-
Coulomb crystals have applications in many areas such as quantum computing and simulation, quantum logic spectroscopy, nonlinear dynamics and chaos, phase transitions, and chemical reaction process. The structure of the Coulomb crystal and the trajectory of each trapped ion are typically determined by the parameters of the trap and the ion species. However, dark ions are often inevitable in experiment, which introduces uncertainty into the desired crystal structures and ion trajectories. Few researches have been conducted to investigate the configuration change of the crystal in the presence of dark ions and the influence of a dark ion on its surrounding ion trajectories in a multi-ion system. In this work, we utilize the molecular dynamics simulation software LAMMPS and the (py)LIon package (modified to adapt the semi-classical theory of laser cooling) for simulating the three-dimensional ion trajectories of Coulomb crystals. The formation process of 40Ca+ Coulomb crystal in a linear trap is simulated. With the micromotion and secular motion trajectories of each ion, we calculate the temperature of Coulomb crystal and the average velocity of specific ions. It is observed that the crystal structure exhibits obvious layering phenomenon when the trapped ions yield a large difference in their charge-to-mass ratio (CMR), however, layering is not obvious with a small difference in the CMR. In addition, we simulate and compare the Coulomb crystal structure formed by pure 40Ca+ ions with that formed by 40Ca+ ions mixed with a small number of dark ions including isotopic ions (44Ca+) and impurity ions (CaH+). Three different cases are investigated, namely the one-dimensional ion string, two-dimensional planar structure and three-dimensional helical structure. The results show that the ions in the neighborhood of a dark ion exhibit around micron-order position change compared with their positions before the dark ion is formed. Such a change can be measured in experiment through microscopic imaging, thereby providing a way to identify the formation of dark ions in Column crystals with a large ion number.
-
Keywords:
- linear ion traps /
- molecular dynamics simulations /
- Coulomb crystals /
- calcium ions
[1] Paul W, Steinwedel H 1953 Z. Naturforsch. A 8 448
[2] Fischer E 1959 Z. Physik 156 1
Google Scholar
[3] Van Dyck R S, Farnham D L, Schwinberg P B 1993 Phys. Rev. Lett. 70 2888
Google Scholar
[4] Drewsen M 2015 Physica B 460 105
Google Scholar
[5] Kjærgaard N, Mølhave K, Drewsen M 2002 Phys. Rev. E 66 015401
Google Scholar
[6] Ulm S, Roßnagel J, Jacob G, Degünther C, Dawkins S T, Poschinger U G, Nigmatullin R, Retzker A, Plenio M B, Schmidt-Kaler F, Singer K 2013 Nat. Commun. 4 2290
Google Scholar
[7] García-Mata I, Zhirov O V, Shepelyansky D L 2007 Eur. Phys. J. D 41 325
Google Scholar
[8] Anderegg F, Dubin D H E, O’Neil T M, Driscoll C F 2009 Phys. Rev. Lett. 102 185001
Google Scholar
[9] Herskind P F, Dantan A, Marler J P, Albert M, Drewsen M 2009 Nat. Phys. 5 494
Google Scholar
[10] Chiaverini J, Blakestad R B, Britton J, Jost J D, Langer C, Leibfried D, Ozeri R, Wineland D J 2005 Quant. Inf. Comput. 5 419
Google Scholar
[11] Schmidt P O, Rosenband T, Langer C, Itano W M, Bergquist J C, Wineland D J 2005 Science 309 749
Google Scholar
[12] 李海霞 2019 博士学位论文(武汉: 中国科学院武汉物数所)
Li H X 2019 Ph. D. Dissertation (Wuhan: Wuhan Institute of Physics and Mathematics, Chinese Academy of Sciences) (in Chinese)
[13] Block M, Drakoudis A, Leuthner H, Seibert P, Werth G, Block M, Drakoudis A, Leuthner H, Seibert P 2000 J. Phys. B At. Mol. Opt. Phys. 33 375
Google Scholar
[14] Hornekær L, Kjærgaard N, Thommesen A M, Drewsen M 2001 Phys. Rev. Lett. 86 1994
Google Scholar
[15] Li H X, Li M, Zhang Q Y, Tong X 2019 Chin. Phys. Lett. 36 073701
Google Scholar
[16] Berkeland D J, Miller J D, Bergquist J C, Itano W M, Wineland D J 1998 J. Appl. Phys. 83 5025
Google Scholar
[17] Weckesser P, Thielemann F, Hoenig D, Lambrecht A, Karpa L, Schaetz T 2021 Phys. Rev. A 103 013112
Google Scholar
[18] Okada K, Yasuda K, Takayanagi T, Wada M, Schuessler H A, Ohtani S 2007 Phys. Rev. A 75 033409
Google Scholar
[19] Caplan M E 2020 Phys. Rev. E 101 023201
Google Scholar
[20] Schiller S, Lämmerzahl C 2003 Phys. Rev. A 68 053406
Google Scholar
[21] Bonitz M, Filinov V S, Fortov V E, Levashov P R, Fehske H 2005 Phys. Rev. Lett. 95 235006
Google Scholar
[22] Zhang C B, Offenberg D, Roth B, Wilson M A, Schiller S 2007 Phys. Rev. A 76 012719
Google Scholar
[23] Romanova A V, Rudyi S S, Rozhdestvensky Y V 2021 arXiv: 2102.08912 [physics. chem-ph]
[24] Sillitoe N, Karr J P, Heinrich J, et al. 2017 Proceedings of the 12th International Conference on Low Energy Antiproton Physics (LEAP2016) Kanazawa, Japan, September 24, 2017 p011014
[25] Drewsen M, Jensen I, Lindballe J, Nissen N, Martinussen R, Mortensen A, Staanum P, Voigt D 2003 J. Mass. Spectrom. 229 83
Google Scholar
[26] Mirkhalaf S, Mølmer K 2012 Phys. Rev. A 85 042109
Google Scholar
[27] Lee S, Ravi K, Rangwala S A 2013 Phys. Rev. A 87 052701
Google Scholar
[28] Thompson A P, Aktulga H M, Berger R, et al. 2022 Comput. Phys. Commun. 271 108171
Google Scholar
[29] Bentine E, Foot C J, Trypogeorgos D 2020 Comput. Phys. Commun. 253 107187
Google Scholar
[30] Thompson R C 2015 Contemp. Phys. 56 1
Google Scholar
[31] Schiller S 2013 Phys. Rev. A 87 033823
[32] Christian F R 2000 Ph. D. Dissertation (Graz, Austria: Karl-Franzens-Univ. Graz)
[33] 方长达人 2021 硕士学位论文 (武汉: 中国科学院精密测量与创新研究院)
Fang C D R 2021 M. S. Thesis (Wuhan: Innovation Academy for Precision Measurement Science and Technology, Chinese Academy of Sciences) (in Chinese)
[34] Okada K, Wada M, Takayanagi T, Ohtani S, Schuessler H A 2010 Phys. Rev. A 81 013420
Google Scholar
[35] Coplen T B, Böhlke J K, De Bièvre P, Ding T, Holden N E, Hopple J A, Krouse H R, Lamberty A, Peiser H S, Revesz K, Rieder S E, Rosman K J R, Roth E, Taylor P D P, Vocke R D, Xiao Y K 2002 Pure Appl. Chem. 74 1987
Google Scholar
-
图 1 激光冷却下不同位置离子的微运动和宏运动轨迹比较 (a)34个40Ca+组成的库仑晶体在10个微运动周期下的平均位置, “×”和“+”所在位置为选取的离子1和2; (b)两个离子在径向平面上加载了微运动的宏运动轨迹, 灰度代表时间演化; (c)两个离子与旋转对称轴的距离随时间的演化, 红色平滑曲线是离子1的变化曲线, 蓝色曲线是离子2的变化曲线
Fig. 1. Micromotion and secular motion of ions at different positions under laser cooling: (a) The average position of Coulomb crystals composed of 34 40Ca+ in 10 micromotion cycles, the positions of × and + are the selected particles 1 and 2; (b) the secular motion trajectory loaded with micromotion on the radial plane of the two particles, the gray scale represents the time evolution; (c) the evolution of the distance between the particle and axial rotational axis of symmetry evolving over time. The red smooth curve is for particle 1, and the blue curve is for particle 2.
图 2 激光冷却下离子1和离子2的径向微运动和宏运动对比（1000个时间步长）. 不同颜色表示不同演化时间后的运动轨迹：0.8×107个时间步长(黄色上三角), 107个时间步长(红色“×”), 1.5×107个时间步长(蓝色圆形), 2×107个时间步长(绿色下三角)
Fig. 2. Comparison of radial micromotion and secular motion of ion 1 and ion 2 over 1000 timesteps under lasercooling. Different colors represent the trajectory of motion after different evolution times: 8×106 timesteps (yellow), 107 timesteps (red), 1.5×107 timesteps (blue), 2×107 timesteps (green).
图 3 激光冷却下34个40Ca+形成的库仑晶体温度随时间的变化曲线, 时间范围是0—0.4×106个时间步长
Fig. 3. Temperature of Coulomb crystals formed by 34 40Ca+ under laser cooling, the time range is 0—0.4 × 106 timesteps.
图 4 单个40Ca+在线型离子阱中的冷却过程(a)温度随时间的变化(b)速度随时间的变化, 蓝色、绿色和红色曲线分别对应在x, y和z方向上的速度平均值变化
Fig. 4. The cooling process for a single 40Ca+ in a linear ion trap: (a) The change in temperature over time; (b) the change in speed over time. The blue, green, and red curves correspond to changes in the average velocity in the x, y, and z direction respectively.
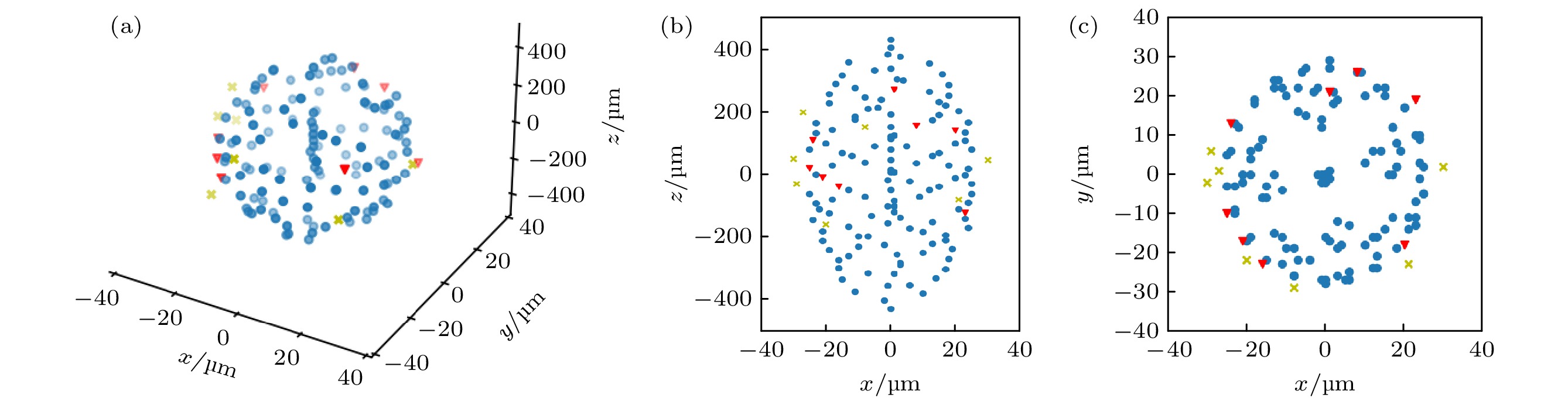
图 5 4种不同荷质比的离子在库仑晶体中的排布. 离子种类分别为1∶40(蓝色圆形), 1∶80(红色下三角), 1∶120(黄色“×”), 1∶160(绿色上三角) (a)为三维图片; (b)为轴向平面投影; (c)为径向平面投影
Fig. 5. The arrangement of ions with four different charge-to-mass ratios in the Coulomb crystal. Ion types are 1∶40 (blue circle), 1∶80 (red lower triangle), 1∶120 (yellow ×), 1∶160 (green upper triangle) separately: (a) Three-dimensional image; (b) axial plane image projection; (c) radial plane image projection.
图 6 多组分库仑晶体结构, 包含36个40Ca+(蓝色圆形), 8个CaH+(红色下三角形)和8个44Ca+(黄色“×”) (a)三维图片; (b)轴向平面投影; (c)径向平面投影
Fig. 6. Multicomponent Coulomb crystal structures, 36 40Ca+ (blue circle), 8 CaH+ (red upper triangle) and 8 44Ca+ (yellow ×): (a) Three-dimensional image; (b) axial plane image projection; (c)radial plane image projection.
图 7 由8个40Ca+形成的离子串在两种混入杂质的情况下排布方式的对比, 两种情况分别为混入1个氢化离子(CaH+)或者1个同位素离子(44Ca+)
Fig. 7. Comparison of the arrangement of the ion string formed by pure 40Ca+ and ion string containing 1 hydride ion (CaH+) or 1 isotopic ion (44Ca+).
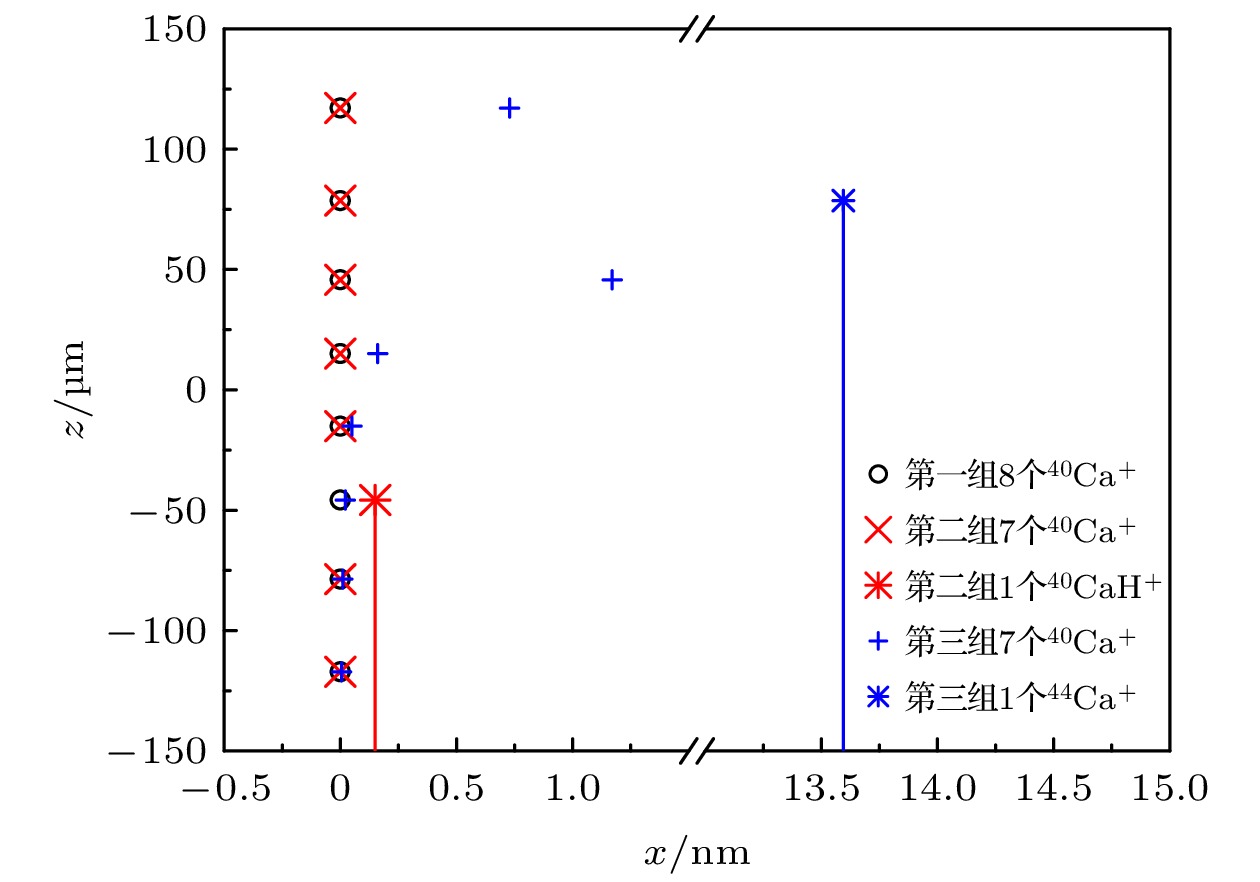
图 8 由16个40Ca+形成的平面库仑晶体在两种混入杂质的情况下排布方式的对比. 两种情况分别为混入1个氢化离子(CaH+)和1个同位素离子(44Ca+) (a)三维图片; (b)轴向平面投影的对比
Fig. 8. Comparison of the arrangement of the planar Coulomb crystal formed by 16 pure 40Ca+ and Coulomb crystal containing 1 hydride ion (CaH+) or 1 isotopic ion (44Ca+): (a) three-dimensional image; (b) axial plane image projection.
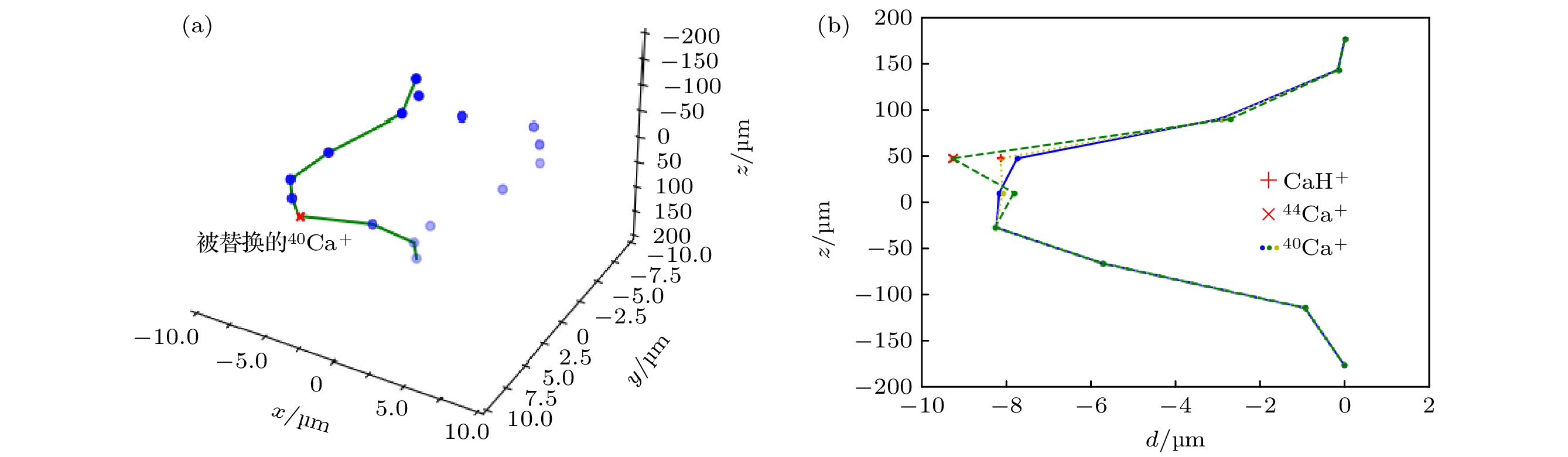
图 9 由36个40Ca+形成的三维库仑晶体在两种混入杂质的情况下排布方式的对比. 两种情况分别为混入1个氢化离子(CaH+)和1个同位素离子(44Ca+) (a)三维图片; (b)螺旋结构的对比
Fig. 9. Comparison of the arrangement of the three-dimensional Coulomb crystal formed by 36 40Ca+ and Coulomb crystals containing 1 hydride ion (CaH+) or 1 isotopic ion (44Ca+): (a) Three-dimensional image; (b) comparison of helical structure.
表 1 4种荷质比离子组成的类圆排布结构信息
Table 1. Information on the circle-like arrangement of four charge-to-mass ratio ions.
离子种类(荷质比) 平均半径/μm 间隔/μm 1∶40 15.564 — 1∶80 45.712 30.148 1∶120 76.110 30.399 1∶160 110.679 35.569 
下载: 导出CSV
-
[1] Paul W, Steinwedel H 1953 Z. Naturforsch. A 8 448
[2] Fischer E 1959 Z. Physik 156 1
Google Scholar
[3] Van Dyck R S, Farnham D L, Schwinberg P B 1993 Phys. Rev. Lett. 70 2888
Google Scholar
[4] Drewsen M 2015 Physica B 460 105
Google Scholar
[5] Kjærgaard N, Mølhave K, Drewsen M 2002 Phys. Rev. E 66 015401
Google Scholar
[6] Ulm S, Roßnagel J, Jacob G, Degünther C, Dawkins S T, Poschinger U G, Nigmatullin R, Retzker A, Plenio M B, Schmidt-Kaler F, Singer K 2013 Nat. Commun. 4 2290
Google Scholar
[7] García-Mata I, Zhirov O V, Shepelyansky D L 2007 Eur. Phys. J. D 41 325
Google Scholar
[8] Anderegg F, Dubin D H E, O’Neil T M, Driscoll C F 2009 Phys. Rev. Lett. 102 185001
Google Scholar
[9] Herskind P F, Dantan A, Marler J P, Albert M, Drewsen M 2009 Nat. Phys. 5 494
Google Scholar
[10] Chiaverini J, Blakestad R B, Britton J, Jost J D, Langer C, Leibfried D, Ozeri R, Wineland D J 2005 Quant. Inf. Comput. 5 419
Google Scholar
[11] Schmidt P O, Rosenband T, Langer C, Itano W M, Bergquist J C, Wineland D J 2005 Science 309 749
Google Scholar
[12] 李海霞 2019 博士学位论文(武汉: 中国科学院武汉物数所)
Li H X 2019 Ph. D. Dissertation (Wuhan: Wuhan Institute of Physics and Mathematics, Chinese Academy of Sciences) (in Chinese)
[13] Block M, Drakoudis A, Leuthner H, Seibert P, Werth G, Block M, Drakoudis A, Leuthner H, Seibert P 2000 J. Phys. B At. Mol. Opt. Phys. 33 375
Google Scholar
[14] Hornekær L, Kjærgaard N, Thommesen A M, Drewsen M 2001 Phys. Rev. Lett. 86 1994
Google Scholar
[15] Li H X, Li M, Zhang Q Y, Tong X 2019 Chin. Phys. Lett. 36 073701
Google Scholar
[16] Berkeland D J, Miller J D, Bergquist J C, Itano W M, Wineland D J 1998 J. Appl. Phys. 83 5025
Google Scholar
[17] Weckesser P, Thielemann F, Hoenig D, Lambrecht A, Karpa L, Schaetz T 2021 Phys. Rev. A 103 013112
Google Scholar
[18] Okada K, Yasuda K, Takayanagi T, Wada M, Schuessler H A, Ohtani S 2007 Phys. Rev. A 75 033409
Google Scholar
[19] Caplan M E 2020 Phys. Rev. E 101 023201
Google Scholar
[20] Schiller S, Lämmerzahl C 2003 Phys. Rev. A 68 053406
Google Scholar
[21] Bonitz M, Filinov V S, Fortov V E, Levashov P R, Fehske H 2005 Phys. Rev. Lett. 95 235006
Google Scholar
[22] Zhang C B, Offenberg D, Roth B, Wilson M A, Schiller S 2007 Phys. Rev. A 76 012719
Google Scholar
[23] Romanova A V, Rudyi S S, Rozhdestvensky Y V 2021 arXiv: 2102.08912 [physics. chem-ph]
[24] Sillitoe N, Karr J P, Heinrich J, et al. 2017 Proceedings of the 12th International Conference on Low Energy Antiproton Physics (LEAP2016) Kanazawa, Japan, September 24, 2017 p011014
[25] Drewsen M, Jensen I, Lindballe J, Nissen N, Martinussen R, Mortensen A, Staanum P, Voigt D 2003 J. Mass. Spectrom. 229 83
Google Scholar
[26] Mirkhalaf S, Mølmer K 2012 Phys. Rev. A 85 042109
Google Scholar
[27] Lee S, Ravi K, Rangwala S A 2013 Phys. Rev. A 87 052701
Google Scholar
[28] Thompson A P, Aktulga H M, Berger R, et al. 2022 Comput. Phys. Commun. 271 108171
Google Scholar
[29] Bentine E, Foot C J, Trypogeorgos D 2020 Comput. Phys. Commun. 253 107187
Google Scholar
[30] Thompson R C 2015 Contemp. Phys. 56 1
Google Scholar
[31] Schiller S 2013 Phys. Rev. A 87 033823
[32] Christian F R 2000 Ph. D. Dissertation (Graz, Austria: Karl-Franzens-Univ. Graz)
[33] 方长达人 2021 硕士学位论文 (武汉: 中国科学院精密测量与创新研究院)
Fang C D R 2021 M. S. Thesis (Wuhan: Innovation Academy for Precision Measurement Science and Technology, Chinese Academy of Sciences) (in Chinese)
[34] Okada K, Wada M, Takayanagi T, Ohtani S, Schuessler H A 2010 Phys. Rev. A 81 013420
Google Scholar
[35] Coplen T B, Böhlke J K, De Bièvre P, Ding T, Holden N E, Hopple J A, Krouse H R, Lamberty A, Peiser H S, Revesz K, Rieder S E, Rosman K J R, Roth E, Taylor P D P, Vocke R D, Xiao Y K 2002 Pure Appl. Chem. 74 1987
Google Scholar
下载:
计量
- 文章访问数: 4375
- PDF下载量: 149
- 被引次数: 0
