用光晶格模拟狄拉克、外尔和麦克斯韦方程

朱燕清; 张丹伟; 朱诗亮

doi:10.7498/aps.68.20181929

摘要

相对论性量子力学波动方程, 如狄拉克、外尔和麦克斯韦方程, 是描述微观粒子运动的基石. 最近的实验和理论研究表明, 冷原子系统中几乎所有参数都可精确调控, 因此冷原子系统被认为是实现量子模拟的理想平台, 可以用来研究高能和凝聚态物理中的一些基本问题. 本文介绍了设计原子光晶格哈密顿量的思路和方法, 主要涉及激光辅助跳跃的理论. 基于这些方法, 物理学界提出了利用光晶格体系模拟相对论性量子力学波动方程, 包括狄拉克、外尔和麦克斯韦方程等, 并且预言了一些在基本粒子物理中很难观察到, 但在冷原子体系可能观察到的物理现象. 本文综述了国际上此领域的研究进展.

关键词:

Abstract

Relativistic wave equations, such as Dirac, Weyl or Maxwell equations, are fundamental equations which we use to describe the dynamics of the microscopic particles. On the other hand, recent experimental and theoretical studies have shown that almost all parameters in cold atomic systems are precisely tunable, so the cold atom systems are considered as an ideal platform to perform quantum simulations. It can be used to study some topics in high energy and condensed matter physics. In this article, we will first introduce the ideas and methods for engineering the Hamiltonian of atoms, mainly related to the theories of laser-assisted tunneling. Based on these methods, one can simulate the equations of motion of relativistic particles and observe some interesting behaviors which are hard to be observed in other systems. The article reviews these recent advances.

Keywords:

作者及机构信息

1.
南京大学物理学院, 固体微结构国家实验室, 南京　210093

2.
华南师范大学物理与电信工程学院, 广东省量子调控工程与材料重点实验室, 广州　510006

通信作者: 张丹伟, zdanwei@126.com ; 朱诗亮, slzhu@nju.edu.cn

基金项目: 国家重点研发计划(批准号: 2016YFA0301803)、国家自然科学基金(批准号: 11604103, 91636218, 11474153)和广东省自然科学基金(批准号: 2016A030313436).

Authors and contacts

1.
National Laboratory of Solid State Microstructures, School of Physics, Nanjing University, Nanjing 210093, China

2.
Guangdong Provincial Key Laboratory of Quantum Engineering and Quantum Materials, School of Physics and Telecommunication Engineering, South China Normal University, Guangzhou 510006, China

Corresponding author: Zhang Dan-Wei, zdanwei@126.com ; Zhu Shi-Liang, slzhu@nju.edu.cn

Funds: Project supported by the National Key Research and Development Program of China (Grant No. 2016YFA0301803), the National Natural Science Foundation of China (Grant Nos. 11604103, 91636218, 11474153), and the Natural Science Foundation of Guangdong Province, China (Grant No. 2016A030313436).

文章全文 : translate this paragraph

参考文献

[1]	Chu S 1998 Rev. Mod. Phys. 70 685 Google Scholar
[2]	Cohen-Tannoudji C N 1998 Rev. Mod. Phys. 70 707 Google Scholar
[3]	Phillips W D 1998 Rev. Mod. Phys. 70 721 Google Scholar
[4]	Anderson M H, Ensher J R, Matthews M R, Wieman C E, Cornell E A 1995 Science 269 198 Google Scholar
[5]	Davis K B, Mewes M O, Andrews M R, van Druten N J, Durfee D S, Kurn D M, Ketterle W 1995 Phys. Rev. Lett. 75 3969 Google Scholar
[6]	Chin C, Grimm R, Julienne P, Tiesinga E 2010 Rev. Mod. Phys. 82 1225 Google Scholar
[7]	Jessen P, Deutsch I 1996 Adv. At. Mol. Opt. Phys. 37 95 Google Scholar
[8]	Dalibard J, Gerbier F, Juzeliūnas G, Öhberg P 2011 Rev. Mod. Phys. 83 1523 Google Scholar
[9]	Goldman N, Juzeliūnas G, Öhberg P, Spielman I B 2014 Rep. Prog. Phys. 77 126401 Google Scholar
[10]	Zhai H 2015 Rep. Prog. Phys. 78 026001 Google Scholar
[11]	Zhang D W, Zhu Y Q, Zhao Y X, Hui Y, Zhu S L 2018 arXiv: 1810.09228
[12]	Zhu S L, Zhang D W, Wang Z D 2009 Phys. Rev. Lett. 102 210403 Google Scholar
[13]	Lewenstein M, Sanpera A, Ahufinger V, Damski B, Sen A, Sen U 2007 Adv. Phys. 56 243 Google Scholar
[14]	Jaksch D, Zoller P 2003 New J. Phys. 5 56 Google Scholar
[15]	Gerbier F, Dalibard J 2010 New J. Phys. 12 033007 Google Scholar
[16]	Struck J, Olschlager C, Weinberg M, et al. 2012 Phys. Rev. Lett. 108 225304 Google Scholar
[17]	Grimm R, Weidemüller M 2000 Adv. At. Mol. Opt. Phys. 42 95 Google Scholar
[18]	Zhu S L, Wang B, Duan L M 2007 Phys. Rev. Lett. 98 260402 Google Scholar
[19]	Zhang D W, Shan C J, Mei F, Yang M, Wang R Q, Zhu S L 2014 Phys. Rev. A 89 015601 Google Scholar
[20]	Mandel O, Greiner M, Widera A, Rom T, Hansch T W, Bloch I 2003 Phys. Rev. Lett. 91 010407 Google Scholar
[21]	Lee P J, Anderlini M, Brown B L, Sebby-Strabley J, Phillips W D, Porto J V 2007 Phys. Rev. Lett. 99 020402 Google Scholar
[22]	Mazza L, Bermudez A, Goldman N, Rizzi M, Martin-Delgado M A, Lewenstein M 2012 New J. Phys. 14 015007 Google Scholar
[23]	Aidelsburger M, Atala M, Nascimbène M, Trotzky S, Chen Y A, Bloch I 2011 Phys. Rev. Lett. 107 255301 Google Scholar
[24]	Aidelsburger M, Atala M, Lohse M, Barreiro J T, Paredes B, Bloch I 2013 Phys. Rev. Lett. 111 185301 Google Scholar
[25]	Miyake H, Siviloglou G A, Kennedy C J, Burton W C, Ketterle W 2013 Phys. Rev. Lett. 111 185302 Google Scholar
[26]	Tarruell L, Greif D, Uehlinger T, Jotzu G, Esslinger T 2012 Nature 483 302 Google Scholar
[27]	Lim L K, Fuchs J N, Montambaux G 2012 Phys. Rev. Lett. 108 175303 Google Scholar
[28]	Uehlinger T, Greif D, Jotzu G, Tarruell L, Esslinger T, Wang L, Troyer M 2013 Eur. Phys. J. Special Topics 217 121 Google Scholar
[29]	Duca L, Li T, Reitter M, Bloch I, Schleier-Smith M, Schneider U 2015 Science 347 288 Google Scholar
[30]	Armitage N P, Mele E J, Vishwanath A 2018 Rev. Mod. Phys. 90 015001 Google Scholar
[31]	Bermudez A, Mazza L, Rizzi M, Goldman N, Lewenstein M, Martin-Delgado M A 2010 Phys. Rev. Lett. 105 190404 Google Scholar
[32]	Mazza L, Bermudez A, Goldman N, Rizzi M, Martin-Delgado M A, Lewenstein M 2012 New J. Phys. 14 015007
[33]	Yang M, Zhu S L 2010 Phys. Rev. A 82 064102 Google Scholar
[34]	Lepori L, Mussardo G, Trombettoni A 2010 Europhys. Lett. 92 50003 Google Scholar
[35]	Wilson K, New Phenomena in Subnuclear Physics, Plenum, New York, 1977.
[36]	Zhang D W, Mei F, Xue Z Y, Zhu S L, Wang Z D 2015 Phys. Rev. A 92 013612 Google Scholar
[37]	Ganeshan S, Sarma S D 2015 Phys. Rev. B 91 125438 Google Scholar
[38]	Jiang J H 2012 Phys. Rev. A 85 033640 Google Scholar
[39]	He W Y, Zhang S, Law K T 2016 Phys. Rev. A 94 013606 Google Scholar
[40]	Hou J M, Chen W 2016 Sci. Rep. 6 33512 Google Scholar
[41]	Dubček T, Kennedy C J, Lu L, Ketterle W, Soljačić M, Buljan H 2015 Phys. Rev. Lett. 114 225301 Google Scholar
[42]	Xu Y, Duan L M 2016 Phys. Rev. A 94 053619 Google Scholar
[43]	Shastri K, Yang Z, Zhang B 2017 Phys. Rev. B 95 014306 Google Scholar
[44]	Kong X, He J, Liang Y, Kou S 2017 Phys. Rev. A 95 33629 Google Scholar
[45]	Zhu Y Q, Zhang D W, Yan H, Xing D Y, Zhu S L 2017 Phys. Rev. A 96 033634 Google Scholar
[46]	Tan X, Zhang D W, Liu Q, Xue G, Yu H F, Zhu Y Q, Yan H, Zhu S L, Yu Y 2018 Phys. Rev. Lett. 120 130503 Google Scholar
[47]	Liang L, Yu Y 2016 Phys. Rev. B 93 045113 Google Scholar
[48]	Lan Z, Goldman N, Bermudez A, Lu W, Öhberg P 2011 Phys. Rev. B 84 165115 Google Scholar
[49]	Kitaev A, Laumann C 2009 arXiv: 0904.2771
[50]	Trebst S, Troyer M, Wang Z, Ludwig A W W 2008 Prog. Theor. Phys. Supp. 176 384 Google Scholar
[51]	Nayak C, Simon S H, Stern A, Freedman M, Sarma S D 2008 Rev. Mod. Phys. 80 1083 Google Scholar
[52]	Read N, Rezayi E 1999 Phys. Rev. B 59 8084 Google Scholar
[53]	Liu S, Shan C J, Zhang Z M, Xue Z Y 2014 Quantum Inf. Process. 13 1813 Google Scholar
[54]	Vaishnav J Y, Clark C W 2008 Phys. Rev. Lett. 100 153002 Google Scholar
[55]	Zhang D W, Xue Z Y, Yan H, Wang Z D, Zhu S L 2012 Phys. Rev. A 85 013628 Google Scholar
[56]	Li Z, Wang H Q, Zhang D W, Zhu S L, Xing D Y 2016 Phys. Rev. A 94 043617 Google Scholar
[57]	Xu Y, Duan L M 2017 Phys. Rev. B 96 155301 Google Scholar
[58]	Shen X, Zhu Y Q, Li Z (In preparation)
[59]	Bliokh K Y, Smirnova D, Nori F 2015 Science 348 1448 Google Scholar
[60]	邱英, 何军, 王彦华, 王婧, 张天才, 王军民 2008 57 6227 Google Scholar Qiu Y, He J, Wang Y H, Wang J, Zhang T C, Wang J M 2008 Acta Phys. Sin. 57 6227 Google Scholar
[61]	Atala M, Aidelsburger M, Barreiro J T, Abanin D, Kitagawa T, Demler E, Bloch I 2013 Nat. Phys. 9 795 Google Scholar
[62]	Fisher M P A, Weichwan P B, Grinstein G, Fisher D S 1989 Phys. Rev. B 40 546 Google Scholar
[63]	Jaksch D, Bruder C, Cirac J I, Zoller P 1998 Phys. Rev. Lett. 81 3108 Google Scholar
[64]	Jotzu G, Messer M, Desbuquois R, Lebrat M, Uehlinger T, Greif D, Esslinger T 2014 Nature 515 237 Google Scholar
[65]	Aidelsburger M, Lohse M, Schweizer C, Atala M, Barreiro J T, Nascimbène S, Cooper N R, Bloch I, Goldman N 2015 Nat. Phys. 11 162 Google Scholar
[66]	杨圆, 陈帅, 李小兵 2018 67 237101 Google Scholar Yang Y, Chen S, Li X B 2018 Acta Phys. Sin. 67 237101 Google Scholar
[67]	范桁 2018 67 120301 Google Scholar Fan H 2018 Acta Phys. Sin. 67 120301 Google Scholar

施引文献

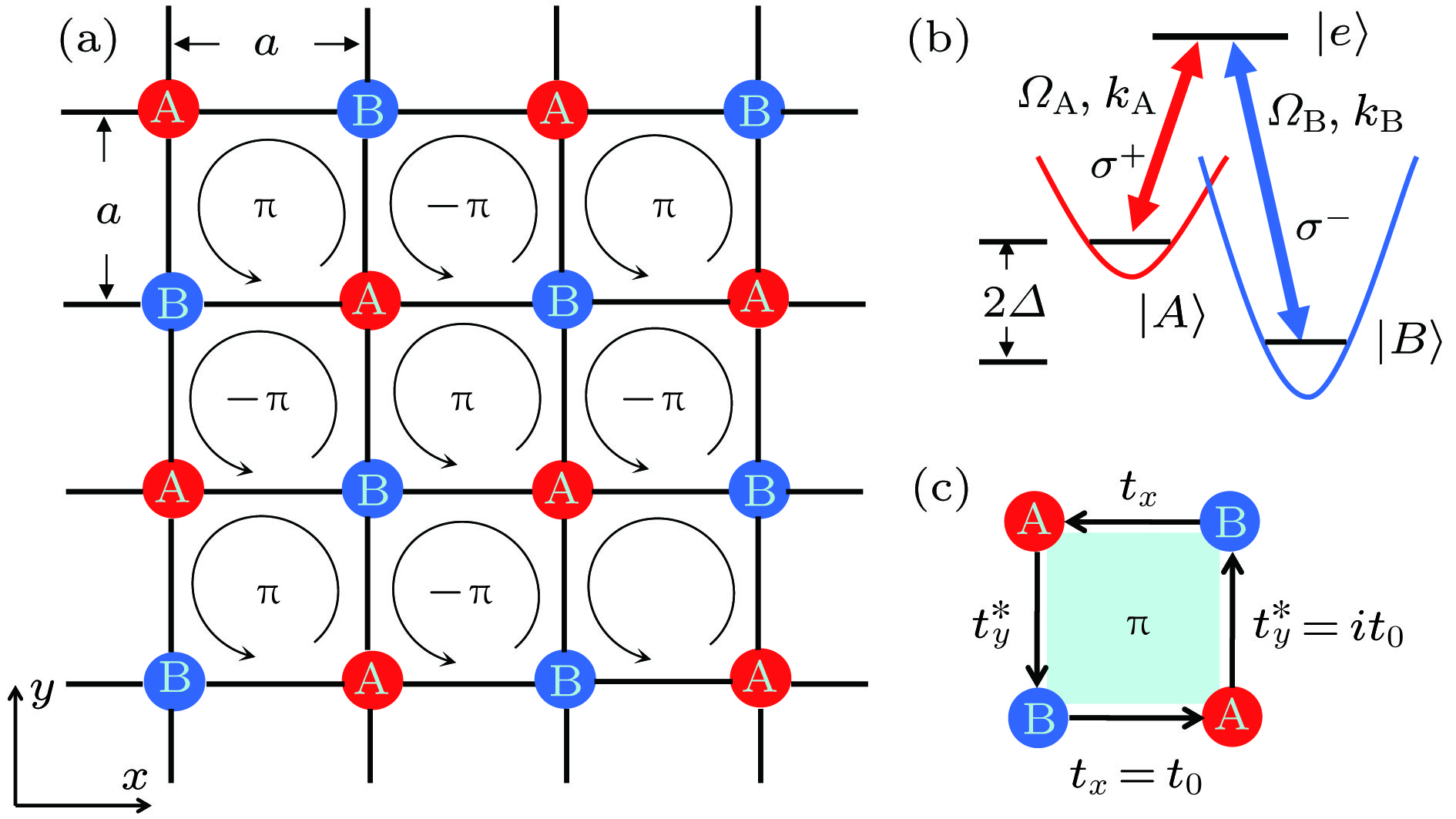
图 1 基于激光辅助跳跃实现人工磁场, 黑(灰)色圆分别表示内态为$ |g\rangle $$ (|e\rangle) $的Yb原子 (a)内态被标记为$ |g\rangle $和$ |e\rangle $的原子被囚禁在自旋依赖的光晶格势$ V_g $和$ V_e $中, 其中$ V_g=-V_e $; (b) $ x $方向上的激光辅助跃迁; (c)自旋依赖光晶格示意图. $ y $方向存在自然跳跃, $ x $方向由一束拉曼光$ \varOmega_{\rm R} $诱导跳跃

Fig. 1. Realization of artificial magnetic field based on laser-assisted tunneling. Gray and black dots represent the Yb atoms correspond to internal states $|g\rangle$ and $|e\rangle$, respectively: (a) The atoms $|g\rangle$ and $|e\rangle$ are trapped in the state-dependent optical lattice potentials $V_g$ and $V_e$, where $V_g=-V_e$; (b) laser-assisted tunneling along $x$ direction; (c) sketch of state-dependent optical lattice. Nature tunneling occurs along the $y$ direction, and the tunneling along $x$ direction is induced by a Raman beam $\varOmega_{\rm R}$.

下载: 全尺寸图片幻灯片

图 2 (a)交错磁通光晶格; (b)双光子拉曼过程; (c)等效${\text{π}}$磁通

Fig. 2. (a) Staggered flux optical lattice; (b) two-photon Raman process; (c) effective ${\text{π}}$ flux.

下载: 全尺寸图片幻灯片

图 3 实现外尔半金属的三维立方晶格示意图. 合理设计$x$和$z$方向跳跃, 在动量空间会出现外尔点. 虚线和实线分别表示获得相位${\text{π}}$和0^[41]

Fig. 3. Schematic diagram of a three-dimensional cubic lattice of a Weyl semimetal. The Weyl points will be created in the momentum space if the tunneling along $x$ and $z$ directions are well-designed . The dashed and solid lines indicate the phase ${\text{π}}$ and 0, respectively.

下载: 全尺寸图片幻灯片

map

[1]	Chu S 1998 Rev. Mod. Phys. 70 685 Google Scholar
[2]	Cohen-Tannoudji C N 1998 Rev. Mod. Phys. 70 707 Google Scholar
[3]	Phillips W D 1998 Rev. Mod. Phys. 70 721 Google Scholar
[4]	Anderson M H, Ensher J R, Matthews M R, Wieman C E, Cornell E A 1995 Science 269 198 Google Scholar
[5]	Davis K B, Mewes M O, Andrews M R, van Druten N J, Durfee D S, Kurn D M, Ketterle W 1995 Phys. Rev. Lett. 75 3969 Google Scholar
[6]	Chin C, Grimm R, Julienne P, Tiesinga E 2010 Rev. Mod. Phys. 82 1225 Google Scholar
[7]	Jessen P, Deutsch I 1996 Adv. At. Mol. Opt. Phys. 37 95 Google Scholar
[8]	Dalibard J, Gerbier F, Juzeliūnas G, Öhberg P 2011 Rev. Mod. Phys. 83 1523 Google Scholar
[9]	Goldman N, Juzeliūnas G, Öhberg P, Spielman I B 2014 Rep. Prog. Phys. 77 126401 Google Scholar
[10]	Zhai H 2015 Rep. Prog. Phys. 78 026001 Google Scholar
[11]	Zhang D W, Zhu Y Q, Zhao Y X, Hui Y, Zhu S L 2018 arXiv: 1810.09228
[12]	Zhu S L, Zhang D W, Wang Z D 2009 Phys. Rev. Lett. 102 210403 Google Scholar
[13]	Lewenstein M, Sanpera A, Ahufinger V, Damski B, Sen A, Sen U 2007 Adv. Phys. 56 243 Google Scholar
[14]	Jaksch D, Zoller P 2003 New J. Phys. 5 56 Google Scholar
[15]	Gerbier F, Dalibard J 2010 New J. Phys. 12 033007 Google Scholar
[16]	Struck J, Olschlager C, Weinberg M, et al. 2012 Phys. Rev. Lett. 108 225304 Google Scholar
[17]	Grimm R, Weidemüller M 2000 Adv. At. Mol. Opt. Phys. 42 95 Google Scholar
[18]	Zhu S L, Wang B, Duan L M 2007 Phys. Rev. Lett. 98 260402 Google Scholar
[19]	Zhang D W, Shan C J, Mei F, Yang M, Wang R Q, Zhu S L 2014 Phys. Rev. A 89 015601 Google Scholar
[20]	Mandel O, Greiner M, Widera A, Rom T, Hansch T W, Bloch I 2003 Phys. Rev. Lett. 91 010407 Google Scholar
[21]	Lee P J, Anderlini M, Brown B L, Sebby-Strabley J, Phillips W D, Porto J V 2007 Phys. Rev. Lett. 99 020402 Google Scholar
[22]	Mazza L, Bermudez A, Goldman N, Rizzi M, Martin-Delgado M A, Lewenstein M 2012 New J. Phys. 14 015007 Google Scholar
[23]	Aidelsburger M, Atala M, Nascimbène M, Trotzky S, Chen Y A, Bloch I 2011 Phys. Rev. Lett. 107 255301 Google Scholar
[24]	Aidelsburger M, Atala M, Lohse M, Barreiro J T, Paredes B, Bloch I 2013 Phys. Rev. Lett. 111 185301 Google Scholar
[25]	Miyake H, Siviloglou G A, Kennedy C J, Burton W C, Ketterle W 2013 Phys. Rev. Lett. 111 185302 Google Scholar
[26]	Tarruell L, Greif D, Uehlinger T, Jotzu G, Esslinger T 2012 Nature 483 302 Google Scholar
[27]	Lim L K, Fuchs J N, Montambaux G 2012 Phys. Rev. Lett. 108 175303 Google Scholar
[28]	Uehlinger T, Greif D, Jotzu G, Tarruell L, Esslinger T, Wang L, Troyer M 2013 Eur. Phys. J. Special Topics 217 121 Google Scholar
[29]	Duca L, Li T, Reitter M, Bloch I, Schleier-Smith M, Schneider U 2015 Science 347 288 Google Scholar
[30]	Armitage N P, Mele E J, Vishwanath A 2018 Rev. Mod. Phys. 90 015001 Google Scholar
[31]	Bermudez A, Mazza L, Rizzi M, Goldman N, Lewenstein M, Martin-Delgado M A 2010 Phys. Rev. Lett. 105 190404 Google Scholar
[32]	Mazza L, Bermudez A, Goldman N, Rizzi M, Martin-Delgado M A, Lewenstein M 2012 New J. Phys. 14 015007
[33]	Yang M, Zhu S L 2010 Phys. Rev. A 82 064102 Google Scholar
[34]	Lepori L, Mussardo G, Trombettoni A 2010 Europhys. Lett. 92 50003 Google Scholar
[35]	Wilson K, New Phenomena in Subnuclear Physics, Plenum, New York, 1977.
[36]	Zhang D W, Mei F, Xue Z Y, Zhu S L, Wang Z D 2015 Phys. Rev. A 92 013612 Google Scholar
[37]	Ganeshan S, Sarma S D 2015 Phys. Rev. B 91 125438 Google Scholar
[38]	Jiang J H 2012 Phys. Rev. A 85 033640 Google Scholar
[39]	He W Y, Zhang S, Law K T 2016 Phys. Rev. A 94 013606 Google Scholar
[40]	Hou J M, Chen W 2016 Sci. Rep. 6 33512 Google Scholar
[41]	Dubček T, Kennedy C J, Lu L, Ketterle W, Soljačić M, Buljan H 2015 Phys. Rev. Lett. 114 225301 Google Scholar
[42]	Xu Y, Duan L M 2016 Phys. Rev. A 94 053619 Google Scholar
[43]	Shastri K, Yang Z, Zhang B 2017 Phys. Rev. B 95 014306 Google Scholar
[44]	Kong X, He J, Liang Y, Kou S 2017 Phys. Rev. A 95 33629 Google Scholar
[45]	Zhu Y Q, Zhang D W, Yan H, Xing D Y, Zhu S L 2017 Phys. Rev. A 96 033634 Google Scholar
[46]	Tan X, Zhang D W, Liu Q, Xue G, Yu H F, Zhu Y Q, Yan H, Zhu S L, Yu Y 2018 Phys. Rev. Lett. 120 130503 Google Scholar
[47]	Liang L, Yu Y 2016 Phys. Rev. B 93 045113 Google Scholar
[48]	Lan Z, Goldman N, Bermudez A, Lu W, Öhberg P 2011 Phys. Rev. B 84 165115 Google Scholar
[49]	Kitaev A, Laumann C 2009 arXiv: 0904.2771
[50]	Trebst S, Troyer M, Wang Z, Ludwig A W W 2008 Prog. Theor. Phys. Supp. 176 384 Google Scholar
[51]	Nayak C, Simon S H, Stern A, Freedman M, Sarma S D 2008 Rev. Mod. Phys. 80 1083 Google Scholar
[52]	Read N, Rezayi E 1999 Phys. Rev. B 59 8084 Google Scholar
[53]	Liu S, Shan C J, Zhang Z M, Xue Z Y 2014 Quantum Inf. Process. 13 1813 Google Scholar
[54]	Vaishnav J Y, Clark C W 2008 Phys. Rev. Lett. 100 153002 Google Scholar
[55]	Zhang D W, Xue Z Y, Yan H, Wang Z D, Zhu S L 2012 Phys. Rev. A 85 013628 Google Scholar
[56]	Li Z, Wang H Q, Zhang D W, Zhu S L, Xing D Y 2016 Phys. Rev. A 94 043617 Google Scholar
[57]	Xu Y, Duan L M 2017 Phys. Rev. B 96 155301 Google Scholar
[58]	Shen X, Zhu Y Q, Li Z (In preparation)
[59]	Bliokh K Y, Smirnova D, Nori F 2015 Science 348 1448 Google Scholar
[60]	邱英, 何军, 王彦华, 王婧, 张天才, 王军民 2008 57 6227 Google Scholar Qiu Y, He J, Wang Y H, Wang J, Zhang T C, Wang J M 2008 Acta Phys. Sin. 57 6227 Google Scholar
[61]	Atala M, Aidelsburger M, Barreiro J T, Abanin D, Kitagawa T, Demler E, Bloch I 2013 Nat. Phys. 9 795 Google Scholar
[62]	Fisher M P A, Weichwan P B, Grinstein G, Fisher D S 1989 Phys. Rev. B 40 546 Google Scholar
[63]	Jaksch D, Bruder C, Cirac J I, Zoller P 1998 Phys. Rev. Lett. 81 3108 Google Scholar
[64]	Jotzu G, Messer M, Desbuquois R, Lebrat M, Uehlinger T, Greif D, Esslinger T 2014 Nature 515 237 Google Scholar
[65]	Aidelsburger M, Lohse M, Schweizer C, Atala M, Barreiro J T, Nascimbène S, Cooper N R, Bloch I, Goldman N 2015 Nat. Phys. 11 162 Google Scholar
[66]	杨圆, 陈帅, 李小兵 2018 67 237101 Google Scholar Yang Y, Chen S, Li X B 2018 Acta Phys. Sin. 67 237101 Google Scholar
[67]	范桁 2018 67 120301 Google Scholar Fan H 2018 Acta Phys. Sin. 67 120301 Google Scholar

[1]	高吉明, 狄国文, 鱼自发, 唐荣安, 徐红萍, 薛具奎. 人工磁场下各向异性偶极玻色气体的量子相变. , 2024, 73(13): 130503. doi: 10.7498/aps.73.20240376
[2]	成恩宏, 郎利君. 非互易Aubry-André 模型的经典电路模拟. , 2022, 71(16): 160301. doi: 10.7498/aps.71.20220219
[3]	徐达, 王逸璞, 李铁夫, 游建强. 微波驱动下超导量子比特与磁振子的相干耦合. , 2022, 71(15): 150302. doi: 10.7498/aps.71.20220260
[4]	高雪儿, 李代莉, 刘志航, 郑超. 非厄米系统的量子模拟新进展. , 2022, 71(24): 240303. doi: 10.7498/aps.71.20221825
[5]	王晨旭, 贺冉, 李睿睿, 陈炎, 房鼎, 崔金明, 黄运锋, 李传锋, 郭光灿. 量子计算与量子模拟中离子阱结构研究进展. , 2022, 71(13): 133701. doi: 10.7498/aps.71.20220224
[6]	李婷, 汪涛, 王叶兵, 卢本全, 卢晓同, 尹默娟, 常宏. 浅光晶格中量子隧穿现象的实验观测. , 2022, 71(7): 073701. doi: 10.7498/aps.71.20212038
[7]	陈阳, 张天炀, 郭光灿, 任希锋. 基于集成光芯片的量子模拟研究进展. , 2022, 71(24): 244207. doi: 10.7498/aps.71.20221938
[8]	罗雨晨, 李晓鹏. 相互作用费米子的量子模拟. , 2022, 71(22): 226701. doi: 10.7498/aps.71.20221756
[9]	林键, 叶梦, 朱家纬, 李晓鹏. 机器学习辅助绝热量子算法设计. , 2021, 70(14): 140306. doi: 10.7498/aps.70.20210831
[10]	卢晓同, 李婷, 孔德欢, 王叶兵, 常宏. 锶原子光晶格钟碰撞频移的测量. , 2019, 68(23): 233401. doi: 10.7498/aps.68.20191147
[11]	赵兴东, 张莹莹, 刘伍明. 光晶格中超冷原子系统的磁激发. , 2019, 68(4): 043703. doi: 10.7498/aps.68.20190153
[12]	林弋戈, 方占军. 锶原子光晶格钟. , 2018, 67(16): 160604. doi: 10.7498/aps.67.20181097
[13]	孔祥宇, 朱垣晔, 闻经纬, 辛涛, 李可仁, 龙桂鲁. 核磁共振量子信息处理研究的新进展. , 2018, 67(22): 220301. doi: 10.7498/aps.67.20180754
[14]	赵士平, 刘玉玺, 郑东宁. 新型超导量子比特及量子物理问题的研究. , 2018, 67(22): 228501. doi: 10.7498/aps.67.20180845
[15]	喻祥敏, 谭新生, 于海峰, 于扬. 利用超导量子电路模拟拓扑量子材料. , 2018, 67(22): 220302. doi: 10.7498/aps.67.20181857
[16]	范桁. 量子计算与量子模拟. , 2018, 67(12): 120301. doi: 10.7498/aps.67.20180710
[17]	田晓, 王叶兵, 卢本全, 刘辉, 徐琴芳, 任洁, 尹默娟, 孔德欢, 常宏, 张首刚. 锶玻色子的“魔术”波长光晶格装载实验研究. , 2015, 64(13): 130601. doi: 10.7498/aps.64.130601
[18]	赵旭, 赵兴东, 景辉. 利用光晶格自旋链中磁振子的激发模拟有限温度下光子的动力学 Casimir 效应. , 2013, 62(6): 060302. doi: 10.7498/aps.62.060302
[19]	周骏, 任海东, 冯亚萍. 强非局域光晶格中空间孤子的脉动传播. , 2010, 59(6): 3992-4000. doi: 10.7498/aps.59.3992
[20]	张科智, 王建军, 刘国荣, 薛具奎. 两组分BECs在光晶格中的隧穿动力学及其周期调制效应. , 2010, 59(5): 2952-2961. doi: 10.7498/aps.59.2952

计量

文章访问数: 12288
PDF下载量: 254
被引次数: 0

姓名
邮箱
手机号码
标题
留言内容
验证码

搜索

留言板

用光晶格模拟狄拉克、外尔和麦克斯韦方程