基于超导量子系统的量子纠错研究进展

陈子杰; 潘啸轩; 华子越; 王韦婷; 马雨玮; 李明; 邹旭波; 孙麓岩; 邹长铃

doi:10.7498/aps.71.20221824

摘要

基于量子力学基本原理的信息处理技术, 在计算、传感等领域具有远超经典技术的巨大潜力. 随着实验技术的进步, 量子调控技术得到突飞猛进的发展. 在所有的量子信息处理平台中, 基于固体材料的超导系统, 具有精确的量子调控能力、优异的量子相干性以及适合大规模集成化等优点. 因此, 超导量子系统成为当前最有潜力的量子信息处理平台之一. 目前的超导芯片能集成约一百个量子比特, 已经可以展示量子系统的优势, 但进一步的发展受到系统噪声的制约. 为了突破这一瓶颈, 借鉴经典信息中的纠错技术发展而来的量子纠错技术受到广泛的关注. 本文介绍了超导量子系统中量子纠错的研究进展, 主要包括超导量子系统的基本原理、常用的量子纠错编码方案、纠错相关的控制技术以及近期超导量子纠错的应用. 最后, 总结了超导量子纠错领域面临的七个关键问题.

关键词:

Abstract

Information processing technology based on the basic principle of quantum mechanics shows great potential applications in computing, sensing and other fields, and is far superior to classical technology. With the advance of experimental technology, quantum control technology develops rapidly. Compared with other quantum information processing platforms, the superconducting system based on solid materials has the advantages of accurate quantum controllability, excellent quantum coherence and the potential for large-scale integration. Therefore, superconducting quantum system is one of the most promising platforms for quantum information processing. The existing superconducting circuits, which can integrate about one hundred qubits, have already demonstrated the advantages of quantum systems, but further development is limited by system noise. In order to break through this bottleneck, quantum error correction technology, which is developed from the classical error correction technology, has attracted extensive attention. Here, we mainly summarize the research progress of quantum error correction in superconducting quantum systems including the basic principles of superconducting quantum systems, the quantum error correction codes, the related control techniques and the recent applications. At the end of the article, we summarize seven key problems in this field.

Keywords:

作者及机构信息

1.
中国科学技术大学, 中国科学院量子信息重点实验室, 合肥　230026

2.
清华大学, 交叉信息研究院, 量子信息中心, 北京　100084

通信作者: 孙麓岩, luyansun@mail.tsinghua.edu.cn ; 邹长铃, clzou321@ustc.edu.cn

基金项目: 国家重点研发计划 (批准号: 2017YFA0304303)、国家自然科学基金(批准号: 92165209, 11925404, 11874342, 11922411, 12061131011)和中国博士后科学基金(批准号: BX2021167)资助的课题

Authors and contacts

1.
Key Laboratory of Quantum Information, Chinese Academy of Sciences, University of Science and Technology of China, Hefei 230026, China

2.
Center for Quantum Information, Institute for Interdisciplinary Information Sciences, Tsinghua University, Beijing 100084, China

Corresponding author: Sun Lu-Yan, luyansun@mail.tsinghua.edu.cn ; Zou Chang-Ling, clzou321@ustc.edu.cn

Funds: Project supported by the National Key R&D Program of China (Grant No. 2017YFA0304303), the National Natural Science Foundation of China (Grant Nos. 92165209, 11925404, 11874342, 11922411, 12061131011), and the China Postdoctoral Science Foundation (Grant No. BX2021167)

文章全文 : translate this paragraph

参考文献

[1]	Shor P W 1994 Proc. 35th Annu. Symp. Found. Comput. Sci. (IEEE) Santa Fe, NM, USA, November 20–22, 1994 p124
[2]	Shor P W 1995 Phys. Rev. A 52 R2493 Google Scholar
[3]	Kudra M, Biznárová J, Fadavi Roudsari A, Burnett J J, Niepce D, Gasparinetti S, Wickman B, Delsing P 2020 Appl. Phys. Lett. 117 70601 Google Scholar
[4]	Reagor M, Pfaff W, Axline C, et al. 2016 Phys. Rev. B 94 14506 Google Scholar
[5]	Romanenko A, Pilipenko R, Zorzetti S, Frolov D, Awida M, Belomestnykh S, Posen S, Grassellino A 2020 Phys. Rev. Appl. 13 34032 Google Scholar
[6]	Magnard P, Storz S, Kurpiers P, Schär J, Marxer F, Lütolf J, Walter T, Besse J C, Gabureac M, Reuer K, Akin A, Royer B, Blais A, Wallraff A 2020 Phys. Rev. Lett. 125 260502 Google Scholar
[7]	Xu X B, Wang W, Sun L, Zou C L 2022 Chip 100016 Google Scholar
[8]	Acharya R, Aleiner I, Allen R, et al. 2022 arXiv: 2207.06431 [quant-ph]
[9]	Jurcevic P, Javadi-Abhari A, Bishop L S, et al. 2021 Quantum Sci. Technol. 6 25020 Google Scholar
[10]	Zhu Q, Cao S, Chen F, et al. 2022 Sci. Bull. 67 240 Google Scholar
[11]	Guo Q, Cheng C, Li H, et al. 2021 Phys. Rev. Lett. 127 240502 Google Scholar
[12]	Xu K, Zhang Y R, Sun Z H, et al. 2022 Phys. Rev. Lett. 128 150501 Google Scholar
[13]	Xu H, Zhang J, Han J, Li Z, Xue G, Liu W, Jin Y, Yu H 2021 arXiv: 2108.00942 [quant-ph]
[14]	Arute F, Arya K, Babbush R, et al. 2019 Nature 574 505 Google Scholar
[15]	Wu Y, Bao W S, Cao S, et al. 2021 Phys. Rev. Lett. 127 180501 Google Scholar
[16]	Farhi E, Goldstone J, Gutmann S 2014 arXiv: 1411.4028 [quant-ph]
[17]	Peruzzo A, McClean J, Shadbolt P, Yung M H, Zhou X Q, Love P J, Aspuru-Guzik A, O’brien J L 2014 Nat. Commun. 5 1 Google Scholar
[18]	Wendin G 2017 Rep. Prog. Phys. 80 106001 Google Scholar
[19]	Blais A, Grimsmo A L, Girvin S M, Wallraff A 2021 Rev. Mod. Phys. 93 25005 Google Scholar
[20]	Xu Y, Hua Z, Chen T, et al. 2020 Phys. Rev. Lett. 124 230503 Google Scholar
[21]	Cai T Q, Han X Y, Wu Y K, Ma Y L, Wang J H, Wang Z L, Zhang H Y, Wang H Y, Song Y P, Duan L M 2021 Phys. Rev. Lett. 127 060505 Google Scholar
[22]	Tan X, Zhang D W, Zheng W, et al. 2021 Phys. Rev. Lett. 126 017702 Google Scholar
[23]	Ni Z, Li S, Zhang L, et al. 2022 Phys. Rev. Lett. 129 040502 Google Scholar
[24]	Marques J F, Varbanov B M, Moreira M S, et al. 2022 Nat. Phys. 18 80 Google Scholar
[25]	Riste D, Poletto S, Huang M Z, Bruno A, Vesterinen V, Saira O P, DiCarlo L 2015 Nat. Commun. 6 1 Google Scholar
[26]	Yan F, Krantz P, Sung Y, Kjaergaard M, Campbell D L, Orlando T P, Gustavsson S, Oliver W D 2018 Phys. Rev. Appl. 10 054062 Google Scholar
[27]	Mundada P, Zhang G Y, Hazard T, Houck A 2019 Phys. Rev. Appl. 12 54023 Google Scholar
[28]	Sung Y, Ding L, Braumüller J, Vepsäläinen A, Kannan B, Kjaergaard M, Greene A, Samach G O, McNally C, Kim D, Melville A, Niedzielski B M, Schwartz M E, Yoder J L, Orlando T P, Gustavsson S, Oliver W D 2021 Phys. Rev. X 11 21058 Google Scholar
[29]	Li X, Cai T, Yan H, Wang Z, Pan X, Ma Y, Cai W, Han J, Hua Z, Han X, Wu Y, Zhang H, Wang H, Song Y P, Duan L M, Sun L Y 2020 Phys. Rev. Appl. 14 24070 Google Scholar
[30]	Song C, Xu K, Li H, Zhang Y R, Zhang X, Liu W, Guo Q, Wang Z, Ren W, Hao J, Feng H, Fan H, Zheng D, Wang D W, Wang H, Zhu S Y 2019 Science 365 574 Google Scholar
[31]	Zhao Y, Ye Y, Huang H L, et al. 2021 arXiv: 2112.13505 [quant-ph]
[32]	Negirneac V, Ali H, Muthusubramanian N, Battistel F, Sagastizabal R, Moreira M S, Marques J F, Vlothuizen W J, Beekman M, Zachariadis C, Haider N, Bruno A, DiCarlo L 2021 Phys. Rev. Lett. 126 220502 Google Scholar
[33]	Kjaergaard M, Schwartz M E, Greene A, et al 2020 arXiv: 2001.08838 [quant-ph]
[34]	Kandala A, Wei K X, Srinivasan S, Magesan E, Carnevale S, Keefe G A, Klaus D, Dial O, McKay D C 2021 Phys. Rev. Lett. 127 130501 Google Scholar
[35]	Blais A, Huang R S, Wallraff A, Girvin S M, Schoelkopf R J 2004 Phys. Rev. A 69 62320 Google Scholar
[36]	Koch J, Yu T M, Gambetta J, Houck A A, Schuster D I, Majer J, Blais A, Devoret M H, Girvin S M, Schoelkopf R J 2007 Phys. Rev. A 76 042319 Google Scholar
[37]	Houck A A, Schreier J A, Johnson B R, Chow J M, Koch J, Gambetta J M, Schuster D I, Frunzio L, Devoret M H, Girvin S M, Schoelkopf R J 2008 Phys. Rev. Lett. 101 80502 Google Scholar
[38]	Reed M D, Johnson B R, Houck A A, DiCarlo L, Chow J M, Schuster D I, Frunzio L, Schoelkopf R J 2010 Appl. Phys. Lett. 9 6 Google Scholar
[39]	Jeffrey E, Sank D, Mutus J Y, White T C, Kelly J, Barends R, Chen Y, Chen Z, Chiaro B, Dunsworth A, Megrant A, O’Malley P J, Neill C, Roushan P, Vainsencher A, Wenner J, Cleland A N, Martinis J M 2014 Phys. Rev. Lett. 112 190504 Google Scholar
[40]	Yurke B, Corruccini L R, Kaminsky P G, Rupp L W, Smith A D, Silver A H, Simon R W, Whittaker E A 1989 Phys. Rev. A 39 2519 Google Scholar
[41]	Siddiqi I, Vijay R, Pierre F, Wilson C M, Metcalfe M, Rigetti C, Frunzio L, Devoret M H 2004 Phys. Rev. Lett. 93 207002 Google Scholar
[42]	Castellanos-Beltran M A, Lehnert K W 2007 Appl. Phys. Lett. 91 83509 Google Scholar
[43]	Walter T, Kurpiers P, Gasparinetti S, et al. 2017 Phys. Rev. Appl. 7 054020 Google Scholar
[44]	Reagor M, Paik H, Catelani G, et al. 2013 Appl. Phys. Lett. 102 192604 Google Scholar
[45]	Xu Y, Ma Y, Cai W, et al. 2020 Phys. Rev. Lett. 124 120501 Google Scholar
[46]	Chamberland C, Noh K, Arrangoiz-Arriola P, Campbell E T, Hann C T, Iverson J, Putterman H, Bohdanowicz T C, Flammia S T, Keller A, Refael G, Preskill J, Jiang L, Safavi-Naeini A H, Painter O, Brandão F G S L 2022 PRX Quantum 3 10329 Google Scholar
[47]	Chu Y, Gröblacher S 2020 Appl. Phys. Lett. 117 150503 Google Scholar
[48]	Place A P M, Rodgers L V H, Mundada P, et al. 2021 Nat. Commun. 12 1779 Google Scholar
[49]	Wang C, Li X, Xu H, et al. 2021 arXiv: 2105.09890 [quant-ph]
[50]	Bao F, Deng H, Ding D, et al. 2021 arXiv: 2111.13504 [quant-ph]
[51]	Nuerbolati W, Han Z, Chu J, Zhou Y, Tan X, Yu Y, Liu S, Yan F 2022 Appl. Phys. Lett. 120 174001 Google Scholar
[52]	Zhao P, Linghu K, Li Z, Xu P, Wang R, Xue G, Jin Y, Yu H 2022 PRX Quantum 3 20301 Google Scholar
[53]	Joshi A, Noh K, Gao Y Y 2021 Quantum Sci. Technol. 6 33001 Google Scholar
[54]	Shor P W 1996 Proc. 37th Conf. Found. Comput. Sci. (IEEE) Burlington, VT, USA, October 14–16 1996, p56
[55]	Gottesman D 2009 arXiv: 0904.2557 [quant-ph]
[56]	Knill E, Laflamme R 1997 Phys. Rev. A 55 900 Google Scholar
[57]	Nielsen M A, Chuang I 2010 Quantum Computation and Quantum Information (New York: Cambridge University Press) pp1–12
[58]	Gottesman D 1996 Phys. Rev. A 54 1862 Google Scholar
[59]	Michael M H, Silveri M, Brierley R T, Albert V V, Salmilehto J, Jiang L, Girvin S M 2016 Phys. Rev. X 6 31006 Google Scholar
[60]	Leghtas Z, Kirchmair G, Vlastakis B, Schoelkopf R J, Devoret M H, Mirrahimi M 2013 Phys. Rev. Lett. 111 120501 Google Scholar
[61]	Mirrahimi M, Leghtas Z, Albert V V, Touzard S, Schoelkopf R J, Jiang L, Devoret M H 2014 New J. Phys. 16 45014 Google Scholar
[62]	Gottesman D, Kitaev A, Preskill J 2001 Phys. Rev. A 64 12310 Google Scholar
[63]	Noh K, Chamberland C, Brandão F G S L 2022 PRX Quantum 3 10315 Google Scholar
[64]	Vuillot C, Asasi H, Wang Y, Pryadko L P, Terhal B M 2019 Phys. Rev. A 99 32344 Google Scholar
[65]	Guillaud J, Mirrahimi M 2019 Phys. Rev. X 9 041053 Google Scholar
[66]	Darmawan A S, Brown B J, Grimsmo A L, Tuckett D K, Puri S 2021 PRX Quantum 2 30345 Google Scholar
[67]	Kapit E 2017 Quantum Sci. Technol. 2 33002 Google Scholar
[68]	Reed M D, DiCarlo L, Nigg S E, Sun L, Frunzio L, Girvin S M, Schoelkopf R J 2012 Nature 482 382 Google Scholar
[69]	Kelly J, Barends R, Fowler A G, et al. 2015 Nature 519 66 Google Scholar
[70]	Cramer J, Kalb N, Rol M A, Hensen B, Blok M S, Markham M, Twitchen D J, Hanson R, Taminiau T H 2016 Nat. Commun. 7 1 Google Scholar
[71]	Takita M, Cross A W, Córcoles A D, Chow J M, Gambetta J M 2017 Phys. Rev. Lett. 119 180501 Google Scholar
[72]	Wootton J R, Loss D 2018 Phys. Rev. A 97 52313 Google Scholar
[73]	Chen Z, Satzinger K J, Atalaya J, et al. 2021 Nature 595 383 Google Scholar
[74]	Kitaev A Y 1997 Russ. Math Surv. 52 1191 Google Scholar
[75]	Bravyi S B, Kitaev A Y 1998 arXiv: quant-ph/9811052 [quant-ph]
[76]	Fowler A G, Mariantoni M, Martinis J M, Cleland A N 2012 Phys. Rev. A 86 32324 Google Scholar
[77]	Raussendorf R, Harrington J, Goyal K 2006 Ann. Phys. 321 2242 Google Scholar
[78]	Raussendorf R, Harrington J 2007 Phys. Rev. Lett. 98 190504 Google Scholar
[79]	Raussendorf R, Harrington J, Goyal K 2007 New J. Phys. 9 199 Google Scholar
[80]	Fowler A G, Whiteside A C, McInnes A L, Rabbani A 2012 Phys. Rev. X 2 41003 Google Scholar
[81]	Dennis E, Kitaev A, Landahl A, Preskill J 2002 J. Math. Phys. 43 4452 Google Scholar
[82]	Knill E 2005 Nature 434 39 Google Scholar
[83]	Zeng B, Chen X, Zhou D L, Wen X G 2019 Quantum Information Meets Quantum Matter (New York: Springer) pp3–361
[84]	Satzinger K J, Liu Y J, Smith A, Knapp C, Newman M, Jones C, Chen Z, Quintana C, Mi X, Dunsworth A, Others 2021 Science 374 1237 Google Scholar
[85]	Liu Y J, Shtengel K, Smith A, Pollmann F 2021 arXiv: 2110.02020 [quant-ph]
[86]	Horsman C, Fowler A G, Devitt S, Van Meter R 2012 New J. Phys. 14 123011 Google Scholar
[87]	Bonilla Ataides J P, Tuckett D K, Bartlett S D, Flammia S T, Brown B J 2021 Nat. Commun. 12 1 Google Scholar
[88]	Bombin H, Martin-Delgado M A 2006 Phys. Rev. Lett. 97 180501 Google Scholar
[89]	Fowler A G 2011 Phys. Rev. A 83 42310 Google Scholar
[90]	Willsch D, Willsch M, Jin F, De Raedt H, Michielsen K 2018 Phys. Rev. A 98 52348 Google Scholar
[91]	Harper R, Flammia S T 2019 Phys. Rev. Lett. 122 80504 Google Scholar
[92]	Gong M, Yuan X, Wang S, et al. 2022 Natl. Sci. Rev. 9 nwab011 Google Scholar
[93]	Andersen C K, Remm A, Lazar S, Krinner S, Lacroix N, Norris G J, Gabureac M, Eichler C, Wallraff A 2020 Nat. Phys. 16 875 Google Scholar
[94]	Krinner S, Lacroix N, Remm A, et al. 2021 arXiv: 2112.03708 [quant-ph]
[95]	Sundaresan N, Yoder T J, Kim Y, Li M, Chen E H, Harper G, Thorbeck T, Cross A W, Córcoles A D, Takita M 2022 arXiv: 2203.07205 [quant-ph]
[96]	Khaneja N, Reiss T, Kehlet C, Schulte-Herbrüggen T, Glaser S J 2005 J. Magn. Reson. 172 296 Google Scholar
[97]	De Fouquieres P, Schirmer S G, Glaser S J, Kuprov I 2011 J. Magn. Reson. 212 412 Google Scholar
[98]	Hu L, Ma Y, Cai W, et al. 2019 Nat. Phys. 15 503 Google Scholar
[99]	Gao Y Y, Lester B J, Chou K S, Frunzio L, Devoret M H, Jiang L, Girvin S M, Schoelkopf R J 2019 Nature 566 509 Google Scholar
[100]	Chou K S, Blumoff J Z, Wang C S, Reinhold P C, Axline C J, Gao Y Y, Frunzio L, Devoret M H, Jiang L, Schoelkopf R J 2018 Nature 561 368 Google Scholar
[101]	Ma Y, Xu Y, Mu X, et al. 2020 Nat. Phys. 16 827 Google Scholar
[102]	Li L, Zou C L, Albert V V, Muralidharan S, Girvin S M, Jiang L 2017 Phys. Rev. Lett. 119 30502 Google Scholar
[103]	Puri S, Boutin S, Blais A 2017 npj Quantum Inf. 3 1 Google Scholar
[104]	Bourassa J, Beaudoin F, Gambetta J M, Blais A 2012 Phys. Rev. A 86 13814 Google Scholar
[105]	Grimsmo A L, Combes J, Baragiola B Q 2020 Phys. Rev. X 10 11058 Google Scholar
[106]	Ofek N, Petrenko A, Heeres R, et al. 2016 Nature 536 441 Google Scholar
[107]	Heeres R W, Reinhold P, Ofek N, Frunzio L, Jiang L, Devoret M H, Schoelkopf R J 2017 Nat. Commun. 8 94 Google Scholar
[108]	Gertler J M, Baker B, Li J, Shirol S, Koch J, Wang C 2021 Nature 590 243 Google Scholar
[109]	Touzard S, Grimm A, Leghtas Z, et al. 2018 Phys. Rev. X 8 21005 Google Scholar
[110]	Lescanne R, Villiers M, Peronnin T, Sarlette A, Delbecq M, Huard B, Kontos T, Mirrahimi M, Leghtas Z 2020 Nat. Phys. 16 509 Google Scholar
[111]	Grimm A, Frattini N E, Puri S, Mundhada S O, Touzard S, Mirrahimi M, Girvin S M, Shankar S, Devoret M H 2020 Nature 584 205 Google Scholar
[112]	Albert V V, Noh K, Duivenvoorden K, et al. 2018 Phys. Rev. A 97 32346 Google Scholar
[113]	Noh K, Albert V V, Jiang L 2019 IEEE Trans. Inf. Theory 65 2563 Google Scholar
[114]	Flühmann C, Nguyen T L, Marinelli M, Negnevitsky V, Mehta K, Home J P 2019 Nature 566 513 Google Scholar
[115]	de Neeve B, Nguyen T L, Behrle T, Home J P 2022 Nat. Phys. 18 296 Google Scholar
[116]	Campagne-Ibarcq P, Eickbusch A, Touzard S, et al. 2020 Nature 584 368 Google Scholar
[117]	Terhal B M, Weigand D 2016 Phys. Rev. A 93 12315 Google Scholar
[118]	Royer B, Singh S, Girvin S M 2020 Phys. Rev. Lett. 125 260509 Google Scholar
[119]	Eastin B, Knill E 2009 Phys. Rev. Lett. 102 110502 Google Scholar
[120]	Gottesman D, Chuang I L 1999 Nature 402 390 Google Scholar
[121]	Zhou X, Leung D W, Chuang I L 2000 Phys. Rev. A 62 52316 Google Scholar
[122]	Bravyi S, Kitaev A 2005 Phys. Rev. A 71 22316 Google Scholar
[123]	Meier A M, Eastin B, Knill E 2012 arXiv: 1204.4221 [quant-ph]
[124]	Chamberland C, Cross A W 2019 Quantum 3 143 Google Scholar
[125]	Chamberland C, Jochym-O’Connor T, Laflamme R 2017 Phys. Rev. A 95 22313 Google Scholar
[126]	Campbell E T, Terhal B M, Vuillot C 2017 Nature 549 172 Google Scholar
[127]	Rosenblum S, Reinhold P, Mirrahimi M, Jiang L, Frunzio L, Schoelkopf R J 2018 Science 361 266 Google Scholar
[128]	Krastanov S, Albert V V, Shen C, Zou C L, Heeres R W, Vlastakis B, Schoelkopf R J, Jiang L 2015 Phys. Rev. A 92 40303 Google Scholar
[129]	Heeres R W, Vlastakis B, Holland E, Krastanov S, Albert V V, Frunzio L, Jiang L, Schoelkopf R J 2015 Phys. Rev. Lett. 115 137002 Google Scholar
[130]	Wang W, Hu L, Xu Y, Liu K, Ma Y, Zheng S B, Vijay R, Song Y P, Duan L M, Sun L 2017 Phys. Rev. Lett. 118 223604 Google Scholar
[131]	Lloyd S, Viola L 2001 Phys. Rev. A 65 10101 Google Scholar
[132]	Shen C, Noh K, Albert V V, Krastanov S, Devoret M H, Schoelkopf R J, Girvin S M, Jiang L 2017 Phys. Rev. B 95 134501 Google Scholar
[133]	Hu L, Mu X, Cai W, Ma Y, Xu Y, Wang H, Song Y, Zou C L, Sun L 2018 Sci. Bull. 63 1551 Google Scholar
[134]	Cai W, Han J, Hu L, et al. 2021 Phys. Rev. Lett. 127 90504 Google Scholar
[135]	Giovannetti V, Lloyd S, Maccone L 2011 Nat. Photonics 5 222 Google Scholar
[136]	Backes K M, Palken D A, Kenany S A, et al. 2021 Nature 590 238 Google Scholar
[137]	Wang W, Wu Y, Ma Y, Cai W, Hu L, Mu X, Xu Y, Chen Z J, Wang H, Song Y P, Yuan H, Zou C L, Duan L M, Sun L 2019 Nat. Commun. 10 4382 Google Scholar
[138]	Wang W, Chen Z J, Liu X, et al. 2022 Nat. Commun. 13 1 Google Scholar
[139]	Zhou S, Zhang M, Preskill J, Jiang L 2018 Nat. Commun. 9 1 Google Scholar
[140]	Górecki W, Zhou S, Jiang L, Demkowicz-Dobrzański R 2020 Quantum 4 288 Google Scholar
[141]	Pfaff W, Axline C J, Burkhart L D, Vool U, Reinhold P, Frunzio L, Jiang L, Devoret M H, Schoelkopf R J 2017 Nat. Phys. 13 882 Google Scholar
[142]	Muralidharan S, Li L, Kim J, Lütkenhaus N, Lukin M D, Jiang L 2016 Sci. Rep. 6 1 Google Scholar
[143]	Preskill J 2018 Quantum 2 79 Google Scholar
[144]	Endo S, Cai Z, Benjamin S C, Yuan X 2021 J. Phys. Soc. Jpn. 90 32001 Google Scholar
[145]	McArdle S, Yuan X, Benjamin S 2019 Phys. Rev. Lett. 122 180501 Google Scholar
[146]	Koh J M, Tai T, Lee C H 2022 arXiv: 2207.14322 [cond-mat.str-el]
[147]	Li Y, Benjamin S C 2016 Phys. Rev. A 94 42303 Google Scholar
[148]	Gottesman D 2016 arXiv: 1610.03507 [quant-ph]
[149]	Chao R, Reichardt B W 2018 Phys. Rev. Lett. 121 50502 Google Scholar
[150]	Ma W L, Zhang M, Wong Y, Noh K, Rosenblum S, Reinhold P, Schoelkopf R J, Jiang L 2020 Phys. Rev. Lett. 125 110503 Google Scholar
[151]	Jahn A, Eisert J 2021 Quantum Sci. Technol. 6 33002 Google Scholar
[152]	Almheiri A, Dong X, Harlow D 2015 J. High Energy Phys. 2015(4) 1 Google Scholar
[153]	Pastawski F, Yoshida B, Harlow D, Preskill J 2015 J. High Energy Phys. 2015(6) 1 Google Scholar
[154]	Vijay S, Haah J, Fu L 2016 Phys. Rev. B 94 235157 Google Scholar
[155]	Hong Y, Young J T, Kaufman A M, Lucas A 2022 arXiv: 2205.12998 [quant-ph]

施引文献

图 1 (a)二维transmon量子比特结构示意图(图片来自文献[15]). 左右两边黄色电路分别表示一个transmon量子比特, 其中交叉表示约瑟夫森结, 其两端并联大旁路电容, 而中间的黑色电路表示辅助模式, 用于两个量子比特之间的可调耦合. (b)三维超导谐振腔与transmon量子比特耦合结构示意图(图片来自文献[45]). 橙色和绿色区域为高纯铝制备的三维超导谐振腔, 两腔通过铝块侧面开孔与辅助超导量子比特进行耦合. (c)基于二维transmon量子比特的架构(图片修改自文献[30]). 图中黄色线路为读取用微波传输线, 末端接隔离器和约瑟夫森参量放大器, 用于读取信号的单向传输和放大; 绿色区域为读取谐振腔; 浅蓝色区域为可调频transmon量子比特, 量子比特之间通过一个共同的辅助模式B耦合; 红色线路为transmon量子比特的微波驱动线, 蓝色线路为transmon量子比特的磁通驱动线. (d)三维谐振腔架构拓展示意图^[53]. 红色和绿色方块为transmon量子比特, 浅渌色部分为高Q超导谐振腔(用于存储量子信息), 灰色部分为低Q超导谐振腔(用于transmon量子比特的读取). 谐振腔与transmon量子比特通过电容直接耦合

Fig. 1. (a) Structure of coupled two dimensional (2D) transmon qubits (Reprinted with permission from Ref. [15]). The left and right circuits (yellow) represent two transmon qubits, where each cross represents a Josephson junction and its two ends are coupled with a large capacitor. The middle black circuit represents the auxiliary mode for adjustable coupling between the two qubits. (b) Structure of 3D superconducting cavities coupled with transmon qubits (Reprinted with permission from Ref. [45]). The orange and green parts are the three dimensional (3D) superconducting cavities made of high-purity aluminum, and the two cavities are coupled to the auxiliary superconducting qubits through trenches on the sides of the aluminum block. (c) Architecture based on 2D transmon qubits (Reprinted with permission from Ref. [30]). The yellow lines in the figure are the microwave transmission lines for readout, and are connected with an isolator and a Josephson parametric amplifier, which are used for one-way transmission and amplification of the readout signal. The green parts are the readout resonators. The light blue parts are the tunable transmon qubits, which are coupled by a common auxiliary mode B. The red and the blue lines are the microwave drive and the flux drive lines for the transmon qubits respectively. (d) Architecture based on 3D superconducting resonators^[53]. The red and green squares are transmon qubits, the light green parts are the high-Q superconducting resonators (for storing quantum information), and the gray parts are the low-Q superconducting resonators (for readout of transmon qubits). The resonator is directly coupled to the transmon qubit through a capacitor

下载: 全尺寸图片幻灯片

图 2 纠错流程图. 蓝色的圆圈表示编码空间, 绿色的圆圈表示错误空间, 黄色的箭头表示要保护的量子态

Fig. 2. Diagram of quantum error correction. The blue circles represent the code space, the green circles represent the error space, and the yellow arrows represent the quantum states to be protected

下载: 全尺寸图片幻灯片

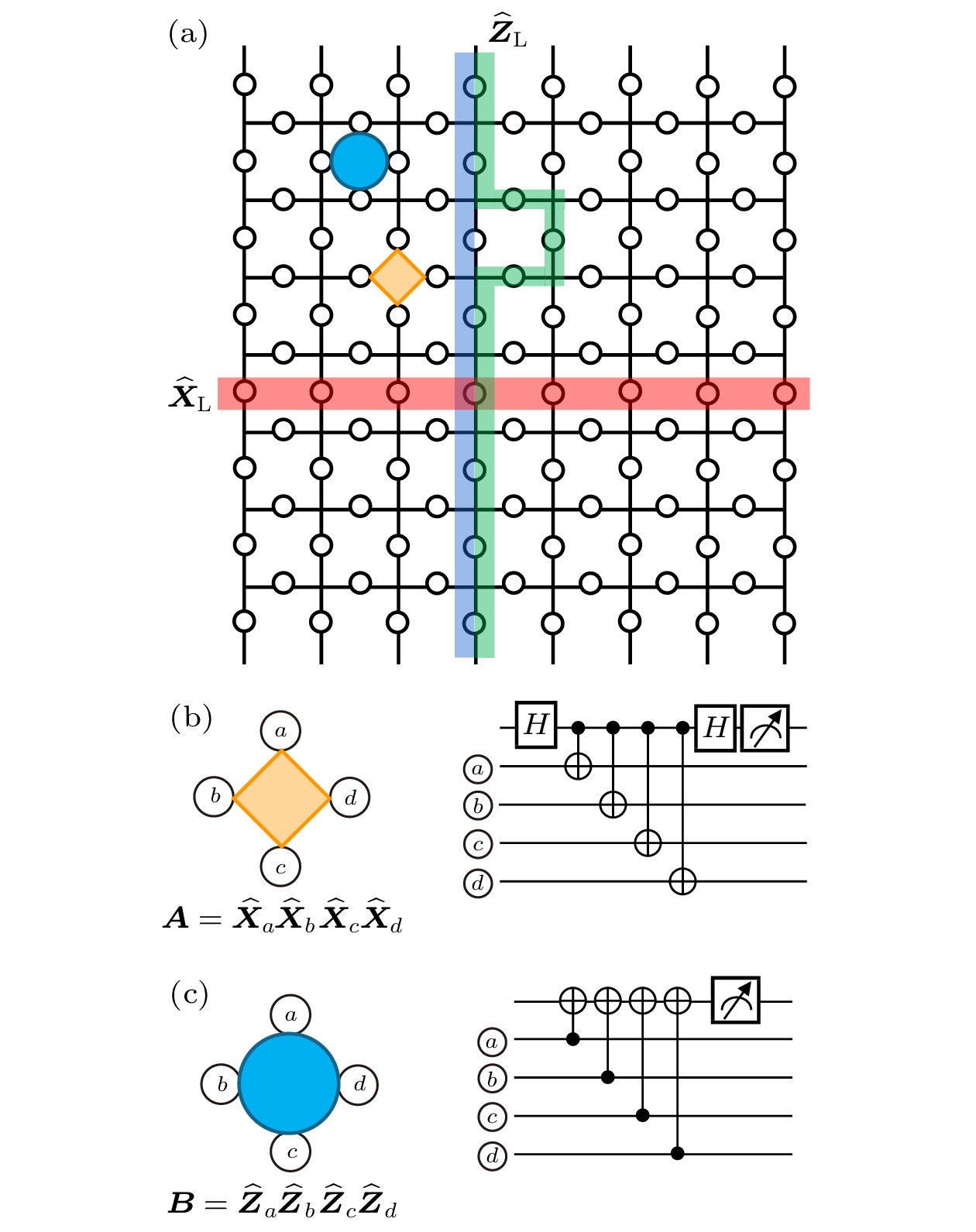
图 3 (a) $ d=8 $的表面码及其逻辑算符$ {\boldsymbol{\hat{Z}}}_{{\rm{L}}} $与$ {\boldsymbol{\hat{X}}}_{{\rm{L}}} $的示意图. 图中网格的每条边上都有一个白点表示一个数据量子比特. 黄色菱形以及蓝色圆形分别表示其中一个A和B类型的稳定子. 蓝色和红色阴影线分别表示逻辑编码的$ {\boldsymbol{\hat{Z}}}_{{\rm{L}}} $和$ {\boldsymbol{\hat{X}}}_{{\rm{L}}} $算符. 绿色阴影线表示蓝色阴影线对应的算符乘上一个稳定算符, 其也是逻辑$ {\boldsymbol{\hat{Z}}}_{{\rm{L}}} $算符. (b)和(c)分别是A, B类型稳定子算符测量的量子线路图. 此图由文献[76]改编

Fig. 3. (a) Schematic of $ d=8 $ surface code and the corresponding logical operators $ {\boldsymbol{\hat{Z}}}_{{\rm{L}}} $ and $ {\boldsymbol{\hat{X}}}_{{\rm{L}}} $. The white dots on each edge of the grid represent data qubits. The yellow diamonds and the blue circles represent A and B types of stabilizers, respectively. The blue and red shaded lines represent the logical $ {\boldsymbol{\hat{Z}}}_{{\rm{L}}} $ and $ {\boldsymbol{\hat{X}}}_{{\rm{L}}} $ operators, respectively. The green shaded line represents the operator corresponding to the blue shaded line multiplied by a stablizer operator, which is also the logical $ {\boldsymbol{\hat{Z}}}_{{\rm{L}}} $ operator. (b) and (c) are quantum circuits that measure the stabilizer operators of type A and B, respectively. This figure is adapted from Ref. [76]

下载: 全尺寸图片幻灯片

图 4 表面码的错误症状及纠错操作示意图. 图中红色交叉表示对应物理比特发生了位翻转噪声, 蓝色圆形表示测量结果异常的B类型稳定子的位置, 即缺陷的位置, 阴影线均表示对线上的物理比特执行的$ {\boldsymbol{\hat{X}}} $操作. 四个区域分别对应以下情况: (a)网格中单个比特发生噪声产生了两个相邻的缺陷; (b)网格中的连续的几个比特发生噪声产生了位于错误链两端的缺陷, 而蓝色和绿色阴影线对应的操作均能纠正逻辑错误; (c)含有网格左边界的比特的错误链导致单个缺陷的产生, 浅绿色和黄色的阴影线对应的操作均能纠正逻辑错误; (d)含有网格左边界的比特的错误链导致单个缺陷的产生, 红色阴影线对应的操作能纠正逻辑错误, 但是紫色阴影线的操作会导致无法被错误诊断识别的逻辑错误

Fig. 4. Schematic of error syndromes and error correction operations of surface codes. The red cross in the figure indicates a bit-flip error occuring in the corresponding physical qubit, while the blue circle indicates the position of the B type stabilizer with abnormal measurement results, i.e., the position of the defect, and the shaded lines indicate an $ {\boldsymbol{\hat{X}}} $ operation performed on each of the physical qubit on the line. The four areas correspond to the following situations: (a) A single bit-flip error in the grid results in two adjacent defects. (b) Several consecutive bit-flip errors in the grid result in two defects located at the two ends of the error chain. Both the blue and green shaded lines can correct these errors. (c) The error chain containing a qubit on the left boundary of the grid results in a single defect, and the operations corresponding to either the light green or the yellow shaded line can orrect these errors. (d) The error chain containing a qubit on the left boundary of the grid results in a single defect. The operation corresponding to the red shaded line can correct these errors, but the operation corresponding to the purple shaded line causes a logic error that cannot be identified by the error syndrome

下载: 全尺寸图片幻灯片

图 5 (a)谷歌公司实验^[84]中制备表面码初态所用超导芯片的架构以及对应稳定子测量结果. 图中白色的十字为数据比特, 紫色和蓝色的图形分别代表$ {\boldsymbol{B}_{p}} $类型和$ {\boldsymbol{A}_{s}} $类型的稳定子测量, 图中的数值是初态对应的稳定子测量结果的平均值. (b)表面码初态制备对应的门操作线路

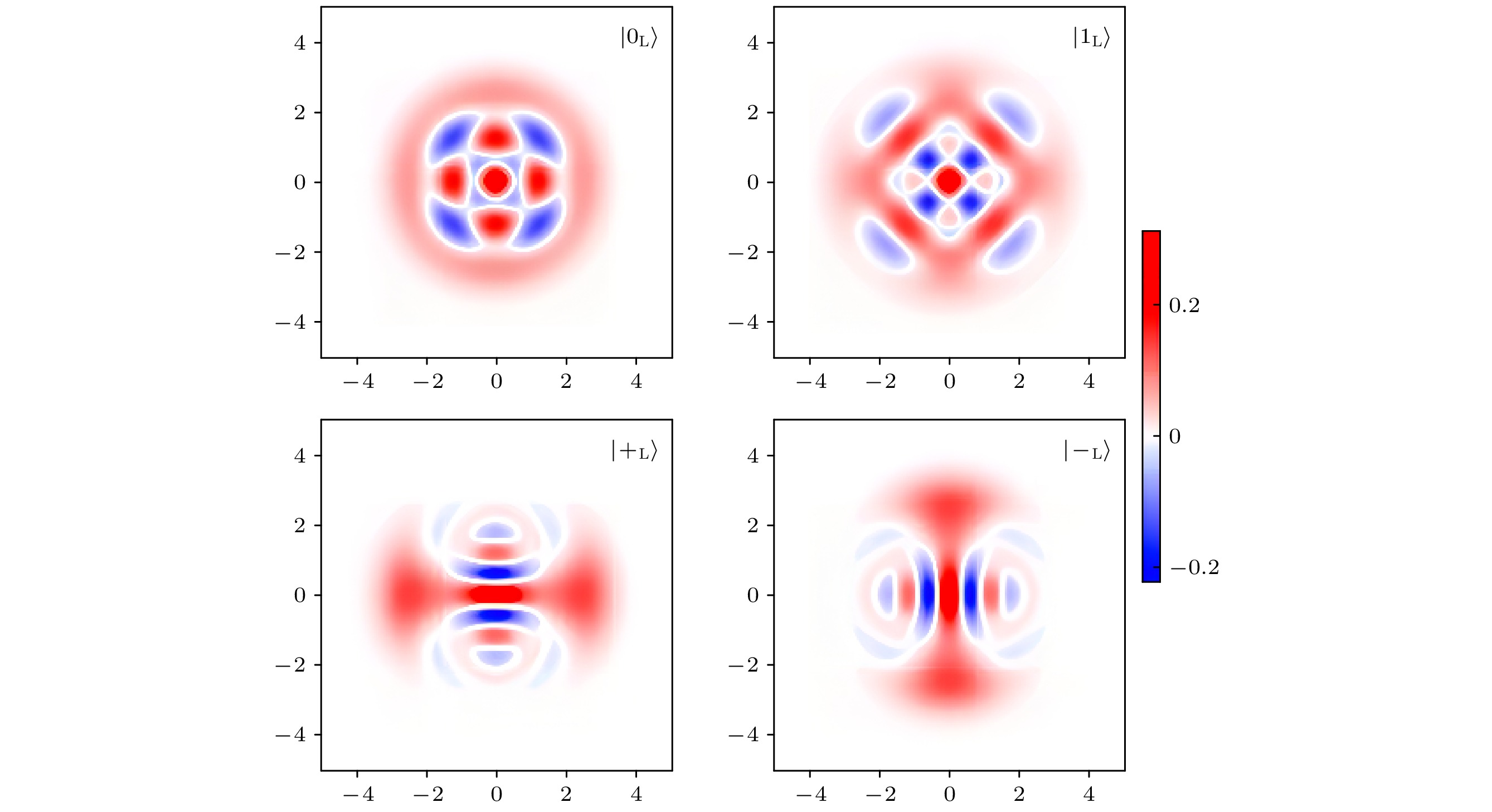
Fig. 5. (a) Architecture of the superconducting circuit used to prepare the initial state of the surface code in Google’s experiment^[84] and the corresponding stabilizer measurement results. The white crosses are data qubits, the purple and blue regions represent stabilizer measurement results of type $ {\boldsymbol{B}_{p}} $ and $ {\boldsymbol{A}_{s}} $, respectively. The values in the figure are the average values of the stabilizer measurement results corresponding to the initial state. (b) Operation circuit to prepare the initial state of the surface code

下载: 全尺寸图片幻灯片

图 6 一种二项式编码逻辑态的维格纳函数图像. 左上: 逻辑态$ |0_{{\rm{L}}}\rangle=( | 0\rangle +\sqrt{3}|4\rangle)/2 $; 右上: $ |1_{{\rm{L}}}\rangle=(\sqrt{3}|2\rangle +|6\rangle)/2 $; 左下: $ |+_{{\rm{L}}}\rangle=(|0_{{\rm{L}}}\rangle+|1_{{\rm{L}}}\rangle)/\sqrt{2} $; 右下: $ |-_{{\rm{L}}}\rangle=(|0_{{\rm{L}}}\rangle-|1_{{\rm{L}}}\rangle)/\sqrt{2} $. 这是平均光子数最小的且能纠正错误集合$ \{{\boldsymbol{\hat{I}}},\; {\boldsymbol{\hat{a}}},\; {\boldsymbol{\hat{a}}}^{\dagger}{\boldsymbol{\hat{a}}}\} $的二项式编码, 可以看到其$ |0/1_{{\rm{L}}}\rangle $本身具有$ {\text{π}}/4 $的旋转对称性, 而$ |+/-_{{\rm{L}}}\rangle $在相空间中接近正交

Fig. 6. Wigner functions of the logical states of one binomial code. Upper left: Logical state $ |0_{{\rm{L}}}\rangle=( | 0\rangle +\sqrt{3}|4\rangle)/2 $; Upper right: Logical state $ |1_{{\rm{L}}}\rangle=(\sqrt{3}|2\rangle +|6\rangle)/2 $; Lower left: $ |+_{{\rm{L}}}\rangle=(|0_{{\rm{L}}}\rangle+|1_{{\rm{L}}}\rangle)/\sqrt{2} $; Lower right: $ |-_{{\rm{L}}}\rangle=(|0_{{\rm{L}}}\rangle-|1_{{\rm{L}}}\rangle)/\sqrt{2} $. This is the binomial code that has the minimal average photon number and can correct the error set $ \{{\boldsymbol{\hat{I}}}, \;{\boldsymbol{\hat{a}}},\; {\boldsymbol{\hat{a}}}^{\dagger}{\boldsymbol{\hat{a}}}\} $. The logical state $ |0/1_{{\rm{L}}}\rangle $ has a rotational symmetry of $ {\text{π}}/4 $ and $ |+/-_{{\rm{L}}}\rangle $ are almost orthogonal in phase space

下载: 全尺寸图片幻灯片

图 7 猫态编码逻辑态的维格纳函数图像, 其中$ \alpha=2.5,\; n=4 $. 左上: 逻辑态$ |0_{{\rm{L}}}\rangle $; 右上: $ |1_{{\rm{L}}}\rangle $; 左下: $ |+_{{\rm{L}}}\rangle=(|0_{{\rm{L}}}\rangle+|1_{{\rm{L}}}\rangle)/\sqrt{2} $; 右下: $ |-_{{\rm{L}}}\rangle=(|0_{{\rm{L}}}\rangle-|1_{{\rm{L}}}\rangle)/\sqrt{2} $

Fig. 7. Wigner functions of the logical states of the cat code with $ \alpha=2.5,\; n=4 $. Upper left: Logical state $ |0_{{\rm{L}}}\rangle $; Upper right: Logical state $ |1_{{\rm{L}}}\rangle $; Lower left:$ |+_{{\rm{L}}}\rangle=(|0_{{\rm{L}}}\rangle+|1_{{\rm{L}}}\rangle)/\sqrt{2} $; Lower right:$ |-_{{\rm{L}}}\rangle=(|0_{{\rm{L}}}\rangle-|1_{{\rm{L}}}\rangle)/\sqrt{2} $

下载: 全尺寸图片幻灯片

图 8 近似GKP编码逻辑态的维格纳函数图像, 其中$\varDelta=0.3$. 左上: 逻辑态$ |0_{{\rm{L}}}\rangle $; 右上: $ |1_{{\rm{L}}}\rangle $; 左下: $ |+_{{\rm{L}}}\rangle=(|0_{{\rm{L}}}\rangle+|1_{{\rm{L}}}\rangle)/\sqrt{2} $; 右下: $ |-_{{\rm{L}}}\rangle=(|0_{{\rm{L}}}\rangle-|1_{{\rm{L}}}\rangle)/\sqrt{2} $

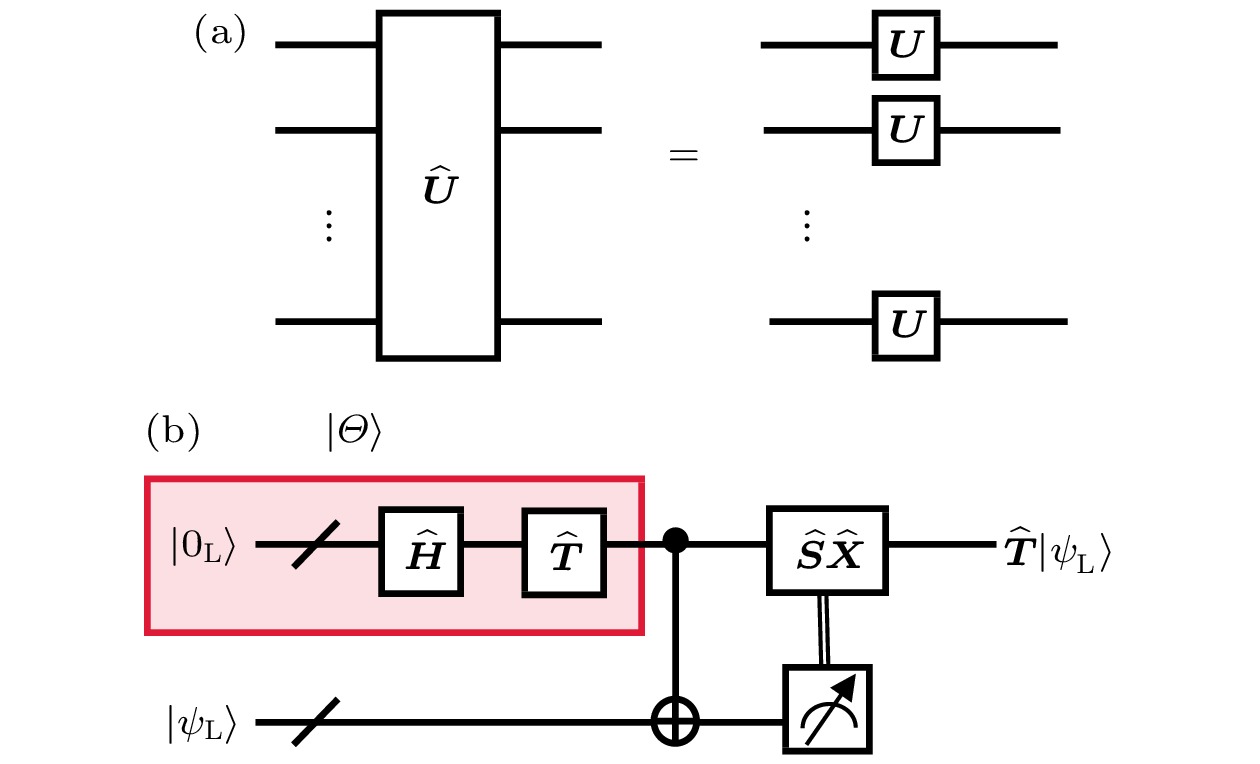
Fig. 8. Wigner functions of the logical states of an approximate GKP code with $\varDelta=0.3$. Upper left: Logical state $ |0_{{\rm{L}}}\rangle $; Upper right: $ |1_{{\rm{L}}}\rangle $; Lower left: $ |+_{{\rm{L}}}\rangle=(|0_{{\rm{L}}}\rangle+|1_{{\rm{L}}}\rangle)/\sqrt{2} $; Lower right: $ |-_{{\rm{L}}}\rangle=(|0_{{\rm{L}}}\rangle-|1_{{\rm{L}}}\rangle)/\sqrt{2} $

下载: 全尺寸图片幻灯片

图 9 (a)横向逻辑门操作示意图; (b)单比特态传输的方式实现逻辑${{\hat{{\boldsymbol{T}}}}}$门. 图中斜线表示此逻辑比特包括多个物理比特, 而图中红色阴影区域的线路等价于将辅助比特初态制备成$\left|\varTheta\right\rangle$, 红色区域外的门操作全是横向逻辑门

Fig. 9. (a) Schematic of the transversal logical operation; (b) logical ${{\hat{{\boldsymbol{T}}}}}$ gate implemented through one-bit teleportation. The slash in the figure indicates that the logical qubit is encoded with several physical qubits, and the red shaded area is equivalent to initializing the auxiliary qubit as $\left|\varTheta\right\rangle$. All logical gates outside the red shaded area are transversal

下载: 全尺寸图片幻灯片

表 1 超导系统中二能级编码的纠错实验进展. 带*号的是物理比特中最优的数据, /表示文献中没有直接给出相关数据. 其中, 文献[72, 90, 91]的实验均在国际商用机器公司的IBMQ平台上进行

Table 1. Experimental progress on quantum error correction with two-level codes in superconducting systems. Datas with * refer to the optimal datas among the physical qubits. / indicate that the relevant datas are not directly given in the documents. The experiments in the Refs. [72, 90, 91] were implemented on IBMQ

时间	文献	编码	逻辑$ T_{1} $(物理$ T_{1} $)$/\text{µ} {\rm{s}}$	逻辑 $ T_{2} $(物理$ T_{2} $)$/\text{µ} {\rm{s}}$
2012	耶鲁大学^[68]	$ \left[3, 1, 3\right] $重复码	/	/
2014	加州大学圣芭芭拉分校^[69]	$ \left[3, 1, 3\right] $, $ \left[5, 1, 5\right] $重复码	/	/
2015	代尔夫特理工大学^[25]	$ \left[3, 1, 3\right] $重复码	/	/
2017	IBM^[71]	4比特颜色码	/	/
2018	巴塞尔大学(University of Basel)^[72]	$ \left[8, 1, 8\right] $重复码	/	/
2018	德国于利希研究中心(Forschungszentrum Jülich)^[90]	4比特颜色码	/	/
2019	悉尼大学^[91]	$ [4, 2, 2] $错误检测码	/	/
2019	中国科学技术大学^[92]	$ [[5, 1, 3]] $编码	/	/
2020	苏黎世联邦理工学院^[93]	$ [[4, 1, 2]] $表面码	$ 62.7\pm9.4 $($ 16.8^{*} $)	$ 72.5\pm32.9 $($ 21.5^{*} $)
2021	谷歌公司^[84]	实现表面码的基态	/	/
2021	中国科学技术大学^[31]	$ [[9, 1, 3]] $表面码	$ 137.8 $($ 36.6^{*} $)	/
2021	苏黎世联邦理工学院^[94]	$ [[9, 1, 3]] $表面码	$ 16.4 $($ 32.5 $)	$ 18.2 $($ 37.5 $)
2021	谷歌公司^[73]	$ [11, 1, 11] $重复码以及$ [[4, 1, 2]] $表面码	/	/
2022	苏黎世联邦理工学院^[24]	$ [[4, 1, 2]] $表面码	/	/
2022	IBM^[95]	$ [[9, 1, 3]] $Heavy-hexagon编码	/	/
2022	谷歌公司^[8]	$ [[25, 1, 5]] $表面码以及$ [25, 1, 25] $重复码	/	/

下载: 导出CSV

map

[1]	Shor P W 1994 Proc. 35th Annu. Symp. Found. Comput. Sci. (IEEE) Santa Fe, NM, USA, November 20–22, 1994 p124
[2]	Shor P W 1995 Phys. Rev. A 52 R2493 Google Scholar
[3]	Kudra M, Biznárová J, Fadavi Roudsari A, Burnett J J, Niepce D, Gasparinetti S, Wickman B, Delsing P 2020 Appl. Phys. Lett. 117 70601 Google Scholar
[4]	Reagor M, Pfaff W, Axline C, et al. 2016 Phys. Rev. B 94 14506 Google Scholar
[5]	Romanenko A, Pilipenko R, Zorzetti S, Frolov D, Awida M, Belomestnykh S, Posen S, Grassellino A 2020 Phys. Rev. Appl. 13 34032 Google Scholar
[6]	Magnard P, Storz S, Kurpiers P, Schär J, Marxer F, Lütolf J, Walter T, Besse J C, Gabureac M, Reuer K, Akin A, Royer B, Blais A, Wallraff A 2020 Phys. Rev. Lett. 125 260502 Google Scholar
[7]	Xu X B, Wang W, Sun L, Zou C L 2022 Chip 100016 Google Scholar
[8]	Acharya R, Aleiner I, Allen R, et al. 2022 arXiv: 2207.06431 [quant-ph]
[9]	Jurcevic P, Javadi-Abhari A, Bishop L S, et al. 2021 Quantum Sci. Technol. 6 25020 Google Scholar
[10]	Zhu Q, Cao S, Chen F, et al. 2022 Sci. Bull. 67 240 Google Scholar
[11]	Guo Q, Cheng C, Li H, et al. 2021 Phys. Rev. Lett. 127 240502 Google Scholar
[12]	Xu K, Zhang Y R, Sun Z H, et al. 2022 Phys. Rev. Lett. 128 150501 Google Scholar
[13]	Xu H, Zhang J, Han J, Li Z, Xue G, Liu W, Jin Y, Yu H 2021 arXiv: 2108.00942 [quant-ph]
[14]	Arute F, Arya K, Babbush R, et al. 2019 Nature 574 505 Google Scholar
[15]	Wu Y, Bao W S, Cao S, et al. 2021 Phys. Rev. Lett. 127 180501 Google Scholar
[16]	Farhi E, Goldstone J, Gutmann S 2014 arXiv: 1411.4028 [quant-ph]
[17]	Peruzzo A, McClean J, Shadbolt P, Yung M H, Zhou X Q, Love P J, Aspuru-Guzik A, O’brien J L 2014 Nat. Commun. 5 1 Google Scholar
[18]	Wendin G 2017 Rep. Prog. Phys. 80 106001 Google Scholar
[19]	Blais A, Grimsmo A L, Girvin S M, Wallraff A 2021 Rev. Mod. Phys. 93 25005 Google Scholar
[20]	Xu Y, Hua Z, Chen T, et al. 2020 Phys. Rev. Lett. 124 230503 Google Scholar
[21]	Cai T Q, Han X Y, Wu Y K, Ma Y L, Wang J H, Wang Z L, Zhang H Y, Wang H Y, Song Y P, Duan L M 2021 Phys. Rev. Lett. 127 060505 Google Scholar
[22]	Tan X, Zhang D W, Zheng W, et al. 2021 Phys. Rev. Lett. 126 017702 Google Scholar
[23]	Ni Z, Li S, Zhang L, et al. 2022 Phys. Rev. Lett. 129 040502 Google Scholar
[24]	Marques J F, Varbanov B M, Moreira M S, et al. 2022 Nat. Phys. 18 80 Google Scholar
[25]	Riste D, Poletto S, Huang M Z, Bruno A, Vesterinen V, Saira O P, DiCarlo L 2015 Nat. Commun. 6 1 Google Scholar
[26]	Yan F, Krantz P, Sung Y, Kjaergaard M, Campbell D L, Orlando T P, Gustavsson S, Oliver W D 2018 Phys. Rev. Appl. 10 054062 Google Scholar
[27]	Mundada P, Zhang G Y, Hazard T, Houck A 2019 Phys. Rev. Appl. 12 54023 Google Scholar
[28]	Sung Y, Ding L, Braumüller J, Vepsäläinen A, Kannan B, Kjaergaard M, Greene A, Samach G O, McNally C, Kim D, Melville A, Niedzielski B M, Schwartz M E, Yoder J L, Orlando T P, Gustavsson S, Oliver W D 2021 Phys. Rev. X 11 21058 Google Scholar
[29]	Li X, Cai T, Yan H, Wang Z, Pan X, Ma Y, Cai W, Han J, Hua Z, Han X, Wu Y, Zhang H, Wang H, Song Y P, Duan L M, Sun L Y 2020 Phys. Rev. Appl. 14 24070 Google Scholar
[30]	Song C, Xu K, Li H, Zhang Y R, Zhang X, Liu W, Guo Q, Wang Z, Ren W, Hao J, Feng H, Fan H, Zheng D, Wang D W, Wang H, Zhu S Y 2019 Science 365 574 Google Scholar
[31]	Zhao Y, Ye Y, Huang H L, et al. 2021 arXiv: 2112.13505 [quant-ph]
[32]	Negirneac V, Ali H, Muthusubramanian N, Battistel F, Sagastizabal R, Moreira M S, Marques J F, Vlothuizen W J, Beekman M, Zachariadis C, Haider N, Bruno A, DiCarlo L 2021 Phys. Rev. Lett. 126 220502 Google Scholar
[33]	Kjaergaard M, Schwartz M E, Greene A, et al 2020 arXiv: 2001.08838 [quant-ph]
[34]	Kandala A, Wei K X, Srinivasan S, Magesan E, Carnevale S, Keefe G A, Klaus D, Dial O, McKay D C 2021 Phys. Rev. Lett. 127 130501 Google Scholar
[35]	Blais A, Huang R S, Wallraff A, Girvin S M, Schoelkopf R J 2004 Phys. Rev. A 69 62320 Google Scholar
[36]	Koch J, Yu T M, Gambetta J, Houck A A, Schuster D I, Majer J, Blais A, Devoret M H, Girvin S M, Schoelkopf R J 2007 Phys. Rev. A 76 042319 Google Scholar
[37]	Houck A A, Schreier J A, Johnson B R, Chow J M, Koch J, Gambetta J M, Schuster D I, Frunzio L, Devoret M H, Girvin S M, Schoelkopf R J 2008 Phys. Rev. Lett. 101 80502 Google Scholar
[38]	Reed M D, Johnson B R, Houck A A, DiCarlo L, Chow J M, Schuster D I, Frunzio L, Schoelkopf R J 2010 Appl. Phys. Lett. 9 6 Google Scholar
[39]	Jeffrey E, Sank D, Mutus J Y, White T C, Kelly J, Barends R, Chen Y, Chen Z, Chiaro B, Dunsworth A, Megrant A, O’Malley P J, Neill C, Roushan P, Vainsencher A, Wenner J, Cleland A N, Martinis J M 2014 Phys. Rev. Lett. 112 190504 Google Scholar
[40]	Yurke B, Corruccini L R, Kaminsky P G, Rupp L W, Smith A D, Silver A H, Simon R W, Whittaker E A 1989 Phys. Rev. A 39 2519 Google Scholar
[41]	Siddiqi I, Vijay R, Pierre F, Wilson C M, Metcalfe M, Rigetti C, Frunzio L, Devoret M H 2004 Phys. Rev. Lett. 93 207002 Google Scholar
[42]	Castellanos-Beltran M A, Lehnert K W 2007 Appl. Phys. Lett. 91 83509 Google Scholar
[43]	Walter T, Kurpiers P, Gasparinetti S, et al. 2017 Phys. Rev. Appl. 7 054020 Google Scholar
[44]	Reagor M, Paik H, Catelani G, et al. 2013 Appl. Phys. Lett. 102 192604 Google Scholar
[45]	Xu Y, Ma Y, Cai W, et al. 2020 Phys. Rev. Lett. 124 120501 Google Scholar
[46]	Chamberland C, Noh K, Arrangoiz-Arriola P, Campbell E T, Hann C T, Iverson J, Putterman H, Bohdanowicz T C, Flammia S T, Keller A, Refael G, Preskill J, Jiang L, Safavi-Naeini A H, Painter O, Brandão F G S L 2022 PRX Quantum 3 10329 Google Scholar
[47]	Chu Y, Gröblacher S 2020 Appl. Phys. Lett. 117 150503 Google Scholar
[48]	Place A P M, Rodgers L V H, Mundada P, et al. 2021 Nat. Commun. 12 1779 Google Scholar
[49]	Wang C, Li X, Xu H, et al. 2021 arXiv: 2105.09890 [quant-ph]
[50]	Bao F, Deng H, Ding D, et al. 2021 arXiv: 2111.13504 [quant-ph]
[51]	Nuerbolati W, Han Z, Chu J, Zhou Y, Tan X, Yu Y, Liu S, Yan F 2022 Appl. Phys. Lett. 120 174001 Google Scholar
[52]	Zhao P, Linghu K, Li Z, Xu P, Wang R, Xue G, Jin Y, Yu H 2022 PRX Quantum 3 20301 Google Scholar
[53]	Joshi A, Noh K, Gao Y Y 2021 Quantum Sci. Technol. 6 33001 Google Scholar
[54]	Shor P W 1996 Proc. 37th Conf. Found. Comput. Sci. (IEEE) Burlington, VT, USA, October 14–16 1996, p56
[55]	Gottesman D 2009 arXiv: 0904.2557 [quant-ph]
[56]	Knill E, Laflamme R 1997 Phys. Rev. A 55 900 Google Scholar
[57]	Nielsen M A, Chuang I 2010 Quantum Computation and Quantum Information (New York: Cambridge University Press) pp1–12
[58]	Gottesman D 1996 Phys. Rev. A 54 1862 Google Scholar
[59]	Michael M H, Silveri M, Brierley R T, Albert V V, Salmilehto J, Jiang L, Girvin S M 2016 Phys. Rev. X 6 31006 Google Scholar
[60]	Leghtas Z, Kirchmair G, Vlastakis B, Schoelkopf R J, Devoret M H, Mirrahimi M 2013 Phys. Rev. Lett. 111 120501 Google Scholar
[61]	Mirrahimi M, Leghtas Z, Albert V V, Touzard S, Schoelkopf R J, Jiang L, Devoret M H 2014 New J. Phys. 16 45014 Google Scholar
[62]	Gottesman D, Kitaev A, Preskill J 2001 Phys. Rev. A 64 12310 Google Scholar
[63]	Noh K, Chamberland C, Brandão F G S L 2022 PRX Quantum 3 10315 Google Scholar
[64]	Vuillot C, Asasi H, Wang Y, Pryadko L P, Terhal B M 2019 Phys. Rev. A 99 32344 Google Scholar
[65]	Guillaud J, Mirrahimi M 2019 Phys. Rev. X 9 041053 Google Scholar
[66]	Darmawan A S, Brown B J, Grimsmo A L, Tuckett D K, Puri S 2021 PRX Quantum 2 30345 Google Scholar
[67]	Kapit E 2017 Quantum Sci. Technol. 2 33002 Google Scholar
[68]	Reed M D, DiCarlo L, Nigg S E, Sun L, Frunzio L, Girvin S M, Schoelkopf R J 2012 Nature 482 382 Google Scholar
[69]	Kelly J, Barends R, Fowler A G, et al. 2015 Nature 519 66 Google Scholar
[70]	Cramer J, Kalb N, Rol M A, Hensen B, Blok M S, Markham M, Twitchen D J, Hanson R, Taminiau T H 2016 Nat. Commun. 7 1 Google Scholar
[71]	Takita M, Cross A W, Córcoles A D, Chow J M, Gambetta J M 2017 Phys. Rev. Lett. 119 180501 Google Scholar
[72]	Wootton J R, Loss D 2018 Phys. Rev. A 97 52313 Google Scholar
[73]	Chen Z, Satzinger K J, Atalaya J, et al. 2021 Nature 595 383 Google Scholar
[74]	Kitaev A Y 1997 Russ. Math Surv. 52 1191 Google Scholar
[75]	Bravyi S B, Kitaev A Y 1998 arXiv: quant-ph/9811052 [quant-ph]
[76]	Fowler A G, Mariantoni M, Martinis J M, Cleland A N 2012 Phys. Rev. A 86 32324 Google Scholar
[77]	Raussendorf R, Harrington J, Goyal K 2006 Ann. Phys. 321 2242 Google Scholar
[78]	Raussendorf R, Harrington J 2007 Phys. Rev. Lett. 98 190504 Google Scholar
[79]	Raussendorf R, Harrington J, Goyal K 2007 New J. Phys. 9 199 Google Scholar
[80]	Fowler A G, Whiteside A C, McInnes A L, Rabbani A 2012 Phys. Rev. X 2 41003 Google Scholar
[81]	Dennis E, Kitaev A, Landahl A, Preskill J 2002 J. Math. Phys. 43 4452 Google Scholar
[82]	Knill E 2005 Nature 434 39 Google Scholar
[83]	Zeng B, Chen X, Zhou D L, Wen X G 2019 Quantum Information Meets Quantum Matter (New York: Springer) pp3–361
[84]	Satzinger K J, Liu Y J, Smith A, Knapp C, Newman M, Jones C, Chen Z, Quintana C, Mi X, Dunsworth A, Others 2021 Science 374 1237 Google Scholar
[85]	Liu Y J, Shtengel K, Smith A, Pollmann F 2021 arXiv: 2110.02020 [quant-ph]
[86]	Horsman C, Fowler A G, Devitt S, Van Meter R 2012 New J. Phys. 14 123011 Google Scholar
[87]	Bonilla Ataides J P, Tuckett D K, Bartlett S D, Flammia S T, Brown B J 2021 Nat. Commun. 12 1 Google Scholar
[88]	Bombin H, Martin-Delgado M A 2006 Phys. Rev. Lett. 97 180501 Google Scholar
[89]	Fowler A G 2011 Phys. Rev. A 83 42310 Google Scholar
[90]	Willsch D, Willsch M, Jin F, De Raedt H, Michielsen K 2018 Phys. Rev. A 98 52348 Google Scholar
[91]	Harper R, Flammia S T 2019 Phys. Rev. Lett. 122 80504 Google Scholar
[92]	Gong M, Yuan X, Wang S, et al. 2022 Natl. Sci. Rev. 9 nwab011 Google Scholar
[93]	Andersen C K, Remm A, Lazar S, Krinner S, Lacroix N, Norris G J, Gabureac M, Eichler C, Wallraff A 2020 Nat. Phys. 16 875 Google Scholar
[94]	Krinner S, Lacroix N, Remm A, et al. 2021 arXiv: 2112.03708 [quant-ph]
[95]	Sundaresan N, Yoder T J, Kim Y, Li M, Chen E H, Harper G, Thorbeck T, Cross A W, Córcoles A D, Takita M 2022 arXiv: 2203.07205 [quant-ph]
[96]	Khaneja N, Reiss T, Kehlet C, Schulte-Herbrüggen T, Glaser S J 2005 J. Magn. Reson. 172 296 Google Scholar
[97]	De Fouquieres P, Schirmer S G, Glaser S J, Kuprov I 2011 J. Magn. Reson. 212 412 Google Scholar
[98]	Hu L, Ma Y, Cai W, et al. 2019 Nat. Phys. 15 503 Google Scholar
[99]	Gao Y Y, Lester B J, Chou K S, Frunzio L, Devoret M H, Jiang L, Girvin S M, Schoelkopf R J 2019 Nature 566 509 Google Scholar
[100]	Chou K S, Blumoff J Z, Wang C S, Reinhold P C, Axline C J, Gao Y Y, Frunzio L, Devoret M H, Jiang L, Schoelkopf R J 2018 Nature 561 368 Google Scholar
[101]	Ma Y, Xu Y, Mu X, et al. 2020 Nat. Phys. 16 827 Google Scholar
[102]	Li L, Zou C L, Albert V V, Muralidharan S, Girvin S M, Jiang L 2017 Phys. Rev. Lett. 119 30502 Google Scholar
[103]	Puri S, Boutin S, Blais A 2017 npj Quantum Inf. 3 1 Google Scholar
[104]	Bourassa J, Beaudoin F, Gambetta J M, Blais A 2012 Phys. Rev. A 86 13814 Google Scholar
[105]	Grimsmo A L, Combes J, Baragiola B Q 2020 Phys. Rev. X 10 11058 Google Scholar
[106]	Ofek N, Petrenko A, Heeres R, et al. 2016 Nature 536 441 Google Scholar
[107]	Heeres R W, Reinhold P, Ofek N, Frunzio L, Jiang L, Devoret M H, Schoelkopf R J 2017 Nat. Commun. 8 94 Google Scholar
[108]	Gertler J M, Baker B, Li J, Shirol S, Koch J, Wang C 2021 Nature 590 243 Google Scholar
[109]	Touzard S, Grimm A, Leghtas Z, et al. 2018 Phys. Rev. X 8 21005 Google Scholar
[110]	Lescanne R, Villiers M, Peronnin T, Sarlette A, Delbecq M, Huard B, Kontos T, Mirrahimi M, Leghtas Z 2020 Nat. Phys. 16 509 Google Scholar
[111]	Grimm A, Frattini N E, Puri S, Mundhada S O, Touzard S, Mirrahimi M, Girvin S M, Shankar S, Devoret M H 2020 Nature 584 205 Google Scholar
[112]	Albert V V, Noh K, Duivenvoorden K, et al. 2018 Phys. Rev. A 97 32346 Google Scholar
[113]	Noh K, Albert V V, Jiang L 2019 IEEE Trans. Inf. Theory 65 2563 Google Scholar
[114]	Flühmann C, Nguyen T L, Marinelli M, Negnevitsky V, Mehta K, Home J P 2019 Nature 566 513 Google Scholar
[115]	de Neeve B, Nguyen T L, Behrle T, Home J P 2022 Nat. Phys. 18 296 Google Scholar
[116]	Campagne-Ibarcq P, Eickbusch A, Touzard S, et al. 2020 Nature 584 368 Google Scholar
[117]	Terhal B M, Weigand D 2016 Phys. Rev. A 93 12315 Google Scholar
[118]	Royer B, Singh S, Girvin S M 2020 Phys. Rev. Lett. 125 260509 Google Scholar
[119]	Eastin B, Knill E 2009 Phys. Rev. Lett. 102 110502 Google Scholar
[120]	Gottesman D, Chuang I L 1999 Nature 402 390 Google Scholar
[121]	Zhou X, Leung D W, Chuang I L 2000 Phys. Rev. A 62 52316 Google Scholar
[122]	Bravyi S, Kitaev A 2005 Phys. Rev. A 71 22316 Google Scholar
[123]	Meier A M, Eastin B, Knill E 2012 arXiv: 1204.4221 [quant-ph]
[124]	Chamberland C, Cross A W 2019 Quantum 3 143 Google Scholar
[125]	Chamberland C, Jochym-O’Connor T, Laflamme R 2017 Phys. Rev. A 95 22313 Google Scholar
[126]	Campbell E T, Terhal B M, Vuillot C 2017 Nature 549 172 Google Scholar
[127]	Rosenblum S, Reinhold P, Mirrahimi M, Jiang L, Frunzio L, Schoelkopf R J 2018 Science 361 266 Google Scholar
[128]	Krastanov S, Albert V V, Shen C, Zou C L, Heeres R W, Vlastakis B, Schoelkopf R J, Jiang L 2015 Phys. Rev. A 92 40303 Google Scholar
[129]	Heeres R W, Vlastakis B, Holland E, Krastanov S, Albert V V, Frunzio L, Jiang L, Schoelkopf R J 2015 Phys. Rev. Lett. 115 137002 Google Scholar
[130]	Wang W, Hu L, Xu Y, Liu K, Ma Y, Zheng S B, Vijay R, Song Y P, Duan L M, Sun L 2017 Phys. Rev. Lett. 118 223604 Google Scholar
[131]	Lloyd S, Viola L 2001 Phys. Rev. A 65 10101 Google Scholar
[132]	Shen C, Noh K, Albert V V, Krastanov S, Devoret M H, Schoelkopf R J, Girvin S M, Jiang L 2017 Phys. Rev. B 95 134501 Google Scholar
[133]	Hu L, Mu X, Cai W, Ma Y, Xu Y, Wang H, Song Y, Zou C L, Sun L 2018 Sci. Bull. 63 1551 Google Scholar
[134]	Cai W, Han J, Hu L, et al. 2021 Phys. Rev. Lett. 127 90504 Google Scholar
[135]	Giovannetti V, Lloyd S, Maccone L 2011 Nat. Photonics 5 222 Google Scholar
[136]	Backes K M, Palken D A, Kenany S A, et al. 2021 Nature 590 238 Google Scholar
[137]	Wang W, Wu Y, Ma Y, Cai W, Hu L, Mu X, Xu Y, Chen Z J, Wang H, Song Y P, Yuan H, Zou C L, Duan L M, Sun L 2019 Nat. Commun. 10 4382 Google Scholar
[138]	Wang W, Chen Z J, Liu X, et al. 2022 Nat. Commun. 13 1 Google Scholar
[139]	Zhou S, Zhang M, Preskill J, Jiang L 2018 Nat. Commun. 9 1 Google Scholar
[140]	Górecki W, Zhou S, Jiang L, Demkowicz-Dobrzański R 2020 Quantum 4 288 Google Scholar
[141]	Pfaff W, Axline C J, Burkhart L D, Vool U, Reinhold P, Frunzio L, Jiang L, Devoret M H, Schoelkopf R J 2017 Nat. Phys. 13 882 Google Scholar
[142]	Muralidharan S, Li L, Kim J, Lütkenhaus N, Lukin M D, Jiang L 2016 Sci. Rep. 6 1 Google Scholar
[143]	Preskill J 2018 Quantum 2 79 Google Scholar
[144]	Endo S, Cai Z, Benjamin S C, Yuan X 2021 J. Phys. Soc. Jpn. 90 32001 Google Scholar
[145]	McArdle S, Yuan X, Benjamin S 2019 Phys. Rev. Lett. 122 180501 Google Scholar
[146]	Koh J M, Tai T, Lee C H 2022 arXiv: 2207.14322 [cond-mat.str-el]
[147]	Li Y, Benjamin S C 2016 Phys. Rev. A 94 42303 Google Scholar
[148]	Gottesman D 2016 arXiv: 1610.03507 [quant-ph]
[149]	Chao R, Reichardt B W 2018 Phys. Rev. Lett. 121 50502 Google Scholar
[150]	Ma W L, Zhang M, Wong Y, Noh K, Rosenblum S, Reinhold P, Schoelkopf R J, Jiang L 2020 Phys. Rev. Lett. 125 110503 Google Scholar
[151]	Jahn A, Eisert J 2021 Quantum Sci. Technol. 6 33002 Google Scholar
[152]	Almheiri A, Dong X, Harlow D 2015 J. High Energy Phys. 2015(4) 1 Google Scholar
[153]	Pastawski F, Yoshida B, Harlow D, Preskill J 2015 J. High Energy Phys. 2015(6) 1 Google Scholar
[154]	Vijay S, Haah J, Fu L 2016 Phys. Rev. B 94 235157 Google Scholar
[155]	Hong Y, Young J T, Kaufman A M, Lucas A 2022 arXiv: 2205.12998 [quant-ph]

[1]	邵凯花, 席忠红, 席保龙, 涂朴, 王青青, 马金萍, 赵茜, 石玉仁. 双组分玻色-爱因斯坦凝聚体中PT对称势下的异步量子Kármán涡街. , 2024, 73(11): 110501. doi: 10.7498/aps.73.20232003
[2]	高吉明, 狄国文, 鱼自发, 唐荣安, 徐红萍, 薛具奎. 人工磁场下各向异性偶极玻色气体的量子相变. , 2024, 73(13): 130503. doi: 10.7498/aps.73.20240376
[3]	王东升. 通用量子计算模型: 一个资源理论的视角. , 2024, 73(22): 220302. doi: 10.7498/aps.73.20240893
[4]	范桁. 量子计算纠错取得突破性进展. , 2023, 72(7): 070303. doi: 10.7498/aps.72.20230330
[5]	王美红, 郝树宏, 秦忠忠, 苏晓龙. 连续变量量子计算和量子纠错研究进展. , 2022, 71(16): 160305. doi: 10.7498/aps.71.20220635
[6]	董毕远, 徐志君. 多个子玻色-爱因斯坦凝聚气体膨胀叠加形成的量子涡旋现象研究. , 2018, 67(1): 010501. doi: 10.7498/aps.67.20171708
[7]	赵文静, 文灵华. 半无限深势阱中自旋相关玻色-爱因斯坦凝聚体的量子反射与干涉. , 2017, 66(23): 230301. doi: 10.7498/aps.66.230301
[8]	贺丽, 余增强. 自旋-轨道耦合作用下玻色-爱因斯坦凝聚在量子相变附近的朗道临界速度. , 2017, 66(22): 220301. doi: 10.7498/aps.66.220301
[9]	吴向艳, 徐艳玲, 於亚飞, 张智明. 利用非稳定子态容错实现密集旋转操作. , 2014, 63(22): 220304. doi: 10.7498/aps.63.220304
[10]	刘妮. 激光驱动下腔与玻色-爱因斯坦凝聚中的量子相变. , 2013, 62(1): 013402. doi: 10.7498/aps.62.013402
[11]	赵峰. 单向量子密钥纠错协议的纠错性能仿真分析. , 2013, 62(20): 200303. doi: 10.7498/aps.62.200303
[12]	赵文垒, 豆福全, 王建忠. 玻色-爱因斯坦凝聚体中非线性相互作用对量子共振棘流的影响. , 2012, 61(22): 220503. doi: 10.7498/aps.61.220503
[13]	王建忠, 曹辉, 豆福全. 玻色-爱因斯坦凝聚体Rosen-Zener跃迁中的多体量子涨落效应. , 2012, 61(22): 220305. doi: 10.7498/aps.61.220305
[14]	宋立军, 严冬, 刘烨. 玻色-爱因斯坦凝聚系统的量子Fisher信息与混沌. , 2011, 60(12): 120302. doi: 10.7498/aps.60.120302
[15]	李高清, 陈海军, 薛具奎. 一维双组分玻色-爱因斯坦凝聚体系的量子隧穿特性. , 2010, 59(3): 1449-1455. doi: 10.7498/aps.59.1449
[16]	王鹏军, 陈海霞, 熊德智, 于旭东, 高峰, 张靖. 实现玻色-费米混合气体量子简并的四极Ioffe组合磁阱设计. , 2008, 57(8): 4840-4845. doi: 10.7498/aps.57.4840
[17]	马云, 傅立斌, 杨志安, 刘杰. 玻色-爱因斯坦凝聚体自囚禁现象的动力学相变及其量子纠缠特性. , 2006, 55(11): 5623-5628. doi: 10.7498/aps.55.5623
[18]	张权, 张尔扬, 唐朝京. 基于无消相干子空间的量子避错码设计. , 2002, 51(8): 1675-1683. doi: 10.7498/aps.51.1675
[19]	王治国, 许伯威. Ashkin-Teller量子链的玻色化形式及其新的临界点. , 1997, 46(5): 841-845. doi: 10.7498/aps.46.841
[20]	刘文森, 马桂荣, 张九安, 梁九卿. 量子玻色流体中的压缩玻色子对数态. , 1997, 46(9): 1699-1709. doi: 10.7498/aps.46.1699

计量

文章访问数: 8449
PDF下载量: 371
被引次数: 0

姓名
邮箱
手机号码
标题
留言内容
验证码

搜索

留言板