-
流动超材料与变换流体动力学的发展丰富了人们对于流体流动控制的方法. 本文基于变换流体动力学, 耦合流动旋转与放大功能, 设计出了具有张量化黏度的流动旋聚器. 从数值模拟层面验证了旋聚器可在蠕动流状态下同时实现对流速的放大和旋转功能. 在旋聚器中心流域, 流体流速被放大, 呈现出文丘里效应; 在旋聚器外部区域, 流体流动状态不会因旋聚器的存在而受到干扰, 保持原有的流动状态. 除此之外, 本文发现并解释了空间坐标变换的非互易性所造成的旋转滞后现象的本质. 本文所研究内容扩展并优化了现有的流体流动聚集功能; 提出了文丘里效应相关应用的一种新途径; 为超材料的非互易坐标变换设计提供了新的思路.The development of hydrodynamics metamaterials and transformation hydrodynamics has enriched the methods of fluid flow control. In the proposed study, coupling flow rotation and amplification functions, hydrodynamic rotating concentrators with tensorized viscosity are designed based on transformation hydrodynamics. Through numerical simulations, we have demonstrated that the rotating concentrators can simultaneously magnify and rotate the velocity in creeping flows. In the central area of the rotating concentrators, the fluid velocity is amplified, exhibiting the venturi effect; in the external area of the rotating concentrators, the flow state is not interfered with due to the presence of the rotating concentrators, maintaining the original flow state. Additionally, we discover and explain the mechanisms of the rotational hysteresis phenomena that are caused by the nonreciprocity of spatial coordinate transformations. The proposed studies 1) extend and optimize the traditional flow concentrators, 2) raise new approaches for applications related to Venturi effects, and 3) shed light on the design of nonreciprocal coordinate transformations for metamaterials.
-
Keywords:
- Venturi effect /
- hydrodynamic rotating concentrator /
- nonreciprocity /
- transformation hydrodynamics
[1] Pendry J B, Schurig D, Smith D R 2006 Science 312 1780
Google Scholar
[2] Leonhardt U 2006 Science 312 1777
Google Scholar
[3] Li C, Liu X, Liu G C, Li F, Fang G Y 2011 Appl. Phys. Lett. 99 084104
Google Scholar
[4] Ergin T, Stenger N, Brenner P, Pendry J B, Wegener M 2010 Science 328 337
Google Scholar
[5] Leonhardt U, Tyc T 2009 Science 323 110
Google Scholar
[6] Zhang S, Xia C, Fang N 2011 Phys. Rev. Lett. 106 024301
Google Scholar
[7] Fang N, Xi D, Xu J, Ambati M, Srituravanich W, Sun C, Zhang X 2006 Nat. Mater. 5 452
Google Scholar
[8] Torrent D, Sánchez-Dehesa J 2008 New J. Phys. 10 063015
Google Scholar
[9] Cummer SA Schurig D 2007 New J. Phys. 9 45
Google Scholar
[10] 高东宝, 曾新吾 2012 61 184301
Google Scholar
Gao D B, Zeng X W 2012 Acta Phys. Sin. 61 184301
Google Scholar
[11] Fan C Z, Gao Y, Huang J P 2008 Appl. Phys. Lett. 92 251907
Google Scholar
[12] Guenneau S, Amra C, Veynante D 2012 Opt. Express 20 8207
Google Scholar
[13] Schittny R, Kadic M, Guenneau S, Wegener M 2013 Phys. Rev. Lett. 110 195901
Google Scholar
[14] 沈翔瀛, 黄吉平 2016 65 178103
Google Scholar
Sheng X Y, Huang J P 2016 Acta Phys. Sin. 65 178103
Google Scholar
[15] Yang S, Wang J, Dai G L, Yang F B, Huang J P 2021 Phys. Rep. 908 1
Google Scholar
[16] 夏舸, 杨立, 寇蔚, 杜永成 2017 66 104401
Google Scholar
Xia K, Yang L, Kou W, Du Y C 2017 Acta Phys. Sin. 66 104401
Google Scholar
[17] Hu R, Zhou S, Li Y, Lei D Y, Luo X B, Qiu C W 2018 Adv. Mater. 30 1707237
Google Scholar
[18] Shen X, Li Y, Jiang C R, Huang J P 2016 Phys. Rev. Lett. 117 055501
Google Scholar
[19] Xu L J, Huang J P 2020 Chin. Phys. Lett. 32 120501
[20] De de, E M, Nomura T, Schmalenberg P, Lee J S 2013 Appl. Phys. Lett. 103 063501
Google Scholar
[21] Urzhumov Y A, Smith D R 2011 Phys. Rev. Lett. 107 074501
Google Scholar
[22] Urzhumov Y A, Smith D R 2012 Phys. Rev. Lett. 86 056313
[23] Park J, Youn J R, Song Y S 2019 Phys. Rev. Lett. 123 074502
Google Scholar
[24] Wang B, Shi T M, Huang J P 2021 Appl. Therm. Eng. 190 116726
Google Scholar
[25] Park J, Song Y S 2020 J. Fluid Struct. 98 103136
Google Scholar
[26] Tay F, Zhang Y, Xu H, Goh H H, Luo Y, Zhang B L 2019 arXiv: 190807169
[27] Wang B, Shi T M, Xu L J, Dai G L, Huang J P 2021 Phys. Rev. Appl. 15 034014
Google Scholar
[28] Boyko E, Bacheva V, Eigenbrod M 2021 Phys. Rev. Lett. 126 184502
Google Scholar
[29] Ren F, Wang C, Tang H 2021 Phys. Fluids 33 093602
Google Scholar
[30] Park J, Youn J R, Song Y S 2019 Phys. Rev. Appl. 12 061002
Google Scholar
[31] Park J, Youn J R, Song Y S 2021 Extreme Mech. Lett. 42 101061
Google Scholar
[32] Wang W, Lin L, Ma J, Wang C, Cui J, Du C, Luo X 2008 Opt. Express 16 11431
Google Scholar
[33] Navau C, Prat-Camps J, Sanchez A 2012 Phys. Rev. Lett. 109 263903
Google Scholar
[34] Shen X Y, Li Y, Jiang C R, Ni Y S, Huang J P 2016 Appl. Phys. Lett. 109 031907
Google Scholar
[35] Li C Y, Xu L, Zhu L L, Zou S Y, Liu Q H, Wang Z Y, Chen H Y 2018 Phys. Rev. Lett. 121 104501
Google Scholar
[36] Wang H, Yao N Z, Wang B, Shi T M, Wang X S 2022 Appl. Therm. Eng. 206 118012
Google Scholar
[37] Kadic M, Bückmann T, Schittny R, Wegener M 2013 Rep. Prog. Phys. 76 126501
Google Scholar
[38] Hele-Shaw H S 1898 Nature 58 520
[39] Kundu P K, Cohen I M 2002 Fluid Mech.
[40] Bertotti G, Mayergoyz I D 2005 A. P.
[41] Bertotti G 1998 A. P.
-
图 1 文丘里效应旋聚器模型示意图 (a) 坐标变换; (b) 边界条件
Fig. 1. Schematic models of Venturi-effect rotating concentrators: (a) the coordinate transformation; (b) boundary conditions.
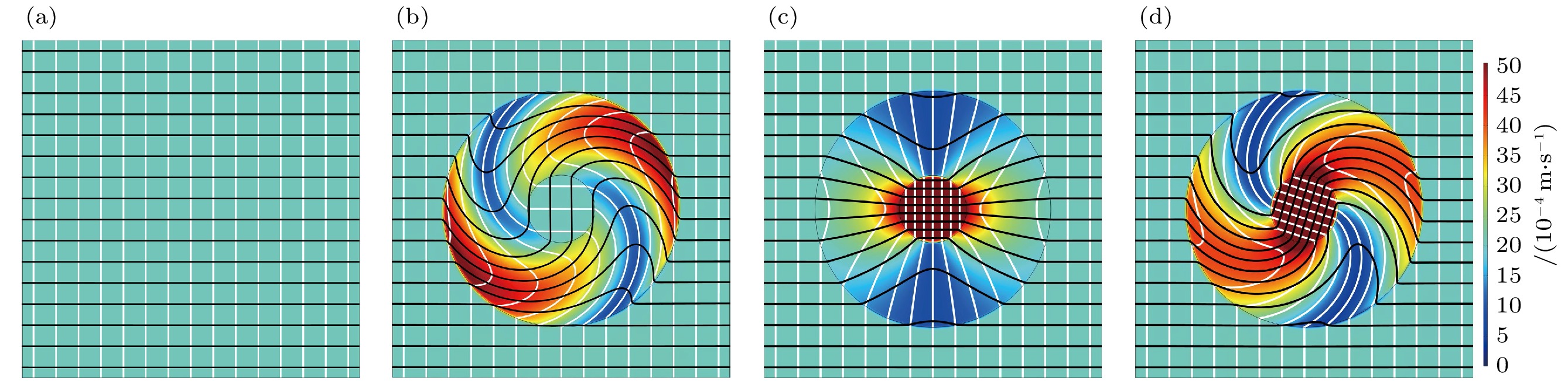
图 2 不同流动功能在均匀来流下的速度场分布, 其中黑色线条代表流线, 白色线条表示等压线 (a) 背景流场; (b) 流动旋转; (c) 流动聚集; (d) 流动旋转聚集
Fig. 2. Velocity distributions of different hydrodynamic meta-devices in uniform flow fields with streamlines (black color) and isobars (white color): (a) Background flow fields; (b) hydrodynamic rotators; (c) hydrodynamic concentrators; (d) Venturi-effect rotating concentrators
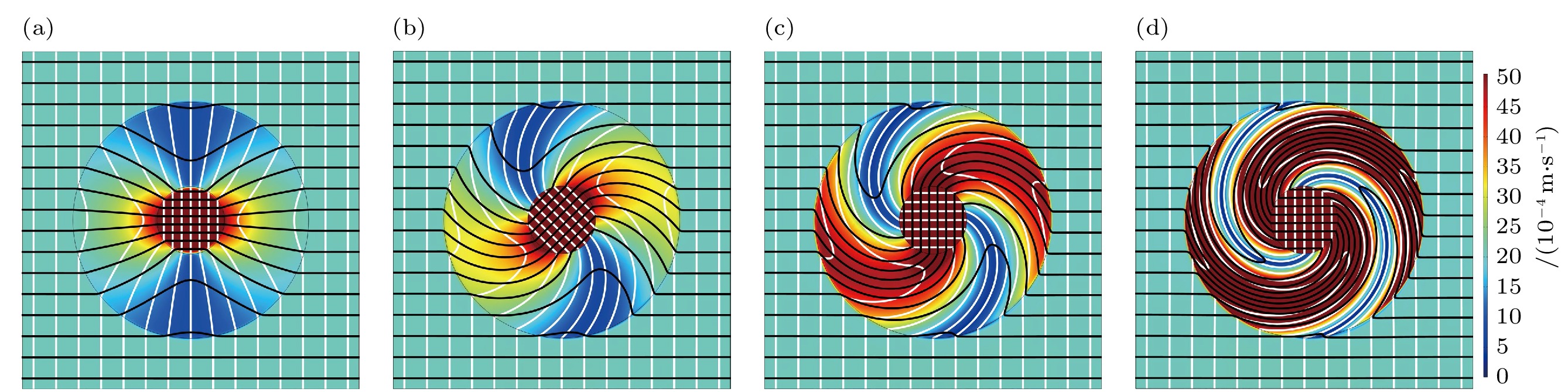
图 3 文丘里效应旋聚器在不同旋转角下的速度场分布, 其中黑色线条代表流线, 白色线条表示等压线 (a)
$ \theta_0 $ = 0 rad; (b)$ \theta_0 = \pi/4 $ rad; (c)$ \theta_0 = \pi/2 $ rad; (d)$ \theta_0 = \pi $ rad. 从图中可以看出, 在不同旋转角下, 流体在中心区域的旋转均出现滞后现象Fig. 3. Velocity distributions of Venturi-effect rotating concentrators at different predesigned rotation angles with streamlines (black color) and isobars (white color): (a)
$ \theta_0 $ = 0 rad; (b)$ \theta_0 = \pi/4 $ rad; (c)$ \theta_0 = \pi/2 $ rad; (d)$ \theta_0 = \pi $ rad. It can be seen that the rotation angles of the central region appear hysteresis at various predesigned rotation angles ($ \theta_0 $ )
图 4 文丘里效应旋聚器旋转角度无滞后时的速度场分布, 其中黑色线条代表流线, 白色线条表示等压线 (a)
$ \theta_0 $ = 0 rad; (b)$ \theta_0 = \pi/4 $ rad; (c)$ \theta_0 = \pi/2 $ rad; (d)$ \theta_0 = \pi $ radFig. 4. Velocity distributions of Venturi-effect rotating concentrators at rotation angles without hysteresis. The black lines represent streamlines and the white lines indicate isobars: (a)
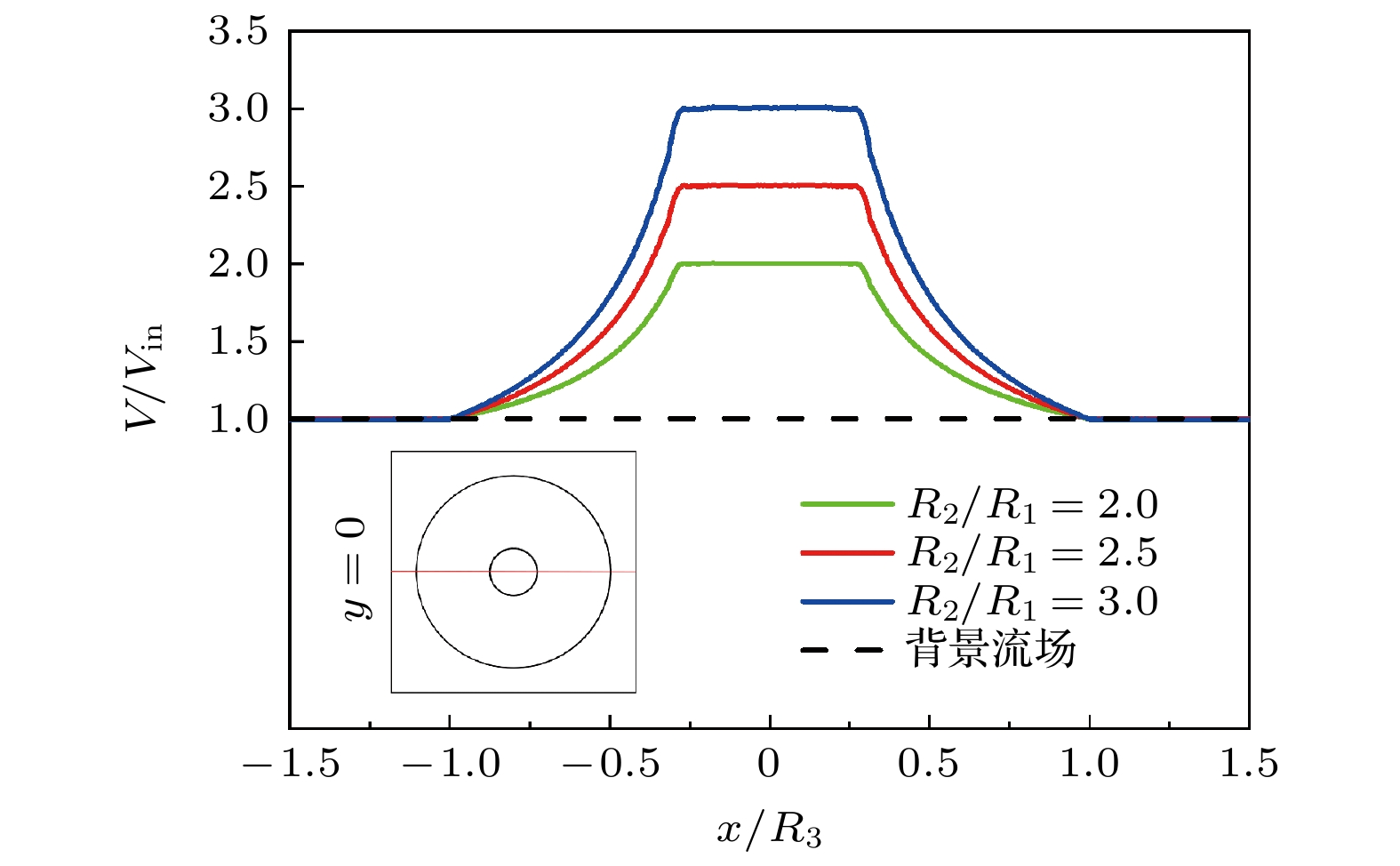
$ \theta_0 =0 $ rad; (b)$ \theta_0 = \pi/4 $ rad; (c)$ \theta_0 = \pi/2 $ rad; (d)$ \theta_0 = \pi $ rad
图 5 不同R2/R1情况下的文丘里效应旋聚器在
$ \theta_0 = 0 $ 时和y = 0处的速度分布Fig. 5. Velocity distributions of Venturi-effect rotating concentrators parameterized in R2/R1 at
$ \theta_0 = 0 $ and at the centerline y = 0.
图 6 文丘里效应旋聚器在非均匀来流下的流场分布图, 其中黑色线条代表流线, 白色线条表示等压线. (a) 背景流场; (b) θ0 = 0 rad; (c) θ0 = π/2 rad; (d) θ0 = π rad
Fig. 6. Velocity distributions of Venturi-effect rotating concentrators in non-uniform flow fields with streamlines (black color) and isobars (white color): (a) background flow fields; (b) θ0 = 0 rad; (c) θ0 = π/2 rad; (d) θ0 = π rad.
-
[1] Pendry J B, Schurig D, Smith D R 2006 Science 312 1780
Google Scholar
[2] Leonhardt U 2006 Science 312 1777
Google Scholar
[3] Li C, Liu X, Liu G C, Li F, Fang G Y 2011 Appl. Phys. Lett. 99 084104
Google Scholar
[4] Ergin T, Stenger N, Brenner P, Pendry J B, Wegener M 2010 Science 328 337
Google Scholar
[5] Leonhardt U, Tyc T 2009 Science 323 110
Google Scholar
[6] Zhang S, Xia C, Fang N 2011 Phys. Rev. Lett. 106 024301
Google Scholar
[7] Fang N, Xi D, Xu J, Ambati M, Srituravanich W, Sun C, Zhang X 2006 Nat. Mater. 5 452
Google Scholar
[8] Torrent D, Sánchez-Dehesa J 2008 New J. Phys. 10 063015
Google Scholar
[9] Cummer SA Schurig D 2007 New J. Phys. 9 45
Google Scholar
[10] 高东宝, 曾新吾 2012 61 184301
Google Scholar
Gao D B, Zeng X W 2012 Acta Phys. Sin. 61 184301
Google Scholar
[11] Fan C Z, Gao Y, Huang J P 2008 Appl. Phys. Lett. 92 251907
Google Scholar
[12] Guenneau S, Amra C, Veynante D 2012 Opt. Express 20 8207
Google Scholar
[13] Schittny R, Kadic M, Guenneau S, Wegener M 2013 Phys. Rev. Lett. 110 195901
Google Scholar
[14] 沈翔瀛, 黄吉平 2016 65 178103
Google Scholar
Sheng X Y, Huang J P 2016 Acta Phys. Sin. 65 178103
Google Scholar
[15] Yang S, Wang J, Dai G L, Yang F B, Huang J P 2021 Phys. Rep. 908 1
Google Scholar
[16] 夏舸, 杨立, 寇蔚, 杜永成 2017 66 104401
Google Scholar
Xia K, Yang L, Kou W, Du Y C 2017 Acta Phys. Sin. 66 104401
Google Scholar
[17] Hu R, Zhou S, Li Y, Lei D Y, Luo X B, Qiu C W 2018 Adv. Mater. 30 1707237
Google Scholar
[18] Shen X, Li Y, Jiang C R, Huang J P 2016 Phys. Rev. Lett. 117 055501
Google Scholar
[19] Xu L J, Huang J P 2020 Chin. Phys. Lett. 32 120501
[20] De de, E M, Nomura T, Schmalenberg P, Lee J S 2013 Appl. Phys. Lett. 103 063501
Google Scholar
[21] Urzhumov Y A, Smith D R 2011 Phys. Rev. Lett. 107 074501
Google Scholar
[22] Urzhumov Y A, Smith D R 2012 Phys. Rev. Lett. 86 056313
[23] Park J, Youn J R, Song Y S 2019 Phys. Rev. Lett. 123 074502
Google Scholar
[24] Wang B, Shi T M, Huang J P 2021 Appl. Therm. Eng. 190 116726
Google Scholar
[25] Park J, Song Y S 2020 J. Fluid Struct. 98 103136
Google Scholar
[26] Tay F, Zhang Y, Xu H, Goh H H, Luo Y, Zhang B L 2019 arXiv: 190807169
[27] Wang B, Shi T M, Xu L J, Dai G L, Huang J P 2021 Phys. Rev. Appl. 15 034014
Google Scholar
[28] Boyko E, Bacheva V, Eigenbrod M 2021 Phys. Rev. Lett. 126 184502
Google Scholar
[29] Ren F, Wang C, Tang H 2021 Phys. Fluids 33 093602
Google Scholar
[30] Park J, Youn J R, Song Y S 2019 Phys. Rev. Appl. 12 061002
Google Scholar
[31] Park J, Youn J R, Song Y S 2021 Extreme Mech. Lett. 42 101061
Google Scholar
[32] Wang W, Lin L, Ma J, Wang C, Cui J, Du C, Luo X 2008 Opt. Express 16 11431
Google Scholar
[33] Navau C, Prat-Camps J, Sanchez A 2012 Phys. Rev. Lett. 109 263903
Google Scholar
[34] Shen X Y, Li Y, Jiang C R, Ni Y S, Huang J P 2016 Appl. Phys. Lett. 109 031907
Google Scholar
[35] Li C Y, Xu L, Zhu L L, Zou S Y, Liu Q H, Wang Z Y, Chen H Y 2018 Phys. Rev. Lett. 121 104501
Google Scholar
[36] Wang H, Yao N Z, Wang B, Shi T M, Wang X S 2022 Appl. Therm. Eng. 206 118012
Google Scholar
[37] Kadic M, Bückmann T, Schittny R, Wegener M 2013 Rep. Prog. Phys. 76 126501
Google Scholar
[38] Hele-Shaw H S 1898 Nature 58 520
[39] Kundu P K, Cohen I M 2002 Fluid Mech.
[40] Bertotti G, Mayergoyz I D 2005 A. P.
[41] Bertotti G 1998 A. P.
下载:
计量
- 文章访问数: 3903
- PDF下载量: 60
- 被引次数: 0
