基于准简谐格林-久保理论结合流体动力学外推方法的非晶二氧化铪导热机制研究

朱雄飞; 孙健时; 熊玉成; 李寿航; 刘向军

doi:10.7498/aps.74.20250350

摘要

非晶态材料二氧化铪在微电子器件中具有广泛应用, 理解其微观导热机制对于提升电子器件的性能和可靠性至关重要. 以往的研究大多基于分子动力学和单一准简谐格林-久保方法, 难以准确考虑低频振动模式的导热贡献. 本文基于准简谐格林-久保理论, 结合流体动力学外推法, 对不同有序度的非晶二氧化铪结构的热输运机制进行全面研究. 该方法可有效克服单一准简谐格林-久保方法中的有限尺寸问题. 理论预测表明, 非晶二氧化铪的热导率与微观结构有序度呈现弱相关性. 基于模态分析表明, 中低频振动模式对热导率具有显著贡献, 是单一准简谐格林-久保方法低估非晶二氧化铪热导率的主要原因. 同时, 本文基于非谐动态结构因子分离了传播子和扩散子对非晶二氧化铪导热的贡献, 计算表明扩散子在所有非晶二氧化铪结构导热中均占据主导作用. 然而, 传播子的导热贡献仍不可忽略, 其占比可高达20%以上, 且随着有序度的增大而增大.

关键词:

Abstract

Amorphous hafnia (a-HfO₂) has attracted considerable attention due to its excellent dielectric properties and broad applicability in the electronic industry. Considering that the self-heating is becoming the bottleneck for the performance and reliability of microelectronic devices, it is necessary to clarify the thermal transport mechanism in a-HfO₂. The microstructures of a-HfO₂ can be significantly changed during the fabrication process, whose effects on thermal transport remain to be revealed. Here, we conduct a comprehensive investigation of thermal transport in a-HfO₂ based on the quasi-harmonic Green-Kubo (QHGK) theory combined with hydrodynamic extrapolation. The calculation scheme fully considers the contributions from low-frequency vibrational modes, overcoming the drawbacks of finite size in the single QHGK method and molecular dynamics simulation. It is found that the thermal conductivity (κ) of a-HfO₂ is weakly related to its degree of order. The amorphous structures with slower quenching speed and higher degree of order have higher thermal conductivities due to their slightly larger relaxation times. Modal analyses show that the mid- and low-frequency vibrational modes have significant contributions to thermal transport in a-HfO₂, which is the main reason for the underestimation of the κ in other methods. Based on the anharmonic dynamic structure factor, we further separate the contributions of two fundamental heat carriers in amorphous materials: propagons and diffusons. It is found that diffusons dominate the κ in all a-HfO₂ structures. Nevertheless, the contribution of the propagons is non-negligible, accounting for more than 20% and increasing with the degree of structural ordering. This study provides new insights into the microscopic mechanisms and guidance for manipulating thermal transport in a-HfO₂.

Keywords:

作者及机构信息

1.
东华大学机械工程学院, 微纳机电系统与集成电路研究所, 上海　201620

2.
巴黎萨克雷大学, 法国国家科学研究中心, 纳米科学与纳米技术中心, 帕莱索 91120, 法国

通信作者: 李寿航, shouhang.li@universite-paris-saclay.fr ; 刘向军, xjliu@dhu.edu.cn

基金项目: 国家自然科学基金(批准号: 12304039, 52150610495, 12374027)、上海市自然科学基金(批准号: 22YF1400100, 21TS1401500)和中央高校基本科研业务费(批准号: 2232022D-22, CUSF-DH-T-2024061)资助的课题.

Authors and contacts

1.
Institute of Micro/Nano Electromechanical System and Integrated Circuit, College of Mechanical Engineering, Donghua University, Shanghai 201620, China

2.
Centre de Nanosciences et de Nanotechnologies, CNRS, Université Paris-Saclay, 10 Boulevard Thomas Gobert, Palaiseau 91120, France

Corresponding author: LI Shouhang, shouhang.li@universite-paris-saclay.fr ; LIU Xiangjun, xjliu@dhu.edu.cn

Funds: Project supported by the National Natural Science Foundation of China (Grant Nos. 12304039, 52150610495, 12374027), the Natural Science Foundation of Shanghai, China (Grant Nos. 22YF1400100, 21TS1401500), and the Fundamental Research Funds for the Central Universities of Ministry of Education of China (Grant Nos. 2232022D-22, CUSF-DH-T-2024061).

文章全文

参考文献

[1]	Wilk G D, Wallace R M, Anthony J 2001 J. Appl. Phys. 89 5243 Google Scholar
[2]	Chen J H, Liang M F, Song Y, Yuan J J, Zhang M Y, Luo Y M, Wang N N 2024 Chin. Phys. B 33 047503 Google Scholar
[3]	Wang Y, Zahid F, Wang J, Guo H 2012 Phys. Rev. B 85 224110 Google Scholar
[4]	董典萌, 汪成, 张清怡, 张涛, 杨永涛, 夏翰驰, 王月晖, 吴真平 2023 72 097302 Google Scholar Dong D M, Wang C, Zhang Q Y, Zhang T, Yang Y T, Xia H C, Wang Y H, Wu Z P 2023 Acta. Phys. Sin. 72 097302 Google Scholar
[5]	Gao R, Liu C, Shi B, Li Y, Luo B, Chen R, Ouyang W, Gao H, Hu S, Wang Y 2024 Chin. Phys. Lett. 41 087701 Google Scholar
[6]	Chen S, Chen M, Liu Y, Cao D, Chen G 2024 Chin. Phys. B 33 098701 Google Scholar
[7]	McKenna K, Shluger A, Iglesias V, Porti M, Nafría M, Lanza M, Bersuker G 2011 Microelectron. Eng. 88 1272 Google Scholar
[8]	袁国亮, 王琛皓, 唐文彬, 张睿, 陆旭兵 2023 72 097703 Google Scholar Yuan G L, Wang C H, Tang W B, Zhang R, Lu X B 2023 Acta. Phys. Sin. 72 097703 Google Scholar
[9]	Liu K, Liu K, Zhang X, Fang J, Jin F, Wu W, Ma C, Wang L 2024 Chin. Phys. Lett. 41 117701 Google Scholar
[10]	Scott E A, Gaskins J T, King S W, Hopkins P E 2018 APL Mater. 6 058302 Google Scholar
[11]	Lu S X, Cebe P 1996 Polymer 37 4857 Google Scholar
[12]	何宇亮, 周衡南, 刘湘娜, 程光煦 1990 39 1796 Google Scholar He Y L, Zhou H N, Liu X N, Cheng G X, Yu S D 1990 Acta Phys. Sin. 39 1796 Google Scholar
[13]	Wang S, Wang C, Li M, Huang L, Ott R, Kramer M, Sordelet D, Ho K 2008 Phys. Rev. B 78 184204 Google Scholar
[14]	Wang Y, Fan Z, Qian P, Caro M A, Ala-Nissila T 2023 Phys. Rev. B 107 054303 Google Scholar
[15]	林揆训, 林璇英, 梁厚蕴, 池凌飞, 余楚迎, 黄创君 2002 51 863 Google Scholar Lin K X, Lin X Y, Liang H Y, Chi L F, Yu C Y, Huang C J 2002 Acta. Phys. Sin. 51 863 Google Scholar
[16]	Kittel C 1949 Phys. Rev. 75 972 Google Scholar
[17]	Allen P B, Feldman J L 1989 Phys. Rev. Lett. 62 645 Google Scholar
[18]	Zhu X, Shao C 2022 Phys. Rev. B 106 014305 Google Scholar
[19]	Qiu R, Zeng Q Y, Han J S, Chen K, Kang D D, Yu X X, Dai J Y 2025 Phys. Rev. B 111 064103 Google Scholar
[20]	Luo T, Lloyd J R 2012 Adv. Funct. Mater. 22 2495 Google Scholar
[21]	Li S H, Yu X X, Bao H, Yang N 2018 J. Phys. Chem. C 122 13140 Google Scholar
[22]	Xi Q, Zhong J, He J, Xu X, Nakayama T, Wang Y, Liu J, Zhou J, Li B 2020 Chin. Phys. Lett. 37 104401 Google Scholar
[23]	Prasai K, Biswas P, Drabold D 2016 Semicond. Sci. Techn. 31 073002 Google Scholar
[24]	朱美芳 1996 45 499 Google Scholar Zhu M F 1996 Acta Phys. Sin. 45 499 Google Scholar
[25]	Mu X, Wu X, Zhang T, Go D B, Luo T 2014 Sci. Rep. 4 3909 Google Scholar
[26]	王学智, 汤雨婷, 车军伟, 令狐佳珺, 侯兆阳 2023 72 056101 Google Scholar Wang X Z, Tang Y T, Che J W, Linghu J J, Hou Z Y 2023 Acta Physica Sinica 72 056101 Google Scholar
[27]	Yang F H, Zeng Q Y, Chen B, Kang D D, Zhang S, Wu J H, Yu X X, Dai J Y 2022 Chin. Phys. Lett. 39 116301 Google Scholar
[28]	鲍华 2013 62 1 Google Scholar Bao H 2013 Acta Phys. Sin. 62 1 Google Scholar
[29]	Qiu R, Zeng Q Y, Wang H, Kang D D, Yu X X, Dai J Y 2023 Chin. Phys. Lett. 40 116301 Google Scholar
[30]	Isaeva L, Barbalinardo G, Donadio D, Baroni S 2019 Nat. Commun. 10 3853 Google Scholar
[31]	Simoncelli M, Marzari N, Mauri F 2019 Nat. Phys. 15 809 Google Scholar
[32]	Harper A F, Iwanowski K, Witt W C, Payne M C, Simoncelli M 2024 Phys. Rev. Mater. 8 043601 Google Scholar
[33]	Fiorentino A, Pegolo P, Baroni S 2023 npj Comput. Mater. 9 157 Google Scholar
[34]	Barbalinardo G, Chen Z, Lundgren N W, Donadio D 2020 J. Appl. Phys. 128 135104 Google Scholar
[35]	Fan Z Y, Wang Y Z, Ying P H, Song K K, Wang J J, Wang Y, Zeng Z Z, Xu K, Lindgren E, Rahm J M, Gabourie A J, Liu J H, Dong H K, Wu J Y, Chen Y, Zhong Z, Sun J, Erhart P, Su Y J, Ala-Nissila T 2022 J. Chem. Phys. 157 114801 Google Scholar
[36]	Fan Z Y, Zeng Z Z, Zhang C Z, Wang Y Z, Song K K, Dong H K, Chen Y, Ala-Nissila T 2021 Phys. Rev. B 104 104309 Google Scholar
[37]	Zhang H, Gu X, Fan Z, Bao H 2023 Phys. Rev. B 108 045422 Google Scholar
[38]	Sivaraman G, Krishnamoorthy A N, Baur M, Holm C, Stan M, Csányi G, Benmore C, Vázquez-Mayagoitia Á 2020 npj Comput. Mater. 6 104 Google Scholar
[39]	Plimpton S 1995 J. Comput. Phys. 117 1 Google Scholar
[40]	Zeng Q Y, Yu X X, Yao Y P, Gao T Y, Chen B, Zhang S, Kang D D, Wang H, Dai J Y 2021 Phys. Rev. Res. 3 033116 Google Scholar
[41]	Franzblau D 1991 Phys. Rev. B 44 4925 Google Scholar
[42]	Le Roux S, Petkov V 2010 J. Appl. Crystallogr. 43 181 Google Scholar
[43]	Xiang X, Fan H, Zhou Y G 2024 J. Appl. Phys. 135 125102 Google Scholar
[44]	Zhang S L, Yi S L, Yang J Y, Liu J, Liu L H 2023 Int. J. Heat Mass Tran. 207 123971 Google Scholar
[45]	Panzer M A, Shandalov M, Rowlette J A, Oshima Y, Chen Y W, McIntyre P C, Goodson K E 2009 IEEE Electron Dev. Lett. 30 1269 Google Scholar
[46]	Lee S M, Cahill D G, Allen T H 1995 Phys. Rev. B 52 253 Google Scholar
[47]	Chaubey G S, Yao Y, Makongo J P, Sahoo P, Misra D, Poudeu P F, Wiley J B 2012 RSC Adv. 2 9207 Google Scholar
[48]	Tritt T M 2005 Thermal Conductivity: Theory, Properties, and Applications (Springer Science & Business Media
[49]	Shenogin S, Bodapati A, Keblinski P, McGaughey A J 2009 J. Appl. Phys. 105 034906 Google Scholar
[50]	Seyf H R, Henry A 2016 J. Appl. Phys. 120 025101 Google Scholar

施引文献

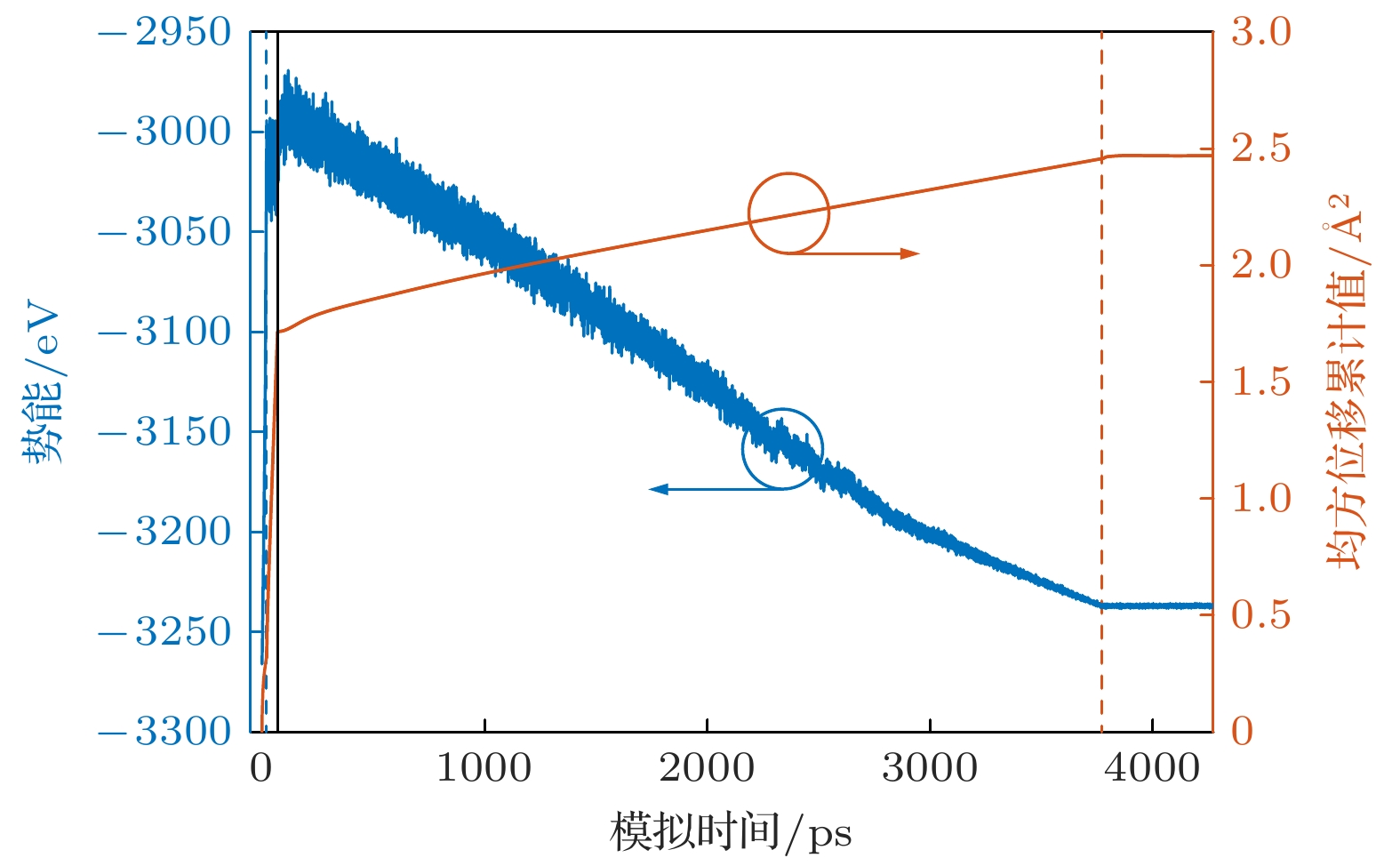
图 1 生成非晶结构过程中势能和均方位移累计值随模拟时间的变化, 图中灰色虚线之前为熔融过程, 灰色虚线与黑色实线之间为在温度4000 K下的弛豫过程, 红色点划线之后为退火过程

Fig. 1. Variation of potential energy and accumulated mean square displacement with simulation time during the generation of amorphous structures, the melting process is before the gray dashed line, the relaxation process at 4000 K is between the gray dashed line and the black solid line, and the annealing process is after the red dotted line.

下载: 全尺寸图片幻灯片

图 2 非晶HfO₂在不同淬火速度下的(a)径向分布函数和(b)环数分布

Fig. 2. (a) Radial distribution function and (b) ring distribution of amorphous HfO₂ at different quenching rates.

下载: 全尺寸图片幻灯片

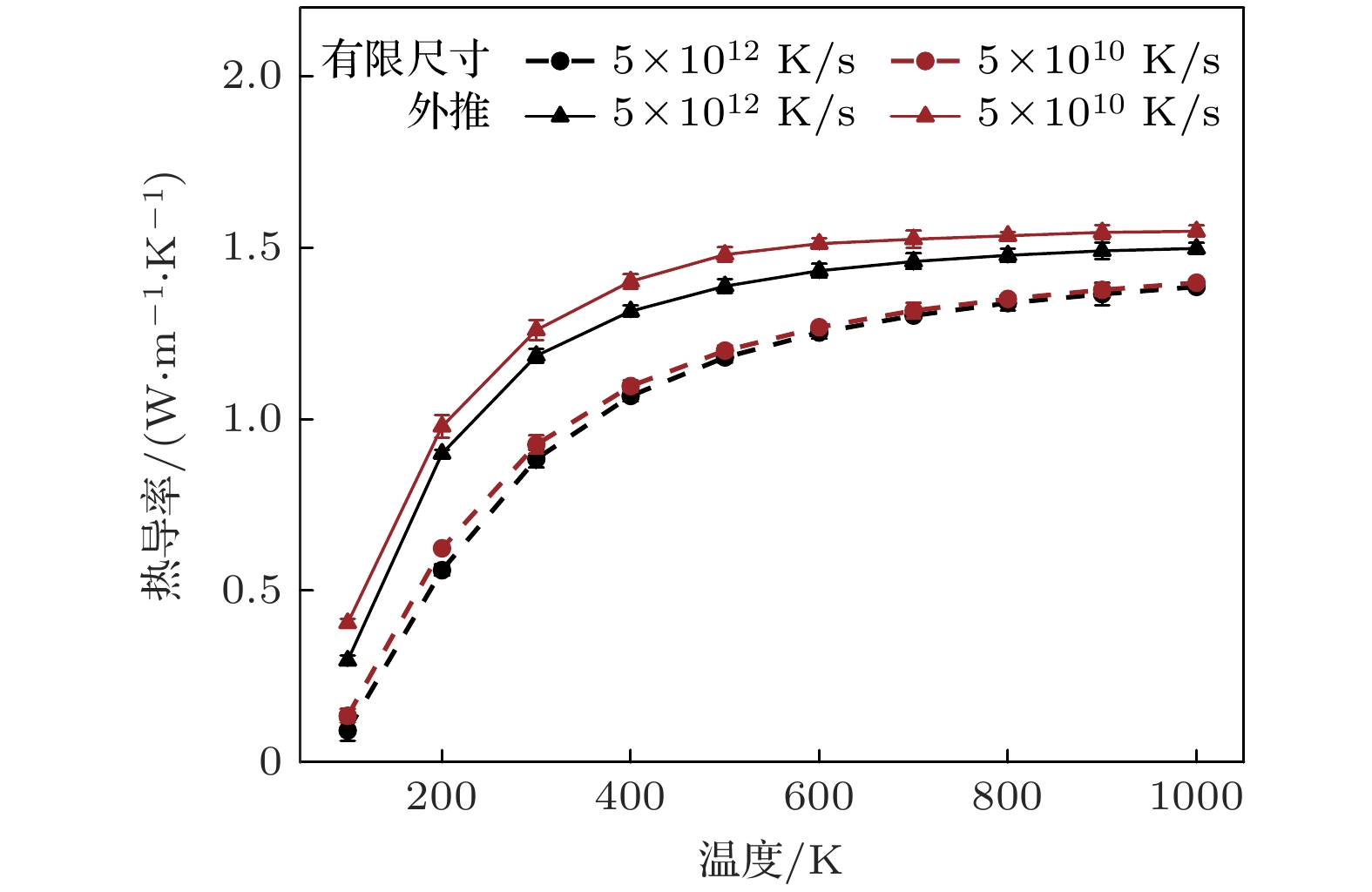
图 3 有限尺寸(2592个原子)和流体动力学外推法的非晶HfO₂随温度变化的热导率, 图中图例的数值表示淬火速度, 误差棒为热导率标准差

Fig. 3. Thermal conductivity of amorphous HfO₂ with temperature for finite size (2592 atoms) and the hydrodynamic extrapolation. The values of the legend denote the quenching rate, error bar is standard deviations of thermal conductivity.

下载: 全尺寸图片幻灯片

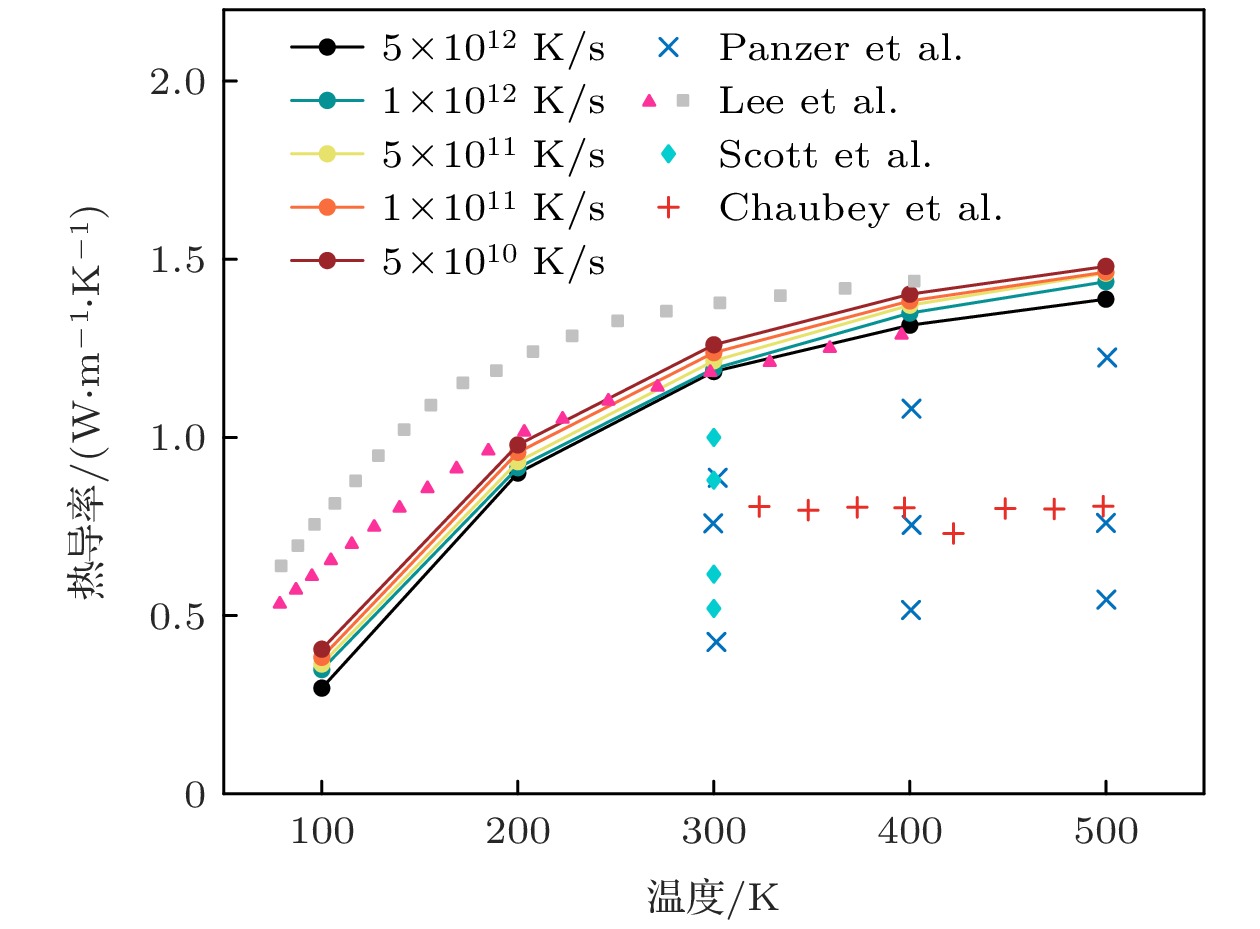
图 4 非晶HfO₂热导率随温度变化关系, 图中散点是Panzer等^[45]、Lee等^[46]、Scott等^[10]和Chaubey等^[47]报道的非晶HfO₂实验数据

Fig. 4. Temperature-dependent thermal conductivity of amorphous HfO₂, scattered points in the figure are experimental data for amorphous HfO₂ reported by Panzer et al.^[45], Lee et al.^[46], Scott et al.^[10] and Chaubey et al.^[47].

下载: 全尺寸图片幻灯片

图 5 300 K温度下不同淬火速度非晶HfO₂　(a) 热容量; (b) 弛豫时间; (c) 模态扩散率; (d) 参与比

Fig. 5. (a) Heat capacity; (b) lifetime; (c) modal diffusivity; (d) participation ratio of amorphous HfO₂ with different quenching rates at 300 K.

下载: 全尺寸图片幻灯片

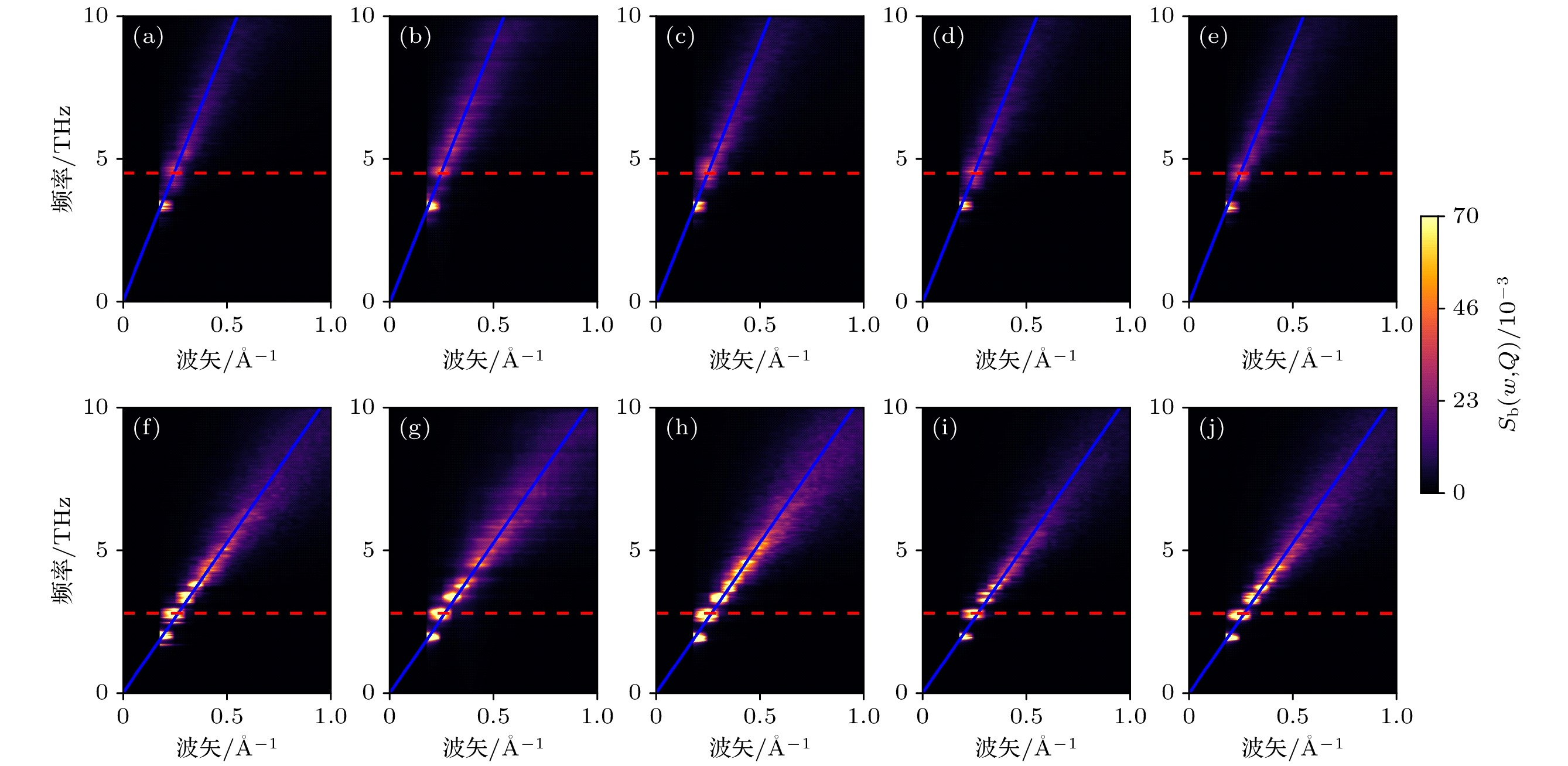
图 6 (a)—(e) 淬火速度分别为5×10¹², 1×10¹², 5×10¹¹, 1×10¹¹, 5×10¹⁰ K/s的非晶HfO₂的纵向非谐动态结构因子; (f)—(j) 为对应淬火速度下的横向非谐动态结构因子; 图中颜色条是根据(8)式计算的非谐动态结构因子强度, 蓝色直线是非谐动态结构因子在低频部分的线性拟合, 红色虚线是选取的截止频率

Fig. 6. (a)–(e) Longitudinal anharmonic dynamic structure factors of amorphous HfO₂ with different quenching rates of 5×10¹², 1×10¹², 5×10¹¹, 1×10¹¹, and 5×10¹⁰ K/s; (f)–(j) transverse anharmonic dynamic structure factors at corresponding quenching rates. The colorbar indicates the strength of the anharmonic dynamic structure factor calculated by Eq. (8), the blue straight line is a linear fit of the anharmonic dynamic structure factor in the low frequency part, and the red dashed line is the selected cut-off frequency.

下载: 全尺寸图片幻灯片

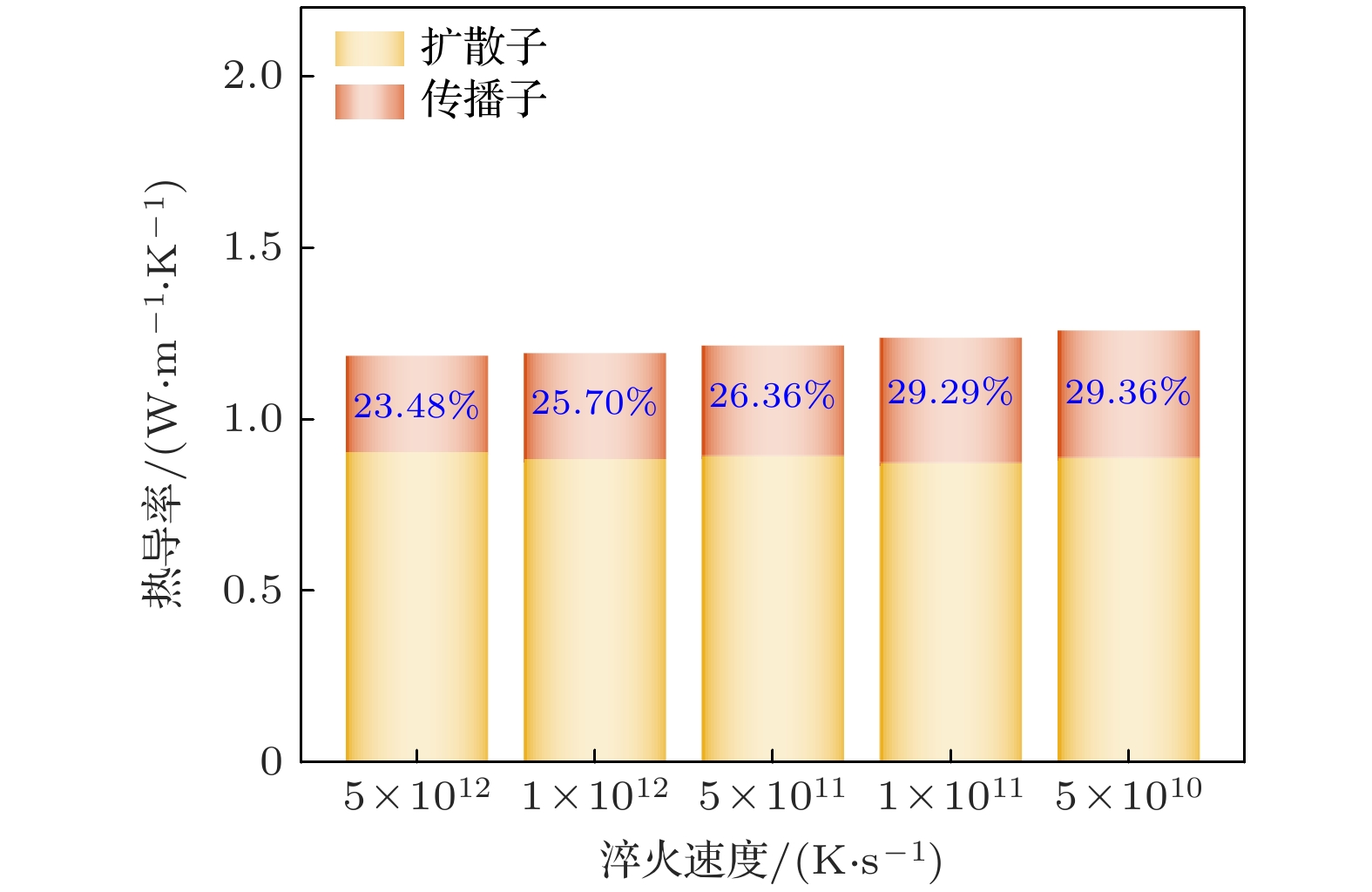
图 7 300 K温度下不同淬火速度非晶HfO₂的传播子和扩散子对热导率的贡献, 图中的蓝色文字代表传播子对总热导率的贡献百分比

Fig. 7. Contributions of propagon and diffuson to thermal conductivity of amorphous HfO₂ with different quenching rates at 300 K, the blue text in the figure represents the percentage contribution of propagon to the total thermal conductivity.

下载: 全尺寸图片幻灯片

map

[1]	Wilk G D, Wallace R M, Anthony J 2001 J. Appl. Phys. 89 5243 Google Scholar
[2]	Chen J H, Liang M F, Song Y, Yuan J J, Zhang M Y, Luo Y M, Wang N N 2024 Chin. Phys. B 33 047503 Google Scholar
[3]	Wang Y, Zahid F, Wang J, Guo H 2012 Phys. Rev. B 85 224110 Google Scholar
[4]	董典萌, 汪成, 张清怡, 张涛, 杨永涛, 夏翰驰, 王月晖, 吴真平 2023 72 097302 Google Scholar Dong D M, Wang C, Zhang Q Y, Zhang T, Yang Y T, Xia H C, Wang Y H, Wu Z P 2023 Acta. Phys. Sin. 72 097302 Google Scholar
[5]	Gao R, Liu C, Shi B, Li Y, Luo B, Chen R, Ouyang W, Gao H, Hu S, Wang Y 2024 Chin. Phys. Lett. 41 087701 Google Scholar
[6]	Chen S, Chen M, Liu Y, Cao D, Chen G 2024 Chin. Phys. B 33 098701 Google Scholar
[7]	McKenna K, Shluger A, Iglesias V, Porti M, Nafría M, Lanza M, Bersuker G 2011 Microelectron. Eng. 88 1272 Google Scholar
[8]	袁国亮, 王琛皓, 唐文彬, 张睿, 陆旭兵 2023 72 097703 Google Scholar Yuan G L, Wang C H, Tang W B, Zhang R, Lu X B 2023 Acta. Phys. Sin. 72 097703 Google Scholar
[9]	Liu K, Liu K, Zhang X, Fang J, Jin F, Wu W, Ma C, Wang L 2024 Chin. Phys. Lett. 41 117701 Google Scholar
[10]	Scott E A, Gaskins J T, King S W, Hopkins P E 2018 APL Mater. 6 058302 Google Scholar
[11]	Lu S X, Cebe P 1996 Polymer 37 4857 Google Scholar
[12]	何宇亮, 周衡南, 刘湘娜, 程光煦 1990 39 1796 Google Scholar He Y L, Zhou H N, Liu X N, Cheng G X, Yu S D 1990 Acta Phys. Sin. 39 1796 Google Scholar
[13]	Wang S, Wang C, Li M, Huang L, Ott R, Kramer M, Sordelet D, Ho K 2008 Phys. Rev. B 78 184204 Google Scholar
[14]	Wang Y, Fan Z, Qian P, Caro M A, Ala-Nissila T 2023 Phys. Rev. B 107 054303 Google Scholar
[15]	林揆训, 林璇英, 梁厚蕴, 池凌飞, 余楚迎, 黄创君 2002 51 863 Google Scholar Lin K X, Lin X Y, Liang H Y, Chi L F, Yu C Y, Huang C J 2002 Acta. Phys. Sin. 51 863 Google Scholar
[16]	Kittel C 1949 Phys. Rev. 75 972 Google Scholar
[17]	Allen P B, Feldman J L 1989 Phys. Rev. Lett. 62 645 Google Scholar
[18]	Zhu X, Shao C 2022 Phys. Rev. B 106 014305 Google Scholar
[19]	Qiu R, Zeng Q Y, Han J S, Chen K, Kang D D, Yu X X, Dai J Y 2025 Phys. Rev. B 111 064103 Google Scholar
[20]	Luo T, Lloyd J R 2012 Adv. Funct. Mater. 22 2495 Google Scholar
[21]	Li S H, Yu X X, Bao H, Yang N 2018 J. Phys. Chem. C 122 13140 Google Scholar
[22]	Xi Q, Zhong J, He J, Xu X, Nakayama T, Wang Y, Liu J, Zhou J, Li B 2020 Chin. Phys. Lett. 37 104401 Google Scholar
[23]	Prasai K, Biswas P, Drabold D 2016 Semicond. Sci. Techn. 31 073002 Google Scholar
[24]	朱美芳 1996 45 499 Google Scholar Zhu M F 1996 Acta Phys. Sin. 45 499 Google Scholar
[25]	Mu X, Wu X, Zhang T, Go D B, Luo T 2014 Sci. Rep. 4 3909 Google Scholar
[26]	王学智, 汤雨婷, 车军伟, 令狐佳珺, 侯兆阳 2023 72 056101 Google Scholar Wang X Z, Tang Y T, Che J W, Linghu J J, Hou Z Y 2023 Acta Physica Sinica 72 056101 Google Scholar
[27]	Yang F H, Zeng Q Y, Chen B, Kang D D, Zhang S, Wu J H, Yu X X, Dai J Y 2022 Chin. Phys. Lett. 39 116301 Google Scholar
[28]	鲍华 2013 62 1 Google Scholar Bao H 2013 Acta Phys. Sin. 62 1 Google Scholar
[29]	Qiu R, Zeng Q Y, Wang H, Kang D D, Yu X X, Dai J Y 2023 Chin. Phys. Lett. 40 116301 Google Scholar
[30]	Isaeva L, Barbalinardo G, Donadio D, Baroni S 2019 Nat. Commun. 10 3853 Google Scholar
[31]	Simoncelli M, Marzari N, Mauri F 2019 Nat. Phys. 15 809 Google Scholar
[32]	Harper A F, Iwanowski K, Witt W C, Payne M C, Simoncelli M 2024 Phys. Rev. Mater. 8 043601 Google Scholar
[33]	Fiorentino A, Pegolo P, Baroni S 2023 npj Comput. Mater. 9 157 Google Scholar
[34]	Barbalinardo G, Chen Z, Lundgren N W, Donadio D 2020 J. Appl. Phys. 128 135104 Google Scholar
[35]	Fan Z Y, Wang Y Z, Ying P H, Song K K, Wang J J, Wang Y, Zeng Z Z, Xu K, Lindgren E, Rahm J M, Gabourie A J, Liu J H, Dong H K, Wu J Y, Chen Y, Zhong Z, Sun J, Erhart P, Su Y J, Ala-Nissila T 2022 J. Chem. Phys. 157 114801 Google Scholar
[36]	Fan Z Y, Zeng Z Z, Zhang C Z, Wang Y Z, Song K K, Dong H K, Chen Y, Ala-Nissila T 2021 Phys. Rev. B 104 104309 Google Scholar
[37]	Zhang H, Gu X, Fan Z, Bao H 2023 Phys. Rev. B 108 045422 Google Scholar
[38]	Sivaraman G, Krishnamoorthy A N, Baur M, Holm C, Stan M, Csányi G, Benmore C, Vázquez-Mayagoitia Á 2020 npj Comput. Mater. 6 104 Google Scholar
[39]	Plimpton S 1995 J. Comput. Phys. 117 1 Google Scholar
[40]	Zeng Q Y, Yu X X, Yao Y P, Gao T Y, Chen B, Zhang S, Kang D D, Wang H, Dai J Y 2021 Phys. Rev. Res. 3 033116 Google Scholar
[41]	Franzblau D 1991 Phys. Rev. B 44 4925 Google Scholar
[42]	Le Roux S, Petkov V 2010 J. Appl. Crystallogr. 43 181 Google Scholar
[43]	Xiang X, Fan H, Zhou Y G 2024 J. Appl. Phys. 135 125102 Google Scholar
[44]	Zhang S L, Yi S L, Yang J Y, Liu J, Liu L H 2023 Int. J. Heat Mass Tran. 207 123971 Google Scholar
[45]	Panzer M A, Shandalov M, Rowlette J A, Oshima Y, Chen Y W, McIntyre P C, Goodson K E 2009 IEEE Electron Dev. Lett. 30 1269 Google Scholar
[46]	Lee S M, Cahill D G, Allen T H 1995 Phys. Rev. B 52 253 Google Scholar
[47]	Chaubey G S, Yao Y, Makongo J P, Sahoo P, Misra D, Poudeu P F, Wiley J B 2012 RSC Adv. 2 9207 Google Scholar
[48]	Tritt T M 2005 Thermal Conductivity: Theory, Properties, and Applications (Springer Science & Business Media
[49]	Shenogin S, Bodapati A, Keblinski P, McGaughey A J 2009 J. Appl. Phys. 105 034906 Google Scholar
[50]	Seyf H R, Henry A 2016 J. Appl. Phys. 120 025101 Google Scholar

[1]	刘秀成, 杨智, 郭浩, 陈颖, 罗向龙, 陈健勇. 金刚石/环氧树脂复合物热导率的分子动力学模拟. , 2023, 72(16): 168102. doi: 10.7498/aps.72.20222270
[2]	郑翠红, 杨剑, 谢国锋, 周五星, 欧阳滔. 离子辐照对磷烯热导率的影响及其机制分析. , 2022, 71(5): 056101. doi: 10.7498/aps.71.20211857
[3]	唐道胜, 华钰超, 周艳光, 曹炳阳. GaN薄膜的热导率模型研究. , 2021, 70(4): 045101. doi: 10.7498/aps.70.20201611
[4]	方文玉, 陈粤, 叶盼, 魏皓然, 肖兴林, 黎明锴, AhujaRajeev, 何云斌. 二维XO₂ (X = Ni, Pd, Pt)弹性、电子结构和热导率. , 2021, 70(24): 246301. doi: 10.7498/aps.70.20211015
[5]	徐文雪, 梁新刚, 徐向华, 祝渊. 交联对硅橡胶热导率影响的分子动力学模拟. , 2020, 69(19): 196601. doi: 10.7498/aps.69.20200737
[6]	刘英光, 张士兵, 韩中合, 赵豫晋. 纳晶铜晶粒尺寸对热导率的影响. , 2016, 65(10): 104401. doi: 10.7498/aps.65.104401
[7]	甘渝林, 王丽, 苏雪琼, 许思维, 孔乐, 沈祥. 用拉曼光谱测量GeSbSe玻璃的热导率. , 2014, 63(13): 136502. doi: 10.7498/aps.63.136502
[8]	张程宾, 程启坤, 陈永平. 分形结构纳米复合材料热导率的分子动力学模拟研究. , 2014, 63(23): 236601. doi: 10.7498/aps.63.236601
[9]	惠治鑫, 贺鹏飞, 戴瑛, 吴艾辉. 硅功能化石墨烯热导率的分子动力学模拟. , 2014, 63(7): 074401. doi: 10.7498/aps.63.074401
[10]	郑伯昱, 董慧龙, 陈非凡. 基于量子修正的石墨烯纳米带热导率分子动力学表征方法. , 2014, 63(7): 076501. doi: 10.7498/aps.63.076501
[11]	李屹同, 沈谅平, 王浩, 汪汉斌. 水基ZnO纳米流体电导和热导性能研究　. , 2013, 62(12): 124401. doi: 10.7498/aps.62.124401
[12]	李静, 冯妍卉, 张欣欣, 黄丛亮, 杨穆. 考虑界面散射的金属纳米线热导率修正. , 2013, 62(18): 186501. doi: 10.7498/aps.62.186501
[13]	黄丛亮, 冯妍卉, 张欣欣, 李静, 王戈, 侴爱辉. 金属纳米颗粒的热导率. , 2013, 62(2): 026501. doi: 10.7498/aps.62.026501
[14]	鲍华. 固体氩的晶格热导率的非简谐晶格动力学计算. , 2013, 62(18): 186302. doi: 10.7498/aps.62.186302
[15]	杨平, 王晓亮, 李培, 王欢, 张立强, 谢方伟. 氮掺杂和空位对石墨烯纳米带热导率影响的分子动力学模拟. , 2012, 61(7): 076501. doi: 10.7498/aps.61.076501
[16]	黄丛亮, 冯妍卉, 张欣欣, 李威, 杨穆, 李静, 王戈. 介孔二氧化硅基导电聚合物复合材料热导率的实验研究. , 2012, 61(15): 154402. doi: 10.7498/aps.61.154402
[17]	杨平, 吴勇胜, 许海锋, 许鲜欣, 张立强, 李培. TiO2/ZnO纳米薄膜界面热导率的分子动力学模拟. , 2011, 60(6): 066601. doi: 10.7498/aps.60.066601
[18]	侯泉文, 曹炳阳, 过增元. 碳纳米管的热导率:从弹道到扩散输运. , 2009, 58(11): 7809-7814. doi: 10.7498/aps.58.7809
[19]	李世彬, 吴志明, 袁凯, 廖乃镘, 李伟, 蒋亚东. 氢化非晶硅薄膜的热导率研究. , 2008, 57(5): 3126-3131. doi: 10.7498/aps.57.3126
[20]	吴国强, 孔宪仁, 孙兆伟, 王亚辉. 氩晶体薄膜法向热导率的分子动力学模拟. , 2006, 55(1): 1-5. doi: 10.7498/aps.55.1

计量

文章访问数: 405
PDF下载量: 17
被引次数: 0

姓名
邮箱
手机号码
标题
留言内容
验证码

搜索

留言板

基于准简谐格林-久保理论结合流体动力学外推方法的非晶二氧化铪导热机制研究