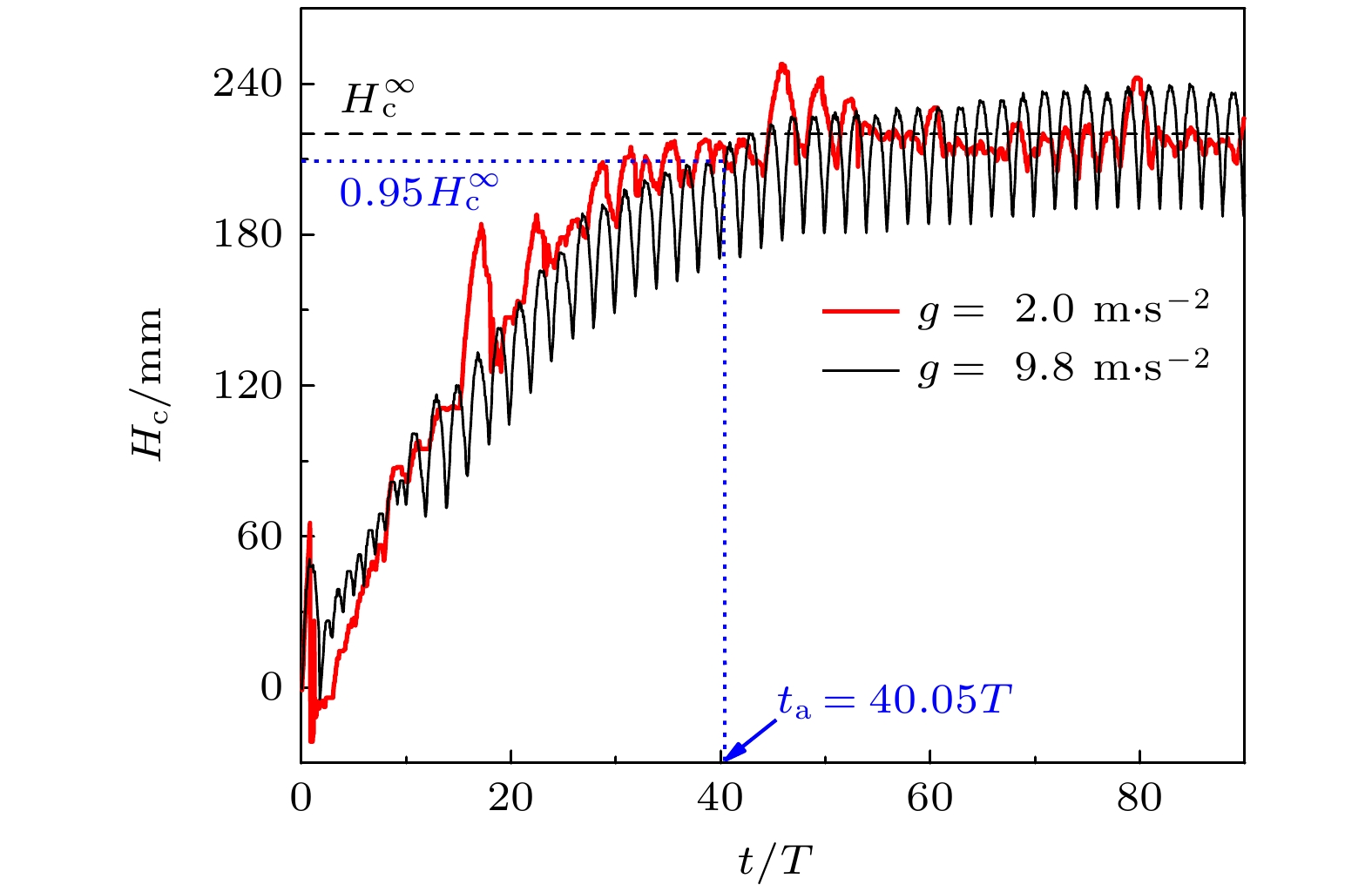
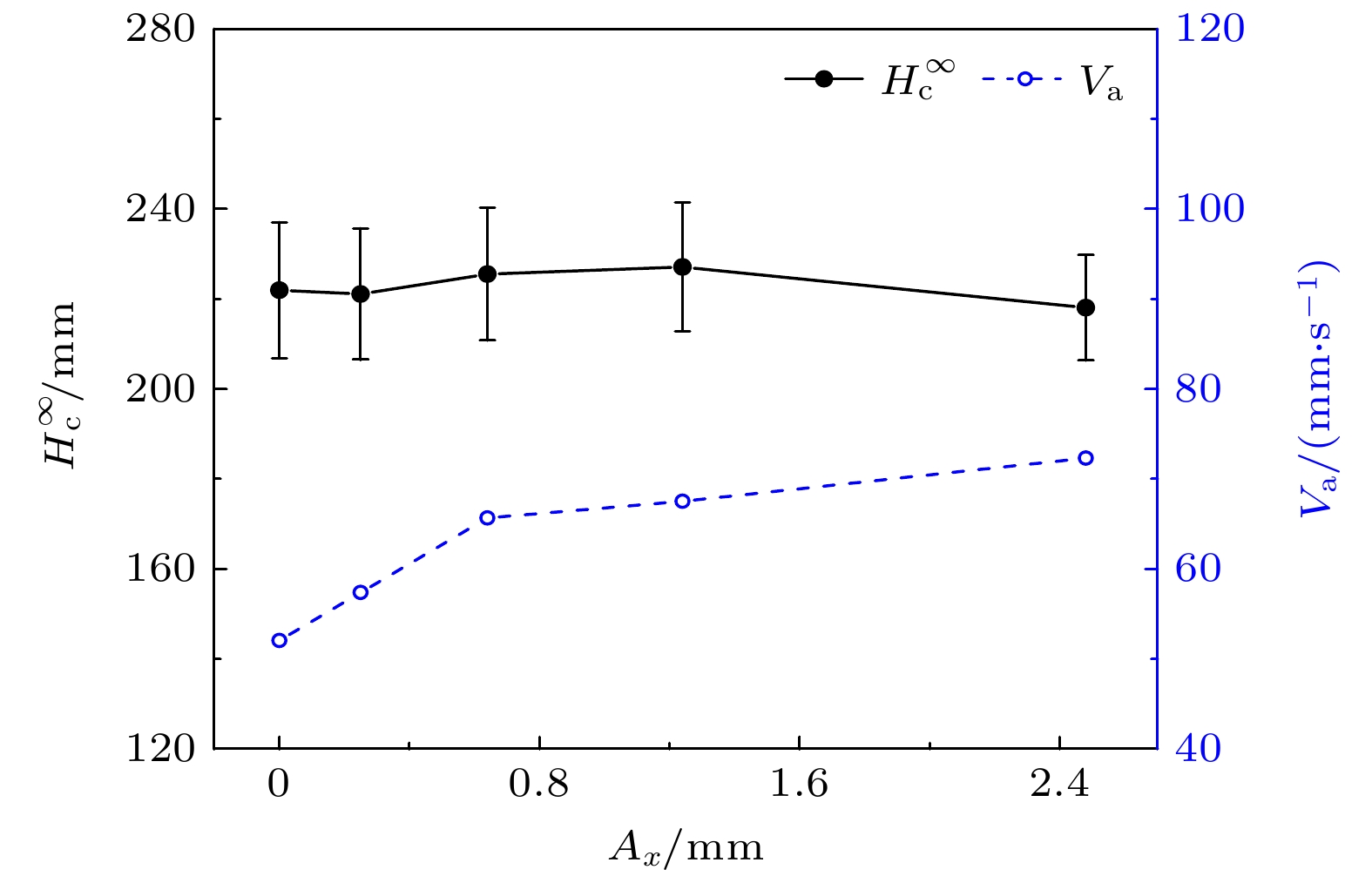
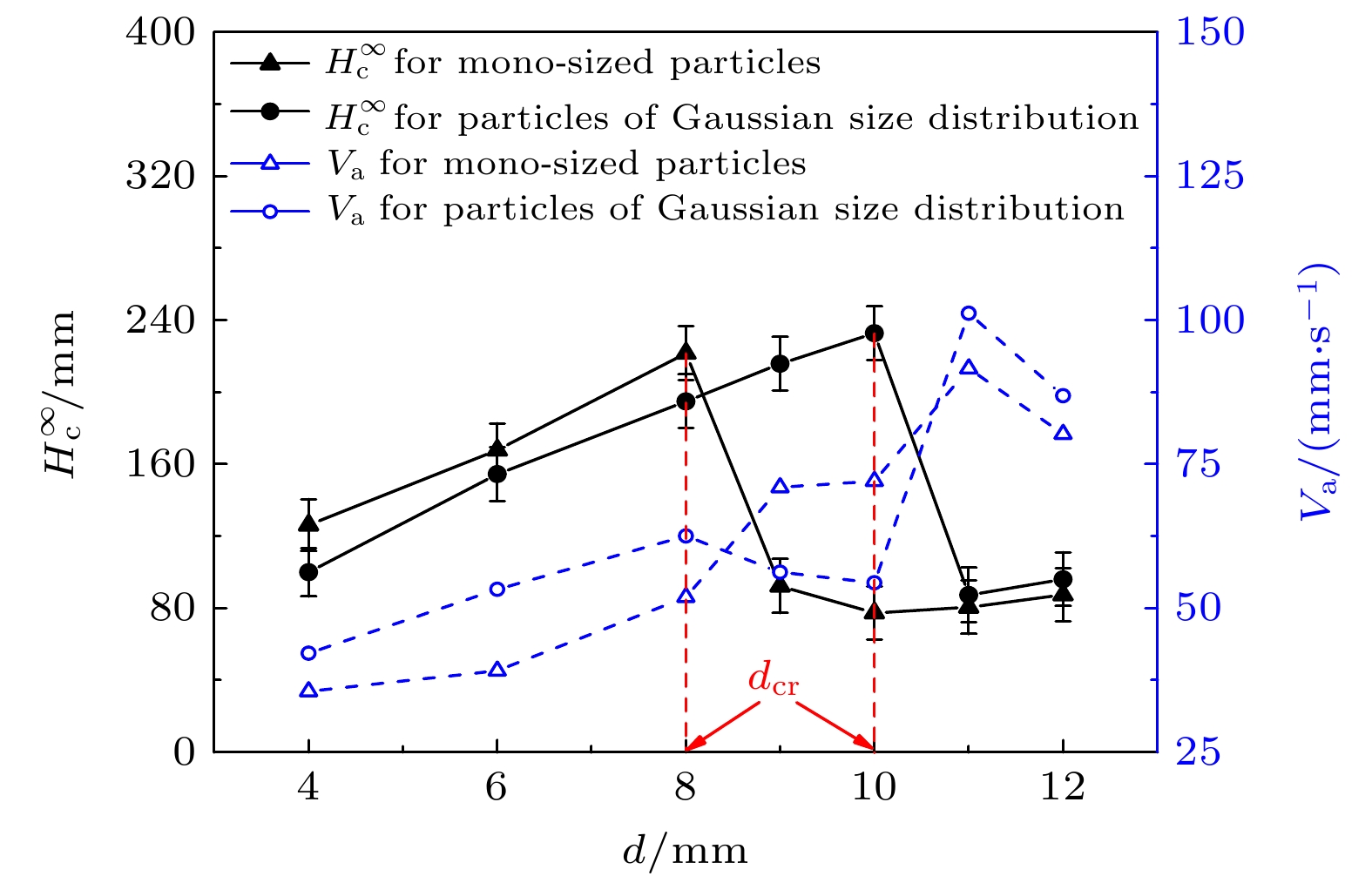
竖直振动激励下颗粒毛细上升行为研究

于天林; 凡凤仙

doi:10.7498/aps.71.20212333

摘要

竖直振动激励下颗粒毛细上升现象为颗粒物料的提升、输运和采集提供了一种全新的技术路径. 然而, 已有颗粒毛细上升行为研究仍存在明显不足, 特别是缺乏对重力加速度、水平振动分量、颗粒粒径分布影响的深入探究. 针对这些问题, 采用离散元方法, 对不同操作条件下颗粒毛细上升现象开展数值模拟研究, 并对颗粒最终毛细上升高度和平均毛细上升速度进行计算分析. 结果表明, 在低重力条件下, 颗粒毛细效应仍能发生, 颗粒最终毛细上升高度和平均毛细上升速度随重力加速度均呈现先增加后减小的趋势; 颗粒最终毛细上升高度对水平振动分量的变化不敏感, 而平均毛细上升速度随水平振动分量的增大而增加; 在平均粒径相等的情况下, 粒径服从高斯分布的颗粒比单一粒径颗粒的最终毛细上升高度最大值对应的临界管径更大, 并且同处于堵塞效应影响的管径区域时平均毛细上升速度也更快.

关键词:

Abstract

The phenomenon of granular capillary rising under vertical vibration provides a novel technical route for hoisting, transporting and collecting granular materials. However, there are still obvious deficiencies in the existing studies of the granular capillary rising behavior, especially the intensive investigation on the effects of gravitational acceleration, horizontal vibration component and particle size distribution are still lacking. To address these problems, the discrete element method is used to numerically simulate the granular capillary rising phenomenon under different operating conditions. The final capillary rising height and average capillary rising velocity of the granular matter are computed and analyzed based on the numerical simulations. The results show that the granular capillarity can also occur under low gravity conditions, and that the final capillary rising height and the average capillary rising velocity first increase and then decrease with the gravitational acceleration. It is also found that the final capillary rising height is insensitive to the variation of horizontal vibrational component, whereas the average capillary rising velocity increases with the augmentation of horizontal vibrational component. Compared with the mono-sized particles, the particles with the same mean size but having a Gaussian size distribution exhibit a maximal capillary rising height at a larger critical tube diameter. Meanwhile, the average capillary rising velocity of the particles having a Gaussian size distribution is faster in the tube diameter range where the granular capillary dynamics for both size distributions is dominated by the jamming effect.

Keywords:

作者及机构信息

于天林¹,
凡凤仙^1,2

1.
上海理工大学能源与动力工程学院, 上海　200093

2.
上海理工大学上海市动力工程多相流动与传热重点实验室, 上海　200093

通信作者: 凡凤仙, fanfengxian@usst.edu.cn

基金项目: 国家自然科学基金(批准号: 51976130)和上海市科委科研计划(批准号: 13DZ2260900)资助的课题

Authors and contacts

Yu Tian-Lin¹,
Fan Feng-Xian^1,2

1.
School of Energy and Power Engineering, University of Shanghai for Science and Technology, Shanghai 200093, China

2.
Shanghai Key Laboratory of Multiphase Flow and Heat Transfer in Power Engineering, University of Shanghai for Science and Technology, Shanghai 200093, China

Corresponding author: Fan Feng-Xian, fanfengxian@usst.edu.cn

Funds: Project supported by the National Natural Science Foundation of China (Grant No. 51976130) and the Science and Technology Commission of Shanghai Municipality, China (Grant No. 13DZ2260900)

文章全文 : translate this paragraph

参考文献

[1]	Xing Y, Zheng J, Li J D, Cao Y X, Pan W, Zhang J, Wang Y J 2021 Phys. Rev. Lett. 126 048002 Google Scholar
[2]	Li Z F, Zeng Z K, Xing Y, Li J D, Zheng J, Mao Q H, Zhang J, Hou M Y, Wang Y J 2021 Sci. Adv. 7 eabe8737 Google Scholar
[3]	Then H Z, Sekiguchi T, Okumura K 2020 Soft Matter 16 8612 Google Scholar
[4]	Kogane A, Kuwagi K, Mawatari Y, Mawatari Y, Davoren L, Seville J P K, Parker D J 2020 J. Phys. Commun. 4 075012 Google Scholar
[5]	van Gerner H J, van der Weele K, van der Meer D, van der Hoef M A 2015 Phys. Rev. E Stat. Nonlinear Soft Matter Phys. 92 042203 Google Scholar
[6]	Sánchez I, Díaz A A, Guerrero B, Trosel Y, Rojas C 2015 Mech. Res. Commun. 67 1 Google Scholar
[7]	郭宇, 凡凤仙, 白鹏博, 刘举 2019 上海理工大学学报 41 409 Google Scholar Guo Y, Fan F X, Bai P B, Lu J 2019 J. Univ. Shanghai for Sci. Technol. 41 409 Google Scholar
[8]	Sánchez I, Darias J R, Paredes R, Lobb C J, Gutiérrez G 2009 Traffic Granular Flow 545
[9]	Liu C P, Wu P, Wang L 2013 Soft Matter 9 4762 Google Scholar
[10]	张富翁, 王立, 刘传平, 吴平 2014 63 014501 Google Scholar Zhang F W, Wang L, Liu C P, Wu P 2014 Acta. Phys. Sin. 63 014501 Google Scholar
[11]	Fan F X, Parteli E J R, Pöschel T 2017 Phys. Rev. Lett. 118 218001 Google Scholar
[12]	张华腾, 凡凤仙, 王志强 2020 力学学报 52 442 Google Scholar Zhang H T, Fan F X, Wang Z Q 2020 Chin. J. Theo. Appl. Mech. 52 442 Google Scholar
[13]	凡凤仙, 王志强, 刘举, 张华腾 2019 力学学报 51 415 Google Scholar Fan F X, Wang Z Q, Liu J, Zhang H T 2019 Chin. J. Theo. Appl. Mech. 51 415 Google Scholar
[14]	Fan F X, Liu J, Parteli E J R, Pschel T 2017 EPJ Web of Conferences 140 16008 Google Scholar
[15]	刘举, 白鹏博, 凡凤仙, 胡晓红 2016 化工进展 35 1956 Google Scholar Liu J, Bai P B, Fan F X, Hu X H 2016 Chem. Ind. Eng. Prog. 35 1956 Google Scholar
[16]	Zhang F W, Cronin K, Lin Y H, Miao S, Liu C P, Wang L 2019 Powder Technol. 343 383 Google Scholar
[17]	Zhang F W, Cronin K, Lin Y, Liu C, Wang L 2018 Powder Technol. 333 421 Google Scholar
[18]	Zhang F W, Wang L, Liu C P, Wu P 2017 Adv Powder Technol. 28 356 Google Scholar
[19]	Liu C P, Zhang F W, Wu P, Wang 2014 Powder Technol. 259 137 Google Scholar
[20]	Kawamoto H, Kubo K, Kikumiya R, Adachi M 2021 J. Aerosp. Eng. 34 04021097 Google Scholar
[21]	Liu Y, Zhao J H 2015 Chin. Phys. B 24 034502 Google Scholar
[22]	Xu Y P, Musser J, Li T, Padding J T, Rogers W A 2017 Powder Technol. 320 304 Google Scholar
[23]	Zhang N, Cheng B, Baoyin H 2019 Appl. Math. Mech. Engl. Ed. 40 127 Google Scholar
[24]	Brilliantov N V, Spahn F, Hertzsch J M, Pöschel T 1996 Phys. Rev. E 53 5382 Google Scholar
[25]	Cundall P A, Strack O D 1979 Géotechnique 29 47 Google Scholar
[26]	Ai J, Chen J F, Rotter J M, Ooi J Y 2011 Powder Technol. 206 269 Google Scholar
[27]	Kloss C, Goniva C, Hager A, Amberger S, Pirker S 2012 Prog. Comput. Fluid Dyn. 12 140 Google Scholar
[28]	Shäfer J, Dippel S, Wolf D E 1996 J. Phys. I 6 5 Google Scholar
[29]	赵永志, 程易, 郑津洋 2009 计算力学学报 26 239 Zhao Y Z, Cheng Y, Zheng J Y 2009 Chin. J. Comput. Mech. 26 239
[30]	Ng T T, Zhou W, Ma G, Chang X L 2014 J. Eng. Mech. 141 04014167 Google Scholar

施引文献

图 1 颗粒系统示意图

Fig. 1. Schematic diagram of granular system.

下载: 全尺寸图片幻灯片

图 2 不同重力加速度下颗粒毛细上升动力学过程

Fig. 2. Dynamic process of granular capillary rising under different gravitational accelerations.

下载: 全尺寸图片幻灯片

图 3 毛细上升高度随时间的演变

Fig. 3. Evolution of capillary rising height with time.

下载: 全尺寸图片幻灯片

图 4 最终毛细上升高度和平均毛细上升速度随重力加速度的变化

Fig. 4. Dependence of final capillary rising height and average capillary rising velocity on gravitational acceleration.

下载: 全尺寸图片幻灯片

图 5 最终毛细上升高度和平均毛细上升速度随水平振动分量的变化

Fig. 5. Dependence of final capillary rising height and average capillary rising velocity on horizontal vibrational component.

下载: 全尺寸图片幻灯片

图 6 不同粒径分布下最终毛细上升高度和平均毛细上升速度随管径的变化

Fig. 6. Dependence of final capillary rising height and average capillary rising velocity on tube diameter under different particle size distribution.

下载: 全尺寸图片幻灯片

表 1 数值模拟参数

Table 1. Parameters used in numerical simulations

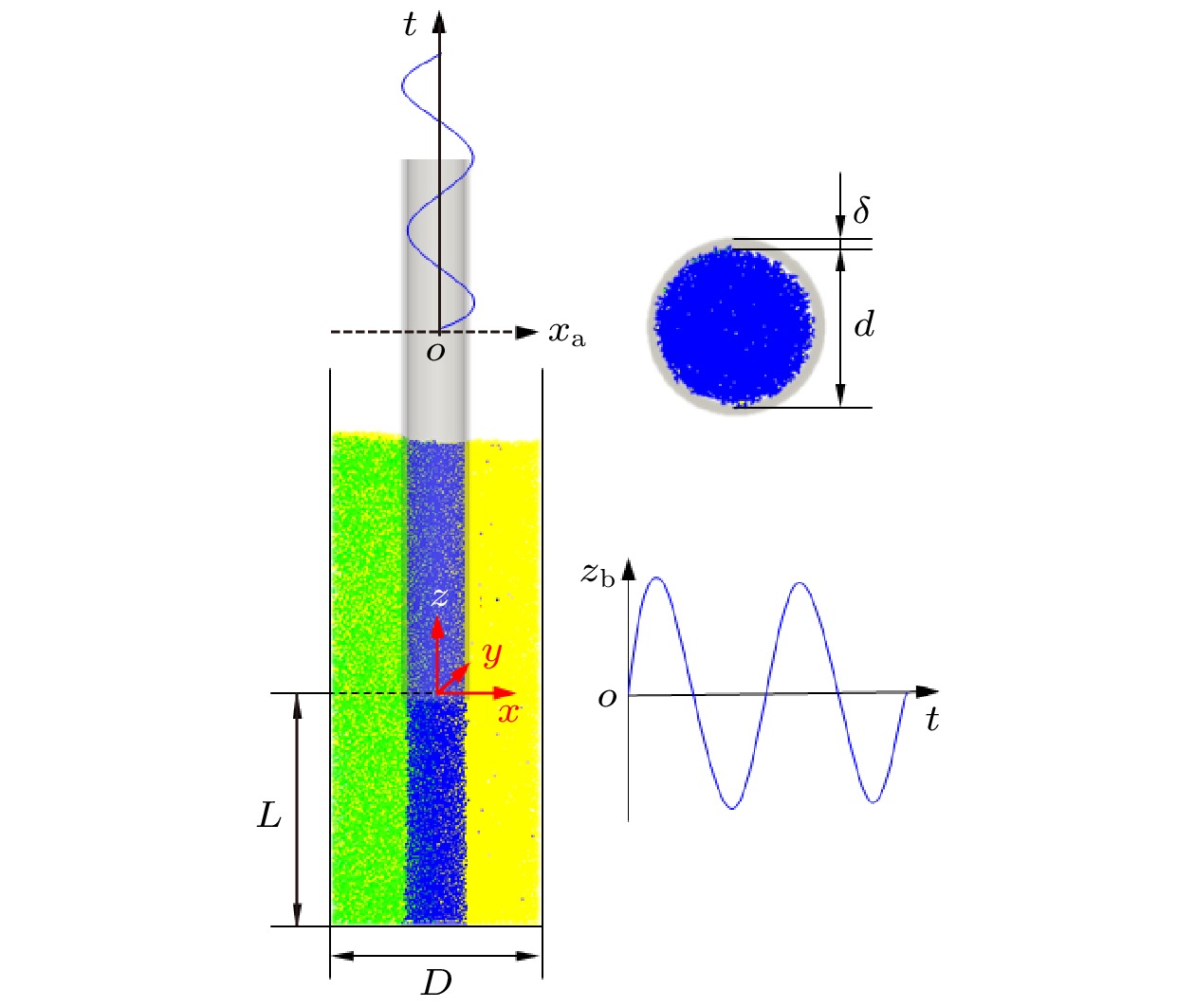
参数	符号	数值
容器内径/mm	D	28.2
管内径/mm	d	8
颗粒数目	N_p	200000
管壁厚度/mm	δ	0.6
管底面距容器底面的距离/mm	L	30
颗粒密度/(kg⋅m^–3)	ρ_p	2500
杨氏模量/MPa	Y	10
泊松比	υ	0.25
恢复系数	ε	0.5
颗粒间滑动摩擦系数	μ_pp,s	0.8
颗粒间滚动摩擦系数	μ_pp,r	0.1
颗粒-壁面间滑动摩擦系数	μ_pw,s	0.58
颗粒-壁面间滚动摩擦系数	μ_pw,r	0.05
振幅/mm	A_z	12.42
频率/Hz	f	10

下载: 导出CSV

map

[1]	Xing Y, Zheng J, Li J D, Cao Y X, Pan W, Zhang J, Wang Y J 2021 Phys. Rev. Lett. 126 048002 Google Scholar
[2]	Li Z F, Zeng Z K, Xing Y, Li J D, Zheng J, Mao Q H, Zhang J, Hou M Y, Wang Y J 2021 Sci. Adv. 7 eabe8737 Google Scholar
[3]	Then H Z, Sekiguchi T, Okumura K 2020 Soft Matter 16 8612 Google Scholar
[4]	Kogane A, Kuwagi K, Mawatari Y, Mawatari Y, Davoren L, Seville J P K, Parker D J 2020 J. Phys. Commun. 4 075012 Google Scholar
[5]	van Gerner H J, van der Weele K, van der Meer D, van der Hoef M A 2015 Phys. Rev. E Stat. Nonlinear Soft Matter Phys. 92 042203 Google Scholar
[6]	Sánchez I, Díaz A A, Guerrero B, Trosel Y, Rojas C 2015 Mech. Res. Commun. 67 1 Google Scholar
[7]	郭宇, 凡凤仙, 白鹏博, 刘举 2019 上海理工大学学报 41 409 Google Scholar Guo Y, Fan F X, Bai P B, Lu J 2019 J. Univ. Shanghai for Sci. Technol. 41 409 Google Scholar
[8]	Sánchez I, Darias J R, Paredes R, Lobb C J, Gutiérrez G 2009 Traffic Granular Flow 545
[9]	Liu C P, Wu P, Wang L 2013 Soft Matter 9 4762 Google Scholar
[10]	张富翁, 王立, 刘传平, 吴平 2014 63 014501 Google Scholar Zhang F W, Wang L, Liu C P, Wu P 2014 Acta. Phys. Sin. 63 014501 Google Scholar
[11]	Fan F X, Parteli E J R, Pöschel T 2017 Phys. Rev. Lett. 118 218001 Google Scholar
[12]	张华腾, 凡凤仙, 王志强 2020 力学学报 52 442 Google Scholar Zhang H T, Fan F X, Wang Z Q 2020 Chin. J. Theo. Appl. Mech. 52 442 Google Scholar
[13]	凡凤仙, 王志强, 刘举, 张华腾 2019 力学学报 51 415 Google Scholar Fan F X, Wang Z Q, Liu J, Zhang H T 2019 Chin. J. Theo. Appl. Mech. 51 415 Google Scholar
[14]	Fan F X, Liu J, Parteli E J R, Pschel T 2017 EPJ Web of Conferences 140 16008 Google Scholar
[15]	刘举, 白鹏博, 凡凤仙, 胡晓红 2016 化工进展 35 1956 Google Scholar Liu J, Bai P B, Fan F X, Hu X H 2016 Chem. Ind. Eng. Prog. 35 1956 Google Scholar
[16]	Zhang F W, Cronin K, Lin Y H, Miao S, Liu C P, Wang L 2019 Powder Technol. 343 383 Google Scholar
[17]	Zhang F W, Cronin K, Lin Y, Liu C, Wang L 2018 Powder Technol. 333 421 Google Scholar
[18]	Zhang F W, Wang L, Liu C P, Wu P 2017 Adv Powder Technol. 28 356 Google Scholar
[19]	Liu C P, Zhang F W, Wu P, Wang 2014 Powder Technol. 259 137 Google Scholar
[20]	Kawamoto H, Kubo K, Kikumiya R, Adachi M 2021 J. Aerosp. Eng. 34 04021097 Google Scholar
[21]	Liu Y, Zhao J H 2015 Chin. Phys. B 24 034502 Google Scholar
[22]	Xu Y P, Musser J, Li T, Padding J T, Rogers W A 2017 Powder Technol. 320 304 Google Scholar
[23]	Zhang N, Cheng B, Baoyin H 2019 Appl. Math. Mech. Engl. Ed. 40 127 Google Scholar
[24]	Brilliantov N V, Spahn F, Hertzsch J M, Pöschel T 1996 Phys. Rev. E 53 5382 Google Scholar
[25]	Cundall P A, Strack O D 1979 Géotechnique 29 47 Google Scholar
[26]	Ai J, Chen J F, Rotter J M, Ooi J Y 2011 Powder Technol. 206 269 Google Scholar
[27]	Kloss C, Goniva C, Hager A, Amberger S, Pirker S 2012 Prog. Comput. Fluid Dyn. 12 140 Google Scholar
[28]	Shäfer J, Dippel S, Wolf D E 1996 J. Phys. I 6 5 Google Scholar
[29]	赵永志, 程易, 郑津洋 2009 计算力学学报 26 239 Zhao Y Z, Cheng Y, Zheng J Y 2009 Chin. J. Comput. Mech. 26 239
[30]	Ng T T, Zhou W, Ma G, Chang X L 2014 J. Eng. Mech. 141 04014167 Google Scholar

[1]	杜清馨, 孙其诚, 丁红胜, 张国华, 范彦丽, 安飞飞. 垂直振动下干湿颗粒样品的体积模量与耗散. , 2022, 71(18): 184501. doi: 10.7498/aps.71.20220329
[2]	牛晓娜, 张国华, 孙其诚, 赵雪丹, 董远湘. 二维有摩擦颗粒体系振动态密度与玻色峰的研究. , 2016, 65(3): 036301. doi: 10.7498/aps.65.036301
[3]	季顺迎, 樊利芳, 梁绍敏. 基于离散元方法的颗粒材料缓冲性能及影响因素分析. , 2016, 65(10): 104501. doi: 10.7498/aps.65.104501
[4]	何菲菲, 彭政, 颜细平, 蒋亦民. 振动颗粒混合物中的周期性分聚现象与能量耗散. , 2015, 64(13): 134503. doi: 10.7498/aps.64.134503
[5]	吴迪平, 李星祥, 秦勤, 管奔, 臧勇. 离散颗粒层被横向推移过程中的力学行为研究. , 2014, 63(9): 098201. doi: 10.7498/aps.63.098201
[6]	张富翁, 王立, 刘传平, 吴平. 竖直振动管中颗粒的上升运动. , 2014, 63(1): 014501. doi: 10.7498/aps.63.014501
[7]	彭政, 蒋亦民, 刘锐, 厚美瑛. 垂直振动激发下颗粒物质的能量耗散. , 2013, 62(2): 024502. doi: 10.7498/aps.62.024502
[8]	黄德财, 冯耀东, 解为梅, 陆明, 吴海平, 胡凤兰, 邓开明. 颗粒密度对旋转筒内二元颗粒体系分离的影响. , 2012, 61(12): 124501. doi: 10.7498/aps.61.124501
[9]	张祺, 厚美瑛. 直剪颗粒体系的尺寸效应研究. , 2012, 61(24): 244504. doi: 10.7498/aps.61.244504
[10]	彭亚晶, 张卓, 王勇, 刘小嵩. 振动颗粒物质“巴西果”分离效应实验和理论研究. , 2012, 61(13): 134501. doi: 10.7498/aps.61.134501
[11]	姜泽辉, 张峰, 郭波, 赵海发, 郑瑞华. 受振颗粒“毛细”系统中的对流与有序化. , 2010, 59(8): 5581-5587. doi: 10.7498/aps.59.5581
[12]	姜泽辉, 荆亚芳, 赵海发, 郑瑞华. 振动颗粒物质中倍周期运动对尺寸分离的影响. , 2009, 58(9): 5923-5929. doi: 10.7498/aps.58.5923
[13]	梁宣文, 李粮生, 侯兆国, 吕震, 杨雷, 孙刚, 史庆藩. 垂直振动作用下二元混合颗粒分层的动态循环反转. , 2008, 57(4): 2300-2305. doi: 10.7498/aps.57.2300
[14]	彭政, 厚美瑛, 史庆藩, 陆坤权. 颗粒介质的离散态特性研究. , 2007, 56(2): 1195-1202. doi: 10.7498/aps.56.1195
[15]	姜泽辉, 王运鹰, 吴晶. 窄振动颗粒床中的运动模式. , 2006, 55(9): 4748-4753. doi: 10.7498/aps.55.4748
[16]	杜学能, 胡林, 孔维姝, 王伟明, 吴宇. 颗粒物质内部滑动摩擦力的非线性振动现象. , 2006, 55(12): 6488-6493. doi: 10.7498/aps.55.6488
[17]	姜泽辉, 刘新影, 彭雅晶, 李建伟. 竖直振动颗粒床中的倍周期运动. , 2005, 54(12): 5692-5698. doi: 10.7498/aps.54.5692
[18]	姜泽辉, 李斌, 赵海发, 王运鹰, 戴智斌. 竖直振动颗粒物厚层中冲击力分岔现象. , 2005, 54(3): 1273-1278. doi: 10.7498/aps.54.1273
[19]	胡国琦, 张训生, 鲍德松, 唐孝威. 二维颗粒流通道宽度效应的分子动力学模拟. , 2004, 53(12): 4277-4281. doi: 10.7498/aps.53.4277
[20]	姜泽辉, 陆坤权, 厚美瑛, 陈唯, 陈相君. 振动颗粒混合物中的三明治式分离. , 2003, 52(9): 2244-2248. doi: 10.7498/aps.52.2244

计量

文章访问数: 3964
PDF下载量: 76
被引次数: 0

姓名
邮箱
手机号码
标题
留言内容
验证码

搜索

留言板