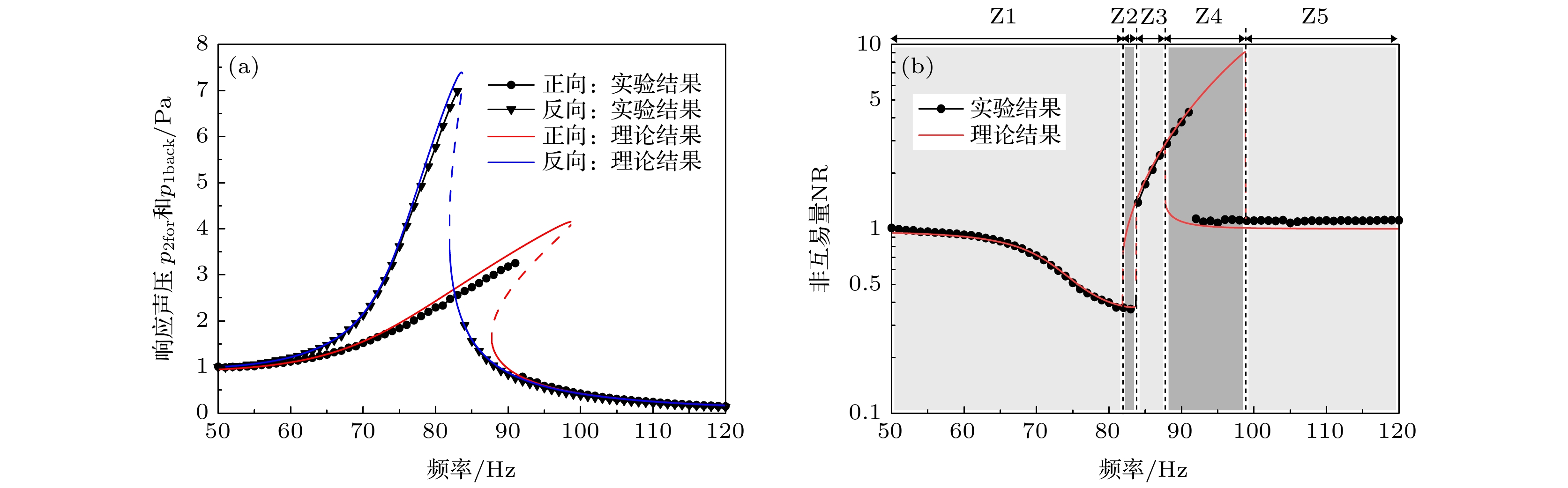
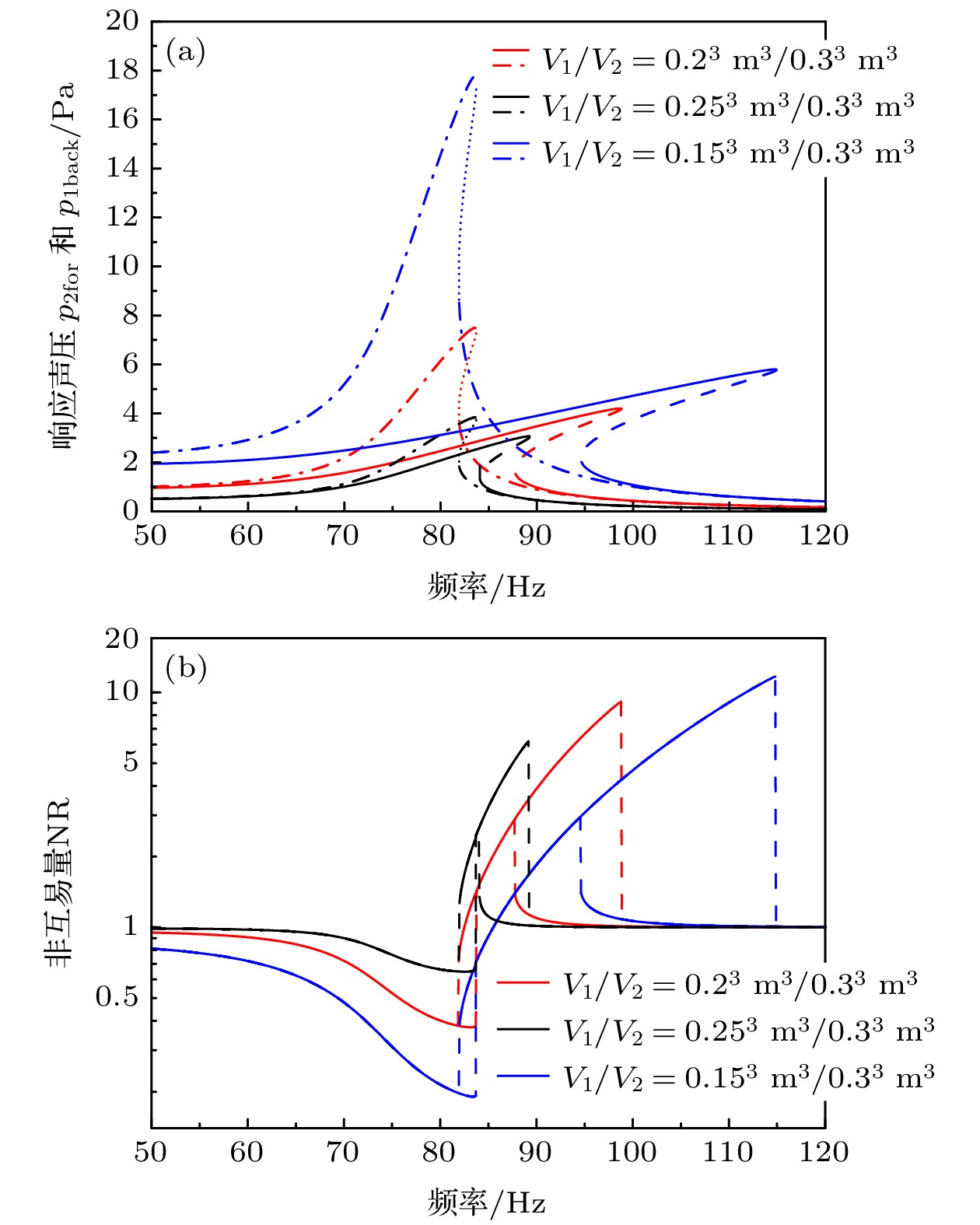
-
声能量非互易传递机理及声非互易系统构建是近年来声学领域的研究热点. 本文开展了由非线性薄膜和两个不同尺寸声腔组成的实验系统中声能量非互易传递的实验研究. 该系统利用简化为Duffing振子的薄膜频响函数的不对称性, 实现了声能量的非互易传递. 采用复化平均法获得系统频响函数的渐近解, 理论计算结果与实验测量结果吻合. 理论计算和实验结果表明: 该系统理论上存在最大9.1倍的非互易量, 实验测得的最大非互易量为4.3倍, 归一化跳变区频率带宽为0.56. 研究结果揭示了实验系统中声能量非互易传递机理, 为实现空气介质声系统中声能量的非对称传递提供了一种新方法.Mechanisms for the nonreciprocal transmission of acoustic energy and the construction of non-reciprocal vibro-acoustic systems have been subjects of intense research in recent years. An experimental study of acoustic nonreciprocal transmission in an experimental system with a nonlinear membrane and two acoustic cavities of different sizes is reported. The membrane can be simplified into a Duffing oscillator, and the asymmetry of the frequency response function of this oscillator is used to realize the non-reciprocal transmission of acoustic energy. The asymptotic solution of the frequency response function of the nonlinear membrane is obtained by the complexification-averaging method. The theoretical simulation results accord well with the experimental results. The results show that the experimental system has a maximum non-reciprocal quantity of 9.1 times in theory, 4.3 times in the experiment, and the normalized frequency bandwidth of the jump phenomenon region is up to 0.56. The research results reveal the mechanism of non-reciprocal transfer of acoustic energy in the experimental system and demonstrate a new way to realize the asymmetric transfer of acoustic energy in an acoustic system with an air medium.
-
Keywords:
- acoustic non-reciprocity /
- one-way transmission /
- nonlinear membrane vibration /
- Duffing oscillator
[1] Moore K J, Vakakis A F 2018 Acta Mech. 229 4057
Google Scholar
[2] Mojahed A, Moore K, Bergman L A, Vakakis A F 2018 Int. J. Non Linear Mech. 107 94
Google Scholar
[3] Spadoni A, Daraio C 2010 Proc. Natl. Acad. Sci. U. S. A. 107 7230
Google Scholar
[4] Zhu X H, Li J F, Shen C, Peng X Y, Song A L, Li L Q, Cummer S A 2020 Appl. Phys. Lett. 116 34101
Google Scholar
[5] 梁彬, 袁樱, 程建春 2015 64 094305
Google Scholar
Liang B, Yuan Y, Cheng J C 2015 Acta Phys. Sin. 64 094305
Google Scholar
[6] 邹欣晔, 袁樱, 梁彬, 程建春 2013 应用声学 32 169
Google Scholar
Zou X Y, Yuan Y, Liang B, Cheng J C 2013 Appl. Acoust. 32 169
Google Scholar
[7] Zhu X F, Ramezani H, Shi C Z, Zhu J, Zhang X 2014 Phys. Rev. X 4 031042
[8] Liu T, Zhu X F, Chen F, Liang S J, Zhu J 2018 Phys. Rev. Lett. 120 124502
Google Scholar
[9] Nassar H, Xu X C, Norris A N, Huang G L 2017 J. Mech. Phys. Solids 101 10
Google Scholar
[10] Nassar H, Chen H, Norris A N, Huang G L 2018 Phys. Rev. B 97 014305
Google Scholar
[11] Fleury R, Sounas D L, Sieck C F, Haberman M R, Alù A 2014 Science 343 516
Google Scholar
[12] Khanikaev A B, Fleury R, Mousavi S H, Alù A 2015 Nat. Commun. 6 8260
Google Scholar
[13] Zhu X F, Zou X Y, Liang B, Cheng J C 2010 J. Appl. Phys. 108 124909
Google Scholar
[14] Peng Y G, Qin C Z, Zhao D G, Shen Y X, Xu X Y, Bao M, Jia H, Zhu X F 2016 Nat. Commun. 7 13368
Google Scholar
[15] Ding Y J, Peng Y G, Zhu Y F, Fan X D, Yang J, Liang B, Zhu X F, Wan X G, Cheng J C 2019 Phys. Rev. Lett. 122 014302
Google Scholar
[16] Chen Z X, Peng Y G, Li H X, Liu J J, Ding Y J, Liang B, Zhu X F, Lu Y Q, Cheng J C, Alù A 2021 Sci. Adv. 7 eabj1198
Google Scholar
[17] Nassar H, Yousefzadeh B, Fleury R, Ruzzene M, Alù A, Daraio C, Norris A N, Huang G L, Haberman M R 2020 Nat. Rev. Mater. 5 667
Google Scholar
[18] Liang B, Guo X S, Tu J, Zhang D, Cheng J C 2010 Nat. Mater. 9 989
Google Scholar
[19] Zhu Y F, Zou X Y, Liang B, Cheng J C 2015 Appl. Phys. Lett. 107 113501
Google Scholar
[20] Boechler N, Theocharis G, Daraio C 2011 Nat. Mater. 10 665
Google Scholar
[21] Wang Y F, Yousefzadeh B, Chen H, Nassar H, Huang G L, Daraio C 2018 Phys. Rev. Lett. 121 194301
Google Scholar
[22] Bunyan J, Moore K J, Mojahed A, Fronk M D, Leamy M, Tawfick S, Vakakis A F 2018 Phys. Rev. E 97 052211
Google Scholar
[23] Wang C G, Tawfick S, Vakakis A F 2020 Physica D 402 132229
Google Scholar
[24] Mojahed A, Bunyan J, Tawfick S, Vakakis A F 2019 Phys. Rev. Appl. 12 034033
Google Scholar
[25] Wei L S, Wang Y Z, Wang Y S 2020 Int. J. Mech. Sci. 173 105433
Google Scholar
[26] Bellet R, Cochelin B, Herzog P, Mattei P O 2010 J. Sound Vib. 329 2768
Google Scholar
[27] Bellet R, Cochelin B, Côte R, Mattei P O 2012 J. Sound Vib. 331 5657
Google Scholar
[28] Shao J W, Cochelin B 2014 Int. J. Non Linear Mech. 64 85
Google Scholar
[29] Bryk P Y, Côte R, Bellizzi S 2019 J. Sound Vib. 460 114868
Google Scholar
[30] Chauvin A, Monteil M, Bellizzi S, Côte R, Herzog P, Pachebat M 2018 J. Sound Vib. 416 244
Google Scholar
[31] Leissa A W 1969 Vibration of Plates (New York: Acoustical Society of America) pp44–45
[32] Manevitch L I 1999 Mathematical Models of Non-Linear Excitations, Transfer, Dynamics, and Control in Condensed Systems and Other Media (New York: Springer) pp269–300
[33] McFarland D M, Bergman L A, Vakakis A F 2005 Int. J. Non Linear Mech. 40 891
Google Scholar
-
图 1 结构声非互易系统构成 (a) 实验系统全貌; (b) 非互易实验装置
Fig. 1. Configuration of the non-reciprocal vibro-acoustic experimental system: (a) The overview of the experimental set-up; (b) the non-reciprocal experimental apparatus.
图 2 薄膜非线性立方刚度测量实验系统图
Fig. 2. Experimental system for measuring nonlinear cubic stiffness of membrane.
图 3 结构声非互易系统理论计算与实验测量结果对比 (a) 激励声压; (b) 薄膜平均速度
Fig. 3. Comparison of the theoretical and experimental results for non-reciprocal vibro-acoustic system: (a) Excitation sound pressure; (b) average membrane velocity.
图 4 结构声非互易系统的系统响应 (a)正向响应声压和反向响应声压; (b)非互易量
Fig. 4. Response of non-reciprocal vibro-acoustic system: (a) Forward response sound pressure and backward response sound pressure; (b) non-reciprocal quantity.
图 5 不同源强输入下系统响应 (a) 正向响应声压(实线)和反向响应声压(点划线); (b) 非互易量
Fig. 5. System responses under different VVS: (a) Forward response sound pressure (solid line) and backward response sound pressure (dot dash line); (b) non-reciprocal quantity.
图 6 不同声腔下系统响应 (a) 正向响应声压(实线)和反向响应声压(点划线); (b) 非互易量
Fig. 6. System responses with different acoustic cavities: (a) Forward response sound pressure (solid line) and backward response sound pressure (dot-dash line); (b) non-reciprocal quantity.
表 1 变量和参数表
Table 1. Nomenclature.
参数名称 符号 上声腔边长 ${L_1}$ 下声腔边长 ${L_2}$ 上声腔体积 ${V_1}$ 下声腔体积 ${V_2}$ 薄膜半径 $R$ 薄膜厚度 $h$ 薄膜面积 ${S_{\rm me} }$ 薄膜质量 ${m_{\rm me} }$ 薄膜表面附加空气质量 ${m_{\rm{a}}}$ 实验测得薄膜的一阶共振频率 ${f_1}$ 无预应力的薄膜共振频率 ${f_0}$ 薄膜密度 ${\rho _{\rm me} }$ 薄膜杨氏模量 $E$ 薄膜线性刚度 ${k_1}$ 薄膜立方非线性刚度 ${k_3}$ 薄膜泊松比 $\upsilon $ 薄膜阻尼系数 $ \eta $ 薄膜中心点横向位移 ${\dot q_{\rm me} }$ 薄膜平均速度 ${\bar v_n}$ 空气声速 $ {c_0} $ 空气密度 ${\rho _{\rm{a}}}$ 激励频率 ${\omega _{\rm{S}}}$ 源强幅值 ${Q_{\rm{s}}}$ 非互易量 $NR$ 
下载: 导出CSV
表 2 系统参数
Table 2. System parameters.
参数名称 符号 数值 单位 上声腔边长 ${L_1}$ 0.2 m 下声腔边长 ${L_2}$ 0.3 m 薄膜半径 $R$ 0.017 m 薄膜厚度 $h$ 1×10–4 m 薄膜密度 ${\rho _{\rm me} }$ 980 kg/m3 薄膜杨氏模量 $E$ 2.1 MPa 薄膜泊松比 $\upsilon $ 0.49 实验测得的薄膜线性固有频率 $ {f_1} $ 77 Hz 薄膜立方非线性刚度 ${k_3}$ 3.50×106 N/m3 薄膜阻尼系数 $ \eta $ 8×10–5 s–1 空气声速 $ {c_0} $ 340 m/s 空气密度 ${\rho _{\rm{a}}}$ 1.29 kg/m3
下载: 导出CSV
-
[1] Moore K J, Vakakis A F 2018 Acta Mech. 229 4057
Google Scholar
[2] Mojahed A, Moore K, Bergman L A, Vakakis A F 2018 Int. J. Non Linear Mech. 107 94
Google Scholar
[3] Spadoni A, Daraio C 2010 Proc. Natl. Acad. Sci. U. S. A. 107 7230
Google Scholar
[4] Zhu X H, Li J F, Shen C, Peng X Y, Song A L, Li L Q, Cummer S A 2020 Appl. Phys. Lett. 116 34101
Google Scholar
[5] 梁彬, 袁樱, 程建春 2015 64 094305
Google Scholar
Liang B, Yuan Y, Cheng J C 2015 Acta Phys. Sin. 64 094305
Google Scholar
[6] 邹欣晔, 袁樱, 梁彬, 程建春 2013 应用声学 32 169
Google Scholar
Zou X Y, Yuan Y, Liang B, Cheng J C 2013 Appl. Acoust. 32 169
Google Scholar
[7] Zhu X F, Ramezani H, Shi C Z, Zhu J, Zhang X 2014 Phys. Rev. X 4 031042
[8] Liu T, Zhu X F, Chen F, Liang S J, Zhu J 2018 Phys. Rev. Lett. 120 124502
Google Scholar
[9] Nassar H, Xu X C, Norris A N, Huang G L 2017 J. Mech. Phys. Solids 101 10
Google Scholar
[10] Nassar H, Chen H, Norris A N, Huang G L 2018 Phys. Rev. B 97 014305
Google Scholar
[11] Fleury R, Sounas D L, Sieck C F, Haberman M R, Alù A 2014 Science 343 516
Google Scholar
[12] Khanikaev A B, Fleury R, Mousavi S H, Alù A 2015 Nat. Commun. 6 8260
Google Scholar
[13] Zhu X F, Zou X Y, Liang B, Cheng J C 2010 J. Appl. Phys. 108 124909
Google Scholar
[14] Peng Y G, Qin C Z, Zhao D G, Shen Y X, Xu X Y, Bao M, Jia H, Zhu X F 2016 Nat. Commun. 7 13368
Google Scholar
[15] Ding Y J, Peng Y G, Zhu Y F, Fan X D, Yang J, Liang B, Zhu X F, Wan X G, Cheng J C 2019 Phys. Rev. Lett. 122 014302
Google Scholar
[16] Chen Z X, Peng Y G, Li H X, Liu J J, Ding Y J, Liang B, Zhu X F, Lu Y Q, Cheng J C, Alù A 2021 Sci. Adv. 7 eabj1198
Google Scholar
[17] Nassar H, Yousefzadeh B, Fleury R, Ruzzene M, Alù A, Daraio C, Norris A N, Huang G L, Haberman M R 2020 Nat. Rev. Mater. 5 667
Google Scholar
[18] Liang B, Guo X S, Tu J, Zhang D, Cheng J C 2010 Nat. Mater. 9 989
Google Scholar
[19] Zhu Y F, Zou X Y, Liang B, Cheng J C 2015 Appl. Phys. Lett. 107 113501
Google Scholar
[20] Boechler N, Theocharis G, Daraio C 2011 Nat. Mater. 10 665
Google Scholar
[21] Wang Y F, Yousefzadeh B, Chen H, Nassar H, Huang G L, Daraio C 2018 Phys. Rev. Lett. 121 194301
Google Scholar
[22] Bunyan J, Moore K J, Mojahed A, Fronk M D, Leamy M, Tawfick S, Vakakis A F 2018 Phys. Rev. E 97 052211
Google Scholar
[23] Wang C G, Tawfick S, Vakakis A F 2020 Physica D 402 132229
Google Scholar
[24] Mojahed A, Bunyan J, Tawfick S, Vakakis A F 2019 Phys. Rev. Appl. 12 034033
Google Scholar
[25] Wei L S, Wang Y Z, Wang Y S 2020 Int. J. Mech. Sci. 173 105433
Google Scholar
[26] Bellet R, Cochelin B, Herzog P, Mattei P O 2010 J. Sound Vib. 329 2768
Google Scholar
[27] Bellet R, Cochelin B, Côte R, Mattei P O 2012 J. Sound Vib. 331 5657
Google Scholar
[28] Shao J W, Cochelin B 2014 Int. J. Non Linear Mech. 64 85
Google Scholar
[29] Bryk P Y, Côte R, Bellizzi S 2019 J. Sound Vib. 460 114868
Google Scholar
[30] Chauvin A, Monteil M, Bellizzi S, Côte R, Herzog P, Pachebat M 2018 J. Sound Vib. 416 244
Google Scholar
[31] Leissa A W 1969 Vibration of Plates (New York: Acoustical Society of America) pp44–45
[32] Manevitch L I 1999 Mathematical Models of Non-Linear Excitations, Transfer, Dynamics, and Control in Condensed Systems and Other Media (New York: Springer) pp269–300
[33] McFarland D M, Bergman L A, Vakakis A F 2005 Int. J. Non Linear Mech. 40 891
Google Scholar
下载:
计量
- 文章访问数: 4173
- PDF下载量: 81
- 被引次数: 0
