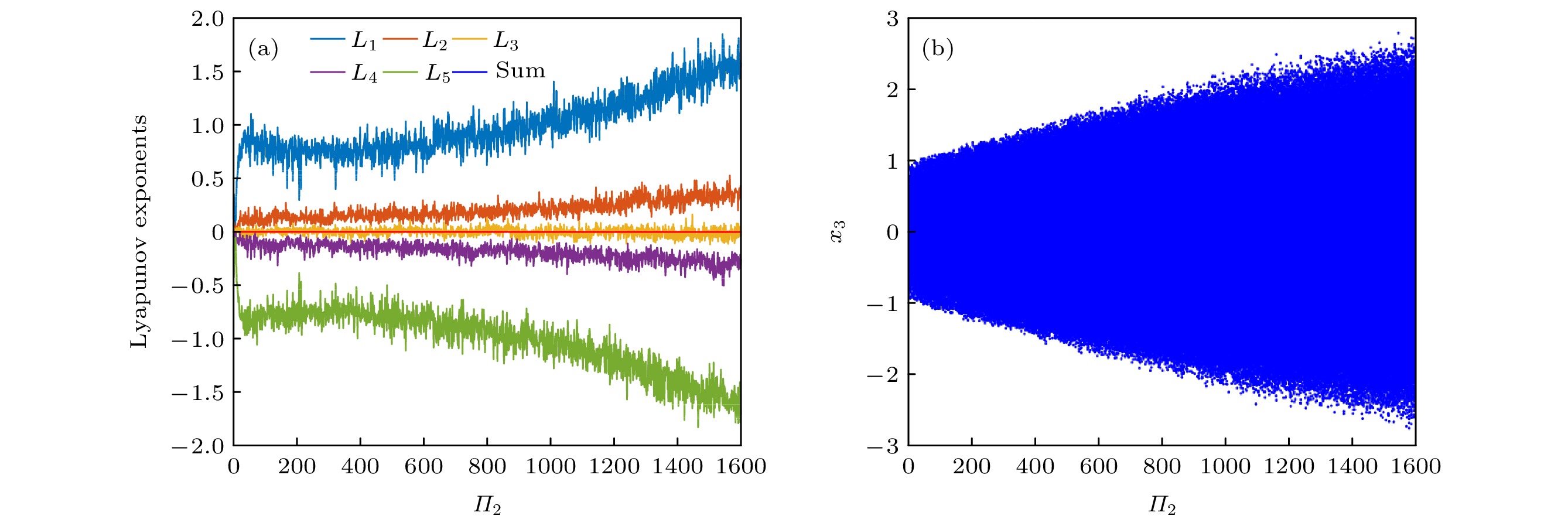
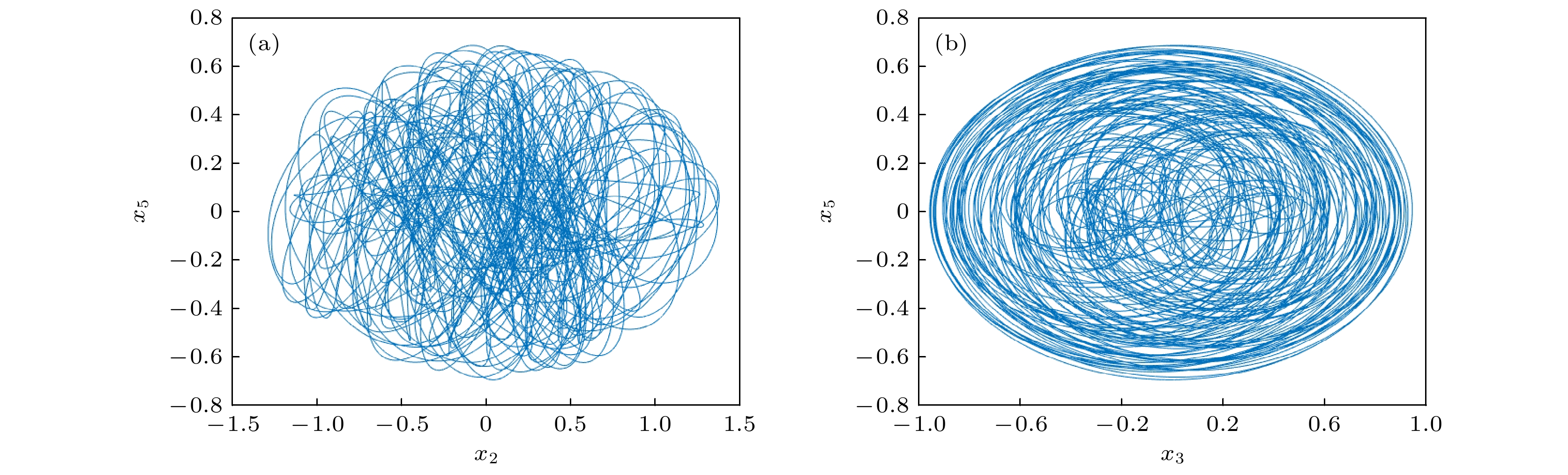
-
保守系统因为没有吸引子, 与常见的耗散系统相比, 它的遍历性更好, 伪随机性更强, 安全性更高, 更适合应用于混沌保密通信等领域. 基于此, 设计了一个新的具有宽参数范围的五维保守超混沌系统. 首先, 进行 Hamilton 能量和 Casimir 能量分析, 证明了新系统满足 Hamilton 能量保守且能够产生混沌. 然后进行动力学分析, 包括保守性证明、平衡点分析、Lyapunov 指数谱和分岔图分析, 证明了新系统具有保守系统的特点, 且能够在宽参数范围内一直保持超混沌状态, 同时对比宽参数范围内系统的相图和 Poincaré 截面图, 结果表明随着参数增大, 系统的随机性和遍历性得到增强. 接着, 对新系统进行 NIST 测试, 结果显示该系统在宽参数范围内产生的混沌随机序列具有很强的伪随机性. 最后对保守超混沌系统进行电路仿真和硬件电路实验, 实验结果证实了新系统具有良好的遍历性和可实现性.Conservative systems have no attractors. Therefore, compared with common dissipative systems, conservative systems have good ergodicity, strong pseudo-randomness and high security performance, thereby making them more suitable for applications in chaotic secure communication and other fields. Owing to these features, a new five-dimensional conservative hyperchaotic system with a wide parameter range is designed. Firstly, the Hamiltonian energy and Casimir energy are analyzed, showing that the new system satisfies the Hamiltonian energy conservation and can generate chaos. Next, the dynamic analysis is carried out, including conservativeness proof, equilibrium point analysis, Lyapunov exponential spectrum, and bifurcation diagrams analysis, thereby proving that the new system has the characteristics of conservative system and can always maintain a hyperchaotic state in a wide parameter range. At the same time, the phase diagram and Poincaré section diagram of the new system in a wide parameter range are compared. The results show that the randomness and ergodicity of the system are enhanced with the increase of parameters. Then, the NIST test shows that the chaotic random sequences generated by the new system in a wide parameter range have strong pseudo-randomness. Finally, the circuit simulation and hardware circuit experiment of the conservative hyperchaotic system are carried out, which proves that the new system has good ergodicity and realizability.
[1] 禹思敏, 吕金虎, 李澄清 2016 电子与信息学报 38 735
Yu S M, Lü J H, Li C Q 2016 J. Elec. Info. Tech. 38 735
[2] Lorenz E N 1963 J. Atmos. Sci. 20 130
[3] Sprott J C 1994 Phys. Rev. E 50 647
Google Scholar
[4] Chen G R, Ueta T 1999 Int. J. Bifurcation Chaos 9 1465
Google Scholar
[5] Lü J H, Chen G R 2002 Int. J. Bifurcation Chaos 12 659
Google Scholar
[6] Dang X Y, Li C B, Bao B C, Wu H G 2015 Chin. Phys. B 24 050503
Google Scholar
[7] 鲜永菊, 扶坤荣, 徐昌彪 2021 振动与冲击 40 15
Xian Y J, Fu K R, Xu C B 2021 J. Vib. Shock. 40 15
[8] Wang G Y, Yuan F, Chen G R, Zhang Y 2018 Chaos 28 013125
Google Scholar
[9] Akhshani A, Akhavan A, Mobaraki A, Lim S C, Hassan Z 2014 Commun. Nonlinear Sci. Numer. Simul. 19 101
Google Scholar
[10] Kadhim A F, Mhaibes H I 2018 Int. J. Appl. Eng. Res. 13 2141
[11] Qi G Y 2018 Nonlinear Dyn. 95 2063
Google Scholar
[12] Vaidyanathan S, Volos C 2015 Arch. Control Sci. 25 333
Google Scholar
[13] Cang S J, Wu A G, Wang Z H, Chen Z Q 2017 Nonlinear Dyn. 89 2495
Google Scholar
[14] Dong E Z, Yuan M F, Du S Z, Chen Z Q 2019 Appl. Math. Model. 73 40
Google Scholar
[15] Gu S Q, Du B X, Wan Y J 2020 Int. J. Bifurcation Chaos 30 2050242
Google Scholar
[16] Chen M, Wang C, Wu H G, Xu Q, Bao B C 2021 Nonlinear Dyn. 103 643
Google Scholar
[17] Bouteghrine B, Tanougast C, Sadoudi S 2021 J. Circuits Syst. Comput. 30 2150280
Google Scholar
[18] Lin Z S, Wang G Y, Wang X Y, Yu S M, Lü J H 2018 Nonlinear Dyn. 94 1003
Google Scholar
[19] 徐昌彪, 钟德, 夏诚, 黎周 2019 振动与冲击 38 125
Xu C B, Zhong D, Xia C, Li Z 2019 J. Vib. Shock. 38 125
[20] Barboza R 2007 Int. J. Bifurcation Chaos 17 4285
Google Scholar
[21] 贾红艳, 陈增强, 袁著祉 2009 58 4469
Google Scholar
Jia H Y, Chen Z Q, Yuan Z Z 2009 Acta Phys. Sin. 58 4469
Google Scholar
[22] Liu J M, Zhang W 2013 Optik 124 5528
Google Scholar
[23] Xian Y J, Xia C, Guo T T, Fu K R, Xu C B 2018 Results Phys. 11 368
Google Scholar
[24] 徐昌彪, 黎周 2019 浙江大学学报(工学版) 53 1552
Google Scholar
Xu C B, Li Z 2019 J. Zhejiang Univ. (Eng. Sci.) 53 1552
Google Scholar
[25] Sprott J C 2011 Int. J. Bifurcation Chaos 21 2391
Google Scholar
[26] Dong E Z, Jiao X D, Du S Z, Chen Z Q, Qi G Y 2020 Complexity 2020 4627597
Google Scholar
[27] Lakshmanan M, Rajasekar S 2003 Nonlinear Dynamics (Berlin Heidelberg: Springer-Verlag) pp191–238
[28] Wolf A, Swift J B, Swinney H L, Vastano J A 1985 Physica D 16 285
Google Scholar
[29] 包伯成 2013 混沌电路导论 (北京: 科学出版社) 第45—49页
Bao B C 2013 An Introduction to Chaotic Circuits (Beijing: Science Press) pp45−49 (in Chinese)
[30] Ramasubramanian K, Sriram M S 2000 Physica D 139 72
Google Scholar
[31] Rukhin A, Soto J, Nechvatal J, Smid M, Barker E, Leigh S, Levenson M, Vangel M, Banks D, Heckert A, Dray J, Vo S 2021https://csrc.nist.gov/publications/detail/sp/800-22/rev-1 a/final [2021-06-26]
[32] 禹思敏 2011 混沌系统与混沌电路 (西安: 西安电子科技大学出版社) 第293—312页
Yu S M 2011 Chaotic Systems and Chaotic Circuits (Xi’an: Xidian University Press) pp293−312 (in Chinese)
-
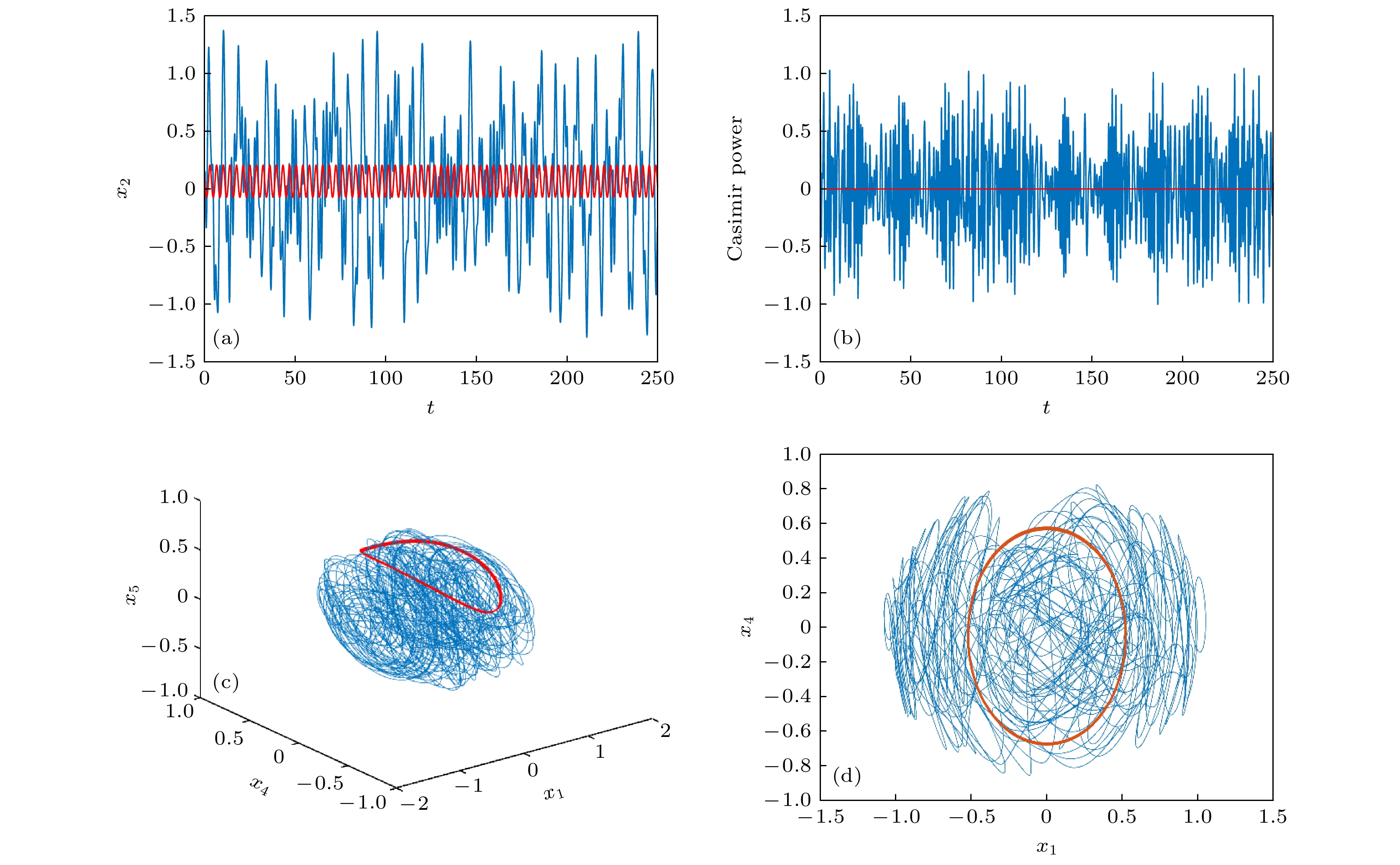
图 1 数值仿真, 红色部分为系统
${\varSigma _1}$ , 蓝色部分为系统$\varSigma _1^{\rm{H}}$ (a)时域波形; (b)Casimir功率; (c)${x_1}{\rm{ \text- }}{x_4}{\rm{ \text- }}{x_5}$ 相图; (d)${x_1}{\rm{ \text- }}{x_4}$ 相图Fig. 1. Numerical simulation, the red part is system
${\varSigma_1}$ , the blue part is system$\varSigma _1^{\rm{H}}$ : (a) Time domain waveforms; (b) Casimir power; (c)${x_1}{\rm{ \text- }}{x_4}{\rm{\text-}}{x_5}$ plane; (d)${x_1}{\rm{ \text- }}{x_4}$ plane.
图 2 数值仿真 (a)系统
$\varSigma_1^{\rm{H}}$ 的Lyapunov指数谱; (b)系统$\varSigma_1^{\rm{H}}$ 的分岔图Fig. 2. Numerical simulation: (a) Lyapunov exponent spectrum of system
$\varSigma _1^{\rm{H}}$ ; (b) bifurcation diagram of system$\varSigma _1^{ {{\rm{H}}}}$ 
图 3 系统
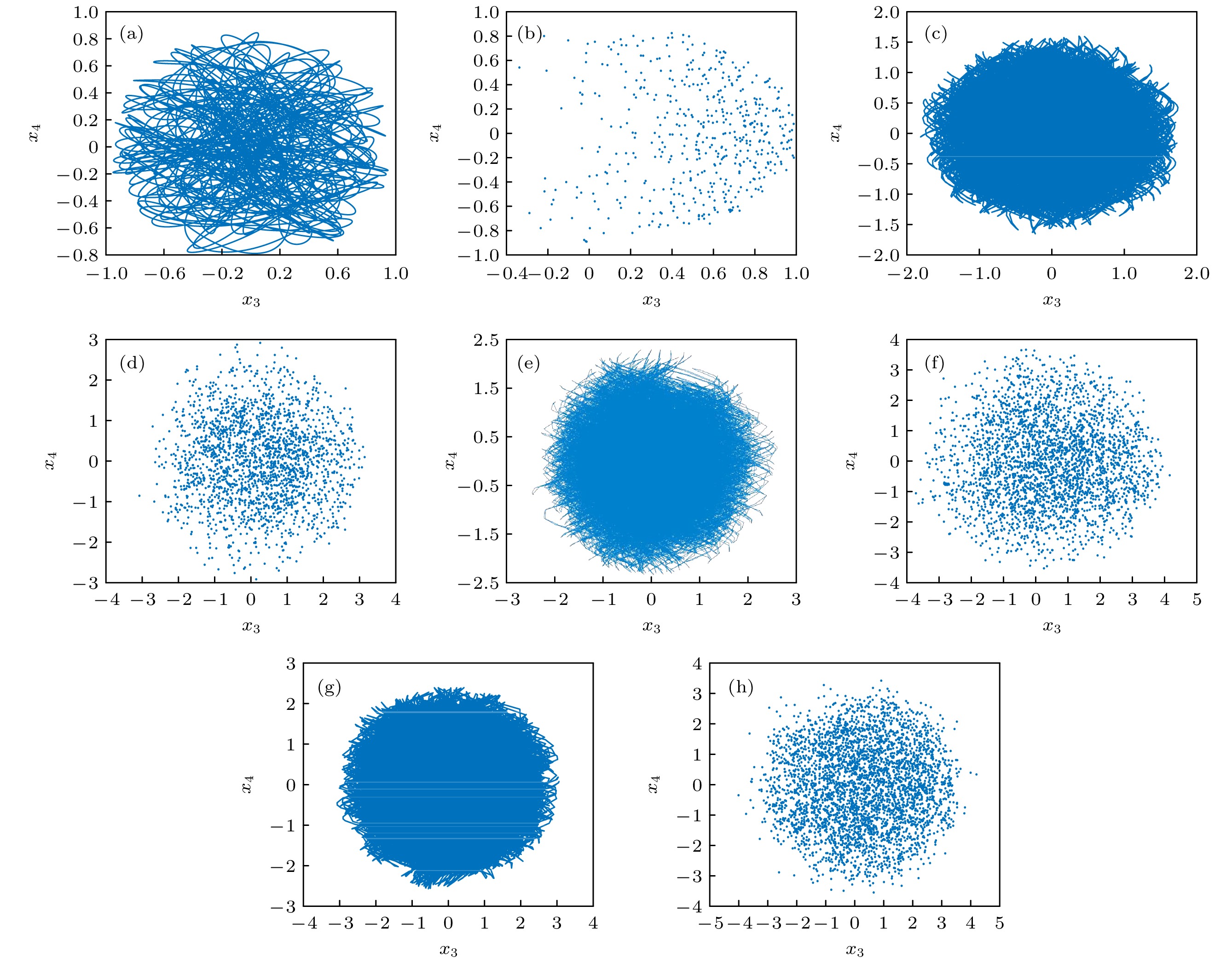
$\varSigma _1^{\rm{H}}$ 的相图和Poincaré截面图 (a)$ {\varPi _2} = 2 $ 时的相图; (b)$ {\varPi _2} = 2 $ 时的Poincaré截面图; (c)$ {\varPi _2} = 500 $ 时的相图; (d)$ {\varPi _2} = 500 $ 时的Poincaré截面图; (e)$ {\varPi _2} = 1000 $ 时的相图; (f)$ {\varPi _2} = 1000 $ 时的Poincaré截面图; (g)$ {\varPi _2} = 1500 $ 时的相图; (h)$ {\varPi _2} = 1500 $ 时的Poincaré截面图Fig. 3. Phase diagrams and Poincaré maps of system
$\varSigma _1^{\rm{H}}$ : (a) The phase diagram when$ {\varPi _2} = 2 $ ; (b) the Poincaré map when$ {\varPi _2} = 2 $ ; (c) the phase diagram when$ {\varPi _2} = 500 $ ; (d) the Poincaré map when$ {\varPi _2} = 500 $ ; (e) the phase diagram when$ {\varPi _2} = 1000 $ ; (f) the Poincaré map when$ {\varPi _2} = 1000 $ ; (g) the phase diagram when$ {\varPi _2} = 1500 $ ; (h) the Poincaré map when$ {\varPi _2} = 1500 $ .
图 4 系统
$\varSigma_1^{\rm{H}}$ 在$ {\varPi _2} = 2 $ 的相图 (a)${x_2}{\rm{ \text- }}{x_5}$ 平面; (b)${x_3}{\rm{ \text- }}{x_5}$ 平面Fig. 4. Phase diagrams of system
$\varSigma_1^{\rm{H}}$ when$ {\varPi _2} = 2 $ : (a)${x_2}{\rm{ \text- }}{x_5}$ plane; (b)${x_3}{\rm{ \text- }}{x_5}$ plane.
图 5 系统
$\varSigma_1^{\rm{H}}$ 非重叠模块匹配检验的P-values的直方图Fig. 5. P-values histogram of non-overlapping template matching test of system
$\varSigma _1^{\rm{H}}$ .
图 6 系统
$\varSigma_1^{\rm{H}}$ 的电路设计Fig. 6. Circuit design of system
$\varSigma_1^{\rm{H}}$ .
图 7 系统
$\varSigma _1^{\rm{H}}$ 的仿真电路 (a)${x_2}{\rm{ \text- }}{x_5}$ 相图; (b)${x_3}{\rm{ \text- }}{x_5}$ 相图Fig. 7. Simulation circuit of system
$\varSigma _1^{\rm{H}}$ : (a)${x_2}{\rm{ \text- }}{x_5}$ plane; (b)${x_3}{\rm{ \text- }}{x_5}$ plane.
图 8 系统
$\varSigma _1^{\rm{H}}$ 的实际电路 (a)硬件实验电路; (b)实验结果Fig. 8. Actual circuit of system
$\varSigma _1^{\rm{H}}$ : (a) Hardware experimental circuit; (b) experimental result.表 1 系统
$\varSigma_1^{\rm{H}}$ 的平衡点和特征值Table 1. Equilibrium points and characteristic values of system
$\varSigma _1^{\rm{H}}$ .系统 平衡点($ {k_1}, {k_4} \in \mathbb{R} $) 特征值($ \sigma , \omega \in {\mathbb{R}^ + } $) 平衡点类型 $\varSigma _1^{\rm{H} }$ $ (0, 0, 0, 0, 0) $ $ (0, {\rm{j}}{\omega _1}, - {\rm{j}}{\omega _1}, {\rm{j}}{\omega _2}, - {\rm{j}}{\omega _2}) $ 中心点 $ (0, {\sigma _1}, - {\sigma _2}, {\sigma _3} + {\rm{j}}\omega , {\sigma _3} - {\rm{j}}\omega ) $ 鞍焦点 $ ({k_1}, 0, 0, 0, 0) $ $ (0, {\sigma _1}, - {\sigma _2}, - {\sigma _3} + {\rm{j}}\omega , - {\sigma _3} - {\rm{j}}\omega ) $ 鞍焦点 $ (0, \sigma + {\rm{j}}{\omega _1}, \sigma - {\rm{j}}{\omega _1}, - \sigma + {\rm{j}}{\omega _2}, - \sigma - {\rm{j}}{\omega _2}) $ 鞍焦点 $ (0, {\sigma _1}, {\sigma _2}, - {\sigma _3}, - {\sigma _4}) $ 鞍焦点 $ (\sqrt 2 , 0, \sqrt 2 {k_4}, {k_4}, 0) $ $ (0, 0, - {\sigma _1}, {\sigma _2} + {\rm{j}}\omega , {\sigma _2} - {\rm{j}}\omega ) $ 鞍焦点 $ (0, \sigma + {\rm{j}}{\omega _1}, \sigma - {\rm{j}}{\omega _1}, - \sigma + {\rm{j}}{\omega _2}, - \sigma - {\rm{j}}{\omega _2}) $ 鞍焦点 $ (0, {\sigma _1}, {\sigma _2}, - {\sigma _3}, - {\sigma _4}) $ 鞍焦点 $ ( - \sqrt 2 , 0, - \sqrt 2 {k_4}, {k_4}, 0) $ $ (0, 0, {\sigma _1}, - {\sigma _2} + {\rm{j}}\omega , - {\sigma _2} - {\rm{j}}\omega ) $ 鞍焦点 $ (0, \sigma + {\rm{j}}{\omega _1}, \sigma - {\rm{j}}{\omega _1}, - \sigma + {\rm{j}}{\omega _2}, - \sigma - {\rm{j}}{\omega _2}) $ 鞍焦点 
下载: 导出CSV
表 2 系统
$\varSigma _1^{\rm{H}}$ 的NIST测试结果Table 2. NIST test results of System
$\varSigma _1^{\rm{H}}$ .No. Statistical test P-value Proportion 1 Frequency 0.759756 0.99 2 Block frequency 0.494392 1.00 3 Cumulative sums 0.595549 1.00 4 Runs 0.867692 0.99 5 Longest run 0.102526 0.98 6 Rank 0.115387 1.00 7 FFT 0.455937 1.00 8 Nonoverlapping template 0.015598 0.98 9 Overlapping template 0.699313 0.99 10 Universal 0.678686 0.98 11 Approximate entropy 0.574903 1.00 12 Random excursions 0.186566 0.9836 13 Random excursions variant 0.023812 1.00 14 Serial 0.514124 0.99 15 Linear complexity 0.350485 0.99
下载: 导出CSV
-
[1] 禹思敏, 吕金虎, 李澄清 2016 电子与信息学报 38 735
Yu S M, Lü J H, Li C Q 2016 J. Elec. Info. Tech. 38 735
[2] Lorenz E N 1963 J. Atmos. Sci. 20 130
[3] Sprott J C 1994 Phys. Rev. E 50 647
Google Scholar
[4] Chen G R, Ueta T 1999 Int. J. Bifurcation Chaos 9 1465
Google Scholar
[5] Lü J H, Chen G R 2002 Int. J. Bifurcation Chaos 12 659
Google Scholar
[6] Dang X Y, Li C B, Bao B C, Wu H G 2015 Chin. Phys. B 24 050503
Google Scholar
[7] 鲜永菊, 扶坤荣, 徐昌彪 2021 振动与冲击 40 15
Xian Y J, Fu K R, Xu C B 2021 J. Vib. Shock. 40 15
[8] Wang G Y, Yuan F, Chen G R, Zhang Y 2018 Chaos 28 013125
Google Scholar
[9] Akhshani A, Akhavan A, Mobaraki A, Lim S C, Hassan Z 2014 Commun. Nonlinear Sci. Numer. Simul. 19 101
Google Scholar
[10] Kadhim A F, Mhaibes H I 2018 Int. J. Appl. Eng. Res. 13 2141
[11] Qi G Y 2018 Nonlinear Dyn. 95 2063
Google Scholar
[12] Vaidyanathan S, Volos C 2015 Arch. Control Sci. 25 333
Google Scholar
[13] Cang S J, Wu A G, Wang Z H, Chen Z Q 2017 Nonlinear Dyn. 89 2495
Google Scholar
[14] Dong E Z, Yuan M F, Du S Z, Chen Z Q 2019 Appl. Math. Model. 73 40
Google Scholar
[15] Gu S Q, Du B X, Wan Y J 2020 Int. J. Bifurcation Chaos 30 2050242
Google Scholar
[16] Chen M, Wang C, Wu H G, Xu Q, Bao B C 2021 Nonlinear Dyn. 103 643
Google Scholar
[17] Bouteghrine B, Tanougast C, Sadoudi S 2021 J. Circuits Syst. Comput. 30 2150280
Google Scholar
[18] Lin Z S, Wang G Y, Wang X Y, Yu S M, Lü J H 2018 Nonlinear Dyn. 94 1003
Google Scholar
[19] 徐昌彪, 钟德, 夏诚, 黎周 2019 振动与冲击 38 125
Xu C B, Zhong D, Xia C, Li Z 2019 J. Vib. Shock. 38 125
[20] Barboza R 2007 Int. J. Bifurcation Chaos 17 4285
Google Scholar
[21] 贾红艳, 陈增强, 袁著祉 2009 58 4469
Google Scholar
Jia H Y, Chen Z Q, Yuan Z Z 2009 Acta Phys. Sin. 58 4469
Google Scholar
[22] Liu J M, Zhang W 2013 Optik 124 5528
Google Scholar
[23] Xian Y J, Xia C, Guo T T, Fu K R, Xu C B 2018 Results Phys. 11 368
Google Scholar
[24] 徐昌彪, 黎周 2019 浙江大学学报(工学版) 53 1552
Google Scholar
Xu C B, Li Z 2019 J. Zhejiang Univ. (Eng. Sci.) 53 1552
Google Scholar
[25] Sprott J C 2011 Int. J. Bifurcation Chaos 21 2391
Google Scholar
[26] Dong E Z, Jiao X D, Du S Z, Chen Z Q, Qi G Y 2020 Complexity 2020 4627597
Google Scholar
[27] Lakshmanan M, Rajasekar S 2003 Nonlinear Dynamics (Berlin Heidelberg: Springer-Verlag) pp191–238
[28] Wolf A, Swift J B, Swinney H L, Vastano J A 1985 Physica D 16 285
Google Scholar
[29] 包伯成 2013 混沌电路导论 (北京: 科学出版社) 第45—49页
Bao B C 2013 An Introduction to Chaotic Circuits (Beijing: Science Press) pp45−49 (in Chinese)
[30] Ramasubramanian K, Sriram M S 2000 Physica D 139 72
Google Scholar
[31] Rukhin A, Soto J, Nechvatal J, Smid M, Barker E, Leigh S, Levenson M, Vangel M, Banks D, Heckert A, Dray J, Vo S 2021https://csrc.nist.gov/publications/detail/sp/800-22/rev-1 a/final [2021-06-26]
[32] 禹思敏 2011 混沌系统与混沌电路 (西安: 西安电子科技大学出版社) 第293—312页
Yu S M 2011 Chaotic Systems and Chaotic Circuits (Xi’an: Xidian University Press) pp293−312 (in Chinese)
下载:
计量
- 文章访问数: 4932
- PDF下载量: 158
- 被引次数: 0
