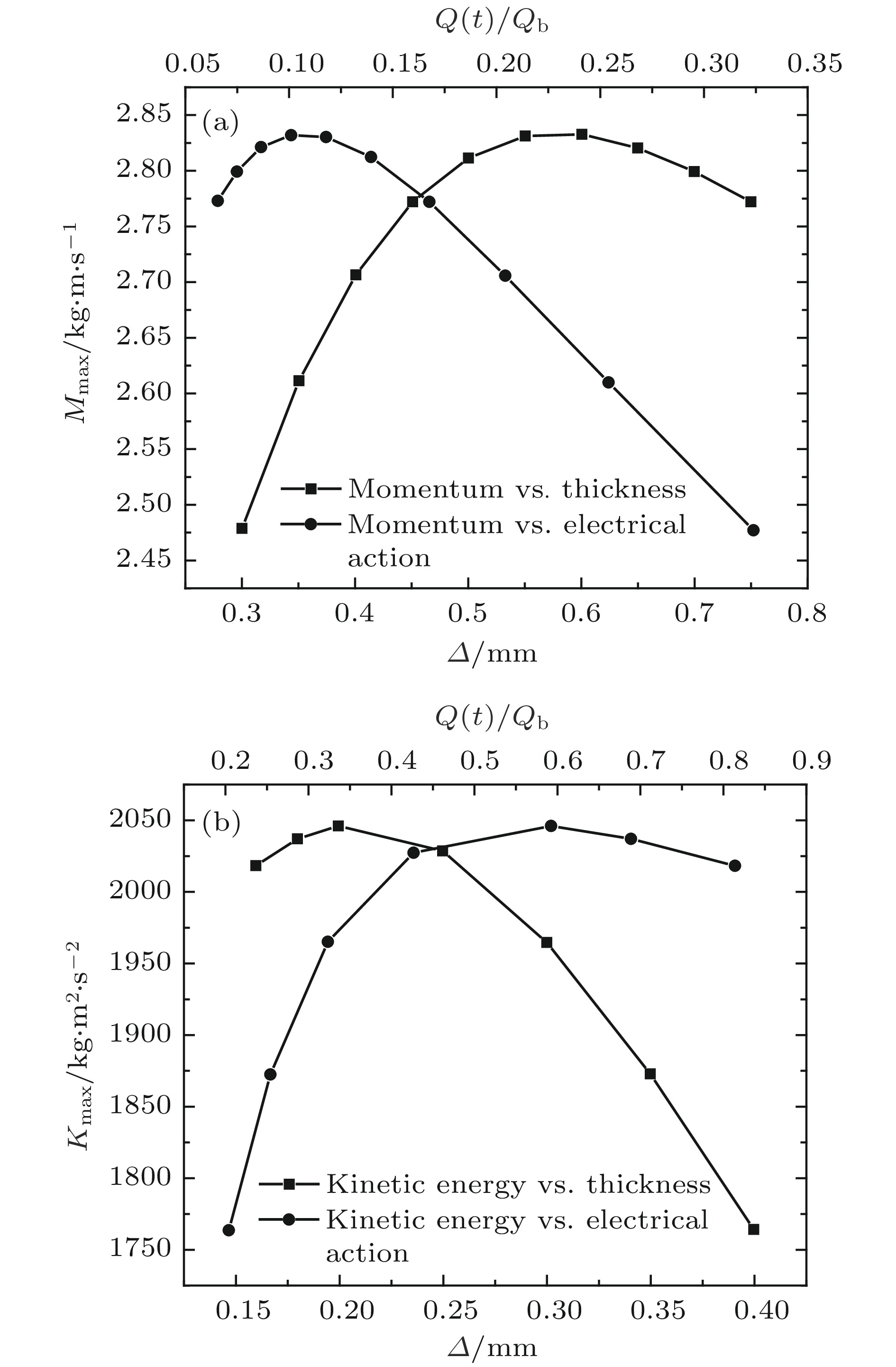
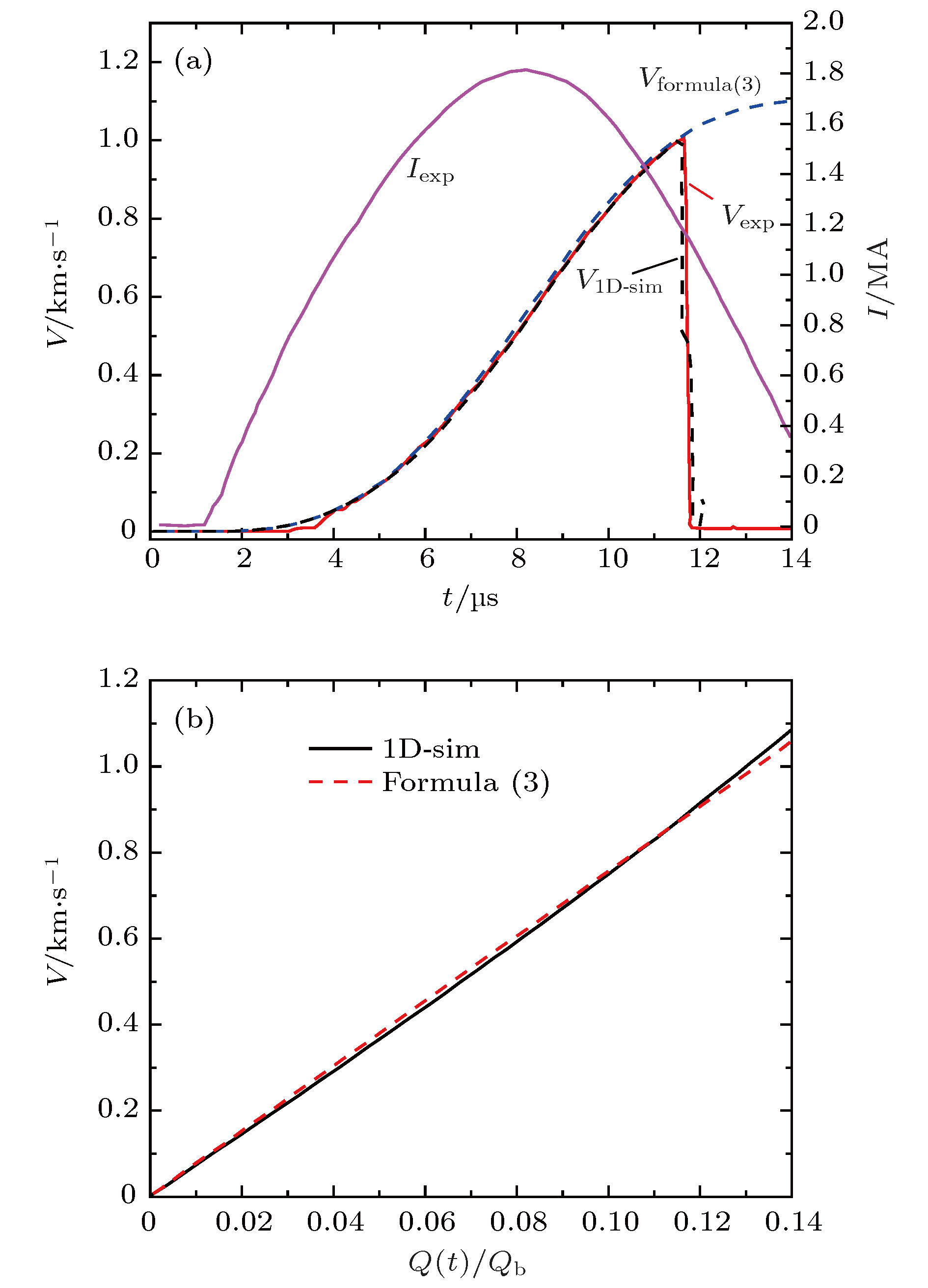
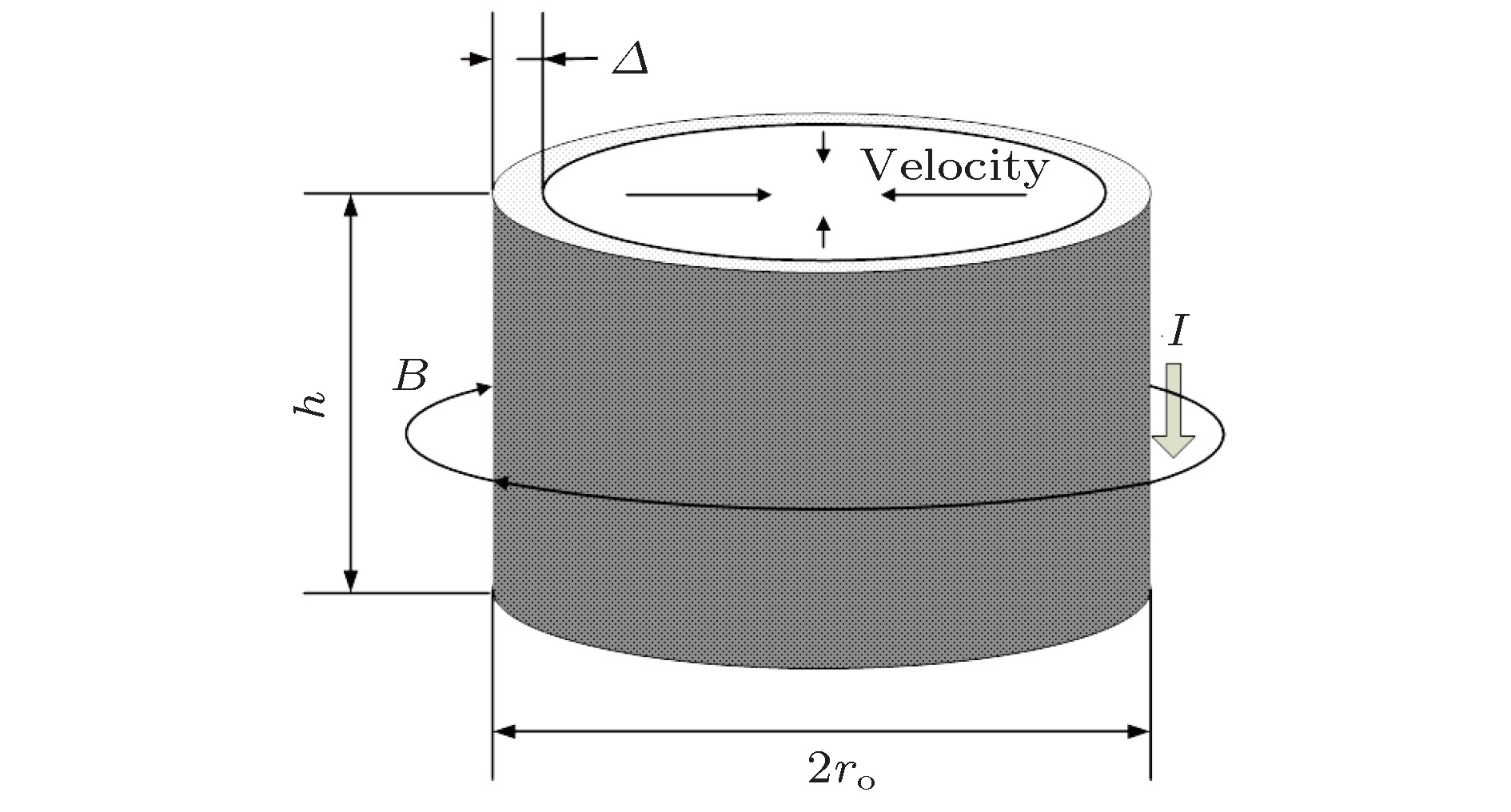
-
磁驱动固体套筒内爆作为标准柱面冲击/准等熵汇聚压缩加载方式, 在流体动力学、材料物性和聚变能源等领域具有广泛应用前景. 在特定加载条件下, 套筒飞层材料、半径和厚度的选择决定了套筒内爆力学行为, 而电流烧蚀限制了所能选择的参数范围. 通过薄壁套筒假定引入作为动力学参量的电作用量概念, 利用不可压缩零维模型给出了低线电流密度下薄壁套筒尺寸优化设计方法和套筒飞层材料选择的原则; 将修正后的电阻率-电作用量模型嵌入自编的一维弹塑性磁流体力学程序SOL1D进行模拟计算, 分别与FP-1装置及ZR装置上的实验结果进行比对, 表明在大径厚比和低线电流密度加载下, 利用电作用量估算内爆速度及利用电爆炸丝实验获取的各阶段电作用量判断套筒物理状态是有效的.As a typical cylindrical-convergent drive technique, magnetically driven solid liner implosion could compress interior substance with a shock or quasi-isentropic manner, which has been widely used to investigate the hydrodynamic behavior, the dynamic characteristics of material and fusion energy and so on. For aspecific facility, the implosion parameters depend on material, radius and thickness of the liner, and the ablation of liner restrict the optional parameters. The concept of electrical action is introduced via thin shell model, which not only is the representation of states for conductive metal, but also indicates the change of liner velocity under the condition of thin shell hypothesis. The result shows that the outer velocity of liner increases linearly with electrical action and is directly proportional to liner thickness but inversely proportional to liner density. The incompressible zero-dimensional model is used to calculate the dynamic parameters of thin shell liner, including the implosion time, the outer interface velocity, the implosion kinetic energy, and the electrical action under the condition of low linear current density. There exist optimal radius and thickness which can achieve the maximum velocity, momentum, and kinetic energy. The aluminum is suitable for reaching higher velocity and the copper can obtain higher pressure according to a proportionality coefficient Qb/ρ which is an intrinsic quality of metal. A one-dimensional (1D) elastic plastic magnetic hydrodynamic code which is called SOL1D is developed to simulate liner implosion behavior. The modified relationship between resistivity and electrical action is introduced to SOL1D, which can adapt higher hydrodynamic pressure. According to current waves, the 1D code can be used to simulate liner implosion behavior for all kinds of current densities. The 1D simulation liner velocity is in agreement with both the experimental results and the electrical action model for liner implosion experiment on FP-1 facility. The simulation of isentropic compression experiment at ZR facility shows that the magnetic diffusion process is suppressed at extra high current density and hydrodynamic pressure, and the electrical action is larger than the experimental value of wire electrical explosion. The zero-dimensional (0D) and 1D simulation show that estimating the liner velocity and liner phase changing via the electrical action are suitable when thin shell hypothesis and low current density assumption are satisfied.
-
Keywords:
- solid liner /
- electrical action /
- zero-dimensional model /
- magneto-hydrodynamics simulation
[1] Bowers R L, Brownell J H, Lee H, Mclenithan K D, Scannapieco A J, Shananhan W R 1998 J. Appl. Phys. 83 4146
Google Scholar
[2] Hanmmerberg J E, Kyrala G A, Oro D M, Fulton R D, Anderson W E, Obst A W, Oona H, Stokes J 1999 Los Alamos National Laboratory Report LA-UR-99-3378 (New Mexico: Los Alamos National Laboratory)
[3] Degnan J H, Alme M L, Austin B S, et al. 1999 Phys. Rev. Lett. 82 2681
Google Scholar
[4] Reinovsky R E 2000 IEEE Trans. Plasma Sci. 28 1563
Google Scholar
[5] Rodriguez G, Roberts J P, Echave J A, Taylor A J 2001 Rev. Sci. Instrum. 72 3230
Google Scholar
[6] Rodriguez G, Roberts J P, Echave J A, Taylor A J 2003 J. Appl. Phys. 93 1791
Google Scholar
[7] Turchi P J, Reass W A, Rousculp C L, Reinovsky R E, Griego J R, Oro D M 2011 IEEE Trans. Plasma Sci. 39 2006
Google Scholar
[8] Rousculp C L, Oro D M, Margolin L G, Griego J R, Reinovsky R E, Turchi P J 2015 Los Alamos National Laboratory Report LA-UR-15-25643 (New Mexico: Los Alamos National Laboratory)
[9] Freeman M S, Cousculp C, Oro D, Kreher S, Cheng B L, Griego J, Patten A, Neukirch L, Reinovsky R, Truchi P, Bradley J, Reass W, Fierro F, Randolph R, Donovan J, Saunders A, Mariam F, Tang Z W 2018 AIP Conf. Proc. 1979 080005
[10] 张扬, 戴自换, 孙奇志, 章征伟, 孙海权, 王裴, 丁宁, 薛创, 王冠琼, 沈智军, 李肖, 王建国 2018 67 080701
Google Scholar
Zhang Y, Dai Z H, Sun Q Z, Zhang Z W, Sun H Q, Wang P, Ding N, Xue C, Wang G Q, Shen Z J, Li X, Wang J G 2018 Acta Phys. Sin. 67 080701
Google Scholar
[11] Atchison W L, Faehl R J, Lindemuth I R, Reinovsky R E 2005 Los Alamos National Laboratory Report LA-UR-04-9044 (New Mexico: Los Alamos National Laboratory)
[12] Lemke R W, Dolan D H, Dalton D G, Brown J L, Tomlinson K, Robertson G R, Knudson M D, Harding E, Mattsson A E, Carpenter J H, Drake R R, Cochrane K, Blue B E, Robinson A C, Mattsson T R 2016 J. Appl. Phys. 119 015904
Google Scholar
[13] Degnan J H, Taccetti J M, Cavazos T, Clark D, Coffey S K, Faehl R J, Frese M H, Fulton D, Gueits J C, Gale D, Hussey T W, Intrator T P, Kirkpatrick R C, Kiuttu G H, Lehr F M, Letterio J D, Lindemuth I, McCullough W F, Moses R, Peterkin R E, Jr., Reinovsky R E, Roderick N F, Ruden E L, Shlachter J S, Schoenberg K F, Siemon R E, Sommars W, Turchi P J, Wurden G A, Wysocki F 2001 IEEE Trans. Plasma Sci. 29 93
Google Scholar
[14] Intrator T, Taccetti M, Clark D A, et al. 2002 Nucl. Fusion 42 211
Google Scholar
[15] Sun Q Z, Yang X J, Jia Y S, Li L L, Fang D F, Zhao X M, Qin W D, Liu Z F, Liu W, Li J, Chi Y, Wang X G 2017 Matter Radiat. Extremes 2 263
Google Scholar
[16] Turchi P J, Baker W L 1973 J. Appl. Phys. 44 4936
Google Scholar
[17] 章征伟, 魏懿, 孙奇志, 刘伟, 赵小明, 张朝辉, 王贵林, 郭帅, 谢卫平 2016 强激光与粒子束 28 045017
Google Scholar
Zhang Z W, Wei Y, Sun Q Z, Liu W, Zhao X M, Zhang Z H, Wang G L, Guo S, Xie W P 2016 High Power Laser and Particle Beams 28 045017
Google Scholar
[18] 张绍龙, 章征伟, 孙奇志, 刘伟, 赵小明, 张朝辉, 王贵林, 贾月松 2017 强激光与粒子束 29 105002
Google Scholar
Zhang S L, Zhang Z W, Sun Q Z, Liu W, Zhao X M, Zhang Z H, Wang G L, Jia Y S 2017 High Power Laser and Particle Beams 29 105002
Google Scholar
[19] Zhang S L, Liu W, Wang G L, Zhang Z W, Sun Q Z, Zhang Z H, Li J, Chi Y, Zhang N C 2019 Chin. Phys. B 28 044702
Google Scholar
[20] Faehl R J, Anderson B G, Clark D A, et al. 2004 IEEE Trans.Plasma Sci. 32 1972
Google Scholar
[21] Goforth J H, Atchison W L, Colgate S A, et al. 2009 Los Alamos National Laboratory Report LA-UR-09-04121 (New Mexico: Los Alamos National Laboratory)
[22] 孙奇志, 刘伟, 刘正芬, 池原, 戴文峰, 方东凡, 孙承伟 2009 强激光与粒子束 21 1571
Sun Q Z, Liu W, Liu Z F, Chi Y, Dai W F, Fang D F, Sun C W 2009 High Power Laser and Particle Beams 21 1571
[23] 王贵林, 郭帅, 沈兆武, 等 2014 63 196201
Google Scholar
Wang G L, Guo S, Shen Z W, et al. 2014 Acta Phys. Sin. 63 196201
Google Scholar
[24] 蔡进涛, 王桂吉, 赵剑衡, 莫建军, 翁继东, 吴刚, 赵峰 2010 高压 6 455
Google Scholar
Cai J T, Wang G J, Zhao J H, Mo J J, Weng J D, Wu G, Zhao F 2010 Chinese Journal of High Pressure Physics 6 455
Google Scholar
[25] Tucker T J, Toth R P 1975 Sandia National Laboratory Report SAND-75-0041 (New Mexico: Sandia National Laboratory)
[26] Wilkins M L 1999 Computer Simulation of Dynamic Phenomena (Berlin: Springer) pp63–64
[27] Brugess T J 1986 Sandia National Laboratory Report SAND-86-1093 C (New Mexico: Sandia National Laboratory)
[28] Steinberg D J, Cochran S G, Guinan M W 1980 J. Appl. Phys. 51 1498
Google Scholar
[29] Kraus R G, Davis J P, Seagle C T, Fratanduono D E, Swift D C, Brown J L, Eggert J H 2016 Phys. Rev. B 93 134105
Google Scholar
-
图 2 (a) 不同厚度套筒外界面速度随电作用量的变化; (b) 套筒初始外半径为15.5 mm时套筒外界面最大速度随厚度的变化
Fig. 2. (a) The relationship between outer surface velocity and electrical action with various liner thicknesses; (b) the change of outer surface velocity with the liner thickness for initial outer radius R0 = 15.5 mm.
图 3 (a) 最大动量和 (b) 最大动能随套筒厚度及电作用量的变化
Fig. 3. Change of (a) the maximum momentum and (b) the maximum kinetic energy vs. thickness and electrical action.
图 4 优化后的套筒速度及对应厚度随初始外半径的变化
Fig. 4. The optimal velocity and thickness of liner vs. initial outer radius.
图 5 (a) 冲击撞靶实验负载示意图; (b) 测速探针支架布局
Fig. 5. (a) The configration of impact experiment liner; (b) the layout of PDV probe.
图 7 ZR上的偏离雨贡纽实验结果和模拟对比 (a)测速曲线; (b)压力、密度剖面
Fig. 7. The comparison of experiment and simulation: (a) The velocity profile; (b) the pressure and density profile.
表 1 铝的电作用量常数
Table 1. Electrical action constants for aluminum
物态 电作用量Q/1016 A2·s·m–4 Qmb 2.52 Qme 3.20 Qv 4.86 Qb 6.58 
下载: 导出CSV
表 2 典型金属的材料特性数据
Table 2. The material constants for typical metals.
材料 电阻率η/μΩ·cm 密度ρ/g·cm–3 爆炸电作用量Qb/1016 A2·s·m–4 (Qb/ρ)/1010 A2·s·g–1·m–1 铝(Aluminum) 2.82 2.70 6.58 2.44 铜(Copper) 1.77 8.95 17.30 1.93 金(Gold) 2.44 19.30 8.30 0.43 铀(Uranium) 28.00 18.70 3.50 0.19
下载: 导出CSV
表 3 典型金属的碰撞压力
Table 3. The impact pressure of typical metals.
铝靶PI/GPa 铜靶PI/GPa 金靶PI/GPa 铀靶PI/GPa 铝飞层(2.44 km/s) 23.5 34.4 40.4 39.6 铜飞层(1.93 km/s) 26.1 46.4 60.4 59.3 金飞层(0.43 km/s) 5.5 10.3 14 12.9 铀飞层(0.19 km/s) 2.2 4.0 5.3 4.8
下载: 导出CSV
-
[1] Bowers R L, Brownell J H, Lee H, Mclenithan K D, Scannapieco A J, Shananhan W R 1998 J. Appl. Phys. 83 4146
Google Scholar
[2] Hanmmerberg J E, Kyrala G A, Oro D M, Fulton R D, Anderson W E, Obst A W, Oona H, Stokes J 1999 Los Alamos National Laboratory Report LA-UR-99-3378 (New Mexico: Los Alamos National Laboratory)
[3] Degnan J H, Alme M L, Austin B S, et al. 1999 Phys. Rev. Lett. 82 2681
Google Scholar
[4] Reinovsky R E 2000 IEEE Trans. Plasma Sci. 28 1563
Google Scholar
[5] Rodriguez G, Roberts J P, Echave J A, Taylor A J 2001 Rev. Sci. Instrum. 72 3230
Google Scholar
[6] Rodriguez G, Roberts J P, Echave J A, Taylor A J 2003 J. Appl. Phys. 93 1791
Google Scholar
[7] Turchi P J, Reass W A, Rousculp C L, Reinovsky R E, Griego J R, Oro D M 2011 IEEE Trans. Plasma Sci. 39 2006
Google Scholar
[8] Rousculp C L, Oro D M, Margolin L G, Griego J R, Reinovsky R E, Turchi P J 2015 Los Alamos National Laboratory Report LA-UR-15-25643 (New Mexico: Los Alamos National Laboratory)
[9] Freeman M S, Cousculp C, Oro D, Kreher S, Cheng B L, Griego J, Patten A, Neukirch L, Reinovsky R, Truchi P, Bradley J, Reass W, Fierro F, Randolph R, Donovan J, Saunders A, Mariam F, Tang Z W 2018 AIP Conf. Proc. 1979 080005
[10] 张扬, 戴自换, 孙奇志, 章征伟, 孙海权, 王裴, 丁宁, 薛创, 王冠琼, 沈智军, 李肖, 王建国 2018 67 080701
Google Scholar
Zhang Y, Dai Z H, Sun Q Z, Zhang Z W, Sun H Q, Wang P, Ding N, Xue C, Wang G Q, Shen Z J, Li X, Wang J G 2018 Acta Phys. Sin. 67 080701
Google Scholar
[11] Atchison W L, Faehl R J, Lindemuth I R, Reinovsky R E 2005 Los Alamos National Laboratory Report LA-UR-04-9044 (New Mexico: Los Alamos National Laboratory)
[12] Lemke R W, Dolan D H, Dalton D G, Brown J L, Tomlinson K, Robertson G R, Knudson M D, Harding E, Mattsson A E, Carpenter J H, Drake R R, Cochrane K, Blue B E, Robinson A C, Mattsson T R 2016 J. Appl. Phys. 119 015904
Google Scholar
[13] Degnan J H, Taccetti J M, Cavazos T, Clark D, Coffey S K, Faehl R J, Frese M H, Fulton D, Gueits J C, Gale D, Hussey T W, Intrator T P, Kirkpatrick R C, Kiuttu G H, Lehr F M, Letterio J D, Lindemuth I, McCullough W F, Moses R, Peterkin R E, Jr., Reinovsky R E, Roderick N F, Ruden E L, Shlachter J S, Schoenberg K F, Siemon R E, Sommars W, Turchi P J, Wurden G A, Wysocki F 2001 IEEE Trans. Plasma Sci. 29 93
Google Scholar
[14] Intrator T, Taccetti M, Clark D A, et al. 2002 Nucl. Fusion 42 211
Google Scholar
[15] Sun Q Z, Yang X J, Jia Y S, Li L L, Fang D F, Zhao X M, Qin W D, Liu Z F, Liu W, Li J, Chi Y, Wang X G 2017 Matter Radiat. Extremes 2 263
Google Scholar
[16] Turchi P J, Baker W L 1973 J. Appl. Phys. 44 4936
Google Scholar
[17] 章征伟, 魏懿, 孙奇志, 刘伟, 赵小明, 张朝辉, 王贵林, 郭帅, 谢卫平 2016 强激光与粒子束 28 045017
Google Scholar
Zhang Z W, Wei Y, Sun Q Z, Liu W, Zhao X M, Zhang Z H, Wang G L, Guo S, Xie W P 2016 High Power Laser and Particle Beams 28 045017
Google Scholar
[18] 张绍龙, 章征伟, 孙奇志, 刘伟, 赵小明, 张朝辉, 王贵林, 贾月松 2017 强激光与粒子束 29 105002
Google Scholar
Zhang S L, Zhang Z W, Sun Q Z, Liu W, Zhao X M, Zhang Z H, Wang G L, Jia Y S 2017 High Power Laser and Particle Beams 29 105002
Google Scholar
[19] Zhang S L, Liu W, Wang G L, Zhang Z W, Sun Q Z, Zhang Z H, Li J, Chi Y, Zhang N C 2019 Chin. Phys. B 28 044702
Google Scholar
[20] Faehl R J, Anderson B G, Clark D A, et al. 2004 IEEE Trans.Plasma Sci. 32 1972
Google Scholar
[21] Goforth J H, Atchison W L, Colgate S A, et al. 2009 Los Alamos National Laboratory Report LA-UR-09-04121 (New Mexico: Los Alamos National Laboratory)
[22] 孙奇志, 刘伟, 刘正芬, 池原, 戴文峰, 方东凡, 孙承伟 2009 强激光与粒子束 21 1571
Sun Q Z, Liu W, Liu Z F, Chi Y, Dai W F, Fang D F, Sun C W 2009 High Power Laser and Particle Beams 21 1571
[23] 王贵林, 郭帅, 沈兆武, 等 2014 63 196201
Google Scholar
Wang G L, Guo S, Shen Z W, et al. 2014 Acta Phys. Sin. 63 196201
Google Scholar
[24] 蔡进涛, 王桂吉, 赵剑衡, 莫建军, 翁继东, 吴刚, 赵峰 2010 高压 6 455
Google Scholar
Cai J T, Wang G J, Zhao J H, Mo J J, Weng J D, Wu G, Zhao F 2010 Chinese Journal of High Pressure Physics 6 455
Google Scholar
[25] Tucker T J, Toth R P 1975 Sandia National Laboratory Report SAND-75-0041 (New Mexico: Sandia National Laboratory)
[26] Wilkins M L 1999 Computer Simulation of Dynamic Phenomena (Berlin: Springer) pp63–64
[27] Brugess T J 1986 Sandia National Laboratory Report SAND-86-1093 C (New Mexico: Sandia National Laboratory)
[28] Steinberg D J, Cochran S G, Guinan M W 1980 J. Appl. Phys. 51 1498
Google Scholar
[29] Kraus R G, Davis J P, Seagle C T, Fratanduono D E, Swift D C, Brown J L, Eggert J H 2016 Phys. Rev. B 93 134105
Google Scholar
下载:
计量
- 文章访问数: 6146
- PDF下载量: 51
- 被引次数: 0
