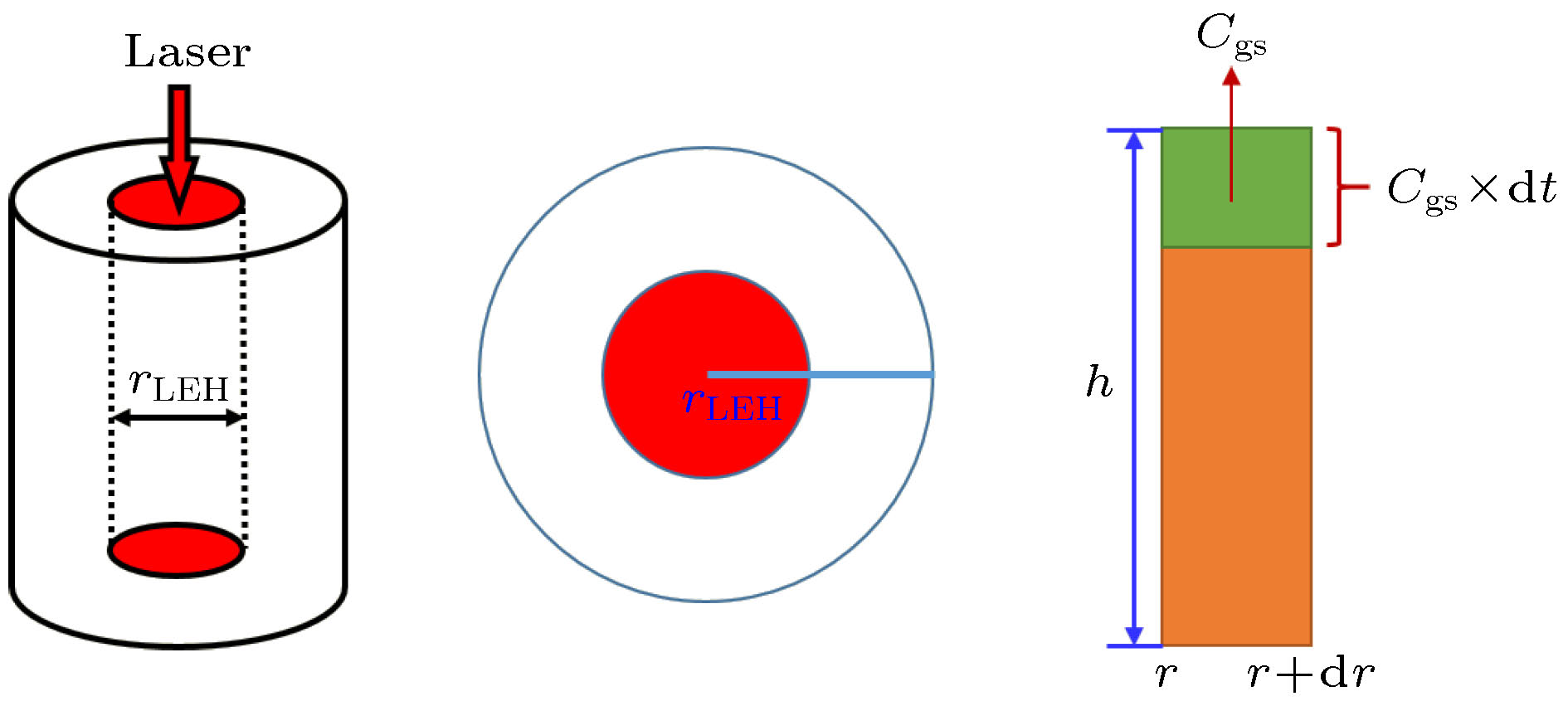
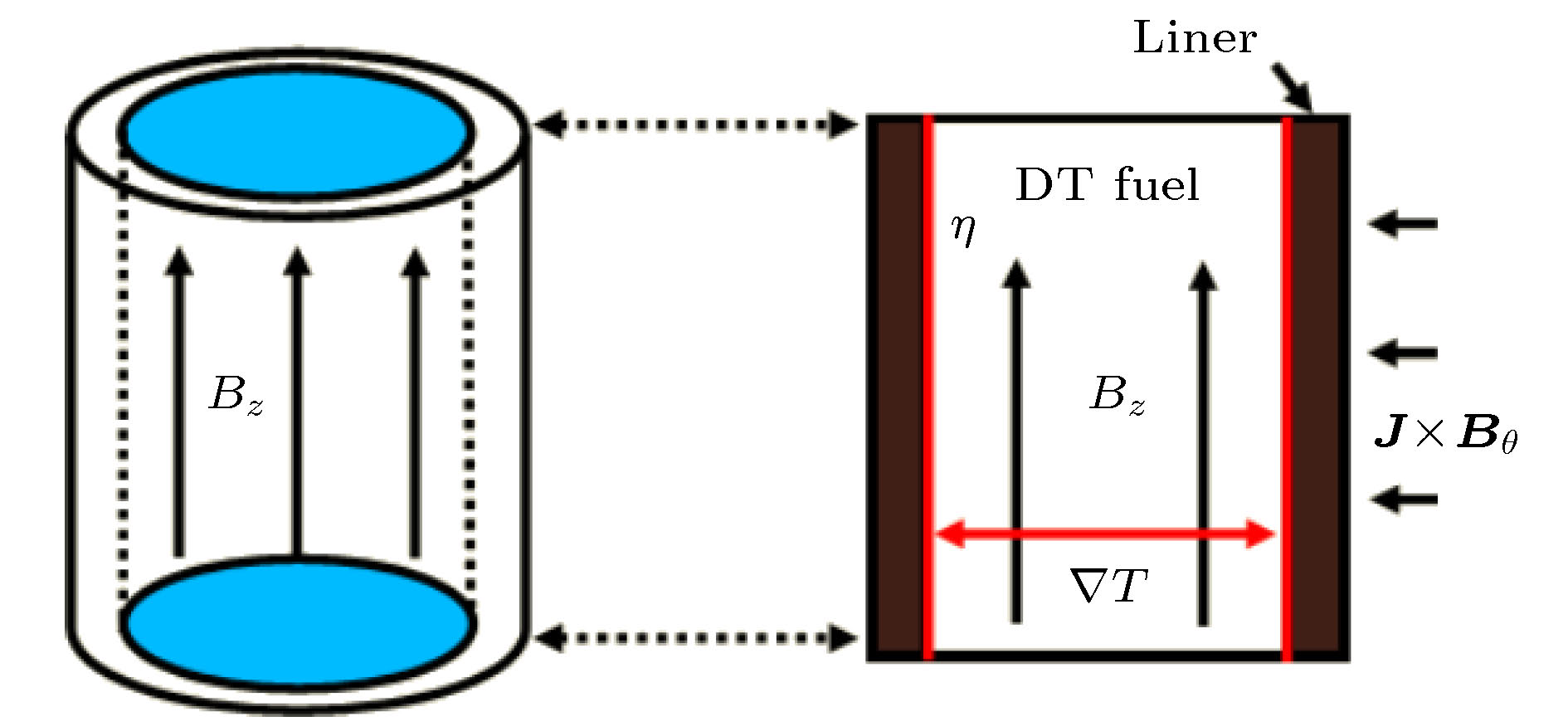
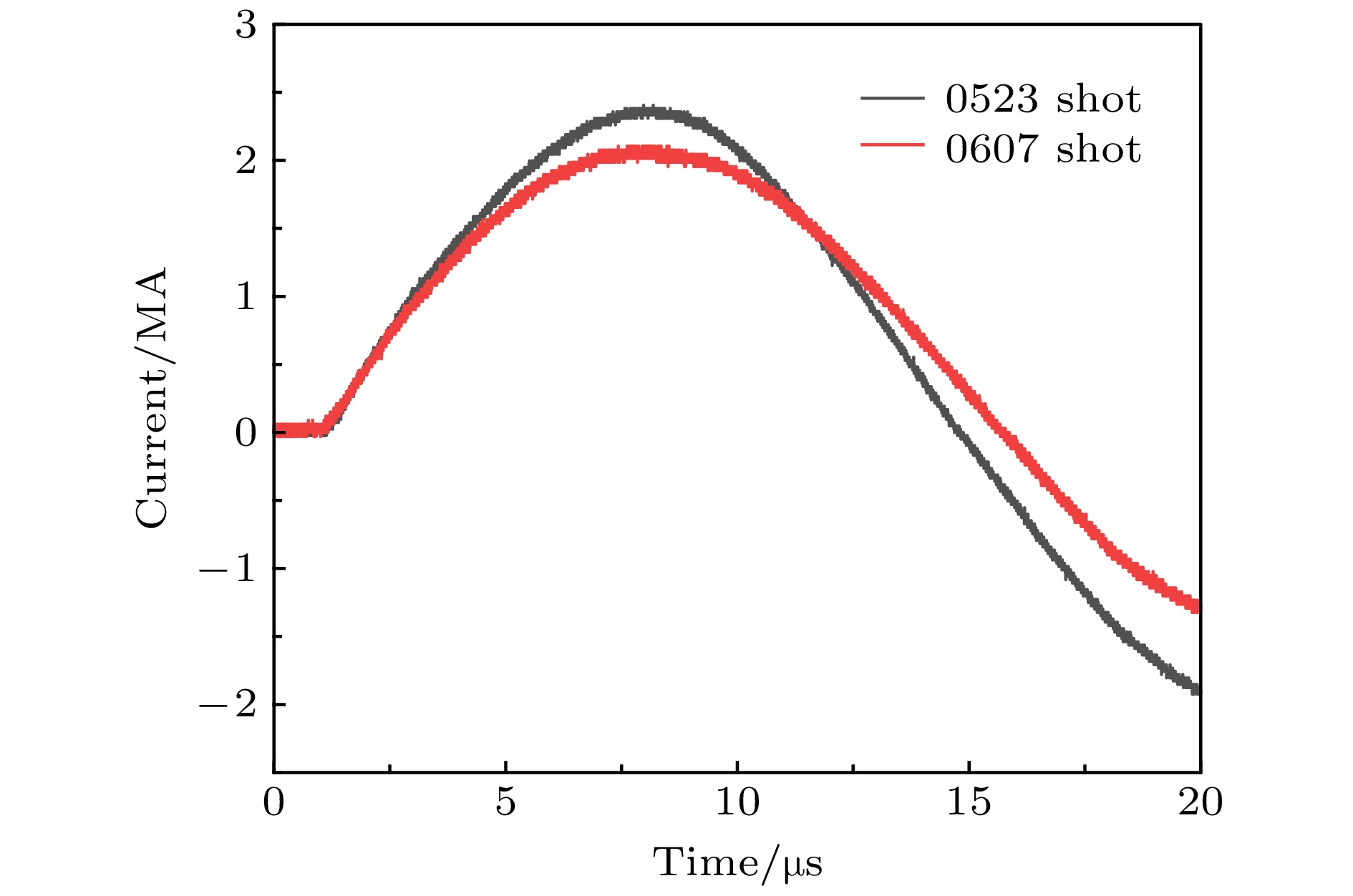
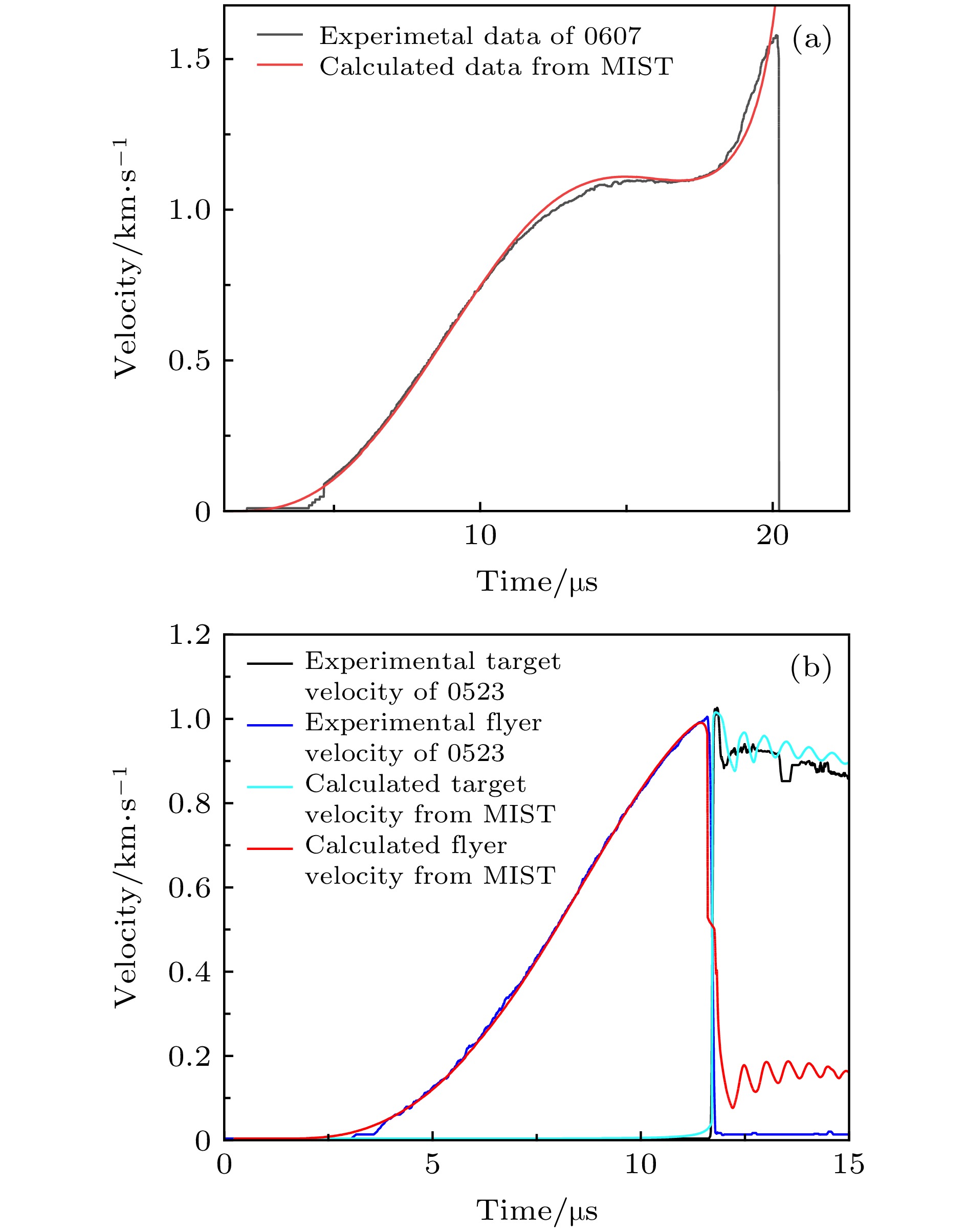
-
磁化套筒惯性聚变(magnetized liner inertial fusion, MagLIF)结合了传统磁约束聚变和惯性约束聚变的优点, 理论上可以显著地降低聚变实现的难度, 具有极大的应用潜力. 以研究MagLIF中的关键问题为目标, 建立能够综合考虑磁化、预加热、套筒内爆、聚变反应、端面效应、磁通压缩等多种复杂机制在内的集成化物理模型, 特别是通过引入流体喷射模型, 使得可以在一维计算条件下考虑具有二维特性的端面损失情况, 并额外考虑Nernst扩散项对磁通损失的影响. 在此基础上编写实现一维集成化MagLIF数值模拟程序MIST (magnetic implosion simulation tools), 与FP-1装置(2 MA, 7.2 μs)上铝套筒内爆实验结果的对比验证了程序磁流体模块的正确性; 将聚变模块纳入后与国外同类程序LASNEX和HYDRA计算结果进行整体比较, 所得数值结果总体接近, 主要差异体现在燃料温度的计算上, 对可能影响的原因进行了简要分析. 所建立的集成化模型与程序将为未来开展MagLIF聚变实验研究提供坚实的理论基础和重要工具.Magnetized liner inertial fusion (MagLIF) integrates the advantages of traditional magnetic confinement fusion with those of inertial confinement fusion, and thus has promising potentials because theoretically it can dramatically lower the difficulties in realizing the controlled fusion. For the systematic simulating of MagLIF, we build up an integrated one-dimensional (1D) model to describe the complex process, which includes the terms of magnetization, laser preheating, liner implosion, fusion reaction, end loss effect, and magnetic flux compression. According to this model we develop an integrated 1D code–MIST (magnetic implosion simulation tools) , and specifically we propose a simplified model to describe the end loss effect based on the flow bursting theory, so the code is able to consider two-dimensional effects within 1D calculations. We also present a specific expression of magnetic diffusion equation where the Nernst effect term is taken into consideration, which is very important if there exists a temperature gradient perpendicular to magnetic field lines. Such conditions are fully satisfied in the MagLIF process. We use experimental data of aluminum liner implosions to verify the magneto-hydrodynamic module of our code, those shots (0607 & 0523) are performed on FP-1 facility (2 MA, 7.2 μs), and results show good agreement with the calculated velocity of inner flyer or target surface and other measurements. Comparison with code LASNEX and HYDRA (used by Sandia Laboratory) is also made to assess the fusion module, and the results show that our calculations are physically self-consistent and roughly coincide with the results from LASNEX and HYDRA, a key difference appears at fuel temperature, and the factors that might cause this difference are discussed. With this integrated model and 1D code, our work would provide a powerful tool for the future experimental research of MagLIF.
-
Keywords:
- magnetized liner inertial fusion /
- integrated simulation /
- end loss /
- Nernst effect
[1] Sinars D B, Campbell E M, Cuneo M E, Jennings C A, Peterson K J, Sefkow A B 2016 J Fusion Energy 35 78
Google Scholar
[2] Ding B J, Bonoli P T, Tuccillo A, Goniche M, Kirov K, Li M, Li Y, Cesario R, Peysson Y, Ekedahl A, Amicucci L, Baek S, Faust I, Parker R, Shiraiwa S, Wallace G M, Cardinali A, Castaldo C, Ceccuzzi S, Mailloux J, Napoli F, Liu F, Wan B 2018 Nucl. Fusion 58 095003
Google Scholar
[3] Makwana K D, Keppens R, Lapenta G 2018 Phys. Plasmas 25 082904
Google Scholar
[4] Shimomura Y, Spears W 2004 IEEE Trans. Plasma Sci. 14 1369
[5] Clark D S, Weber C R, Milovich J L, Pak A E, Casey D T, Hammel B A, Ho D D, Jones O S, Koning J M, Kritcher A L, Marinak M M, Masse L P, Munro D H, Patel M V, Patel P K, Robey H F, Schroeder C R, Sepke S M, Edwards M J 2019 Phys. Plasmas 26 050601
Google Scholar
[6] Perkins L J, Logan B G, Zimmerman G B, Werner C J 2013 Phys. Plasmas 20 072708
Google Scholar
[7] McCrory R L, Meyerhofer D D, Betti R, Craxton R S, Delettrez J A, Edgell D H, Glebov V Yu, Goncharov V N, Harding D R, Jacobs-Perkins D W, Knauer J P, Marshall F J, McKenty P W, Radha P B, Regan S P 2008 Phys. Plasmas 15 055503
Google Scholar
[8] Chen Y Y, Bao X H, Fu P, Gao G 2019 Chin. Phys. B 28 015201
Google Scholar
[9] Zhang Y K, Zhou R J, Hu L Q, Chen M W, Chao Y 2018 Chin. Phys. B 27 055206
Google Scholar
[10] Tikhonchuk V, Gu Y J, Klimo O, Limpouch J, Weber S 2019 Matter Radiat. Extremes 4 045402
Google Scholar
[11] 薛全喜, 江少恩, 王哲斌, 王峰, 赵学庆, 易爱平, 丁永坤, 刘晶儒 2018 24 094701
Google Scholar
Xue Q X, Jiang S E, Wang Z B, Wang F, Zhao X Q, Yi A P, Ding Y K, Liu J R 2018 Acta Phys. Sin. 24 094701
Google Scholar
[12] Wu F Y, Chu Y Y, Ramis R, Li Z H, Ma Y Y, Yang J L, Wang Z, Ye F, Huang Z C, Qi J M, Zhou L, Liang C, Chen S J, Ge Z Y, Yang X H, Wang S W 2018 Matter Radiat. Extremes 3 248
Google Scholar
[13] Ding N, Zhang Y, Xiao D L, Wu J M, Dai Z H, Yin L, Gao Z M, Sun S K, Xue C, Ning C, Shu X J, Wang J G 2016 Matter Radiat. Extremes 1 135
Google Scholar
[14] Slutz S A, Herrmann M C, Vesey R A, Sefkow A B, Sinars D B, Rovang D C, Peterson K J, Cuneo M E 2010 Phys. Plasmas 17 056303
Google Scholar
[15] Slutz S A, Vesey R A 2012 Phys. Rev. Lett. 108 025003
Google Scholar
[16] Sefkow A B, Slutz S A, Koning J M, Marinak M M, Peterson K J, Sinars D B, Vesey R A 2014 Phys. Plasmas 21 072711
Google Scholar
[17] Slutz S A 2018 Phys. Plasmas 25 082707
Google Scholar
[18] Gomez M R, Slutz S A, Sefkow A B, Sinars D B, Hahn K D, Hansen S B, Harding E C, Knapp P F, Schmit P F, Jennings C A, Awe T J, Geissel M, Rovang D C, Chandler G A, Cooper G W, Cuneo M E, Harvey-Thompson A J, Herrmann M C, Hess M H, Johns O, Lamppa D C, Martin M R, McBride R D, Peterson K J, Porter J L, Robertson G K, Rochau G A, Ruiz C L, Savage M E, Smith I C, Stygar W A, Vesey R A 2014 Phys. Rev. Lett. 113 155003
Google Scholar
[19] Awe T J, McBride R D, Jennings C A, Lamppa D C, Martin M R, Rovang D C, Slutz S A, Cuneo M E, Owen A C, Sinars D B, Tomlinson K, Gomez M R, Hansen S B, Herrmann M C, McKenney J L, Nakhleh C, Robertson G K, Rochau G A, Savage M E, Schroen D G, Stygar W A 2013 Phys. Rev. Lett. 111 235005
Google Scholar
[20] Seyler C E, Martin M R, Hamlin N D 2018 Phys. Plasmas 25 062711
Google Scholar
[21] 赵海龙, 张恒第, 王刚华, 王强 2017 强激光与粒子束 29 072001
Zhao H L, Zhang H D, Wang G H, Wang Q 2017 High Power Laser and Particle Beams 29 072001
[22] Basko M M, Kemp A J, Meyer-ter-Vehn J 2000 Nucl. Fusion 40 59
Google Scholar
[23] Ramis R, Meyer-ter-Vehn J 2016 Comput. Phys. Commun. 203 226
Google Scholar
[24] Madrid E A, Rose D V, Welch D R, Clark R E, Mostrom C B, Stygar W A, Cuneo M E, Gomez M R, Hughes T P, Pointon T D, and Seidel D B 2013 Phys. Rev. ST Accel. Beams 16 120401
Google Scholar
[25] Gomez M R, Gilgenbach R M, Cuneo M E, Jennings C A, McBride R D, Waisman E M, Hutsel B T, Stygar W A, Rose D V, and Maron Y 2017 Phys. Rev. ST Accel. Beams 20 010401
Google Scholar
[26] Slutz S A 2012 Sandia National Laboratory Report SAND2012-1734 C
[27] Sefkow A B, Koning J M, Marinak M M, Nakhleh C W, Peterson K J, Sinars D B, Slutz S A, Vesey R A 2012 Sandia National Laboratory Report SAND2012-0876C
-
图 1 MagLIF过程示意图(包含3个主要阶段)
Fig. 1. Schematic of MagLIF process, including three main stages.
图 3 磁通压缩与扩散过程示意图
Fig. 3. Schematic of magnetic flux compression and diffusion process.
图 4 FP-1装置0523与0607发次实验驱动电流测量曲线
Fig. 4. Experimental current curves of shot 0523 & 0607.
图 5 MIST计算得到的自由面速度曲线与实验测量结果的比较 (a) 0607发次; (b) 0523发次
Fig. 5. Comparison of inner surface velocity curves between the calculations and measurements: (a) 0607 shot; (b) 0523 shot.
图 6 MIST程序计算得到的(a)监测点、(b)套筒内爆速度、(c)燃料温度, 以及(d)聚变产额等随时间的演化曲线
Fig. 6. Calculated results of (a) grid position, (b) implosion velocity, (c) fuel temperature, and (d) fusion yield evolving with time.
图 7 端面效应与Nernst效应影响下, 套筒内(a)燃料质量与(b)磁通随时间的演化
Fig. 7. (a) Fuel mass and (b) magnetic flux evolving with time with consideration of end loss and Nernst effect.
表 1 系数C0—C7的取值
Table 1. Values of coefficient C0–C7
C0 /keV1/3 C1/cm3·s–1 C2/keV–1 C3/keV–1 6.661 643.41×10–16 15.136×10–3 75.189×10–3 C4/keV–2 C5/keV–2 C6/keV–3 C7/keV–3 4.6064×10–3 13.5×10–3 –0.10675×10–3 0.01366×10–3 
下载: 导出CSV
表 2 MIST与LASNEX和HYDRA程序一维计算结果的对比
Table 2. Comparison of calculated results between MIST and LASNEX, HYDRA.
程序名称 燃料密度/g·cm–3 燃料温度/keV 磁场强度/103 T 压缩比 峰值压力/Gbar 聚变产额/kJ LASNEX 0.5 8 6—13 23 3 500 MIST 0.47 8.5 7 16 2.7 620 HYDRA 0.8—1.0 6—8 8—22 22 5 565 MIST 0.56 9.5 8 17 3.3 725
下载: 导出CSV
-
[1] Sinars D B, Campbell E M, Cuneo M E, Jennings C A, Peterson K J, Sefkow A B 2016 J Fusion Energy 35 78
Google Scholar
[2] Ding B J, Bonoli P T, Tuccillo A, Goniche M, Kirov K, Li M, Li Y, Cesario R, Peysson Y, Ekedahl A, Amicucci L, Baek S, Faust I, Parker R, Shiraiwa S, Wallace G M, Cardinali A, Castaldo C, Ceccuzzi S, Mailloux J, Napoli F, Liu F, Wan B 2018 Nucl. Fusion 58 095003
Google Scholar
[3] Makwana K D, Keppens R, Lapenta G 2018 Phys. Plasmas 25 082904
Google Scholar
[4] Shimomura Y, Spears W 2004 IEEE Trans. Plasma Sci. 14 1369
[5] Clark D S, Weber C R, Milovich J L, Pak A E, Casey D T, Hammel B A, Ho D D, Jones O S, Koning J M, Kritcher A L, Marinak M M, Masse L P, Munro D H, Patel M V, Patel P K, Robey H F, Schroeder C R, Sepke S M, Edwards M J 2019 Phys. Plasmas 26 050601
Google Scholar
[6] Perkins L J, Logan B G, Zimmerman G B, Werner C J 2013 Phys. Plasmas 20 072708
Google Scholar
[7] McCrory R L, Meyerhofer D D, Betti R, Craxton R S, Delettrez J A, Edgell D H, Glebov V Yu, Goncharov V N, Harding D R, Jacobs-Perkins D W, Knauer J P, Marshall F J, McKenty P W, Radha P B, Regan S P 2008 Phys. Plasmas 15 055503
Google Scholar
[8] Chen Y Y, Bao X H, Fu P, Gao G 2019 Chin. Phys. B 28 015201
Google Scholar
[9] Zhang Y K, Zhou R J, Hu L Q, Chen M W, Chao Y 2018 Chin. Phys. B 27 055206
Google Scholar
[10] Tikhonchuk V, Gu Y J, Klimo O, Limpouch J, Weber S 2019 Matter Radiat. Extremes 4 045402
Google Scholar
[11] 薛全喜, 江少恩, 王哲斌, 王峰, 赵学庆, 易爱平, 丁永坤, 刘晶儒 2018 24 094701
Google Scholar
Xue Q X, Jiang S E, Wang Z B, Wang F, Zhao X Q, Yi A P, Ding Y K, Liu J R 2018 Acta Phys. Sin. 24 094701
Google Scholar
[12] Wu F Y, Chu Y Y, Ramis R, Li Z H, Ma Y Y, Yang J L, Wang Z, Ye F, Huang Z C, Qi J M, Zhou L, Liang C, Chen S J, Ge Z Y, Yang X H, Wang S W 2018 Matter Radiat. Extremes 3 248
Google Scholar
[13] Ding N, Zhang Y, Xiao D L, Wu J M, Dai Z H, Yin L, Gao Z M, Sun S K, Xue C, Ning C, Shu X J, Wang J G 2016 Matter Radiat. Extremes 1 135
Google Scholar
[14] Slutz S A, Herrmann M C, Vesey R A, Sefkow A B, Sinars D B, Rovang D C, Peterson K J, Cuneo M E 2010 Phys. Plasmas 17 056303
Google Scholar
[15] Slutz S A, Vesey R A 2012 Phys. Rev. Lett. 108 025003
Google Scholar
[16] Sefkow A B, Slutz S A, Koning J M, Marinak M M, Peterson K J, Sinars D B, Vesey R A 2014 Phys. Plasmas 21 072711
Google Scholar
[17] Slutz S A 2018 Phys. Plasmas 25 082707
Google Scholar
[18] Gomez M R, Slutz S A, Sefkow A B, Sinars D B, Hahn K D, Hansen S B, Harding E C, Knapp P F, Schmit P F, Jennings C A, Awe T J, Geissel M, Rovang D C, Chandler G A, Cooper G W, Cuneo M E, Harvey-Thompson A J, Herrmann M C, Hess M H, Johns O, Lamppa D C, Martin M R, McBride R D, Peterson K J, Porter J L, Robertson G K, Rochau G A, Ruiz C L, Savage M E, Smith I C, Stygar W A, Vesey R A 2014 Phys. Rev. Lett. 113 155003
Google Scholar
[19] Awe T J, McBride R D, Jennings C A, Lamppa D C, Martin M R, Rovang D C, Slutz S A, Cuneo M E, Owen A C, Sinars D B, Tomlinson K, Gomez M R, Hansen S B, Herrmann M C, McKenney J L, Nakhleh C, Robertson G K, Rochau G A, Savage M E, Schroen D G, Stygar W A 2013 Phys. Rev. Lett. 111 235005
Google Scholar
[20] Seyler C E, Martin M R, Hamlin N D 2018 Phys. Plasmas 25 062711
Google Scholar
[21] 赵海龙, 张恒第, 王刚华, 王强 2017 强激光与粒子束 29 072001
Zhao H L, Zhang H D, Wang G H, Wang Q 2017 High Power Laser and Particle Beams 29 072001
[22] Basko M M, Kemp A J, Meyer-ter-Vehn J 2000 Nucl. Fusion 40 59
Google Scholar
[23] Ramis R, Meyer-ter-Vehn J 2016 Comput. Phys. Commun. 203 226
Google Scholar
[24] Madrid E A, Rose D V, Welch D R, Clark R E, Mostrom C B, Stygar W A, Cuneo M E, Gomez M R, Hughes T P, Pointon T D, and Seidel D B 2013 Phys. Rev. ST Accel. Beams 16 120401
Google Scholar
[25] Gomez M R, Gilgenbach R M, Cuneo M E, Jennings C A, McBride R D, Waisman E M, Hutsel B T, Stygar W A, Rose D V, and Maron Y 2017 Phys. Rev. ST Accel. Beams 20 010401
Google Scholar
[26] Slutz S A 2012 Sandia National Laboratory Report SAND2012-1734 C
[27] Sefkow A B, Koning J M, Marinak M M, Nakhleh C W, Peterson K J, Sinars D B, Slutz S A, Vesey R A 2012 Sandia National Laboratory Report SAND2012-0876C
下载:
计量
- 文章访问数: 6892
- PDF下载量: 70
- 被引次数: 0
