-
钝体是目前各种工程中广泛应用的一种结构. 钝体绕流的尾迹涡动力学也是经典的流体力学研究对象之一. 本文通过直接数值模拟, 针对低雷诺数下各种钝体结构的不可压缩绕流, 当形成三维尾迹时, 研究具有特定符号的涡量分布特征. 通过分析两类钝体结构, 基本的直柱体和受到几何扰动的柱体, 总结并得到了更为广泛适用的涡量符号律. 通过对比并分析这两类钝体结构, 结合理论证明的结果, 进一步厘清了对产生涡量符号律的这两类钝体结构之间的内在物理关联, 即引起自然失稳的小扰动在惯性力作用下产生的表面涡量只能向下游演化发展, 而几何扰动则根据扰动位置, 产生的表面涡量可以向扰动上游或下游演化发展. 从而可以推测所有钝体结构尾迹中的各种型式的涡脱落模态, 从涡量符号律的演化角度来看, 实际上是一致的, 都是起源于壁面产生特定符号组合规律的Π型涡.Bluff bodies possess many engineering applications. The flow past a bluff body is a classical issue in fluid mechanics. In most of previous studies, the role of streamwise vorticity is mainly stressed in three-dimensional wake flow, such as in the physical origin of streamwise vortices in the mode A, and the complete suppression of alternatively shedding Kármán vortices under the effect of geometric disturbances introduced in the bluff body. However, through the careful investigation of two examples above, the vertical vorticity actually plays a key role. Furthermore, there is a physical phenomenon, special relationship among dominant vorticity components with specific signs or vorticity sign law, occurring in the wake of a bluff body with geometric disturbances. In the present paper, through direct numerical simulations at low Reynolds numbers, such a phenomenon is summarized in two kinds of cylinders, i.e. basic straight cylinder and geometrically disturbed cylinder. Two typical cross-sections are examined, including the circular and square sections. Three sub-regimes (front surfaces, shear layers and wake) are mainly investigated. The numerical results show that two generalized vorticity sign laws exist in the wake of a bluff body. For example, the first sign law shows that the sign of streamwise vorticity is always the same as that of vertical vorticity in the upper shear layer, but opposite in the lower shear layer. The second sign law shows that the sign combination of three components of vorticity is always negative in the shear layers and wake. As for the physical mechanism of sign laws appearing in the present two kinds of cylinders, the main difference between the small perturbance which induces the natural three-dimensional instability and the geometric disturbance leads to the evolution of generated surface vorticity under the effect of inertial forces. These generalized sign laws have been already verified theoretically in the previous work recently. Moreover, sign laws also indicate that the different vortex-shedding patterns in the wake of different bluff bodies are inherently identical from the point of vorticity sign. Considering the physical fact that the wall is the only source of new vorticity in the present vortex dynamics, the theoretical results also indicate that the Π-type vortex with specific groups of vorticity components is a basic vortex pattern generated on the walls, once the three-dimensional wake first appears in the wake at low Reynolds number.
-
Keywords:
- vorticity /
- sign law /
- bluff body /
- wake
[1] Karniadakis G E, Triantafyllou G S 1992 J. Fluid Mech. 238 1
Google Scholar
[2] 武作兵, 凌国灿 1993 力学学报 25 264
Wu Z B, Ling G C 1993 Chin. J. Theoret. Appl. Mech. 25 264
[3] Barkely D, Henderson R D 1996 J. Fluid Mech. 322 215
Google Scholar
[4] Williamson C H K 1996 Annu. Rev. Fluid Mech. 28 477
Google Scholar
[5] Williamson C H K 1996 J. Fluid Mech. 328 345
Google Scholar
[6] Henderson R D 1997 J. Fluid Mech. 352 65
Google Scholar
[7] Leweke T, Williamson C H K 1998 Euro. J. Mech. B/Fluids 17 571
Google Scholar
[8] 凌国灿, 常勇 1999 力学学报 31 652
Ling G C, Chang Y 1999 Chin. J. Theoret. Appl. Mech. 31 652
[9] Barkley D, Tuckerman L S, Golubitsky M 2000 Phys. Rev. E 61 5247
Google Scholar
[10] Thompson M C, Leweke T, Williamson C H K 2001 J. Fluid. Struct. 15 607
Google Scholar
[11] Posdziech O, Grundmann R 2001 Theo. Comput. Fluid Dyn. 15 121
Google Scholar
[12] Rao A, Thompson M C, Leweke T, Hourigan K 2013 J. Fluid.Struct. 41 9
Google Scholar
[13] Sheard G J, Thompson M C, Hourigan K 2003 Phys. Fluids 15 L68
Google Scholar
[14] Jiang H, Cheng L, Draper S, An H, Tong F 2016 J. Fluid Mech. 801 353
Google Scholar
[15] Jiang H, Cheng L, Draper S, An H 2017 Comput. Fluids 149 172
Google Scholar
[16] Sarpkaya T 2004 J. Fluid. Struct. 19 389
Google Scholar
[17] Williamson C H K, Govardhan R 2004 Annu. Rev. Fluid Mech. 36 413
Google Scholar
[18] Gabbai R D, Benaroya H 2005 J. Sound Vib. 282 575
Google Scholar
[19] Williamson C H K, Govardhan R 2008 J. Wind Eng. Ind. Aerodyn. 96 713
Google Scholar
[20] Kumar R A, Sohn C H, Gowda B H L 2008 Recent Patents Mech. Eng. 1 1
Google Scholar
[21] Darekar R M, Sherwin S J 2001 J. Fluid Mech. 426 263
Google Scholar
[22] Lam K, Lin Y F 2008 Int. J. Heat Fluid Flow 29 1071
Google Scholar
[23] 林黎明 2007 博士学位论文 (北京: 中国科学院力学研究所)
Lin L M 2007 Ph. D. Dissertation (Beijing: Institute of Mechanics, Chinese Academy of Sciences) (in Chinese)
[24] Lin L M, Ling G C, Wu Y X 2010 Chin. Phys. Lett. 27 034702
Google Scholar
[25] Lin L M, Shi S Y, Wu Y X 2019 Acta Mech. Sin. 35 411
Google Scholar
[26] Lin L M, Zhong X F, Wu Y X 2018 Acta Mech. Sin. 34 812
Google Scholar
[27] Lin L M, Shi S Y, Zhong X F, Wu Y X 2019 Acta Mech. Sin. 35 1
Google Scholar
[28] Lin L M, Shi S Y, Wu Y X 2018 Theo. App. Mech. Lett. 8 320
Google Scholar
[29] Lin L M, Tan Z R 2019 Acta Mech. Sin. 35 1131
Google Scholar
[30] Meiburg E, Lasheras J C 1988 J. Fluid Mech. 190 1
Google Scholar
-
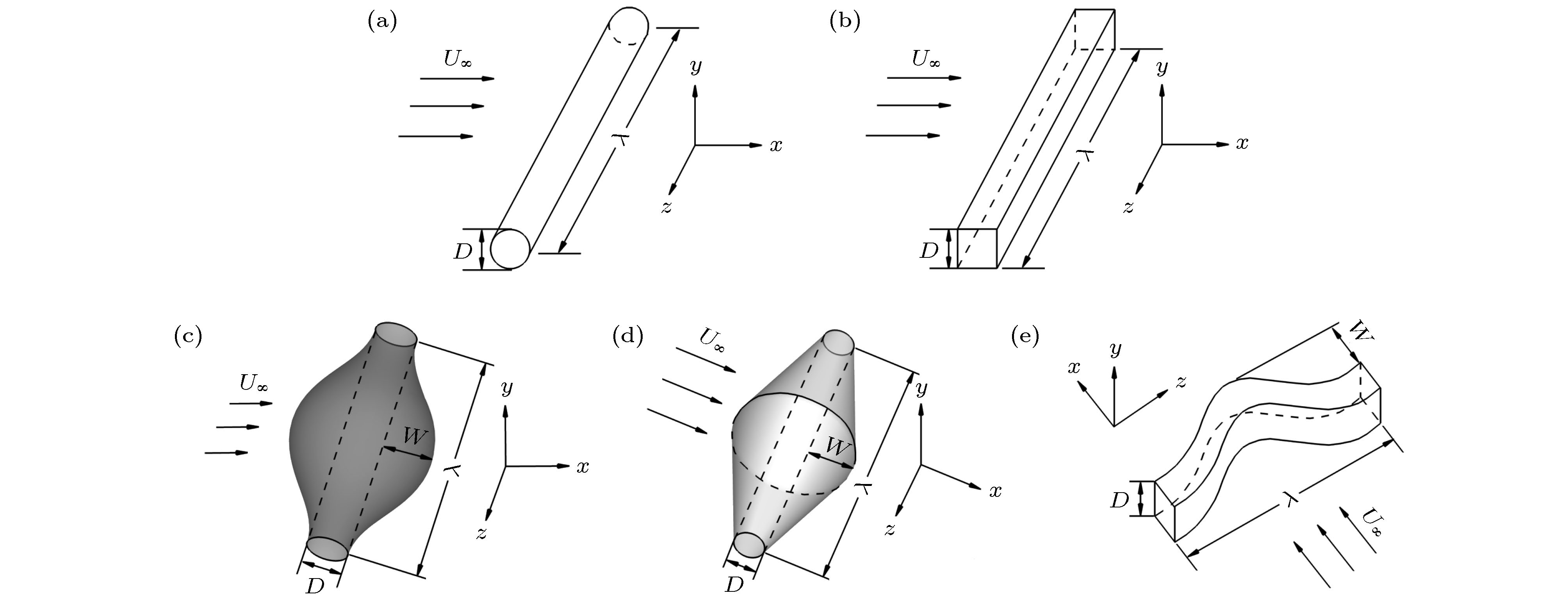
图 1 各种几何结构形式的钝体绕流示意图 (a)圆形截面的直圆柱; (b)方形截面的直方柱; (c)圆形截面的谐波柱; (d)圆形截面的圆锥柱; (e)方形截面的全弯曲方柱
Fig. 1. Schematics of a flow past a bluff body with different geometry: (a) The straight cylinder with circular cross-section; (b) the straight cylinder with square cross-section; (c) the harmonic cylinder with circular cross-section; (d) the conic cylinder with circular cross-section; (e) the wholly wavy cylinder with square cross-section.
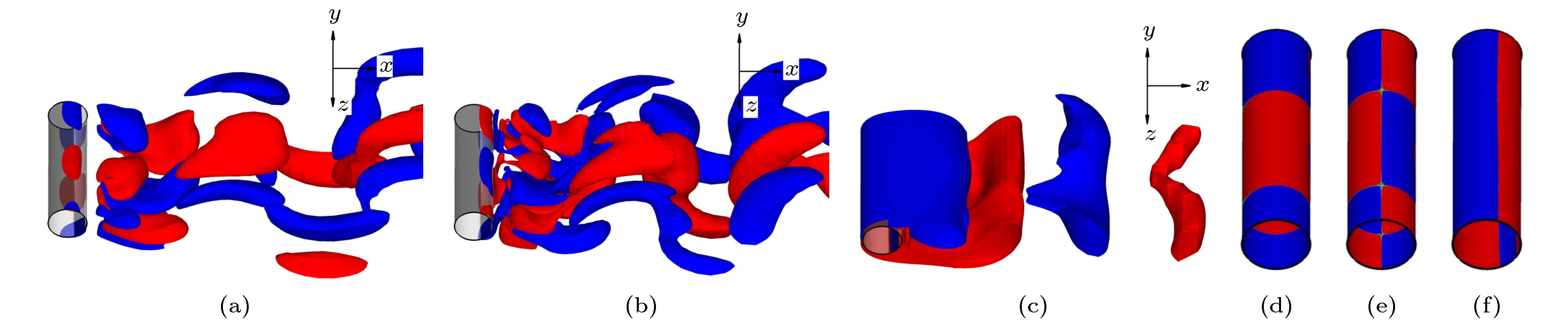
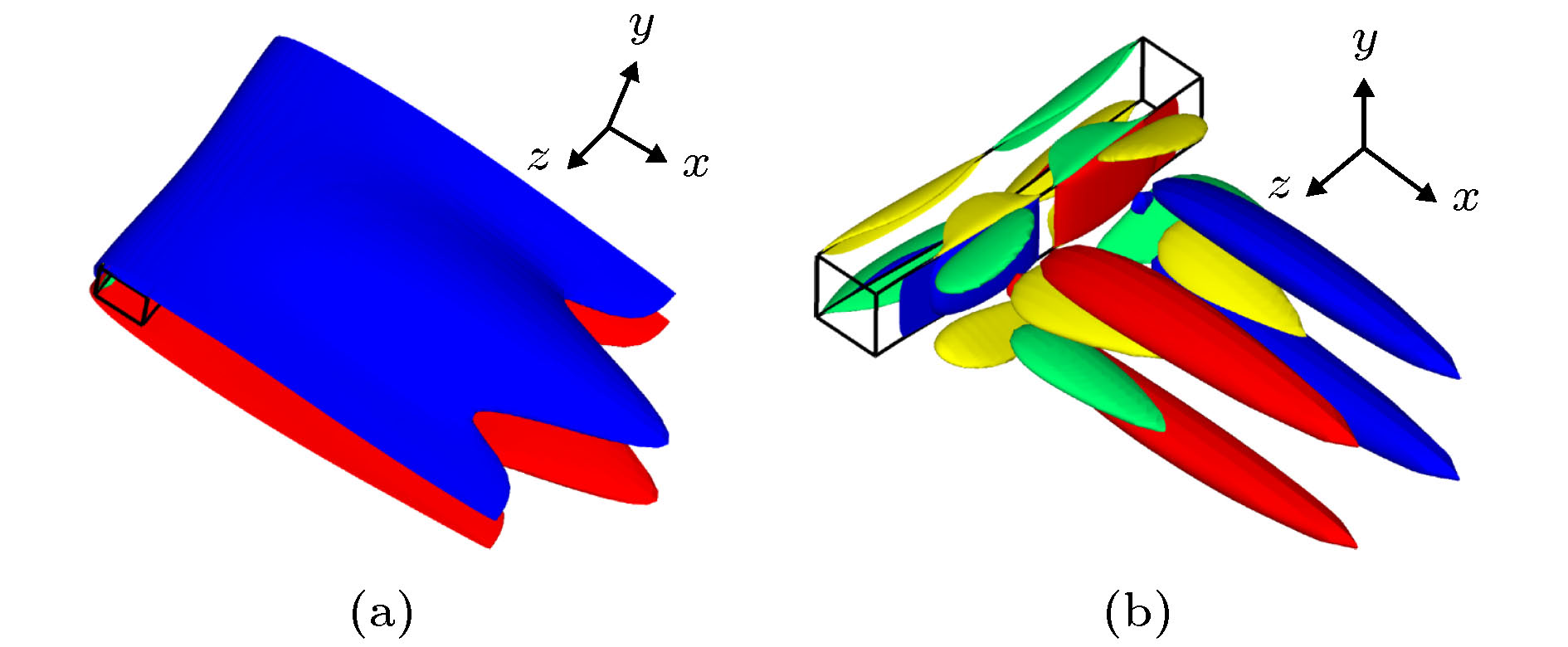
图 2 Re = 200时直圆柱尾迹中各个涡分量等值面以及柱体表面各个涡分量等值线(其中红色和蓝色分别表示正值和负值, 注意等值面图中采用半透明灰色面来表示圆柱体, 且流动从左至右) (a)
${\omega _x} = \pm 0.4$ 等值面; (b)${\omega _y} = \pm 0.2$ 等值面; (c)${\omega _z} = \pm 0.8$ 等值面; (d)${\omega _x}$ 等值线; (e)${\omega _y}$ 等值线; (f)${\omega _z}$ 等值线Fig. 2. At Re = 200, iso-surfaces of
${{\omega}}$ in the wake of a straight circular cylinder, and contours of${{\omega}}$ on cylinder surfaces, where red and blue colors denote positive and negative values, respectively: (a) Iso-surfaces of${\omega _x} = \pm 0.4$ ; (b) iso-surfaces of${\omega _y} = \pm 0.2$ ; (c) iso-surfaces of${\omega _z} = \pm 0.8$ ; (d) contours of${\omega _x}$ ; (e) contours of${\omega _y}$ ; (f) contours of${\omega _z}$ . Note that the cylinder is denoted by the grey translucent surface in iso-surfaces and the flow is from left to right.
图 3 Re = 300时直圆柱尾迹中各个涡分量等值面以及柱体表面各个涡分量等值线(其中红色和蓝色分别表示正值和负值, 以及等值线图中的绿色则表示
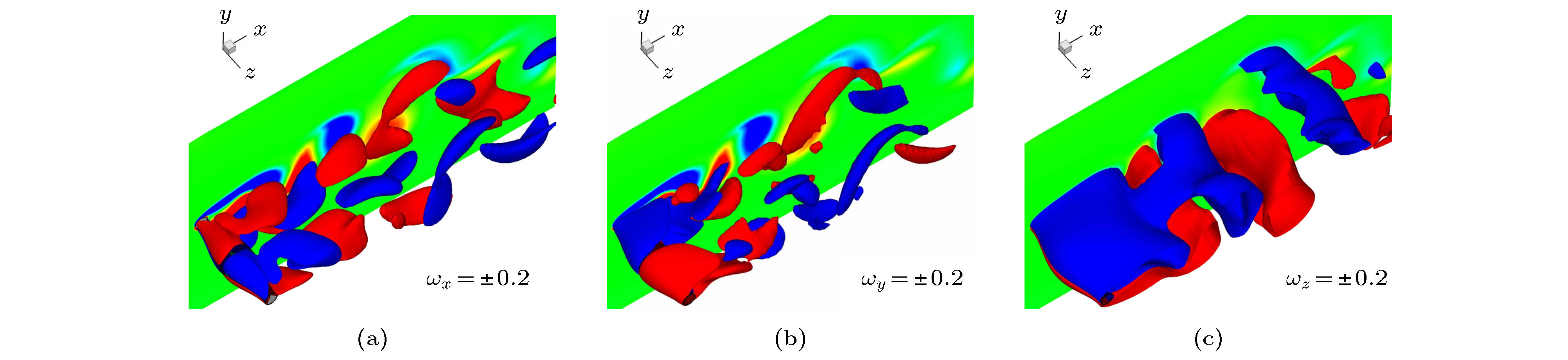
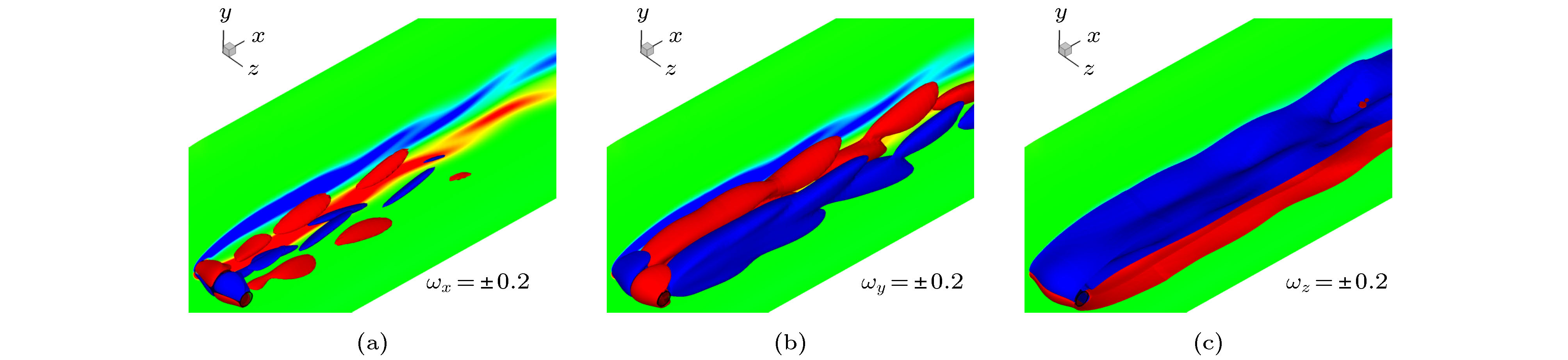
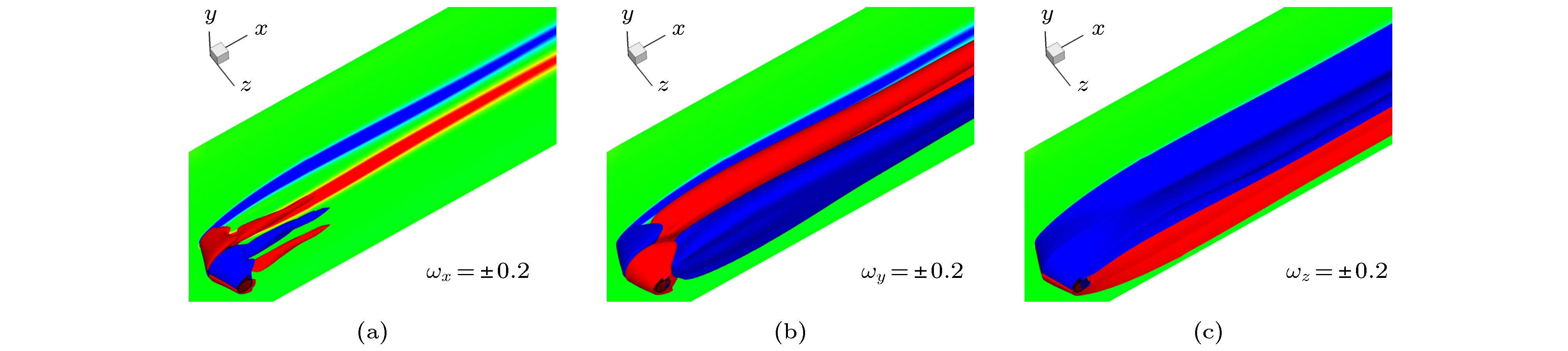
$\left| {{\omega _x}} \right|$ 或$\left| {{\omega _y}} \right|$ 小于0.001; 注意, 等值面图中采用半透明灰色面来表示圆柱体, 且流动从左至右) (a)${\omega _x} = $ $ \pm 0.2$ 等值面; (b)${\omega _y} = \pm 0.2$ 等值面; (c)${\omega _z} = \pm 1$ 等值面; (d)${\omega _x}$ 等值线; (e)${\omega _y}$ 等值线; (f)${\omega _z}$ 等值线Fig. 3. At Re = 300, iso-surfaces of
${{\omega}}$ in the wake of a straight circular cylinder, and contours of${{\omega}}$ on cylinder surfaces, where red and blue colors denote positive and negative values, respectively, and green color in contours denotes$\left| {{\omega _x}} \right|$ or$\left| {{\omega _y}} \right|$ less than 0.001: (a) Iso-surfaces of${\omega _x} = \pm 0.2$ ; (b) iso-surfaces of${\omega _y} = \pm 0.2$ ; (c) iso-surfaces of${\omega _z} = \pm 1$ ; (d) contours of${\omega _x}$ ; (e) contours of${\omega _y}$ ; (f) contours of${\omega _z}$ . Note that the cylinder is denoted by the grey translucent surface in iso-surfaces and the flow is from left to right.
图 4 Re = 180时直方柱尾迹中 (a)
${\omega _x} = \pm 0.8$ (黄/绿)和${\omega _z} = \pm 1$ (红/蓝)等值面图, 其中背景为$z = 0$ 处的${\omega _z}$ 等值线色图; (b)$z = {\lambda / 4}$ 处${\omega _x}$ 的等值线色图; (c)$z = {\lambda / 4}$ 处${\omega _y}$ 的等值线色图; 图中红色和蓝色, 以及${\omega _z}$ 等值线的实线和虚线分别表示正值和负值Fig. 4. In the wake of a square cylinder at Re = 180: (a) Iso-surfaces of
${\omega _x} = \pm 0.8$ (yellow/green) and${\omega _z} = \pm 1$ (red/blue), where the background is colorful contours of${\omega _z}$ at$z = 0$ ; (b) colorful contours of${\omega _x}$ at$z = {\lambda / 4}$ ; (c) colorful contours of${\omega _y}$ at$z = {\lambda / 4}$ . In Fig. 4, red and blue colors, as well as solid and dashed lines in contours of${\omega _z}$ , denote positive and negative values, respectively.
图 5 Re = 250时直方柱尾迹中 (a)
${\omega _x} = \pm 0.8$ (黄/绿)和${\omega _z} = \pm 1$ (红/蓝)等值面图, 其中背景为$z = 0$ 处的${\omega _z}$ 等值线色图; (b)$z = {\lambda / 4}$ 处${\omega _x}$ 的等值线色图; (c)$z = {\lambda / 4}$ 处${\omega _y}$ 的等值线色图, 其中红色和蓝色, 以及${\omega _z}$ 等值线的实线和虚线分别表示正值和负值Fig. 5. In the wake of a square cylinder at Re = 250: (a) Iso-surfaces of
${\omega _x} = \pm 0.8$ (yellow/green) and${\omega _z} = \pm 1$ (red/blue), where the background is colorful contours of${\omega _z}$ at$z = 0$ ; (b) colorful contours of${\omega _x}$ at$z = {\lambda / 4}$ ; (c) colorful contours of${\omega _y}$ at$z = {\lambda / 4}$ . In Fig. 5, red and blue colors, as well as solid and dashed lines in contours of${\omega _z}$ , denote positive and negative values, respectively.
图 6 Re = 100,
${W / \lambda } = 0.1$ 且$\lambda = 8$ 时谐波柱尾迹中3个涡分量等值面图(其中红色和蓝色分别为正值和负值, 背景为$z = 0$ 处${\omega _z}$ 的等值线色图) (a)${\omega _x}$ ; (b)${\omega _y}$ ; (c)${\omega _z}$ Fig. 6. At Re = 100,
${W / \lambda } = 0.1$ and$\lambda = 8$ , iso-surfaces of three components of vorticity in the wake of a harmonic cylinder: (a)${\omega _x}$ ; (b)${\omega _y}$ ; (c)${\omega _z}$ . In Fig. 6, red and blue colors denote positive and negative values, respectively, and the background is the colorful contour of${\omega _z}$ at$z = 0$ .
图 7 Re = 100,
${W / \lambda } = 0.1$ 且$\lambda = 4$ 时谐波柱尾迹中3个涡分量等值面图(其中红色和蓝色分别为正值和负值, 背景为$z = 0$ 处${\omega _z}$ 的等值线色图) (a)${\omega _x}$ ; (b)${\omega _y}$ ; (c)${\omega _z}$ Fig. 7. At Re = 100,
${W / \lambda } = 0.1$ and$\lambda = 4$ , iso-surfaces of three components of vorticity in the wake of a harmonic cylinder: (a)${\omega _x}$ ; (b)${\omega _y}$ ; (c)${\omega _z}$ . In Fig. 7, red and blue colors denote positive and negative values, respectively, and the background is the colorful contour of${\omega _z}$ at$z = 0$ .
图 8 Re = 100,
${W / \lambda } = 0.1$ 且$\lambda = 8$ 时圆锥柱尾迹中三个涡分量等值面图(其中红色和蓝色分别为正值和负值, 背景为$z = 0$ 处${\omega _z}$ 的等值线色图) (a)${\omega _x}$ ; (b)${\omega _y}$ ; (c)${\omega _z}$ Fig. 8. At Re = 100,
${W / \lambda } = 0.1$ and$\lambda = 8$ , iso-surfaces of three components of vorticity in the wake of a conic cylinder: (a)${\omega _x}$ ; (b)${\omega _y}$ ; (c)${\omega _z}$ . In Fig. 8, red and blue colors denote positive and negative values, respectively, and the background is the colorful contour of${\omega _z}$ at$z = 0$ .
图 9 Re = 100,
${W / \lambda } = 0.2$ 且$\lambda = 4$ 时圆锥柱尾迹中3个涡分量等值面图(其中红色和蓝色分别为正值和负值, 背景为$z = 0$ 处${\omega _z}$ 的等值线色图) (a)${\omega _x}$ ; (b)${\omega _y}$ ; (c)${\omega _z}$ Fig. 9. At Re = 100,
${W / \lambda } = 0.2$ and$\lambda = 4$ , iso-surfaces of three components of vorticity in the wake of a conic cylinder: (a)${\omega _x}$ ; (b)${\omega _y}$ ; (c)${\omega _z}$ . In Fig. 9, red and blue colors denote positive and negative values, respectively, and the background is the colorful contour of${\omega _z}$ at$z = 0$ .
图 10 典型的全弯曲方柱迎风面表面涡量分布(Re = 100,
$\lambda = 5.6$ 和${W / \lambda } = 0.025$ ) (a)${\omega _x}$ ; (b)${\omega _y}$ ; (c)${\omega _z}$ Fig. 10. Typical distributions of surface vorticity on the wholly wavy cylinder with a square cross-section (Re = 100,
$\lambda = 5.6$ and${W / \lambda } = 0.025$ ): (a)${\omega _x}$ ; (b)${\omega _y}$ ; (c)${\omega _z}$ .
图 11 Re = 100,
$\lambda = 5.6$ 和${W / \lambda } = 0.025$ 时全弯曲方柱尾迹中涡量等值面分布 (a)${\omega _z} = \pm 1$ (红/蓝); (b)${\omega _x} = $ $\pm 0.25 $ (黄/绿)和${\omega _y} = \pm 0.5$ (红/蓝)Fig. 11. At Re = 100,
$\lambda = 5.6$ and${W / \lambda } = 0.025$ , iso-surfaces of$\omega $ in the wake of the wholly wavy cylinder with a square corss-section: (a)${\omega _z} = \pm 1$ (red/blue); (b)${\omega _x} = $ $\pm 0.25 $ (yellow/green) and${\omega _y} = \pm 0.5$ (red/blue).
图 12 Re = 100,
$\lambda = 5.6$ 和${W / \lambda } = 0.167$ 时全弯曲方柱尾迹中涡量等值面分布 (a)${\omega _z} = \pm 1$ (红/蓝)和${\omega _x} =\pm 0.25$ (黄/绿); (b)${\omega _x} = \pm 0.25$ (黄/绿)和${\omega _y} = \pm 0.5$ (红/蓝)Fig. 12. At Re = 100,
$\lambda = 5.6$ and${W / \lambda } = 0.167$ , iso-surfaces of$\omega $ in the wake of the wholly wavy cylinder with a square corss-section: (a)${\omega _z} = \pm 1$ (red/blue) and${\omega _x} = \pm 0.25$ (yellow/green); (b)${\omega _x} = \pm 0.25$ (yellow/green) and${\omega _y} =$ $ \pm 0.5 $ (red/blue).表 1 不同几何结构的钝体绕流所采用的计算域及近壁网格尺度汇总
Table 1. Summary of computational domain and the nearest-wall grid used in a flow past a bluff body with different geometry.
钝体结构类型 计算域尺度 近壁网格尺度 入口 出口 两侧垂向 圆形截面的直圆柱 20 30 40 0.001 方形截面的直方柱 9 18 18 0.008 圆形截面的谐波柱 10 30 20 0.005 圆形截面的圆锥柱 10 30 20 0.005 方形截面的全弯曲方柱 9 18 18 0.008 
下载: 导出CSV
-
[1] Karniadakis G E, Triantafyllou G S 1992 J. Fluid Mech. 238 1
Google Scholar
[2] 武作兵, 凌国灿 1993 力学学报 25 264
Wu Z B, Ling G C 1993 Chin. J. Theoret. Appl. Mech. 25 264
[3] Barkely D, Henderson R D 1996 J. Fluid Mech. 322 215
Google Scholar
[4] Williamson C H K 1996 Annu. Rev. Fluid Mech. 28 477
Google Scholar
[5] Williamson C H K 1996 J. Fluid Mech. 328 345
Google Scholar
[6] Henderson R D 1997 J. Fluid Mech. 352 65
Google Scholar
[7] Leweke T, Williamson C H K 1998 Euro. J. Mech. B/Fluids 17 571
Google Scholar
[8] 凌国灿, 常勇 1999 力学学报 31 652
Ling G C, Chang Y 1999 Chin. J. Theoret. Appl. Mech. 31 652
[9] Barkley D, Tuckerman L S, Golubitsky M 2000 Phys. Rev. E 61 5247
Google Scholar
[10] Thompson M C, Leweke T, Williamson C H K 2001 J. Fluid. Struct. 15 607
Google Scholar
[11] Posdziech O, Grundmann R 2001 Theo. Comput. Fluid Dyn. 15 121
Google Scholar
[12] Rao A, Thompson M C, Leweke T, Hourigan K 2013 J. Fluid.Struct. 41 9
Google Scholar
[13] Sheard G J, Thompson M C, Hourigan K 2003 Phys. Fluids 15 L68
Google Scholar
[14] Jiang H, Cheng L, Draper S, An H, Tong F 2016 J. Fluid Mech. 801 353
Google Scholar
[15] Jiang H, Cheng L, Draper S, An H 2017 Comput. Fluids 149 172
Google Scholar
[16] Sarpkaya T 2004 J. Fluid. Struct. 19 389
Google Scholar
[17] Williamson C H K, Govardhan R 2004 Annu. Rev. Fluid Mech. 36 413
Google Scholar
[18] Gabbai R D, Benaroya H 2005 J. Sound Vib. 282 575
Google Scholar
[19] Williamson C H K, Govardhan R 2008 J. Wind Eng. Ind. Aerodyn. 96 713
Google Scholar
[20] Kumar R A, Sohn C H, Gowda B H L 2008 Recent Patents Mech. Eng. 1 1
Google Scholar
[21] Darekar R M, Sherwin S J 2001 J. Fluid Mech. 426 263
Google Scholar
[22] Lam K, Lin Y F 2008 Int. J. Heat Fluid Flow 29 1071
Google Scholar
[23] 林黎明 2007 博士学位论文 (北京: 中国科学院力学研究所)
Lin L M 2007 Ph. D. Dissertation (Beijing: Institute of Mechanics, Chinese Academy of Sciences) (in Chinese)
[24] Lin L M, Ling G C, Wu Y X 2010 Chin. Phys. Lett. 27 034702
Google Scholar
[25] Lin L M, Shi S Y, Wu Y X 2019 Acta Mech. Sin. 35 411
Google Scholar
[26] Lin L M, Zhong X F, Wu Y X 2018 Acta Mech. Sin. 34 812
Google Scholar
[27] Lin L M, Shi S Y, Zhong X F, Wu Y X 2019 Acta Mech. Sin. 35 1
Google Scholar
[28] Lin L M, Shi S Y, Wu Y X 2018 Theo. App. Mech. Lett. 8 320
Google Scholar
[29] Lin L M, Tan Z R 2019 Acta Mech. Sin. 35 1131
Google Scholar
[30] Meiburg E, Lasheras J C 1988 J. Fluid Mech. 190 1
Google Scholar
下载:
计量
- 文章访问数: 9124
- PDF下载量: 98
- 被引次数: 0
