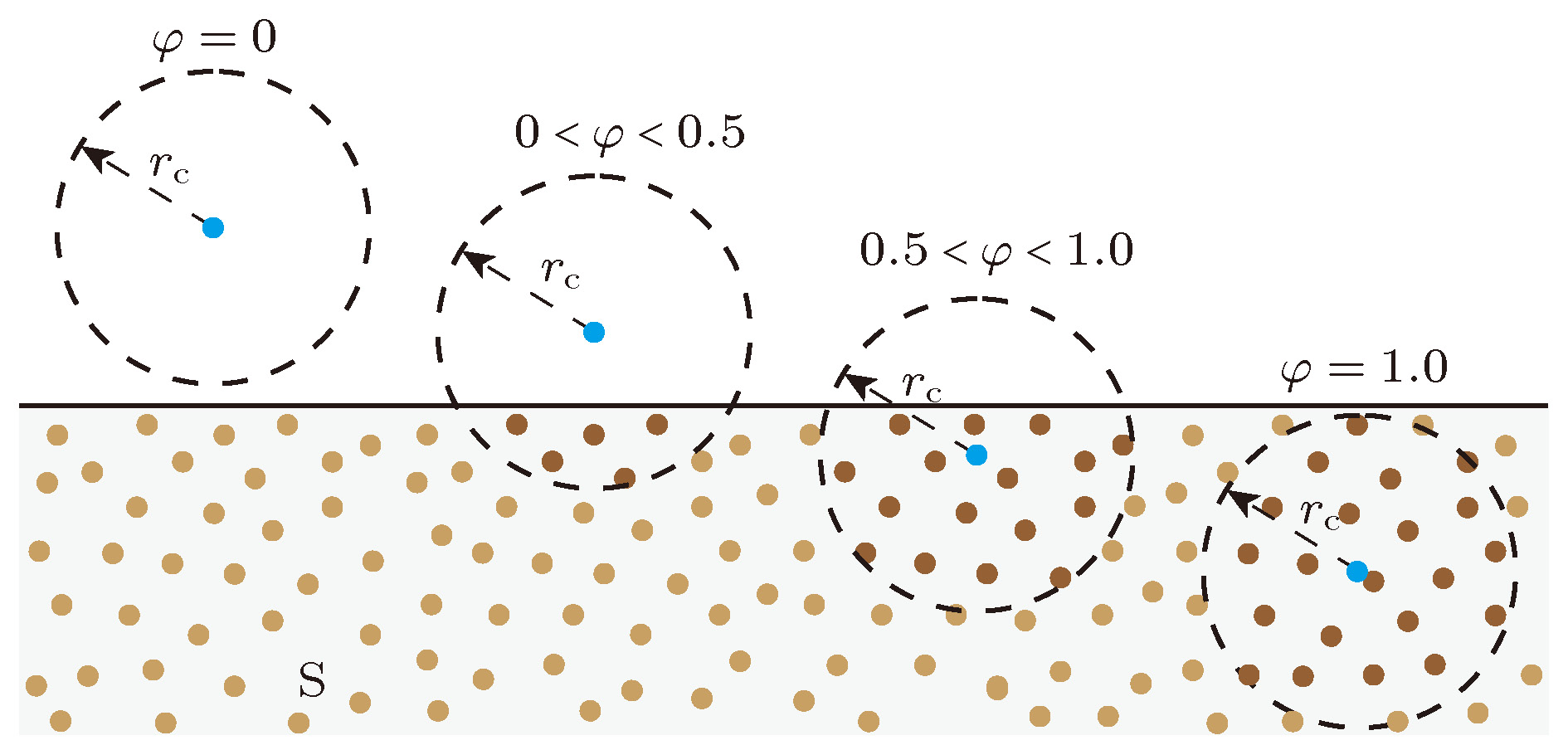
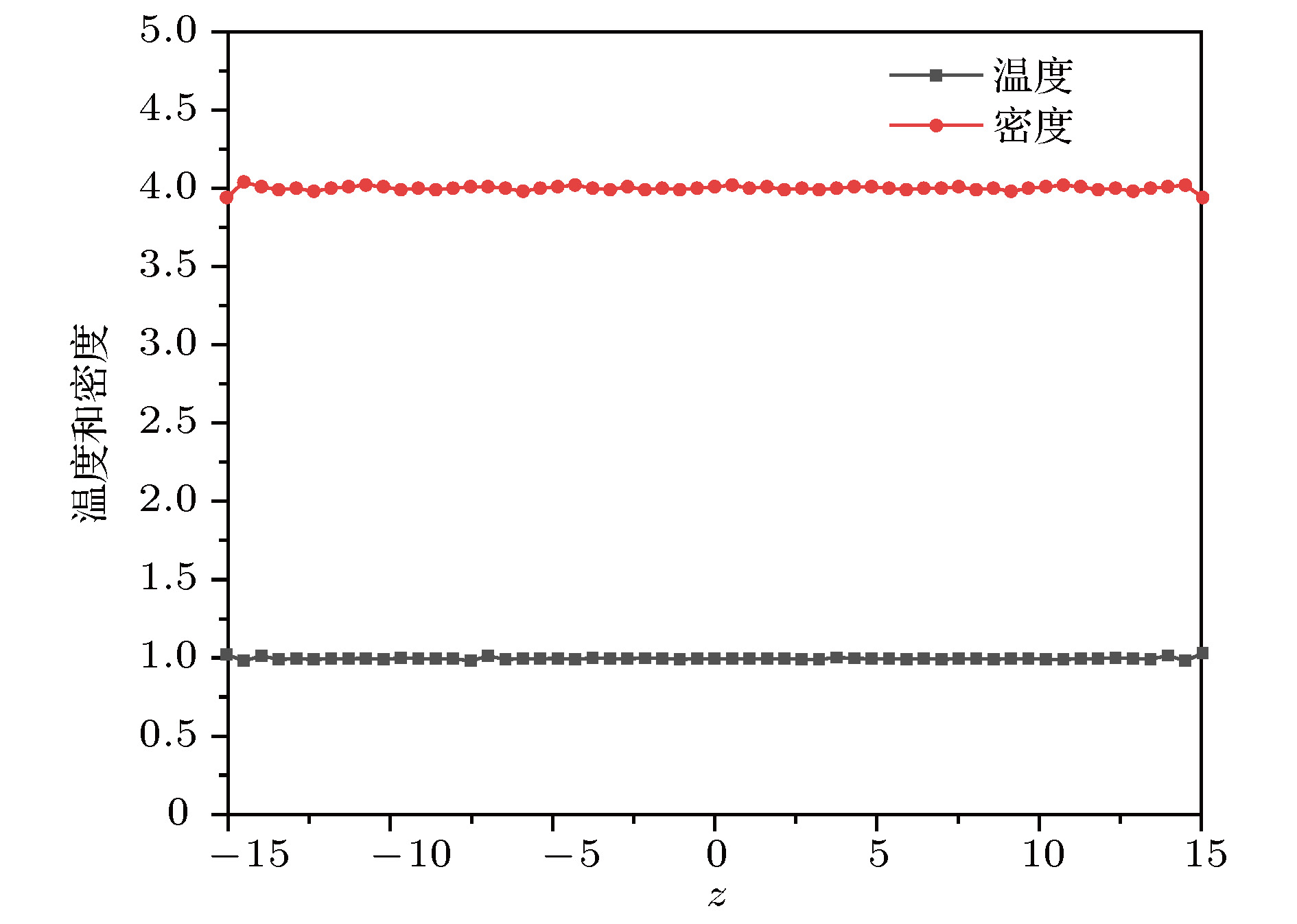
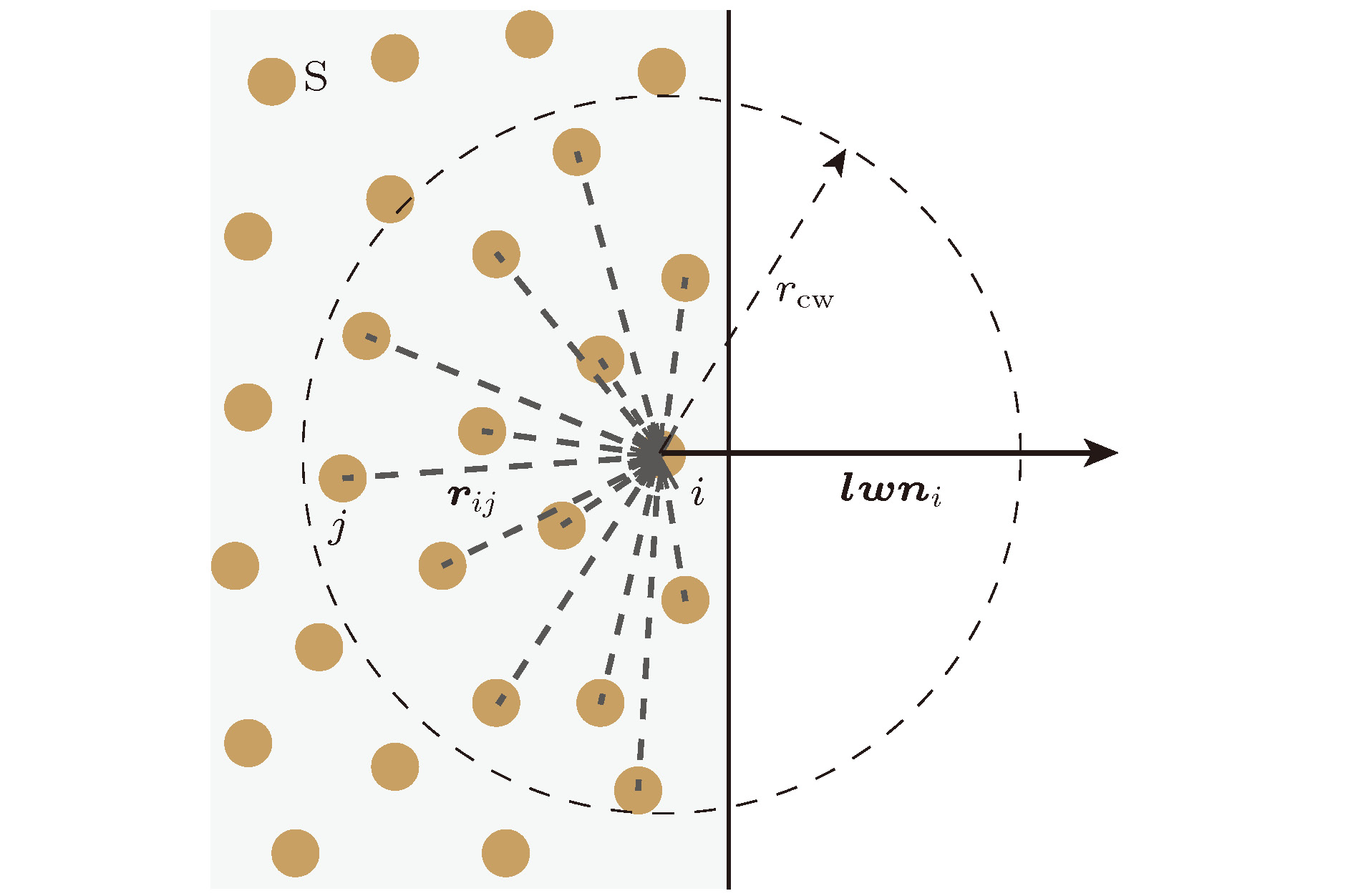
-
耗散粒子动力学(DPD)是一种针对介观流体的高效的粒子模拟方法, 经过二十多年发展已经在诸如聚合物、红细胞、液滴浸润性等方面有了很多研究应用. 但是因为其边界处理手段的不完善, 耗散粒子动力学模拟仍局限于相对简单的几何边界问题中. 本文提出一种能自适应各种复杂几何边界的处理方法, 并能同时满足三大边界要求：流体粒子不穿透壁面、边界处速度无滑移、边界处密度和温度波动小. 具体地, 通过给每个壁面粒子赋予一个新的矢量属性—局部壁面法向量, 该属性通过加权计算周围壁面粒子的位置得到；然后通过定义周围固体占比概念, 仅提取固体壁面的表层粒子参与模拟计算, 减少了模拟中无效的粒子；最后在运行中, 实时计算每个流体粒子周围固体粒子占比, 判断是否进入固体壁面内, 如果进入则修正速度和位置. 我们将这种方法应用于Poiseuille流动, 验证了该方法符合各项要求, 随后还在复杂血管网络和结构化固体壁面上展示了该边界处理方法的应用. 这种方法使得DPD模拟不再局限于简单函数描述的壁面曲线, 而是可以直接从各种设计图纸和实验扫描影像中提取壁面, 极大地拓展了DPD的应用范围.Dissipative particle dynamics (DPD) is a thriving particle-based simulation method of modeling mesoscale fluids. After two decades of evolution, DPD has shown unique advantages in researches about polymer, red blood cell, droplets wetting, etc. However, DPD is limited to relatively simple geometries due to the lack of a satisfactory boundary method. In this paper, we propose an adaptive boundary method for complex geometry, which fulfills the three basic requirements of boundary method: no penetration into the solid, no-slip near boundary, negligible fluctuation of density or temperature near boundary. Specifically, first, a new vector attribution is added to each solid particle, the attribution is named local wall normal (LWN) attribution and it is a function of its neighbor solid particle’s position, the LWN attribution is used to correct the penetrating fluid particles’ velocity and position and is computed only once if the wall is stationary. Second the surface wall particles are identified by neighbor solid fraction (φ), which indicates the percentage of surrounding space occupied by solid particles, then the wall is reconstructed by only the surface particles instead of all solid particles. By doing so, the redundant bulk particles are removed from the simulation. Third, it is detected on-the-fly whether the moving fluid particle penetrates the wall by computing its φ, the fluid particles with φ greater than 0.5 are considered to enter into the solid wall, their position and velocity will be corrected based on the local wall normal attribution. We verify that the method causes negligible density and temperature fluctuation in Poiseuille flow. Then, we illustrate the implementation of LWNM in the cases of complex blood vessel network and micro-structured surface. With this method, the obstacles in flow are no longer restricted to shapes described by functions but can be generated by CAD software, and blood vessels can also be generated by CT scan images or other experimental data. Moreover, we show a case with a bent tube and droplets inside, demonstrating the practicability of constructing complex geometry and the effectiveness of LWNM. This new boundary approach empowered DPD to simulate more realistic problems.
[1] Hoogerbrugge P J, Koelman J 1992 Europhys. Lett. 19 155
Google Scholar
[2] Español P, Warren P 1995 Europhys. Lett. 30 191
Google Scholar
[3] Groot R D, Warren P B 1997 J. Chem. Phys. 107 4423
Google Scholar
[4] Xiao L L, Chen S, Lin C S, Liu Y 2014 Mol. Cell. Biomech. 11 67
[5] Xiao L L, Liu Y, Chen S, Fu B M 2017 Int. J. Comput. Methods Exp. Meas. 6 303
[6] Arienti M, Pan W, Li X J, Karniadakis G E 2011 J. Chem. Phys. 134 204114
Google Scholar
[7] Lin C S, Chen S, Xiao L L, Liu Y 2018 Langmuir 34 2708
Google Scholar
[8] Wang Y X, Chen S 2015 Appl. Surf. Sci. 327 159
Google Scholar
[9] 林晨森, 陈硕, 李启良, 杨志刚 2014 63 104702
Google Scholar
Lin C S, Chen S, Li Q L, Yang Z G 2014 Acta Phys. Sin. 63 104702
Google Scholar
[10] Reddy H, Abraham 2009 J. Phys. Fluids 21 053303
Google Scholar
[11] 陈硕, 金亚斌, 张明焜, 尚智 2012 同济大学学报 01 137
Google Scholar
Chen S, Jin Y B, Zhang M K, Shang Z 2012 J. Tongji Univ. 01 137
Google Scholar
[12] Kang S H, Hwang W S, Lin Z, Kwon S H, Hong S W 2015 Nano Lett. 15 7913
Google Scholar
[13] Liu M B, Liu G R, Zhou L W, Chang J Z 2014 Arch. Comp. Meth. Eng. 22 529
[14] Kreder M J, Alvarenga J, Kim P, Aizenberg J 2016 J. Nat. Rev. Mater. 1 20153
[15] Revenga M, Zúñiga I, Español P 1999 Comput. Phys. Commun. 121 309
[16] 许少锋, 汪久根 2013 浙江大学学报 47 1603
Google Scholar
Xu S F, Wang J G 2013 J. Zhejiang Univ. 47 1603
Google Scholar
[17] Mehboudi A, Saidi M S 2011 Scientia Iranica 18 6
[18] 刘谋斌, 常建忠 2010 59 7556
Google Scholar
Liu M B, Chang J Z 2010 Acta Phys. Sin. 59 7556
Google Scholar
[19] Li Z, Bian X, Tang Y H, Karniadakis G E 2018 J. Comput. Phys. 355 534
Google Scholar
[20] Pivkin I V, Karniadakis G E 2005 J. Comput. Phys. 207 114
Google Scholar
[21] Duong-Hong D, Phan-Thien N, Fan X J 2004 Comput. Mech. 35 24
Google Scholar
[22] Lei H, Fedosov D A, Karniadakis G E 2011 J. Comput. Phys. 230 3765
Google Scholar
[23] Ranjith S K, Patnaik B S V, Vedantam S 2013 J. Comput. Phys. 232 174
Google Scholar
[24] Sigalotti L D, Klapp J, Sira E, Meleán Y, Hasmy A 2003 J. Comput. Phys. 191 622
Google Scholar
[25] Liu T, Kim C J 2014 Science 346 1096
[26] Malouin B A, Koratkar N A, Hirsa A H, Wang Z 2010 Appl. Phys. Lett. 96 234103
Google Scholar
[27] Fedosov D A, Caswell B, Karniadakis G E 2010 Comput. Meth. Appl. Mech. Eng. 199 1937
[28] Xiao L L, Liu Y, Chen S, Fu B M 2016 Cell Biochem. Biophys. 74 513
Google Scholar
[29] Ye T, Phan-Thien N, Khoo B C, Lim C T 2014 J. Appl. Phys. 116 124703
Google Scholar
-
图 1 计算计算壁面粒子i的法向量lwni
Fig. 1. Computing the local wall normal vector lwni of wall particle i.
图 2 流体粒子固体体积分数(φ)的四种情况(φ = 0远离壁面, 0 < φ < 0.5未穿透壁面, 0.5 < φ < 1.0已穿透壁面, φ = 1.0完全浸入壁面)
Fig. 2. Four scenarios for solidfraction (φ): φ = 0 particle away from wall; 0 < φ < 0.5 particle near the wall; 0.5 < φ < 1.0 particle penetrating the wall; φ = 1.0 particle submerged in wall.
图 3 选用一定范围内固体粒子的lwni计算修正流体粒子时的法向量en
Fig. 3. Computing en from nearby lwni for correcting penetrating fluid particle.
图 4 LWNM边界条件的实施过程图 (a) 固体粒子构造壁面; (b) 提取表面层固体粒子; (c)计算LWN; (d)模拟时效果
Fig. 4. Workflow of LWNM: (a) Constructing wall with frozen particles; (b) identifying surface wall particles; (c) com-puting LWN; (d) snapshot during simulation.
图 6 LWNM边界方法统计结果和理论解的对比(温度和密度)
Fig. 6. Comparison of LWNM and theoretical results (temperature and density).
图 7 (a)微结构表面对液滴亲疏水性的影响[26]; (b)粒子模拟中微结构表面的LWN
Fig. 7. (a) Microstructures on surface affect the hydrophilicity; (b) LWNs (grey arrows) of surface with microstructures.
图 9 应用LWNM实现液滴在TJU(同济大学)形状的复杂管道中运动
Fig. 9. Droplets in TJU (Tongji University) shape tube with LWNM.
-
[1] Hoogerbrugge P J, Koelman J 1992 Europhys. Lett. 19 155
Google Scholar
[2] Español P, Warren P 1995 Europhys. Lett. 30 191
Google Scholar
[3] Groot R D, Warren P B 1997 J. Chem. Phys. 107 4423
Google Scholar
[4] Xiao L L, Chen S, Lin C S, Liu Y 2014 Mol. Cell. Biomech. 11 67
[5] Xiao L L, Liu Y, Chen S, Fu B M 2017 Int. J. Comput. Methods Exp. Meas. 6 303
[6] Arienti M, Pan W, Li X J, Karniadakis G E 2011 J. Chem. Phys. 134 204114
Google Scholar
[7] Lin C S, Chen S, Xiao L L, Liu Y 2018 Langmuir 34 2708
Google Scholar
[8] Wang Y X, Chen S 2015 Appl. Surf. Sci. 327 159
Google Scholar
[9] 林晨森, 陈硕, 李启良, 杨志刚 2014 63 104702
Google Scholar
Lin C S, Chen S, Li Q L, Yang Z G 2014 Acta Phys. Sin. 63 104702
Google Scholar
[10] Reddy H, Abraham 2009 J. Phys. Fluids 21 053303
Google Scholar
[11] 陈硕, 金亚斌, 张明焜, 尚智 2012 同济大学学报 01 137
Google Scholar
Chen S, Jin Y B, Zhang M K, Shang Z 2012 J. Tongji Univ. 01 137
Google Scholar
[12] Kang S H, Hwang W S, Lin Z, Kwon S H, Hong S W 2015 Nano Lett. 15 7913
Google Scholar
[13] Liu M B, Liu G R, Zhou L W, Chang J Z 2014 Arch. Comp. Meth. Eng. 22 529
[14] Kreder M J, Alvarenga J, Kim P, Aizenberg J 2016 J. Nat. Rev. Mater. 1 20153
[15] Revenga M, Zúñiga I, Español P 1999 Comput. Phys. Commun. 121 309
[16] 许少锋, 汪久根 2013 浙江大学学报 47 1603
Google Scholar
Xu S F, Wang J G 2013 J. Zhejiang Univ. 47 1603
Google Scholar
[17] Mehboudi A, Saidi M S 2011 Scientia Iranica 18 6
[18] 刘谋斌, 常建忠 2010 59 7556
Google Scholar
Liu M B, Chang J Z 2010 Acta Phys. Sin. 59 7556
Google Scholar
[19] Li Z, Bian X, Tang Y H, Karniadakis G E 2018 J. Comput. Phys. 355 534
Google Scholar
[20] Pivkin I V, Karniadakis G E 2005 J. Comput. Phys. 207 114
Google Scholar
[21] Duong-Hong D, Phan-Thien N, Fan X J 2004 Comput. Mech. 35 24
Google Scholar
[22] Lei H, Fedosov D A, Karniadakis G E 2011 J. Comput. Phys. 230 3765
Google Scholar
[23] Ranjith S K, Patnaik B S V, Vedantam S 2013 J. Comput. Phys. 232 174
Google Scholar
[24] Sigalotti L D, Klapp J, Sira E, Meleán Y, Hasmy A 2003 J. Comput. Phys. 191 622
Google Scholar
[25] Liu T, Kim C J 2014 Science 346 1096
[26] Malouin B A, Koratkar N A, Hirsa A H, Wang Z 2010 Appl. Phys. Lett. 96 234103
Google Scholar
[27] Fedosov D A, Caswell B, Karniadakis G E 2010 Comput. Meth. Appl. Mech. Eng. 199 1937
[28] Xiao L L, Liu Y, Chen S, Fu B M 2016 Cell Biochem. Biophys. 74 513
Google Scholar
[29] Ye T, Phan-Thien N, Khoo B C, Lim C T 2014 J. Appl. Phys. 116 124703
Google Scholar
下载:
计量
- 文章访问数: 8778
- PDF下载量: 100
- 被引次数: 0
