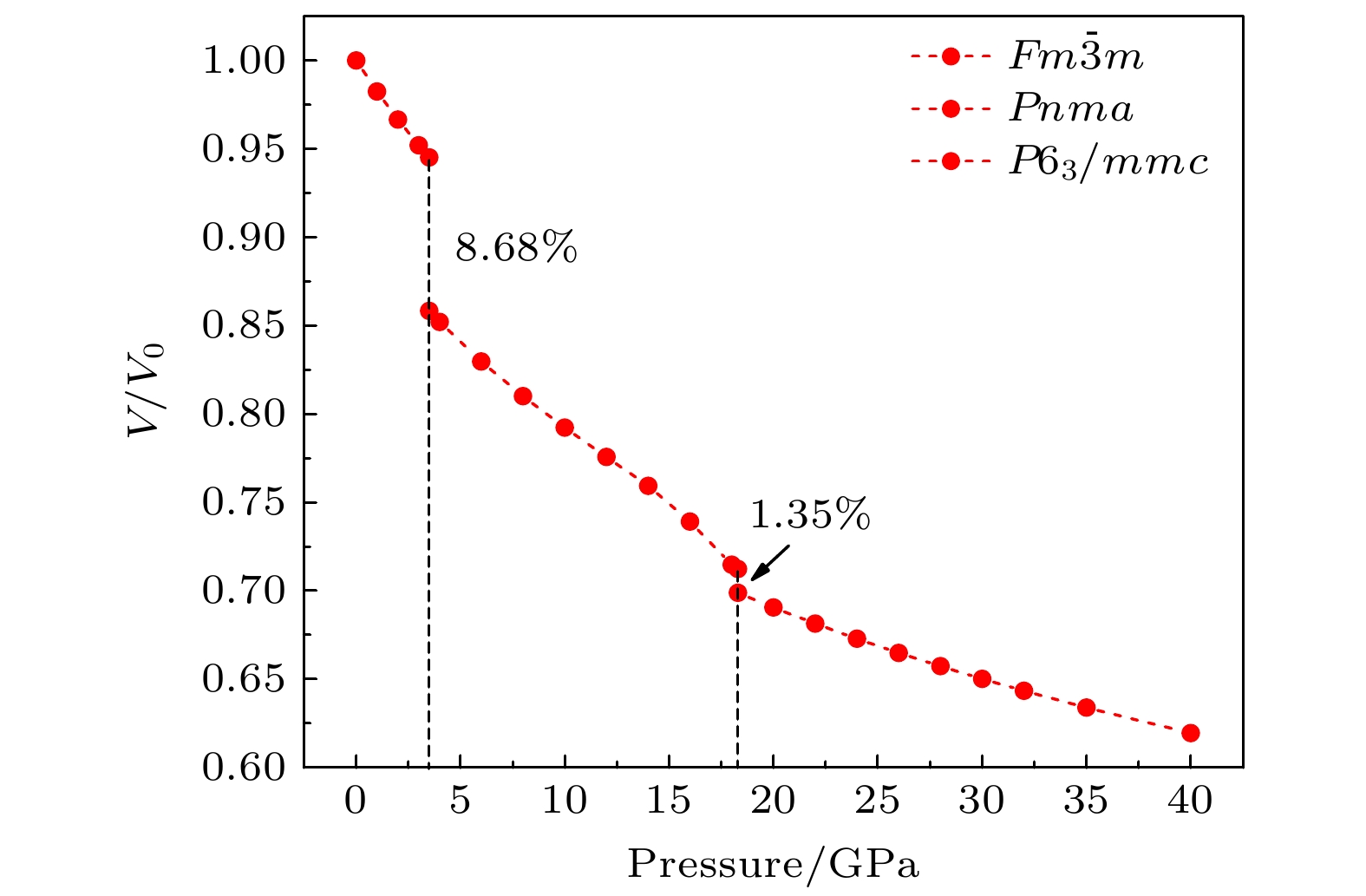
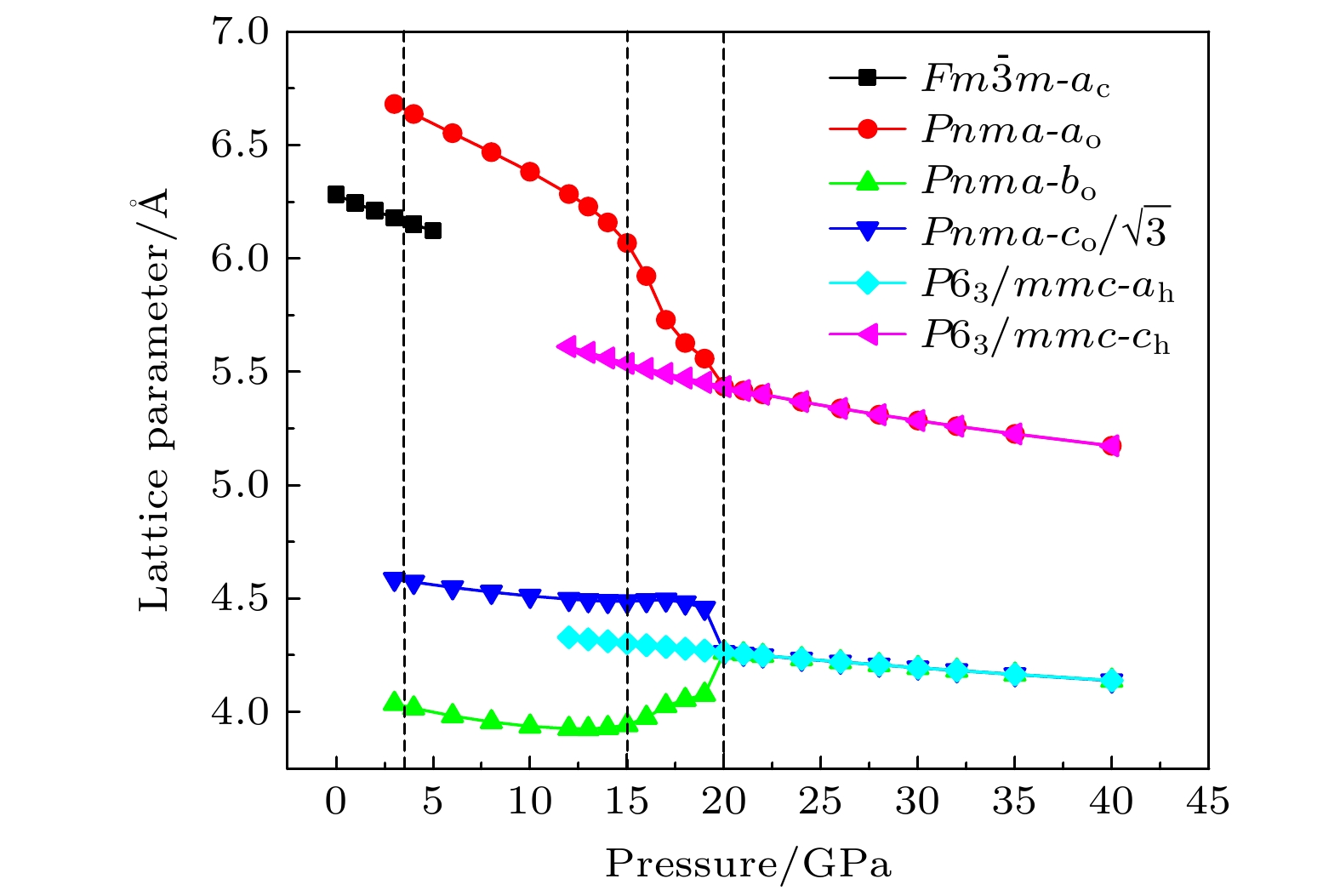
-
通过理论计算研究了BaF 2在高压下的晶体结构及物理性质. 结果表明, 在3.5和18.3 GPa, BaF 2依次经历了 Fm
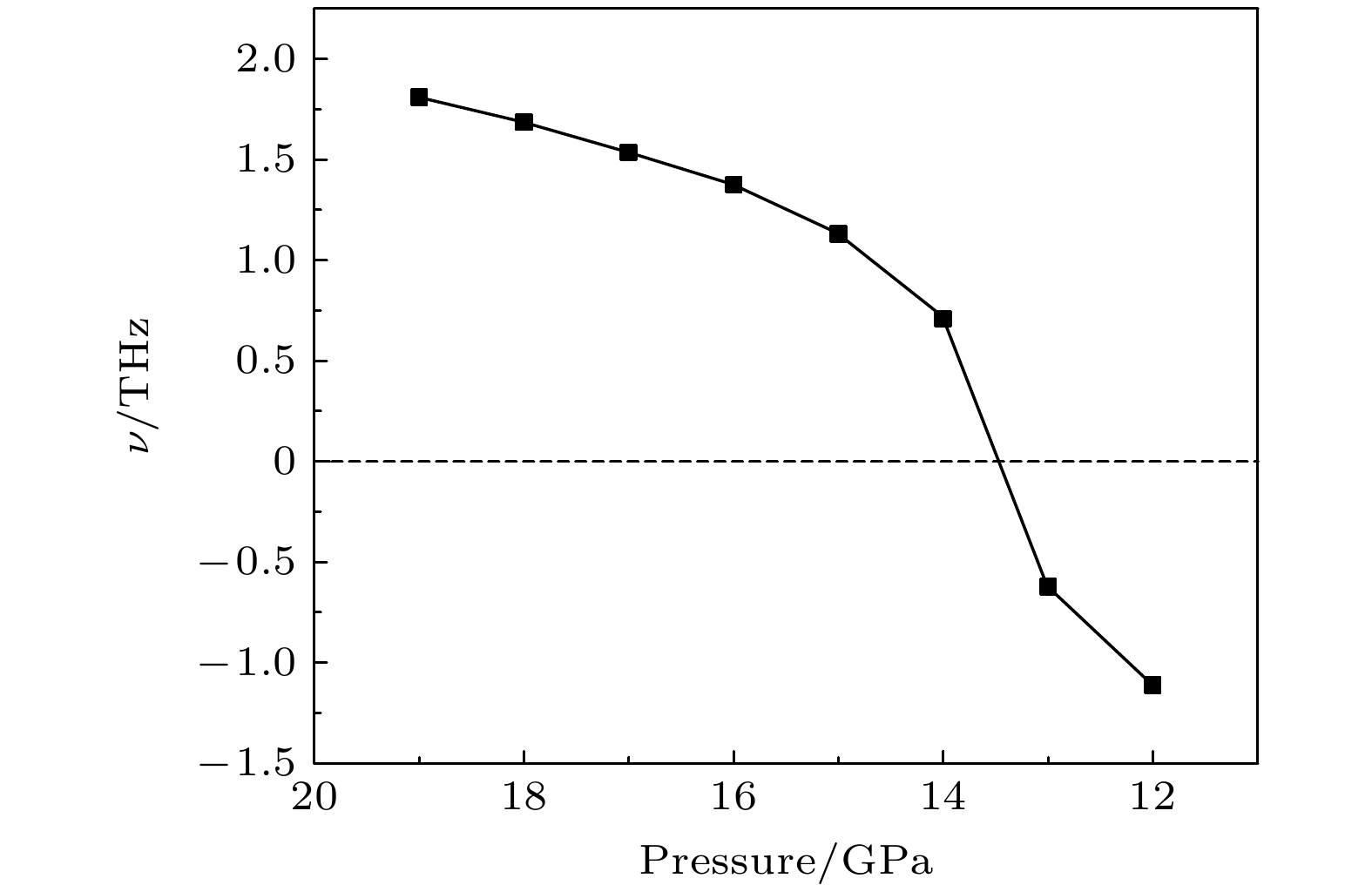
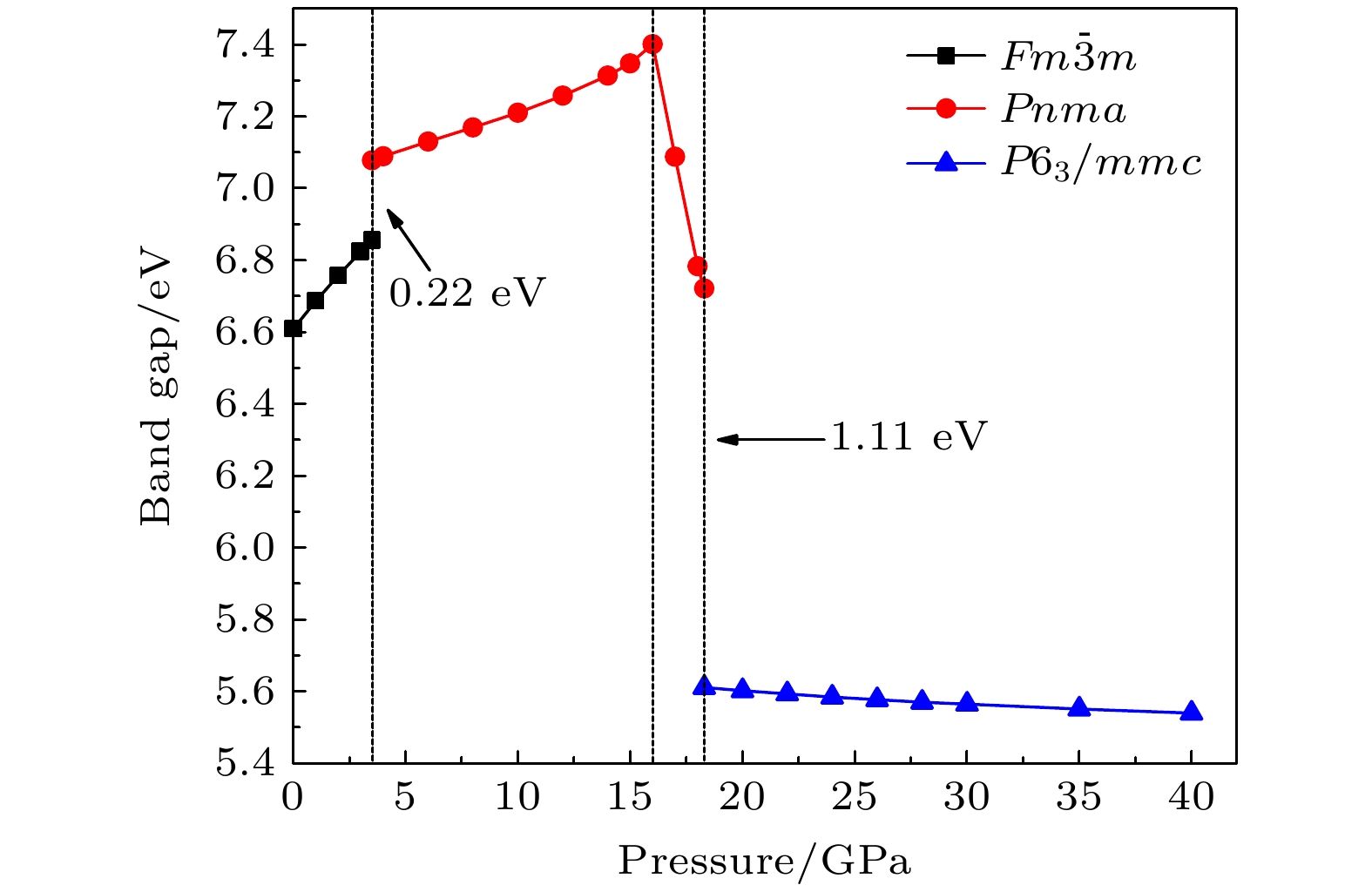
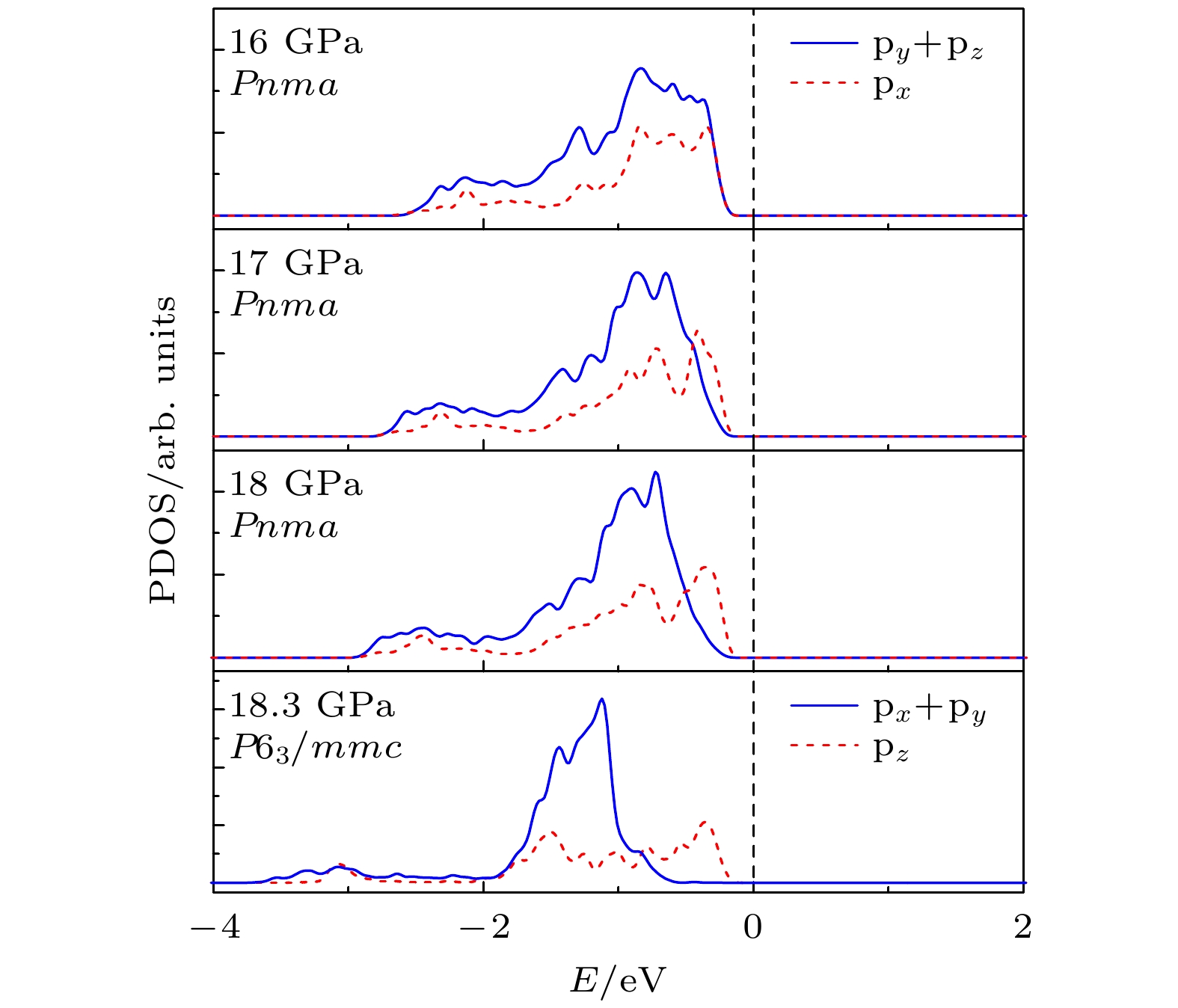
$ \overline {3} $ m- Pnma- P6 3/ mmc两次结构相变, 相变过程伴随着体积的塌缩, 均为一级相变. 约15 GP时, Pnma相晶轴压缩性出现异常, 表现为随压强增大, 晶轴 b o轻微增加, a o略微减小. 对其电子态密度进行分析发现, 在16 GPa以后, 由于F1原子的p y + p z 与p x 轨道电子离域, 导致其带隙随压强增加而降低. 在约20 GPa时, Pnma相完全转变为 P6 3/ mmc相, 相变完成. 对BaF 2的拉曼峰位随压强变化进行了计算, 为其高压拉曼光谱行为提供了相应的理论依据. 计算了 P6 3/ mmc相在不同压强下的声子色散曲线, 揭示了其卸压过程中的滞后机制, 计算结果还预测该物相至少可以稳定到80 GPa.There have been some theoretical studies of high pressure phase transition behavior of BaF 2, while in most cases the attention is paid mainly to the optical and electrical properties of BaF 2 under increasing pressure. To date, there has been still a lack of theoretical explanation for the hysteresis phenomenon of high-pressure phase of BaF 2 when the pressure is released. In addition, the pressure-dependent behavior of the BaF 2 band gap is still under controversy, and there are few studies of its high-pressure Raman spectra. Therefore, first principle is used to make a supplementary calculation of the high pressure behavior of BaF 2. For a given pressure P and temperature T, the thermodynamic stable phase has the lowest Gibbs free energy. The calculations are performed at zero temperature and hence, the Gibbs free energy becomes equal to the enthalpy. Thus, the variation of enthalpy is calculated as a function of pressure to study the high-pressure phase stability of BaF 2 based on density functional theory as implemented in the Vienna ab initio simulation package (VASP). The results show that the BaF 2 undergoes two structural phase transitions from Fm3 m(cubic) to Pnma (orthorhombic) and then to P6 3/ mmc(hexagonal) with increasing pressure, and their corresponding transition pressures are 3.5 and 18.3 GPa, respectively. By calculating the evolution of lattice constant with pressure, it is found that at about 15 GPa (near the second phase transition pressure), the lattice constants of the Pnma structure show abnormal behavior (a slight increase in b o and a slight decrease in a o). We suggest that this behavior leads the band gap to decrease, indicated by analyzing the calculated results of Pnma structure of other materials. The Pnma structure completely transforms into P6 3/ mmc structure at about 20 GPa. By analyzing the phonon dispersion curves of BaF 2 as a function of pressure, the structural stability information of the material can also be obtained. Then the density functional perturbation theory (DFPT) is used to calculate the phonon dispersion curves of BaF 2 by VASP code and Phonopy code. The hysteresis phenomenon of the P6 3/ mmc structure, when the pressure is released, is explained by the kinetic stability. The results predict that the P6 3/ mmc structure can be stabilized at least to 80 GPa.-
Keywords:
- first-principles /
- BaF 2 /
- phase transition /
- hysteresis
[1] Snider E, Dasenbrock-Gammon N, McBride R, Debessai M, Vindana H, Vencatasamy K, Lawler K V, Salamat A, Dias R P 2020 Nature 586 373
Google Scholar
[2] Xia J, Yan J, Wang Z, He Y, Gong Y, Chen W, Sum T C, Liu Z, Ajayan P M, Shen Z 2021 Nat. Phys. 17 92
Google Scholar
[3] 徐波, 田永君 2017 66 036201
Google Scholar
Xu B, Tian Y J 2017 Acta Phys. Sin. 66 036201
Google Scholar
[4] Ayala A P 2001 J. Phys. Condens. Matter 13 11741
Google Scholar
[5] Kavner A 2008 Phys. Rev. B 77 224102
Google Scholar
[6] Leger J M, Haines J, Atouf A, Schulte O, Hull S 1995 Phys. Rev. B 52 13247
Google Scholar
[7] Wang J S, Ma C L, Zhou D, Xu Y S, Zhang M Z, Gao W, Zhu H Y, Cui Q L 2012 J. Solid State Chem. 186 231
Google Scholar
[8] Speziale S, Duffy T S 2002 Phys. Chem. Miner. 29 465
Google Scholar
[9] Dorfman S M, Jiang F M, Mao Z, Kubo A, Meng Y, Prakapenka V B, Duffy T S 2010 Phys. Rev. B 81 174121
Google Scholar
[10] Smith J S, Desgreniers S, Tse J S, Sun J, Klug D D, Ohishi Y 2009 Phys. Rev. B 79 134101
Google Scholar
[11] Kourouklis G A, Anastassakis E 1989 Phys. Status Solidi B 152 89
Google Scholar
[12] Kessler J R, Monberg E, Nicol M 1974 J. Chem. Phys. 60 5057
Google Scholar
[13] Gao G Y, Oganov A R, Li P F, Li Z W, Wang H, Cui T, Ma Y M, Bergara A, Lyakhov A O, Iitaka T, Zou G T 2010 Proc. Natl. Acad. Sci. U. S. A. 107 1317
Google Scholar
[14] Jin X L, Meng X, He Z, Ma Y M, Liu B, Cui T A, Zou G T, Mao H K 2010 Proc. Natl. Acad. Sci. U. S. A. 107 9969
Google Scholar
[15] Yang X C, Hao A M, Wang X M, Liu X, Zhu Y 2010 Comput. Mater. Sci. 49 530
Google Scholar
[16] Jiang H T, Pandey R, Darrigan C, Rerat M 2003 J. Phys. Condens. Matter 15 709
Google Scholar
[17] Kanchana V, Vaitheeswaran G, Rajagopalan M 2003 J. Alloys Compd. 359 66
Google Scholar
[18] Blochl P E 1994 Phys. Rev. B 50 17953
Google Scholar
[19] Kresse G, Furthmuller J 1996 Comput. Mater. Sci. 6 15
Google Scholar
[20] Perdew J P, Burke K, Ernzerhof M 1996 Phys. Rev. Lett. 77 3865
Google Scholar
[21] Dai J J, Feng Q G 2020 Phys. Status Solidi B 257 1900726
Google Scholar
[22] Xiao H Y, Jiang X D, Duan G, Gao F, Zu X T, Weber W J 2010 Comput. Mater. Sci. 48 768
Google Scholar
[23] Cui S X, Feng W X, Hua H Q, Feng Z B, Wang Y X 2009 Comput. Mater. Sci. 47 41
Google Scholar
[24] Kessair S, Arbouche O, Amara K, Benallou Y, Azzaz Y, Zemouli M, Bekki M, Ameri M, Bouazza B S 2016 Indian J. Phys. 90 1403
Google Scholar
[25] Boudjemline A, Louail L, Islam M M, Diawara B 2011 Comput. Mater. Sci. 50 2280
Google Scholar
[26] Guo Y, Fang Y M, Li J 2021 Chin. Phys. B 30 030502
Google Scholar
[27] Wu X, Qin S, Wu Z Y 2006 Phys. Rev. B 73 134103
Google Scholar
[28] Verma A K, Modak P, Sharma S M 2017 J. Alloys Compd. 710 460
Google Scholar
[29] Tse J S, Klug D D, Desgreniers S, Smith J S, Flacau R, Liu Z, Hu J, Chen N, Jiang D T 2007 Phys. Rev. B 75 134108
Google Scholar
[30] Song H X, Liu L, Geng H Y, Wu Q 2013 Phys. Rev. B 87 184103
Google Scholar
[31] Kunc K, Loa I, Syassen K 2008 Phys. Rev. B 77 094110
Google Scholar
[32] Ji D P, Chong X Y, Ge Z H, Feng J 2019 J. Alloys Compd. 773 988
Google Scholar
[33] Liu G, Wang H, Ma Y M, Ma Y M 2011 Solid State Commun. 151 1899
Google Scholar
[34] Gonze X, Lee C 1997 Phys. Rev. B 55 10355
Google Scholar
[35] Togo A, Oba F, Tanaka I 2008 Phys. Rev. B 78 134106
Google Scholar
[36] Kroumova E, Aroyo M I, Perez-Mato J M, Kirov A, Capillas C, Ivantchev S, Wondratschek H 2003 Phase Transitions 76 155
Google Scholar
[37] Soni H R, Gupta S K, Talati M, Jha P K 2011 J. Phys. Chem. Solids 72 934
Google Scholar
[38] Kinoshita K, Nishimura M, Akahama Y, Kawamura H 2007 Solid State Commun. 141 69
Google Scholar
[39] Luo D B, Wang Y C, Yang G C, Ma Y M 2018 J. Phys. Chem. C 122 12448
Google Scholar
[40] Rubloff G W 1972 Phys. Rev. B 5 662
Google Scholar
[41] Kanchana V, Vaitheeswaran G, Rajagopalan M 2003 Physica B 328 283
Google Scholar
[42] Shi H, Luo W, Johansson B, Ahujia R 2009 J. Phys. Condens. Matter 21 415501
Google Scholar
[43] Hao A M, Yang X C, Li J, Xin W, Zhang S H, Zhang X Y, Liu R P 2009 Chin. Phys. Lett. 26 077103
Google Scholar
[44] 朱春野, 刘欢欢, 刘艳辉 2011 延边大学学报(自然科学版) 37 19
Google Scholar
Zhu C Y, Liu H H, Liu Y H 2011 J. Yanbian Univ. (Natural Science Edition) 37 19
Google Scholar
[45] 吴成国, 武文远, 龚艳春, 戴斌飞, 何苏红, 黄雁华 2015 64 114213
Google Scholar
Wu C G, Wu W Y, Gong Y C, Dai B F, He S H, Huang Y H 2015 Acta Phys. Sin. 64 114213
Google Scholar
-
图 2 BaF 2的相对体积随压强的变化
Fig. 2. Relative volume ( V/ V 0) variation of BaF 2 as a function of pressure.
图 3 BaF 23种物相晶格常数随压强的变化
Fig. 3. Evolution of the lattice constants of BaF 2 with three structures under pressure.
图 4 BaF 2(a) Fm
$ \overline {3} $ m结构T 2g模和(b) P6 3/ mmc结构2E 2g模拉曼峰位随压强的变化Fig. 4. Raman shift as a function of pressure for (a) T 2g of Fm
$ \overline {3} $ m and (b) 2E 2g of P6 3/ mmc.
图 5 不同压强下BaF 2的 P6 3/ mmc相声子谱 (a) 12 GPa; (b) 14 GPa; (c) 40 GPa; (d) 80 GPa
Fig. 5. Phonon dispersion curves for P6 3/ mmc structure of BaF 2 at different pressures: (a) 12 GPa; (b) 14 GPa; (c) 40 GPa; (d) 80 GPa.
图 6 P6 3/ mmc结构 M点声学支声子振动频率随压强的变化
Fig. 6. Phonon frequencies at M point as a function of pressure for P6 3/ mmc structure.
图 7 GGA泛函计算BaF 23种物相带隙随压强的变化
Fig. 7. Band gap as a function of pressure for three structures with GGA of BaF 2.
图 9 Pnma相F1原子投影电子态密度(PDOS)随压强的变化
Fig. 9. Projected DOS onto p y + p z and px orbitals of F1 atoms for Pnma and P6 3/ mmc structure.
表 1 10 GPa压强下 Pnma结构BaF 2拉曼峰位计算结果
Table 1. Calculated Raman shift of Pnma structure BaF 2 under 10 GPa.
Mode ω/cm –1 Mode ω/cm –1 Mode ω/cm –1 A g 81.2 A g 190.6 B 2g 268.7 B 3g 81.4 B 1g 203.3 A g 283.3 B 1g 90.2 A g 211.2 B 1g 304.4 A g 112.9 B 3g 218.7 B 3g 309.6 B 2g 151.5 B 2g 224.0 A g 321.6 B 2g 174.7 B 2g 251.2 B 2g 363.8 
下载: 导出CSV
-
[1] Snider E, Dasenbrock-Gammon N, McBride R, Debessai M, Vindana H, Vencatasamy K, Lawler K V, Salamat A, Dias R P 2020 Nature 586 373
Google Scholar
[2] Xia J, Yan J, Wang Z, He Y, Gong Y, Chen W, Sum T C, Liu Z, Ajayan P M, Shen Z 2021 Nat. Phys. 17 92
Google Scholar
[3] 徐波, 田永君 2017 66 036201
Google Scholar
Xu B, Tian Y J 2017 Acta Phys. Sin. 66 036201
Google Scholar
[4] Ayala A P 2001 J. Phys. Condens. Matter 13 11741
Google Scholar
[5] Kavner A 2008 Phys. Rev. B 77 224102
Google Scholar
[6] Leger J M, Haines J, Atouf A, Schulte O, Hull S 1995 Phys. Rev. B 52 13247
Google Scholar
[7] Wang J S, Ma C L, Zhou D, Xu Y S, Zhang M Z, Gao W, Zhu H Y, Cui Q L 2012 J. Solid State Chem. 186 231
Google Scholar
[8] Speziale S, Duffy T S 2002 Phys. Chem. Miner. 29 465
Google Scholar
[9] Dorfman S M, Jiang F M, Mao Z, Kubo A, Meng Y, Prakapenka V B, Duffy T S 2010 Phys. Rev. B 81 174121
Google Scholar
[10] Smith J S, Desgreniers S, Tse J S, Sun J, Klug D D, Ohishi Y 2009 Phys. Rev. B 79 134101
Google Scholar
[11] Kourouklis G A, Anastassakis E 1989 Phys. Status Solidi B 152 89
Google Scholar
[12] Kessler J R, Monberg E, Nicol M 1974 J. Chem. Phys. 60 5057
Google Scholar
[13] Gao G Y, Oganov A R, Li P F, Li Z W, Wang H, Cui T, Ma Y M, Bergara A, Lyakhov A O, Iitaka T, Zou G T 2010 Proc. Natl. Acad. Sci. U. S. A. 107 1317
Google Scholar
[14] Jin X L, Meng X, He Z, Ma Y M, Liu B, Cui T A, Zou G T, Mao H K 2010 Proc. Natl. Acad. Sci. U. S. A. 107 9969
Google Scholar
[15] Yang X C, Hao A M, Wang X M, Liu X, Zhu Y 2010 Comput. Mater. Sci. 49 530
Google Scholar
[16] Jiang H T, Pandey R, Darrigan C, Rerat M 2003 J. Phys. Condens. Matter 15 709
Google Scholar
[17] Kanchana V, Vaitheeswaran G, Rajagopalan M 2003 J. Alloys Compd. 359 66
Google Scholar
[18] Blochl P E 1994 Phys. Rev. B 50 17953
Google Scholar
[19] Kresse G, Furthmuller J 1996 Comput. Mater. Sci. 6 15
Google Scholar
[20] Perdew J P, Burke K, Ernzerhof M 1996 Phys. Rev. Lett. 77 3865
Google Scholar
[21] Dai J J, Feng Q G 2020 Phys. Status Solidi B 257 1900726
Google Scholar
[22] Xiao H Y, Jiang X D, Duan G, Gao F, Zu X T, Weber W J 2010 Comput. Mater. Sci. 48 768
Google Scholar
[23] Cui S X, Feng W X, Hua H Q, Feng Z B, Wang Y X 2009 Comput. Mater. Sci. 47 41
Google Scholar
[24] Kessair S, Arbouche O, Amara K, Benallou Y, Azzaz Y, Zemouli M, Bekki M, Ameri M, Bouazza B S 2016 Indian J. Phys. 90 1403
Google Scholar
[25] Boudjemline A, Louail L, Islam M M, Diawara B 2011 Comput. Mater. Sci. 50 2280
Google Scholar
[26] Guo Y, Fang Y M, Li J 2021 Chin. Phys. B 30 030502
Google Scholar
[27] Wu X, Qin S, Wu Z Y 2006 Phys. Rev. B 73 134103
Google Scholar
[28] Verma A K, Modak P, Sharma S M 2017 J. Alloys Compd. 710 460
Google Scholar
[29] Tse J S, Klug D D, Desgreniers S, Smith J S, Flacau R, Liu Z, Hu J, Chen N, Jiang D T 2007 Phys. Rev. B 75 134108
Google Scholar
[30] Song H X, Liu L, Geng H Y, Wu Q 2013 Phys. Rev. B 87 184103
Google Scholar
[31] Kunc K, Loa I, Syassen K 2008 Phys. Rev. B 77 094110
Google Scholar
[32] Ji D P, Chong X Y, Ge Z H, Feng J 2019 J. Alloys Compd. 773 988
Google Scholar
[33] Liu G, Wang H, Ma Y M, Ma Y M 2011 Solid State Commun. 151 1899
Google Scholar
[34] Gonze X, Lee C 1997 Phys. Rev. B 55 10355
Google Scholar
[35] Togo A, Oba F, Tanaka I 2008 Phys. Rev. B 78 134106
Google Scholar
[36] Kroumova E, Aroyo M I, Perez-Mato J M, Kirov A, Capillas C, Ivantchev S, Wondratschek H 2003 Phase Transitions 76 155
Google Scholar
[37] Soni H R, Gupta S K, Talati M, Jha P K 2011 J. Phys. Chem. Solids 72 934
Google Scholar
[38] Kinoshita K, Nishimura M, Akahama Y, Kawamura H 2007 Solid State Commun. 141 69
Google Scholar
[39] Luo D B, Wang Y C, Yang G C, Ma Y M 2018 J. Phys. Chem. C 122 12448
Google Scholar
[40] Rubloff G W 1972 Phys. Rev. B 5 662
Google Scholar
[41] Kanchana V, Vaitheeswaran G, Rajagopalan M 2003 Physica B 328 283
Google Scholar
[42] Shi H, Luo W, Johansson B, Ahujia R 2009 J. Phys. Condens. Matter 21 415501
Google Scholar
[43] Hao A M, Yang X C, Li J, Xin W, Zhang S H, Zhang X Y, Liu R P 2009 Chin. Phys. Lett. 26 077103
Google Scholar
[44] 朱春野, 刘欢欢, 刘艳辉 2011 延边大学学报(自然科学版) 37 19
Google Scholar
Zhu C Y, Liu H H, Liu Y H 2011 J. Yanbian Univ. (Natural Science Edition) 37 19
Google Scholar
[45] 吴成国, 武文远, 龚艳春, 戴斌飞, 何苏红, 黄雁华 2015 64 114213
Google Scholar
Wu C G, Wu W Y, Gong Y C, Dai B F, He S H, Huang Y H 2015 Acta Phys. Sin. 64 114213
Google Scholar
下载:
计量
- 文章访问数: 5047
- PDF下载量: 135
- 被引次数: 0
