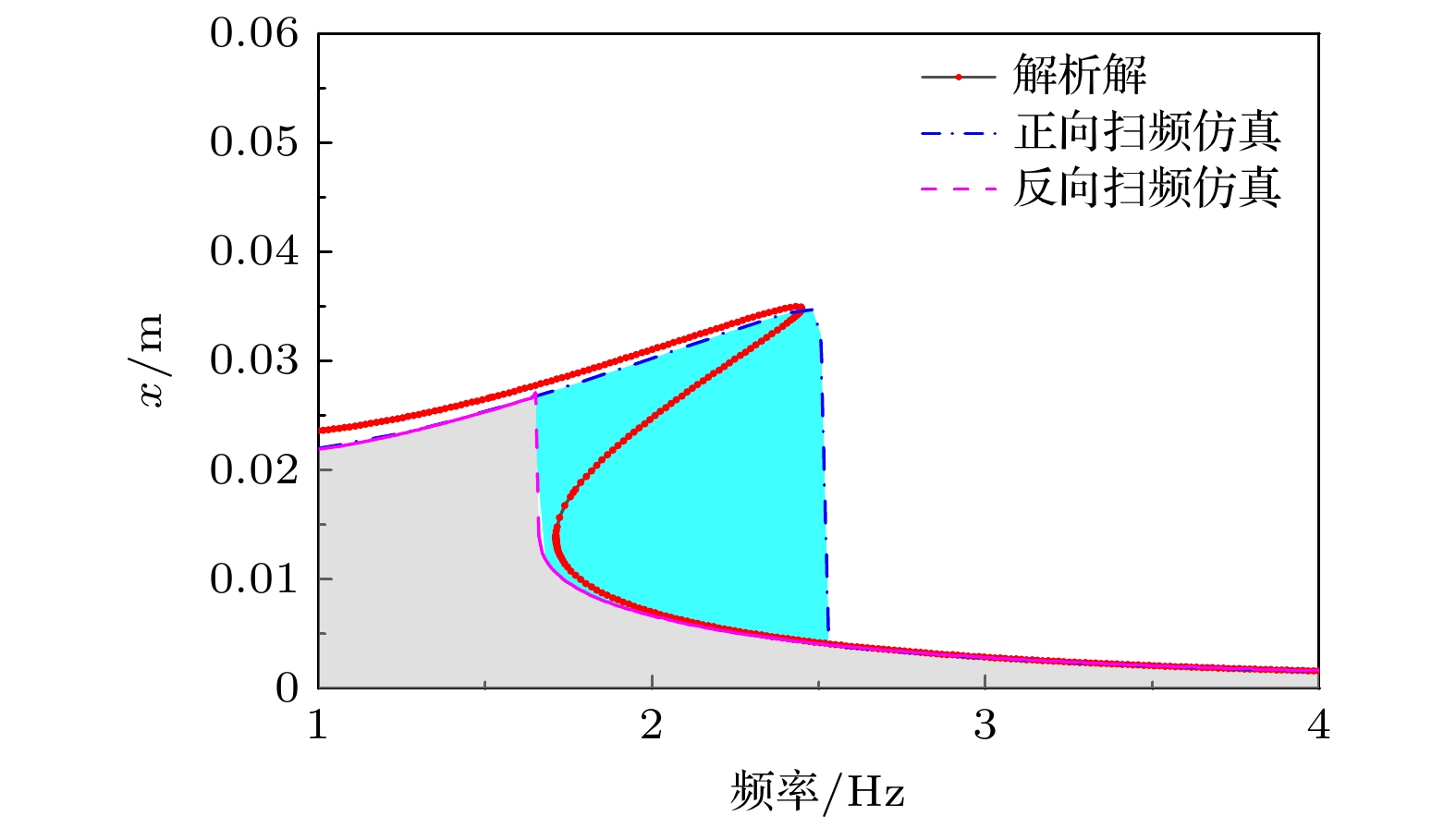
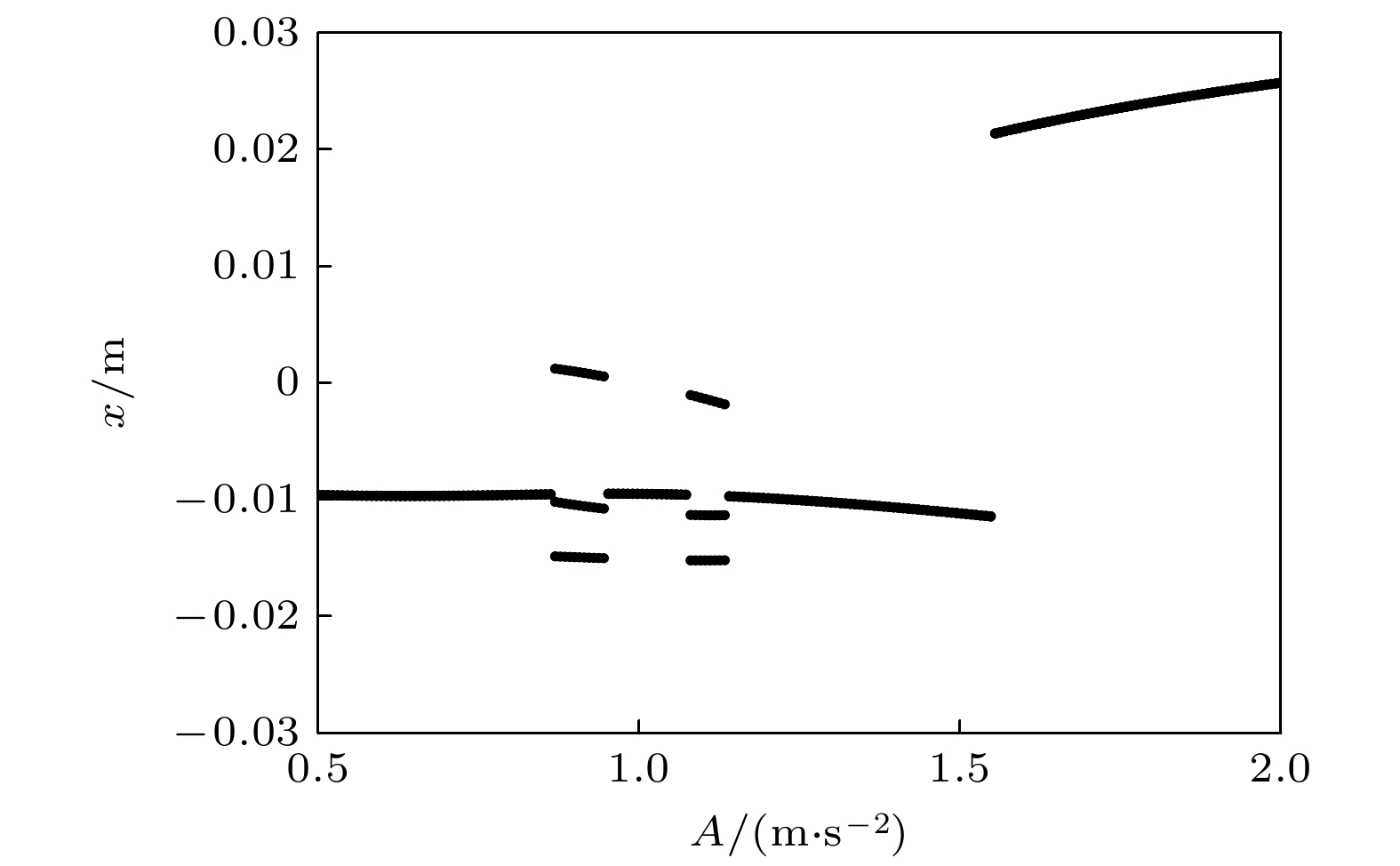
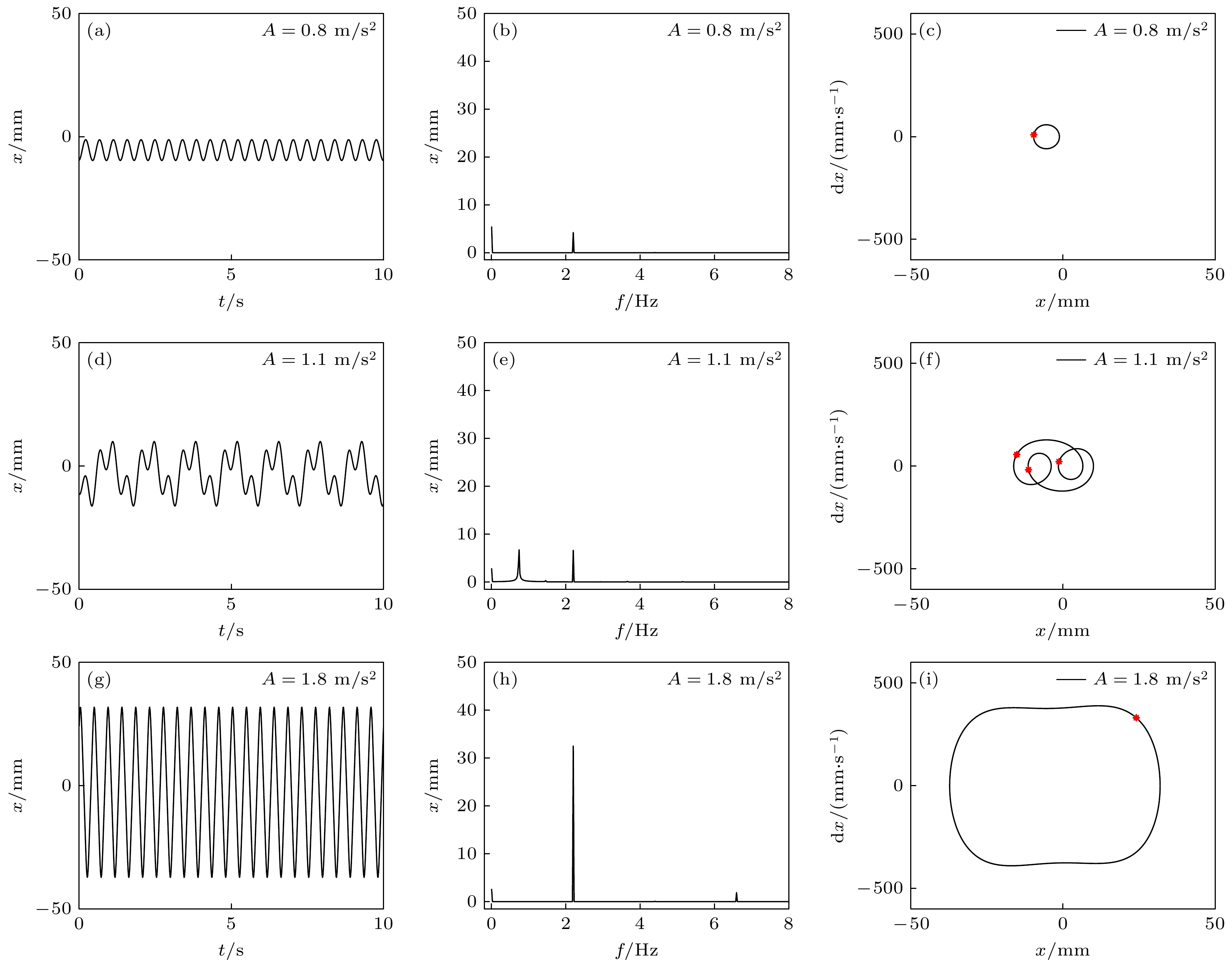
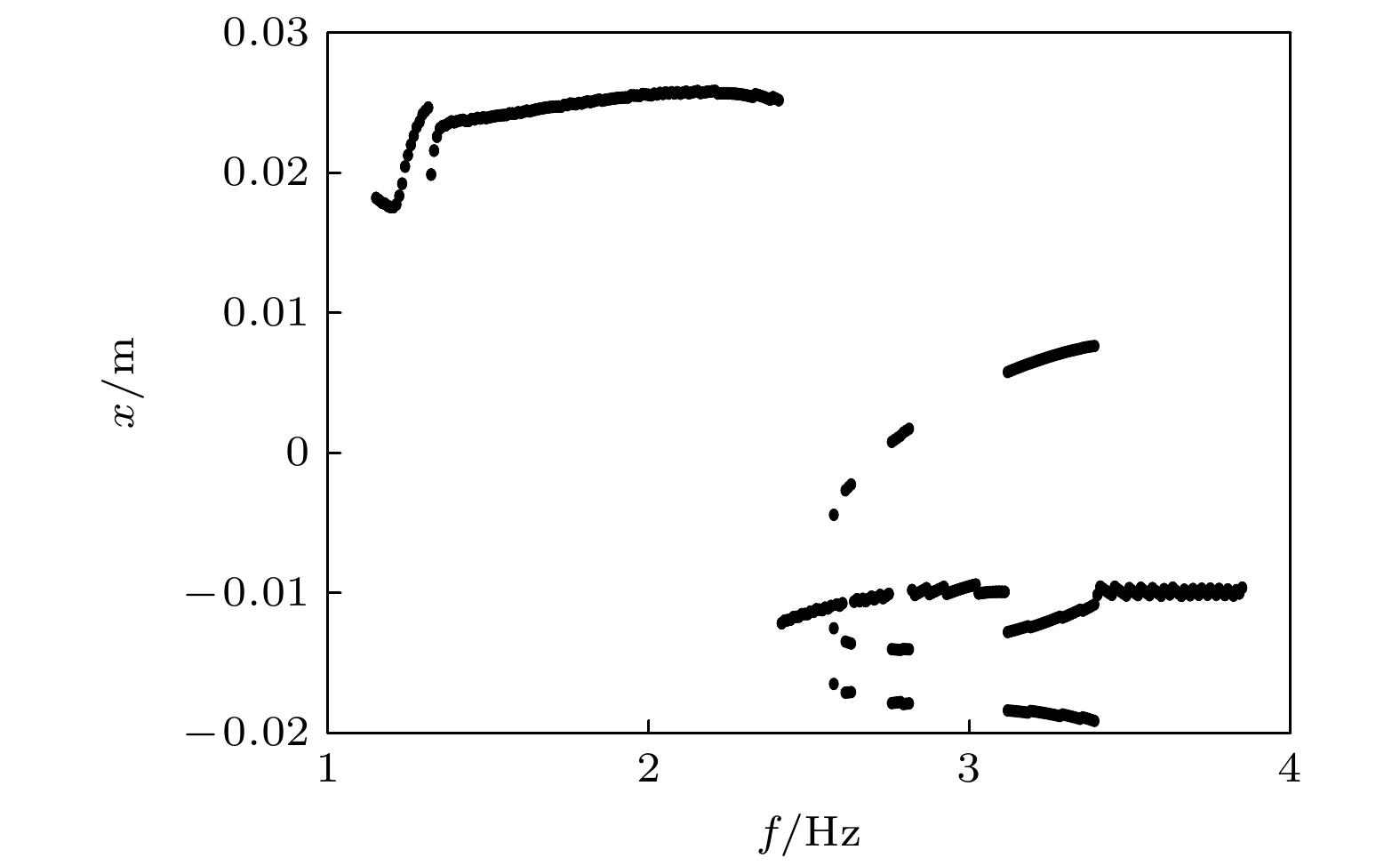
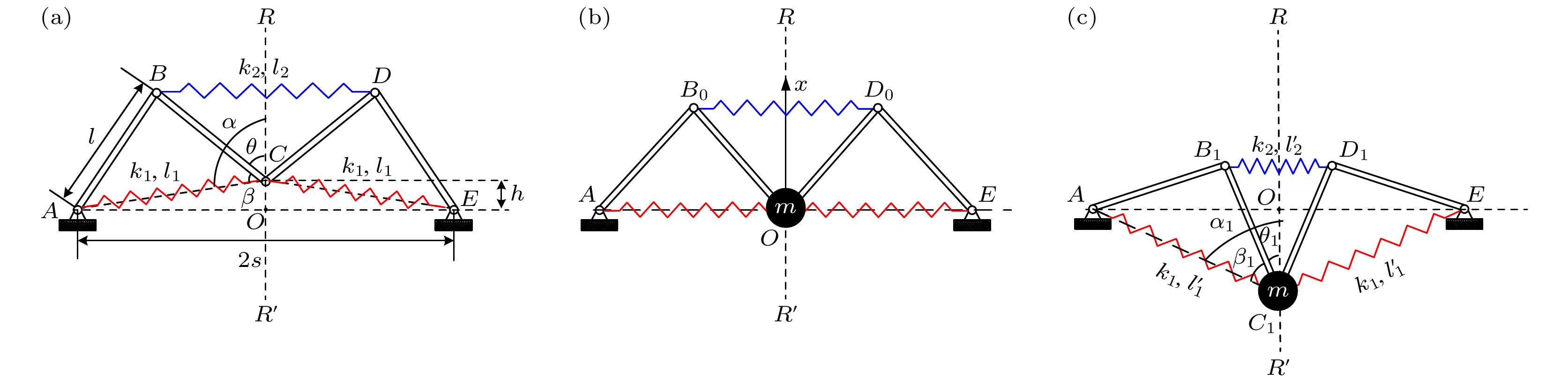
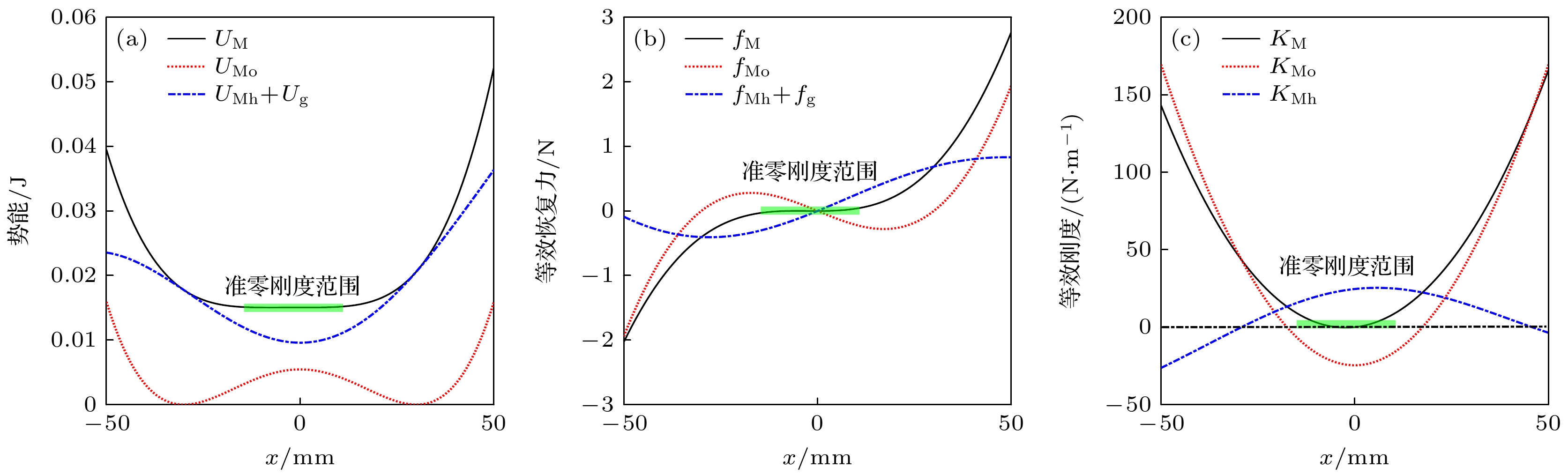
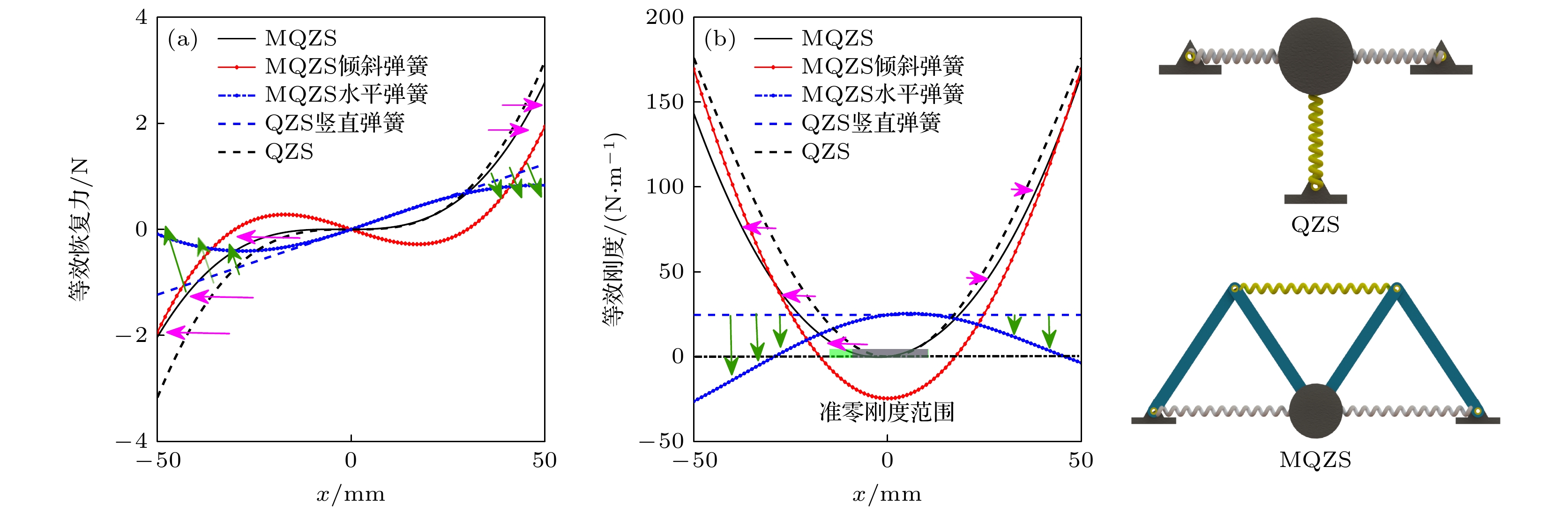
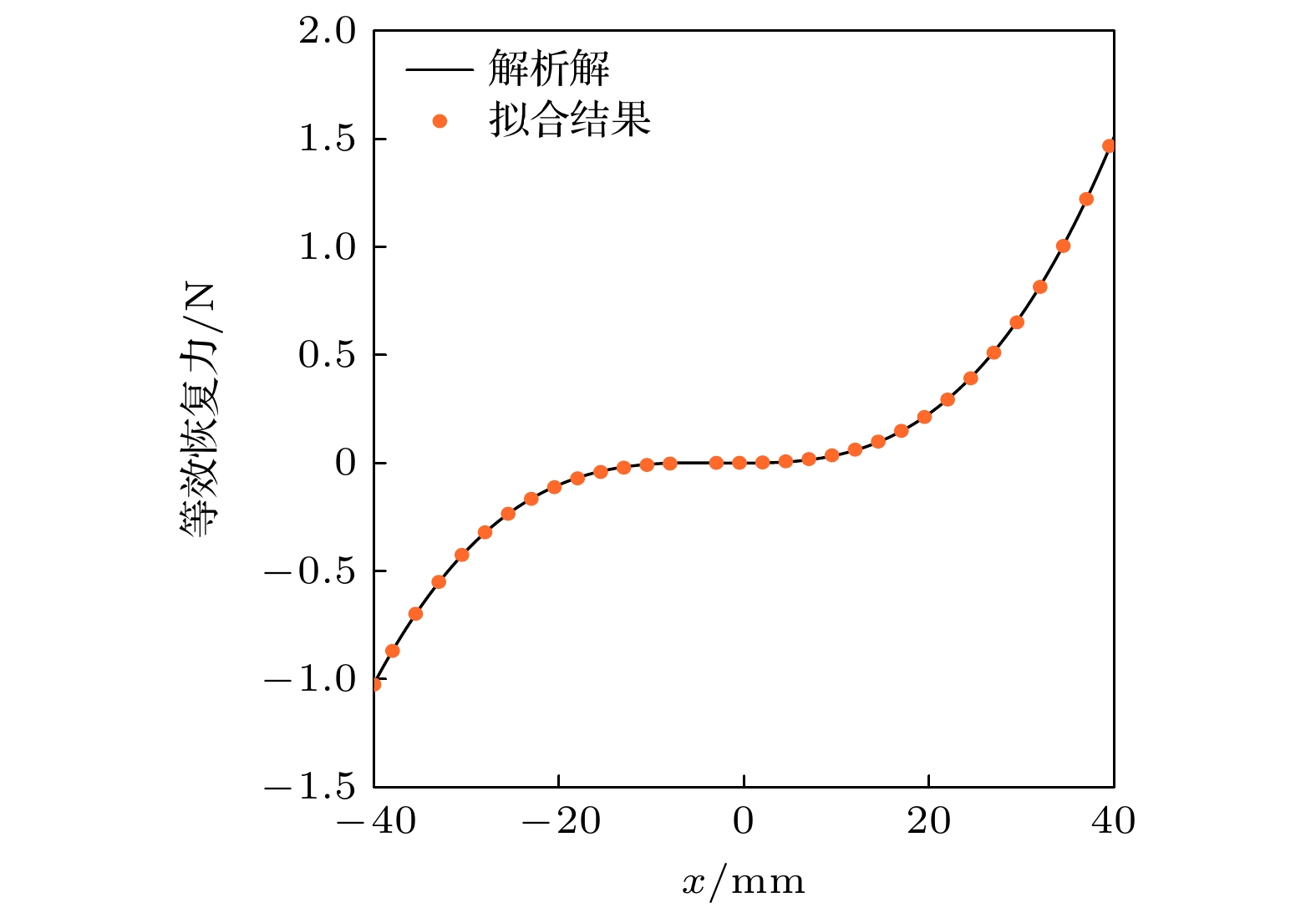
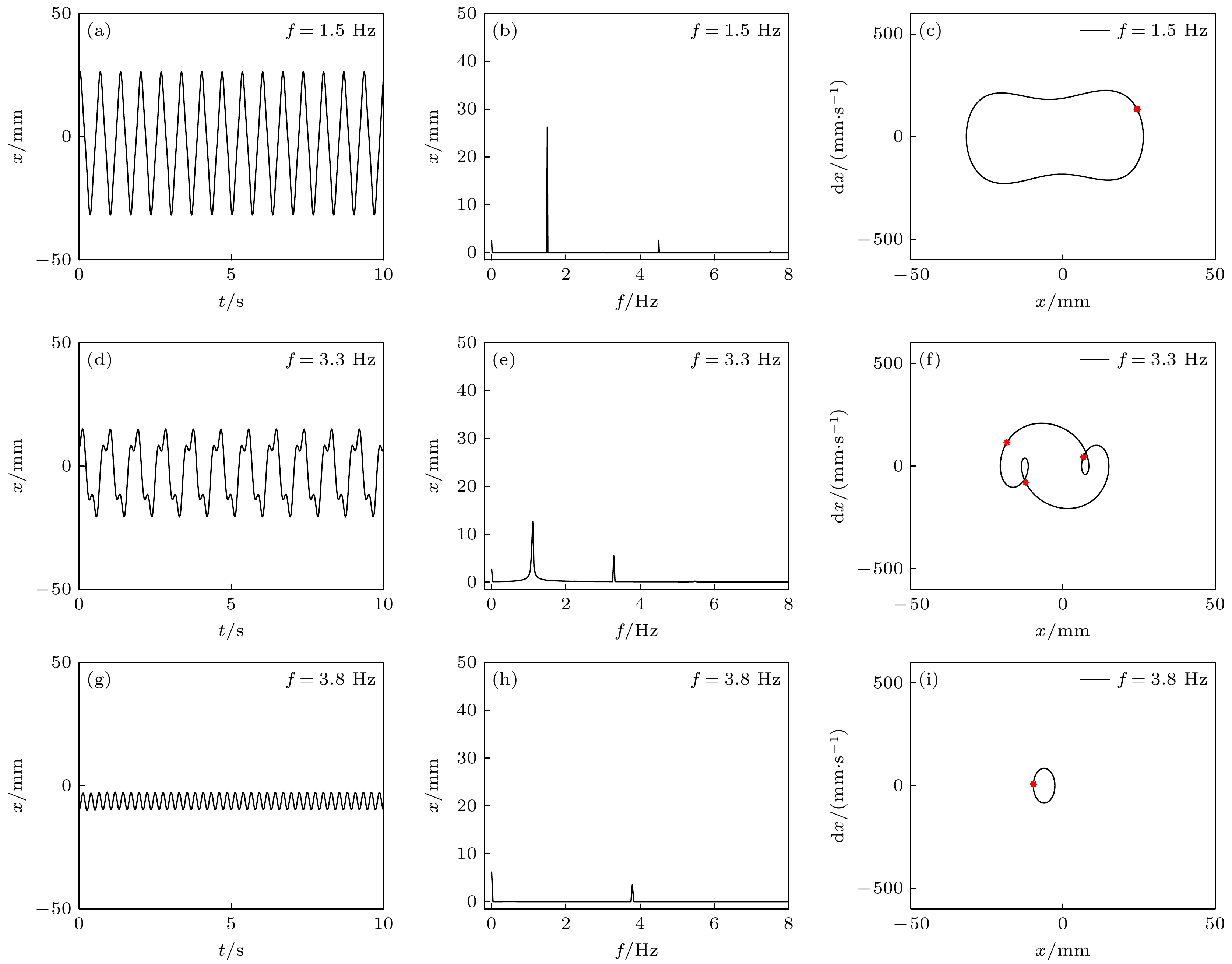
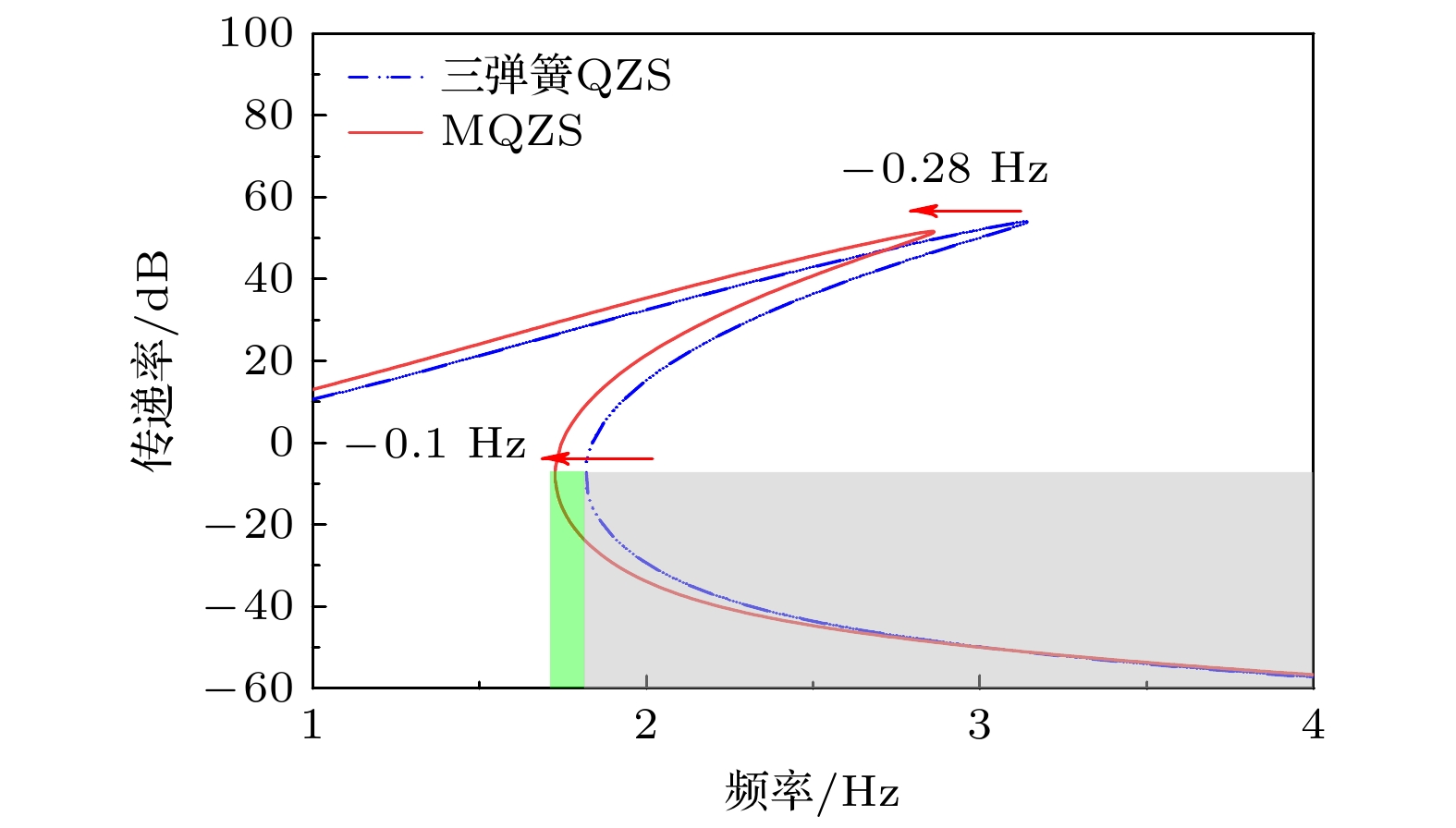
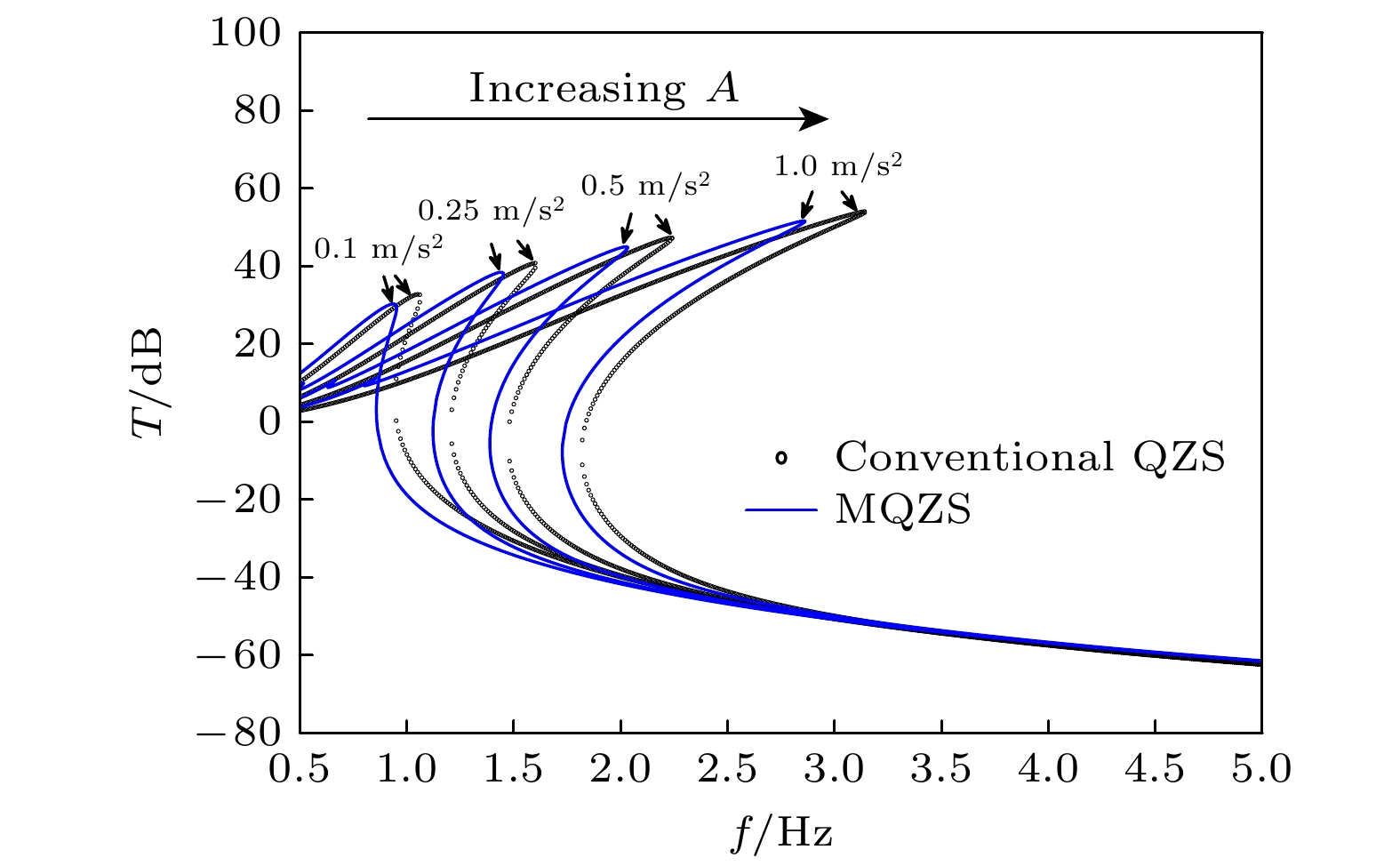
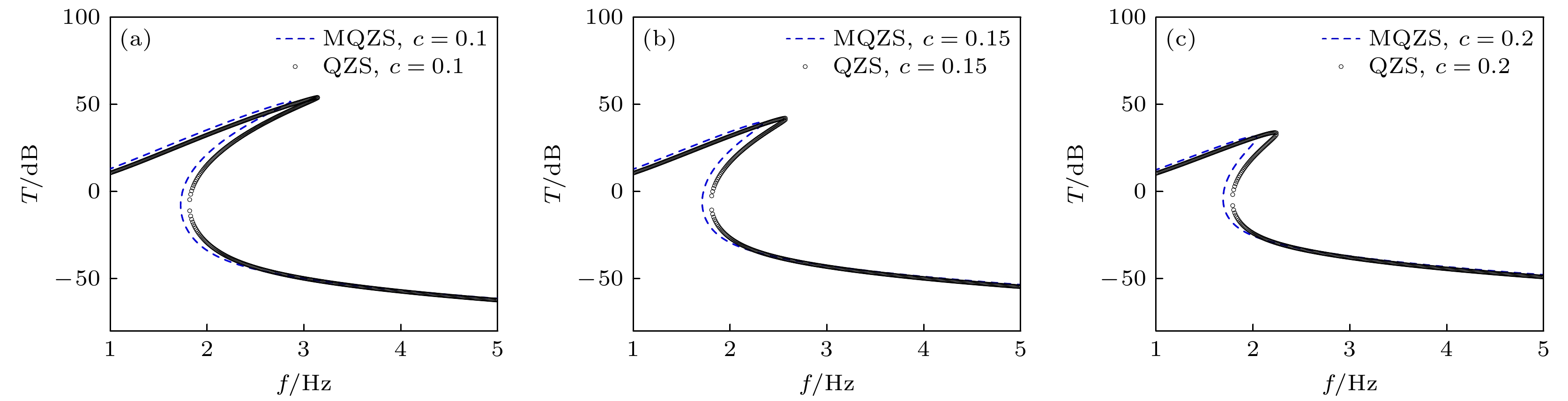
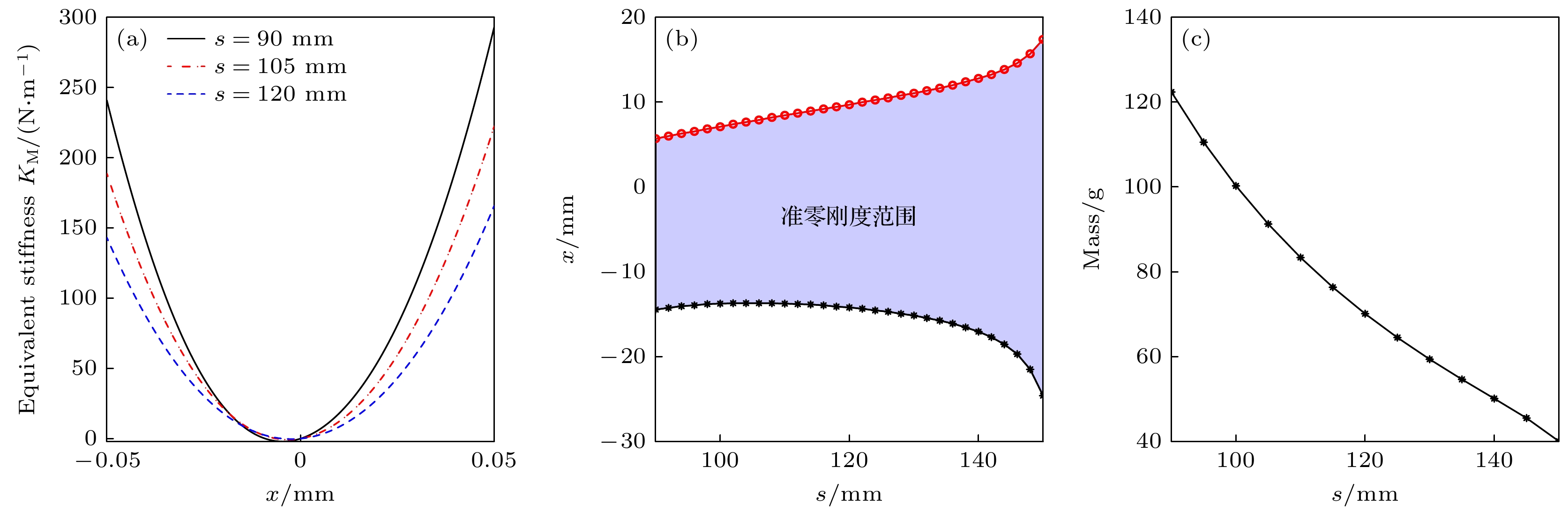
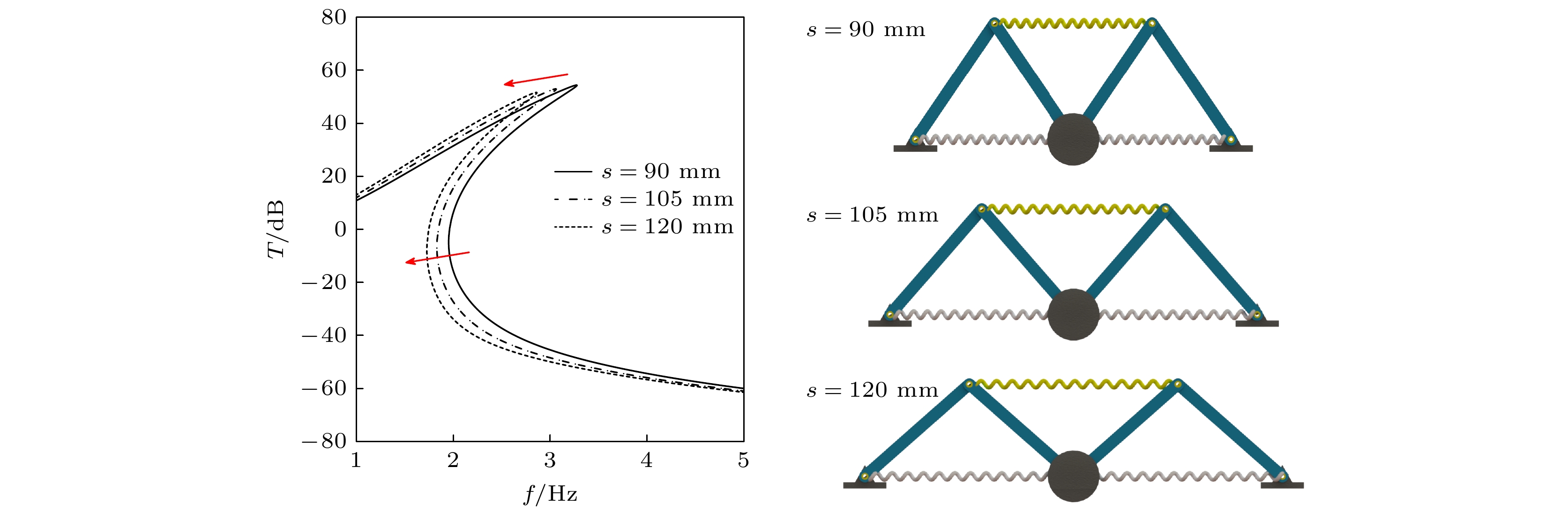
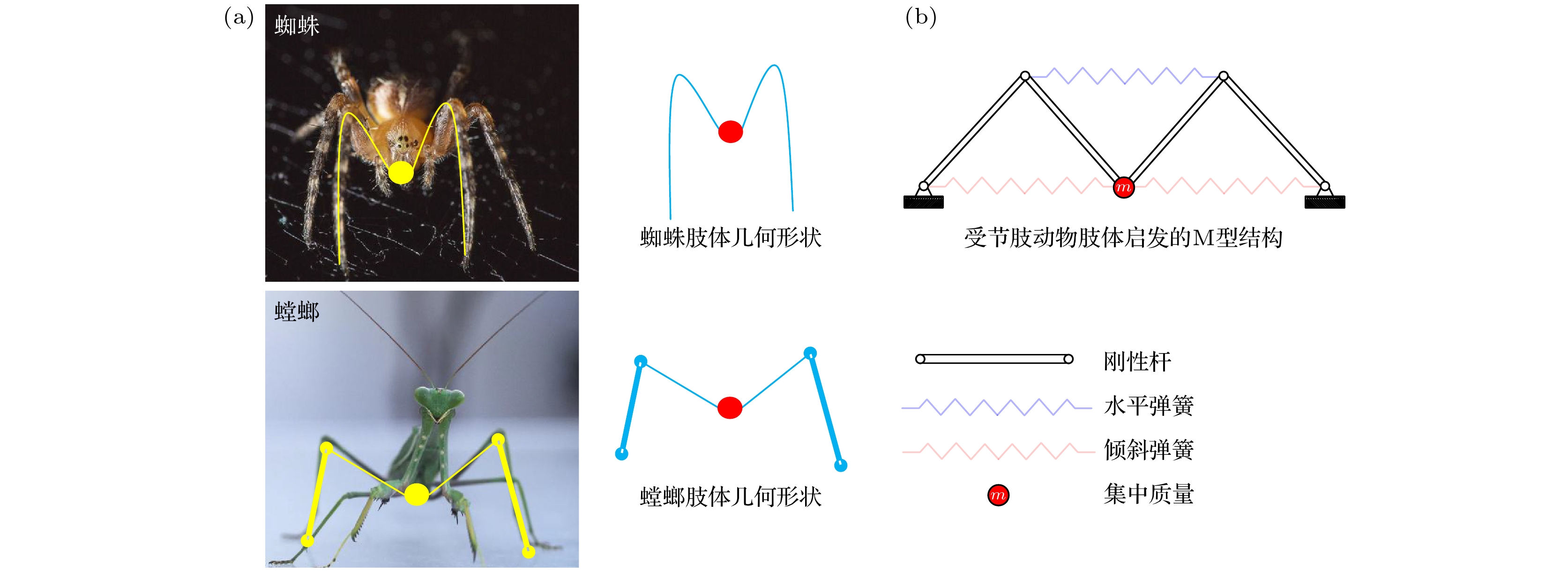
-
Arthropods, including spiders and mantises, are capable of maintaining their body stability on shaking surfaces, such as spiderwebs or leaves. This impressive stability can be attributed to the specific geometry of their limbs, which exhibit an M-shaped structure. Inspired by this geometry, this paper proposes an arthropod-limb-inspired M-shaped structure for low-frequency vibration isolation. First, the design methodology of the M-shaped quasi-zero-stiffness (QZS) structure is presented. A static analysis of potential energy, restoring force, and equivalent stiffness is conducted. It is revealed that the M-shaped structure enables a horizontal linear spring to generate nonlinear stiffness in the vertical direction. More importantly, this nonlinear stiffness effectively compensates for the negative stiffness in large-displacement responses, thereby achieving a wider quasi-zero-stiffness region compared to the conventional three-spring-based QZS structure. Subsequently, the harmonic balance method was employed to derive approximate analytical solutions for the M-shaped QZS structure, which were well validated through numerical simulation. A comparison between the proposed M-shaped QZS structure and the conventional three-spring-based QZS structure was performed. Results show that the M-shaped QZS structure is advantageous for reducing both the cut-in isolation frequency and the resonance frequency. In particular, under large excitation or small damping conditions, the performance improvement of the M-shaped QZS structure in terms of reducing the resonance frequency and maximum response becomes more pronounced. The underlying mechanism behind this feature is primarily attributed to the expanded QZS region induced by the M-shaped structure. Lastly, since the M-shaped structures vary among different arthropods, the effect of the geometry of M-shaped structures on low-frequency vibration performance was investigated. Interestingly, a trade-off between vibration isolation performance and loading mass was observed. As the M-shaped structure becomes flatter, the QZS region expands, and both the cut-in isolation frequency, the resonance frequency/peak, and the loading mass decrease. This occurs because a flatter M-shaped structure leads to a reduction in the equivalent stiffness generated by the horizontal stiffness. Consequently, while the loading mass capacity decreases, the low-frequency vibration isolation performance is enhanced. This novel finding provides a reasonable explanation for why most arthropods possess many pairs of limbs, allowing the loading mass to be distributed and enabling excellent low-frequency vibration isolation to be achieved simultaneously.
-
Keywords:
- Bio-inspired Structure /
- Low-frequency Vibration Isolation /
- Nonlinear Vibration /
- Arthropods
-
[1] Jiao X L, Zhang J X, Li W B, Wang Y Y, Ma W L, Zhao Y 2023 Prog. Aerosp. Sci. 138 100898
[2] Li L, Wang L, Yuan L, Zheng R, Wu Y P, Sui J, Zhong J 2021Acta Astronaut. 180 417
[3] Spacecraft Line-of-Sight Jitter Management and Mitigation Lessons Learned and Engineering Best Practices, Dennehy C J, Wolf A A, Swanson D K https://ntrs.nasa.gov/citations/20210017871[2025-05-07]
[4] Meng G, Dong Y H, Zhou X B, Shen J F, Liu X T 2019 Sci. Sin-Phys. Mech. As. 49 74（in Chinese） [孟光，董瑶海，周徐斌，申军烽，刘兴天2019中国科学：物理学、力学、天文学49 74]
[5] McPherson K, Hrovat K, Kelly E, Keller J 2015A Researcher’s Guide to Acceleration Environment on the International Space Station (Washington, D.C.: NASA) pp37-41
[6] Liu H P, Zhang S C, Men L L, He Z Q 2022Acta Phys. Sin. 71 157（in Chinese）[刘海平，张世乘，门玲鸰，何振强2022 71 157]
[7] Luo H T, Fan C H, Li Y X, Liu G M, Yu C S 2023Eur. J. Mech. A-Solid. 97 104833
[8] Molyneux W G 1958 Aircr. Eng. Aerosp. Tec. 30 160
[9] Carrella A, Brennan M J, Waters T P 2007J. Sound Vib. 301 678
[10] Zhang Y Y 2014M.S. Thesis (Hunan: Hunan University) (in Chinese) [张月英2014硕士学位论文(湖南: 湖南大学)]
[11] Kovacic I, Brennan M J, Waters T P 2008J. Sound Vib. 315 700
[12] Zhou J X, Wang X L, Xu D L, Bishop S 2015J. Sound Vib. 346 53
[13] Zhao F, Ji J C, Ye K, Luo Q T 2020Mech. Syst. Signal Pr. 144 106975
[14] Deng T C, Wen G L, Ding H, Lu Z Q, Chen L Q 2020Mech. Syst. Signal Pr. 145 106967
[15] Liu C R, Yu K P, Liao B P, Hu R P 2021Commun. Nonlinear Sci. Numer. Simulat. 95 105654
[16] Hao Z F 2016Ph.D. Dissertation (Harbin: Harbin Institute of Technology) (in Chinese) [郝志峰2016博士学位论文(哈尔滨: 哈尔滨工业大学)]
[17] Ran Z R 2023M.S. Thesis (Shijiazhuang: Shijiazhuang TieDao University) (in Chinese) [阮子悦2023硕士学位论文(石家庄: 石家庄铁道大学)]
[18] Yan B, Yu N, Wang Z H, Wu C Y, Wang S, Zhang W M 2022 J. Sound Vib. 527 116865
[19] Liu X T, Huang X C, Hua H X 2013 J. Sound Vib. 332 3359
[20] Wang K, Zhou J X, Chang Y P, Ouyang H J, Xu D L, Yang Y 2020Nonlinear Dynam. 101755
[21] Wu W J, Chen X D, Shan Y H 2014J. Sound Vib. 333 2958
[22] An J H, 2021M.S. Thesis (Nanjing: Nanjing University of Aeronautics and Astronautics) (in Chinese) [安隽翰2021硕士学位论文(南京: 南京航空航天大学)]
[23] Yan G, Zou H X, Wang S, Zhao L C, Wu Z Y, Zhang W M 2021Appl. Mech. Rev. 73020801
[24] Wu Z J, Jing X J, Bian J, Li F M, Allen R 2015Bioinspir. Biomim. 10 056015
[25] Yan G, Wang S, Zou H X, Zhao L C, Gao Q H, Zhang W M 2020Sci. China Tech. Sci. 63 2617
[26] Shi X J, Xu J, Chen T K, Qian C, Tian W J 2023J. Bionic Eng. 20 2194
[27] Zeng R, Wen G L, Zhou J X, Zhao G 2021Acta Mech. Sinica-PRC. 37 1152
[28] Yan G, Zou H X, Wang S, Zhao L C, Wu Z Y, Zhang W M 2022Mech. Syst. Signal Pr. 162 108010
[29] Jin G X, Wang Z H, Yang T Z 2022Appl. Math. Mech.-Engl. Ed. 43 813
[30] Ling P, Miao L L, Zhang W M, Wu C Y, Yan B 2022Mech. Syst. Signal Pr. 171 108955
[31] Long S M, Leonard A, Carey A, Jakob E M 2015J. Arachnol. 43 111
Metrics
- Abstract views: 25
- PDF Downloads: 0
- Cited By: 0
下载:
