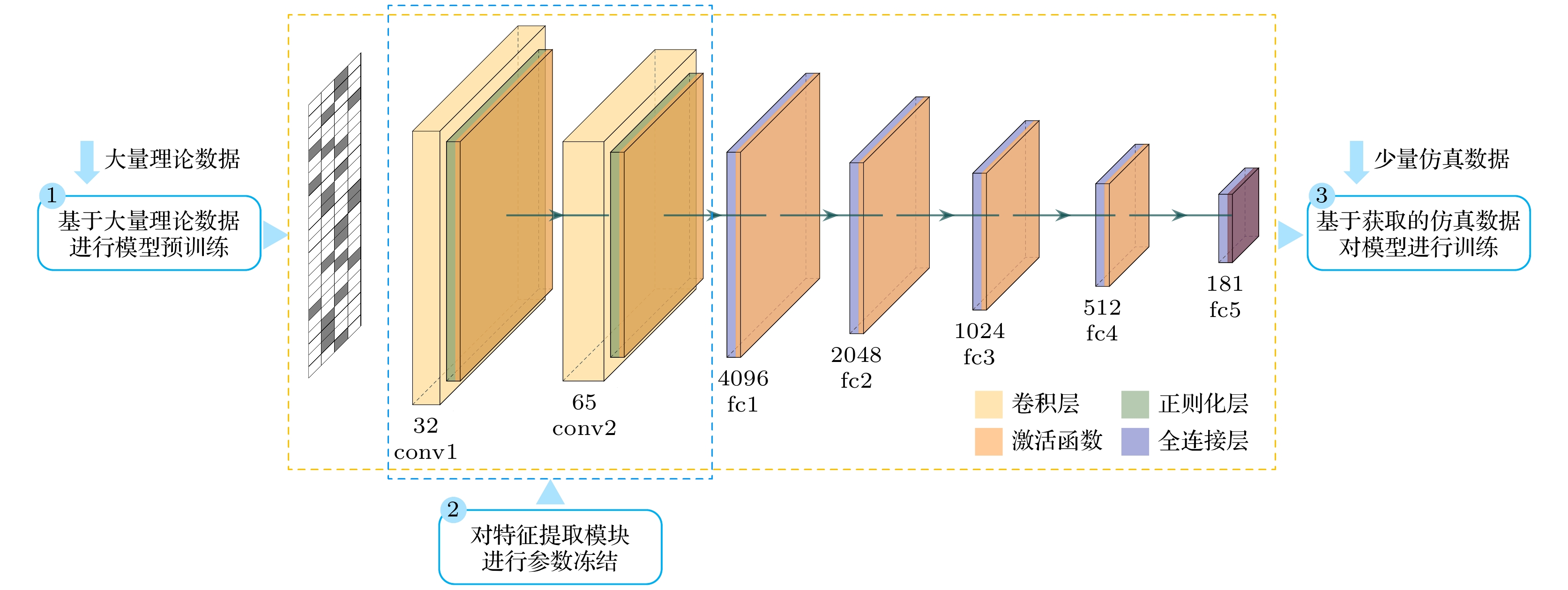
-
Conformal metasurfaces with flexible structures can fit complicated platforms and have obvious advantages in moving platforms scattering manipulations. However, the far-field simulation of conformal metasurface is time-consuming and difficult to optimize, thereby making the its agile design difficult. Here, an efficient and intelligent scattering field calculation method is proposed based on transfer learning for conformal metasurfaces. Firstly, according to the consistency in physical mechanism between antenna theory and full wave simulation, an initial mapping model between phase distribution and far-field of metasurface is constructed and pre-trained based on a large quantity of theoretical data in source domain. Secondly, by pre-training, parameter freezing and model fine-tuning, the far-field prediction model for full wave simulation is transferred and achieved successfully, based on a small quantity of full wave simulation data in target domain. Finally, the transfer learning model for far-field prediction is transferred once again for conformal metasurfaces with different structures. Results indicate that the proposed method only consumes 0.1% of full wave simulation time for conformal metasurface far-field calculation. In fewer samples, the model with transfer learning can improve the average accuracy by 19.8%, and the training data account for only 42.9% for the models without transfer learning, which reduces the training data collection time by 50.1%. Moreover, our far-field calculation method demonstrates good transfer performance between conformal metasurfaces with different structures.
-
Keywords:
- conformal metasurface /
- transfer learning /
- scattering field
-
图 1 共形超构表面迁移学习框架
Figure 1. Transfer learning framework of conformal metasurface.
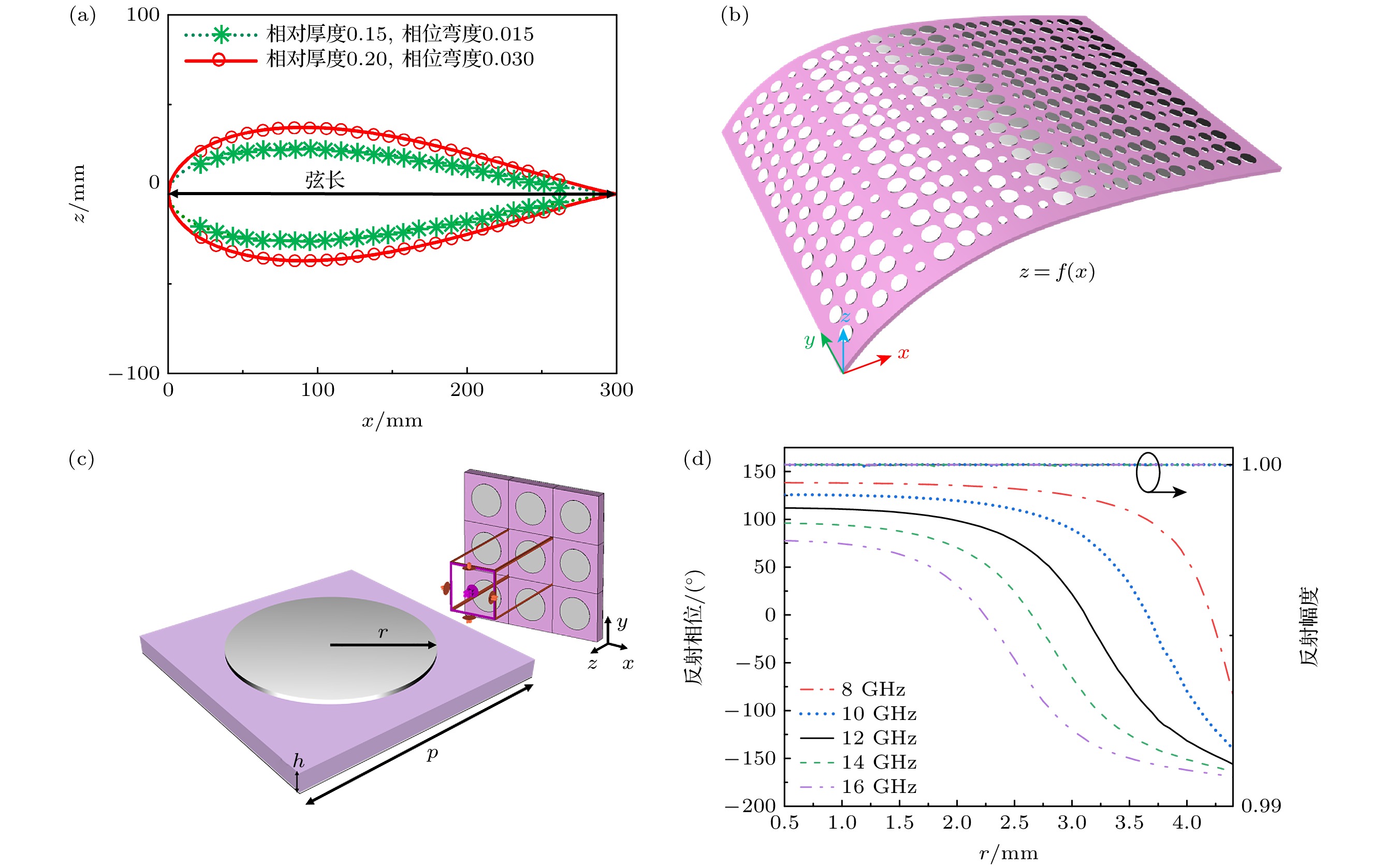
图 2 共型超构表面剖面结构和单元电磁特性 (a) 茹科夫斯基翼型函数曲线; (b) 共型超构表面结构, 其中x和y方向设置为unit cell边界, z方向为open边界; (c) 超构单元结构及其仿真设置; (d) 超构单元的同极化反射相位和幅度
Figure 2. The structure of conformal metasurface and electromagnetic response of meta-atom: (a) Жуковский airfoil function; (b) the structure of conformal metasurface, where unit cell conditions are applied in x and y directions and open condition is applied in z direction; (c) prototype of the meta-atom and simulation setup ; (d) reflection phase and amplitude of co-polarization.
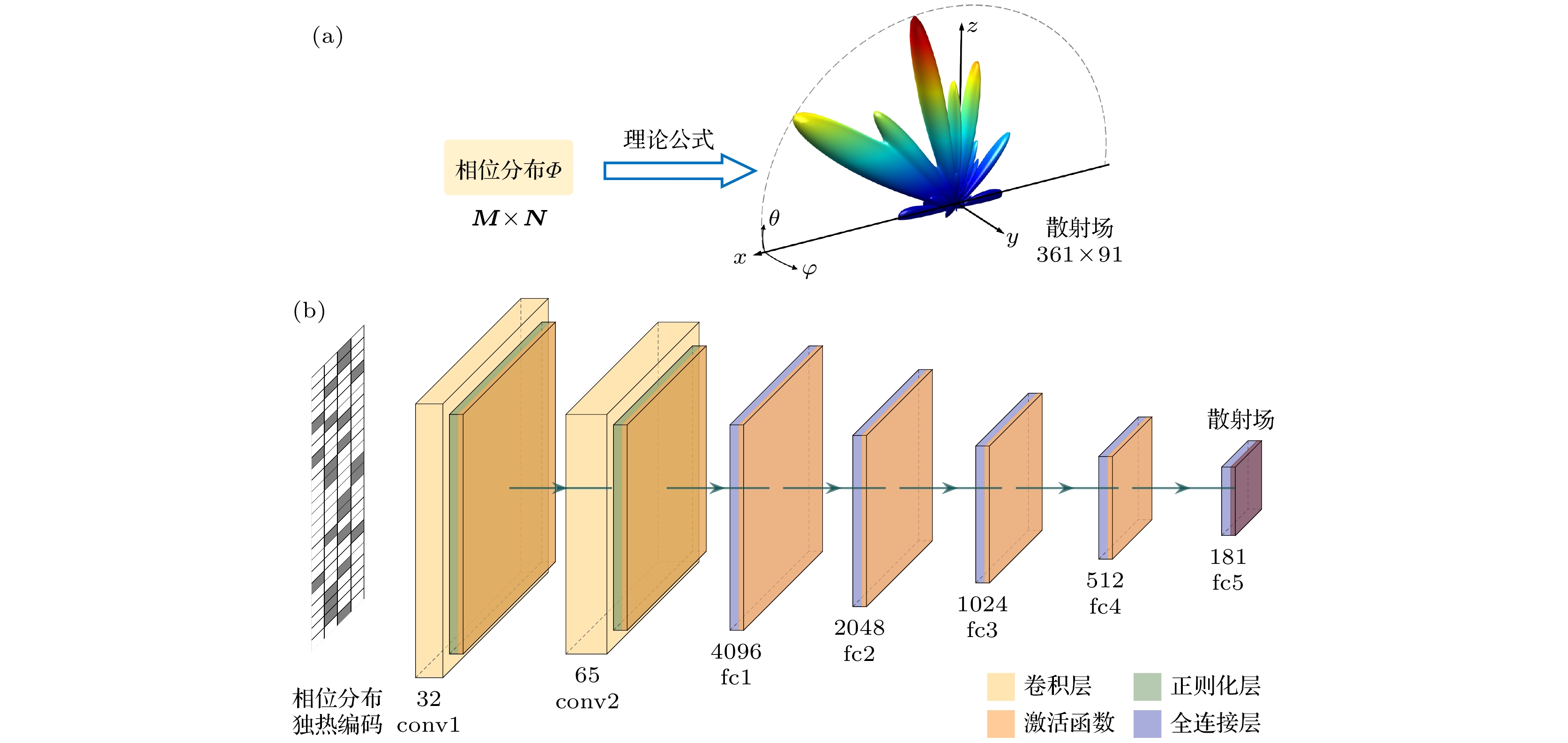
图 3 源域训练数据生成和模型构建 (a) 基于天线理论计算得到大量相位分布和散射场数据; (b) 预训练模型${\mathcal{M}_0}$的网络架构
Figure 3. Training data generation and model network construction of source domain: (a) Numerous phase distribution and scattering data can be generated based on antenna theory; (b) paradigm of pre-trained network ${\mathcal{M}_0}$.
图 4 全波仿真数据获取设置 (a) 联合自动化仿真流程; (b) 共形超构表面全波仿真设置
Figure 4. Configurations of full wave simulations: (a) The flowchart of associated automation simulation; (b) the full wave simulation setup of conformal metasurface.
图 5 迁移学习策略
Figure 5. Transfer learning strategy.
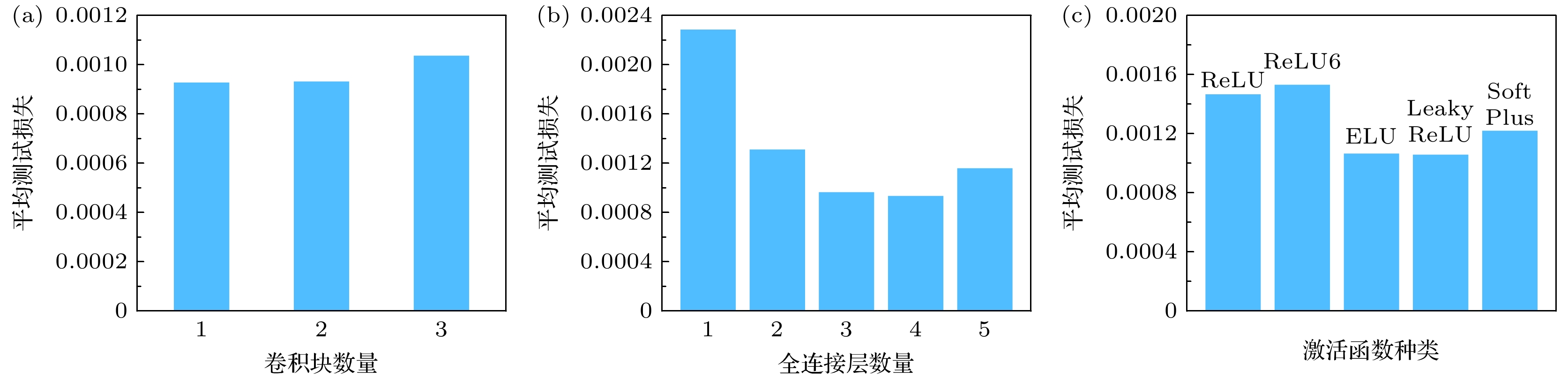
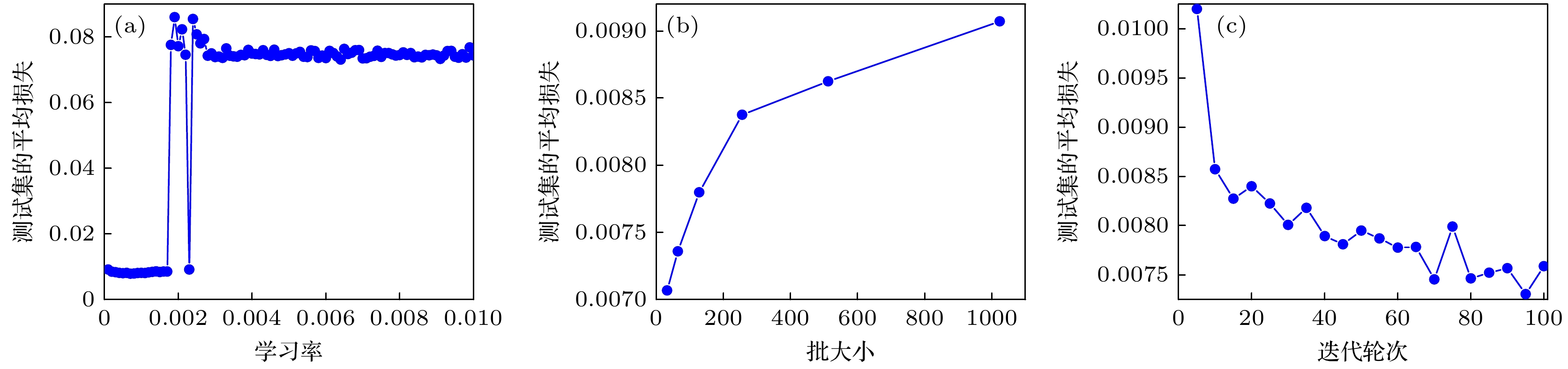
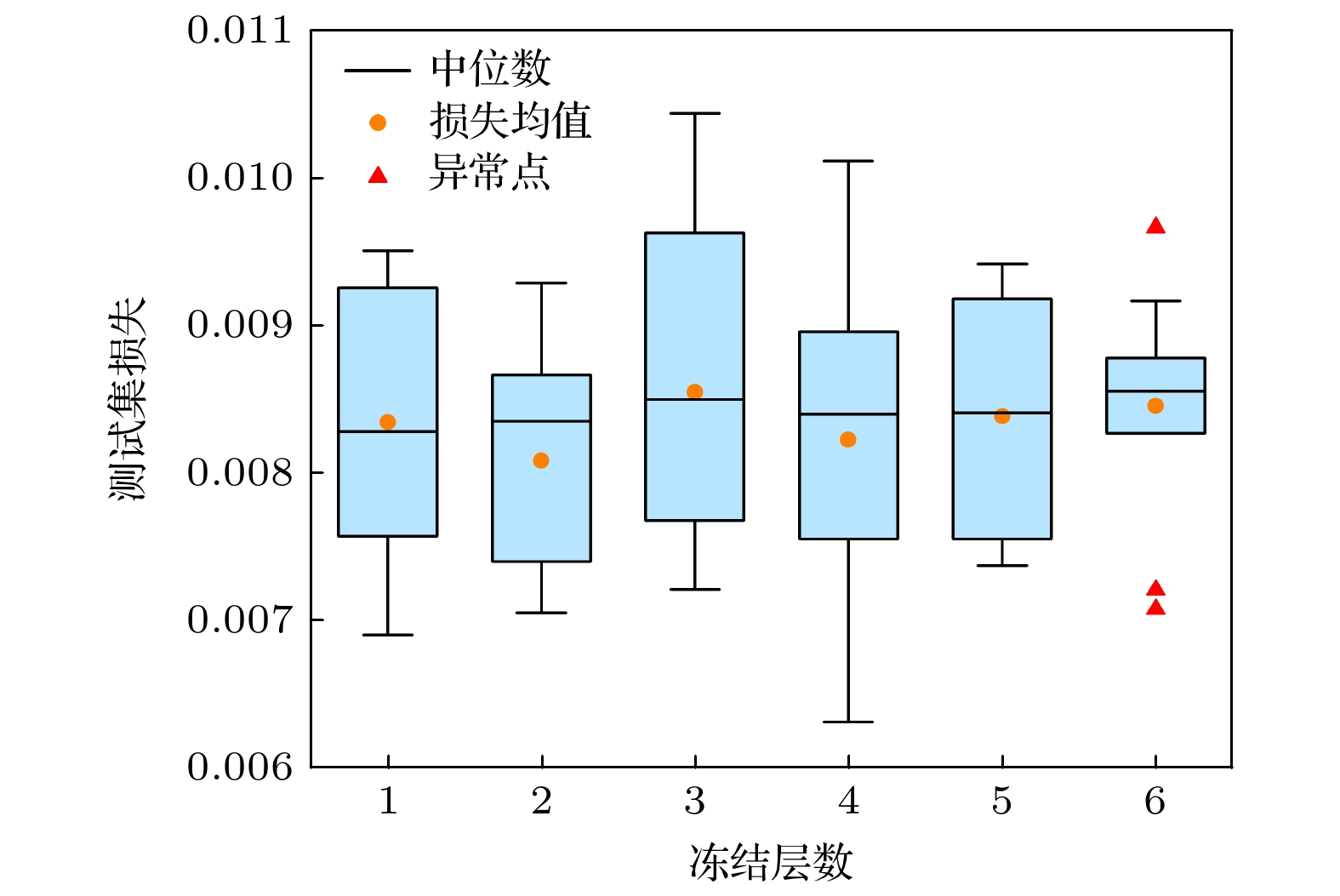
图 6 模型结构分析 (a) 卷积块数量取1, 2, 3时模型的平均测试损失值; (b) 全连接层数量为1, 2, 3, 4, 5时模型的平均测试损失值; (c) 激活函数分别为ReLU, ReLU6, ELU, Leaky ReLU和Soft Plus模型平均测试损失值
Figure 6. Network structure analysis. Model average train loss with (a) convolution blocks number of 1, 2, 3, (b) fully connected layer number of 1, 2, 3, 4, 5, and (c) activation function of ReLU, ReLU6, ELU, Leaky ReLU and Soft Plus.
图 7 模型超参数寻优. 测试集的平均损失随 (a) 学习率, (b) 批大小, (c) 迭代轮次变化曲线
Figure 7. Model hyperparameter optimization. The average loss of the test set varies with (a) learning rate, (b) batch size, and (c) iteration rounds.
图 8 迁移学习冻结层数对测试集损失值的影响.
Figure 8. The impact of transfer learning frozen layers numbers on loss value.
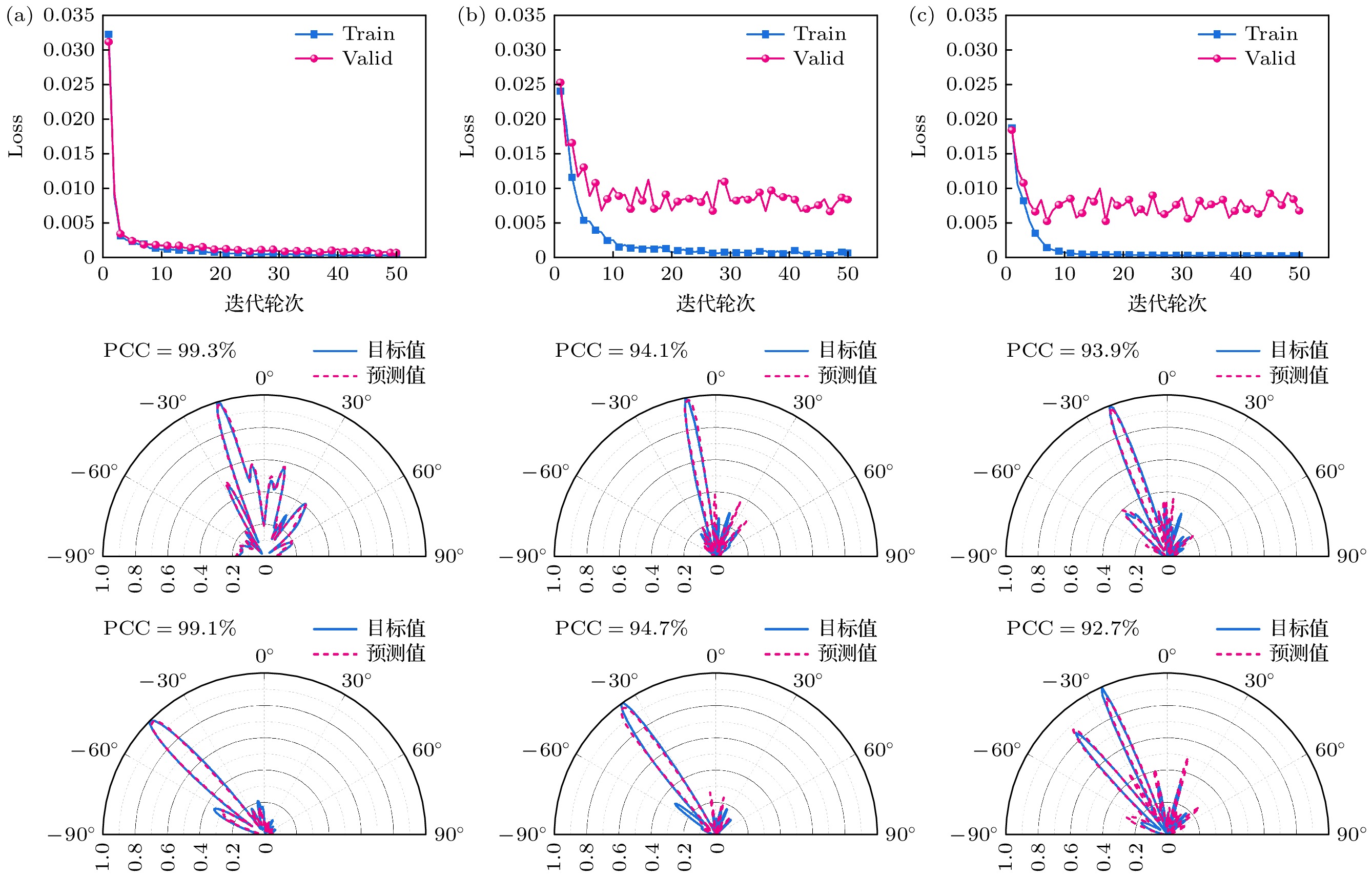
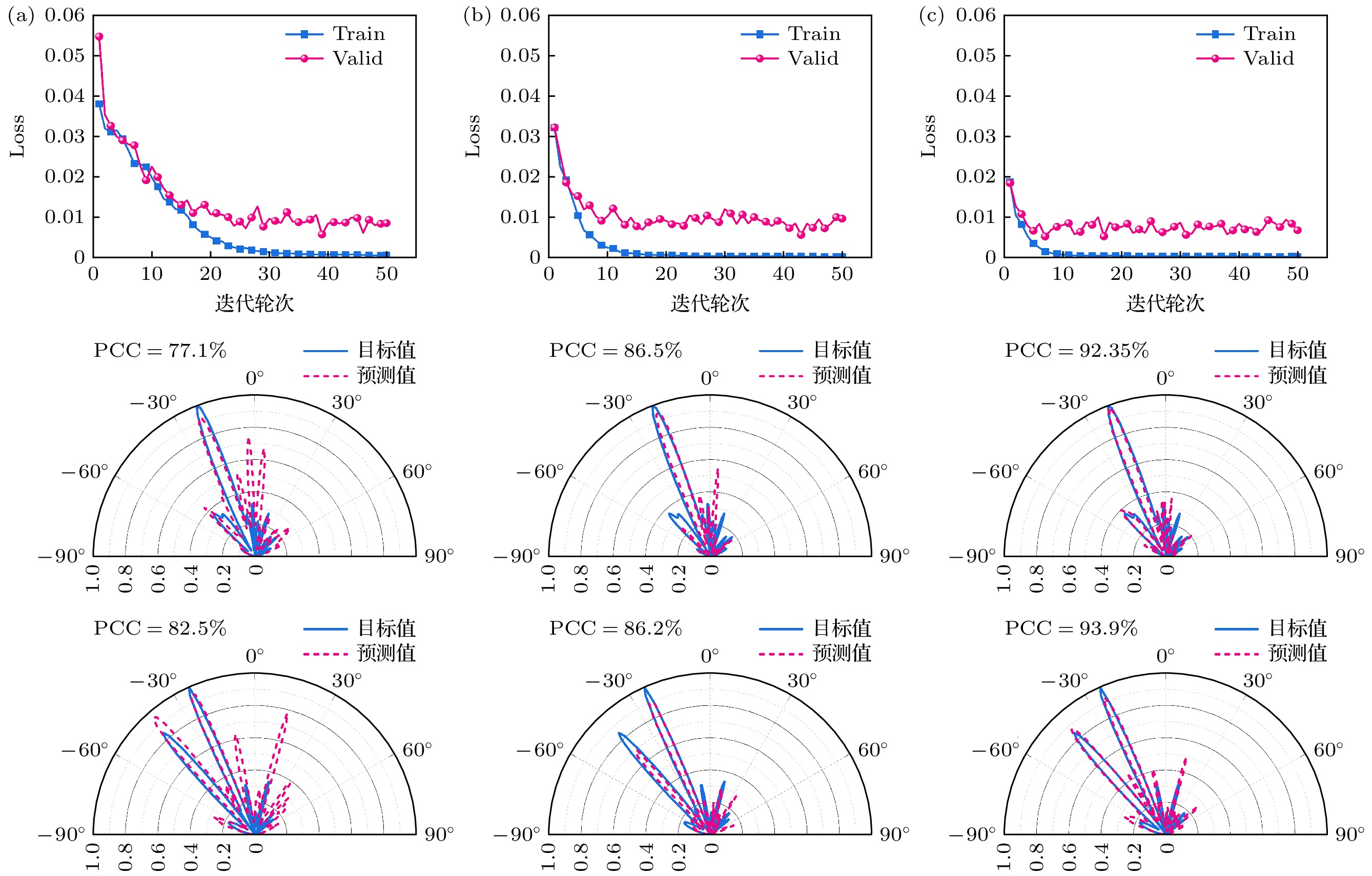
图 9 模型${\mathcal{M}_0}$, ${\mathcal{M}_1}$和${\mathcal{M}_2}$的平均损失值和效果验证 模型${\mathcal{M}_0}$(a), ${\mathcal{M}_1}$(b), ${\mathcal{M}_2}$(c)的损失值随迭代轮次的变化曲线以及两种测试算例下的拟合效果
Figure 9. Loss value and verification of ${\mathcal{M}_0}$, ${\mathcal{M}_1}$ and ${\mathcal{M}_2}$: Loss over the epoch and prediction results under two testing instances of ${\mathcal{M}_0}$(a), ${\mathcal{M}_1}$(b), ${\mathcal{M}_2}$(c).
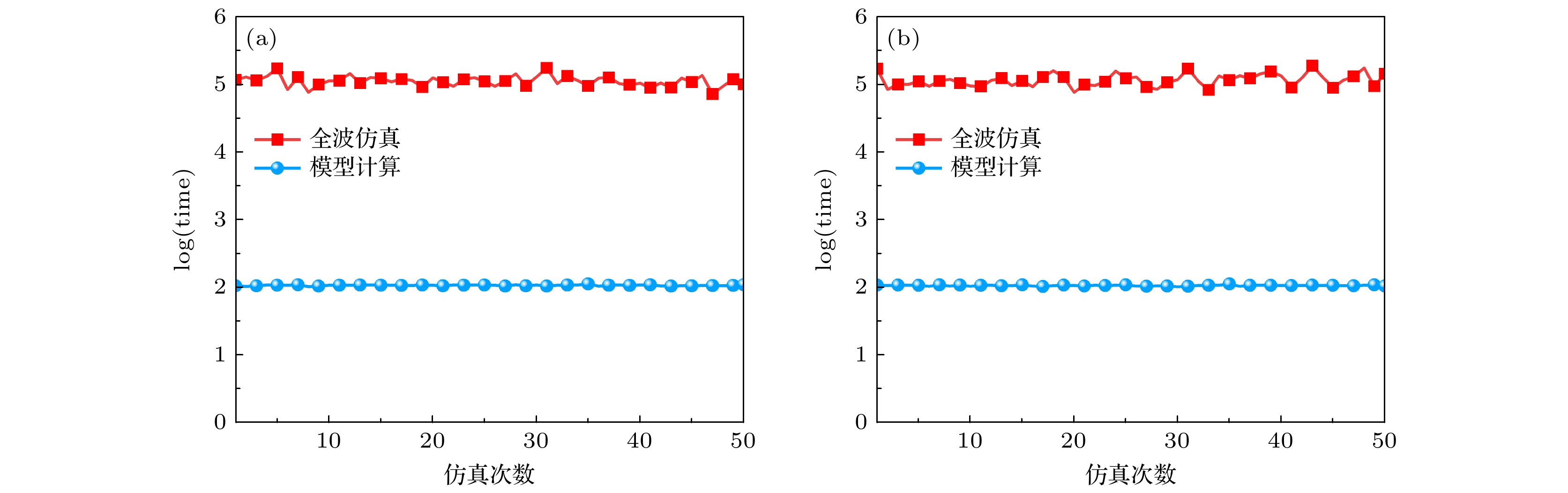
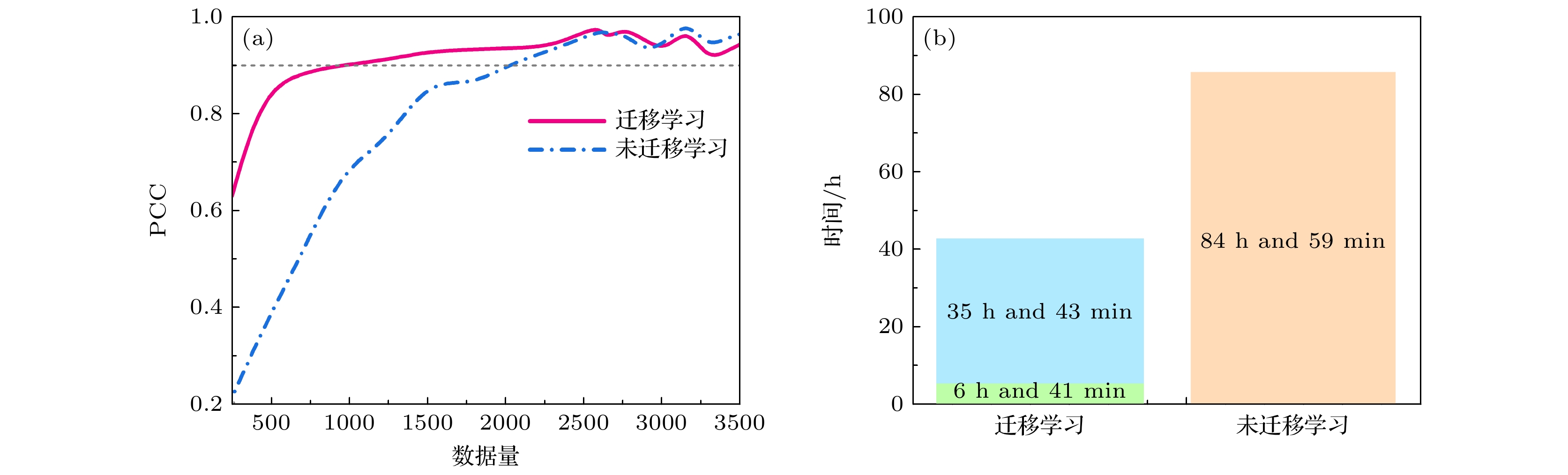
图 10 迁移学习模型与全波仿真时间对比 (a) 结构1共形超构表面在软件中进行全波仿真计算散射场, 与利用模型${\mathcal{M}_1}$计算散射场的时间对数值; (b) 结构2共形超构表面在软件中进行全波仿真计算散射场, 与利用模型${\mathcal{M}_2}$计算散射场的时间对数值
Figure 10. Time comparison of transfer learning model and full-wave simulation: (a) Logarithmic value of full-wave simulation time in CST and model ${\mathcal{M}_1}$ calculation time for conformal metasurface with structure 1; (b) logarithmic value of full-wave simulation time in CST and model ${\mathcal{M}_2}$ calculation time for conformal metasurface with structure 2.
图 11 迁移学习模型和未迁移学习模型性能对比分析 (a) 模型精度随训练数据量的变化关系; (b) 数据集收集时间柱状图
Figure 11. Performances comparative analysis of models with and without transfer learning: (a) Model accuracy varies with the amount of training data; (b) bar chart of dataset collection time.
图 12 结构2共形超构表面散射场计算模型平均损失函数及效果验证 (a) 基于结构2全波仿真数据直接训练得到的远场计算模型${\mathcal{M}'_2}$(未迁移学习); (b) 基于结构1理论数据散射场计算模型${\mathcal{M}_0}$迁移训练得到的结构2共形超构表面远场计算模型${\mathcal{M}''_2}$(经历一次迁移学习); (c) 基于结构1迁移学习模型${\mathcal{M}_1}$迁移训练得到的结构2共形超构表面远场计算模型${\mathcal{M}_2}$(经历两次迁移学习)
Figure 12. Average loss value and performance verifications of structure 2 conformal metasurface far-field prediction models: (a) Far-field prediction model ${\mathcal{M}'_2}$(without transfer learning) for structure 2 conformal metasurface, trained based on structure 2 conformal metasurface full wave calculation data; (b) far-field prediction model ${\mathcal{M}''_2}$ (with once transfer learning) for structure 2 conformal metasurface, transferred from the structure 1 conformal metasurface theoretical far-field prediction model ${\mathcal{M}_0}$; (c) far-field prediction model ${\mathcal{M}_2}$ (with twice transfer learning) for structure 2 conformal metasurface, transferred from the structure 1 conformal metasurface full wave calculation far-field prediction model ${\mathcal{M}_1}$.
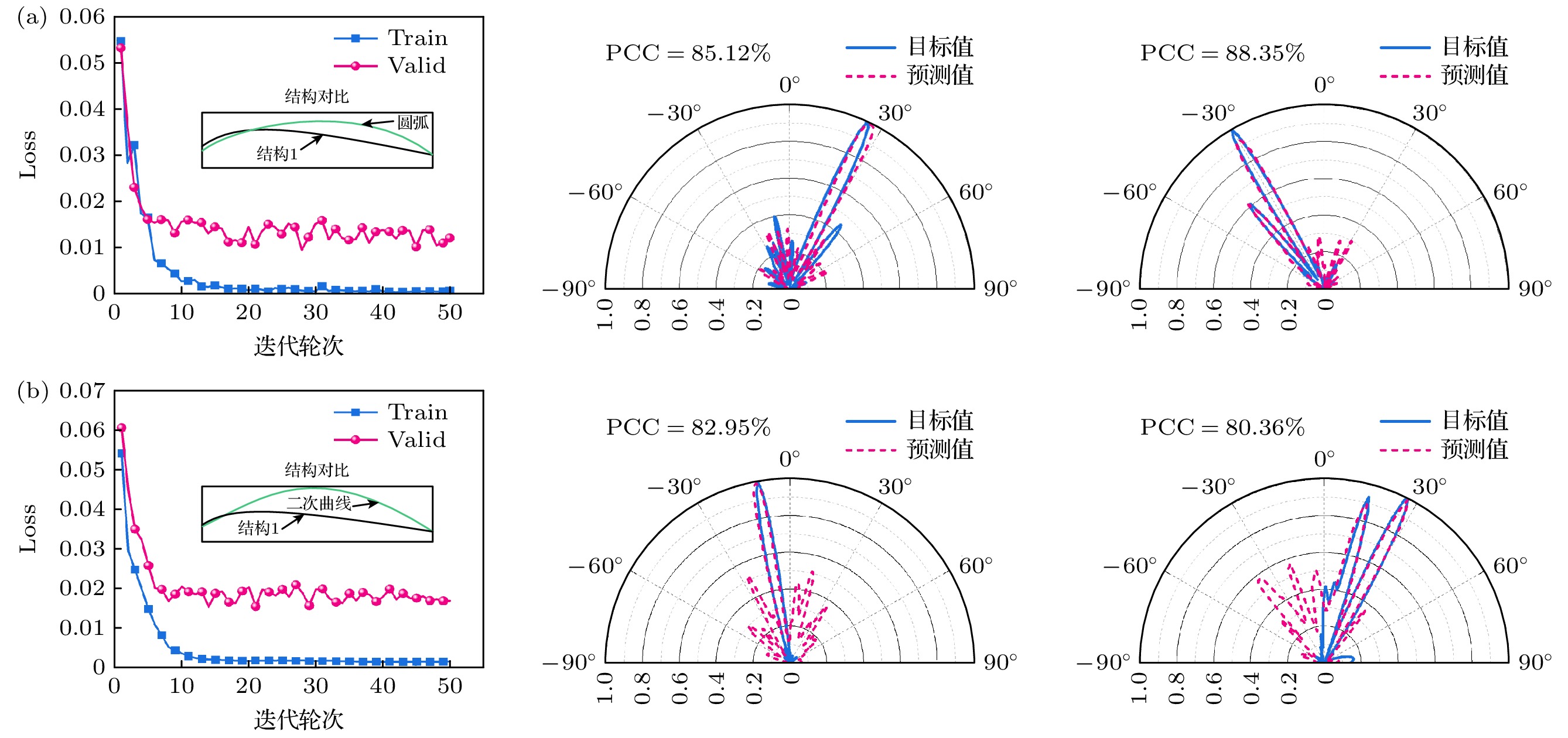
图 13 不同轮廓方程结构迁移学习效果 (a) 轮廓方程为圆弧的共形超构表面散射场预测模型${\mathcal{M}_{\text{c}}}$的平均损失值和效果验证; (b) 轮廓方程为的二次曲线的共形超构表面散射场预测模型${\mathcal{M}_{\text{q}}}$的平均损失值和效果验证. 其中左图中的插图表示结构1轮廓和圆弧、二次曲线结构对比图
Figure 13. The transfer learning performance of different contour equation structures: (a) Average loss value and performance verifications of far-field prediction model ${\mathcal{M}_{\text{c}}}$ for conformal metasurface with contour equation of a circular arc; (b) average loss value and performance verifications of far-field prediction model ${\mathcal{M}_{\text{q}}}$ for conformal metasurface with contour equation of a quadratic curve. The illustration in the left figure represents the comparison between the outline of structure 1 and the structure of arc and quadratic curves.
表 1 模型结构的搜索空间
Table 1. Search space of model structure.
序号 控制变量 候选集合 1 卷积块数量 $ \{1, 2, 3\} $ 2 全连接块数量(不含输出层) $ \{1, 2, 3, 4, 5\} $ 3 激活函数类型 {ReLU, ReLU6, ELU, LeakyReLU, SoftPlus} 
DownLoad: CSV
表 2 模型超参数的搜索空间
Table 2. Search space of model hyperparameters.
序号 控制变量 候选集合 1 学习率 {0.0001, 0.0002, . .., 0.0099, 0.01}, 步长为0.0001 2 批量大小 {32, 64, 128, 256, 512, 1024} 3 迭代轮次 {5, 10, 15, 20, . .., 90, 95, 100}, 步长为5
DownLoad: CSV
表 3 模型迁移关系
Table 3. The transfer relationship between models.
序号 模型 预训练模型 迁移次数 1 ${\mathcal{M}_0}$ 无 0 2 ${\mathcal{M}_1}$ ${\mathcal{M}_0}$ 1 3 ${\mathcal{M}'_2}$ 无 0 4 ${\mathcal{M}''_2}$ ${\mathcal{M}_0}$ 1 5 ${\mathcal{M}_2}$ ${\mathcal{M}_1}$ 2
DownLoad: CSV
-
[1] Liu K Y, Wang G M, Cai T, Guo W L, Zhuang Y Q, Liu G 2018 Chin. Phys. B 27 084101
Google Scholar
[2] Liu K T, Wang G M, Cai T, Dai B J, Xiao Y, Li H P, Guo W L 2019 J. Phys. D: Appl. Phys. 52 255002
Google Scholar
[3] Bai H, Wang G M, Zou X J , Xie P, Shi Y P 2022 Chin. Phys. B 31 54102
[4] Liu K Y, Wang G M, Cai T, Li H P, Li T Y 2021 IEEE Trans. Antennas Propag. 69 3349
Google Scholar
[5] Germain D, Seetharamdoo D, Burokur S N, de Lustrac A 2013 Appl. Phys. Lett. 103 124102
Google Scholar
[6] Wang Y C, Feng Q, Kong X D, Liu H X, Han J Q, Li L 2024 IEEE Antennas Wirel. Propag. Lett. 23 970
Google Scholar
[7] Fu B, Yu S X, Kou N, Ding Z, Zhang Z P 2022 Chin. Phys. B 31 40703
Google Scholar
[8] Gupta E, Bonner C, Lazarus N, Mirotznik M S, Nicholson K J 2023 IEEE Antennas Wirel. Propag. Lett. 22 2629
[9] Fu C F, Han L F, Liu C, Lu X L, Sun Z J 2022 IEEE Trans. Antennas Propag. 70 2352
[10] Wang Y J, Su J X, Li Z R, Guo Q X, Song J M 2020 IEEE Antennas Wirel. Propag. Lett. 19 631
[11] Luo X Y, Chen K, Guo W L, Feng Y J 2019 International Conference on Microwave and Millimeter Wave Technology (ICMMT) Guangzhou China, May 19-22, 2019 pp 1
[12] Xu H X, Hu G W, Wang Y Z, Wang C H, Wang M Z, Wang S J, Huang Y J, Genevet P, Huang W, Qiu C W 2021 Light Sci. Appl. 10 75
Google Scholar
[13] 王朝辉, 许河秀, 逄智超, 王明照, 王少杰 2022 红外与毫米波学报 41 210
Google Scholar
Wang C H, Xu H X, Pang Z C, Wang M Z, Wang S J 2022 J. Infrared Millimeter Waves 41 210
Google Scholar
[14] Srilatha K., Madhav B. T. P., babu B. Anil, Das Sudipta, Rao M. C. 2022 Appl. Phys. A 128 1091
Google Scholar
[15] 刘梦蛟, 李添悦, 戈钦, 王漱明, 王振林, 祝世宁 2022 光学学报 42 2126004
Liu M J, Li T Y, Ge Q, Wang S M, Wang Z L, Zhu S N 2022 Acta Opt. Sin. 42 21260049
[16] 王朝辉, 许河秀, 逄智超, 王明照, 王少杰 2022 红外与毫米波学报 41 8
Google Scholar
Wang Z H, Xu H X, Pang Z C, Wang M Z, Wang S J 2022 J. Infrared Millimeter Waves 41 8
Google Scholar
[17] 杨斯雯, 黄玲玲, 王涌天 2023 光学技术 49 522
Yang S W, Huang L L, Wang Y T 2023 Opt. Tech. 49 522
[18] Ma Y C, Chen S, Ermon S, Lobell David B 2024 Remote Sens. Environ. 301 113924
Google Scholar
[19] Fu S Y, Tao S Y, Fan H T, He K, Liu X T, Tao Y L, Zuo J X, Zhang X, Wang Y, Sun Y J 2024 Appl. Energy 353 121991
Google Scholar
[20] Chen L C, Zhu Y, Papandreou G, Schroff F, Adam H, 2018 European Conference on Computer Vision Berlin Germany, September 8-14, 2018 p833
[21] Treviso M, Ji T C, Lee J U, van Aken B, Cao Q Q, Ciosici M R, Hassid M, Heafield K, Hooker S, Martins P H, Martins A F T, Milder P, Raffel C, Simpson E, Slonim N, Dodge J, Strubell E, Balasubramanian N, Derczynski L, Gurevych I, Schwartz R 2023 Trans. Assoc. Comput. Linguist. 11 826
[22] Zhu R C, Qiu T S, Wang J F, Sui S, Hao C L, Liu T, Li Y F, Feng M D, Zhang A X, Qiu C W, Qu S B 2021 Nat. Commun. 12 2974
Google Scholar
[23] Xu Y, Li F, Gu J Q, Bi Z W, Cao B, Yang Q L, Han J G, Hu Q H, Zhang W L 2024 Adv. Photonics Nexus 3 026002
[24] Qu Y R, Jing L Shen Y C, Qiu M, Soljačić M 2019 ACS Photonics 6 1168
Google Scholar
[25] Xu D, Luo Y, Luo J, Pu M B, Zhang Y X, Ha Y L, Luo X G 2021 Opt. Mater. Express 11 1852
[26] Zhang J, Qian C, Fan Z X, Chen J T, Li E P, Jin J M, Chen H S 2022 Adv. Opt. Mater. 10 2200748
Google Scholar
[27] 张森, 席德科, 李华星 2019 工程热 40 1058
Zhang S, Xi D K, Li H X 2019 J. Eng. Thermophys. 40 1058
[28] Jia Y T, Qian C, Fan Z X, Ding Y Z, Wang Z D, Wang D P, Li E P, Zheng B, Cai T, Chen H S 2022 Adv. Funct. Mater. 32 2109331
Google Scholar
DownLoad:
Metrics
- Abstract views: 111
- PDF Downloads: 4
- Cited By: 0
