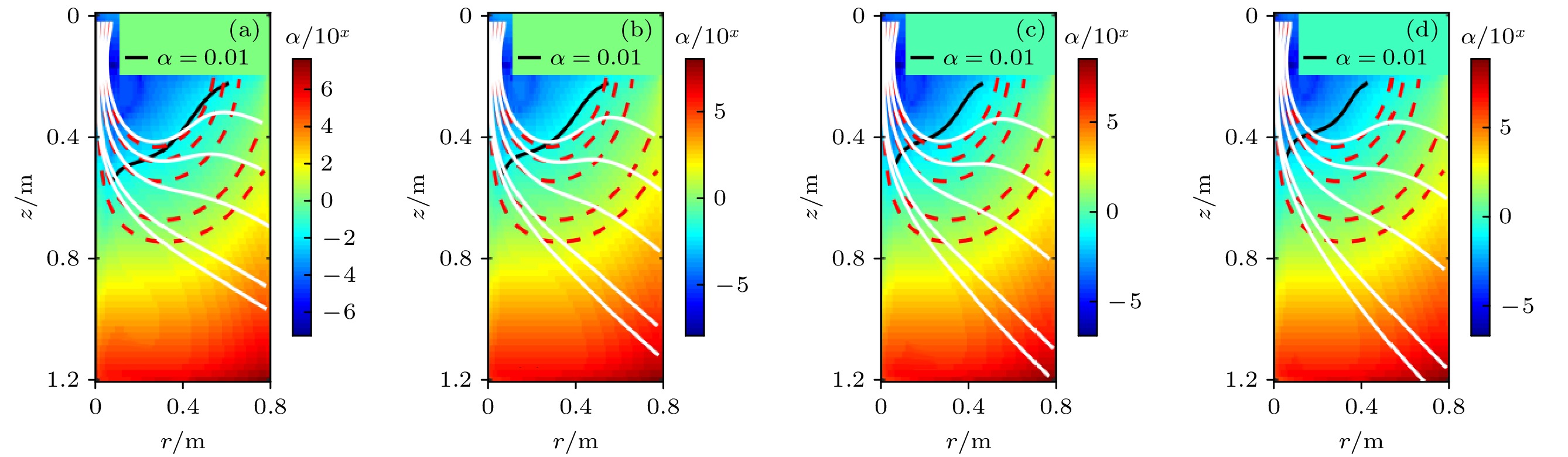
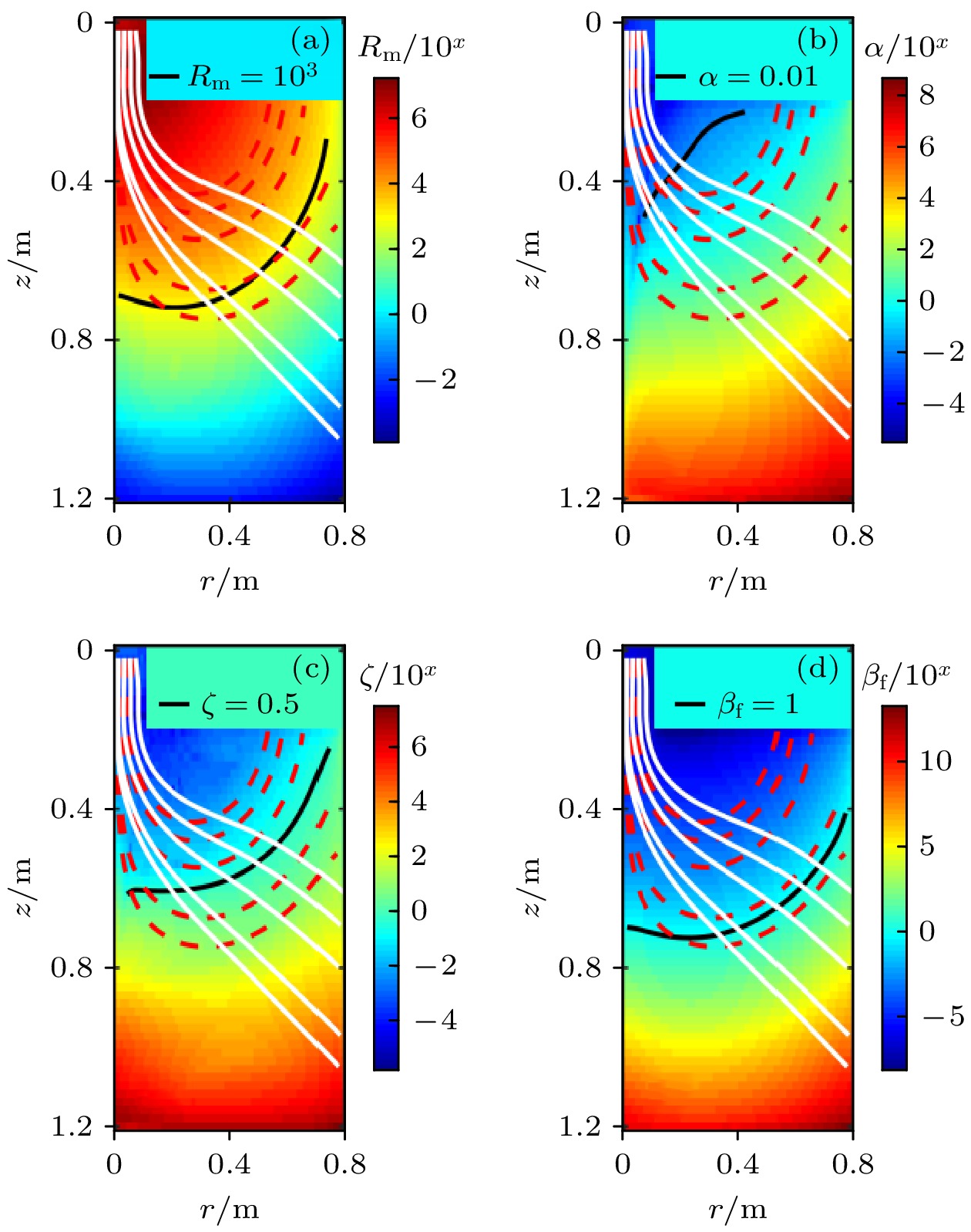
-
Magnetoplasma rocket engine has a broad application prospect in the deep space exploration, manned space flight and other space missions. The ion energy is converted into the directed velocity in the magnetic nozzle of the engine. The investigation into the detachment process of the plasma with the magnetic field is of great significance for improving the engine propulsion efficiency. However, there are roughly five kinds of physical mechanisms which can all contribute to the detachment process and make the detachment in the magnetic nozzle quite complicated. Furthermore, the ion temperature is much higher than the electron temperature in the magnetic nozzle of the magnetoplasma rocket engine due to the heating effect of the ion cyclotron resonance stage. As a result, previous numerical model which were based on the assumption of cold ions are unapplicable for the simulation of the engine. In this work, a fluid simulation model is developed which is used for simulating the magnetic nozzle in the magnetoplasma rocket engine. The model includes the electron and the ion of single charge. For the characteristics of the magnetoplasma rocket engine, the ion energy equation is added into the governing equations. In order to analyze the effect of the inertial detachment, the static electric field due to the charge separation is also included. The simulations are performed under the conditions of different inlet ion temperatures and background magnetic fields. The results show that the ion axial velocity gradually increases in the magnetic nozzle and the ion stream lines detach from the magnetic field lines gradually. The loss of adiabaticity is the dominant mechanism in the detachment process. The ion axial velocity increases with the inlet ion temperature rising, and the ion streamlines detach earlier from the magnetic field lines. The resistive diffusion is unaffected by the inlet ion temperature while the detachment interfaces of other three mechanisms all move toward the upstream. With the increase of the background magnetic field, ion axial velocity decreases and the angle included between the streamline and the axis becomes smaller. The loss of adiabaticity is still the dominant physical mechanism when the magnetic field is changed.
-
Keywords:
- magnetoplasma rocket engine /
- magnetic nozzle /
- plasma detachment /
- fluid simulation
[1] 于达仁, 乔磊, 蒋文嘉 刘辉 2020 推进技术 41 1
Google Scholar
Yu D R, Qiao L, Jiang W J, Liu H 2020 J. Propuls. Technol. 41 1
Google Scholar
[2] Chang F R, Fisher J L 1982 Nucl. Fusion 22 8
Google Scholar
[3] Chang F R, Giambusso M, Corrigan A M H, Dean L O, Warrayat M F 2022 37th International Electric Propulsion Conference Cambridge, USA, June 19–23, 2022 pp1–10
[4] 龙建飞, 张天平, 杨威, 孙明明, 贾艳辉, 刘明正 2018 67 011901
Google Scholar
Long J F, Zhang T P, Yang W, Sun M M, Jia Y H, Liu M Z 2018 Acta Phys. Sin. 67 011901
Google Scholar
[5] 段萍, 曹安宁, 沈鸿娟, 周新维, 覃海娟, 刘金远, 卿绍伟 2013 62 205205
Google Scholar
Duan P, Cao A N, Shen H J, Zhou X W, Qin H J, Liu J Y, Qing S W 2013 Acta Phys. Sin. 62 205205
Google Scholar
[6] Longmier B, Squire J, Olsen C 2012 48th AIAA/ASME/SAE/ASEE Joint Propulsion Conference & Exhibit Atlanta, Georgia, July 29–August 1, 2012 pp1–14
[7] 张海亮, 张天平, 王涛 2018 真空与低温 24 4
Google Scholar
Zhang H L, Zhang T P, Wang T 2018 Vac. Cryogen. 24 4
Google Scholar
[8] Ramos J J, Merino M, Ahedo E 2018 Phys. Plasmas 25 061206
Google Scholar
[9] Merino M, Nuez J, Ahedo E 2021 Plasma Sources Sci. Technol. 30 115006
Google Scholar
[10] Little J M, Choueiri E Y 2010 46th AIAA/ASME/SAE/ASEE Joint Propulsion Conference & Exhibit Nashville, TN, July 25–28, 2010 pp1–14
[11] Moses R W, Gerwin R A, Schoenberg K F 1992 AIP Conf. Proc. 246 1293
Google Scholar
[12] Merino M, Ahedo E 2011 Phys. Plasmas 18 053504
Google Scholar
[13] Dimov G I, Taskaev S Y 2000 27th EPS Conference on Control Fusion and Plasma Physics Budapest, June 12–16, 2000 pp464–467
[14] Ahedo E, Merino M 2010 46th AIAA/ASME/SAE/ASEE Joint Propulsion Conference & Exhibit Nashville, TN, July 25–28, 2010 pp1–12
[15] Merino M, Ahedo E 2011 47th AIAA/ASME/SAE/ASEE Joint Propulsion Conference & Exhibit San Diego, California, July 31–August 3, 2011 pp1–11
[16] Hooper E B 1993 J. Propul. Power 9 758
[17] Arefiev A V, Breizman B N 2005 Phys. Plasmas 12 043504
Google Scholar
[18] Little J M, Choueiri E Y 2011 47th AIAA/ASME/SAE/ASEE Joint Propulsion Conference & Exhibit San Diego, California, July 31–August 3, 2011 pp1–12
[19] Ilin A V, Chang F R, Squire J P, Tarditi A G 2002 40th AIAA Aerospace Sciences Meeting & Exhibit Reno, NV, January 14–17, 2002 pp1–11
[20] Longmier B W, Cassady L D, Ballenger M G, Cater M D, CHANG F R, Glover T W, Ilin A V, McCaskill G E, Olsen C S, Squire J P 2011 J. Propul. Power 27 915
Google Scholar
[21] Olsen C S, Ballenger M G, Carter M D, Chang Díaz F R, Giambusso M, Glover T W, Ilin A V, Squire J P, Longmier B W, Bering E A, Cloutier P A 2015 IEEE Trans. Plasma Sci. 43 252
Google Scholar
[22] 赵转转 2019 硕士学位论文 (大连: 大连理工大学)
Zhang Z Z 2019 M. S. Thesis (Dalian: Dalian University of Technology
[23] Boris J P, Landsberg A M, Oran E S, Gardner J H 1993 LCPFCT-A Flux-Corrected Transport Algorithm for Solving Generalized Continuity Equations
[24] Wu M Y, Xiao C J, Liu Y, Xu M, Tan C 2022 Plasma Sci. Technol. 24 055002
Google Scholar
[25] Lafleur T, Cannat F, Jarrige J, Elias P Q, Packan D 2015 Plasma Sources Sci. Technol. 24 065013
Google Scholar
-
图 1 磁等离子体发动机示意图
Figure 1. Schematic of the magnetoplasma rocket engine.
图 2 几何模型示意图
Figure 2. Schematic of the geometric model.
图 3 磁场强度分布图
Figure 3. Distribution of the magnetic field intensity.
图 4 稳态离子参数分布 (a)离子密度; (b)离子温度
Figure 4. Distribution of the ion parameters in steady state: (a) Ion density; (b) ion temperature.
图 5 稳态离子速度分布 (a) ui, z; (b) ui, r
Figure 5. Distribution of the ion velocity in steady state: (a) ui, z; (b) ui, r.
图 6 离子流线图
Figure 6. Streamlines of the ion.
图 7 不同分离机制的无量纲参数分布 (a) Rm; (b) α; (c) ζ; (d) βf
Figure 7. Distribution of the dimensionless parameters with different detachment mechanisms: (a) Rm; (b) α; (c) ζ; (d) βf.
图 8 离子温度分布 (a) Ti, in = 10 eV; (b) Ti, in = 20 eV; (c) Ti, in = 40 eV; (d) Ti, in = 80 eV
Figure 8. Distribution of the ion temperature: (a) Ti, in = 10 eV; (b) Ti, in = 20 eV; (c) Ti, in = 40 eV; (d) Ti, in = 80 eV.
图 9 离子轴向速度ui,z分布 (a) Ti, in = 10 eV; (b) Ti, in = 20 eV; (c) Ti, in = 40 eV; (d) Ti, in = 80 eV
Figure 9. Distribution of the ion axial velocity ui,z: (a) Ti, in = 10 eV; (b) Ti, in = 20 eV; (c) Ti, in = 40 eV; (d) Ti, in = 80 eV.
图 10 Ti,in = 40 eV不同分离机制的无量纲参数分布 (a) Rm; (b) α; (c) ζ; (d) βf
Figure 10. Distribution of the dimensionless parameters with different detachment mechanisms when Ti,in = 40 eV: (a) Rm; (b) α; (c) ζ; (d) βf.
图 11 不同Ti, in的α分布 (a) Ti, in = 10 eV; (b) Ti, in = 20 eV; (c) Ti, in = 40 eV; (d) Ti, in = 80 eV
Figure 11. Distribution of α with different Ti, in: (a) Ti, in = 10 eV; (b) Ti, in = 20 eV; (c) Ti, in = 40 eV; (d) Ti, in = 80 eV
图 12 离子轴向速度ui, z分布 (a) fB = 0.1; (b) fB = 0.4
Figure 12. Distribution of the ion axial velocity ui, z: (a) fB = 0.1; (b) fB = 0.4.
图 13 fB = 0.1不同分离机制的无量纲参数分布 (a) Rm; (b) α; (c) ζ; (d) βf
Figure 13. Distribution of the dimensionless parameters with different detachment mechanisms when fB = 0.1: (a) Rm; (b) α; (c) ζ; (d) βf.
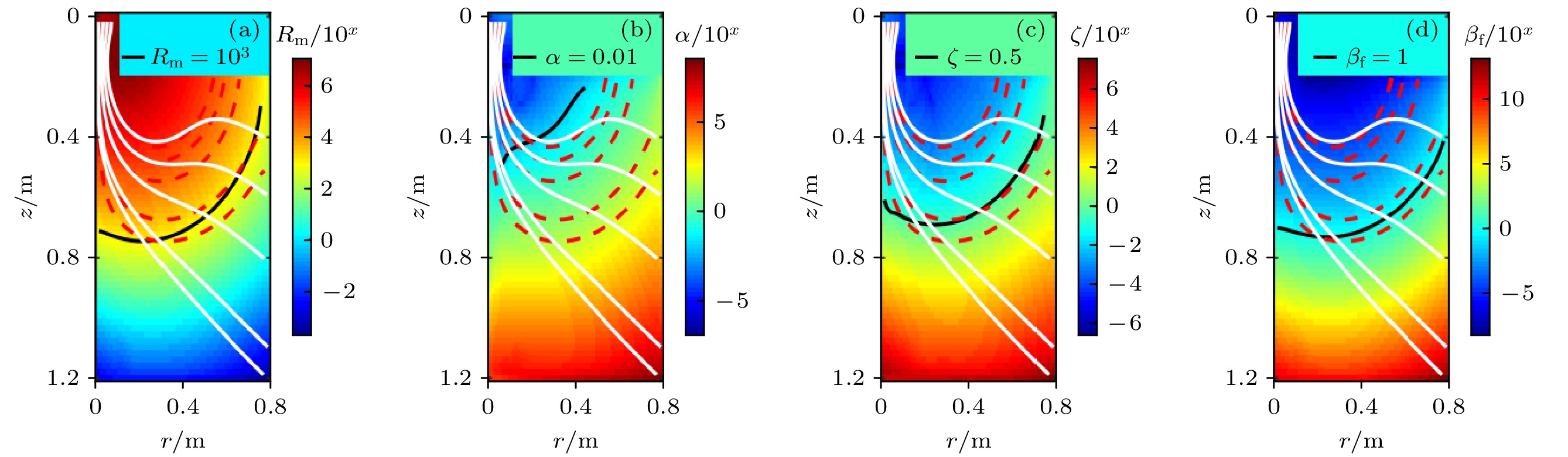
表 1 不同物理机制的特征参数
Table 1. Characteristic parameters of the physical mechanisms.
物理机制 无量纲系数 分离判据 绝热性损失分离 $ \alpha = {r_{\text{L}}}\dfrac{{\left| {\nabla B} \right|}}{{\left| B \right|}} $ 不满足$ \alpha \ll 1 $ 阻性扩散分离 $ {R_{\text{m}}} = \dfrac{{\mu L{V_{\text{A}}}}}{\eta } $ $ 1 < {R_{\text{m}}} < 1000 $ 惯性分离 $ G = \dfrac{{{\text{e}}B}}{{{m_{\text{e}}}}}\dfrac{{{\text{e}}B}}{{{m_{\text{i}}}}}\dfrac{{{L^2}}}{{{U^2}}} $ $ \xi = {G^{ - 1/2}}\left| {\dfrac{{\nabla B}}{B}} \right| \approx 0.5 $ 超阿尔芬速度分离 $ {\beta _{\text{f}}} = \dfrac{{\rho {u^2}}}{{{{{B^2}} \mathord{\left/ {\vphantom {{{B^2}} \mu }} \right. } \mu }}} $ $ {\beta _{\text{f}}} > 1 $ 
DownLoad: CSV
表 2 模型几何参数
Table 2. Geometric parameters of the model.
参数 值/m 参数 值/m rend 0.8 dr 0.01 zend 1.2 dz 0.02 r0 0.12 z0 0.2
DownLoad: CSV
-
[1] 于达仁, 乔磊, 蒋文嘉 刘辉 2020 推进技术 41 1
Google Scholar
Yu D R, Qiao L, Jiang W J, Liu H 2020 J. Propuls. Technol. 41 1
Google Scholar
[2] Chang F R, Fisher J L 1982 Nucl. Fusion 22 8
Google Scholar
[3] Chang F R, Giambusso M, Corrigan A M H, Dean L O, Warrayat M F 2022 37th International Electric Propulsion Conference Cambridge, USA, June 19–23, 2022 pp1–10
[4] 龙建飞, 张天平, 杨威, 孙明明, 贾艳辉, 刘明正 2018 67 011901
Google Scholar
Long J F, Zhang T P, Yang W, Sun M M, Jia Y H, Liu M Z 2018 Acta Phys. Sin. 67 011901
Google Scholar
[5] 段萍, 曹安宁, 沈鸿娟, 周新维, 覃海娟, 刘金远, 卿绍伟 2013 62 205205
Google Scholar
Duan P, Cao A N, Shen H J, Zhou X W, Qin H J, Liu J Y, Qing S W 2013 Acta Phys. Sin. 62 205205
Google Scholar
[6] Longmier B, Squire J, Olsen C 2012 48th AIAA/ASME/SAE/ASEE Joint Propulsion Conference & Exhibit Atlanta, Georgia, July 29–August 1, 2012 pp1–14
[7] 张海亮, 张天平, 王涛 2018 真空与低温 24 4
Google Scholar
Zhang H L, Zhang T P, Wang T 2018 Vac. Cryogen. 24 4
Google Scholar
[8] Ramos J J, Merino M, Ahedo E 2018 Phys. Plasmas 25 061206
Google Scholar
[9] Merino M, Nuez J, Ahedo E 2021 Plasma Sources Sci. Technol. 30 115006
Google Scholar
[10] Little J M, Choueiri E Y 2010 46th AIAA/ASME/SAE/ASEE Joint Propulsion Conference & Exhibit Nashville, TN, July 25–28, 2010 pp1–14
[11] Moses R W, Gerwin R A, Schoenberg K F 1992 AIP Conf. Proc. 246 1293
Google Scholar
[12] Merino M, Ahedo E 2011 Phys. Plasmas 18 053504
Google Scholar
[13] Dimov G I, Taskaev S Y 2000 27th EPS Conference on Control Fusion and Plasma Physics Budapest, June 12–16, 2000 pp464–467
[14] Ahedo E, Merino M 2010 46th AIAA/ASME/SAE/ASEE Joint Propulsion Conference & Exhibit Nashville, TN, July 25–28, 2010 pp1–12
[15] Merino M, Ahedo E 2011 47th AIAA/ASME/SAE/ASEE Joint Propulsion Conference & Exhibit San Diego, California, July 31–August 3, 2011 pp1–11
[16] Hooper E B 1993 J. Propul. Power 9 758
[17] Arefiev A V, Breizman B N 2005 Phys. Plasmas 12 043504
Google Scholar
[18] Little J M, Choueiri E Y 2011 47th AIAA/ASME/SAE/ASEE Joint Propulsion Conference & Exhibit San Diego, California, July 31–August 3, 2011 pp1–12
[19] Ilin A V, Chang F R, Squire J P, Tarditi A G 2002 40th AIAA Aerospace Sciences Meeting & Exhibit Reno, NV, January 14–17, 2002 pp1–11
[20] Longmier B W, Cassady L D, Ballenger M G, Cater M D, CHANG F R, Glover T W, Ilin A V, McCaskill G E, Olsen C S, Squire J P 2011 J. Propul. Power 27 915
Google Scholar
[21] Olsen C S, Ballenger M G, Carter M D, Chang Díaz F R, Giambusso M, Glover T W, Ilin A V, Squire J P, Longmier B W, Bering E A, Cloutier P A 2015 IEEE Trans. Plasma Sci. 43 252
Google Scholar
[22] 赵转转 2019 硕士学位论文 (大连: 大连理工大学)
Zhang Z Z 2019 M. S. Thesis (Dalian: Dalian University of Technology
[23] Boris J P, Landsberg A M, Oran E S, Gardner J H 1993 LCPFCT-A Flux-Corrected Transport Algorithm for Solving Generalized Continuity Equations
[24] Wu M Y, Xiao C J, Liu Y, Xu M, Tan C 2022 Plasma Sci. Technol. 24 055002
Google Scholar
[25] Lafleur T, Cannat F, Jarrige J, Elias P Q, Packan D 2015 Plasma Sources Sci. Technol. 24 065013
Google Scholar
DownLoad:
Catalog
Metrics
- Abstract views: 1579
- PDF Downloads: 64
- Cited By: 0
