-
Long-range, high-precision, and high-refresh rate absolute distance measurement based on double intensity modulation is proposed and experimentally demonstrated. In this scheme, a Mach-Zehnder modulator is utilized to perform bidirectional modulation by a reversible optical path. In the Mach-Zehnder modulator, interference demodulation is completed by bidirectional modulated light with time difference. By adjusting the driving frequency of the modulator, the curve of light intensity versus driving frequency is achieved. Consequently, the distance to be measured can be obtained by extracted the frequency interval between two adjacent light intensity minimum points. In the traditional double polarization modulation ranging, the optical carrier is polarized by a polarizing beam splitter (PBS) before phase modulator. Moreover, a quarter wave or Faraday rotating mirror need to be placed to adjust the polarization in front of the target object. Therefore, the polarization state is an indispensable factor in the traditional double polarization modulation ranging. Due to the advantage of the intensity modulation, absolute distance measurement is achieved without additional polarization control, greatly simplifying the system. Theoretical analysis of the system is developed, which is then demonstrated by experiments. In the experiments, we achieved the following results. Firstly, the relationship between the intensity of the output light of the system and the modulation frequency is theoretically analyzed, which proved to be a cosine form. Secondly, swing method is introduced to realize high-speed absolute distance measurement during the analytical distance algorithm, and we achieved a refresh rate of 2 kHz in the experiments. Thirdly, the relationship between measurement ranging precision and frequency stability is analyzed. When the modulation frequency is 8.9 GHz, the experimentally measured frequency stability is on the order of 10–7. And when the distance to be measured is 2.73 m, the standard deviation of ranging reaches 1 μm, which represents the precision of the system. That is, the relative measurement precision is also on the order of 10–7, which is consistent with theoretical analysis. Finally, when the distance to be measured increases from 1.57 m to 100.83 m, the measurement precision increases from 1 μm to 30 μm. It is worth mentioning that the relative measurement precision of the system is always stable in the order of 10–7. Our scheme has some significant advantages, such as long-range, high-precision, high-refresh rate, and a simple and compact configuration. Moreover, our method can be used in important applications such as precision instruments, metrology, and aerospace.
[1] 王镓, 李达飞, 何锡明, 成子青, 许倩, 钱雪茹, 万文辉 2022 深空探测学报 9 62
Wang J, Li D F, He X M, Cheng Z Q, Xu Q, Qian X R, Wan W H 2022 J. Deep Space Explor. 9 62
[2] 于勇, 陶剑, 范玉青 2009 航空制造技术 11 56
Google Scholar
Yu Y, Tao J, Fan Y Q 2009 Aeronaut. Manuf. Technol. 11 56
Google Scholar
[3] 邵珠法 2005 硕士学位论文 (成都: 电子科技大学)
Shao Z F 2005 M. S. Thesis (Chengdu: University of Electronic Science and Technology of China
[4] Minoshima K, Matsumoto H 2000 Appl. Opt. 39 5512
Google Scholar
[5] Ye J 2004 Opt. Lett. 29 1153
Google Scholar
[6] Cui M, Zeitouny M G, Bhattacharya N, van den Berg S A, Urbach H P, Braat J J M 2009 Opt. Lett. 34 1982
Google Scholar
[7] Lee J, Kim Y J, Lee K, Lee S, Kim S W 2010 Nat. Photonics 4 716
Google Scholar
[8] Minoshima K, Arai K, Inaba H 2011 Opt. Express 19 26095
Google Scholar
[9] Lee J, Han S, Lee K, Bae E, Kim S, Lee S, Kim S W, Kim Y J 2013 Meas. Sci. Technol. 24 045201
Google Scholar
[10] Wu G H, Liao L, Xiong S L, Li G Y, Cai Z J, Zhu Z 2018 Sci. Rep. 8 4362
Google Scholar
[11] Armano M, Audley H, Baird J, et al. 2018 Phys. Rev. Lett. 120 061101
Google Scholar
[12] Gao R H, Liu H S, Luo Z R, Jin G 2019 Chin. Opt. 12 425
Google Scholar
[13] Gong Y G, Luo J, Wang B 2021 Nat. Astron. 5 881
Google Scholar
[14] Nissinen J, Nissinen I, Kostamovaara J 2009 IEEE J. Solid-State Circuits 44 1486
Google Scholar
[15] Wang T S, Huo J, Wang P C, Dong P, Yang R, Li M F 2017 Proceedings of the 2017 Symposium on Quantum Information Technology and Applications Beijing, China, August 6–15, 2017 p50
[16] Kilpela A, Pennala R, Kostamovaara J 2001 Rev. Sci. Instrum. 72 2197
Google Scholar
[17] 刘玉周 2015 硕士学位论文 (武汉: 华中科技大学)
Liu Y Z 2015 M. S. Thesis (Wuhan: Huazhong University of Science and Technology
[18] 许贤泽, 翁名杰, 徐逢秋, 白翔 2017 光学精密工程 8 1979
Xu X Z, Weng M J, Xu F Q, Bai X 2017 Opt. Precis. Eng. 8 1979
[19] 郑大青, 陈伟民, 陈丽, 李存龙 2015 光电子·激光 26 303
Zheng D Q, Chen W M, Chen L, Li C L 2015 J. Optoelectron. Laser 26 303
[20] 黑克非, 于晋龙, 王菊, 王文睿, 贾石, 吴穹, 薛纪强 2014 63 100602
Google Scholar
Hei K F, Yu J L, Wang J, Wang W R, Jia S, Wu Q, Xue J Q 2014 Acta Phys. Sin. 63 100602
Google Scholar
[21] 肖洋, 于晋龙, 王菊, 王文睿, 王子雄, 谢田元 2016 65 100601
Google Scholar
Xiao Y, Yu J L, Wang J, Wang W R, Wang Z X, Xie T Y 2016 Acta Phys. Sin. 65 100601
Google Scholar
[22] 高书苑, 石俊凯, 纪荣祎, 黎尧, 周维虎 2018 中国激光 45 4005
Gao S Y, Shi J K, Ji R W, Li Y, Zhou W H 2018 Chin. J. Lasers 45 4005
[23] 高书苑, 黎尧, 纪荣祎, 石俊凯, 胡哲文, 周维虎 2019 光学精密工程 27 279
Google Scholar
Gao S Y, Li Y, Ji R W, Shi J K, Hu Z W, Zhou W H 2019 Opt. Precis. Eng. 27 279
Google Scholar
[24] 高超, 纪荣祎, 高书苑, 董登峰, 周维虎 2022 光学精密工程 30 246
Gao C, Ji R Y, Gao S Y, Dong D F, Zhou W H 2022 Opt. Precis. Eng. 30 246
[25] 亢洋 2021 硕士学位论文 (北京: 北京邮电大学)
Kang Y 2021 M. S. Thesis (Beijing: Beijing University of Posts and Telecommunications
[26] 张伟婷 2020 硕士学位论文 (成都: 电子科技大学)
Zhang W T 2020 M. S. Thesis (Chengdu: University of Electronic Science and Technology of China
[27] Frankel M Y, Esman R D 1998 J. Lightwave Technol. 16 859
Google Scholar
-
图 1 二次强度调制原理示意图(Cir, 环形器; MZM, 马赫曾德尔调制器; PD, 光电探测器)
Figure 1. Schematic diagram of double intensity modulation (Cir, circulator; MZM, Mach-Zehnder modulator; PD, photo detector).
图 2 马赫-曾德尔调制器传输曲线
Figure 2. Transmission curve of Mach-Zehnder modulator
图 3 第一类贝塞尔函数
Figure 3. Bessel function of the first kind
图 4 二次强度调制测距实验结构图(Cir, 环形器; MZM, 马赫-曾德尔调制器; VOA, 可调光衰减; PD, 光电探测器; A/D, 模数转换)
Figure 4. Experimental structure diagram of double intensity modulation ranging (Cir, circulator; MZM, Mach-Zehnder modulator; VOA, variable optical attenuator; PD, photo detector; A/D, analog to digital converter).
图 5 实验扫频曲线
Figure 5. Experimental sweep curve
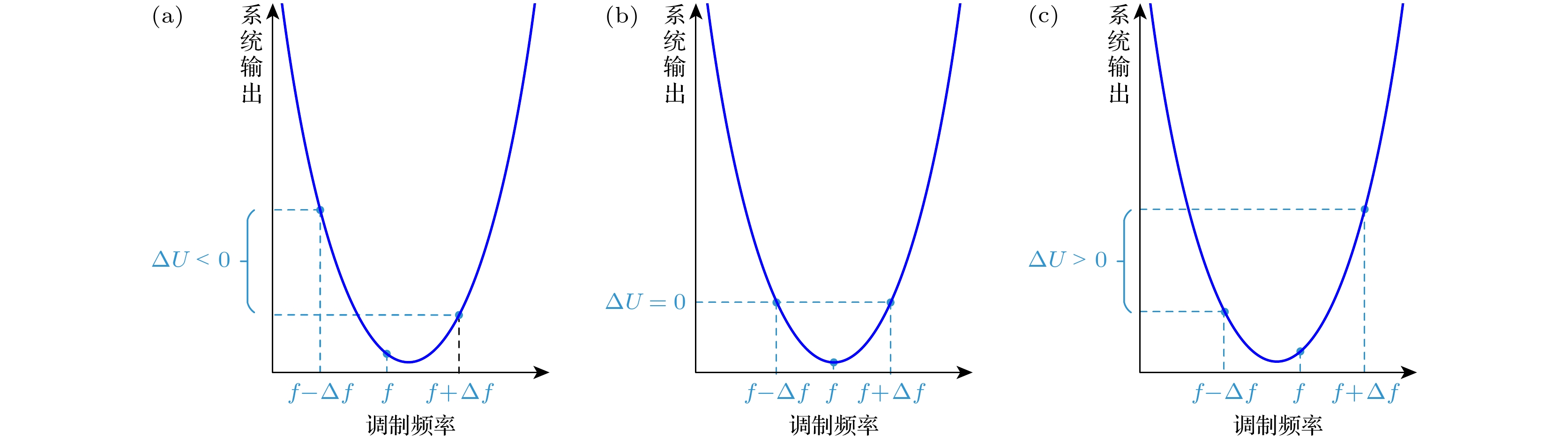
图 6 不同位置下f与
$ \Delta U $ 的关系 (a) f在光强极小值点对应频率的左侧; (b) f为光强极小值点对应的频率; (c) f在光强极小值点对应频率的右侧Figure 6. Relationship between f and
$ \Delta U $ at different positions: (a) f is on the left side of the frequency corresponding to the light intensity minimum point; (b) f is the frequency corresponding to the minimum point of light intensity; (c) f is on the right side of the frequency corresponding to the light intensity minimum point.
图 7 摇摆差值曲线及其零点局部放大 (a)摇摆差值曲线; (b)摇摆差值零点局部放大
Figure 7. Swing difference curve and local amplification at zero point: (a) Swing difference curve; (b) partial amplification of zero point of swing difference.
图 8 系统测距结果
Figure 8. Distance measurement results of the system
表 1 f1的相对稳定度
Table 1. Relative stability of f1.
Group Average of
$ f_{1}$/HzStandard
deviation of
$ f_{1}$/HzRelative
accuracy/10–7Ⅰ 8965550359 2737 3.05 Ⅱ 8965546127 2760 3.07 Ⅲ 8965538910 3736 4.17 
DownLoad: CSV
表 2 相对测距精度
Table 2. Relative distance measurement accuracy.
Group Average of D/m Standard deviation
of D/μmRelative accuracy
/10–7Ⅰ 1.575537 1 6.35 Ⅱ 9.139261 5 5.47 Ⅲ 23.313040 8 3.43 Ⅳ 38.786468 10 2.57 Ⅴ 54.107275 15 2.77 Ⅵ 64.199287 16 2.55 Ⅶ 79.673707 26 3.49 Ⅷ 100.830172 30 2.98
DownLoad: CSV
-
[1] 王镓, 李达飞, 何锡明, 成子青, 许倩, 钱雪茹, 万文辉 2022 深空探测学报 9 62
Wang J, Li D F, He X M, Cheng Z Q, Xu Q, Qian X R, Wan W H 2022 J. Deep Space Explor. 9 62
[2] 于勇, 陶剑, 范玉青 2009 航空制造技术 11 56
Google Scholar
Yu Y, Tao J, Fan Y Q 2009 Aeronaut. Manuf. Technol. 11 56
Google Scholar
[3] 邵珠法 2005 硕士学位论文 (成都: 电子科技大学)
Shao Z F 2005 M. S. Thesis (Chengdu: University of Electronic Science and Technology of China
[4] Minoshima K, Matsumoto H 2000 Appl. Opt. 39 5512
Google Scholar
[5] Ye J 2004 Opt. Lett. 29 1153
Google Scholar
[6] Cui M, Zeitouny M G, Bhattacharya N, van den Berg S A, Urbach H P, Braat J J M 2009 Opt. Lett. 34 1982
Google Scholar
[7] Lee J, Kim Y J, Lee K, Lee S, Kim S W 2010 Nat. Photonics 4 716
Google Scholar
[8] Minoshima K, Arai K, Inaba H 2011 Opt. Express 19 26095
Google Scholar
[9] Lee J, Han S, Lee K, Bae E, Kim S, Lee S, Kim S W, Kim Y J 2013 Meas. Sci. Technol. 24 045201
Google Scholar
[10] Wu G H, Liao L, Xiong S L, Li G Y, Cai Z J, Zhu Z 2018 Sci. Rep. 8 4362
Google Scholar
[11] Armano M, Audley H, Baird J, et al. 2018 Phys. Rev. Lett. 120 061101
Google Scholar
[12] Gao R H, Liu H S, Luo Z R, Jin G 2019 Chin. Opt. 12 425
Google Scholar
[13] Gong Y G, Luo J, Wang B 2021 Nat. Astron. 5 881
Google Scholar
[14] Nissinen J, Nissinen I, Kostamovaara J 2009 IEEE J. Solid-State Circuits 44 1486
Google Scholar
[15] Wang T S, Huo J, Wang P C, Dong P, Yang R, Li M F 2017 Proceedings of the 2017 Symposium on Quantum Information Technology and Applications Beijing, China, August 6–15, 2017 p50
[16] Kilpela A, Pennala R, Kostamovaara J 2001 Rev. Sci. Instrum. 72 2197
Google Scholar
[17] 刘玉周 2015 硕士学位论文 (武汉: 华中科技大学)
Liu Y Z 2015 M. S. Thesis (Wuhan: Huazhong University of Science and Technology
[18] 许贤泽, 翁名杰, 徐逢秋, 白翔 2017 光学精密工程 8 1979
Xu X Z, Weng M J, Xu F Q, Bai X 2017 Opt. Precis. Eng. 8 1979
[19] 郑大青, 陈伟民, 陈丽, 李存龙 2015 光电子·激光 26 303
Zheng D Q, Chen W M, Chen L, Li C L 2015 J. Optoelectron. Laser 26 303
[20] 黑克非, 于晋龙, 王菊, 王文睿, 贾石, 吴穹, 薛纪强 2014 63 100602
Google Scholar
Hei K F, Yu J L, Wang J, Wang W R, Jia S, Wu Q, Xue J Q 2014 Acta Phys. Sin. 63 100602
Google Scholar
[21] 肖洋, 于晋龙, 王菊, 王文睿, 王子雄, 谢田元 2016 65 100601
Google Scholar
Xiao Y, Yu J L, Wang J, Wang W R, Wang Z X, Xie T Y 2016 Acta Phys. Sin. 65 100601
Google Scholar
[22] 高书苑, 石俊凯, 纪荣祎, 黎尧, 周维虎 2018 中国激光 45 4005
Gao S Y, Shi J K, Ji R W, Li Y, Zhou W H 2018 Chin. J. Lasers 45 4005
[23] 高书苑, 黎尧, 纪荣祎, 石俊凯, 胡哲文, 周维虎 2019 光学精密工程 27 279
Google Scholar
Gao S Y, Li Y, Ji R W, Shi J K, Hu Z W, Zhou W H 2019 Opt. Precis. Eng. 27 279
Google Scholar
[24] 高超, 纪荣祎, 高书苑, 董登峰, 周维虎 2022 光学精密工程 30 246
Gao C, Ji R Y, Gao S Y, Dong D F, Zhou W H 2022 Opt. Precis. Eng. 30 246
[25] 亢洋 2021 硕士学位论文 (北京: 北京邮电大学)
Kang Y 2021 M. S. Thesis (Beijing: Beijing University of Posts and Telecommunications
[26] 张伟婷 2020 硕士学位论文 (成都: 电子科技大学)
Zhang W T 2020 M. S. Thesis (Chengdu: University of Electronic Science and Technology of China
[27] Frankel M Y, Esman R D 1998 J. Lightwave Technol. 16 859
Google Scholar
DownLoad:
Catalog
Metrics
- Abstract views: 2355
- PDF Downloads: 135
- Cited By: 0
