Dispersion properties of van der Waals phonon polaritons modulated by Weyl semimetals

Gu Zi-Heng; Zang Qiang; Zheng Gai-Ge

doi:10.7498/aps.72.20230167

Abstract

Surface phonon polaritons (SPhP) as an alternative constituent for mid-infrared (MIR) nanophotonic applications have attracted extensive attention and they maybe solve the intrinsic loss problem of plasmonics. SPhP arise in polar dielectrics due to IR-active phonon resonances, leading to negative permittivity within the Reststrahlen band. Although SPhP have great potential in enhancing the interaction between light and matter in the infrared region, it is still limited to enhance optical fields and fixed resonance band because of the existing Reststrahlen band. Moreover, active manipulating of phonon polaritons in MIR range remains elusive. The significant research progress of natural van der Waals (vdW) crystal and heterostructures have been made, which are characterized by an anisotropic polaritonic response, leading to elliptical, hyperbolic, or biaxial polaritonic dispersions. Among these structures, SPhP with hyperbolicity in α-MoO₃ are of particular interest, due to not only the strong field confinement, low losses, and long lifetimes, but also the natural in-plane anisotropic dispersion. A heterostructure composed of a biaxial vdW material (α-MoO₃) and a Weyl semimetal (WSM) is proposed to study the active tunability of anisotropic SPhP. The control of polaritons can show more degrees of freedom, which has not yet been addressed. Under the incident condition of transverse magnetic incident wave, the reflection coefficient and field distribution in the heterogeneous system are accurately solved by the 4×4 transfer matrix method, and the dispersion properties of anisotropic SPhP are described in detail. Variation of dispersion spectrum with azimuthal angle and α-MoO₃ thickness is presented. The research results indicate that mode hybridization and dispersion manipulation can be realized by controlling the azimuth angle and the thickness of α-MoO₃. More importantly, the Fermi level of WSM enable the adjustment of dynamic dispersion curve, which depends on the change of external temperature. Isofrequency curves of hybridized SPhP at different Fermi levels are also demonstrated. By chemically changing the Femi level of α-MoO₃, the topology of polariton isofrequency surfaces transforms from open shape to closed shape as a result of polariton hybridization. Therefore, our research is helpful in further optimizing and designing active optoelectronic devices based on vdW materials, which have good application prospects in infrared heat radiation and biosensing.

Keywords:

Authors and contacts

1.
School of Automation, Nanjing University of Information Science and Technology, Nanjing 210044, China
2.
Jiangsu Collaborative Innovation Center on Atmospheric Environment and Equipment Technology, Nanjing 210044, China
3.
School of Physics and Optoelectronic Engineering, Nanjing University of Information Science and Technology, Nanjing 210044, China

Corresponding author: Zang Qiang, autozang@163.com ; Zheng Gai-Ge, eriot@126.com

Funds: Project supported by the Natural Science Foundation of Jiangsu Province, China (Grant No. BK20191396).

FullText HTML : translate this paragraph

References

[1]	段嘉华, 陈佳宁 2019 68 110701 Google Scholar Duan J H, Chen J N 2019 Acta Phys. Sin. 68 110701 Google Scholar
[2]	郑嘉璐, 戴志高, 胡光维, 欧清东, 张津瑞, 甘雪涛, 仇成伟, 鲍桥梁 2021 中国光学 14 812 Google Scholar Zheng J L, Dai Z G, Hu G W, Ou Q D, Zhang J R, Gan X T, Qiu C W, Bao Q L 2021 Chin. Opt. 14 812 Google Scholar
[3]	徐琨淇, 胡成, 沈沛约, 马赛群, 周先亮, 梁齐, 史志文 2023 72 027102 Google Scholar Xu K Q, Hu C, Shen P Y, Ma S Q, Zhou X L, Liang Q, Shi Z W 2023 Acta Phys. Sin. 72 027102 Google Scholar
[4]	Hu G W, Ou Q D, Si G Y, Wu Y J, Wu J, Dai Z G, Krasnok A, Mazor Y, Zhang Q, Bao Q L, Qiu C W, Alù A 2020 Nature 582 209 Google Scholar
[5]	Chaudhary K, Tamagnone M, Rezaee M, Bediako D K, Ambrosio A, Kim P, Capasso F 2019 Sci. Adv. 5 eaau7171 Google Scholar
[6]	Álvarez-Pérez G, González-Morán A, Capote-Robayna N, Voronin K V, Duan J H, Volkov V S, Alonso-González P, Nikitin A Y 2022 ACS Photonics 9 383 Google Scholar
[7]	Duan J, Álvarez-Pérez G, Voronin K V, Prieto I, Taboada-Gutiérrez J, Volkov V S, Martín-Sánchez J, Nikitin A Y, Alonso-González P 2021 Sci. Adv. 7 eabf2690 Google Scholar
[8]	Hajian H, Rukhlenko I D, Hanson G W, Low T, Butun B, Ozbay E 2020 Nanophotonics 9 3909 Google Scholar
[9]	Lee I H, He M Z, Zhang X, Luo Y J, Liu S, Edgar J H, Wang K, Avouris P, Low T, Caldwell J D, Oh S H 2020 Nat. Commun. 11 3649 Google Scholar
[10]	Menabde S G, Jahng J, Boroviks S, Ahn J, Heiden J T, Hwang D K, Lee E S, Mortensen N A, Jang M S 2022 Adv. Optical Mater. 10 2201492 Google Scholar
[11]	Erçağlar V, Hajian H, Rukhlenko I D, Ozbay E 2022 Appl. Phys. Lett. 121 182201 Google Scholar
[12]	Schwartz J J, Le Son T, Krylyuk S, Richter C A, Davydov A V, Centrone A 2021 Nanophotonics 10 1517 Google Scholar
[13]	Larciprete M C, Dereshgi S A, Centini M, Aydin K 2022 Opt. Express 30 12788 Google Scholar
[14]	Gong Y, Zhao Y, Zhou Z, Li D, Mao H, Bao Q, Zhang Y, Wang G 2022 Adv. Opt. Mater. 10 2200038 Google Scholar
[15]	Zheng Z, Chen J, Wang Y, Wang X, Chen X, Liu P, Xu J, Xie W, Chen H, Deng S, Xu N 2018 Adv. Mater. 30 1705318 Google Scholar
[16]	Zhang Q, Zhen Z, Yang Y F, Gan G W, Jariwala D, Cui X D 2019 Opt. Express 27 18585 Google Scholar
[17]	Huang W, Sun F, Zheng Z, Folland T G, Chen X, Liao H, Xu N, Caldwell J D, Chen H, Deng S 2021 Adv. Sci. 8 2004872 Google Scholar
[18]	Hu G, Shen J, Qiu C W, Alù A, Dai S 2020 Adv. Optical Mater. 8 1901393 Google Scholar
[19]	Dai S, Zhang J, MaQ, Kittiwatanakul S, McLeod A, Chen X, Corder S N G, Watanabe K, Taniguchi T, Lu J, Dai Q, Jarillo-Herrero P, Liu M, Basov D N 2019 Adv. Mater. 31 1900251 Google Scholar
[20]	Passler N C, Heßler A, Wuttig M, Taubner T, Paarmann A 2020 Adv. Optical Mater. 8 1901056 Google Scholar
[21]	Zhang Q, Ou Q, Hu G, Liu J, Dai Z, Fuhrer M S, Bao Q, Qiu C W 2021 Nano Lett. 21 3112 Google Scholar
[22]	Hofmann J, Das S S 2016 Phys. Rev. B 93 241402 Google Scholar
[23]	Zhao B, Guo C, Garcia C A C, Narang P, Fan S 2020 Nano Lett. 20 1923 Google Scholar
[24]	Kotov O V, Lozovik Y E 2018 Phys. Rev. B 98 195446 Google Scholar
[25]	Tamaya T, Kato T, Tsuchikawa K, Konabe S, Kawabata S 2019 J. Phys. Condens. Matter 31 305001 Google Scholar
[26]	Schubert M 1996 Phys. Rev. B 53 4265 Google Scholar
[27]	Wu X H, Fu C J, Zhang Z M 2019 Int. J. Heat Mass Tran. 135 1207 Google Scholar
[28]	Hajian H, Ghobadi A, Dereshgi S A, Butun B, Ozbay E 2017 J. Opt. Soc. Am. B 34 D29 Google Scholar
[29]	Fandan R, Pedrós J, Schiefele J, Boscá A, Martínez J, Calle F 2018 J. Phys. D: Appl. Phys. 51 204004 Google Scholar
[30]	Wang Y, Khandekar C, Gao X, Li T, Jiao D, Jacob Z 2021 Opt. Mater. Express 11 3880 Google Scholar
[31]	Wu J, Wu B Y, Wang Z M, Wu X H 2022 Int. J. Therm. Sci. 181 107788 Google Scholar
[32]	Ashby P E C, Carbotte J P 2014 Phys. Rev. B 89 245121 Google Scholar
[33]	Wu X H 2020 J. Heat Transfer 142 072802 Google Scholar

Cited By

图 1 (a) α-MoO₃/WSM异质结模型示意图; (b) WSM介电常数张量分量

Figure 1. (a) Schematic diagram of α-MoO₃/WSM heterostructure mode; (b) different parts of permittivity tensor components of WSM.

DownLoad: Full-Size Img PowerPoint

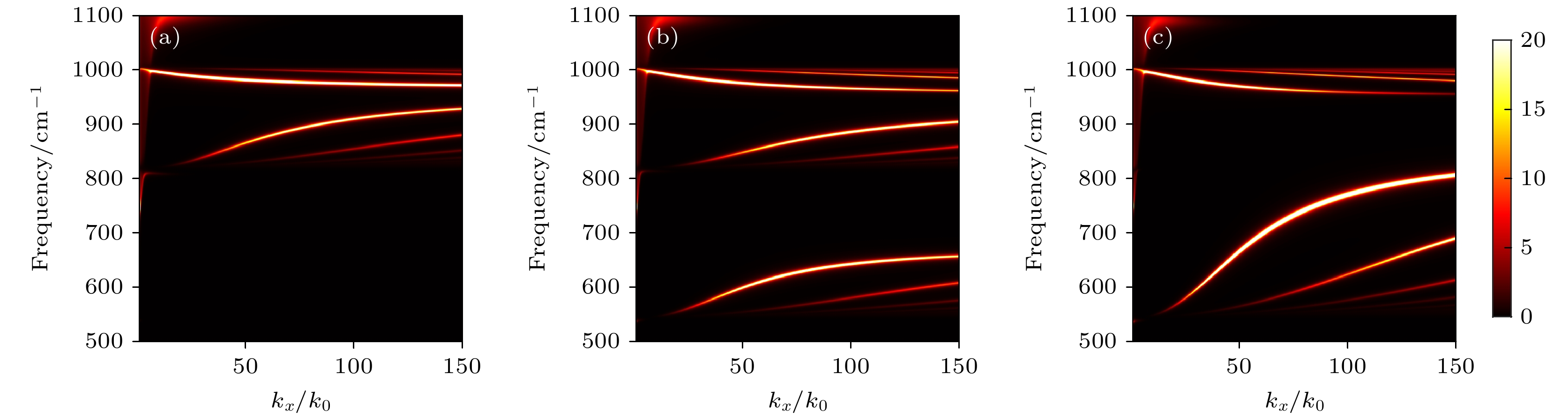
图 2 不同传播角条件下的色散图谱(α-MoO₃的厚度固定在d = 50 nm)　(a) φ = 0°; (b) φ = 45°; (c) φ = 90° . k₀和k_x分别代表真空中和x方向的波矢

Figure 2. Dispersion spectra under different propagation angle conditions (Thickness of α-MoO₃ is fixed at d = 50 nm): (a) φ = 0°; (b) φ = 45°; (c) φ = 90° . k₀ and k_x represent wave vectors in the vacuum and x direction, respectively

DownLoad: Full-Size Img PowerPoint

图 3 色散图谱随方位角和α-MoO₃厚度的变化　(a) 50 nm; (b) 500 nm; (c) 1000 nm; (d) 2000 nm

Figure 3. Variation of dispersion spectra with azimuthal angle and α-MoO₃ thickness: (a) 50 nm; (b) 500 nm; (c) 1000 nm; (d) 2000 nm.

DownLoad: Full-Size Img PowerPoint

图 4 d = 50 nm, φ = 0°时, 不同费米能级下的色散图谱(其他参数同图2)　(a) E_F = 0.1 eV; (b) E_F = 0.4 eV

Figure 4. Dispersion spectra under different propagation angle conditions at d = 50 nm and φ = 0° (Other parameters are the same as used in Fig. 2): (a) E_F = 0.1 eV; (b) E_F = 0.4 eV.

DownLoad: Full-Size Img PowerPoint

图 5 不同费米能级下色散图谱随方位角和频率的变化　(a) E_F = 0.2 eV; (b) E_F = 0.3 eV; (c) E_F = 0. 35 eV; (d) E_F = 0.4 eV

Figure 5. Variation of dispersion spectra with azimuthal angle and frequency with different Femi levels: (a) E_F = 0.2 eV; (b) E_F = 0.3 eV; (c) E_F = 0. 35 eV; (d) E_F = 0.4 eV.

DownLoad: Full-Size Img PowerPoint

图 6 不同费米能级下杂化SPhP的等频线(其他参数同图2)　(a) E_F = 0.2 eV; (b) E_F = 0.25 eV; (c) E_F = 0. 3 eV; (d) E_F = 0.35 eV

Figure 6. Equal-frequency curves of hybridized SPhP at different Fermi levels (Other parameters are the same as used in Fig. 2): (a) E_F = 0.2 eV; (b) E_F = 0.25 eV; (c) E_F = 0. 3 eV; (d) E_F = 0.35 eV.

DownLoad: Full-Size Img PowerPoint

map

[1]	段嘉华, 陈佳宁 2019 68 110701 Google Scholar Duan J H, Chen J N 2019 Acta Phys. Sin. 68 110701 Google Scholar
[2]	郑嘉璐, 戴志高, 胡光维, 欧清东, 张津瑞, 甘雪涛, 仇成伟, 鲍桥梁 2021 中国光学 14 812 Google Scholar Zheng J L, Dai Z G, Hu G W, Ou Q D, Zhang J R, Gan X T, Qiu C W, Bao Q L 2021 Chin. Opt. 14 812 Google Scholar
[3]	徐琨淇, 胡成, 沈沛约, 马赛群, 周先亮, 梁齐, 史志文 2023 72 027102 Google Scholar Xu K Q, Hu C, Shen P Y, Ma S Q, Zhou X L, Liang Q, Shi Z W 2023 Acta Phys. Sin. 72 027102 Google Scholar
[4]	Hu G W, Ou Q D, Si G Y, Wu Y J, Wu J, Dai Z G, Krasnok A, Mazor Y, Zhang Q, Bao Q L, Qiu C W, Alù A 2020 Nature 582 209 Google Scholar
[5]	Chaudhary K, Tamagnone M, Rezaee M, Bediako D K, Ambrosio A, Kim P, Capasso F 2019 Sci. Adv. 5 eaau7171 Google Scholar
[6]	Álvarez-Pérez G, González-Morán A, Capote-Robayna N, Voronin K V, Duan J H, Volkov V S, Alonso-González P, Nikitin A Y 2022 ACS Photonics 9 383 Google Scholar
[7]	Duan J, Álvarez-Pérez G, Voronin K V, Prieto I, Taboada-Gutiérrez J, Volkov V S, Martín-Sánchez J, Nikitin A Y, Alonso-González P 2021 Sci. Adv. 7 eabf2690 Google Scholar
[8]	Hajian H, Rukhlenko I D, Hanson G W, Low T, Butun B, Ozbay E 2020 Nanophotonics 9 3909 Google Scholar
[9]	Lee I H, He M Z, Zhang X, Luo Y J, Liu S, Edgar J H, Wang K, Avouris P, Low T, Caldwell J D, Oh S H 2020 Nat. Commun. 11 3649 Google Scholar
[10]	Menabde S G, Jahng J, Boroviks S, Ahn J, Heiden J T, Hwang D K, Lee E S, Mortensen N A, Jang M S 2022 Adv. Optical Mater. 10 2201492 Google Scholar
[11]	Erçağlar V, Hajian H, Rukhlenko I D, Ozbay E 2022 Appl. Phys. Lett. 121 182201 Google Scholar
[12]	Schwartz J J, Le Son T, Krylyuk S, Richter C A, Davydov A V, Centrone A 2021 Nanophotonics 10 1517 Google Scholar
[13]	Larciprete M C, Dereshgi S A, Centini M, Aydin K 2022 Opt. Express 30 12788 Google Scholar
[14]	Gong Y, Zhao Y, Zhou Z, Li D, Mao H, Bao Q, Zhang Y, Wang G 2022 Adv. Opt. Mater. 10 2200038 Google Scholar
[15]	Zheng Z, Chen J, Wang Y, Wang X, Chen X, Liu P, Xu J, Xie W, Chen H, Deng S, Xu N 2018 Adv. Mater. 30 1705318 Google Scholar
[16]	Zhang Q, Zhen Z, Yang Y F, Gan G W, Jariwala D, Cui X D 2019 Opt. Express 27 18585 Google Scholar
[17]	Huang W, Sun F, Zheng Z, Folland T G, Chen X, Liao H, Xu N, Caldwell J D, Chen H, Deng S 2021 Adv. Sci. 8 2004872 Google Scholar
[18]	Hu G, Shen J, Qiu C W, Alù A, Dai S 2020 Adv. Optical Mater. 8 1901393 Google Scholar
[19]	Dai S, Zhang J, MaQ, Kittiwatanakul S, McLeod A, Chen X, Corder S N G, Watanabe K, Taniguchi T, Lu J, Dai Q, Jarillo-Herrero P, Liu M, Basov D N 2019 Adv. Mater. 31 1900251 Google Scholar
[20]	Passler N C, Heßler A, Wuttig M, Taubner T, Paarmann A 2020 Adv. Optical Mater. 8 1901056 Google Scholar
[21]	Zhang Q, Ou Q, Hu G, Liu J, Dai Z, Fuhrer M S, Bao Q, Qiu C W 2021 Nano Lett. 21 3112 Google Scholar
[22]	Hofmann J, Das S S 2016 Phys. Rev. B 93 241402 Google Scholar
[23]	Zhao B, Guo C, Garcia C A C, Narang P, Fan S 2020 Nano Lett. 20 1923 Google Scholar
[24]	Kotov O V, Lozovik Y E 2018 Phys. Rev. B 98 195446 Google Scholar
[25]	Tamaya T, Kato T, Tsuchikawa K, Konabe S, Kawabata S 2019 J. Phys. Condens. Matter 31 305001 Google Scholar
[26]	Schubert M 1996 Phys. Rev. B 53 4265 Google Scholar
[27]	Wu X H, Fu C J, Zhang Z M 2019 Int. J. Heat Mass Tran. 135 1207 Google Scholar
[28]	Hajian H, Ghobadi A, Dereshgi S A, Butun B, Ozbay E 2017 J. Opt. Soc. Am. B 34 D29 Google Scholar
[29]	Fandan R, Pedrós J, Schiefele J, Boscá A, Martínez J, Calle F 2018 J. Phys. D: Appl. Phys. 51 204004 Google Scholar
[30]	Wang Y, Khandekar C, Gao X, Li T, Jiao D, Jacob Z 2021 Opt. Mater. Express 11 3880 Google Scholar
[31]	Wu J, Wu B Y, Wang Z M, Wu X H 2022 Int. J. Therm. Sci. 181 107788 Google Scholar
[32]	Ashby P E C, Carbotte J P 2014 Phys. Rev. B 89 245121 Google Scholar
[33]	Wu X H 2020 J. Heat Transfer 142 072802 Google Scholar

[1]	Li Wen-Qiu, Tang Yan-Na, Liu Ya-Lin, Ma Wei-Cong, Wang Gang. Radiation enhancement phenomenon of isotropic plasma layer coated cylinderical metal antenna. Acta Physica Sinica, 2023, 72(13): 135202. doi: 10.7498/aps.72.20230101
[2]	Wang Jing-Li, Yang Zhi-Xiong, Dong Xian-Chao, Yin Liang, Wan Hong-Dan, Chen He-Ming, Zhong Kai. VO₂based terahertz anisotropic coding metasurface. Acta Physica Sinica, 2023, 72(12): 124204. doi: 10.7498/aps.72.20222171
[3]	Qian Li-Ming, Sun Meng-Ran, Zheng Gai-Ge. Coupling interactions of anisotropic hyperbolic phonon polaritons in double layered orthorhombic molybdenum trioxide. Acta Physica Sinica, 2023, 72(7): 077101. doi: 10.7498/aps.72.20222144
[4]	Su Rui-Xia, Huang Xia, Zheng Zhi-Gang. Lattice wave solution and its dispersion relation of two coupled Frenkel-Kontorova chains. Acta Physica Sinica, 2022, 71(15): 154401. doi: 10.7498/aps.71.20212362
[5]	Gao Han-Feng, Zhang Xin, Wu Fu-Gen, Yao Yuan-Wei. Semi-Dirac cone and singular features of two-dimensional three-component phononic crystals. Acta Physica Sinica, 2016, 65(4): 044301. doi: 10.7498/aps.65.044301
[6]	Lu Min, Huang Hui-Lian, Yu Dong-Hai, Liu Wei-Qing, Wei Wang-He. Anisotropy of melting of Ag nanocrystal with different crystallographic planes at high temperature. Acta Physica Sinica, 2015, 64(10): 106101. doi: 10.7498/aps.64.106101
[7]	Ren Yi-Chong, Fan Hong-Yi. Solving dispersion relations of one-dimensional diatomic chain with on-site potential by invariant eigen-operator method. Acta Physica Sinica, 2013, 62(15): 156301. doi: 10.7498/aps.62.156301
[8]	Li Xiao-Ze, Teng Yan, Wang Jian-Guo, Song Zhi-Min, Zhang Li-Jun, Zhang Yu-Chuan, Ye Hu. Mode selection in surface wave oscillator with overmoded structure. Acta Physica Sinica, 2013, 62(8): 084103. doi: 10.7498/aps.62.084103
[9]	Wang Guan-Yu, Song Jian-Jun, Zhang He-Ming, Hu Hui-Yong, Ma Jian-Li, Wang Xiao-Yan. Analytical dispersion relation model for conduction band of uniaxial strained Si. Acta Physica Sinica, 2012, 61(9): 097103. doi: 10.7498/aps.61.097103
[10]	Zhang Li-Wei, Zhao Yu-Huan, Wang Qin, Fang Kai, Li Wei-Bin, Qiao Wen-Tao. Resonance properties of surface plasmon in the anisotropic metamaterial waveguide. Acta Physica Sinica, 2012, 61(6): 068401. doi: 10.7498/aps.61.068401
[11]	Liu San-Qiu, Guo Hong-Mei. Transverse dispersion laws in ultra-relativistic plasma with fast electron distribution. Acta Physica Sinica, 2011, 60(5): 055203. doi: 10.7498/aps.60.055203
[12]	Ling Rui-Liang, Feng Jin, Feng Jin-Fu. Quantized energy spectrum and exact wave function of three-dimensional anisotropic coupled harmonic oscillator. Acta Physica Sinica, 2010, 59(12): 8348-8358. doi: 10.7498/aps.59.8348
[13]	Liu Bing-Can, Lu Zhi-Xin, Yu Li. The dispersion relation for surface plasmon at a metal-Kerr nonlinear medium interface. Acta Physica Sinica, 2010, 59(2): 1180-1184. doi: 10.7498/aps.59.1180
[14]	Ji Pei-Yong, Lu Nan, Zhu Jun. Dispersion relation and Landau damping of linear waves in quantum plasma. Acta Physica Sinica, 2009, 58(11): 7473-7478. doi: 10.7498/aps.58.7473
[15]	Zhou Jian-Hua, Liu Hong-Yao, Luo Hai-Lu, Wen Shuang-Chun. Backward wave propagation in anisotropic metamaterials. Acta Physica Sinica, 2008, 57(12): 7729-7736. doi: 10.7498/aps.57.7729
[16]	Song Jian-Jun, Zhang He-Ming, Dai Xian-Ying, Hu Hui-Yong, Xuan Rong-Xi. Dispersion relation model of valence band in strained Si. Acta Physica Sinica, 2008, 57(11): 7228-7232. doi: 10.7498/aps.57.7228
[17]	Cai Li, Han Xiao-Yun, Wen Xi-Sen. The elastic wave propagation in two-dimensional phononic crystal at low frequencies and the anisotropy of effective velocity. Acta Physica Sinica, 2008, 57(3): 1746-1752. doi: 10.7498/aps.57.1746
[18]	Zhao Guo-Wei, Xu Yue-Min, Chen Cheng. Calculation of dispersion relation and radiation pattern of plasma antenna. Acta Physica Sinica, 2007, 56(9): 5298-5303. doi: 10.7498/aps.56.5298
[19]	Mu Quan-Quan, Liu Yong-Jun, Hu Li-Fa, Li Da-Yu, Cao Zhao-Liang, Xuan Li. Determination of anisotropic liquid crystal layer parameters by spectroscopic ellipsometer. Acta Physica Sinica, 2006, 55(3): 1055-1060. doi: 10.7498/aps.55.1055
[20]	FAN ZHI-KAI, LIU QING-XIANG. ANALYTIC RESEARCH ON THE DISPERSION RELATION AND FIELD DISTRIBUTION OF THE RESON ANT CAVITY CHAIN. Acta Physica Sinica, 2000, 49(7): 1249-1255. doi: 10.7498/aps.49.1249

Catalog

Vol. 72, Issue 19 - 2023-10-05

Metrics

Abstract views: 2106
PDF Downloads: 111
Cited By: 0

姓名
邮箱
手机号码
标题
留言内容
验证码

Search

Article

留言板