-
X-ray ghost imaging is a low-dose, non-localized imaging method, which is of great significance in medical diagnosis and biological imaging. In crystal diffraction based X-ray ghost imaging, the blurring patterns in the diffracted beam, caused by the crystal vibration, can result in a reduction in the contrast and spatial resolution of the reconstructed imaged by ensemble average. In the paper, we systematically analyze the influence of the blurring degree of the speckle patterns from the diffracted beam on the normalized second-order intensity correlation function
$ {g}^{\left(2\right)} $ numerically and theoretically. Both demonstrates that as the blurring degree increases, the maximum value of$ {g}^{\left(2\right)} $ decreases and the full width at half maximum broadens, which theoretically proves the blurring degree relating to image quality. In order to solve the above problem, in the paper we propose a$ {G}_{\mathrm{L}\mathrm{H}} $ enhanced ($ {G}_{\mathrm{L}\mathrm{H}}\mathrm{E} $ ) method to optimize the image quality based on the scheme ($ {G}_{\mathrm{L}\mathrm{H}} $ ) which directly correlates the bucket signals in diffracted beam with the high-definition patterns in transmitted beam. The simulation experiments exhibit that the$ {G}_{\mathrm{L}\mathrm{H}}\mathrm{E} $ method can improve both the image contrast and the spatial resolution simultaneously. As the blurring degree increases, the difference between the peak signal-to noise ratio of the reconstructed image by the iterative method and that by the scheme$ {(G}_{\mathrm{L}\mathrm{L}}) $ which preprocess the speckle patterns in the transmitted beam through Gaussian filtering, becomes greater. Furthermore, the${G}_{\mathrm{L}\mathrm{H}}\mathrm{E} $ is almost immune to the additive noise. In summary, the present study provides a feasible idea for the practical application of X-ray ghost imaging based on crystal diffraction.-
Keywords:
- X-ray ghost imaging /
- crystal diffraction /
- imaging quality /
- normalized second-order intensity correlation
[1] Bennink R S, Bentley S J, Boyd R W, Howell J C 2004 Phys. Rev. Lett. 92 033601
Google Scholar
[2] Ferri F, Magatti D, Gatti A, Bache M, Brambilla E, Lugiato L A 2005 Phys. Rev. Lett. 94 183602
Google Scholar
[3] Valencia A, Scarcelli G, D’Angelo M, Shih Y 2005 Phys. Rev. Lett. 94 063601
Google Scholar
[4] Pittman T, Shih Y, Strekalov D, Sergienko A 1995 Phys. Rev. A 52 R3429
Google Scholar
[5] Zhang D, Zhai Y H, Wu L A, Chen X H 2005 Opt. Lett. 30 2354
Google Scholar
[6] Chan K W C, O'Sullivan M N, Boyd R W 2009 Opt. Lett. 34 3343
Google Scholar
[7] Cao D Z, Xiong J, Wang K 2005 Phys. Rev. A 71 013801
Google Scholar
[8] Strekalov D V, Sergienko A V, Klyshko D N, Shih Y H 1995 Phys. Rev. Lett. 74 3600
Google Scholar
[9] Bennink R S, Bentley S J, Boyd R W 2002 Phys. Rev. Lett. 89 113601
Google Scholar
[10] Yu W K, Liu X F, Yao X R, Wang C, Zhai G J, Zhao Q 2014 Phys. Rev. A 378 3406
[11] Cheng J 2009 Opt. Express 17 7916
Google Scholar
[12] Shi D, Fan C, Zhang P, Zhang J, Shen H, Qiao C, Wang Y 2012 Opt. Express 20 27992
Google Scholar
[13] 李明飞, 阎璐, 杨然, 寇军, 刘院省 2019 68 094204
Google Scholar
Li M F, Yan L, Yang R, Kou J, Liu Y X 2019 Acta Phys. Sin. 68 094204
Google Scholar
[14] Oh J E, Cho Y W, Scarcelli G, Kim Y H 2013 Opt. Lett. 38 682
Google Scholar
[15] Zhao C, Gong W, Chen M, Li E, Wang H, Wendong X, Han A 2012 Appl. Phys. Lett. 101 141123
Google Scholar
[16] Ma S, Liu Z, Wang C, Hu C, Li E, Gong W, Tong Z, Wu J, Shen X, Han S 2019 Opt. Express 27 13219
Google Scholar
[17] Boto A N, Kok P, Abrams D S, Braunstein S L, Williams C P, Dowling J P 2000 Phys. Rev. Lett. 85 2733
Google Scholar
[18] D'Angelo M, Chekhova M V, Shih Y 2001 Phys. Rev. Lett. 87 013602
Google Scholar
[19] Li S, Yao X R, Yu W K, Wu L A, Zhai G J 2013 Opt. Lett. 38 2144
Google Scholar
[20] Cheng J, Han S 2004 Phys. Rev. Lett. 92 093903
Google Scholar
[21] Chen X H, Agafonov I N, Luo K H, Liu Q, Xian R, Chekhova M V, Wu L A 2010 Opt. Lett. 35 1166
Google Scholar
[22] Chen X H, Liu Q, Luo K H, Wu L A 2009 Opt. Lett. 34 695
Google Scholar
[23] Li S, Cropp F, Kabra K, Lane T J, Wetzstein G, Musumeci P, Ratner D 2018 Phys. Rev. Lett. 121 114801
Google Scholar
[24] Kingston A M, Myers G R, Pelliccia D, Salvemini F, Bevitt J J, Garbe U, Paganin D M 2020 Phys. Rev. A 101 053844
Google Scholar
[25] Pelliccia D, Olbinado M, Rack A, Kingston A, Myers G, Paganin D 2018 IUCrJ 5 428
Google Scholar
[26] Kingston A M, Pelliccia D, Rack A, Olbinado M P, Cheng Y, Myers G R, Paganin D M 2018 Optica 5 1516
Google Scholar
[27] Zhang A X, He Y H, Wu L A, Chen L M, Wang B B 2018 Optica 5 374
Google Scholar
[28] Klein Y, Schori A, Dolbnya I P, Sawhney K, Shwartz S 2019 Opt. Express 27 3284
Google Scholar
[29] Schori A, Shwartz S 2017 Opt. Express 25 14822
Google Scholar
[30] Schori A, Borodin D, Tamasaku K, Shwartz S 2018 Phys. Rev. A 97 063804
Google Scholar
[31] Pelliccia D, Rack A, Scheel M, Cantelli V, Paganin D M 2016 Phys. Rev. Lett. 117 113902
Google Scholar
[32] Yu H, Lu R, Han S, Xie H, Du G, Xiao T, Zhu D 2016 Phys. Rev. Lett. 117 113901
Google Scholar
[33] He Y H, Zhang A X, Li M F, Huang Y Y, Quan B G, Li D Z, Wu L A, Chen L M 2020 APL Photonics 5 056102
Google Scholar
[34] 孙海峰, 包为民, 方海燕, 李小平 2014 63 069701
Google Scholar
Sun H F, Bao F W, Fang H Y, Li X P 2014 Acta Phys. Sin. 63 069701
Google Scholar
[35] 刘雪峰, 姚旭日, 李明飞, 俞文凯, 陈希浩, 孙志斌, 吴 令安, 翟光杰 2013 62 184205
Google Scholar
Liu X F, Yao X R, Li M F, Yu W K, Chen X H, Sun Z B, Wu L A, Zhai G J 2013 Acta Phys. Sin. 62 184205
Google Scholar
[36] Zhao C Z, Si S Y, Zhang H P, Xue L , Li Z L, Xiao T Q 2021 Acta Phys. Sin. 70
Google Scholar
-
图 1 基于晶体衍射分光的X射线鬼成像示意图
Figure 1. Schematic diagram of X-ray ghost imaging based on the beam splitter of crystal diffraction.
图 2 一致性和模糊程度关系
Figure 2. Consistency vs ambiguity.
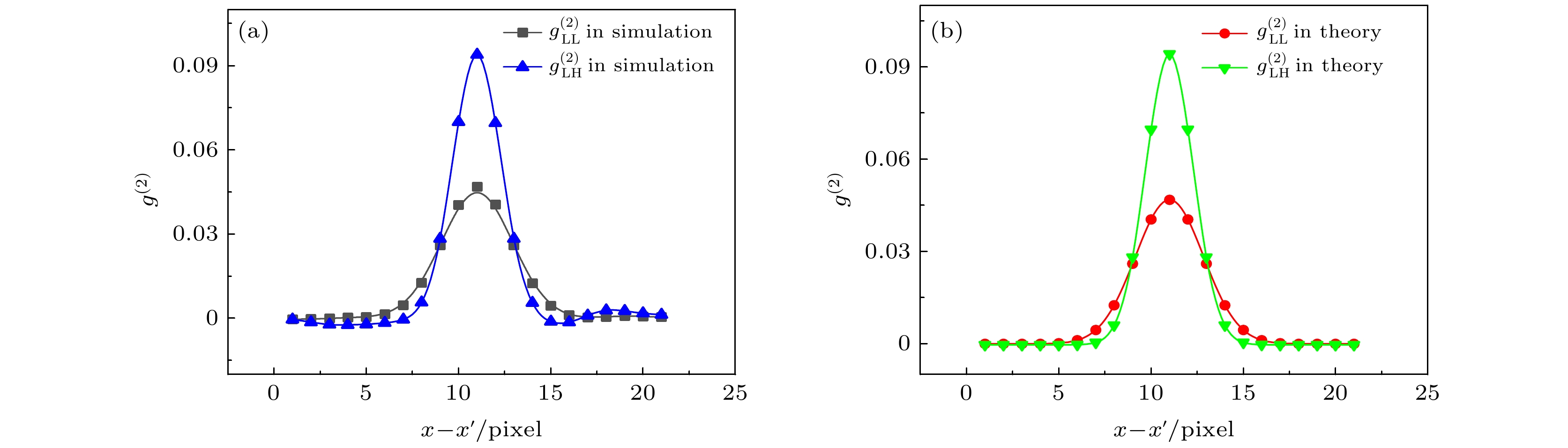
图 3 当
$ \sigma =1.3 $ 时光强归一化二阶关联的理论和模拟在x方向上的曲线图 (a)$ {g}_{\mathrm{L}\mathrm{L}}^{\left(2\right)}\mathrm{和}{g}_{\mathrm{L}\mathrm{H}}^{\left(2\right)} $ 的模拟在x方向上的曲线图; (b)${g}_{\mathrm{L}\mathrm{L}}^{\left(2\right)} $ $ \mathrm{和}{g}_{\mathrm{L}\mathrm{H}}^{\left(2\right)}$ 的理论在x方向上的曲线图Figure 3. The theoretical and simulated curves of the normalized second-order correlation of light intensity in x direction when
$ \sigma =1.3: $ (a) The simulated curves of$ {g}_{\mathrm{L}\mathrm{L}}^{\left(2\right)} $ and$ {g}_{\mathrm{L}\mathrm{H}}^{\left(2\right)} $ in x direction; (b) the theoretical curves of$ {g}_{\mathrm{L}\mathrm{L}}^{\left(2\right)} $ and$ {g}_{\mathrm{L}\mathrm{H}}^{\left(2\right)} $ in x direction.
图 4
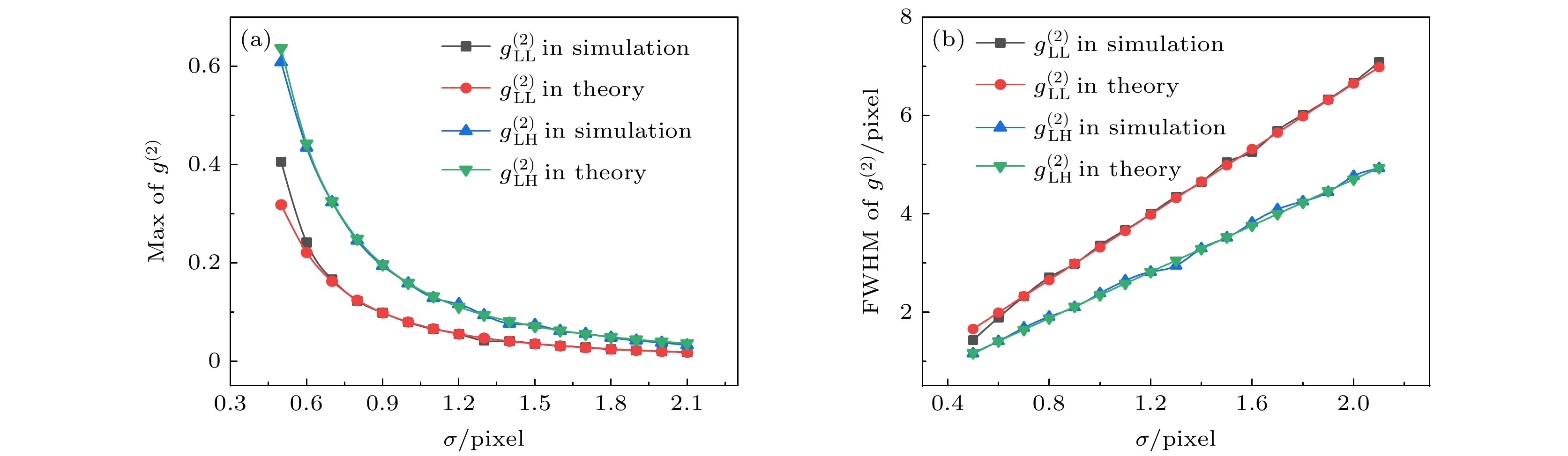
$ {g}_{\mathrm{L}\mathrm{L}}^{\left(2\right)} $ 和$ {g}_{\mathrm{L}\mathrm{H}}^{\left(2\right)} $ 在理论和模拟上随模糊程度$ \sigma $ 的变化曲线图 (a)$ {\mathrm{g}}_{\mathrm{L}\mathrm{L}}^{\left(2\right)} $ 和${g}_{\mathrm{L}\mathrm{H}}^{\left(2\right)}$ 在理论和模拟的最大值随$ \sigma $ 的变化; (b)$ {g}_{\mathrm{L}\mathrm{L}}^{\left(2\right)} $ 和${g}_{\mathrm{L}\mathrm{H}}^{\left(2\right)}$ 在理论和模拟的半高全宽随$ \sigma $ 的变化Figure 4.
${g}_{\mathrm{L}\mathrm{L}}^{\left(2\right)}~\mathrm{and}~{g}_{\mathrm{L}\mathrm{H}}^{\left(2\right)}$ vary with the blur degree$ \sigma $ in theory and simulation: (a) The theoretical and simulated maximum of${g}_{\mathrm{L}\mathrm{L}}^{\left(2\right)}\mathrm{~and~}{g}_{\mathrm{L}\mathrm{H}}^{\left(2\right)}$ vary with$ \sigma $ ; (b) the FWHM of${g}_{\mathrm{L}\mathrm{L}}^{\left(2\right)}~\mathrm{and}~{g}_{\mathrm{L}\mathrm{H}}^{\left(2\right)}$ vary with$ \sigma $ in theory and simulation.
图 5
${G}_{\mathrm{L}\mathrm{L}} $ 和$ {G}_{\mathrm{L}\mathrm{H}}\mathrm{E} $ 方法重构图像 (a) 物体图像; (b)—(f) 不同标准差($ \sigma $ = 0.7, 1.0, 1.3, 1.6, 1.9)时$ {G}_{\mathrm{L}\mathrm{L}} $ 恢复的图像; (g)$ {G}_{\mathrm{H}\mathrm{H}} $ 重构的图像; (h)—(l) 不同标准差($ \sigma $ = 0.7, 1.0, 1.3, 1.6, 1.9)时$ {G}_{\mathrm{L}\mathrm{H}}\mathrm{E} $ 方法恢复的图像.Figure 5. Images reconstructed by
$ {G}_{\mathrm{L}\mathrm{L}} $ and iterative method: (a) The object image; (b)-(f) the images are retrieved by$ {G}_{\mathrm{L}\mathrm{L}} $ with$ \sigma $ set as 0.7, 1.0, 1.3, 1.6, 1.9; (g) the image restored by$ {G}_{\mathrm{H}\mathrm{H}} $ ; (h)-(l) the images are reconstructed by iterative method when$ \sigma $ is 0.7, 1.0, 1.3, 1.6, 1.9.
图 6 不同算法重构图像的PSNR随模糊衬度的变化曲线
Figure 6. The PSNR curves of reconstructed images with different algorithms vary with blur degree.
图 7
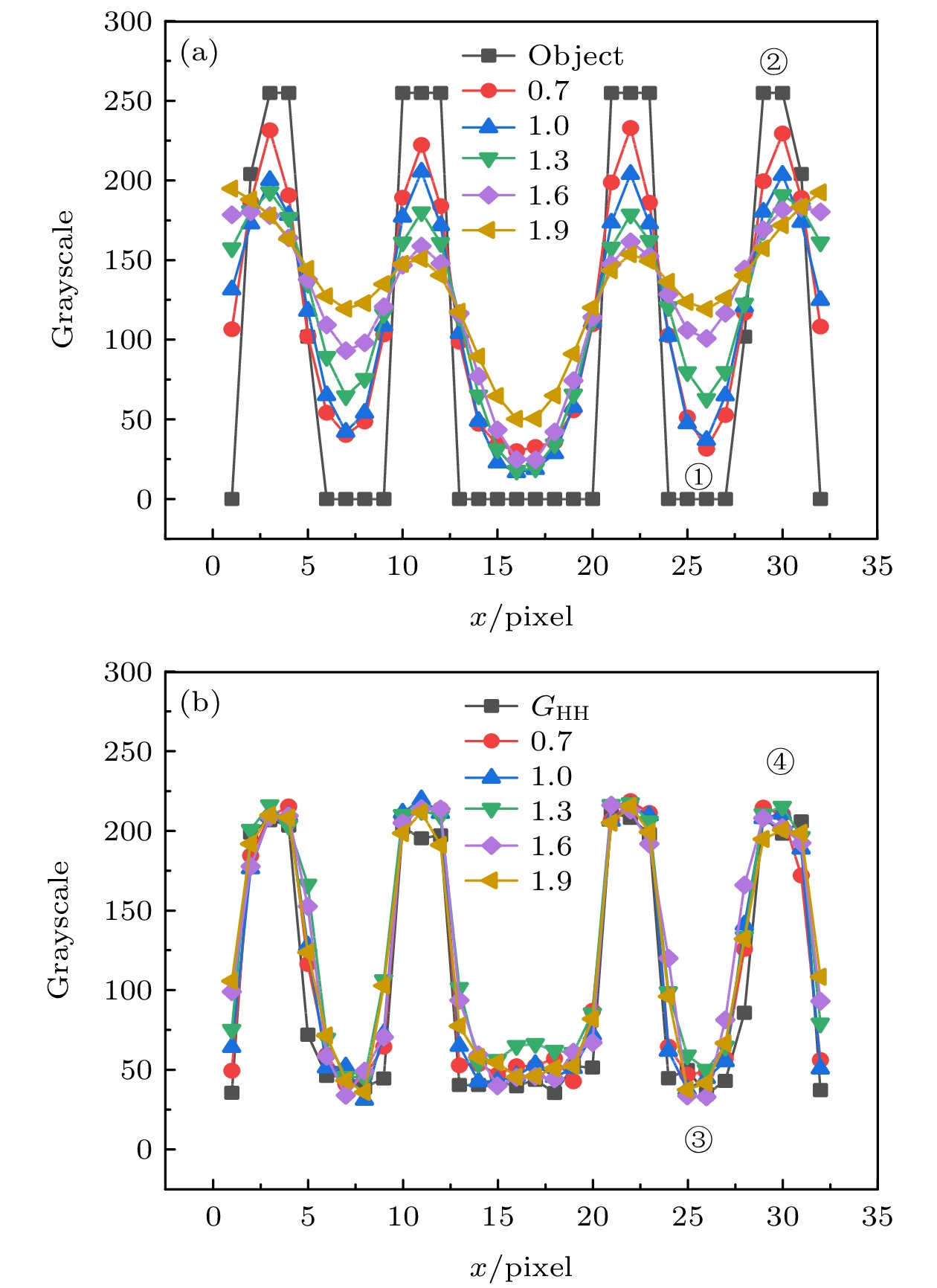
$ {G}_{\mathrm{L}\mathrm{L}} $ 和$ {G}_{\mathrm{L}\mathrm{H}}\mathrm{E} $ 方法重构图像中间部位的截面轮廓线：(a) 黑线是物体的截面轮廓线, 即图5(a)中间区域的平均灰度变化, 其余分别是$ {G}_{\mathrm{L}\mathrm{L}} $ 方法在$ \sigma $ 为0.7, 1.0, 1.3, 1.6, 1.9时重构图像的截面轮廓线, 即图5(b)到图5(f)的中间区域的平均灰度变化; (b) 黑线是GHH重构图像的截面轮廓线, 即图5(g)中间区域的平均灰度变化, 其余是$ {G}_{\mathrm{L}\mathrm{H}}\mathrm{E} $ 方法在$ \sigma $ 为0.7, 1.0, 1.3, 1.6, 1.9时重构图像的截面轮廓线，即图5(h)到图5(l)的中间区域的平均灰度变化.Figure 7. Line profiles of the middle parts in the reconstructed images by
$ {G}_{\mathrm{L}\mathrm{L}} $ and$ {G}_{\mathrm{L}\mathrm{H}}\mathrm{E} $ : (a) The black curve is the line profile of the object, that is the mean grayscale change of the middle part in Fig. 5(a), and the rest is the line profiles of the images retrieved by$ {G}_{\mathrm{L}\mathrm{L}} $ with$ \sigma $ set as 0.7, 1.0, 1.3, 1.6, 1.9, that is, the mean grayscale change of the middle part in Fig. 5(b) to Fig. 5(f); (b) the black curve is the line profile of the image retrieved by$ {G}_{\mathrm{H}\mathrm{H}} $ , that is the mean grayscale change of the middle part in Fig. 5(g), and the rest is the line profiles of the images restored by$ {G}_{\mathrm{L}\mathrm{H}}\mathrm{E} $ when$ \sigma $ is 0.7, 1.0, 1.3, 1.6, 1.9, that is, the mean grayscale change of the middle part in Fig. 5(h) to Fig. 5(l).
图 8
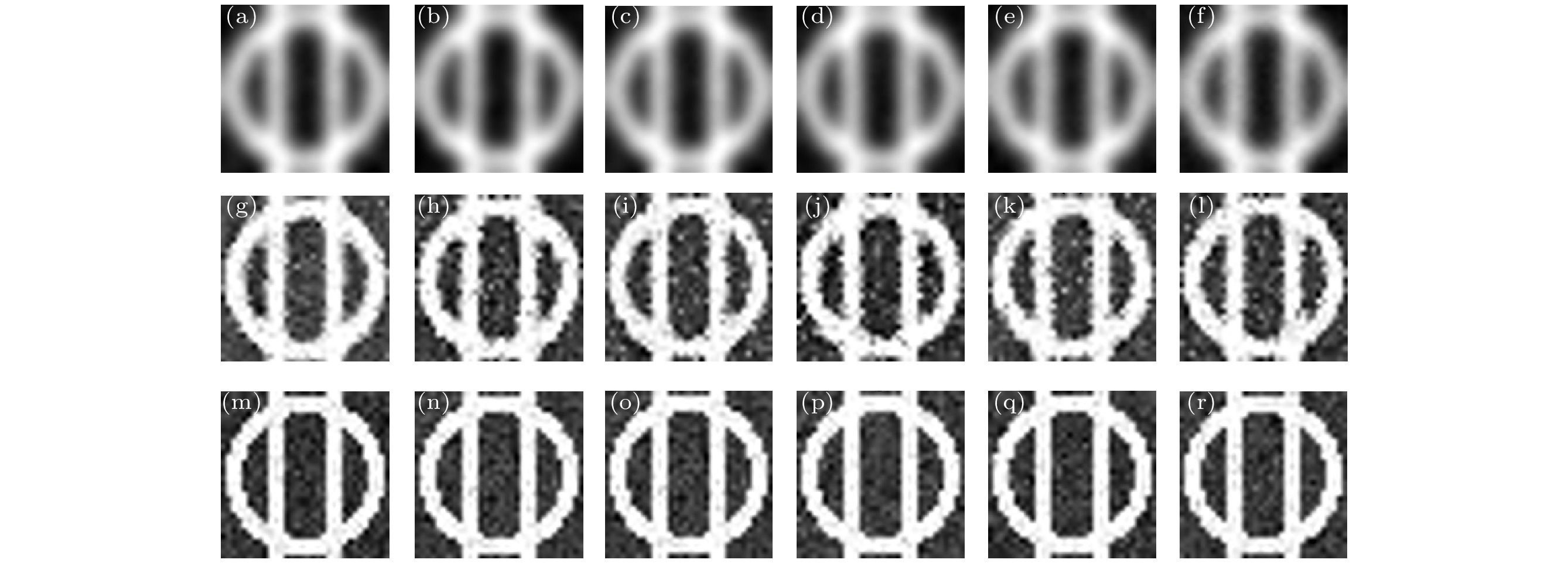
$ {G}_{\mathrm{L}\mathrm{L}} $ ,$ {G}_{\mathrm{L}\mathrm{H}}\mathrm{E} $ ,$ {G}_{\mathrm{H}\mathrm{H}} $ 在不同噪声下重构图像: (a), (g), (m) 无噪声时$ {G}_{\mathrm{L}\mathrm{L}} $ ,$ {G}_{\mathrm{L}\mathrm{H}}\mathrm{E} $ ,$ {G}_{\mathrm{H}\mathrm{H}} $ 重构的图像; (b)—(f)$ {\mathrm{G}}_{\mathrm{L}\mathrm{L}} $ 在均值为0.1, 标准差为0.05, 0.1, 0.15, 0.2, 0.25时重构的图像; (i)—(l)$ {G}_{\mathrm{L}\mathrm{H}}\mathrm{E} $ 在均值为0.1, 标准差为0.05, 0.1, 0.15, 0.2, 0.25时重构的图像; (n)—(r)$ {G}_{\mathrm{H}\mathrm{H}} $ 在均值为0.1, 标准差为0.05, 0.1, 0.15, 0.2, 0.25时重构的图像Figure 8. Images reconstructed by
$ {G}_{\mathrm{L}\mathrm{L}} $ ,$ {G}_{\mathrm{L}\mathrm{H}}\mathrm{E} $ ,$ {G}_{\mathrm{H}\mathrm{H}} $ under different noise: (a), (g), (m) the images reconstructed by$ {G}_{\mathrm{L}\mathrm{L}} $ ,$ {G}_{\mathrm{L}\mathrm{H}}\mathrm{E} $ ,$ {G}_{\mathrm{H}\mathrm{H}} $ without noise; (b)–(f) the images reconstructed by$ {G}_{\mathrm{L}\mathrm{L}} $ under the noise with the mean of 0.1 and the standard deviation of 0.05, 0.1, 0.15, 0.2, 0.25 respectively; (i)–(l) the images reconstructed by$ {G}_{\mathrm{L}\mathrm{H}}\mathrm{E} $ under the noise with the mean of 0.1 and the standard deviation of 0.05, 0.1, 0.15, 0.2, 0.25 respectively; (n)–(r) the images reconstructed by$ {G}_{\mathrm{H}\mathrm{H}} $ under the noise with the mean of 0.1 and the standard deviation of 0.05, 0.1, 0.15, 0.2, 0.25 respectively.
图 9
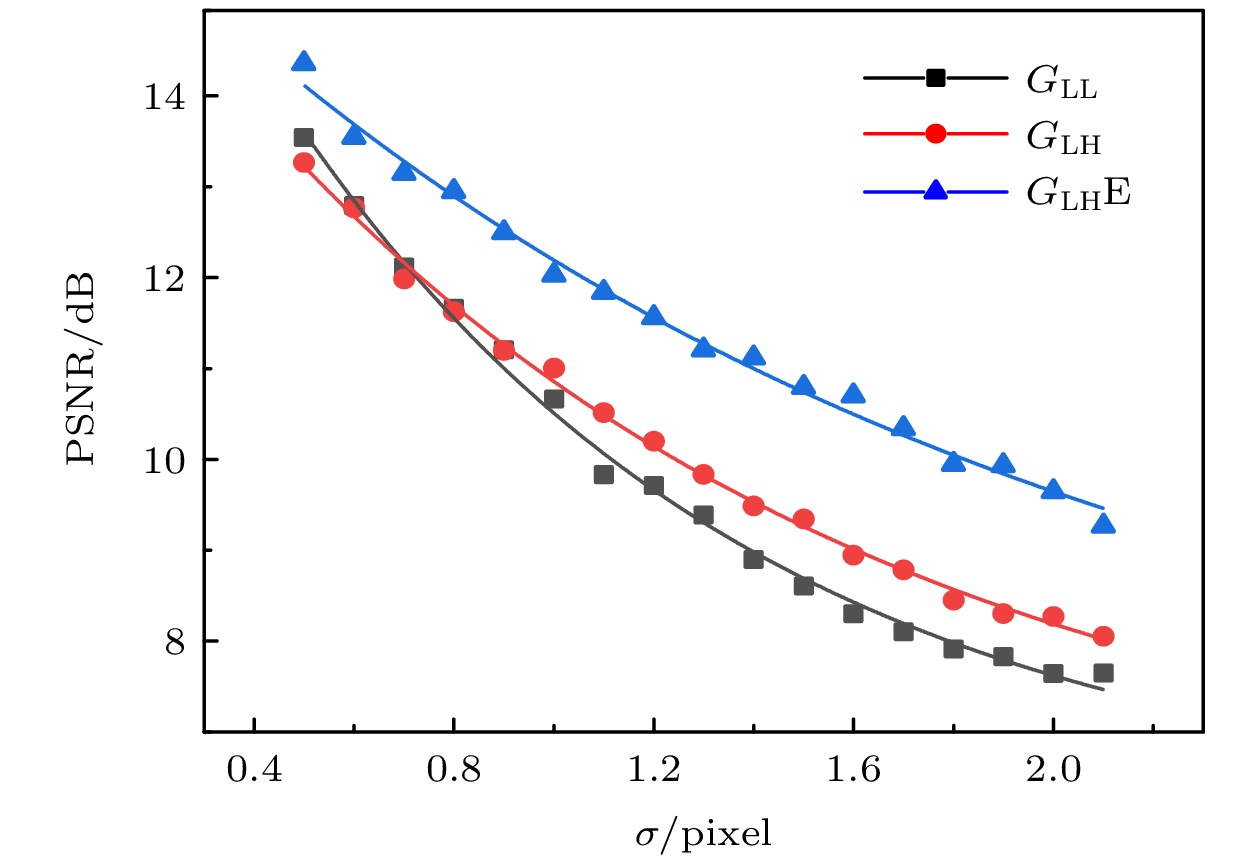
$ {G}_{\mathrm{L}\mathrm{L}} $ ,$ {G}_{\mathrm{L}\mathrm{H}}\mathrm{E} $ ,$ {G}_{\mathrm{H}\mathrm{H}} $ 在不同噪声下重构图像的PSNR, 其中标准差$ {\sigma }_{\mathrm{N}} $ 为0表示没有噪声(此时噪声均值$ {\mu }_{\mathrm{N}} $ 也为0)Figure 9. PSNRs of images reconstructed by
$ {G}_{\mathrm{L}\mathrm{L}} $ ,$ {G}_{\mathrm{L}\mathrm{H}}\mathrm{E} $ ,$ {G}_{\mathrm{H}\mathrm{H}} $ under different noise, where the standard deviation$ {\sigma }_{\mathrm{N}} $ of 0 indicates there is no noise (at this time the mean$ {\mu }_{\mathrm{N}} $ of noise is also 0). -
[1] Bennink R S, Bentley S J, Boyd R W, Howell J C 2004 Phys. Rev. Lett. 92 033601
Google Scholar
[2] Ferri F, Magatti D, Gatti A, Bache M, Brambilla E, Lugiato L A 2005 Phys. Rev. Lett. 94 183602
Google Scholar
[3] Valencia A, Scarcelli G, D’Angelo M, Shih Y 2005 Phys. Rev. Lett. 94 063601
Google Scholar
[4] Pittman T, Shih Y, Strekalov D, Sergienko A 1995 Phys. Rev. A 52 R3429
Google Scholar
[5] Zhang D, Zhai Y H, Wu L A, Chen X H 2005 Opt. Lett. 30 2354
Google Scholar
[6] Chan K W C, O'Sullivan M N, Boyd R W 2009 Opt. Lett. 34 3343
Google Scholar
[7] Cao D Z, Xiong J, Wang K 2005 Phys. Rev. A 71 013801
Google Scholar
[8] Strekalov D V, Sergienko A V, Klyshko D N, Shih Y H 1995 Phys. Rev. Lett. 74 3600
Google Scholar
[9] Bennink R S, Bentley S J, Boyd R W 2002 Phys. Rev. Lett. 89 113601
Google Scholar
[10] Yu W K, Liu X F, Yao X R, Wang C, Zhai G J, Zhao Q 2014 Phys. Rev. A 378 3406
[11] Cheng J 2009 Opt. Express 17 7916
Google Scholar
[12] Shi D, Fan C, Zhang P, Zhang J, Shen H, Qiao C, Wang Y 2012 Opt. Express 20 27992
Google Scholar
[13] 李明飞, 阎璐, 杨然, 寇军, 刘院省 2019 68 094204
Google Scholar
Li M F, Yan L, Yang R, Kou J, Liu Y X 2019 Acta Phys. Sin. 68 094204
Google Scholar
[14] Oh J E, Cho Y W, Scarcelli G, Kim Y H 2013 Opt. Lett. 38 682
Google Scholar
[15] Zhao C, Gong W, Chen M, Li E, Wang H, Wendong X, Han A 2012 Appl. Phys. Lett. 101 141123
Google Scholar
[16] Ma S, Liu Z, Wang C, Hu C, Li E, Gong W, Tong Z, Wu J, Shen X, Han S 2019 Opt. Express 27 13219
Google Scholar
[17] Boto A N, Kok P, Abrams D S, Braunstein S L, Williams C P, Dowling J P 2000 Phys. Rev. Lett. 85 2733
Google Scholar
[18] D'Angelo M, Chekhova M V, Shih Y 2001 Phys. Rev. Lett. 87 013602
Google Scholar
[19] Li S, Yao X R, Yu W K, Wu L A, Zhai G J 2013 Opt. Lett. 38 2144
Google Scholar
[20] Cheng J, Han S 2004 Phys. Rev. Lett. 92 093903
Google Scholar
[21] Chen X H, Agafonov I N, Luo K H, Liu Q, Xian R, Chekhova M V, Wu L A 2010 Opt. Lett. 35 1166
Google Scholar
[22] Chen X H, Liu Q, Luo K H, Wu L A 2009 Opt. Lett. 34 695
Google Scholar
[23] Li S, Cropp F, Kabra K, Lane T J, Wetzstein G, Musumeci P, Ratner D 2018 Phys. Rev. Lett. 121 114801
Google Scholar
[24] Kingston A M, Myers G R, Pelliccia D, Salvemini F, Bevitt J J, Garbe U, Paganin D M 2020 Phys. Rev. A 101 053844
Google Scholar
[25] Pelliccia D, Olbinado M, Rack A, Kingston A, Myers G, Paganin D 2018 IUCrJ 5 428
Google Scholar
[26] Kingston A M, Pelliccia D, Rack A, Olbinado M P, Cheng Y, Myers G R, Paganin D M 2018 Optica 5 1516
Google Scholar
[27] Zhang A X, He Y H, Wu L A, Chen L M, Wang B B 2018 Optica 5 374
Google Scholar
[28] Klein Y, Schori A, Dolbnya I P, Sawhney K, Shwartz S 2019 Opt. Express 27 3284
Google Scholar
[29] Schori A, Shwartz S 2017 Opt. Express 25 14822
Google Scholar
[30] Schori A, Borodin D, Tamasaku K, Shwartz S 2018 Phys. Rev. A 97 063804
Google Scholar
[31] Pelliccia D, Rack A, Scheel M, Cantelli V, Paganin D M 2016 Phys. Rev. Lett. 117 113902
Google Scholar
[32] Yu H, Lu R, Han S, Xie H, Du G, Xiao T, Zhu D 2016 Phys. Rev. Lett. 117 113901
Google Scholar
[33] He Y H, Zhang A X, Li M F, Huang Y Y, Quan B G, Li D Z, Wu L A, Chen L M 2020 APL Photonics 5 056102
Google Scholar
[34] 孙海峰, 包为民, 方海燕, 李小平 2014 63 069701
Google Scholar
Sun H F, Bao F W, Fang H Y, Li X P 2014 Acta Phys. Sin. 63 069701
Google Scholar
[35] 刘雪峰, 姚旭日, 李明飞, 俞文凯, 陈希浩, 孙志斌, 吴 令安, 翟光杰 2013 62 184205
Google Scholar
Liu X F, Yao X R, Li M F, Yu W K, Chen X H, Sun Z B, Wu L A, Zhai G J 2013 Acta Phys. Sin. 62 184205
Google Scholar
[36] Zhao C Z, Si S Y, Zhang H P, Xue L , Li Z L, Xiao T Q 2021 Acta Phys. Sin. 70
Google Scholar
DownLoad:
Catalog
Metrics
- Abstract views: 5808
- PDF Downloads: 214
- Cited By: 0
