Monte-Carlo study of pre-neutron emission mass and energy for neutron-induced <sup>232</sup>Th fission

Liu Chang-Qi; Huo Dong-Ying; Han Chao; Wu Kang; Liu Xing-Yu; Yang Xu; Bai Xiao-Hou; Wang Jun-Run; Zhang Yu; Yao Ze-En; Wei Zheng

doi:10.7498/aps.71.20211333

Abstract

The development of fourth-generation reactors and advanced nuclear energy systems require high-precision, multi-nuclide, and wide-energy-area neutron nuclear data. However, the current nuclear energy-related nuclear fission data in the China Nuclear Data Evaluation Library (CENDL library) are incomplete and cannot meet the current need. It is extremely important to establish the reliable calculation methods and tools for the neutron nuclear data. Based on the Monte-Carlo method, a model for calculating the pre-neutron fission fragment is established in this work. The mass and kinetic energy distribution of ²³²Th(n,f) reaction at the medium- and low- incident neutron energy are studied. The calculations of the mass distribution with the different values of incident energy are compared with the experimental results. The maximum deviation of this work from the experimental data is ~1%, which is advantageous compared with the GEF and TALYS code (maximum deviation from the experimental value is ~2%). The calculation of the pre-neutron fission fragment kinetic energy also shows good agreement with experimental result. The results indicate that this model can well describe and predict the characteristics of pre-neutron fission fragment for ²³²Th(n,f) reaction at the medium- and low- incident neutron energy. It also provides a new idea for calculating the neutron-induced actinide fission reactions.

Keywords:

pre-neutron emission fission fragments /
mass distribution /
total kinetic energy distribution /
Monte-Carlo method

Authors and contacts

1.
School of Nuclear Science and Technology, Lanzhou University, Lanzhou 730000, China
2.
Engineering Research Center for Neutron Application, Ministry of Education, Lanzhou University, Lanzhou 730000, China

Corresponding author: Wei Zheng, weizheng@lzu.edu.cn

Funds: Project supported by the Joint Fund of the National Natural Science Foundation of China and the China Academy of Engineering Physics (Grant No. U1830102), the National Natural Science Foundation of China (Grant Nos. 12075105, 11875155, 11705071), the Joint Fund of the National Natural Science Foundation of China and the Nuclear Technology Innovation Fund of China National Nuclear Corporation (Grant No. U1867213), the Fundamental Research Fund for the Central Universities, China (Grant No. lzujbky-2021-kb09), and the DSTI Foundation of Gansu Province, China (Grant No. 2018ZX-07).

FullText HTML : translate this paragraph

References

[1]	Talou P, Becker B, Kawano T, Chadwick M B, Danon Y 2011 Phys. Rev. C 83 1509
[2]	张竞上 2003 现代物理知识 01 24 Zhang J S 2003 Mod. Phys. 01 24
[3]	Forrest R A 2011 Energy Procedia 7 540 Google Scholar
[4]	Möller P, Sierk A J 2003 Nature 422 485
[5]	Al-Adili A, Hambsch F J, Pomp S, Oberstedt S, Vidali M 2016 Phys. Rev. C 93 34603 Google Scholar
[6]	Salvador-Castineira P, Brys T, Eykens R, Hambsch F-J, Göök A, Moens A, Oberstedt S, Sibbens G, Vanleeuw D, Vidali M 2015 Phys. Rev. C 92 014620 Google Scholar
[7]	Meierbachtol K, Tovesson F, Duke D L, Geppert-Kleinrath V, Manning B, Meharchand R, Mosby S, Shields D 2016 Phys. Rev. C 94 034611 Google Scholar
[8]	蔡翔舟, 戴志敏, 徐洪杰 2016 物理 45 578 Google Scholar Cai X Z, Dai Z M, Xu H J 2016 Physics 45 578 Google Scholar
[9]	Crasta R, Naik H, Suryanarayana S V, Shivashankar B S, Mulik V K, Prajapati P M, Sanjeev G, Sharma S C, Bhagwat P V, Mohanty A K, Ganesan S, Goswami A 2012 Ann. Nucl. Energy 47 160 Google Scholar
[10]	李光超 2017 博士学位论文 (上海: 中国科学院上海应用物理研究所) Li G C 2017 Ph. D. Dissertation (Shanghai: Shanghai Institute of Applied Physics, Chinese Academy of Sciences) (in Chinese)
[11]	Trochon J, Yehia H A, Brisard F, Pranal Y 1979 Nucl. Phys. A 318 63 Google Scholar
[12]	Naik H, Mukherji S, Suryanarayana S V, Jagadeesan K C, Thakare S V, Sharma S C 2016 Nucl. Phys. A 952 100 Google Scholar
[13]	King J, Yanez R, Loveland W, Barrett J S, Oscar B, Fotiades N, Tovesson F, Lee H Y 2017 Eur. Phys. J. A 53 238 Google Scholar
[14]	Sergachev A I, Vorob'Eva V G, Kuz'Minov B D, Mikhailov V B, Tarasko M Z 1968 Yadern. Fiz. 7 778
[15]	Ryzhov I V, Yavshits S G, Tutin G A, Kovalev N V, Saulski A V, Kudryashev N A 2011 Phys. Rev. C 83 054603 Google Scholar
[16]	葛智刚, 陈永静 2015 科学通报 60 3087 Google Scholar Ge Z G, Chen Y J 2015 Chin. Sci. bull. 60 3087 Google Scholar
[17]	Schmidt K H, Jurado B, Amouroux C 2016 Nucl. Data Sheets 131 107 Google Scholar
[18]	Koning A J, Hilaire S, Duijvestijn M C 2007 Proceedings of the International Conference on Nuclear Data for Science and Technology Nice, France, April 22–27, 2007 pp1–214
[19]	郝艺伟, 董国香, 王小保 2019 中国科学: 物理学力学天文学 49 122001 Hao Y W, Dong G X, Wang X B 2019 Scientia Sinica Physica, Mechanica & Astronomica 49 122001
[20]	Brosa U 1985 Phys. Rev. C 32 1438 Google Scholar
[21]	Brosa U, Grossmann S, Muller A, Becker E 1989 Nucl. Phys. A 502 423c Google Scholar
[22]	Hambsch F J, Vivès F, Siegler P, Oberstedt S 2000 Nucl. Phys. A 679 3 Google Scholar
[23]	Agostinelli S, Allison J, Amako K, et al. 2003 Nucl. Instrum. Methods A 506 250 Google Scholar
[24]	Mosby S, Tovesson F, Couture A, Duke D L, et al. 2014 Nucl. Instrum. Methods A 757 75 Google Scholar
[25]	Vivès F, Hambsch F J, Bax H, Oberstedt S 2000 Nucl. Phys. A 662 63 Google Scholar
[26]	Zeynalova O V, Zeynalov S, Hambsch F J, Oberstedt S, Fabry I 2010 Bull. Russ. Acad. Sci. Phys. 74 800 Google Scholar
[27]	Chadwick M B, Herman M, Obložinský P, et al. 2011 Nucl. Data Sheets 112 2887 Google Scholar
[28]	Liu C Q, Hu Z M, Hu Z J, et al. 2021 J. Instrum. 16 P07038 Google Scholar
[29]	Wang D, Zhang C, Zhang J H 2015 Radiat. Meas. 73 46 Google Scholar
[30]	Liu C Q, Wei Z, Han C, et al. 2019 Chin. Phys. C 43 064001 Google Scholar
[31]	Wei Z, Yao Z E, Lan C L, et al. 2015 J Radioanal. Nucl. Chem. 305 455 Google Scholar
[32]	Lan C L, Peng M, Zhang Y, Wei Z, Yao Z E, Xie B L 2017 Nucl. Sci. Technol. 28 8 Google Scholar
[33]	Duke D L, Tovesson F, Laptev A B, Mosby S 2016 Phys. Rev. C 94 054604 Google Scholar
[34]	Al-Adili A, Hambsch F J, Oberstedt S, Pomp S, Zeynalov S H 2010 Nucl. Instrum. Methods A 624 684 Google Scholar
[35]	Higgins D, Greife U, Tovesson F, Manning B, Mayorov D, Mosby S, Schmitt K 2020 Phys. Rev. C 101 014601 Google Scholar
[36]	Goverdovsky A A, Kuzminov B D, Mitrofanov V F, Sergachev A I 1997 Phys. At. Nucl. 60 1787
[37]	Trochon J, Yehia H A, Brisard F, Pranal Y 1979 Nuclear Physics A 318 63
[38]	Stanley L, Whetstone J 1958 Phys. Rev. 114 581
[39]	Albertsson M, Carlsson B G, Døssing T, Möller P, Randrup J, Åberg S 2021 Phys. Rev. C 103 014609 Google Scholar
[40]	Chen Y J, Liu T J 2011 Chin. Phys. C 35 344 Google Scholar
[41]	Göök A, Hambscha F J, Oberstedta S, Vidalia M 2015 Physics Procedia 64 190 Google Scholar
[42]	Schmidt K H, Jurado B 2010 Phys. Rev. Lett. 104 242501
[43]	Dyachenko N P, Kuzminov B D, Mitrofanov V F, Sergachev A I 1977 Yadern. Fiz. 26 691
[44]	Lam S T, Yu L L, Fielding H W, Dawson W K, Neilson G C 1983 Phys. Rev. C 28 1212 Google Scholar

Cited By

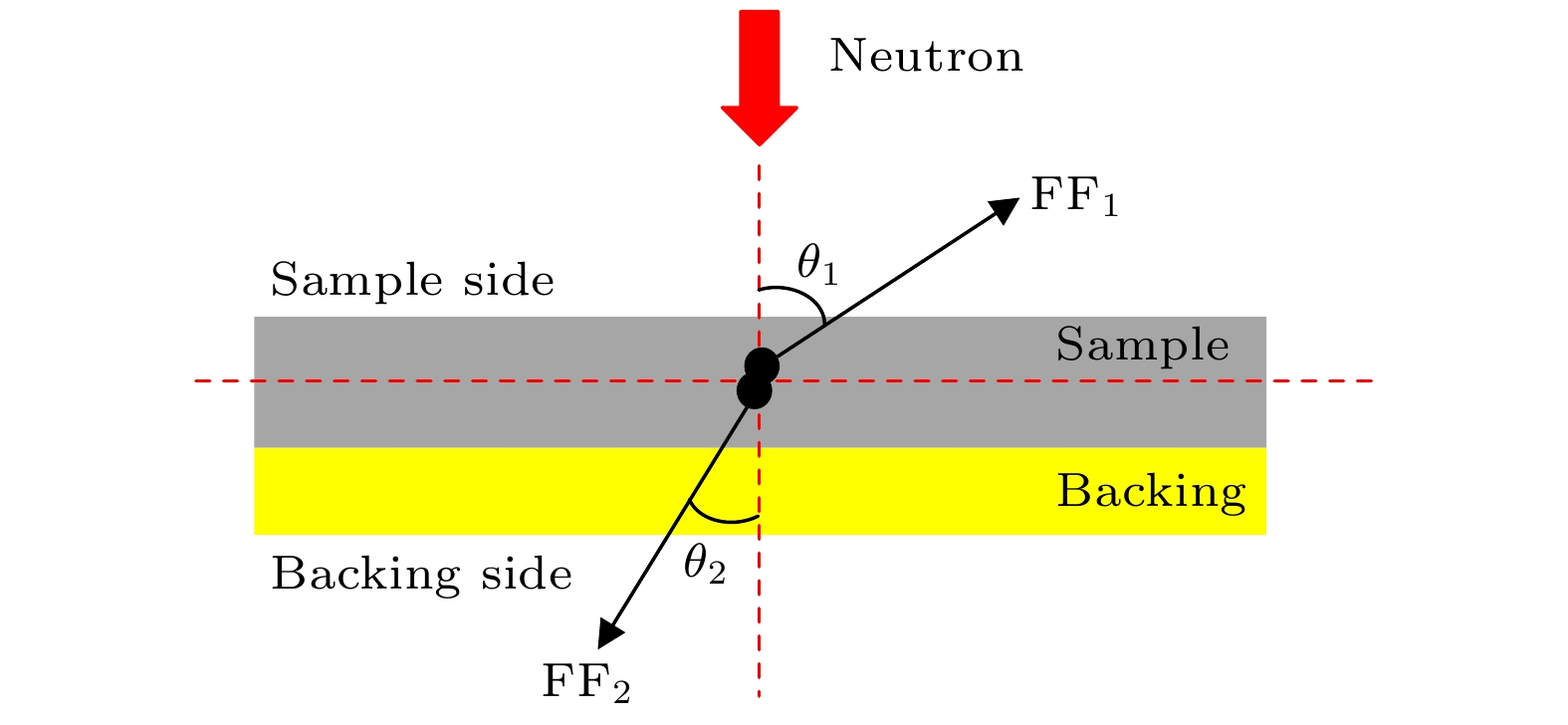
图 1 Geant4几何模型示意图. 灰色区域代表锕系核素样品(Sample), 黄色区域代表衬底(Backing). 面向入射中子一侧为样品侧(Sample side), 远离入射中子一侧为衬底侧(Backing side). FF₁和FF₂分别代表一对互补裂变碎片, 并且它们穿出靶的角度分别为θ₁和θ₂

Figure 1. Schematic illustration of the Geant4 geometric model. The gray layer is the fissile sample of the actinide target, while the yellow one is the backing support for the sample. The sample side faced the impinging neutrons. FF₁ and FF₂ respectively denote the fragments emitted from the different sides. θ₁ and θ₂ are the angles of the fragment axis relative to the axial direction of the incoming neutron.

DownLoad: Full-Size Img PowerPoint

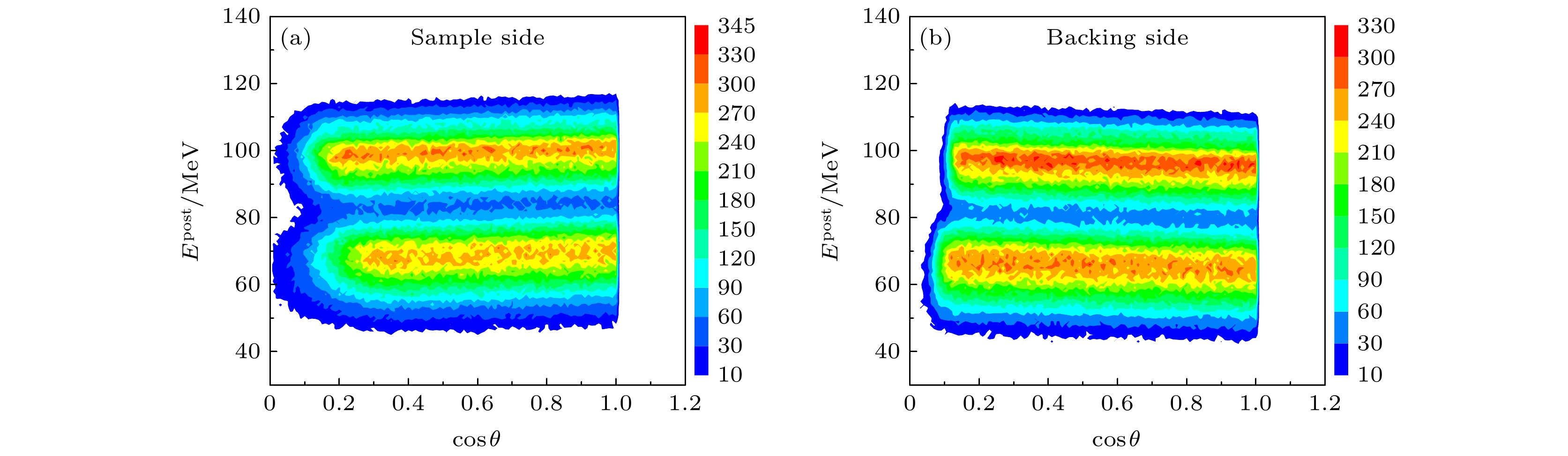
图 2 发射中子后裂变碎片初始动能$ {E^{{\text{post}}}} $与碎片出射方向相对中子入射方向夹角的余弦值$ \cos \theta $的关系　(a) 碎片从样品侧穿出时计算结果; (b) 碎片从衬底侧穿出时计算结果

Figure 2. $ \cos \theta $ versus post-neutron emission kinetic energy $ {E^{{\text{post}}}} $distribution: (a) The case of the fission fragments from sample side; (b) in the case of the fission fragments from backing side.

DownLoad: Full-Size Img PowerPoint

图 3 ²³²Th(n, f)反应发射中子后TKE分布　(a)中子能量为3 MeV; (b)中子能量为6 MeV; (c)中子能量为10 MeV. 黑线为实验数据^[13]; 红线为本文计算数据

Figure 3. Post-neutron emission TKE distribution for ²³²Th(n, f) reaction: (a) E_n = 3 MeV; (b) E_n = 6 MeV; (c) E_n = 10 MeV. The black line denotes experimental data^[13]. The red line denotes the calculated result from this work.

DownLoad: Full-Size Img PowerPoint

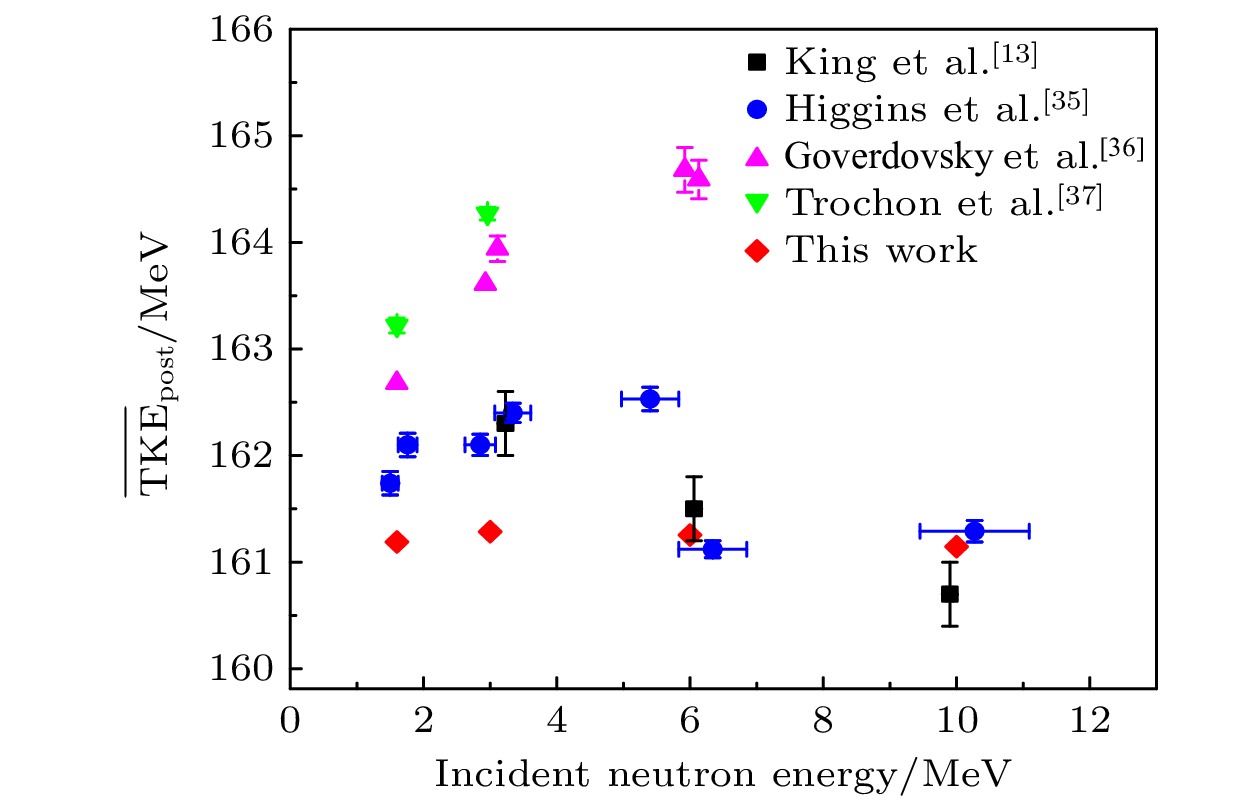
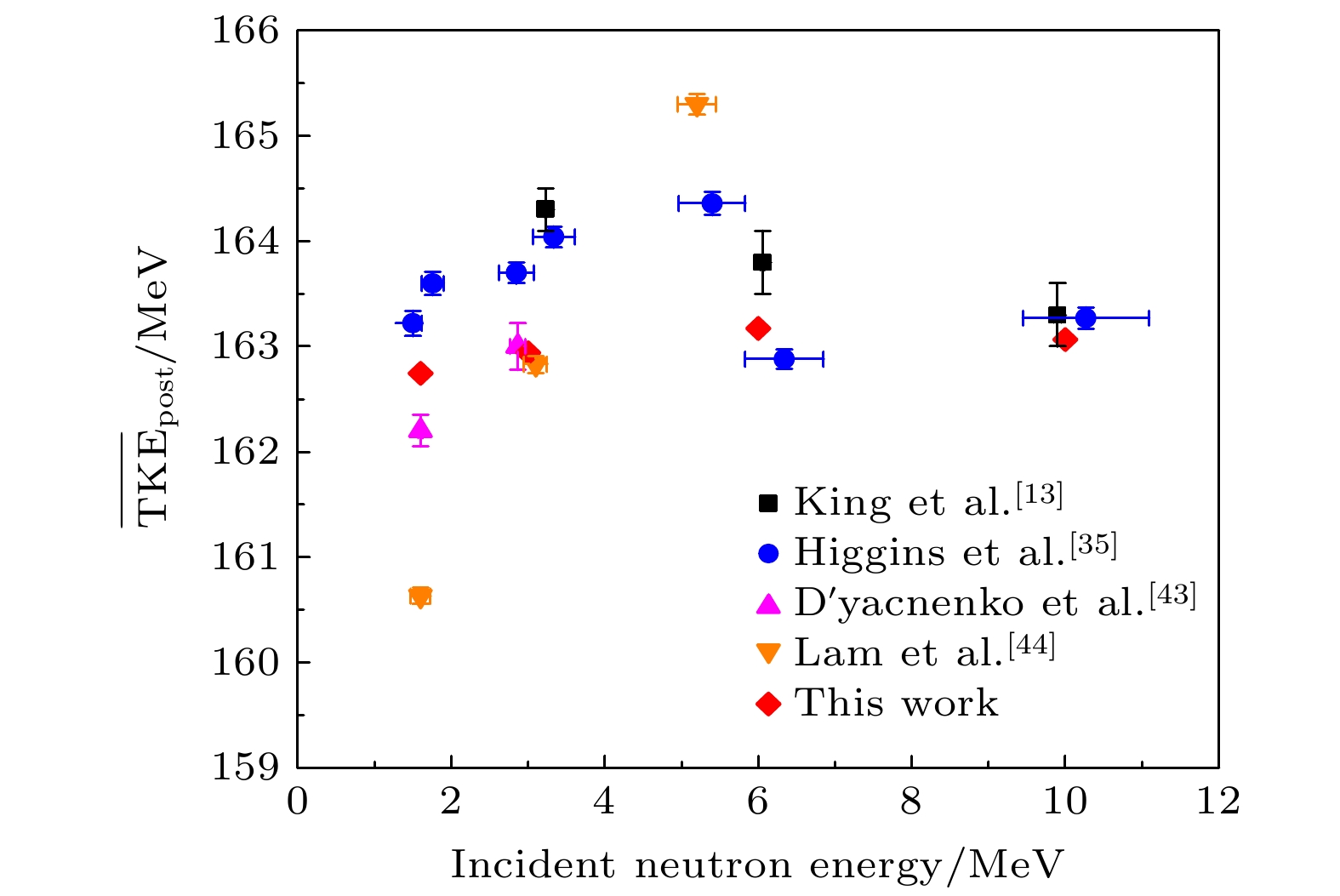
图 4 ²³²Th(n, f)反应发射中子后平均总动能$ {\overline {{\text{TKE}}} _{{\text{post}}}} $随入射中子能量的变化情况. 红点为本文计算数据, 其他颜色点为实验数据^[13,35-37]

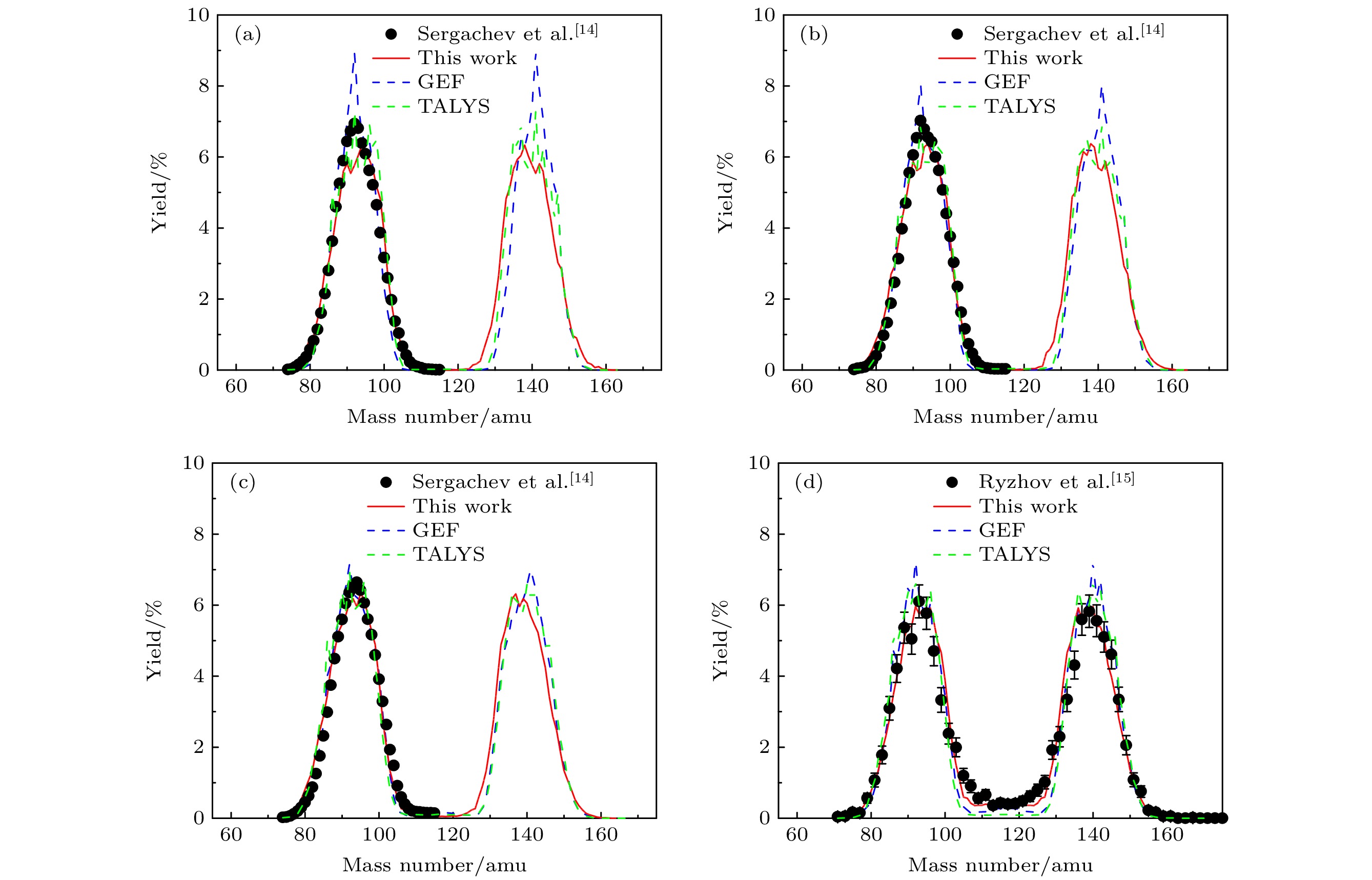
Figure 4. Relationship between the incident neutron energy and $ {\overline {{\text{TKE}}} _{{\text{post}}}} $ for ²³²Th(n, f) reaction. The red dots denote the calculated results from this work. The dots with other colors denote the experimental data^13,35-37].

DownLoad: Full-Size Img PowerPoint

图 5 不同入射中子能量下, ²³²Th(n, f)反应中子多重性$ \overline \nu (m) $的计算结果

Figure 5. Calculation of neutron multiplicity distribution $ \overline \nu (m) $ for ²³²Th(n, f) reaction with the different incident neutron energies.

DownLoad: Full-Size Img PowerPoint

图 6 发射中子前裂变碎片质量、总动能分布计算流程图

Figure 6. Program flow chart for the calculation of the pre-neutron fission fragment mass and TKE distribution.

DownLoad: Full-Size Img PowerPoint

图 7 ²³²Th(n, f)反应发射中子前裂变碎片质量分布　(a)中子能量为1.6 MeV; (b)中子能量为3 MeV; (c)中子能量为6 MeV; (d)中子能量为10 MeV. 黑色实心点代表实验结果^[14,15], 红线为本工作结果, 蓝线为GEF结果, 绿线为TALYS结果

Figure 7. Calculation of the pre-neutron mass distribution for ²³²Th(n, f) reaction: (a) E_n = 1.6 MeV; (b) E_n = 3 MeV; (c) E_n = 6 MeV; (d) E_n = 10 MeV. The black dots line is experimental data ^[14,15]. The red line is the calculated data from this work, while the blue one is from the GEF code and the green one is from the TALYS code.

DownLoad: Full-Size Img PowerPoint

图 8 ²³²Th(n, f)反应质量分布计算与实验结果偏差分析　(a)中子能量为1.6 MeV; (b)中子能量为3 MeV; (c)中子能量为6 MeV; (d)中子能量为10 MeV. 红线为本工作结果, 蓝线为GEF结果, 绿线为TALYS结果

Figure 8. Difference of the mass distribution between calculation and experimental data for ²³²Th(n, f) reaction: (a) E_n = 1.6 MeV; (b) E_n = 3 MeV; (c) E_n = 6 MeV; (d) E_n = 10 MeV. The red line is the calculated data from this work, while the blue one is from the GEF code and the green one is from the TALYS code.

DownLoad: Full-Size Img PowerPoint

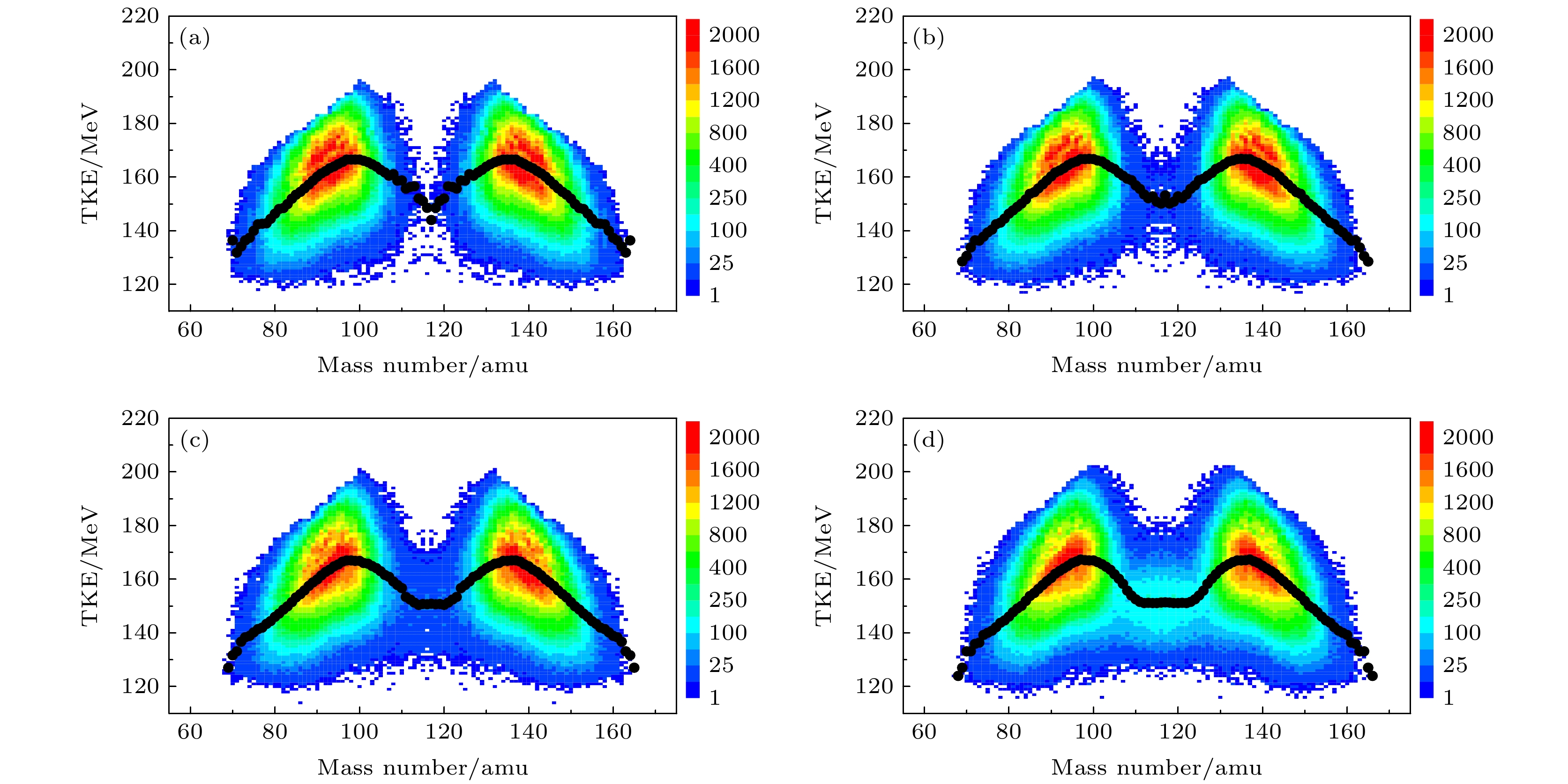
图 9 发射中子前裂变碎片质量-TKE的二维分布　(a)中子能量为1.6 MeV; (b)中子能量为3 MeV; (c)中子能量为6 MeV; (d)中子能量为10 MeV. 黑点表示碎片质量与平均总动能$ {\overline {{\text{TKE}}} _{{\text{pre}}}}({m^{{\text{pre}}}}) $关系. 图例中颜色标度反映了事件数目

Figure 9. Two-dimension distribution of pre-neutron mass versus TKE: (a) E_n = 1.6 MeV; (b) E_n = 3 MeV; (c) E_n = 6 MeV; (d) E_n = 10 MeV. The black dots denote $ {\overline {{\text{TKE}}} _{{\text{pre}}}}({m^{{\text{pre}}}}) $, the relationship between pre-neutron mass and average TKE. The color scale refers to the number of events.

DownLoad: Full-Size Img PowerPoint

图 10 ²³²Th(n, f)反应发射中子前平均总动能$ {\overline {{\text{TKE}}} _{{\text{pre}}}} $随入射中子能量变化情况. 红点为本文计算数据, 其他颜色点为实验数据^{[13,35,43,44]}

Figure 10. Relationship between the incident neutron energy and $ {\overline {{\text{TKE}}} _{{\text{pre}}}} $ for ²³²Th(n, f) reaction. The red dots denote the calculated results from this work. The dots with other colors denote the experimental data^13,35,43,44].

DownLoad: Full-Size Img PowerPoint

map

[1]	Talou P, Becker B, Kawano T, Chadwick M B, Danon Y 2011 Phys. Rev. C 83 1509
[2]	张竞上 2003 现代物理知识 01 24 Zhang J S 2003 Mod. Phys. 01 24
[3]	Forrest R A 2011 Energy Procedia 7 540 Google Scholar
[4]	Möller P, Sierk A J 2003 Nature 422 485
[5]	Al-Adili A, Hambsch F J, Pomp S, Oberstedt S, Vidali M 2016 Phys. Rev. C 93 34603 Google Scholar
[6]	Salvador-Castineira P, Brys T, Eykens R, Hambsch F-J, Göök A, Moens A, Oberstedt S, Sibbens G, Vanleeuw D, Vidali M 2015 Phys. Rev. C 92 014620 Google Scholar
[7]	Meierbachtol K, Tovesson F, Duke D L, Geppert-Kleinrath V, Manning B, Meharchand R, Mosby S, Shields D 2016 Phys. Rev. C 94 034611 Google Scholar
[8]	蔡翔舟, 戴志敏, 徐洪杰 2016 物理 45 578 Google Scholar Cai X Z, Dai Z M, Xu H J 2016 Physics 45 578 Google Scholar
[9]	Crasta R, Naik H, Suryanarayana S V, Shivashankar B S, Mulik V K, Prajapati P M, Sanjeev G, Sharma S C, Bhagwat P V, Mohanty A K, Ganesan S, Goswami A 2012 Ann. Nucl. Energy 47 160 Google Scholar
[10]	李光超 2017 博士学位论文 (上海: 中国科学院上海应用物理研究所) Li G C 2017 Ph. D. Dissertation (Shanghai: Shanghai Institute of Applied Physics, Chinese Academy of Sciences) (in Chinese)
[11]	Trochon J, Yehia H A, Brisard F, Pranal Y 1979 Nucl. Phys. A 318 63 Google Scholar
[12]	Naik H, Mukherji S, Suryanarayana S V, Jagadeesan K C, Thakare S V, Sharma S C 2016 Nucl. Phys. A 952 100 Google Scholar
[13]	King J, Yanez R, Loveland W, Barrett J S, Oscar B, Fotiades N, Tovesson F, Lee H Y 2017 Eur. Phys. J. A 53 238 Google Scholar
[14]	Sergachev A I, Vorob'Eva V G, Kuz'Minov B D, Mikhailov V B, Tarasko M Z 1968 Yadern. Fiz. 7 778
[15]	Ryzhov I V, Yavshits S G, Tutin G A, Kovalev N V, Saulski A V, Kudryashev N A 2011 Phys. Rev. C 83 054603 Google Scholar
[16]	葛智刚, 陈永静 2015 科学通报 60 3087 Google Scholar Ge Z G, Chen Y J 2015 Chin. Sci. bull. 60 3087 Google Scholar
[17]	Schmidt K H, Jurado B, Amouroux C 2016 Nucl. Data Sheets 131 107 Google Scholar
[18]	Koning A J, Hilaire S, Duijvestijn M C 2007 Proceedings of the International Conference on Nuclear Data for Science and Technology Nice, France, April 22–27, 2007 pp1–214
[19]	郝艺伟, 董国香, 王小保 2019 中国科学: 物理学力学天文学 49 122001 Hao Y W, Dong G X, Wang X B 2019 Scientia Sinica Physica, Mechanica & Astronomica 49 122001
[20]	Brosa U 1985 Phys. Rev. C 32 1438 Google Scholar
[21]	Brosa U, Grossmann S, Muller A, Becker E 1989 Nucl. Phys. A 502 423c Google Scholar
[22]	Hambsch F J, Vivès F, Siegler P, Oberstedt S 2000 Nucl. Phys. A 679 3 Google Scholar
[23]	Agostinelli S, Allison J, Amako K, et al. 2003 Nucl. Instrum. Methods A 506 250 Google Scholar
[24]	Mosby S, Tovesson F, Couture A, Duke D L, et al. 2014 Nucl. Instrum. Methods A 757 75 Google Scholar
[25]	Vivès F, Hambsch F J, Bax H, Oberstedt S 2000 Nucl. Phys. A 662 63 Google Scholar
[26]	Zeynalova O V, Zeynalov S, Hambsch F J, Oberstedt S, Fabry I 2010 Bull. Russ. Acad. Sci. Phys. 74 800 Google Scholar
[27]	Chadwick M B, Herman M, Obložinský P, et al. 2011 Nucl. Data Sheets 112 2887 Google Scholar
[28]	Liu C Q, Hu Z M, Hu Z J, et al. 2021 J. Instrum. 16 P07038 Google Scholar
[29]	Wang D, Zhang C, Zhang J H 2015 Radiat. Meas. 73 46 Google Scholar
[30]	Liu C Q, Wei Z, Han C, et al. 2019 Chin. Phys. C 43 064001 Google Scholar
[31]	Wei Z, Yao Z E, Lan C L, et al. 2015 J Radioanal. Nucl. Chem. 305 455 Google Scholar
[32]	Lan C L, Peng M, Zhang Y, Wei Z, Yao Z E, Xie B L 2017 Nucl. Sci. Technol. 28 8 Google Scholar
[33]	Duke D L, Tovesson F, Laptev A B, Mosby S 2016 Phys. Rev. C 94 054604 Google Scholar
[34]	Al-Adili A, Hambsch F J, Oberstedt S, Pomp S, Zeynalov S H 2010 Nucl. Instrum. Methods A 624 684 Google Scholar
[35]	Higgins D, Greife U, Tovesson F, Manning B, Mayorov D, Mosby S, Schmitt K 2020 Phys. Rev. C 101 014601 Google Scholar
[36]	Goverdovsky A A, Kuzminov B D, Mitrofanov V F, Sergachev A I 1997 Phys. At. Nucl. 60 1787
[37]	Trochon J, Yehia H A, Brisard F, Pranal Y 1979 Nuclear Physics A 318 63
[38]	Stanley L, Whetstone J 1958 Phys. Rev. 114 581
[39]	Albertsson M, Carlsson B G, Døssing T, Möller P, Randrup J, Åberg S 2021 Phys. Rev. C 103 014609 Google Scholar
[40]	Chen Y J, Liu T J 2011 Chin. Phys. C 35 344 Google Scholar
[41]	Göök A, Hambscha F J, Oberstedta S, Vidalia M 2015 Physics Procedia 64 190 Google Scholar
[42]	Schmidt K H, Jurado B 2010 Phys. Rev. Lett. 104 242501
[43]	Dyachenko N P, Kuzminov B D, Mitrofanov V F, Sergachev A I 1977 Yadern. Fiz. 26 691
[44]	Lam S T, Yu L L, Fielding H W, Dawson W K, Neilson G C 1983 Phys. Rev. C 28 1212 Google Scholar

[1]	Zhang Xian, Liu Shi-Chang, Wei Jun-Xia, Li Shu, Wang Xin, Shangguan Dan-Hua. Monte Carlo global variance reduction method combining source bias and weight window. Acta Physica Sinica, 2024, 73(4): 042801. doi: 10.7498/aps.73.20231493
[2]	Shangguan Dan-Hua, Yan Wei-Hua, Wei Jun-Xia, Gao Zhi-Ming, Chen Yi-Bing, Ji Zhi-Cheng. Efficient Monte Carlo algorithm of time-dependent particle transport problem in multi-physics coupling calculation. Acta Physica Sinica, 2022, 71(9): 090501. doi: 10.7498/aps.71.20211474
[3]	Deng Li, Li Rui, Wang Xin, Fu Yuan-Guang. Monte Carlo simulation technology based on characteristic γ-ray spectrum analysis. Acta Physica Sinica, 2020, 69(11): 112801. doi: 10.7498/aps.69.20200279
[4]	Shangguan Dan-Hua, Ji Zhi-Cheng, Deng Li, Li Rui, Li Gang, Fu Yuan-Guang. New strategy for global tallying in Monte Carlo criticality calculation. Acta Physica Sinica, 2019, 68(12): 122801. doi: 10.7498/aps.68.20182276
[5]	Chen Zhong, Zhao Zi-Jia, Lü Zhong-Liang, Li Jun-Han, Pan Dong-Mei. Numerical simulation of deuterium-tritium fusion reaction rate in laser plasma based on Monte Carlo-discrete ordinate method. Acta Physica Sinica, 2019, 68(21): 215201. doi: 10.7498/aps.68.20190440
[6]	Li Shu. Photon spectrum and angle distribution for photon scattering with relativistic Maxwellian electrons. Acta Physica Sinica, 2019, 68(1): 015201. doi: 10.7498/aps.68.20181796
[7]	Li Shu. Monte Carlo method for computing relativistic photon-Maxwellian electron scattering cross sections. Acta Physica Sinica, 2018, 67(21): 215201. doi: 10.7498/aps.67.20180932
[8]	ShangGuan Dan-Hua, Deng Li, Li Gang, Zhang Bao-Yin, Ma Yan, Fu Yuan-Guang, Li Rui, Hu Xiao-Li. Algorithm researches for efficient global tallying in criticality calculation of Monte Carlo method. Acta Physica Sinica, 2016, 65(6): 062801. doi: 10.7498/aps.65.062801
[9]	Shangguan Dan-Hua, Li Gang, Deng Li, Zhang Bao-Yin, Li Rui, Fu Yuan-Guan. Modified uniform-fission-site algorithm in Monte Carlo simulation of reactor criticality problem. Acta Physica Sinica, 2015, 64(5): 052801. doi: 10.7498/aps.64.052801
[10]	Lin Shu, Yan Yang-Jiao, Li Yong-Dong, Liu Chun-Liang. Monte-Carlo method of computing multipactor threshold in microwave devices. Acta Physica Sinica, 2014, 63(14): 147902. doi: 10.7498/aps.63.147902
[11]	Yang Liang, Wei Cheng-Yang, Lei Li-Ming, Li Zhen-Xi, Li Sai-Yi. Monte Carlo simulations of microstructure and texture evolution during annealing of a two-phase titanium alloy. Acta Physica Sinica, 2013, 62(18): 186103. doi: 10.7498/aps.62.186103
[12]	Li Peng, Xu Zhou, Li Ming, Yang Xing-Fan. A Monte Carlo simulation of secondary electron transport in diamond. Acta Physica Sinica, 2012, 61(7): 078503. doi: 10.7498/aps.61.078503
[13]	Wen De-Zhi, Zhuo Ren-Hong, Ding Da-Jie, Zheng Hui, Cheng Jing, Li Zheng-Hong. Generation of correlated pseudorandom variables in Monte Carlo simulation. Acta Physica Sinica, 2012, 61(22): 220204. doi: 10.7498/aps.61.220204
[14]	Zhao Xue-Feng, Li San-Wei, Jiang Gang, Wang Chuan-Ke, Li Zhi-Chao, Hu Feng, Li Chao-Guang. Monte Carlo simulation of hard X-ray producedby suprathermal electrons interactionwith golden hohlraum targets. Acta Physica Sinica, 2011, 60(7): 075203. doi: 10.7498/aps.60.075203
[15]	Zhang Bao-Wu, Zhang Ping-Ping, Ma Yan, Li Tong-Bao. Simulations of one-dimensional transverse laser cooling of Cr atomic beam with Monte Carlo method. Acta Physica Sinica, 2011, 60(11): 113701. doi: 10.7498/aps.60.113701
[16]	Dai Qiu-Sheng, Qi Yu-Jin. Spatial resolution of pinhole single photon emission computed tomography imaging. Acta Physica Sinica, 2010, 59(2): 1357-1365. doi: 10.7498/aps.59.1357
[17]	Jin Xiao-Lin, Huang Tao, Liao Ping, Yang Zhong-Hai. The particle-in-cell simulation and Monte Carlo collision simulation of the interaction between electrons and microwave in electron cyclotron resonance discharge. Acta Physica Sinica, 2009, 58(8): 5526-5531. doi: 10.7498/aps.58.5526
[18]	. Monte Carlo simulation of Kα source produced by ultrashort and ultrahigh laser interaction with Cu target. Acta Physica Sinica, 2007, 56(12): 7127-7131. doi: 10.7498/aps.56.7127
[19]	Sun Xian-Ming, Han Yi-Ping, Shi Xiao-Wei. Monte Carlo simulation of backscattering by a melting layer of precipitation. Acta Physica Sinica, 2007, 56(4): 2098-2105. doi: 10.7498/aps.56.2098
[20]	Hao Fan-Hua, Hu Guang-Chun, Liu Su-Ping, Gong Jian, Xiang Yong-Chun, Huang Rui-Liang, Shi Xue-Ming, Wu Jun. Monte-Carlo method in calculating the γ spectrum of plutonium volume source. Acta Physica Sinica, 2005, 54(8): 3523-3529. doi: 10.7498/aps.54.3523

Catalog

Vol. 71, Issue 1 - 2022-01-05

Metrics

Abstract views: 6297
PDF Downloads: 126
Cited By: 0

姓名
邮箱
手机号码
标题
留言内容
验证码

Search

Article

留言板

Monte-Carlo study of pre-neutron emission mass and energy for neutron-induced ²³²Th fission

Abstract

Authors and contacts

Corresponding author: Wei Zheng, weizheng@lzu.edu.cn

FullText HTML : translate this paragraph

References

Cited By

Catalog

Metrics

Authors

Referees

About Journal

About

Search

Article

留言板

Monte-Carlo study of pre-neutron emission mass and energy for neutron-induced 232Th fission

Abstract

Authors and contacts

Corresponding author: Wei Zheng, weizheng@lzu.edu.cn

FullText HTML : translate this paragraph

References

Cited By

Catalog

Metrics

Publishing process

Authors

Referees

About Journal

About

Monte-Carlo study of pre-neutron emission mass and energy for neutron-induced ²³²Th fission