-
For many real world systems ranging from biology to engineering, efficient network computation methods have attracted much attention in many applications. Generally, the performance of a network computation can be improved in two ways, i.e., rewiring and weighting. As a matter of fact, many real-world networks where an interpretation of efficient computation is relevant are weighted and directed. Thus, one can argue that nature might have assigned the optimal structure and weights to adjust the level of functionality. Indeed, in many neural and biochemical networks there is evidence that the synchronized and coordinated behavior may play important roles in the system’s functionality. The importance of the network weighting is not limited to the nature. In computer networks, for example, designing appropriate weights and directions for the connection links may enhance the ability of the network to synchronize the processes, thus leading the performance of computation to improve. In this paper, we propose a new two-mode weighting strategy by employing the network topological centralities including the degree, betweenness, closeness and communication neighbor graph. The weighting strategy consists of two modes, i.e., the original mode, in which the synchronizability is enhanced by increasing the weight of bridge edges, and the inverse version, in which the performance of community detection is improved by reducing the weight of bridge edges. We control the weight strategy by simply tuning a single parameter, which can be easily performed in the real world systems. We test the effectiveness of our model in a number of artificial benchmark networks as well as real-world networks. To the best of our knowledge, the proposed weighting strategy outperforms previously published weighting methods of improving the performance of network computation.
-
Keywords:
- complex networks /
- weighting strategy /
- communication neighbor graph /
- community structure
[1] Watts D J, Strogatz S H 1998 Nature 393 440
Google Scholar
[2] Barabasi A L, Albert R 1999 Science 286 509
Google Scholar
[3] Han Y, Zhu L, Cheng Z, Li J, Liu X 2020 IEEE Trans. Cybern. 50 1697
Google Scholar
[4] 杨博, 刘大有, 刘继明, 金弟, 马海宾 2009 软件学报 20 54
Google Scholar
Yang B, Liu D Y, Liu J M, Jin D, Ma H B 2009 J. Software 20 54
Google Scholar
[5] Ding S, Yue Z, Yang S, Niu F, Zhang Y 2020 IEEE Trans. Ind. Inf. 32 2101
Google Scholar
[6] Liang W, Li K, Long J, Kui X, Zomaya A Y 2020 IEEE Trans. Ind. Inf. 16 2063
Google Scholar
[7] Lu M, Zhang Z, Qu Z, Kang Y 2019 IEEE Trans. Knowl. Data Eng. 31 1736
Google Scholar
[8] Ma X, Dong D, Wang Q 2019 IEEE Trans. Knowl. Data Eng. 31 273
Google Scholar
[9] Newman M E J, Girvan M 2004 Phys. Rev. E 69 026113
Google Scholar
[10] Clauset A, Newman M E J 2004 Phys. Rev. E 70 066111
Google Scholar
[11] Du W B, Zhou X L, Lordan O, Wang Z, Zhao C, Zhu Y B 2016 Transp. Res. Pt. E-Logist. Transp. Rev. 89 108
Google Scholar
[12] Zeng X, Wang W, Chen C, Yen G G 2020 IEEE Trans. Cybern. 50 2502
Google Scholar
[13] Palla G, Derenyi I, Farkas I, Vicsek T 2005 Nature 435 814
Google Scholar
[14] Li J, Wang X, Cui Y 2014 Physica A 415 398
Google Scholar
[15] 李慧嘉, 李慧颖, 李爱华 2015 计算机学报 38 301
Google Scholar
Li H J, Li H Y, Li A H 2015 Chin. J. Comput. 38 301
Google Scholar
[16] Hofman J M, Wiggins C H 2008 Phys. Rev. Lett. 100 258701
Google Scholar
[17] Boccaletti S, Ivanchenko M, LatoraV, Pluchino A 2007 Phys. Rev. E 75 045102
Google Scholar
[18] Xu Y, Wu X, Li N, Liu L, Xie C, Li C 2019 IEEE Trans. Circuits Syst. Express Brief 67 700
Google Scholar
[19] Han M, Zhang M, Qiu T, Xu M 2019 IEEE Trans. Neural Networks Learn. Syst. 30 255
Google Scholar
[20] Hong H, Kim B J, Choi M Y, Park H 2004 Phys. Rev. E 69 067105
Google Scholar
[21] Chavez M, Hwang D U, Amann A, Hentschel H E, Boccaletti S 2005 Phys. Rev. Lett. 94 218701
Google Scholar
[22] Wang X, Lai Y C, Lai C H 2007 Phys. Rev. E 75 056205
Google Scholar
[23] Jalili M, Rad A A, Hasler M 2008 Phys. Rev. E 78 016105
Google Scholar
[24] Rad A A, Jalili M, Hasler M 2008 Chaos 18 037104
Google Scholar
[25] Lu X, Kuzmin K, Chen M, Szymanski B K 2018 Inf. Sci. 424 55
Google Scholar
[26] Zhang Y, Wang M, Gottwalt F, Saberi M, Chang E 2019 J. Informetr. 13 616
Google Scholar
[27] De Meo P, Ferrara E, Fiumara G, Provetti A 2013 J. Informetr. 222 648
Google Scholar
[28] Yang R, Wang W X, Lai Y C, Chen G 2009 Phys. Rev. E 79 026112
Google Scholar
[29] Li H J, Daniels J J 2015 Phys. Rev. E 91 012801
Google Scholar
[30] Meyniel F, Dehaene S 2017 PNAS 114 3859
Google Scholar
[31] Khadivi A, Ajdari R A, Hasler M 2011 Phys. Rev. E 83 046104
Google Scholar
[32] Fortunato S, Barthelemy M 2007 PNAS 104 36
Google Scholar
[33] Good B H, de Montjoye Y A, Clauset A 2010 Phys. Rev. E 81 046106
Google Scholar
[34] Newman M E J 2002 Comput. Phys. Commun. 147 40
Google Scholar
[35] Boccaletti S, Latora V, Moreno Y, Chavez M, Hwang D U 2006 Phys. Rep. 424 175
Google Scholar
[36] LuL Y, Chen D B, Ren X L, Zhang Q M, Zhang Y C, Zhou T 2016 Phys. Rep. 650 1
Google Scholar
[37] Carmi S, Havlin S, Kirkpatrick S, Shavitt Y, Shir E 2007 PNAS 104 11150
Google Scholar
[38] Kitsak M, Gallos L K, Havlin S, Liljeros F, Muchnik L, Stanley H E, Makse H A 2010 Nat. Phys. 6 888
Google Scholar
[39] Motter A E, Zhou C, Kurths J 2005 Phys. Rev. E 71 016116
Google Scholar
[40] Motter A E, Zhou C, Kurths J 2005 EPL 69 334
Google Scholar
[41] Nishikawa T, Motter A E 2006 Phys. Rev. E 73 065106
Google Scholar
[42] Gerschgorin S 1931 Izv. Akad. Nauk USSR Otd. Fiz.-Mat. Nauk 7 749
[43] Radicchi F, Castellano C, Cecconi F, Loreto V, Parisi D 2004 PNAS 101 2658
Google Scholar
[44] 李慧嘉, 严冠, 刘志东, 李桂君, 章祥荪 2017 中国科学: 数学 4 7241
Google Scholar
Li H J, Yan G, Liu Z D, Li G J, Zhang X S 2017 Sci. Sin. Math 4 7241
Google Scholar
[45] Li H J, Wang Y, Wu L Y, Zhang J, Zhang X S 2012 Phys. Rev. E 86 016109
Google Scholar
[46] Li H J, Zhang X S 2013 EPL 103 58002
Google Scholar
[47] Lancichinetti A, Fortunato S, Radicchi F 2008 Phys. Rev. E 78 046110
Google Scholar
[48] Guimera R, Nunes Amaral L A 2005 Nature 433 895
Google Scholar
[49] Duch J, Arenas A 2005 Phys. Rev. E 72 027104
Google Scholar
[50] Zachary W W 1977 J. Anthropol. Res. 33 452
Google Scholar
[51] Knuth D E 1994 The Stanford Graph Base: A Platform for Combinatorial Computing (New York: ACM Press) p592
[52] Lusseau D, Schneider K, Boisseau O J, Haase P, Slooten E, Dawson S M 2003 Behav. Ecol. Sociobiol. 54 396
Google Scholar
[53] Guimera R, Danon L, Diaz-Guilera A, Giralt F, Arenas A 2003 Phys. Rev. E 68 065103
Google Scholar
[54] Gleiser P, Danon L 2003 Adv. Complex Syst. 6 565
Google Scholar
[55] Boguna M, Pastor-Satorras R, Diaz-Guilera A, Arenas A 2004 Phys. Rev. E 70 056122
Google Scholar
[56] Agarwal G, Kempe D 2008 Eur. Phys. J. B 66 409
Google Scholar
[57] Xing N, Zong Q, Dou L, Tian B, Wang Q 2019 IEEE Trans. Veh. Technol. 68 9963
Google Scholar
[58] Yang H, Yao Q, Yu A, Lee Y, Zhang J 2019 IEEE Trans. Commun. 67 3457
Google Scholar
-
图 1 (a)节点4和节点5之间边对应的通讯邻域图; (b)网络中的桥边
Figure 1. (a) Communication neighborhood graph corresponding to the edge between node 4 and node 5; (b) bridge side in the network.
图 2 参数α取不同值时BA模型中节点强度s和节点度k之间的关系(N = 5000) (a)
$ \alpha =2 $ ; (b)$ \alpha =6 $ Figure 2. Relationship between node strength s and node degree k in BA model (N = 5000) with different values of parameter α: (a)
$ \alpha =2 $ ; (b)$ \alpha =6 $ .
图 3 应用加权机制后网络的动态演化示例图
Figure 3. Example of dynamic evolution of network after applying weighting mechanism.
图 4 (a) 无标度网络中
$ {\lambda }_{N}/{\lambda }_{2} $ 与($ \alpha $ ,$ \left\langle k \right\rangle $ )的对应关系(N = 500,$ \beta =0 $ ); (b)无标度网络中$ {\lambda }_{N}/{\lambda }_{2} $ 与($ \alpha $ ,$ \beta $ )的对应关系(N = 500,$ \left\langle k \right\rangle =4 $ )Figure 4. (a) Corresponding relationship (N = 500,
$ \beta =0 $ ) in scale-free networks between$ {\lambda }_{N}/{\lambda }_{2} $ and ($ \alpha $ ,$ \left\langle k \right\rangle $ ); (b) Corresponding relationship (N = 500,$ \left\langle k \right\rangle =4 $ ) in scale-free networks between$ {\lambda }_{N}/{\lambda }_{2} $ and ($ \alpha $ ,$ \beta $ ).
图 5 (a) Watts-Strogatz网络中
$ {\lambda }_{N}/{\lambda }_{2} $ 与($ \alpha $ ,$ \left\langle k \right\rangle $ )的对应关系(N = 500, P = 0.1); (b) Watts-Strogatz网络中$ {\lambda }_{N}/{\lambda }_{2} $ 与($ \alpha $ , P)的对应关系(N = 500,$ \left\langle k \right\rangle =4 $ )Figure 5. (a) Corresponding relationship (N = 500, P = 0.1) in Watts-Strogatz networks between
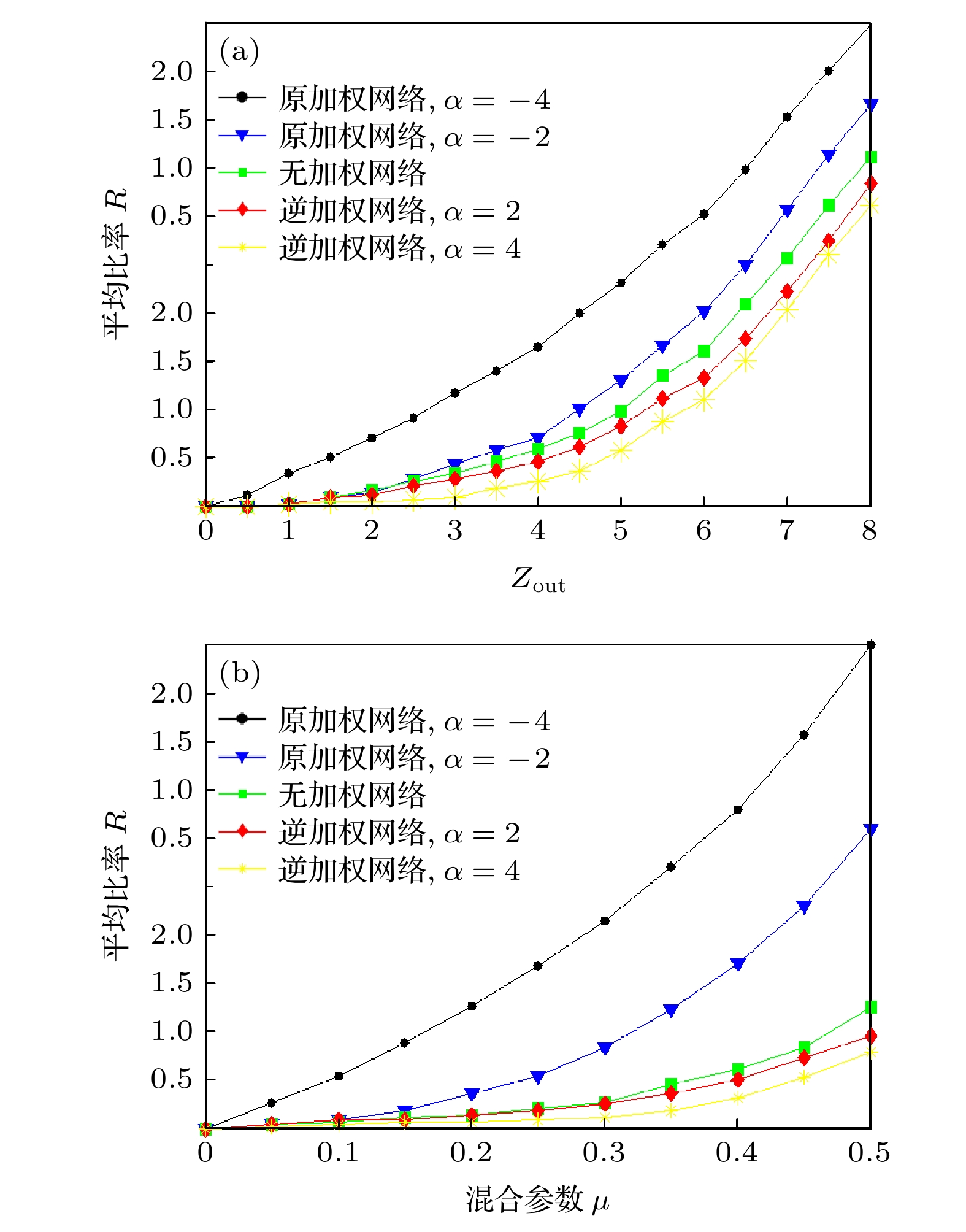
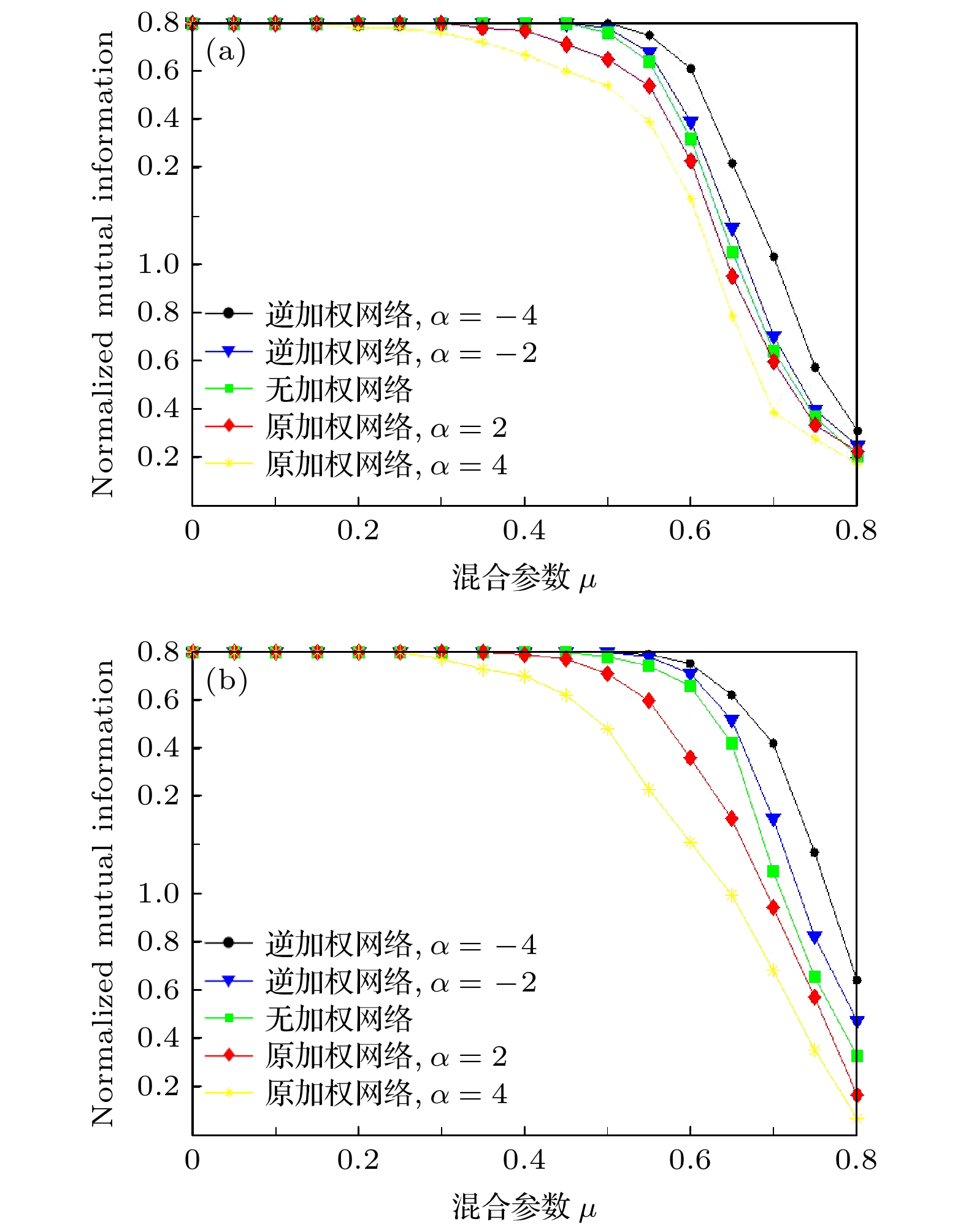
$ {\lambda }_{N}/{\lambda }_{2} $ and ($ \alpha $ ,$ \left\langle k \right\rangle $ ); (b) corresponding relationship (N = 500,$ \left\langle k \right\rangle =4 $ ) in Watts-Strogatz networks between$ {\lambda }_{N}/{\lambda }_{2} $ and ($ \alpha $ , P).
图 6 (a) GN基准网络中使用加权机制(逆加权机制)前后平均比率R的对比; (b) LFR基准网络中使用加权机制(逆加权机制)前后平均比率R的对比
Figure 6. (a) Comparison of average ratio R before and after using weighting mechanism (inverse weighting mechanism) in GN benchmark network; (b) comparison of average ratio R before and after using weighting mechanism (inverse weighting mechanism) in LFR benchmark network.
图 7 在LFR网络中运用加权机制(逆加权机制), 当取不同的
$ \alpha $ 值时, 利用(a) SA算法和(b) DA算法后NMI的计算值Figure 7. Weighted mechanism (inverse weighted mechanism) is used in LFR network. When the
$ \alpha $ value is different, the NMI value is calculated by using (a) SA algorithm and (b) DA algorithm.
图 8 在LFR网络中运用加权机制(逆加权机制), 当
$ \alpha =4 $ ($ \alpha =-4 $ )并考虑聚类规模时, 利用(a) SA算法和(b) DA算法后NMI的计算值Figure 8. The weighted mechanism (inverse weighted mechanism) is used in LFR network. When α = 4 (α = –4) and considering the cluster size, the NMI calculated by (a) SA algorithm and (b) DA algorithm.
表 1 在现实世界网络中使用8种不同加权策略的实验结果对比, 其中RW代表随机游走方法, SA代表模拟退火方法, VB代表变分贝叶斯方法, PL代表概率推断方法
Table 1. Comparison of experimental results using eight different weighting strategies in real world networks, in which RW represents random walk method, SA stands for simulated annealing method, VB stands for variational Bayesian method, PL stands for probability inference method.
现实世界网络 N $ \left\langle k \right\rangle $ $ {\lambda }_{N}/{\lambda }_{2} $ Chavez Wang Jalili Khadivi RW SA VB PL This work 蛋白质结构网络2 53 4.64 20.92 20.54 6.06 5.83 5.61 4.87 4.43 4.59 4.27 海豚网络 62 5.12 16.89 43.01 6.83 6.22 6.04 5.33 5.07 5.30 4.95 蛋白质结构网络1 95 4.48 63.1 262.2 23.5 19.82 15.71 13.65 10.59 11.88 8.45 蛋白质结构网络3 99 4.37 43.75 299.85 13.07 10.84 10.27 9.87 9.14 9.00 8.02 中国航空网络 203 18.48 13.25 5.79 3.29 2.88 2.23 2.08 1.83 1.76 1.55 电子邮件通讯 1133 9.62 8.63 5.81 5.40 4.04 3.86 3.91 3.84 3.54 3.77 酵母蛋白质交互作用 1458 2.67 52.44 269.07 25.60 17.63 15.61 13.21 10.76 12.66 9.52 蛋白质交互作用 2840 2.92 34.87 41.60 16.50 13.85 11.48 10.47 8.94 9.87 5.50 中国电力网络 865 5.20 49.77 133.8 25.43 20.90 23.44 15.19 12.04 10.56 5.04 科学家合作网络 4380 3.25 68.31 273.14 38.69 25.87 20.02 17.36 10.42 11.77 7.21 因特网AS2 7690 4.00 12.90 3.26 2.94 2.15 2.04 2.10 1.91 1.59 1.88 因特网AS5 8063 4.10 12.88 3.41 3.37 2.56 2.27 2.09 1.97 2.20 1.83 
DownLoad: CSV
表 2 在不同现实网络使用加权策略得到的实验结果, 其中“/”左右表示加权后和加权前的模块度Q值
Table 2. Experimental results are obtained by using weighting strategy in different real networks, where /’s left or right represents the modularity Q value after or before weighting.
网络 文献 最优Q SA[48] DA[49] CNM[10] 中国航空网络 [11] — 0.644/0.525 0.589/0.428 0.577/0.483 空手道俱乐部 [50] 0.420 0.416/0.342 0.411/0.351 0.413/0.376 《悲惨世界》 [51] 0.561 0.554/0.389 0.539/0.406 0.531/0.395 海豚社会网络 [52] 0.531 0.527/0.375 0.521/0.362 0.517/0.356 电子邮件 [53] 0.579 0.568/0.462 0.543/0.436 0.538/0.444 爵士乐 [54] 0.446 0.439/0.333 0.437/0.341 0.431/0.328 PGP密钥签名 [55] 0.878 0.883/0.674 0.843/0.705 0.872/0.754
DownLoad: CSV
表 3 在现实世界网络中使用不同加权策略的实验结果对比, 这里网络聚类算法利用CNM算法, 其中RW代表随机游走方法, SA代表模拟退火方法, VB代表变分贝叶斯方法, PL代表概率推断方法
Table 3. Comparison of experimental results using different weighting strategies in the real world network. CNM algorithm is used as the network clustering algorithm, in which RW represents the random walk method, SA represents the simulated annealing method, VB represents the variable dB method, and PL represents the probability inference method.
网络 Chavez Wang Jalili Khadivi RW SA VB PL This work 空手道俱乐部 0.316 0.322 0.351 0.362 0.374 0.381 0.390 0.386 0.413 中国航空网络 0.449 0.478 0.423 0.432 0.506 0.543 0.564 0.578 0.603 《悲惨世界》 0.357 0.369 0.399 0.411 0.439 0.457 0.488 0.433 0.531 爵士乐 0.338 0.347 0.353 0.361 0.383 0.399 0.42 0.387 0.431 PGP密钥签名 0.583 0.678 0.676 0.715 0.744 0.786 0.839 0.820 0.872 海豚社会网络 0.357 0.381 0.371 0.374 0.406 0.444 0.483 0.500 0.517 电子邮件 0.368 0.409 0.431 0.443 0.471 0.499 0.503 0.495 0.538
DownLoad: CSV
-
[1] Watts D J, Strogatz S H 1998 Nature 393 440
Google Scholar
[2] Barabasi A L, Albert R 1999 Science 286 509
Google Scholar
[3] Han Y, Zhu L, Cheng Z, Li J, Liu X 2020 IEEE Trans. Cybern. 50 1697
Google Scholar
[4] 杨博, 刘大有, 刘继明, 金弟, 马海宾 2009 软件学报 20 54
Google Scholar
Yang B, Liu D Y, Liu J M, Jin D, Ma H B 2009 J. Software 20 54
Google Scholar
[5] Ding S, Yue Z, Yang S, Niu F, Zhang Y 2020 IEEE Trans. Ind. Inf. 32 2101
Google Scholar
[6] Liang W, Li K, Long J, Kui X, Zomaya A Y 2020 IEEE Trans. Ind. Inf. 16 2063
Google Scholar
[7] Lu M, Zhang Z, Qu Z, Kang Y 2019 IEEE Trans. Knowl. Data Eng. 31 1736
Google Scholar
[8] Ma X, Dong D, Wang Q 2019 IEEE Trans. Knowl. Data Eng. 31 273
Google Scholar
[9] Newman M E J, Girvan M 2004 Phys. Rev. E 69 026113
Google Scholar
[10] Clauset A, Newman M E J 2004 Phys. Rev. E 70 066111
Google Scholar
[11] Du W B, Zhou X L, Lordan O, Wang Z, Zhao C, Zhu Y B 2016 Transp. Res. Pt. E-Logist. Transp. Rev. 89 108
Google Scholar
[12] Zeng X, Wang W, Chen C, Yen G G 2020 IEEE Trans. Cybern. 50 2502
Google Scholar
[13] Palla G, Derenyi I, Farkas I, Vicsek T 2005 Nature 435 814
Google Scholar
[14] Li J, Wang X, Cui Y 2014 Physica A 415 398
Google Scholar
[15] 李慧嘉, 李慧颖, 李爱华 2015 计算机学报 38 301
Google Scholar
Li H J, Li H Y, Li A H 2015 Chin. J. Comput. 38 301
Google Scholar
[16] Hofman J M, Wiggins C H 2008 Phys. Rev. Lett. 100 258701
Google Scholar
[17] Boccaletti S, Ivanchenko M, LatoraV, Pluchino A 2007 Phys. Rev. E 75 045102
Google Scholar
[18] Xu Y, Wu X, Li N, Liu L, Xie C, Li C 2019 IEEE Trans. Circuits Syst. Express Brief 67 700
Google Scholar
[19] Han M, Zhang M, Qiu T, Xu M 2019 IEEE Trans. Neural Networks Learn. Syst. 30 255
Google Scholar
[20] Hong H, Kim B J, Choi M Y, Park H 2004 Phys. Rev. E 69 067105
Google Scholar
[21] Chavez M, Hwang D U, Amann A, Hentschel H E, Boccaletti S 2005 Phys. Rev. Lett. 94 218701
Google Scholar
[22] Wang X, Lai Y C, Lai C H 2007 Phys. Rev. E 75 056205
Google Scholar
[23] Jalili M, Rad A A, Hasler M 2008 Phys. Rev. E 78 016105
Google Scholar
[24] Rad A A, Jalili M, Hasler M 2008 Chaos 18 037104
Google Scholar
[25] Lu X, Kuzmin K, Chen M, Szymanski B K 2018 Inf. Sci. 424 55
Google Scholar
[26] Zhang Y, Wang M, Gottwalt F, Saberi M, Chang E 2019 J. Informetr. 13 616
Google Scholar
[27] De Meo P, Ferrara E, Fiumara G, Provetti A 2013 J. Informetr. 222 648
Google Scholar
[28] Yang R, Wang W X, Lai Y C, Chen G 2009 Phys. Rev. E 79 026112
Google Scholar
[29] Li H J, Daniels J J 2015 Phys. Rev. E 91 012801
Google Scholar
[30] Meyniel F, Dehaene S 2017 PNAS 114 3859
Google Scholar
[31] Khadivi A, Ajdari R A, Hasler M 2011 Phys. Rev. E 83 046104
Google Scholar
[32] Fortunato S, Barthelemy M 2007 PNAS 104 36
Google Scholar
[33] Good B H, de Montjoye Y A, Clauset A 2010 Phys. Rev. E 81 046106
Google Scholar
[34] Newman M E J 2002 Comput. Phys. Commun. 147 40
Google Scholar
[35] Boccaletti S, Latora V, Moreno Y, Chavez M, Hwang D U 2006 Phys. Rep. 424 175
Google Scholar
[36] LuL Y, Chen D B, Ren X L, Zhang Q M, Zhang Y C, Zhou T 2016 Phys. Rep. 650 1
Google Scholar
[37] Carmi S, Havlin S, Kirkpatrick S, Shavitt Y, Shir E 2007 PNAS 104 11150
Google Scholar
[38] Kitsak M, Gallos L K, Havlin S, Liljeros F, Muchnik L, Stanley H E, Makse H A 2010 Nat. Phys. 6 888
Google Scholar
[39] Motter A E, Zhou C, Kurths J 2005 Phys. Rev. E 71 016116
Google Scholar
[40] Motter A E, Zhou C, Kurths J 2005 EPL 69 334
Google Scholar
[41] Nishikawa T, Motter A E 2006 Phys. Rev. E 73 065106
Google Scholar
[42] Gerschgorin S 1931 Izv. Akad. Nauk USSR Otd. Fiz.-Mat. Nauk 7 749
[43] Radicchi F, Castellano C, Cecconi F, Loreto V, Parisi D 2004 PNAS 101 2658
Google Scholar
[44] 李慧嘉, 严冠, 刘志东, 李桂君, 章祥荪 2017 中国科学: 数学 4 7241
Google Scholar
Li H J, Yan G, Liu Z D, Li G J, Zhang X S 2017 Sci. Sin. Math 4 7241
Google Scholar
[45] Li H J, Wang Y, Wu L Y, Zhang J, Zhang X S 2012 Phys. Rev. E 86 016109
Google Scholar
[46] Li H J, Zhang X S 2013 EPL 103 58002
Google Scholar
[47] Lancichinetti A, Fortunato S, Radicchi F 2008 Phys. Rev. E 78 046110
Google Scholar
[48] Guimera R, Nunes Amaral L A 2005 Nature 433 895
Google Scholar
[49] Duch J, Arenas A 2005 Phys. Rev. E 72 027104
Google Scholar
[50] Zachary W W 1977 J. Anthropol. Res. 33 452
Google Scholar
[51] Knuth D E 1994 The Stanford Graph Base: A Platform for Combinatorial Computing (New York: ACM Press) p592
[52] Lusseau D, Schneider K, Boisseau O J, Haase P, Slooten E, Dawson S M 2003 Behav. Ecol. Sociobiol. 54 396
Google Scholar
[53] Guimera R, Danon L, Diaz-Guilera A, Giralt F, Arenas A 2003 Phys. Rev. E 68 065103
Google Scholar
[54] Gleiser P, Danon L 2003 Adv. Complex Syst. 6 565
Google Scholar
[55] Boguna M, Pastor-Satorras R, Diaz-Guilera A, Arenas A 2004 Phys. Rev. E 70 056122
Google Scholar
[56] Agarwal G, Kempe D 2008 Eur. Phys. J. B 66 409
Google Scholar
[57] Xing N, Zong Q, Dou L, Tian B, Wang Q 2019 IEEE Trans. Veh. Technol. 68 9963
Google Scholar
[58] Yang H, Yao Q, Yu A, Lee Y, Zhang J 2019 IEEE Trans. Commun. 67 3457
Google Scholar
DownLoad:
Catalog
Metrics
- Abstract views: 4326
- PDF Downloads: 55
- Cited By: 0
