Numerical simulation of modal evolution and flow field structure of vibrating droplets on hydrophobic surface

Ye Xin; Shan Yan-Guang

doi:10.7498/aps.70.20210161

Abstract

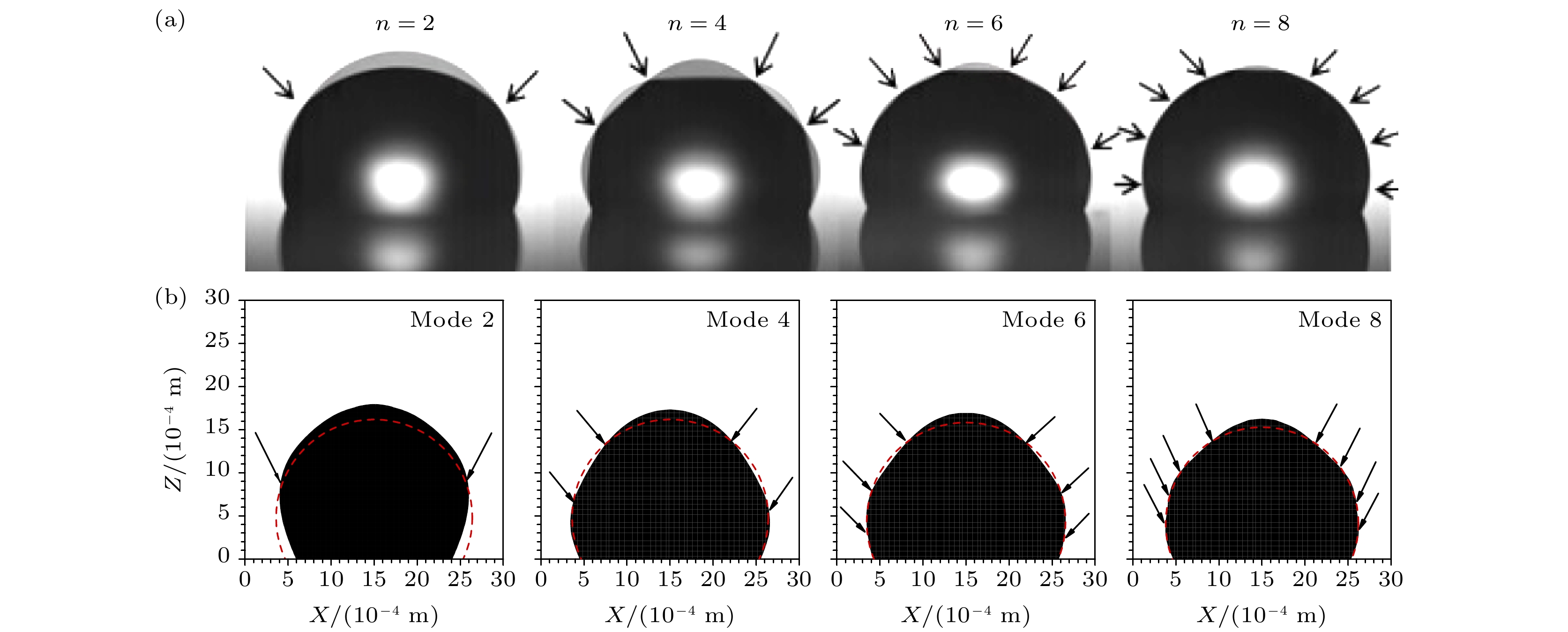
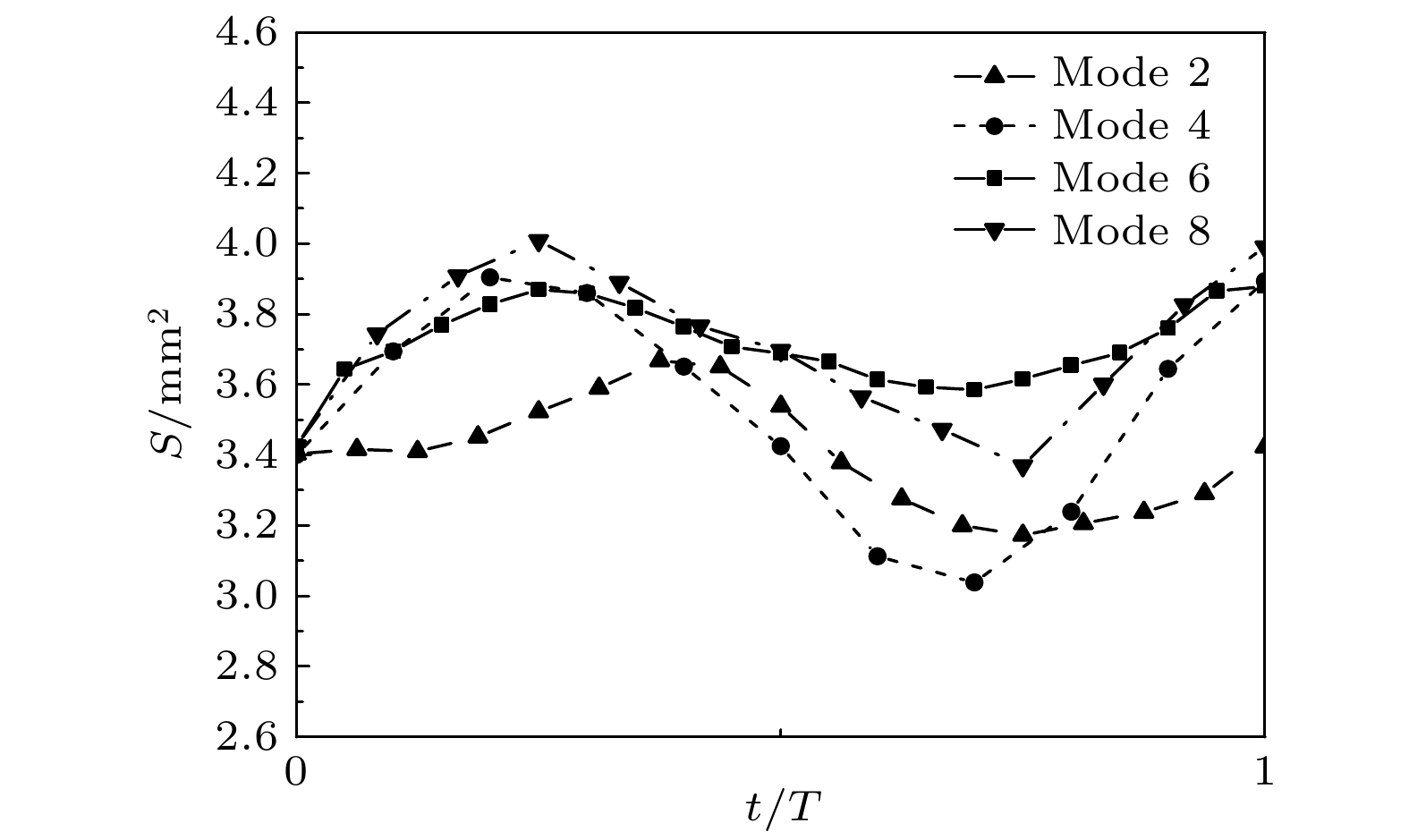
In order to understand the evolution and flow structure within vertical vibrating droplets on hydrophobic surfaces, a three-dimensional model of the vibrating droplet is developed, and the dynamic contact angle of the vibrating droplet is considered. The numerical simulations are performed for the droplet attached to the vertical vibrating plane by the VOF-CSF method, and the four resonance modes of the droplets are obtained. The evolution of modes (2, 4, 6, and 8), internal flow structures and the variation of the dynamic contact angle are predicted. With the change of the vibration acceleration, the droplet can express a wealth of modes, and the specific mode depends on the frequency of the vibrating acceleration. Based on this model, in this paper the internal flow field structure of the droplet is further analyzed. In mode 2 and mode 4, a Y-shaped flow is generated from the bottom of the droplet, while in mode 6 and mode 8, there is a symmetrical eddy flow. And the higher the order of the resonance mode, the larger the average value of the internal velocity of the droplet is. The dynamic contact angle of the vibrating droplet obviously deviates from the static contact angle, indicating the necessity to consider the dynamic contact angle in simulating the vertical vibrating of droplet. The simulation results are compared with the experimental results from the literature, showing that they are in good agreement with each other.

Keywords:

Authors and contacts

School of Energy and Power Engineering, University of Shanghai for Science and Technology, Shanghai 200093, China

Corresponding author: Shan Yan-Guang, shan@usst.edu.cn

Funds: Project supported by the National Natural Science Foundation of China (Grant No. 51676130)

FullText HTML

References

[1]	Singhal V, Garimella S V, Raman A 2004 Appl. Mech. Rev. 57 191 Google Scholar
[2]	Vukasinovic B, Smith M K, Glezer A 2004 Phys. Fluid 16 306 Google Scholar
[3]	Nisisako T, Torri T 2007 Adv. Mater. 19 1489 Google Scholar
[4]	Shan Y G, Wang Y L, Coyle T 2013 Appl. Therm. Eng. 51 690 Google Scholar
[5]	高超, 袁俊杰, 曹进军, 杨荟楠, 单彦广 2019 68 140204 Google Scholar Gao C, Yuan J J, Cao J J, Yang H N, Shan Y G 2019 Acta Phys. Sin. 68 140204 Google Scholar
[6]	张永建 2015 博士学位论文 (西安: 西北工业大学) Zhang Y J 2015 Ph. D. Dissertation (Xian: Northwestern Polytechnical University) (in Chinese)
[7]	Kabi P, Chattopadhyay B, Bhattacharyya S, Chaudhuri S, Basu S 2018 Langmuir 34 12642 Google Scholar
[8]	Kelvin L 1882 Mathematical and Physical Papers (London: Cambridge University Press) pp178−181
[9]	Rayleigh L 1879 Proc. R. Soc. London 29 71 Google Scholar
[10]	Lamb H 1932 Hydrodynamics (London: Cambridge University press) p606
[11]	Strani M, Sabetta F 1984 J. Fluid Mech. 141 233 Google Scholar
[12]	Ko S H, Lee S J, Kang K H 2009 Appl. Phys. Lett. 94 194102 Google Scholar
[13]	邵学鹏, 解文军 2012 61 134302 Google Scholar Shao X P, Xie W J 2012 Acta Phys. Sin. 61 134302 Google Scholar
[14]	Brunet P, Eggers J, Deegan R D 2009 Eur. Phys. J-Spec. Top. 166 11 Google Scholar
[15]	Noblin X, Buguin A, Brochard-Wyart F 2009 Eur. Phys. J. E 166 7 Google Scholar
[16]	Dong L, Chaudhury A, Chaudhury M K 2006 Eur. Phys. J. E 21 231 Google Scholar
[17]	周建臣, 耿兴国, 林可君, 张永建, 臧渡洋 2014 63 216801 Google Scholar Zhou J C, Geng X G, Lin K J, Zhang Y J, Zang D Y 2014 Acta Phys. Sin. 63 216801 Google Scholar
[18]	Noblin X, Buguin A, Brochard-Wyart F 2004 Eur. Phys. J. E 14 395 Google Scholar
[19]	Shin Y S, Lim H C 2014 Eur. Phys. J. E 37 1 Google Scholar
[20]	Kim H, Lim H C 2015 J. Phys. Chem. B 119 6740 Google Scholar
[21]	Park C S, Kim H, Lim H C 2016 Exp. Therm. Fluid Sci. 78 112 Google Scholar
[22]	Ramos S M M 2008 Nucl. Instrum. Methods Phys. Res., Sect. B 266 3143 Google Scholar
[23]	Ehrhorn J, Semke W 2013 Folia Parasit. 5 243 Google Scholar
[24]	Li Y and Umemura A 2014 Int. J. Multiphase Flow 60 64 Google Scholar
[25]	James A J, Smith M K and Glezer A 2003 J. Fluid Mech. 476 29 Google Scholar
[26]	王瑞金, 张凯, 王刚 2007 Fluent技术基础与应用实例 (北京: 清华大学出版社) 第136−150页 Wang R J, Zhang K, Wang G 2007 Fluent Technology Foundation and Application Examples (Beijing: Tsinghua University Press) pp136−150 (in Chinese)
[27]	Brackbill J U, Kothe D B, Zemach C 1992 J. Comput. Phys. 100 335 Google Scholar
[28]	Chernova A A, Kopysov S P, Tonkov L E 2016 IOP Conference Series: Mater. Sci. Eng. 158 1 Google Scholar
[29]	Kistler S F 1993 Wettability (New York: Marcel Dekker) pp311−429

Cited By

图 1 三维模拟计算区域(3 mm × 3 mm × 3 mm)

Figure 1. 3D computational domain (3 mm × 3 mm × 3 mm).

DownLoad: Full-Size Img PowerPoint

图 2 疏水表面上液滴共振模态(2, 4, 6和8)的模拟结果与实验结果对比　(a)实验结果^[20]; (b) 模拟结果

Figure 2. Comparisons of the resonance modes (2, 4, 6, and 8) of a vibrating water drop on a hydrophobic surface: (a) Experimental results^[20]; (b) simulation results.

DownLoad: Full-Size Img PowerPoint

DownLoad: Full-Size Img PowerPoint

图 3 液滴在2, 4, 6和8共振模态下一个振动周期内形貌变化的实验^[21]与模拟结果对比

Figure 3. Comparisons between the experimental^[21] and simulation results of the droplet shape evolution during one cycle of the vibration at resonance modes 2, 4, 6 and 8.

DownLoad: Full-Size Img PowerPoint

图 4 在2, 4, 6和8模态下液滴内部的三维流场图

Figure 4. The three-dimensional flow field inside the droplet at modes 2, 4, 6, and 8.

DownLoad: Full-Size Img PowerPoint

图 5 液滴在2, 4, 6和8共振模态下内部流动结构的实验^[20]与模拟结果对比　(a) 模态2; (b) 模态4; (c) 模态6; (d) 模态8

Figure 5. Comparisons between the experimental^[20]and simulation results of the internal flow structure of the droplet during the vibration at modes 2, 4, 6 and 8: (a) Mode 2; (b) mode 4; (c) mode 6; (d) mode 2.

DownLoad: Full-Size Img PowerPoint

图 6 在2, 4, 6和8共振模态下液滴内部平均速度随时间的变化

Figure 6. The variations of the velocity with time at modes 2, 4, 6, and 8.

DownLoad: Full-Size Img PowerPoint

图 7 在模态2时液滴振动幅值随时间的变化. Num.1: 动态接触角; Num.2: 静态接触角; Exp.: 实验^[20]

Figure 7. The variations of droplet vibration amplitude with time at mode 2. Num.1: dynamic wetting angle; Num.2: static contact angle; Exp.: experiment^[20].

DownLoad: Full-Size Img PowerPoint

图 8 在2, 4, 6和8共振模态下液滴动态接触角随时间的变化

Figure 8. The variations of the dynamic contact angle with time at modes 2, 4, 6, and 8.

DownLoad: Full-Size Img PowerPoint

图 9 在2, 4, 6和8共振模态下液滴润湿面积随时间的变化

Figure 9. The variations of the wetting area with time at modes 2, 4, 6, and 8.

DownLoad: Full-Size Img PowerPoint

表 1 共振频率的理论值和实验值对比

Table 1. Comparisons of theoretical and experimental results for resonance frequency of a 5 ${\text{μ}}\mathrm{L}$ droplet.

Mode n Rayleigh方程
计算值 f/Hz 共振频率
实验值 f/Hz

2 96 85
4 288 226
6 526 469
8 804 635

DownLoad: CSV

表 2 液滴在模态2, 4, 6和8下中心底部的平均垂直速度的实验^[20]与模拟对比

Table 2. Comparisons between the experimental^[20] and simulation results of averaged vertical velocity at the central bottom region of the droplet in modes 2, 4, 6, and 8.

模态模拟速度值/(mm·s^–1) 实验速度值/(mm·s^–1)

2 1.76 0.36
4 3.37 0.79
6 10.43 3.87
8 11.05 3.61

DownLoad: CSV

map

[1]	Singhal V, Garimella S V, Raman A 2004 Appl. Mech. Rev. 57 191 Google Scholar
[2]	Vukasinovic B, Smith M K, Glezer A 2004 Phys. Fluid 16 306 Google Scholar
[3]	Nisisako T, Torri T 2007 Adv. Mater. 19 1489 Google Scholar
[4]	Shan Y G, Wang Y L, Coyle T 2013 Appl. Therm. Eng. 51 690 Google Scholar
[5]	高超, 袁俊杰, 曹进军, 杨荟楠, 单彦广 2019 68 140204 Google Scholar Gao C, Yuan J J, Cao J J, Yang H N, Shan Y G 2019 Acta Phys. Sin. 68 140204 Google Scholar
[6]	张永建 2015 博士学位论文 (西安: 西北工业大学) Zhang Y J 2015 Ph. D. Dissertation (Xian: Northwestern Polytechnical University) (in Chinese)
[7]	Kabi P, Chattopadhyay B, Bhattacharyya S, Chaudhuri S, Basu S 2018 Langmuir 34 12642 Google Scholar
[8]	Kelvin L 1882 Mathematical and Physical Papers (London: Cambridge University Press) pp178−181
[9]	Rayleigh L 1879 Proc. R. Soc. London 29 71 Google Scholar
[10]	Lamb H 1932 Hydrodynamics (London: Cambridge University press) p606
[11]	Strani M, Sabetta F 1984 J. Fluid Mech. 141 233 Google Scholar
[12]	Ko S H, Lee S J, Kang K H 2009 Appl. Phys. Lett. 94 194102 Google Scholar
[13]	邵学鹏, 解文军 2012 61 134302 Google Scholar Shao X P, Xie W J 2012 Acta Phys. Sin. 61 134302 Google Scholar
[14]	Brunet P, Eggers J, Deegan R D 2009 Eur. Phys. J-Spec. Top. 166 11 Google Scholar
[15]	Noblin X, Buguin A, Brochard-Wyart F 2009 Eur. Phys. J. E 166 7 Google Scholar
[16]	Dong L, Chaudhury A, Chaudhury M K 2006 Eur. Phys. J. E 21 231 Google Scholar
[17]	周建臣, 耿兴国, 林可君, 张永建, 臧渡洋 2014 63 216801 Google Scholar Zhou J C, Geng X G, Lin K J, Zhang Y J, Zang D Y 2014 Acta Phys. Sin. 63 216801 Google Scholar
[18]	Noblin X, Buguin A, Brochard-Wyart F 2004 Eur. Phys. J. E 14 395 Google Scholar
[19]	Shin Y S, Lim H C 2014 Eur. Phys. J. E 37 1 Google Scholar
[20]	Kim H, Lim H C 2015 J. Phys. Chem. B 119 6740 Google Scholar
[21]	Park C S, Kim H, Lim H C 2016 Exp. Therm. Fluid Sci. 78 112 Google Scholar
[22]	Ramos S M M 2008 Nucl. Instrum. Methods Phys. Res., Sect. B 266 3143 Google Scholar
[23]	Ehrhorn J, Semke W 2013 Folia Parasit. 5 243 Google Scholar
[24]	Li Y and Umemura A 2014 Int. J. Multiphase Flow 60 64 Google Scholar
[25]	James A J, Smith M K and Glezer A 2003 J. Fluid Mech. 476 29 Google Scholar
[26]	王瑞金, 张凯, 王刚 2007 Fluent技术基础与应用实例 (北京: 清华大学出版社) 第136−150页 Wang R J, Zhang K, Wang G 2007 Fluent Technology Foundation and Application Examples (Beijing: Tsinghua University Press) pp136−150 (in Chinese)
[27]	Brackbill J U, Kothe D B, Zemach C 1992 J. Comput. Phys. 100 335 Google Scholar
[28]	Chernova A A, Kopysov S P, Tonkov L E 2016 IOP Conference Series: Mater. Sci. Eng. 158 1 Google Scholar
[29]	Kistler S F 1993 Wettability (New York: Marcel Dekker) pp311−429

Catalog

Vol. 70, Issue 14 - 2021-07-20

Metrics

Abstract views: 6594
PDF Downloads: 174
Cited By: 0

姓名
邮箱
手机号码
标题
留言内容
验证码

Search

Article

留言板