-
In our study, the unidirectional pedestrian flow in an L-shaped corridor is taken as the research object, and the pedestrian turning behavior is studied based on controllable experiments and micro simulations. First of all, three experimental scenarios, namely, no obstacles in the turning zone, diagonal layout of obstacles along the turning zone, and diagonal layout of obstacles in the vertical turning zone, are constructed. Behavioral characteristics such as pedestrian movement trajectory and velocity distribution are analyzed through controllable experiments of pedestrians. Then, a velocity correction model based on the Voronoi diagram is constructed, and the turning rules of pedestrians passing through a 90-degree L-shaped curve are embedded in the model. Finally, simulation research is conducted on the scene with both obstacles and asymmetric L-shaped corridors as well as the scene with neither of them to simulate and reproduce the turning behavior of pedestrians, and analyze the distributions of pedestrian velocities and individual densities at different stages. The research shows that when pedestrians move in a normal non-panic status, they rarely present disorderly behavior and always approach to the inside of the corner of the L-shaped corridor. In the turning area, pedestrians always follow their original moving mode to pass through the corner like a stable arc. And in the process of moving, pedestrians do not move in a straight line, but keep shaking back and forth for zipper effect. Besides, in the process of turning, the longer the distance from the center of the corner, the longer the distance of the pedestrian around the arc will be. And the L-shaped corridor can be divided into vertical straight area, transition area, turning area, and horizontal straight area. When pedestrians pass through the turning walking area, the “invisible bottleneck” phenomenon and the “curved triangle idle area” phenomenon can be observed. Besides, the streamline compression and multiple rows of pedestrian track clusters can be seen in the region. According to the characteristics of pedestrians walking through the L-shaped corridor, the turning rules of pedestrians are made, and the scene with both of obstacles and asymmetric L-shaped corridor as well as the scene with neither of them is simulated. Then, through the pedestrian simulation by using our model, the turning behavior of pedestrians passing through curve like a smooth arc can be effectively reproduced. Moreover, the “invisible bottleneck” phenomenon and the “curved triangle idle area” phenomenon in the turning walking area can be seen in the simulation. At the same time, when the pedestrian flow passes through the four areas of the L-shaped corridor successively, the velocity distribution is consistent with the experimental data of the pedestrian, showing an increasing-decreasing-increasing “wavy” change characteristic. The simulation model is also used to simulate the local density change of pedestrians due to the turning behavior, which verifies the unity of pedestrian velocity and local density change. The cognition of invisible bottleneck is helpful in rationally utilizing and designing the L-shaped corridor turning area.
-
Keywords:
- pedestrian dynamics /
- L-shaped corridor /
- velocity correction model /
- Voronoi diagram /
- invisible bottleneck
[1] Shiwakoti N, Sarvi M, Rose G, Burd M 2011 Transp. Res. Rec. 2234 97
Google Scholar
[2] Dias C, Sarvi M, Shiwakoti N, Ejtemai O, Burd M 2013 Saf. Sci. 60 87
Google Scholar
[3] Shiwakoti N, Sarvi M 2013 Transp. Res. Part C Emerg. Technol. 37 260
Google Scholar
[4] G uo, R Y, Huang H J, Wong S C 2011 Transp. Res. Part. B Methodol. 45 490
Google Scholar
[5] Xiao Y, Gao Z Y, Jiang R, Li X G, Qu Y C, Huang Q X 2019 Transp. Res. Part C Emerg. Technol. 103 174
Google Scholar
[6] Blue V J, Adler J L 2000 Transp Res Rec. 1710 20
Google Scholar
[7] Yue H, Wang S, Jia X L, Li J, Shao C F 2016 Simul. Trans. Soc. Model. Simul. Int. 92 491
[8] Burstedde C, Klauck K, Schadschneider A, Zittartz J 2001 Physica A 295 507
Google Scholar
[9] Helbing D, Farkas I, Vicsek T 2000 Nature 407 487
Google Scholar
[10] Moussaid M, Helbing D, Garnier S, Johansson A, Combe M, Theraulaz G 2009 Proc. R. Soc. B: Biol. Sci. 276 2755
Google Scholar
[11] Moussaid M, Helbing D, Theraulaz G 2011 Proc. Natl. Acad. Sci. U.S.A. 108 6884
Google Scholar
[12] Qu Y C, Xiao Y, Wu J J, Tang T, Gao Z Y 2018 Physica A 492 1153
Google Scholar
[13] Wu X S, Yue H, Liu Q M, Zhang X, Shao C F 2021 Chin. Phys. B 30 018902
Google Scholar
[14] Haghani M, Sarvi M 2018 Transp. Res. Part B Methodol. 107 253
Google Scholar
[15] Frank G A, Dorso C O 2011 Physica A 390 2135
Google Scholar
[16] Seyfried A, Steffen B, Lippert T 2006 Physica A 368 232
Google Scholar
[17] Dias C, Ejtemai O, Sarvi M, Shiwakoti N 2014 Transp. Res. Rec. 2421 41
Google Scholar
[18] Hou L, Liu J G, Pan X, Wang B H 2014 Physica A 400 93
Google Scholar
[19] Seer S, Brandle N, Ratti C 2014 Transp. Res. Part C Emerg. Technol. 48 212
Google Scholar
[20] Ma X Q, Yin X Y, Xing Y, Liu Y F 2017 In Proceedings of the 3rd International Forum on Energy. Environment Science and Materials (IFEESM) Shenzhen, China, November 25−26, 2017 p154
[21] 武鑫森, 岳昊, 刘秋梅, 张旭, 邵春福 2021 70 068901
Google Scholar
Wu X S, Yue H, Liu Q M, Zhang X, Shao C F 2021 Acta Phys. Sin. 70 068901
Google Scholar
[22] Schadschneider A, Eilhardt C, Nowak S, Will R 2011 International Conference on Pedestrian and Evacuation Dynamics 2010 Gaithersburg, USA, March 8−10, 2010 p557
[23] Li S, Li X, Qu Y, Jia B 2015 Physica A 432 337
Google Scholar
[24] Dias C, Lovreglio R 2018 Phys. Lett. A 382 1255
Google Scholar
[25] Yanagisawa D, Kimura A, Tomoeda A, Nishi R, Suma Y, Ohtsuka K, Nishinari K 2009 Phys. Rev. E 80 036110
Google Scholar
[26] Dias C, Abdullah M, Sarvi M, Lovreglio R, Alhajyaseen W 2019 Sustainability 11 5501
Google Scholar
[27] Zeng J B, Leng B, Xiong Z 2011 Int. J. Mod. Phys. C 22 775
Google Scholar
[28] Guo R Y, Tang T Q 2012 Simul. Modell. Pract. Theory 21 103
Google Scholar
[29] Jing L, Li J Y, Shen C, Yang S C, Han Z G 2014 PLoS One 9 e115463
Google Scholar
[30] Parisi D R, Negri P A, Bruno L 2016 Phys. Rev. E 94 022318
[31] Boltes M, Seyfried A, Steffen B, Schadschneider A 2010 International Conference on Pedestrian and Evacuation Dynamics 2008, Heidelberg, Germany, February 27−29, 2008 p43
[32] Boltes M, Seyfried A 2013 Neurocomputing 100 127
Google Scholar
[33] Hoogendoorm S P, Daamen W 2005 Transp. Sci. 39 147
Google Scholar
[34] Cao S C, Zhang J, Song W G, Shi C A, Zhang R F 2018 J. Stat. Mech.: Theory Exp. 3 033402
[35] Courtine G, Schieppati M 2003 Eur. J. Neurosci. 18 177
Google Scholar
[36] Hicheur H, Vieilledent S, Richardson M J E, Flash T, Berthoz A 2005 Exp. Brain Res. 162 145
Google Scholar
[37] Imai T, Moore S T, Raphan T, Cohen B 2001 Exp. Brain Res. 136 1
Google Scholar
[38] Illera C, Fink M, Hinneberg H, Kath K, Waldau N, Rosic A, Wurzer G 2010 International Conference on Pedestrian and Evacuation Dynamics 2008. Heidelberg, Germany, February 27−29, 2008 p733
[39] Shiwakoti N, Gong Y S, Shi X M, Ye Z R 2015 Saf. Sci. 75 15
Google Scholar
[40] Kirik E, Vitova T, Malyshev A 2019 Nat. Comput. 18 875
Google Scholar
-
图 1 实验场景拍摄设置
Figure 1. Experimental scene shooting settings.
图 2 行人在L型通道移动的实验场景1 (a) L型通道设置; (b) 行人实验截图
Figure 2. Experimental Scenario 1 of pedestrian movement in an L-shaped corridor: (a) The L-shaped corridor setting; (b) pedestrian experiment screenshot.
图 3 行人在带有障碍物的L型通道移动的实验场景2 (a) L型通道设置; (b)行人实验截图
Figure 3. Experimental Scenario 2 of pedestrian movement in an L-shaped corridor with obstacles: (a) The L-shaped corridor setting; (b) pedestrian experiment screenshot.
图 4 行人在带有障碍物的L型通道移动的实验场景3 (a) L型通道设置; (b) 行人实验截图
Figure 4. Experimental Scenario 3 of pedestrian movement in an L-shaped corridor with obstacles: (a) The L-shaped corridor setting; (b) pedestrian experiment screenshot.
图 5 通过Petrack软件对行人进行识别追踪
Figure 5. The pedestrians are identified and tracked by Petrack software.
图 6 行人在场景1无障碍物的L型通道行走的视频截图
Figure 6. The video screenshots of pedestrians walking in the L-shaped passage without obstacles in Scene 1.
图 7 行人在场景1无障碍物L型通道的移动轨迹 (a) 原始移动轨迹; (b)简化移动轨迹
Figure 7. The paths of pedestrians in the L-shaped corridor without obstacles in Scene 1: (a) The original moving track of the pedestrians in the L-shaped corridor; (b) the simplifying moving track of the pedestrians in the L-shaped corridor.
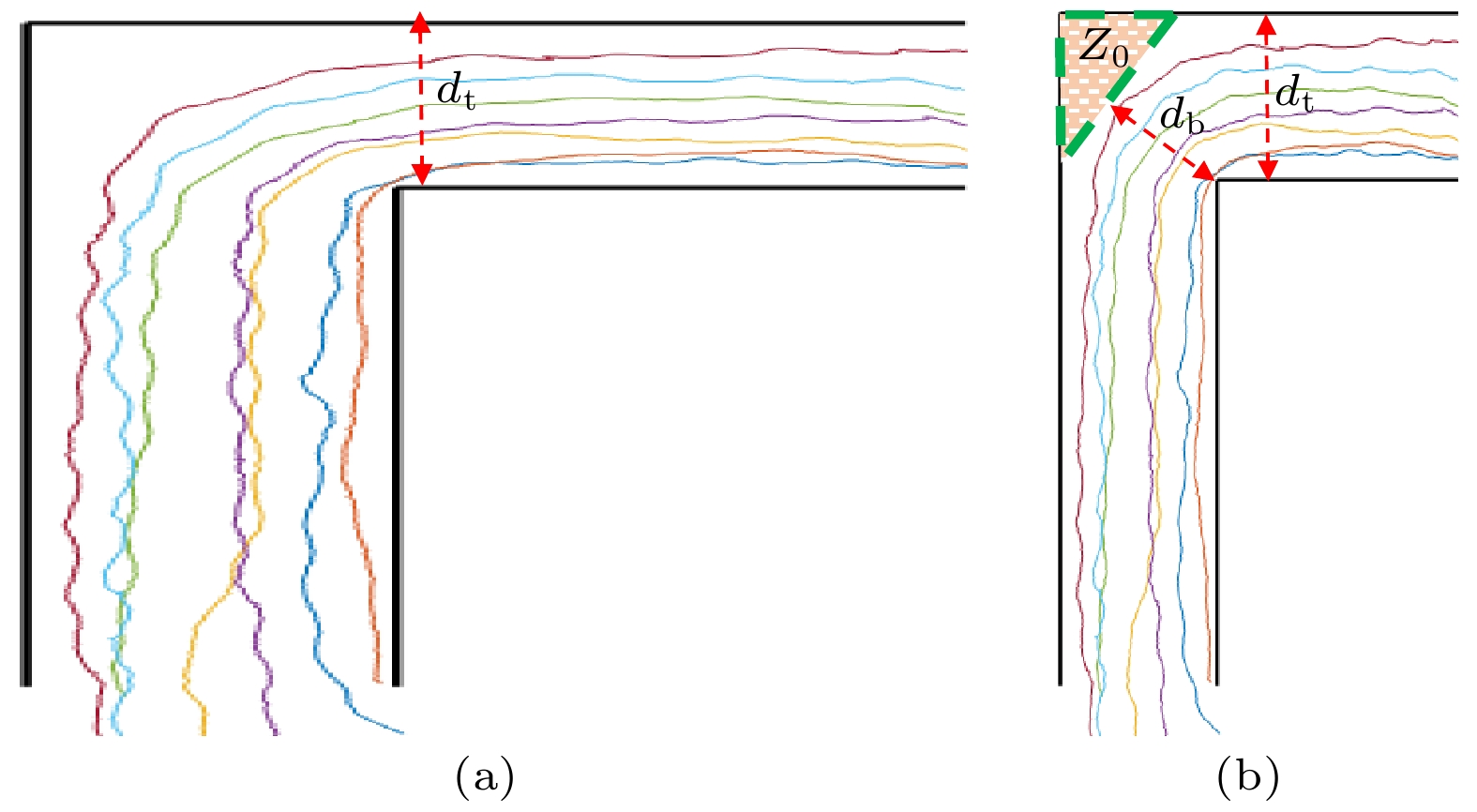
图 8 行人在场景1无障碍物的L型通道移动的特征分析 (a) 行人在通道移动的四区域; (b) 行人在转弯区域的转弯特征; (c) 行人在通道移动的隐形瓶颈
Figure 8. Analysis on the characteristics of pedestrian movement in an L-shaped corridor without obstacles in Scene 1: (a) Four types of areas where pedestrians move in the corridor; (b) the turning characteristics of pedestrians in the turning area; (c) the invisible bottleneck of pedestrian movement in the corridor.
图 9 场景2中L型通道转弯处的小型瓶颈设置
Figure 9. A small bottleneck setting at an L-shaped corridor bend in Scene 2.
图 10 行人在场景2有障碍物的L型通道行走的视频截图
Figure 10. The video screenshots of pedestrians walking in the L-shaped corridor with obstacles in Scene 2.
图 11 行人在场景2有障碍物的L型通道移动的特征分析
Figure 11. Analysis on the characteristics of pedestrian movement in an L-shaped corridor with obstacles in Scene 2.
图 12 行人在场景3有障碍物的L型通道行走的视频截图
Figure 12. The video screenshots of pedestrians walking in the L-shaped corridor with obstacles in Scene 3.
图 13 行人在场景3有障碍物的L型通道移动的特征分析
Figure 13. Analysis on the characteristics of pedestrian movement in an L-shaped corridor with obstacles in Scene 3.
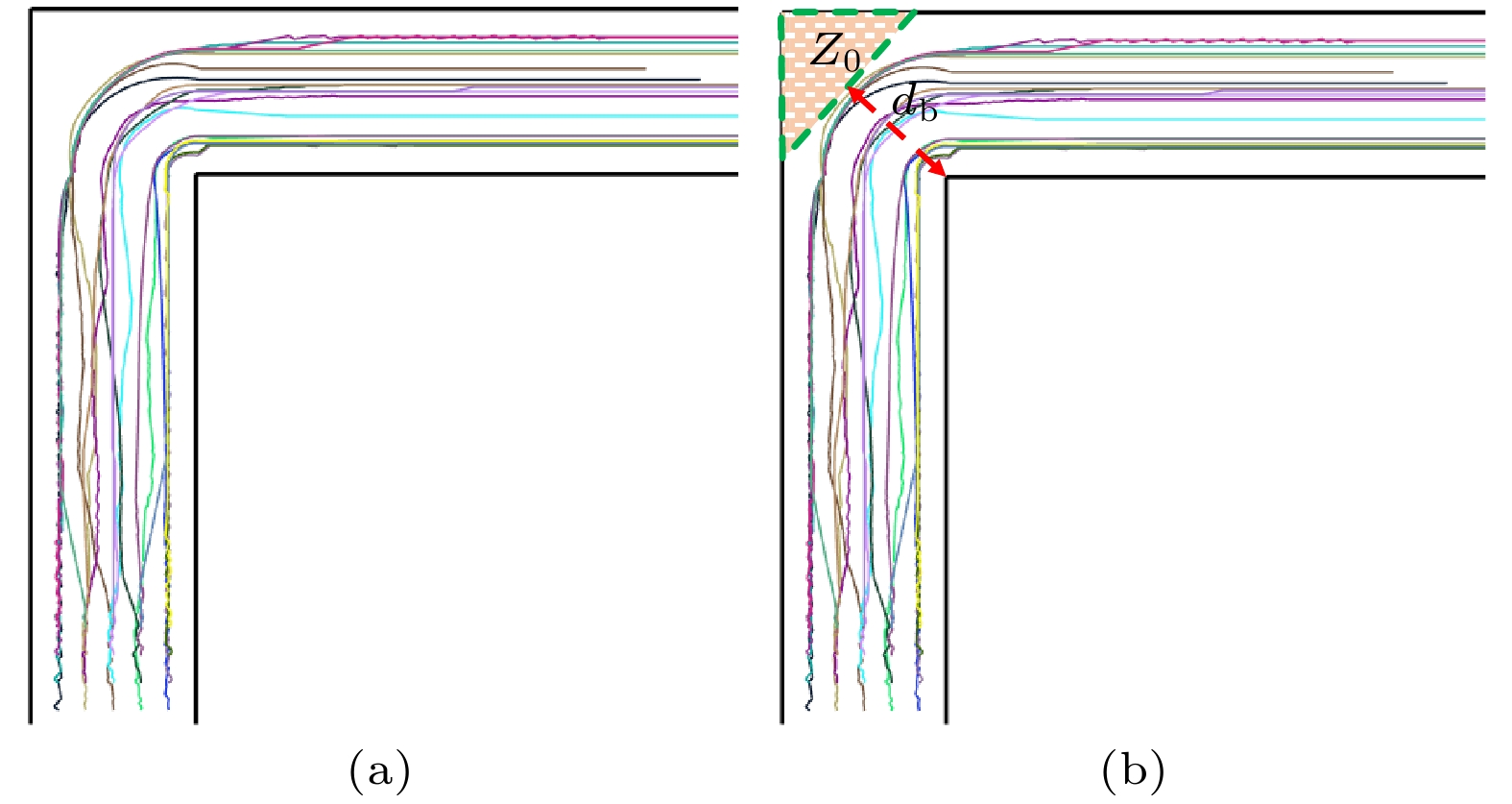
图 14 不同场景的弯道三角形闲置区域面积大小对比 (a) 场景1的弯道三角形闲置区域面积; (b) 场景2的弯道三角形闲置区域面积; (c) 场景3的弯道三角形闲置区域面积
Figure 14. Comparisons of the area size of the curve triangle idle area in different scenes: (a) The area size of the curve triangle idle area in Scene 1; (b) the area size of the curve triangle idle area in Scene 2; (c) the area size of the curve triangle idle area in Scene 3
图 15 行人在L型通道的速度变化过程
Figure 15. The velocity change process of pedestrians in L-shaped corridor.
图 16 通道中的瓶颈 (a) 传统认知的有形瓶颈; (b) 通道中的隐形瓶颈和有形瓶颈
Figure 16. Bottlenecks in the corridor: (a) The physical bottleneck of traditional cognition; (b) invisible and visible bottlenecks in the corridor.
图 18 行人通过90º L型通道的过程分析
Figure 18. Process analysis of pedestrians passing through the 90º L-shaped corridor.
图 19 行人通过转弯区域的自驱动速度时变过程(箭头方向为行人的自驱动速度方向)
Figure 19. The time-varying process of pedestrians' self-driven velocity through the turning area. (The arrow direction is the direction of pedestrians' self-driven velocity).
图 20 行人通过L型无障碍物通道的仿真过程(
$ {W_1} = 3\;{\rm{m}}$ ,$ {L_1} = 13\;{\rm{m}}$ ,$ {W_2} = 3\;{\rm{m}}$ ,$ {L_2} = 10\;{\rm{m}}$ ) (a) t = 0 s; (b) t = 6.0 s; (c) t = 11.8 s; (d) t = 17.4 s; (e) t = 21.2 sFigure 20. The screenshots of the simulation process of pedestrians passing through the L-shaped corridor without obstacles (
${W_1} = 3\;{\rm{m}}$ ,${L_1} = 13\;{\rm{m}}$ ,${W_2} = 3\;{\rm{m}}$ ,${L_2} = 10\;{\rm{m}}$ ).: (a) t = 0 s; (b) t = 6.0 s; (c) t = 11.8 s; (d) t = 17.4 s; (e) t = 21.2 s.
图 21 行人仿真通过L型无障碍通道的轨迹线 (a) 行人移动轨迹线; (b) 在转弯区域形成的弯道三角形闲置区域和隐形瓶颈
Figure 21. Pedestrian simulation of the path lines through the L-shaped corridor without obstacles: (a) The pedestrian movement trajectory; (b) the triangular idle area of the curve and the invisible bottleneck formed in the turning area.
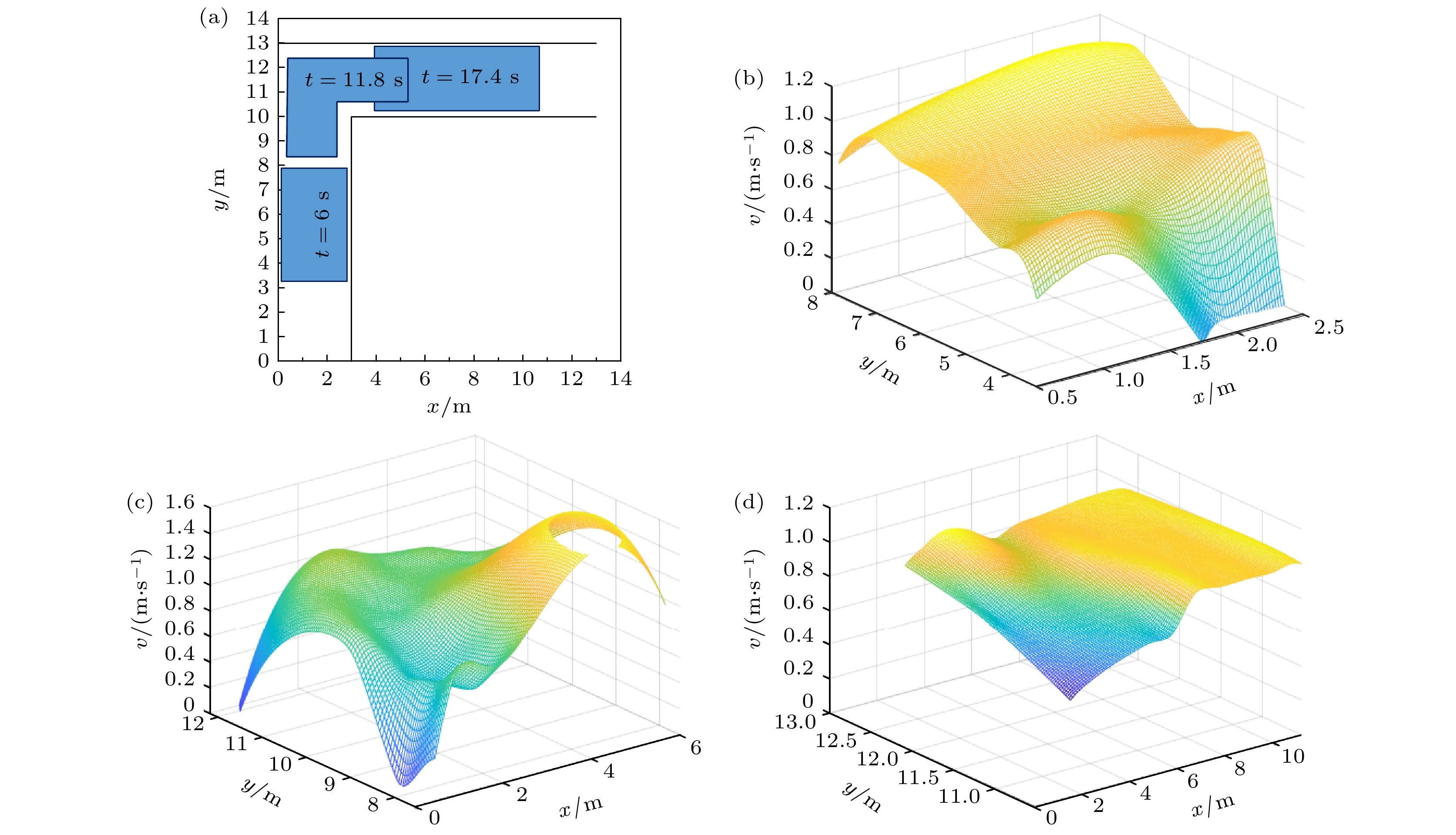
图 22 L型无障碍通道内不同时刻行人速度分布情况 (a) L型无障碍物通道位置与直角坐标系的对应关系; (b) 行人在垂直直行区域的速度, t = 6.0 s; (c) 行人在过渡及转弯区域的速度, t = 11.8 s; (d) 行人在水平直行区域的速度, t = 17.4 s
Figure 22. The velocity distribution of pedestrians at different times in L-shaped corridor without obstacles: (a) Corresponding relation between the position of L-shaped straight corridor without obstacles and Cartesian coordinate system; (b) the velocity of pedestrians in vertical straight-ahead areas, t = 6.0 s; (c) the velocity of pedestrians in transition and turning areas, t = 11.8 s; (d) the velocity of pedestrians in horizontal straight-ahead areas, t = 17.4 s.
图 23 L型无障碍通道行人个体局部密度的变化情况 (a) 行人在垂直直行区域的个体局部密度, t = 6.0 s; (b) 行人在过渡及转弯区域的个体局部密度, t = 11.8 s; (c) 行人在水平直行区域的个体局部密度, t = 17.4 s
Figure 23. The variation trend of the individual local density of pedestrians in L-shaped straight corridor without obstacles: (a) The individual local density of pedestrians in vertical straight-ahead areas, t = 6.0 s; (b) the individual local density of pedestrians in transition and turning areas, t = 11.8 s; (c) the individual local density of pedestrians in horizontal straight-ahead areas, t = 17.4 s.
图 24 行人通过L型有障碍通道的仿真过程(
$ {W_1} = 3\;{\rm{m}}$ ,$ {L_1} = 13\;{\rm{m}}$ ,$ {W_2} = 3\;{\rm{m}}$ ,$ {L_2} = 10\;{\rm{m}}$ ) (a) t = 7.4 s; (b) t = 9.3 s; (c) t = 11.0 s; (d) t = 13.5 sFigure 24. The screenshots of the simulation process of pedestrians passing through the L-shaped corridor with obstacles (
$ {W_1} = 3\;{\rm{m}}$ ,${L_1} = 13\;{\rm{m}}$ ,$ {W_2} = 3\;{\rm{m}}$ ,$ {L_2} = 10\;{\rm{m}}$ ): (a) t = 7.4 s; (b) t = 9.3 s; (c) t = 11.0 s; (d) t = 13.5 s
图 25 L型有障碍通道行人速度的变化趋势 (a) L型有障碍通道位置与直角坐标系的对应关系; (b) 行人接近转弯区域的速度, t = 7.4 s; (c) 行人刚进入转弯区域的速度, t = 9.3 s; (d)行人部分处于转弯区域的速度, t = 11.0 s; (e) 行人大部分通过转弯区域的速度, t = 13.5 s
Figure 25. The variation trend of pedestrian velocity in L-shaped corridor with obstacles: (a) Corresponding relation between the position of L-shaped corridor with obstacles and Cartesian coordinate system; (b) the velocity at which pedestrians approach the turning area, t = 7.4 s; (c) the velocity at which the pedestrians first enter the turning area, t = 9.3 s; (d) the velocity at which the pedestrians part are in the turning area, t = 11.0 s; (e) the velocity at which the pedestrians pass through the turning area for the most part, t = 13.5 s.
图 26 L型有障碍通道行人个体局部密度的分布情况 (a) 行人接近转弯区域的个体局部密度, t = 7.4 s; (b) 行人刚进入转弯区域的个体局部密度, t = 9.3 s; (c) 行人部分处于转弯区域的个体局部密度, t = 11.0 s; (d) 行人大部分通过转弯区域的个体局部密度, t = 13.5 s
Figure 26. The individual local density distribution of pedestrians in L-shaped corridor with obstacles: (a) The individual local density at which pedestrians approach the turning area, t = 7.4 s; (b) the individual local density at which the pedestrians first enter the turning area, t = 9.3 s; (c) the individual local density at which the pedestrians part are in the turning area, t = 11.0 s; (d) the individual local density at which the pedestrians pass through the turning area for the most part, t = 13.5 s.
图 27 行人通过非对称L型通道的仿真过程(
${W_1} = 6\;{\rm{m}}$ ,${L_1} = 12\;{\rm{m}}$ ,${W_2} = 2\;{\rm{m}}$ ,${L_2} = 10\;{\rm{m}}$ ) (a) t = 0.2 s; (b) t = 4.5 s; (c) t = 12.5 s; (d) t = 204 sFigure 27. The screenshots of the simulation process of pedestrians passing through an asymmetric L-shaped corridor (
${W_1} = 6\;{\rm{m}}$ ,${L_1} = 12\;{\rm{m}}$ ,${W_2} = 2\;{\rm{m}}$ ,${L_2} = 10\;{\rm{m}}$ ): (a) t = 0.2 s; (b) t = 4.5 s; (c) t = 12.5 s; (d) t = 204 s.参数 取值 单位 参数 取值 ${v_0}$ 1 ${\rm{m}}/{\rm{s}}$ ${k_1}$ 1.0 ${r_i}$ 0.3 m ${k_2}$ 0.6 ${d_{{\rm{m}}1}}$ 0 m ${k_3}$ 0.2 ${d_{{\rm{m}}2}}$ 0.5 m ${k_4}$ 0 ${d_{{\rm{m}}3}}$ 0.25 m ${k_5}$ 0.8 $\Delta t$ 0.5 s ${k_6}$ 0 
DownLoad: CSV
-
[1] Shiwakoti N, Sarvi M, Rose G, Burd M 2011 Transp. Res. Rec. 2234 97
Google Scholar
[2] Dias C, Sarvi M, Shiwakoti N, Ejtemai O, Burd M 2013 Saf. Sci. 60 87
Google Scholar
[3] Shiwakoti N, Sarvi M 2013 Transp. Res. Part C Emerg. Technol. 37 260
Google Scholar
[4] G uo, R Y, Huang H J, Wong S C 2011 Transp. Res. Part. B Methodol. 45 490
Google Scholar
[5] Xiao Y, Gao Z Y, Jiang R, Li X G, Qu Y C, Huang Q X 2019 Transp. Res. Part C Emerg. Technol. 103 174
Google Scholar
[6] Blue V J, Adler J L 2000 Transp Res Rec. 1710 20
Google Scholar
[7] Yue H, Wang S, Jia X L, Li J, Shao C F 2016 Simul. Trans. Soc. Model. Simul. Int. 92 491
[8] Burstedde C, Klauck K, Schadschneider A, Zittartz J 2001 Physica A 295 507
Google Scholar
[9] Helbing D, Farkas I, Vicsek T 2000 Nature 407 487
Google Scholar
[10] Moussaid M, Helbing D, Garnier S, Johansson A, Combe M, Theraulaz G 2009 Proc. R. Soc. B: Biol. Sci. 276 2755
Google Scholar
[11] Moussaid M, Helbing D, Theraulaz G 2011 Proc. Natl. Acad. Sci. U.S.A. 108 6884
Google Scholar
[12] Qu Y C, Xiao Y, Wu J J, Tang T, Gao Z Y 2018 Physica A 492 1153
Google Scholar
[13] Wu X S, Yue H, Liu Q M, Zhang X, Shao C F 2021 Chin. Phys. B 30 018902
Google Scholar
[14] Haghani M, Sarvi M 2018 Transp. Res. Part B Methodol. 107 253
Google Scholar
[15] Frank G A, Dorso C O 2011 Physica A 390 2135
Google Scholar
[16] Seyfried A, Steffen B, Lippert T 2006 Physica A 368 232
Google Scholar
[17] Dias C, Ejtemai O, Sarvi M, Shiwakoti N 2014 Transp. Res. Rec. 2421 41
Google Scholar
[18] Hou L, Liu J G, Pan X, Wang B H 2014 Physica A 400 93
Google Scholar
[19] Seer S, Brandle N, Ratti C 2014 Transp. Res. Part C Emerg. Technol. 48 212
Google Scholar
[20] Ma X Q, Yin X Y, Xing Y, Liu Y F 2017 In Proceedings of the 3rd International Forum on Energy. Environment Science and Materials (IFEESM) Shenzhen, China, November 25−26, 2017 p154
[21] 武鑫森, 岳昊, 刘秋梅, 张旭, 邵春福 2021 70 068901
Google Scholar
Wu X S, Yue H, Liu Q M, Zhang X, Shao C F 2021 Acta Phys. Sin. 70 068901
Google Scholar
[22] Schadschneider A, Eilhardt C, Nowak S, Will R 2011 International Conference on Pedestrian and Evacuation Dynamics 2010 Gaithersburg, USA, March 8−10, 2010 p557
[23] Li S, Li X, Qu Y, Jia B 2015 Physica A 432 337
Google Scholar
[24] Dias C, Lovreglio R 2018 Phys. Lett. A 382 1255
Google Scholar
[25] Yanagisawa D, Kimura A, Tomoeda A, Nishi R, Suma Y, Ohtsuka K, Nishinari K 2009 Phys. Rev. E 80 036110
Google Scholar
[26] Dias C, Abdullah M, Sarvi M, Lovreglio R, Alhajyaseen W 2019 Sustainability 11 5501
Google Scholar
[27] Zeng J B, Leng B, Xiong Z 2011 Int. J. Mod. Phys. C 22 775
Google Scholar
[28] Guo R Y, Tang T Q 2012 Simul. Modell. Pract. Theory 21 103
Google Scholar
[29] Jing L, Li J Y, Shen C, Yang S C, Han Z G 2014 PLoS One 9 e115463
Google Scholar
[30] Parisi D R, Negri P A, Bruno L 2016 Phys. Rev. E 94 022318
[31] Boltes M, Seyfried A, Steffen B, Schadschneider A 2010 International Conference on Pedestrian and Evacuation Dynamics 2008, Heidelberg, Germany, February 27−29, 2008 p43
[32] Boltes M, Seyfried A 2013 Neurocomputing 100 127
Google Scholar
[33] Hoogendoorm S P, Daamen W 2005 Transp. Sci. 39 147
Google Scholar
[34] Cao S C, Zhang J, Song W G, Shi C A, Zhang R F 2018 J. Stat. Mech.: Theory Exp. 3 033402
[35] Courtine G, Schieppati M 2003 Eur. J. Neurosci. 18 177
Google Scholar
[36] Hicheur H, Vieilledent S, Richardson M J E, Flash T, Berthoz A 2005 Exp. Brain Res. 162 145
Google Scholar
[37] Imai T, Moore S T, Raphan T, Cohen B 2001 Exp. Brain Res. 136 1
Google Scholar
[38] Illera C, Fink M, Hinneberg H, Kath K, Waldau N, Rosic A, Wurzer G 2010 International Conference on Pedestrian and Evacuation Dynamics 2008. Heidelberg, Germany, February 27−29, 2008 p733
[39] Shiwakoti N, Gong Y S, Shi X M, Ye Z R 2015 Saf. Sci. 75 15
Google Scholar
[40] Kirik E, Vitova T, Malyshev A 2019 Nat. Comput. 18 875
Google Scholar
DownLoad:
Catalog
Metrics
- Abstract views: 5043
- PDF Downloads: 92
- Cited By: 0
