-
It is undisputed that complex networks are used to describe the interaction between large-scale complex systems. Different edges have different effects on network controllability. When some edges in a network are attacked or destroyed, the network controllability may be affected very little; when some other edges are attacked, network controllability may be affected very greatly, even results in the uncontrollability of the network. Which edges failure will affect the network controllability? To solve this problem, according to the node classification and edge classification, the concept of quasi-critical edge set is proposed, and the judgment theorem of quasi-critical edge set is given in this paper. In order to study the influence of quasi-critical edge set on the network controllability, the failure model of quasi-critical edge set is proposed, and the network controllability is quantified by the ratio of the number of driver nodes to the number of network nodes. In this failure model, the quasi-critical edge set with the minimum number of edges is removed first, thus destroying the network controllability quickly. By analyzing the failure model of quasi-critical edge set, the failure curve of quasi-critical edge set is obtained. It is found that the failure curve is a piecewise linear function and that the maximum (initial) slope of failure curve is related to the average degree of network. In addition, the failure of quasi-critical edge set has the greatest influence on network controllability. A comparison among the failure of quasi-critical edge set, random failure, degree failure, and betweenness failure verifies that the failure of quasi-critical edge set has the greatest damage to the network controllability in both model networks (ER random network, BA scale-free network, random triangle network and random rectangle network) and real networks in 26 different fields. For some of real networks, such as cancer cell networks, terrorist communication networks and other networks that are harmful to human beings, the failure model of quasi-critical edge set can provide a reference attack method.
-
Keywords:
- complex network /
- structural controllability /
- quasi-critical edge set /
- edge failure model
[1] Watts D J, Strogatz S H 1998 Nature 393 440
Google Scholar
[2] Barabási A L, Albert R 1999 Science 286 509
Google Scholar
[3] 侯绿林, 老松杨, 肖延东, 白亮 2015 64 188901
Google Scholar
Hou L L, Lao S Y, Xiao Y D, Bai L 2015 Acta Phys. Sin. 64 188901
Google Scholar
[4] 徐明, 许传云, 曹克非 2017 66 028901
Google Scholar
Xu M, Xu C Y, Cao K F 2017 Acta Phys. Sin. 66 028901
Google Scholar
[5] Lin C T 1974 IEEE Trans. Autom. Control 19 201
Google Scholar
[6] Liu Y Y, Slotine J J, Barabrási A L 2011 Nature 473 167
Google Scholar
[7] Pequito S, Kar S, Aguiar A P 2016 IEEE Trans. Autom. Control 61 303
Google Scholar
[8] Yin H L, Zhang S Y 2016 Physica A 443 467
Google Scholar
[9] Yuan Z Z, Zhao C, Di Z R, Wang W X, Lai Y C 2013 Nat. Commun. 4 2447
Google Scholar
[10] Olshevsky A 2015 2015 American Control Conference (ACC) Chicago, the United States, July 1–3, 2015 p2218
[11] Olshevsky A 2014 IEEE Trans. Control. Netw. Syst. 1 249
Google Scholar
[12] Pang S P, Wang W X, Hao F, Lai Y C 2017 Sci. Rep. 7 4224
Google Scholar
[13] Menara T, Bassett D S, Pasqualetti F 2019 IEEE Trans. Autom. Control 64 3740
Google Scholar
[14] Lee B H, and Jung W S 2018 Physica A 497 15
Google Scholar
[15] Alec K, Hugo B, Marc B, Gourab G 2018 Nat. Commun. 9 2501
Google Scholar
[16] Gu S, Pasqualetti F, Cieslak M, et al. 2015 Nat. Commun. 6 8414
Google Scholar
[17] Li Y S, Ma D, Zhang H G, Sun Q Y 2015 Appl. Sci. 5 622
Google Scholar
[18] Jia T, Liu Y Y, Csóka E, Pósfai M, Slotine J J, Barabási A L 2013 Nat. Commun. 4 2002
Google Scholar
[19] Wang J J, Yu X H, Stone L 2016 Sci. Rep. 6 25627
Google Scholar
[20] Zhang R, Wang X M, Cheng M, Jia T 2019 Physica A 520 257
Google Scholar
[21] Ruths J, Ruths D 2013 Complex Networks IV. Studies in Computational Intelligence (Berlin Heidelberg: Springer) pp185−192
[22] Lu Z M, Li X F 2016 PloS One 11 e0162289
Google Scholar
[23] Thomas J, Ghosh S, Parek D, Ruths D, Ruths J 2016 Complex Networks & Their Applications V (Cham, Switzerland: Springer) p525
[24] Chen G R, Lou Y, Wang L 2019 IEEE Trans. Circuits Syst. Express Briefs 66 828
Google Scholar
[25] 蒋文君, 刘润然, 范天龙, 刘霜霜, 吕琳媛 2020 69 088904
Google Scholar
Jiang W J, Liu R R, Fan T L, Liu S S, Lü L Y 2020 Acta Phys. Sin. 69 088904
Google Scholar
[26] 陈世明, 邹小群, 吕辉, 徐青刚 2014 63 028902
Google Scholar
Chen S M, Zou X Q, Lü H, Xu Q G 2014 Acta Phys. Sin. 63 028902
Google Scholar
[27] Nie S, Wang X W, Zhang H F, Li Q L, Wang B H 2014 PloS One 9 e89066
Google Scholar
[28] Lou Y, Wang L, Chen G R 2018 IEEE Trans. Circuits Syst. Regul. Pap. 65 2983
Google Scholar
[29] Shang Y L 2019 IEEE Trans. Syst. Man Cybern.-Syst. 49 821
Google Scholar
[30] Edmonds J 1965 Can. J. Math. 17 449
Google Scholar
[31] Hopcroft J E, Karp R M 1973 SIAM J. Comput. 2 225
[32] Kalman R E 1963 J. Soc. Indus. Appl. Math. Ser. A 1 152
Google Scholar
[33] Valiant L G 1979 Theor. Comput. Sci. 8 189
Google Scholar
[34] Erdös P, Rényi A 1964 Acta Math. Hung. 12 261
Google Scholar
[35] Orsini C, Dankulov M M, Colomer-de-Simón P, et al. 2015 Nat. Commun. 6 8627
Google Scholar
[36] Yang D, Chow T W S, Zhang Y C, Chen G R 2017 2017 IEEE 15th International Conference on Industrial Informatics (INDIN) Emden Germany, July 24–26, 2017 p992
[37] Holme P, Kim B J, Yoon C N, Han S K 2002 Phys. Rev. E 65 056109
Google Scholar
[38] Nie S, Wang X W, Wang B H, Jiang L L 2016 Sci. Rep. 6 23952
Google Scholar
[39] 马秀娟 2012 电子设计工程 20 11
Google Scholar
Ma X J 2012 Electronic Design Engineering 20 11
Google Scholar
[40] Linton C F http://moreno.ss.uci.edu/data.html [2020-9-15]
-
图 1 原网络与转置网络 (a) 原网络; (b) 转置网络
Figure 1. Original network and transpose network: (a) Originalnetwork; (b) transpose network.
图 2 有向网络节点分类和边分类 (a) 有向网络所有可能的最大匹配以及对应的MDS; (b) 节点分类和边分类
Figure 2. Directed network node classification and edge classification: (a) All possible maximum matching and corresponding MDS of directed network; (b) node classification and edge classification.
图 3 寻找有向网络中的类关键边集 (a), (b) 原网络和转置网络中的节点分类和边分类; (c) 网络中的类关键边集
Figure 3. Find the quasi-critical edge set in directed network: (a), (b) Node classification and edge classification in original network and transpose network; (c) quasi-critical edge set in the network.
图 4 基于类关键边集的边失效理论曲线
Figure 4. Theoretical curve of edge failure based on quasi-critical edge set.
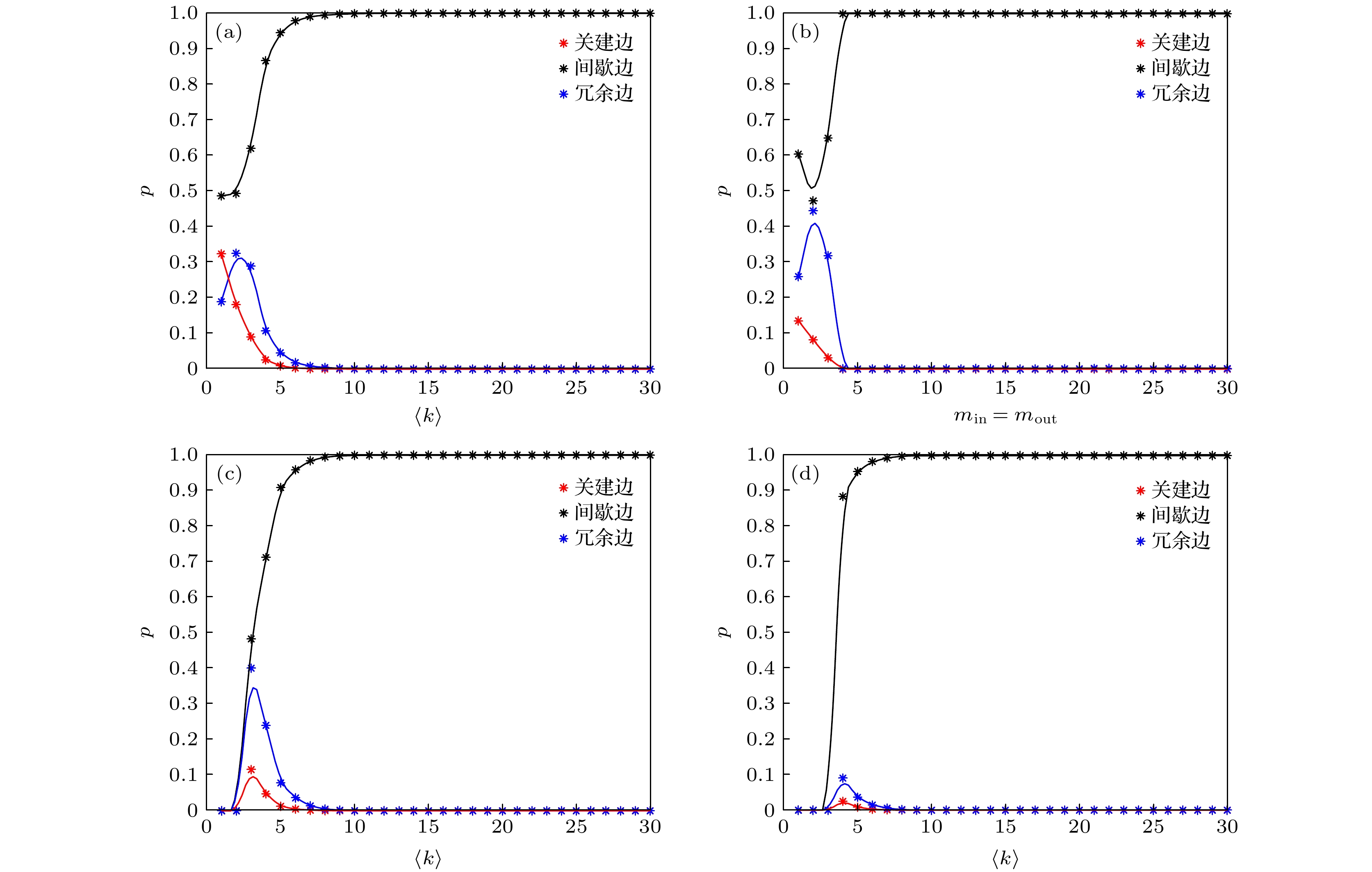
图 7 不同网络中关键边、间歇边和冗余边占网络总边数的比例随网络度的变化曲线 (a) ER随机网络; (b) BA无标度网络; (c) 随机三角形网络; (d) 随机矩形网络
Figure 7. Curve of the ratio of critical edge, intermittent edge and redundant edge to the total number of network edges with network degree in different networks: (a) ER random network; (b) BA scale-free network; (c) random triangle network; (d) random rectangle network.
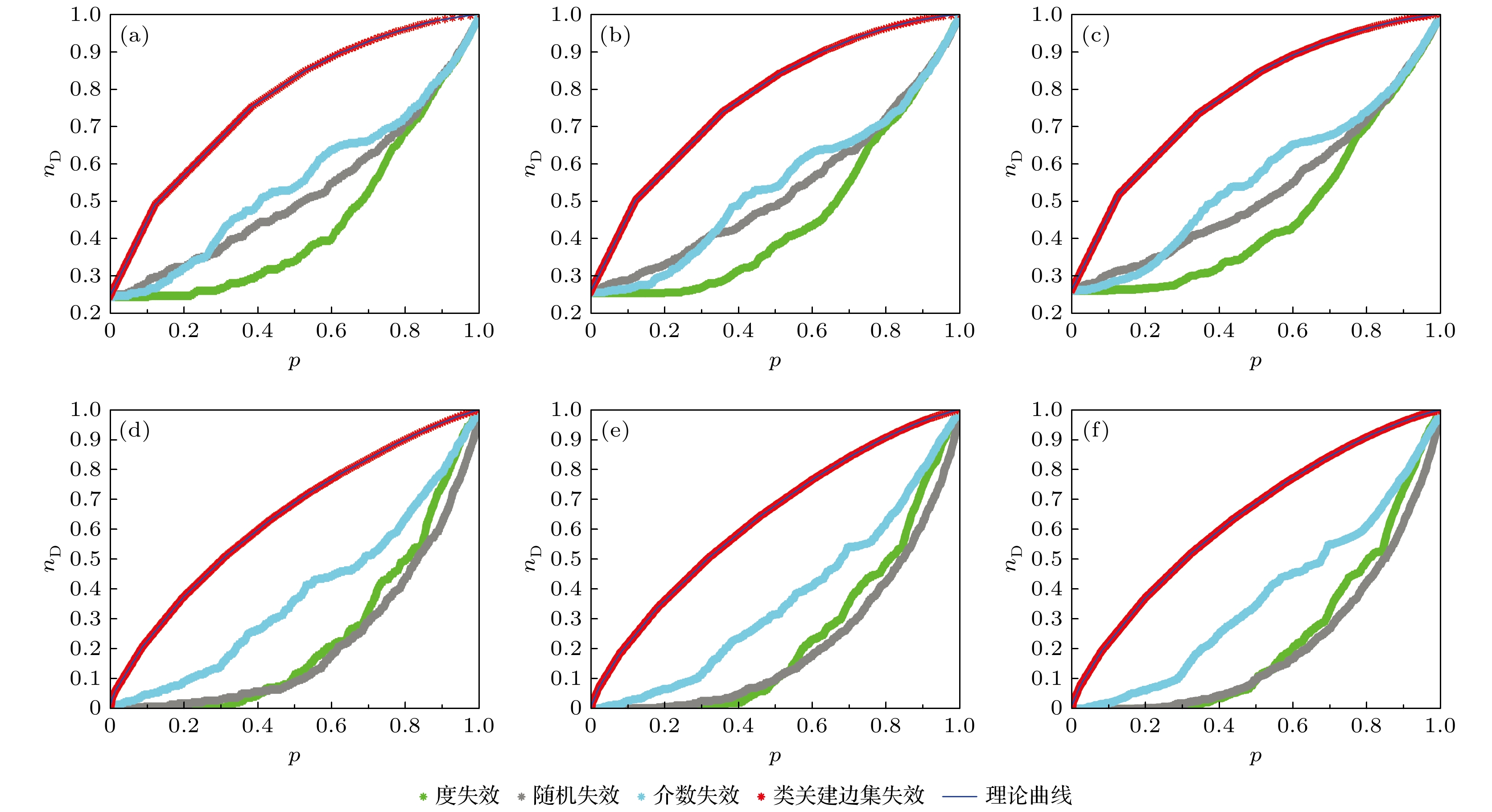
图 8 不同节点总数和平均度的随机网络在4种边失效方式下网络能控性
$n_{\rm D}$ 的变化 (a)节点总数$N=300$ , 平均度$ \left\langle {k_{\rm in}} \right\rangle= \left\langle { k_{ {\rm out}}} \right\rangle=2$ 的随机网络; (b)节点总数$N=500$ , 平均度$\left\langle {k_{\rm in}} \right\rangle= \left\langle { k_{ {\rm out}}} \right\rangle=2$ 的随机网络; (c)节点总数$N=700$ , 平均度$\left\langle {k_{\rm in}} \right\rangle= \left\langle { k_{ {\rm out}}} \right\rangle=2$ 的随机网络; (d)节点总数$N=300$ , 平均度$\left\langle {k_{\rm in}} \right\rangle= \left\langle { k_{ {\rm out}}} \right\rangle=6$ 的随机网络; (e)节点总数$N=500$ , 平均度$\left\langle {k_{\rm in}} \right\rangle= \left\langle { k_{ {\rm out}}} \right\rangle=6$ 的随机网络; (f)节点总数$N=700$ , 平均度$\left\langle {k_{\rm in}} \right\rangle= \left\langle { k_{ {\rm out}}} \right\rangle=6$ 的随机网络Figure 8. The change of controllability
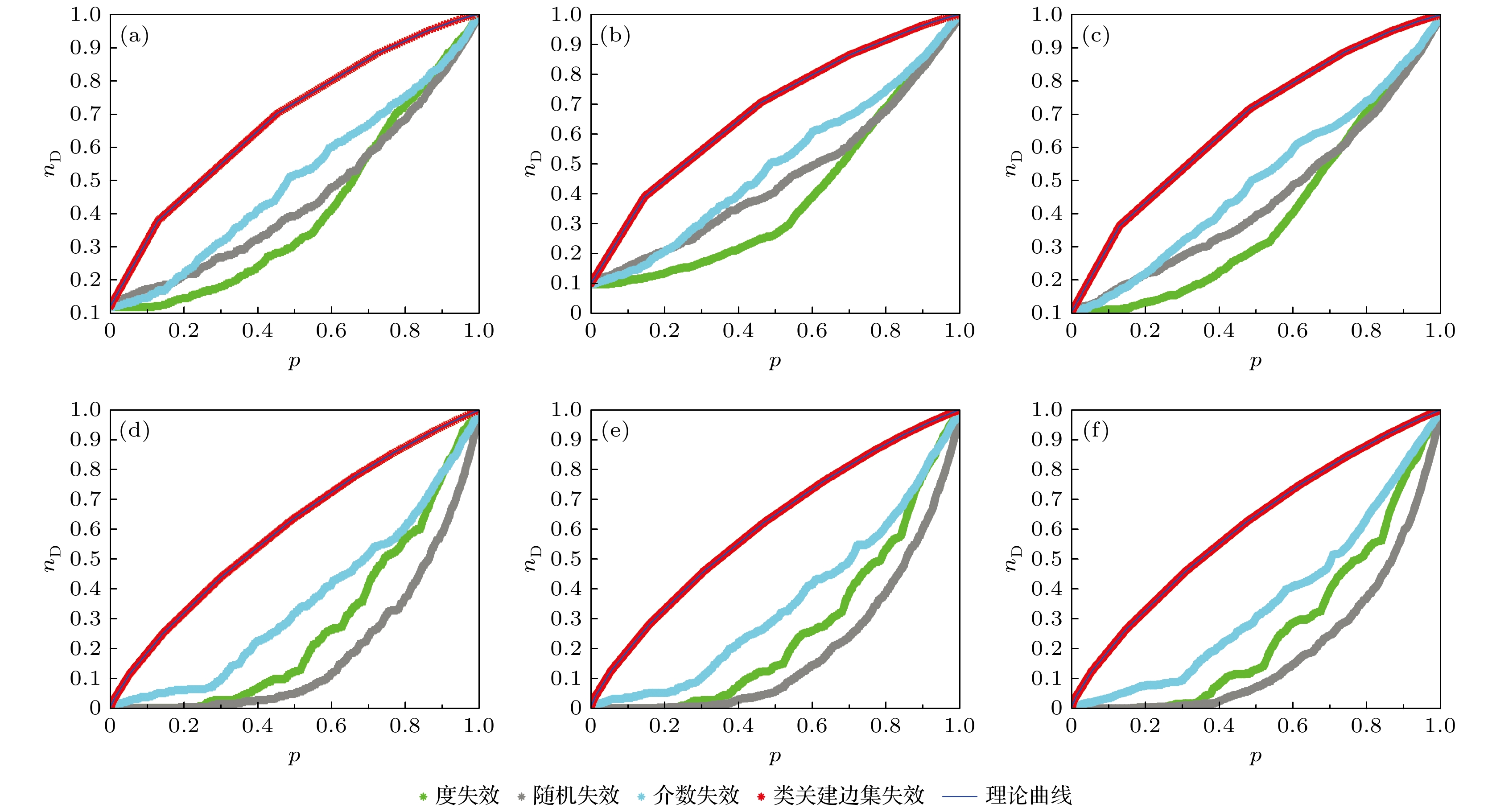
$n_{\rm D}$ of random networks with different number of nodes and average degree under four kinds of edge failure modes: (a) A random network with number of nodes$N=300$ and average degree$\left\langle {k_{\rm in}} \right\rangle= \left\langle { k_{ {\rm out}}} \right\rangle=2$ ; (b) a random network with number of nodes$N=500$ and average degree$ \left\langle {k_{\rm in}} \right\rangle= \left\langle { k_{ {\rm out}}} \right\rangle=2$ ; (c) a random network with number of nodes$N=700$ and average degree$\left\langle {k_{\rm in}} \right\rangle= \left\langle { k_{ {\rm out}}} \right\rangle=2$ ; (d) a random network with number of nodes$N=300$ and average degree$ \left\langle {k_{\rm in}} \right\rangle= \left\langle { k_{ {\rm out}}} \right\rangle=6$ ; (e) a random network with number of nodes$N=500$ and average degree$\left\langle {k_{\rm in}} \right\rangle= \left\langle { k_{ {\rm out}}} \right\rangle=6$ ; (f) a random network with number of nodes$N=700$ and average degree$\left\langle {k_{\rm in}} \right\rangle= \left\langle { k_{ {\rm out}}} \right\rangle=6$ .
图 9 不同节点总数和平均度的无标度网络在4种边失效方式下网络能控性
$n_{\rm D}$ 的变化 (a) 节点总数$N=300$ ,$m_{\rm in}=m_{\rm {out}}=1$ 的无标度网络; (b) 节点总数$N=500$ ,$m_{\rm in}=m_{\rm {out}}=1$ 的无标度网络; (c) 节点总数$N=700$ ,$m_{\rm in}=m_{\rm {out}}=1$ 的无标度网络; (d) 节点总数$N=300$ ,$m_{\rm in}=m_{\rm {out}}=3$ 的无标度网络; (e) 节点总数$N=500$ ,$m_{\rm in}=m_{\rm {out}}=3$ 的无标度网络; (f) 节点总数$N=700$ ,$m_{\rm in}=m_{\rm {out}}=3$ 的无标度网络Figure 9. The change of controllability
$n_{\rm D}$ of scale-free networks with different number of nodes and average degree under four kinds of edge failure modes: (a) A scale-free network with number of nodes$N=300$ and$m_{\rm in}=m_{\rm {out}}=1$ ; (b) a scale-free network with number of nodes$N=500$ and$m_{\rm in}=m_{\rm {out}}=1$ ; (c) a scale-free network with number of nodes$N=700$ and$m_{\rm in}=m_{\rm {out}}=1$ ; (d) a scale-free network with number of nodes$N=300$ and$m_{\rm in}=m_{\rm {out}}=3$ ; (e) a scale-free network with number of nodes$N=500$ and$m_{\rm in}=m_{\rm {out}}=3$ ; (f) a scale-free network with number of nodes$N=700$ and$m_{\rm in}=m_{\rm {out}}=3$ .
图 10 不同节点总数和平均度的随机三角形网络在4种边失效方式下网络能控性
$n_{\rm D}$ 的变化 (a) 节点总数$N=300$ , 平均度$ \left\langle {k_{\rm in}} \right\rangle= \left\langle { k_{ {\rm out}}} \right\rangle=2$ 的随机三角形网络; (b) 节点总数$N=500$ , 平均度$\left\langle {k_{\rm in}} \right\rangle= \left\langle { k_{ {\rm out}}} \right\rangle=2$ 的随机三角形网络; (c) 节点总数$N=700$ , 平均度$ \left\langle {k_{\rm in}} \right\rangle= \left\langle { k_{ {\rm out}}} \right\rangle=2$ 的随机三角形网络; (d) 节点总数$N=300$ , 平均度$ \left\langle {k_{\rm in}} \right\rangle= \left\langle { k_{ {\rm out}}} \right\rangle=6$ 的随机三角形网络; (e) 节点总数$N=500$ , 平均度$\left\langle {k_{\rm in}} \right\rangle= \left\langle { k_{ {\rm out}}} \right\rangle=6$ 的随机三角形网络; (f) 节点总数$N=700$ , 平均度$ \left\langle {k_{\rm in}} \right\rangle= \left\langle { k_{ {\rm out}}} \right\rangle=6$ 的随机三角形网络Figure 10. The change of controllability
$n_{\rm D}$ of random triangle networks with different number of nodes and average degree under four kinds of edge failure modes: (a) A random triangle network with number of nodes$N=300$ and average degree$ \left\langle {k_{\rm in}} \right\rangle= \left\langle { k_{ {\rm out}}} \right\rangle=2$ ; (b) a random triangle network with number of nodes$N=500$ and average degree$\left\langle {k_{\rm in}} \right\rangle= \left\langle { k_{ {\rm out}}} \right\rangle=2$ ; (c) a random triangle network with number of nodes$N=700$ and average degree$\left\langle {k_{\rm in}} \right\rangle= \left\langle { k_{ {\rm out}}} \right\rangle=2$ ; (d) a random triangle network with number of nodes$N=300$ and average degree$\left\langle {k_{\rm in}} \right\rangle= \left\langle { k_{ {\rm out}}} \right\rangle=6$ ; (e) a random triangle network with number of nodes$N=500$ and average degree$ \left\langle {k_{\rm in}} \right\rangle= \left\langle { k_{ {\rm out}}} \right\rangle=6$ ; (f) a random triangle network with number of nodes$N=700$ and average degree$ \left\langle {k_{\rm in}} \right\rangle= \left\langle { k_{ {\rm out}}} \right\rangle=6$ .
图 11 不同节点总数和平均度的随机矩形网络在四4边失效方式下网络能控性
$n_{\rm D}$ 的变化 (a) 节点总数$N=300$ , 平均度$ \left\langle {k_{\rm in}} \right\rangle= \left\langle { k_{ {\rm out}}} \right\rangle=2$ 的随机矩形网络; (b) 节点总数$N=500$ , 平均度$\left\langle {k_{\rm in}} \right\rangle= \left\langle { k_{ {\rm out}}} \right\rangle=2$ 的随机矩形网络; (c) 节点总数$N=700$ , 平均度$ \left\langle {k_{\rm in}} \right\rangle= \left\langle { k_{ {\rm out}}} \right\rangle=2$ 的随机矩形形网络; (d) 节点总数$N=300$ , 平均度$ \left\langle {k_{\rm in}} \right\rangle= \left\langle { k_{ {\rm out}}} \right\rangle=6$ 的随机矩形网络; (e) 节点总数$N=500$ , 平均度$ \left\langle {k_{\rm in}} \right\rangle= \left\langle { k_{ {\rm out}}} \right\rangle=6$ 的随机矩形网络; (f) 节点总数$N=700$ , 平均度$\left\langle {k_{\rm in}} \right\rangle= \left\langle { k_{ {\rm out}}} \right\rangle=6$ 的随机矩形网络Figure 11. The change of controllability
$n_{\rm D}$ of random rectangle networks with different number of nodes and average degree under four kinds of edge failure modes: (a) A random rectangle network with number of nodes$N=300$ and average degree$\left\langle {k_{\rm in}} \right\rangle= \left\langle { k_{ {\rm out}}} \right\rangle=2$ ; (b) a random rectangle network with number of nodes$N=500$ and average degree$ \left\langle {k_{\rm in}} \right\rangle= \left\langle { k_{ {\rm out}}} \right\rangle=2$ ; (c) a random rectangle network with number of nodes$N=700$ and average degree$ \left\langle {k_{\rm in}} \right\rangle= \left\langle { k_{ {\rm out}}} \right\rangle=2$ ; (d) a random rectangle network with number of nodes$N=300$ and average degree$\left\langle {k_{\rm in}} \right\rangle= \left\langle { k_{ {\rm out}}} \right\rangle=6$ ; (e) a random rectangle network with number of nodes$N=500$ and average degree$ \left\langle {k_{\rm in}} \right\rangle= \left\langle { k_{ {\rm out}}} \right\rangle=6$ ; (f) a random rectangle network with number of nodes$N=700$ and average degree$ \left\langle {k_{\rm in}} \right\rangle= \left\langle { k_{ {\rm out}}} \right\rangle=6$ .表 1 实际网络中4种边失效对能控性的影响
Table 1. Influence of four edge failures on controllability in real networks.
网络 N L $n_{\rm D}$ 边移除比例$ p $后网络的$n_{\rm D}$ p = 0.2 p = 0.5 p = 0.8 随机 按度 按介数 FQ 随机 按度 按介数 FQ 随机 按度 按介数 FQ Electronic Circuits_S208 122 189 0.24 0.33 0.29 0.43 0.53 0.48 0.57 0.56 0.77 0.74 0.84 0.85 0.95 Electronic Circuits_S402 252 399 0.23 0.32 0.30 0.42 0.53 0.52 0.56 0.57 0.77 0.76 0.84 0.84 0.95 Electronic Circuits_S838 512 819 0.23 0.33 0.30 0.42 0.53 0.48 0.55 0.57 0.77 0.74 0.84 0.84 0.95 Animal_Hens 32 496 0.03 0.03 0.25 0.19 0.44 0.03 0.59 0.34 0.69 0.19 0.81 0.63 0.88 Collaboration_in jazz 198 5484 0.01 0.01 0.01 0.14 0.43 0.03 0.02 0.32 0.72 0.08 0.38 0.60 0.91 Joint senate press releases 92 954 0.01 0.01 0.01 0.22 0.48 0.07 0.01 0.42 0.76 0.27 0.36 0.53 0.92 Questionnaire for high tech managers_Advice 21 190 0.05 0.05 0.14 0.19 0.43 0.10 0.38 0.43 0.67 0.29 0.62 0.67 0.86 Questionnaire for high tech managers_Friendship 21 102 0.10 0.19 0.14 0.33 0.52 0.24 0.43 0.67 0.76 0.57 0.71 0.86 0.90 Questionnaire for high tech managers_Reports 21 20 0.76 0.76 0.81 0.81 0.81 0.76 0.81 0.81 0.90 0.86 0.86 0.86 0.95 corporate law partnership_law firm 71 892 0.01 0.03 0.04 0.20 0.46 0.06 0.20 0.31 0.73 0.25 0.56 0.65 0.90 Children's network of friendship_Third grade 22 177 0.05 0.05 0.05 0.18 0.36 0.05 0.27 0.27 0.64 0.36 0.68 0.64 0.86 Children's network of friendship_Fourth grade 24 101 0.04 0.04 0.08 0.17 0.29 0.42 0.25 0.33 0.58 0.50 0.71 0.58 0.83 Children's network of friendship_Fifth grade 22 103 0.05 0.05 0.09 0.23 0.36 0.18 0.23 0.41 0.68 0.50 0.64 0.73 0.86 Questionnaire for bank_Advice-seeking 11 30 0.27 0.36 0.45 0.36 0.55 0.45 0.55 0.55 0.73 0.73 0.73 0.73 0.91 Questionnaire for bank_Satisfying 11 51 0.18 0.27 0.27 0.36 0.55 0.36 0.36 0.55 0.73 0.64 0.73 0.64 0.82 Questionnaire for bank_Confiding 11 27 0.18 0.27 0.27 0.36 0.55 0.36 0.45 0.55 0.73 0.64 0.82 0.82 0.91 Questionnaire for bank_Close-friends 11 20 0.36 0.45 0.36 0.45 0.55 0.55 0.64 0.54 0.82 0.82 0.82 0.73 0.91 Trade goods in different countries_Foods 24 307 0.04 0.04 0.08 0.21 0.38 0.04 0.17 0.33 0.67 0.17 0.67 0.58 0.88 Trade goods in different countries_Crude materials 24 307 0.04 0.04 0.04 0.21 0.38 0.04 0.21 0.29 0.71 0.17 0.54 0.71 0.88 Trade goods in different countries_Minerals 24 135 0.13 0.13 0.17 0.38 0.58 0.29 0.50 0.58 0.79 0.58 0.83 0.88 0.92 Trade goods in different countries_Diplomacy 24 369 0.04 0.04 0.04 0.21 0.29 0.04 0.12 0.33 0.58 0.12 0.63 0.75 0.83 Questionnaire for grade seven students_Get on 29 361 0.03 0.03 0.03 0.21 0.34 0.03 0.10 0.34 0.65 0.10 0.52 0.59 0.90 Questionnaire for grade seven students_Best friends 29 181 0.03 0.03 0.03 0.17 0.45 0.14 0.21 0.45 0.72 0.48 0.59 0.62 0.93 Questionnaire for grade seven students_Work with 29 198 0.03 0.07 0.10 0.21 0.45 0.21 0.21 0.41 0.72 0.41 0.59 0.62 0.90 Friendships among high school boys_1957 73 243 0.18 0.25 0.19 0.29 0.53 0.34 0.34 0.49 0.77 0.63 0.67 0.78 0.92 Friendships among high school boys_1958 73 263 0.15 0.19 0.15 0.25 0.52 0.29 0.27 0.47 0.77 0.55 0.64 0.78 0.93 
DownLoad: CSV
-
[1] Watts D J, Strogatz S H 1998 Nature 393 440
Google Scholar
[2] Barabási A L, Albert R 1999 Science 286 509
Google Scholar
[3] 侯绿林, 老松杨, 肖延东, 白亮 2015 64 188901
Google Scholar
Hou L L, Lao S Y, Xiao Y D, Bai L 2015 Acta Phys. Sin. 64 188901
Google Scholar
[4] 徐明, 许传云, 曹克非 2017 66 028901
Google Scholar
Xu M, Xu C Y, Cao K F 2017 Acta Phys. Sin. 66 028901
Google Scholar
[5] Lin C T 1974 IEEE Trans. Autom. Control 19 201
Google Scholar
[6] Liu Y Y, Slotine J J, Barabrási A L 2011 Nature 473 167
Google Scholar
[7] Pequito S, Kar S, Aguiar A P 2016 IEEE Trans. Autom. Control 61 303
Google Scholar
[8] Yin H L, Zhang S Y 2016 Physica A 443 467
Google Scholar
[9] Yuan Z Z, Zhao C, Di Z R, Wang W X, Lai Y C 2013 Nat. Commun. 4 2447
Google Scholar
[10] Olshevsky A 2015 2015 American Control Conference (ACC) Chicago, the United States, July 1–3, 2015 p2218
[11] Olshevsky A 2014 IEEE Trans. Control. Netw. Syst. 1 249
Google Scholar
[12] Pang S P, Wang W X, Hao F, Lai Y C 2017 Sci. Rep. 7 4224
Google Scholar
[13] Menara T, Bassett D S, Pasqualetti F 2019 IEEE Trans. Autom. Control 64 3740
Google Scholar
[14] Lee B H, and Jung W S 2018 Physica A 497 15
Google Scholar
[15] Alec K, Hugo B, Marc B, Gourab G 2018 Nat. Commun. 9 2501
Google Scholar
[16] Gu S, Pasqualetti F, Cieslak M, et al. 2015 Nat. Commun. 6 8414
Google Scholar
[17] Li Y S, Ma D, Zhang H G, Sun Q Y 2015 Appl. Sci. 5 622
Google Scholar
[18] Jia T, Liu Y Y, Csóka E, Pósfai M, Slotine J J, Barabási A L 2013 Nat. Commun. 4 2002
Google Scholar
[19] Wang J J, Yu X H, Stone L 2016 Sci. Rep. 6 25627
Google Scholar
[20] Zhang R, Wang X M, Cheng M, Jia T 2019 Physica A 520 257
Google Scholar
[21] Ruths J, Ruths D 2013 Complex Networks IV. Studies in Computational Intelligence (Berlin Heidelberg: Springer) pp185−192
[22] Lu Z M, Li X F 2016 PloS One 11 e0162289
Google Scholar
[23] Thomas J, Ghosh S, Parek D, Ruths D, Ruths J 2016 Complex Networks & Their Applications V (Cham, Switzerland: Springer) p525
[24] Chen G R, Lou Y, Wang L 2019 IEEE Trans. Circuits Syst. Express Briefs 66 828
Google Scholar
[25] 蒋文君, 刘润然, 范天龙, 刘霜霜, 吕琳媛 2020 69 088904
Google Scholar
Jiang W J, Liu R R, Fan T L, Liu S S, Lü L Y 2020 Acta Phys. Sin. 69 088904
Google Scholar
[26] 陈世明, 邹小群, 吕辉, 徐青刚 2014 63 028902
Google Scholar
Chen S M, Zou X Q, Lü H, Xu Q G 2014 Acta Phys. Sin. 63 028902
Google Scholar
[27] Nie S, Wang X W, Zhang H F, Li Q L, Wang B H 2014 PloS One 9 e89066
Google Scholar
[28] Lou Y, Wang L, Chen G R 2018 IEEE Trans. Circuits Syst. Regul. Pap. 65 2983
Google Scholar
[29] Shang Y L 2019 IEEE Trans. Syst. Man Cybern.-Syst. 49 821
Google Scholar
[30] Edmonds J 1965 Can. J. Math. 17 449
Google Scholar
[31] Hopcroft J E, Karp R M 1973 SIAM J. Comput. 2 225
[32] Kalman R E 1963 J. Soc. Indus. Appl. Math. Ser. A 1 152
Google Scholar
[33] Valiant L G 1979 Theor. Comput. Sci. 8 189
Google Scholar
[34] Erdös P, Rényi A 1964 Acta Math. Hung. 12 261
Google Scholar
[35] Orsini C, Dankulov M M, Colomer-de-Simón P, et al. 2015 Nat. Commun. 6 8627
Google Scholar
[36] Yang D, Chow T W S, Zhang Y C, Chen G R 2017 2017 IEEE 15th International Conference on Industrial Informatics (INDIN) Emden Germany, July 24–26, 2017 p992
[37] Holme P, Kim B J, Yoon C N, Han S K 2002 Phys. Rev. E 65 056109
Google Scholar
[38] Nie S, Wang X W, Wang B H, Jiang L L 2016 Sci. Rep. 6 23952
Google Scholar
[39] 马秀娟 2012 电子设计工程 20 11
Google Scholar
Ma X J 2012 Electronic Design Engineering 20 11
Google Scholar
[40] Linton C F http://moreno.ss.uci.edu/data.html [2020-9-15]
DownLoad:
Catalog
Metrics
- Abstract views: 4169
- PDF Downloads: 67
- Cited By: 0
