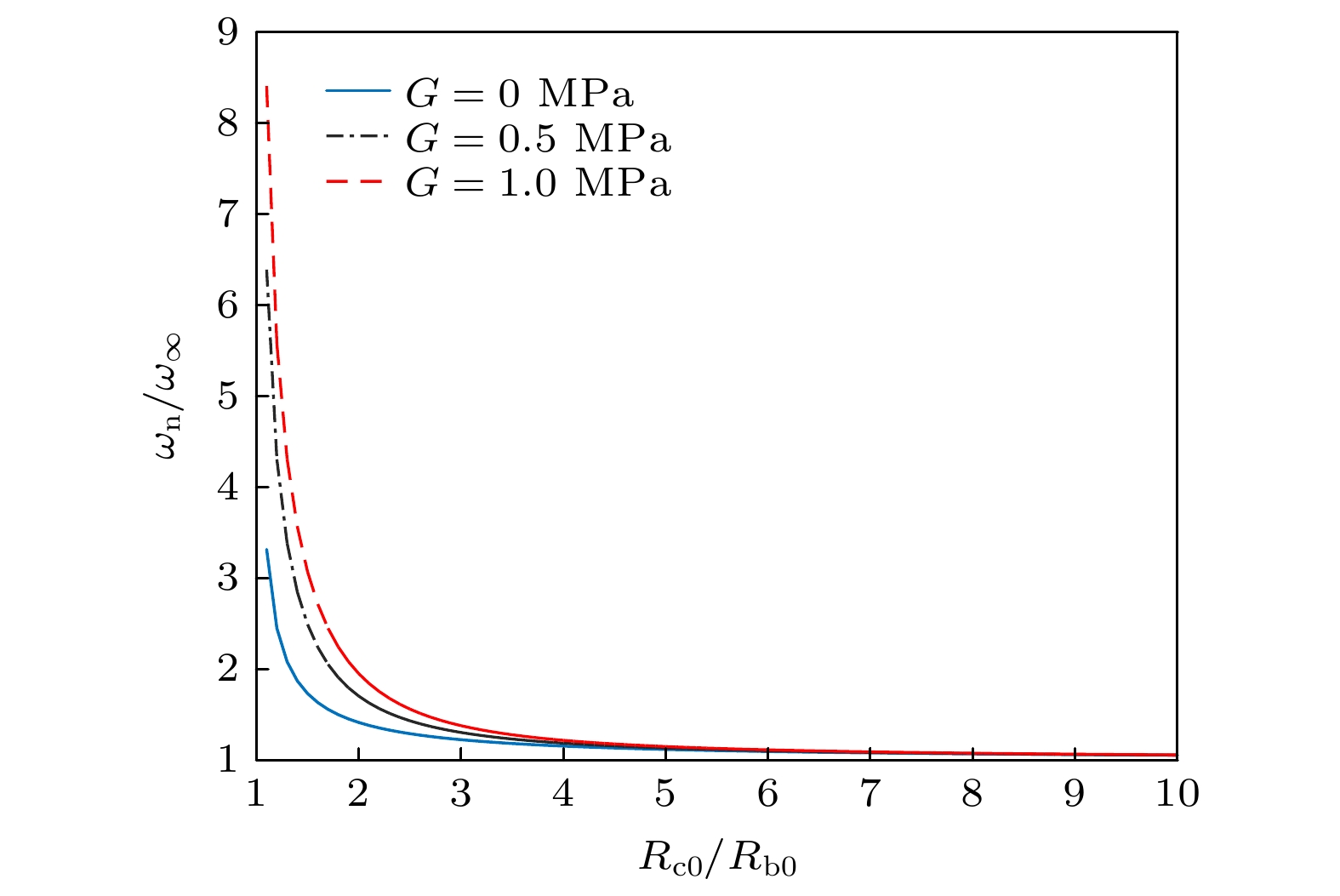
-
Ultrasonic wave with higher intensity will directly cavitate in soft tissue. It is an important issue in ultrasonic therapy that the cavitation bubbles in soft tissues are driven in the ultrasonic field. It is assumed that the medium inside the bubble is gas, the cavity is filled with the incompressible viscous liquid, and the medium surrounding the cavity is viscoelastic solid. To introduce the effect of the surrounding tissue, it is assumed that the tissue is incompressible, linear and Voigt viscoelastic solid. The motion of a cavitation bubble can be affected by many factors, such as acoustic pressure, acoustic frequency, tissue elasticity and cavity size. Numerical simulation shows that the resonance frequency and amplitude of the bubbles decrease with cavity radius decreasing. It is also shown that the amplitude of the radial motion for bubbles decreases with the increase of the tissue shear modulus and the frequency, when the ratio of bubble radius to the cavity radius is constant. The effect of the elasticity is very obvious, which reduces the amplitude greatly. The effect of elasticity will be less when the driving pressure is strong. It is found that the inertial cavitation threshold of bubble is relatively low in a range of 1–5 μm. The inertial cavitation threshold of bubble increases with the increase of shear modulus and driving frequency. The smaller the cavity radius, the higher the inertial cavitation threshold of the bubble is. This report aims to provide a firm theoretical basis for the future study of bubbles in a liquid-filled cavity surrounded by a viscoelasticity tissue.
[1] Coleman A J, Saunders J E, Crum A, Dyson M 1987 Ultrasound Med. Biol. 13 69
Google Scholar
[2] Church C C 1989 J. Acoust. Soc. Am. 86 215
Google Scholar
[3] Zhen X, Fowlkes B J, Edward D R, Albert M L, Charles A C 2005 J. Acoust. Soc. Am. 117 424
Google Scholar
[4] Adam D M, Charles A C, Alexander P D, Ling Q Y, Hitinder S G, Zhen X 2009 Ultrasound Med. Biol. 35 1982
Google Scholar
[5] Yu F Z 2011 World J. Clin. Oncol. 35 1982
Google Scholar
[6] Al-Bataineh O, Juergen J, Huber P 2012 Cancer. Treat. Rev 38 346
Google Scholar
[7] Pahk J P, Andrade M O d, Gélat P, Kim H, Saffari S 2019 Ultrason. Sonochem. 53 164
Google Scholar
[8] Xu S S, Ye D Z, Shentu Y J, Yue Y M, Wan M X, Chen H 2019 Ultrasound Med. & Biol. 45 2758
Google Scholar
[9] Tanasawa I, Yang W J 1970 Appl. Phys. 41 4526
Google Scholar
[10] Yang X M, Church C C 2005 J. Acoust. Soc. Am. 118 3595
Google Scholar
[11] Warnez M T, Johnsen E 2015 Phys. Fluids 27 628
Google Scholar
[12] Catheline S, Gennisson J L, Delon G, Fink M, Sinkus R, Abouelkaram S, Culioli J 2004 J. Acoust. Soc. Am. 116 3734
Google Scholar
[13] Roedder E, Bodnar R J 1980 Annu. Rev. Earth Planet. 8 263
Google Scholar
[14] Stroock A D, Pagay V V, Zwieniecki M A, Holbrook N M 2014 Annu. Rev. Fluid. Mech. 46 615
Google Scholar
[15] Schenk H J, Steppe K, Jansen S 2015 Trends. Plant. Sci. 20 199
Google Scholar
[16] Olivier V, Marmottant P 2012 Phys. Rev. Lett. 108 184502
Google Scholar
[17] Olivier V, Marmottant P 2017 J. Fluid Mech. 827 194
Google Scholar
[18] Wang Q X 2017 Phys. Fluids 29 072101
Google Scholar
[19] Yang W J, Yeh H C 1966 A.I.Ch. E. J. 12 927
Google Scholar
[20] Olivier V, Philippe M, Roberto G A S, Keita A, Ohl C D 2014 Soft Matter 10 1455
Google Scholar
[21] Church C C, Yang X M 2006 AIP Conf. Proc. 838 217
Google Scholar
[22] Doinikov A A, Dollet B, Marmottant P 2018 Phys. Rev. E 97 013108
Google Scholar
[23] Qin S P, Ferrara K W 2009 J. Acoust. Soc. Am. 128 1511
Google Scholar
[24] Solovchuk M A, Hwang S C, Chang H, Thiriet M, Sheu T W H 2014 Med. Phys. 41 052903
Google Scholar
-
图 1 软组织内液体腔中的气泡
Figure 1. Bubbles in the fluid cavity in the soft tissue.
图 2 腔外介质弹性不同时气泡共振频率随半径比的变化
Figure 2. Change of bubble resonance frequency with radius ratio when the elasticity of the medium outside the cavity is different.
图 3 不同模型下气泡振动对比图(本文、文献[21]、文献[18]和文献[22]分别为模型I, II, III和IV) (a) 忽略腔外介质密度模型I、II对比; (b) Pa = 0.5 MPa时模型I, II, III对比; (c) Pa = 0.1 GPa时模型I, IV对比
Figure 3. Vibration of bubbles under different models (The models of this paper, Ref. [21], Ref. [18] and Ref. [22] are called model I, II, III, IV, respectively): (a) Comparison of models I, II when ignoring the density of the medium outside the cavity; (b) Pa = 0.5 MPa, comparison of models I, II, III; (c) Pa = 0.1 GPa, comparison of models I, IV.
图 4 腔与气泡半径比Rc0/Rb0不同时对气泡径向振动的影响
Figure 4. Influence of the radius ratio of cavity to bubble (Rc0/Rb0) on the bubble radial vibration.
图 5 不同声压幅值下腔外介质弹性对气泡振动的影响 (a) Pa = 0.5 MPa, (b) Pa = 1 MPa
Figure 5. Influence of the elasticity of the medium outside the cavity on bubble vibration under different sound pressure amplitudes: (a) Pa = 0.5 MPa; (b) Pa = 1 MPa.
图 6 驱动频率对气泡振动的影响
Figure 6. Influence of driving frequency on bubble vibration.
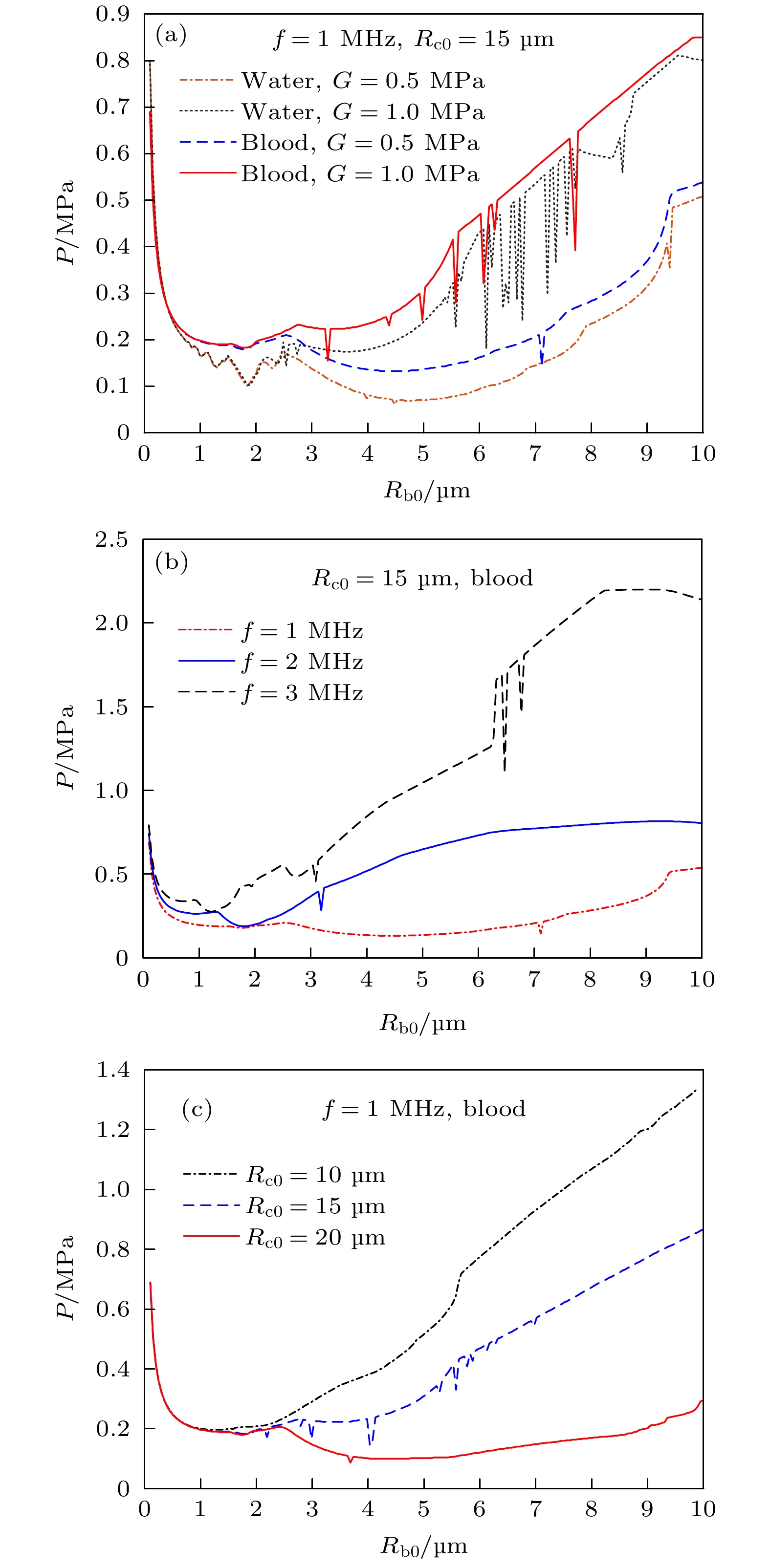
图 7 惯性空化阈值随气泡初始半径的变化趋势 (a)腔内液体及腔外介质弹性对气泡惯性空化阈值的影响; (b)不同驱动频率下气泡的惯性空化阈值; (c)液体腔半径不同时气泡的惯性空化阈值
Figure 7. Variation trend of inertial cavitation threshold with initial bubble radius at different frequencies: (a) Influence of the elasticity of the liquid in the cavity and the medium outside the cavity on the inertial cavitation threshold of the bubble; (b) inertial cavitation threshold of bubbles under different driving frequencies; (c) inertial cavitation threshold of bubbles when the radius of the liquid cavity is different.
-
[1] Coleman A J, Saunders J E, Crum A, Dyson M 1987 Ultrasound Med. Biol. 13 69
Google Scholar
[2] Church C C 1989 J. Acoust. Soc. Am. 86 215
Google Scholar
[3] Zhen X, Fowlkes B J, Edward D R, Albert M L, Charles A C 2005 J. Acoust. Soc. Am. 117 424
Google Scholar
[4] Adam D M, Charles A C, Alexander P D, Ling Q Y, Hitinder S G, Zhen X 2009 Ultrasound Med. Biol. 35 1982
Google Scholar
[5] Yu F Z 2011 World J. Clin. Oncol. 35 1982
Google Scholar
[6] Al-Bataineh O, Juergen J, Huber P 2012 Cancer. Treat. Rev 38 346
Google Scholar
[7] Pahk J P, Andrade M O d, Gélat P, Kim H, Saffari S 2019 Ultrason. Sonochem. 53 164
Google Scholar
[8] Xu S S, Ye D Z, Shentu Y J, Yue Y M, Wan M X, Chen H 2019 Ultrasound Med. & Biol. 45 2758
Google Scholar
[9] Tanasawa I, Yang W J 1970 Appl. Phys. 41 4526
Google Scholar
[10] Yang X M, Church C C 2005 J. Acoust. Soc. Am. 118 3595
Google Scholar
[11] Warnez M T, Johnsen E 2015 Phys. Fluids 27 628
Google Scholar
[12] Catheline S, Gennisson J L, Delon G, Fink M, Sinkus R, Abouelkaram S, Culioli J 2004 J. Acoust. Soc. Am. 116 3734
Google Scholar
[13] Roedder E, Bodnar R J 1980 Annu. Rev. Earth Planet. 8 263
Google Scholar
[14] Stroock A D, Pagay V V, Zwieniecki M A, Holbrook N M 2014 Annu. Rev. Fluid. Mech. 46 615
Google Scholar
[15] Schenk H J, Steppe K, Jansen S 2015 Trends. Plant. Sci. 20 199
Google Scholar
[16] Olivier V, Marmottant P 2012 Phys. Rev. Lett. 108 184502
Google Scholar
[17] Olivier V, Marmottant P 2017 J. Fluid Mech. 827 194
Google Scholar
[18] Wang Q X 2017 Phys. Fluids 29 072101
Google Scholar
[19] Yang W J, Yeh H C 1966 A.I.Ch. E. J. 12 927
Google Scholar
[20] Olivier V, Philippe M, Roberto G A S, Keita A, Ohl C D 2014 Soft Matter 10 1455
Google Scholar
[21] Church C C, Yang X M 2006 AIP Conf. Proc. 838 217
Google Scholar
[22] Doinikov A A, Dollet B, Marmottant P 2018 Phys. Rev. E 97 013108
Google Scholar
[23] Qin S P, Ferrara K W 2009 J. Acoust. Soc. Am. 128 1511
Google Scholar
[24] Solovchuk M A, Hwang S C, Chang H, Thiriet M, Sheu T W H 2014 Med. Phys. 41 052903
Google Scholar
DownLoad:
Catalog
Metrics
- Abstract views: 4965
- PDF Downloads: 72
- Cited By: 0
