A multifunctional quantum teleportation network

Zhou Yao-Yao; Liu Yan-Hong; Yan Zhi-Hui; Jia Xiao-Jun

doi:10.7498/aps.70.20201749

Abstract

Quantum teleportation is one of the most basic quantum protocols, which transfers an unknown quantum state from one location to another through local operation and classical communication by using shared quantum entanglement without physical transfer of the information carrier. And it has been widely used in various quantum information protocols such as entanglement swapping, quantum repeaters, quantum gate teleportation, quantum computation based on measurement, and quantum teleportation networks, which have important application value in quantum computation and quantum information. Quantum teleportation is a naturally bipartite process, in which an unknown quantum state can only be transmitted from one node to another. With the further development of quantum information research, it is necessary to transfer quantum states or quantum information among more and more nodes. Multipartite quantum protocols are expected to form fundamental components for larger-scale quantum communication and computation. A bipartite quantum teleportation should be extended to a multipartite protocol known as a quantum teleportation network. In this paper, a multifunctional quantum teleportation network is proposed theoretically. We first propose a special method of constructing four-partite quantum resources in continuous variables (CVs), and based on this, construct two different types of CV quantum teleportation networks. One type of network contains just one quantum teleportation process consisting of a sender, a receiver and two controllers. In this type of network, the unknown quantum state can be recovered at any other node according to the requirement after the measurement in the input node, which enriches the transfer direction and transfer mode of the unknown quantum state. And meanwhile, the two controllers can control the transfer of a quantum state from the sender to the receiver by restricting the sender and receiver’s access to their information, which makes the quantum teleportation network controllable. The other type of network has two quantum teleportation processes, each containing only a sender, a receiver and no controllers, which increases the number of quantum states that can be transmitted. Then we analyze the dependence of the fidelity of each quantum teleportation network on different physical parameters, and compare the characteristics, advantages and disadvantages among different types of quantum teleportation networks. The scheme for constructing a multifunctional quantum teleportation network in this paper shows some advantages, such as the greater number of quantum nodes, diversity of types, simple operation procedure. And all these advantages provide a broader application prospect for establishing larger and more complex quantum information networks in the future and quicken the pace of the application of quantum information.

Keywords:

Authors and contacts

1.
Department of Physics, Taiyuan Normal University, Jinzhong 030619, China
2.
State Key Laboratory of Quantum Optics and Quantum Optics Devices, Institute of Opto-Electronics, Shanxi University, Taiyuan 030006, China
3.
Collaborative Innovation Center of Extreme Optics, Shanxi University, Taiyuan 030006, China

Corresponding author: Zhou Yao-Yao, zhouyaoyaofangxia@163.com

Funds: Project supported by the National Natural Science Foundation of China (Grant Nos. 11804246, 11805141, 11904218, 12004276, 11847111, 61775127, 11654002), the National Key R&D Program of China (Grant No. 2016YFA0301402), the Natural Science Foundation of Shanxi Province, China (Grant No. 201901D111293), the Program for the Outstanding Innovative Teams of Higher Learning Institutions of Shanxi, Scientific and Technological Innovation Programs of Higher Education Institutions in Shanxi, China (Grant Nos. 2019L0794, 2020L0516), the Program for Sanjin Scholars of Shanxi Province, the Fund for Shanxi “1331Project” Key Subjects Construction, China, the Program for the Outstanding Innovative Teams of Higher Learning Institutions of Shanxi, China and the “1331Program” of Taiyuan Normal University

FullText HTML : translate this paragraph

References

[1]	Bennett C H, Brassard G, Crépeau C, Jozsa R, Peres A, Wootters W K 1993 Phys. Rev. Lett. 70 1895 Google Scholar
[2]	Bouwmeester D, Pan J W, Mattle K, Eibl M, Weinfurter H, Zeilinger A 1997 Nature 390 575 Google Scholar
[3]	Boschi D, Branca S, Martini F D, Hardy L, Popescu S 1998 Phys. Rev. Lett. 80 1121 Google Scholar
[4]	Nielsen M A, Knill E, Laflamme R 1998 Nature 396 52 Google Scholar
[5]	Marcikic I, Riedmatten H D, Tittel W, Zbinden H, Gisin N 2003 Nature 421 509 Google Scholar
[6]	Furusawa A, Sørensen J L, Braunstein S L, Fuchs C A, Kimble H J, Polzik E S 1998 Science 282 706 Google Scholar
[7]	Bowen W P, Treps N, Buchler B C, Schnabel R, Ralph T C, Bachor H A, Symul T, Lam P K 2003 Phys. Rev. A 67 032302 Google Scholar
[8]	Zhang T C, Goh K W, Chou C W, Lodahl P, Kimble H J 2003 Phys. Rev. A 67 033802 Google Scholar
[9]	Su X L, Tian C X, Deng X W, Li Q, Xie C D, Peng K C 2016 Phys. Rev. Lett. 117 240503 Google Scholar
[10]	Pan J W, Bouwmeester D, Weinfurter H, Zeilinger A 1998 Phys. Rev. Lett. 80 3891 Google Scholar
[11]	Makino K, Hashimoto Y, Yoshikawa J I, Ohdan H, Toyama T, Loock P V, Furusawa A 2016 Sci. Adv. 2 e1501772 Google Scholar
[12]	Briegel H J, Dür W, Cirac J I, Zoller P 1998 Phys. Rev. Lett. 81 5932 Google Scholar
[13]	Xu J S, Yung M H, Xu X Y, Tang J S, Li C F, Guo G C 2016 Sci. Adv. 2 e1500672 Google Scholar
[14]	Gottesman D, Chuang I L 1999 Nature 402 390 Google Scholar
[15]	Raussendorf R, Briegel H J 2001 Phys. Rev. Lett. 86 5188 Google Scholar
[16]	Bouchard F, Fickler R, Boyd R W, Karimi E 2017 Sci. Adv. 3 e1601915 Google Scholar
[17]	Vaidman L 1994 Phys. Rev. A 49 1473 Google Scholar
[18]	Ren J G, Xu P, Yong H L, et al. 2017 Nature 549 70 Google Scholar
[19]	Huo M R, Qin J L, Cheng J L, Yan Z H, Qin Z Z, Su X L, Jia X J, Xie C D, Peng K C 2018 Sci. Adv. 4 eaas9401 Google Scholar
[20]	Su X L, Zhao Y P, Hao S H, Jia X J, Xie C D, Peng K C 2012 Opt. Lett. 37 5178 Google Scholar
[21]	Yukawa M, Ukai R, Loock P V, Furusawa A 2008 Phys. Rev. A 78 012301 Google Scholar
[22]	Loock P V, Braunstein S L 2000 Phys. Rev. Lett. 84 3482 Google Scholar
[23]	Yonezawa H, Aoki T, Furusawa A 2004 Nature 431 430 Google Scholar
[24]	Karlsson A, Bourennane M 1998 Phys. Rev. A 58 4394 Google Scholar
[25]	Lee J, Kim M S 2000 Phys. Rev. Lett. 84 4236 Google Scholar
[26]	Lee J, Min H, Oh S D 2002 Phys. Rev. A 66 052318 Google Scholar
[27]	Chen X B, Xu G, Yang Y X, Wen Q Y 2010 Opt. Commun. 283 4802 Google Scholar
[28]	Zheng Y Z, Gu Y J, Guo G C 2002 Chin. Phys. B 11 537 Google Scholar
[29]	Man Z X, Xia Y J, An N B 2007 Phys. Rev. A 75 052306 Google Scholar
[30]	Li S S, Nie Y Y, Hong Z H, Yi X J, Huang Y B 2008 Commun. in Theoretical Phys. 50 633 Google Scholar
[31]	Pirandola S, Eisert J, Weedbrook C, Furusawa A, Braunstein S L 2015 Nat. Photonics 9 641 Google Scholar
[32]	He G Q, Zhang J T, Zeng G H 2008 J. Phys. B: At. Mol. Opt. Phys. 41 215503 Google Scholar
[33]	Ren L J, He G Q, Zeng G H 2008 Phys. Rev. A 78 042302 Google Scholar
[34]	Takeno Y, Yukawa M, Yonezawa H, Furusawa A 2007 Opt. Express 15 4321 Google Scholar
[35]	Vahlbruch H, Mehmet M, Chelkowski S, Hage B, Franzen A, Lastzka N, Goßler S, Danzmann K, Schnabel R 2008 Phys. Rev. Lett. 100 033602 Google Scholar
[36]	Zhou Y Y, Jia X J, Li F, Xie C D, Peng K C 2015 Opt. Express 23 4952 Google Scholar
[37]	Braunstein S L, Fuchs C A, Kimble H J 2000 J. Mod. Opt. 47 267 Google Scholar
[38]	Braunstein S L, Fuchs C A, Kimble H J, Loock P V 2001 Phys. Rev. A 64 022321 Google Scholar
[39]	Yu T, Eberly J H 2009 Science 323 598 Google Scholar
[40]	Almeida M P, Melo F D, Hor-Meyll M, Salles A, Walborn S P, Ribeiro P H S, Davidovich L 2007 Science 316 579 Google Scholar
[41]	Barbara M T 2015 Rev. Mod. Phys. 87 307 Google Scholar
[42]	Duan L, Guo G 1999 Phys. Lett. A 255 209 Google Scholar
[43]	Vahlbruch H, Mehmet M, Danzmann K, Schnabel R 2016 Phys. Rev. Lett. 117 110801 Google Scholar

Cited By

图 1 四组份量子资源的产生装置原理图

Figure 1. Schematic diagram of four-partite quantum resource generation system.

DownLoad: Full-Size Img PowerPoint

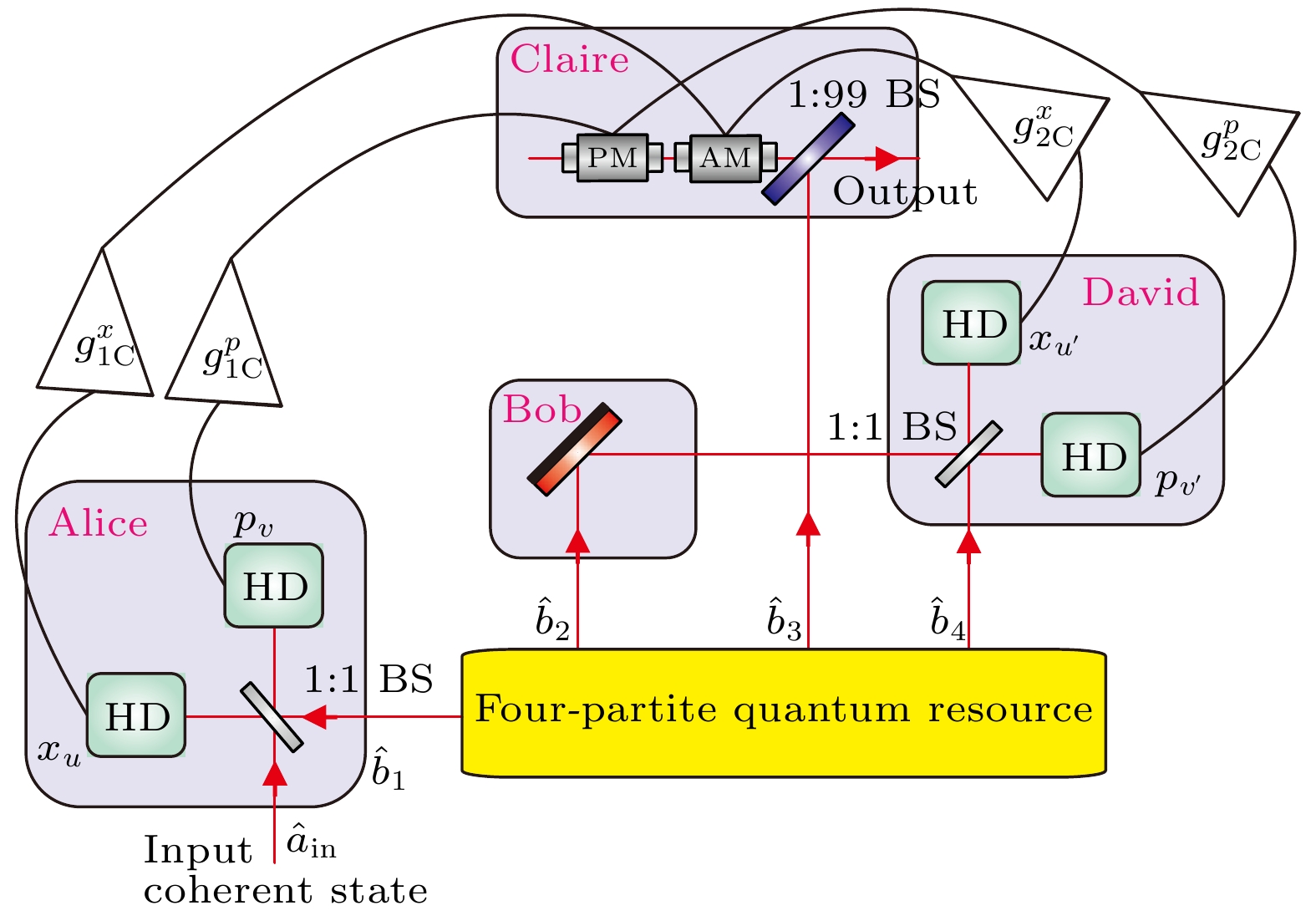
图 2 将一个未知量子态传送至Claire处的四组份量子远程传态网络的结构示意图, 其中AM为振幅调制器, PM为位相调制器, BS为分束器, HD为平衡零拍探测器

Figure 2. Schematic diagram of four-partite quantum teleportation network teleporting an unknown quantum state to Claire, where AM is Amplitude modulator, PM is Phase modulator, BS is Beam splitter, HD is Homodyne detector.

DownLoad: Full-Size Img PowerPoint

图 3 四用户量子远程传态保真度随增益因子g的变化曲线, 曲线1—3分别对应压缩参数为0.5, 0.8和1.5时的保真度大小

Figure 3. Dependences of the fidelity of quantum teleportation with four parties on gain factor g, the traces 1, 2 and 3 are the calculated fidelity when squeezing factor r is selected as 0.5, 0.8 and 1.5, respectively.

DownLoad: Full-Size Img PowerPoint

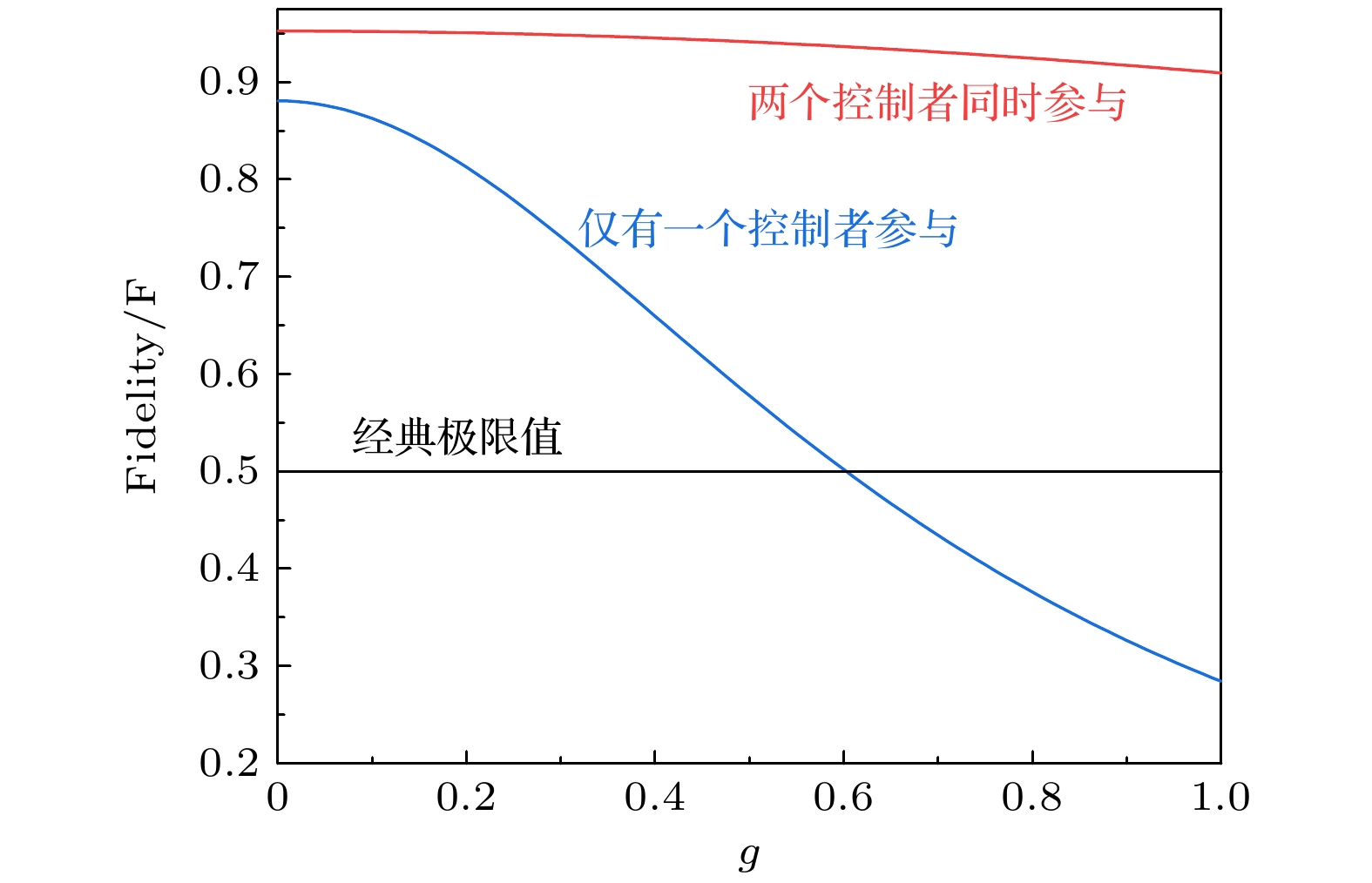
图 4 控制方数量不同的量子远程传态保真度随增益因子g的变化曲线对比图, 曲线1表示有两个控制者参与时的保真度, 曲线2表示仅有一个控制者参与时的保真度, 曲线3表示远程传态保真度的经典极限值

Figure 4. Dependences of the fidelity of quantum teleportation with different number of controllers on gain factor g, trace 1 is the calculated fidelity of quantum teleportation with two controllers, trace 2 is the calculated fidelity of quantum teleportation with only one controller, trace 3 is the classical limit of quantum teleportation.

DownLoad: Full-Size Img PowerPoint

图 5 可同时传送两个未知量子态的量子远程传态网络结构示意图, 其中 AM为振幅调制器, PM为位相调制器, BS为分束器, HD为平衡零拍探测器

Figure 5. Schematic diagram of four-partite quantum teleportation network that can simultaneously teleport two unknown quantum states, where AM is Amplitude modulator; PM is Phase modulator, BS is Beam splitter, HD is Homodyne detector.

DownLoad: Full-Size Img PowerPoint

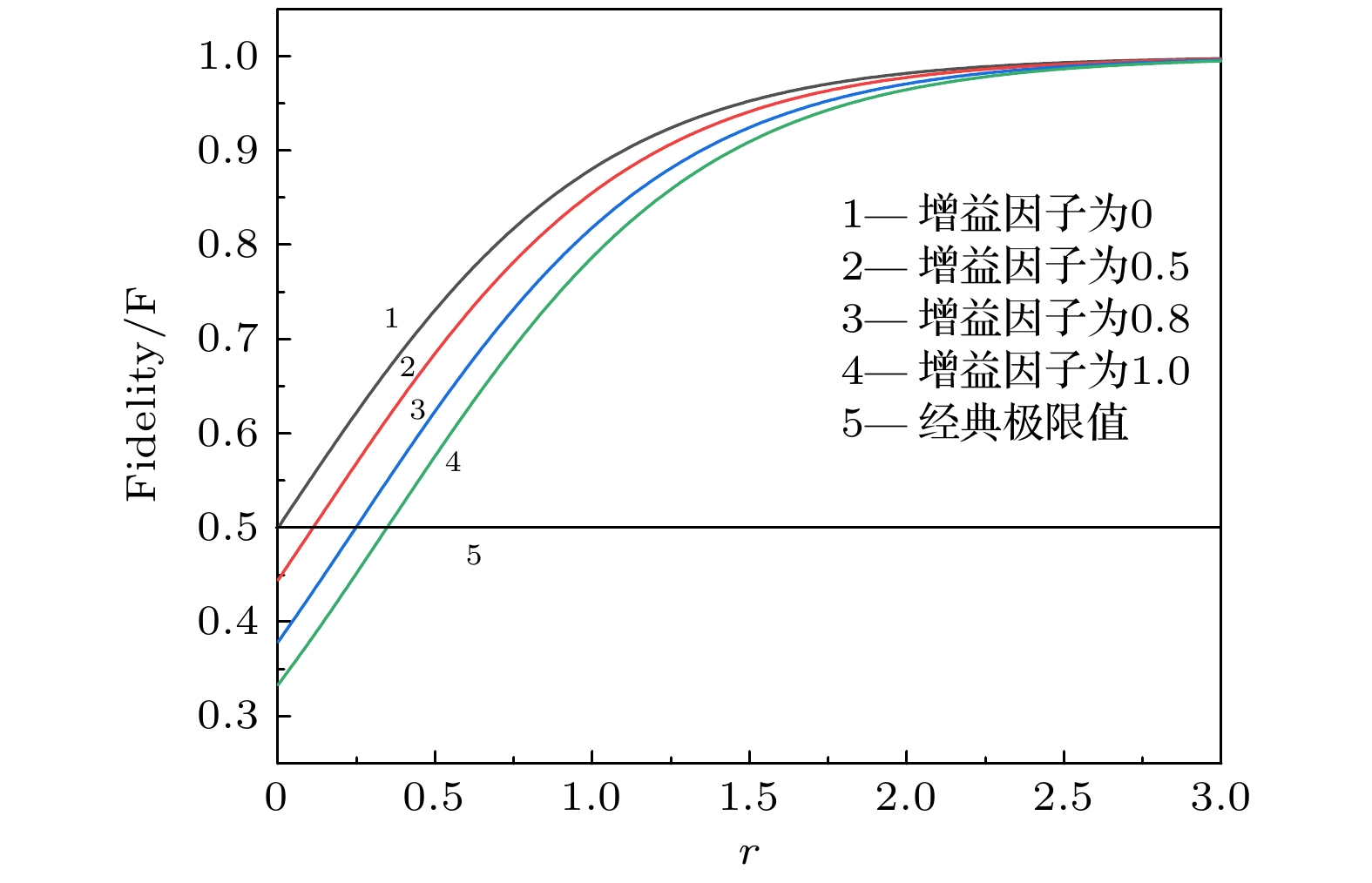
图 6 量子远程传态保真度随压缩参数r的变化曲线, 曲线1—4分别对应增益因子为0, 0.5, 0.8和1时的保真度大小, 曲线5表示远程传态保真度的经典极限值

Figure 6. Dependences of the fidelity of quantum teleportation on squeezing factor r, the traces 1, 2, 3 and 4 are the calculated fidelity when gain factor is selected as 0, 0.5, 0.8 and 1, respectively, trace 5 is the classical limit of quantum teleportation.

DownLoad: Full-Size Img PowerPoint

map

[1]	Bennett C H, Brassard G, Crépeau C, Jozsa R, Peres A, Wootters W K 1993 Phys. Rev. Lett. 70 1895 Google Scholar
[2]	Bouwmeester D, Pan J W, Mattle K, Eibl M, Weinfurter H, Zeilinger A 1997 Nature 390 575 Google Scholar
[3]	Boschi D, Branca S, Martini F D, Hardy L, Popescu S 1998 Phys. Rev. Lett. 80 1121 Google Scholar
[4]	Nielsen M A, Knill E, Laflamme R 1998 Nature 396 52 Google Scholar
[5]	Marcikic I, Riedmatten H D, Tittel W, Zbinden H, Gisin N 2003 Nature 421 509 Google Scholar
[6]	Furusawa A, Sørensen J L, Braunstein S L, Fuchs C A, Kimble H J, Polzik E S 1998 Science 282 706 Google Scholar
[7]	Bowen W P, Treps N, Buchler B C, Schnabel R, Ralph T C, Bachor H A, Symul T, Lam P K 2003 Phys. Rev. A 67 032302 Google Scholar
[8]	Zhang T C, Goh K W, Chou C W, Lodahl P, Kimble H J 2003 Phys. Rev. A 67 033802 Google Scholar
[9]	Su X L, Tian C X, Deng X W, Li Q, Xie C D, Peng K C 2016 Phys. Rev. Lett. 117 240503 Google Scholar
[10]	Pan J W, Bouwmeester D, Weinfurter H, Zeilinger A 1998 Phys. Rev. Lett. 80 3891 Google Scholar
[11]	Makino K, Hashimoto Y, Yoshikawa J I, Ohdan H, Toyama T, Loock P V, Furusawa A 2016 Sci. Adv. 2 e1501772 Google Scholar
[12]	Briegel H J, Dür W, Cirac J I, Zoller P 1998 Phys. Rev. Lett. 81 5932 Google Scholar
[13]	Xu J S, Yung M H, Xu X Y, Tang J S, Li C F, Guo G C 2016 Sci. Adv. 2 e1500672 Google Scholar
[14]	Gottesman D, Chuang I L 1999 Nature 402 390 Google Scholar
[15]	Raussendorf R, Briegel H J 2001 Phys. Rev. Lett. 86 5188 Google Scholar
[16]	Bouchard F, Fickler R, Boyd R W, Karimi E 2017 Sci. Adv. 3 e1601915 Google Scholar
[17]	Vaidman L 1994 Phys. Rev. A 49 1473 Google Scholar
[18]	Ren J G, Xu P, Yong H L, et al. 2017 Nature 549 70 Google Scholar
[19]	Huo M R, Qin J L, Cheng J L, Yan Z H, Qin Z Z, Su X L, Jia X J, Xie C D, Peng K C 2018 Sci. Adv. 4 eaas9401 Google Scholar
[20]	Su X L, Zhao Y P, Hao S H, Jia X J, Xie C D, Peng K C 2012 Opt. Lett. 37 5178 Google Scholar
[21]	Yukawa M, Ukai R, Loock P V, Furusawa A 2008 Phys. Rev. A 78 012301 Google Scholar
[22]	Loock P V, Braunstein S L 2000 Phys. Rev. Lett. 84 3482 Google Scholar
[23]	Yonezawa H, Aoki T, Furusawa A 2004 Nature 431 430 Google Scholar
[24]	Karlsson A, Bourennane M 1998 Phys. Rev. A 58 4394 Google Scholar
[25]	Lee J, Kim M S 2000 Phys. Rev. Lett. 84 4236 Google Scholar
[26]	Lee J, Min H, Oh S D 2002 Phys. Rev. A 66 052318 Google Scholar
[27]	Chen X B, Xu G, Yang Y X, Wen Q Y 2010 Opt. Commun. 283 4802 Google Scholar
[28]	Zheng Y Z, Gu Y J, Guo G C 2002 Chin. Phys. B 11 537 Google Scholar
[29]	Man Z X, Xia Y J, An N B 2007 Phys. Rev. A 75 052306 Google Scholar
[30]	Li S S, Nie Y Y, Hong Z H, Yi X J, Huang Y B 2008 Commun. in Theoretical Phys. 50 633 Google Scholar
[31]	Pirandola S, Eisert J, Weedbrook C, Furusawa A, Braunstein S L 2015 Nat. Photonics 9 641 Google Scholar
[32]	He G Q, Zhang J T, Zeng G H 2008 J. Phys. B: At. Mol. Opt. Phys. 41 215503 Google Scholar
[33]	Ren L J, He G Q, Zeng G H 2008 Phys. Rev. A 78 042302 Google Scholar
[34]	Takeno Y, Yukawa M, Yonezawa H, Furusawa A 2007 Opt. Express 15 4321 Google Scholar
[35]	Vahlbruch H, Mehmet M, Chelkowski S, Hage B, Franzen A, Lastzka N, Goßler S, Danzmann K, Schnabel R 2008 Phys. Rev. Lett. 100 033602 Google Scholar
[36]	Zhou Y Y, Jia X J, Li F, Xie C D, Peng K C 2015 Opt. Express 23 4952 Google Scholar
[37]	Braunstein S L, Fuchs C A, Kimble H J 2000 J. Mod. Opt. 47 267 Google Scholar
[38]	Braunstein S L, Fuchs C A, Kimble H J, Loock P V 2001 Phys. Rev. A 64 022321 Google Scholar
[39]	Yu T, Eberly J H 2009 Science 323 598 Google Scholar
[40]	Almeida M P, Melo F D, Hor-Meyll M, Salles A, Walborn S P, Ribeiro P H S, Davidovich L 2007 Science 316 579 Google Scholar
[41]	Barbara M T 2015 Rev. Mod. Phys. 87 307 Google Scholar
[42]	Duan L, Guo G 1999 Phys. Lett. A 255 209 Google Scholar
[43]	Vahlbruch H, Mehmet M, Danzmann K, Schnabel R 2016 Phys. Rev. Lett. 117 110801 Google Scholar

[1]	Wang Jing-Li, Dong Xian-Chao, Yin Liang, Yang Zhi-Xiong, Wan Hong-Dan, Chen He-Ming, Zhong Kai. Vanadium dioxide based terahertz dual-frequency multi-function coding metasurface. Acta Physica Sinica, 2023, 72(9): 098101. doi: 10.7498/aps.72.20222321
[2]	Shi Tao, Lü Li-Hua, Li You-Quan. Selection of entanglement state in quantum repeater process. Acta Physica Sinica, 2021, 70(23): 230303. doi: 10.7498/aps.70.20211211
[3]	Li Hai-Peng, Wu Xiao, Ding Hai-Yang, Xin Ke-Wei, Wang Guang-Ming. Wideband circularly-polarized bifunction devices employing composite metasurfaces. Acta Physica Sinica, 2021, 70(2): 027803. doi: 10.7498/aps.70.20201150
[4]	Lü Ze-Qi, Xie Yan-Zhao, Gou Ming-Yue, Chen Xiao-Yu, Zhou Jin-Shan, Li Mei, Zhou Yi. Development of 200 kV multi-function pulsed radiation system. Acta Physica Sinica, 2021, 70(20): 205206. doi: 10.7498/aps.70.20210583
[5]	Huang Jiang. The protection of qudit states by weak measurement. Acta Physica Sinica, 2017, 66(1): 010301. doi: 10.7498/aps.66.010301
[6]	Xu Ming, Xu Chuan-Yun, Cao Ke-Fei. Effect of degree correlations on controllability of undirected networks. Acta Physica Sinica, 2017, 66(2): 028901. doi: 10.7498/aps.66.028901
[7]	Jia Fang, Liu Cun-Jin, Hu Yin-Quan, Fan Hong-Yi. New formula for calculating the fidelity of teleportation and its applications. Acta Physica Sinica, 2016, 65(22): 220302. doi: 10.7498/aps.65.220302
[8]	Yang Guang, Lian Bao-Wang, Nie Min. Fidelity recovery scheme for quantum teleportation in amplitude damping channel. Acta Physica Sinica, 2015, 64(1): 010303. doi: 10.7498/aps.64.010303
[9]	Hou Lü-Lin, Lao Song-Yang, Xiao Yan-Dong, Bai Liang. Recent progress in controllability of complex network. Acta Physica Sinica, 2015, 64(18): 188901. doi: 10.7498/aps.64.188901
[10]	Qin Meng, Li Yan-Biao, Bai Zhong, Wang Xiao. Effects of different Dzyaloshinskii-Moriya interaction and magnetic field on entanglement and fidelity intrinsic decoherence in a spin system. Acta Physica Sinica, 2014, 63(11): 110302. doi: 10.7498/aps.63.110302
[11]	Nie Min, Zhang Lin, Liu Xiao-Hui. Poisson survival model of quantum entanglement signaling network and fidelity analysis. Acta Physica Sinica, 2013, 62(23): 230303. doi: 10.7498/aps.62.230303
[12]	Zhao Jian-Hui. Ground state phase diagram of the quantum spin 1 Blume-Capel model: reduced density fidelity study. Acta Physica Sinica, 2012, 61(22): 220501. doi: 10.7498/aps.61.220501
[13]	Guo Zhen, Yan Lian-Shan, Pan Wei, Luo Bin, Xu Ming-Feng. Influence of decoherence of entanglement on deterministic remote state preparation. Acta Physica Sinica, 2011, 60(6): 060301. doi: 10.7498/aps.60.060301
[14]	Fang Mao-Fa, Peng Xiao-Fang, Liao Xiang-Ping, Pan Chang-Ning, Fang Jian-Shu. Fidelity of quantum teleportation of atomic-state in dissipative environment. Acta Physica Sinica, 2011, 60(9): 090303. doi: 10.7498/aps.60.090303
[15]	Lü Jing-Fen, Ma Shan-Jun. Fidelity of the photon subtracted (or added) squeezed vacuum state and squeezed cat state. Acta Physica Sinica, 2011, 60(8): 080301. doi: 10.7498/aps.60.080301
[16]	. Universal telecloning of quantum entangled states. Acta Physica Sinica, 2007, 56(12): 6797-6802. doi: 10.7498/aps.56.6797
[17]	Li Yan-Ling, Feng Jian, Meng Xiang-Guo, Liang Bao-Long. Universal quantum teleflipping and telecloning of qubit. Acta Physica Sinica, 2007, 56(10): 5591-5596. doi: 10.7498/aps.56.5591
[18]	Ye Bin, Gu Rui-Jun, Xu Wen-Bo. Robust quantum computation of the kicked Harper model and quantum chaos. Acta Physica Sinica, 2007, 56(7): 3709-3718. doi: 10.7498/aps.56.3709
[19]	Xia Yun-Jie, Wang Guang-Hui, Du Shao-Jiang. Fidelity of the scheme of continunous variables quantum teleportation via minimum-correlation mixed quantum states. Acta Physica Sinica, 2007, 56(8): 4331-4336. doi: 10.7498/aps.56.4331
[20]	Zhang Deng-Yu, Guo Ping, Gao Feng. Fidelity of two-level atoms’ quantum states in a strong thermal radiation field. Acta Physica Sinica, 2007, 56(4): 1906-1910. doi: 10.7498/aps.56.1906

Catalog

Vol. 70, Issue 10 - 2021-05-20

Metrics

Abstract views: 5558
PDF Downloads: 106
Cited By: 0

姓名
邮箱
手机号码
标题
留言内容
验证码

Search

Article

留言板