-
Based on the three-dimensional spinor Gross-Pitaevskii (GP) equation, the dynamic behavior of the Bose-Einstein condensate under the action of a time-dependent periodic external magnetic field is studied. The results show that the Bose-Einstein condensate with spin-1 in a ferromagnetic state will undergo topological deformation under the action of an external magnetic field periodically varying with time. When the two zero points of the magnetic field enter into the condensate, the density pattern of the spin-up state forms small convexities protruding upward and downward on the z-axis, respectively. As the two zero points of the magnetic field gradually coincide in the condensate, the upward and downward protruding convexities are elongated. Finally, the spin-up state in the shape of a line is distributed on the z-axis, which is consistent with the scenario of the isolated Dirac string predicted by theoretical analysis. As far as we know, magnetic monopole can be divided into positive monopole and negative monopole. The positive magnetic monopole means that all magnetic induction lines are emitted from the center of the circle. And only the Dirac string points to the center of the circle. The negative monopole is that all the magnetic induction lines point from the outside to the center of the circle, and only the Dirac string emits from the center of the circle. Magnetic monopole is a topological defect in vector field, which accords with both quantum mechanics and gauge invariance of electromagnetic field. Single magnetic monopole has been studied a lot in theory, and its analogues have been observed in experiment. But multiple monopoles and the interaction between them are still rarely studied. In this paper, multiple monopoles are produced based on the fact that the periodic magnetic field has multiple zeros. We use a new periodic magnetic field to generate a positive and negative magnetic monopole. Due to the strong external magnetic field, the vorticity in the condensate is consistent with the magnetic field of the monopole. Finally, by calculating the superfluid vorticity of the condensate, the characteristic diagram of the magnetic monopole is obtained. The results show that the condensate forms a pair of positive and negative magnetic monopoles at the two zero points of the magnetic field, corresponding to the two small convexities protruding upward and downward on the z-axis of the spin-up state, respectively. As the two zero points of the magnetic field coincide, the two Dirac strings in the positive and negative magnetic monopole gradually approach to each other, and after about 5 ms, they are completely connected, finally forming an isolated Dirac string. This result provides a new idea for further studying the isolated Dirac strings. -
Keywords:
- magnetic monopole /
- positive and negative monopoles /
- Bose-Einstein condensate /
- isolated Dirac string
[1] Milton K A 2006 Rep. Prog. Phys. 69 1637
Google Scholar
[2] Vilenkin A, Shellard E P S 1994 Cosmic Strings and Other Topological Defects (Britain: Cambridge University Press) pp397−399
[3] Guth A H 1981 Phys. Rev. D 23 347
Google Scholar
[4] Dirac P A 1931 Proc. R. Soc. Lond. A 133 60
Google Scholar
[5] Konstantin Tiurev 2017 Quantum Knots and Monopoles (Finland: School of Science) p19
[6] Blaha S 1976 Phys. Rev. Lett. 36 874
Google Scholar
[7] Salomaa M M 1987 Nature 326 367
Google Scholar
[8] Volovik G E 2009 The Universe in a Helium Droplet (Britain: Oxford University Press) p214
[9] Castelnovo C, Moessner R, Sondhi S L 2008 Nature 451 42
Google Scholar
[10] Morris D J, Tennant D A, Grigera S A, Klemke B, Castelnovo C, Moessner R, Czternasty C, Meissner M, Rule K C, Hoffmann J U, Kiefer K, Gerischer S, Slobinsky D, Perry R S 2009 Science 326 411
Google Scholar
[11] Chuang I L, Durrer R, Turok N, Yurke B 1991 Science 251 1336
Google Scholar
[12] Milde P, Köhler D, Seidel J, Eng L M, Bauer A, Chacon A, Kindervate J, Mühlbauer S, Pfleiderer C, Buhrandt S, Schütte C, Rosch A 2013 Science 340 1076
Google Scholar
[13] Choi J, Kang S, Seo S W, Kwon W J, Shin Y 2013 Phys. Rev. Lett. 111 245301
Google Scholar
[14] Choi J, Kwon W J, Shin Y 2012 Phys. Rev. Lett. 108 035301
Google Scholar
[15] Leanhardt A E, Görlitz A, Chikkatur A P, Kielpinski D, Shin Y, Pritchard D E, Ketterle W 2002 Phys. Rev. Lett. 89 190403
Google Scholar
[16] Leanhardt A E, Shin Y, Kielpinski D, Pritchard D E, Ketterle W 2003 Phys. Rev. Lett. 90 140403
Google Scholar
[17] Ogawa S, Möttönen M, Nakahara M, Ohmi T, Shimada H 2002 Phys. Rev. A 66 013617
Google Scholar
[18] Isoshima T, Nakahara M, Ohmi T, Machida K 2000 Phys. Rev. A 61 063610
Google Scholar
[19] 石康杰 1983 32 1426
Google Scholar
Shi K J 1983 Acta Phys. Sin. 32 1426
Google Scholar
[20] 曾伦武, 宋润霞 2012 61 117302
Google Scholar
Zeng L W, Song R X 2012 Acta Phys. Sin. 61 117302
Google Scholar
[21] 胡国琦, 李康 2002 51 1208
Google Scholar
Hu G Q, Li K 2002 Acta Phys. Sin. 51 1208
Google Scholar
[22] Savage C M, Ruostekoski J 2003 Phys. Rev. A 68 043604
Google Scholar
[23] Ray M W, Ruokokoski E, Kandel S, Möttönen M, Hall D S 2014 Nature 505 657
Google Scholar
[24] Martikainen J P, Collin A, Suominen K A 2002 Phys. Rev. Lett. 88 090404
Google Scholar
[25] Pietilä V, Möttönen M 2009 Phys. Rev. Lett. 103 030401
Google Scholar
[26] Zhong F, Nagaosa N, Takahashi K S, Asamitsu A, Mathieu R, Ogasawara T, Yamada H, Kawasaki M, Tokura Y, Terakura K 2003 Science 302 92
Google Scholar
[27] Pietilä V, Möttönen M 2009 Phys. Rev. Lett. 102 080403
Google Scholar
[28] Stoof H T C, Vliegen E, Khawaja U A 2001 Phys. Rev. Lett. 87 120407
Google Scholar
[29] Jaubert L D C, Holdsworth P C W 2009 Nature Phys. 5 258
Google Scholar
[30] Qi X L, Li R D, Zang J D, Zhang S C 2009 Science 323 1184
Google Scholar
[31] Ohmi T, Machida K 1998 J. Phys. Soc. Jpn. 67 1822
Google Scholar
[32] Ho T L 1998 Phys. Rev. Lett. 81 742
Google Scholar
[33] Luo H B, Li L, Liu W M 2019 Sci. Rep. 9 18804
Google Scholar
-
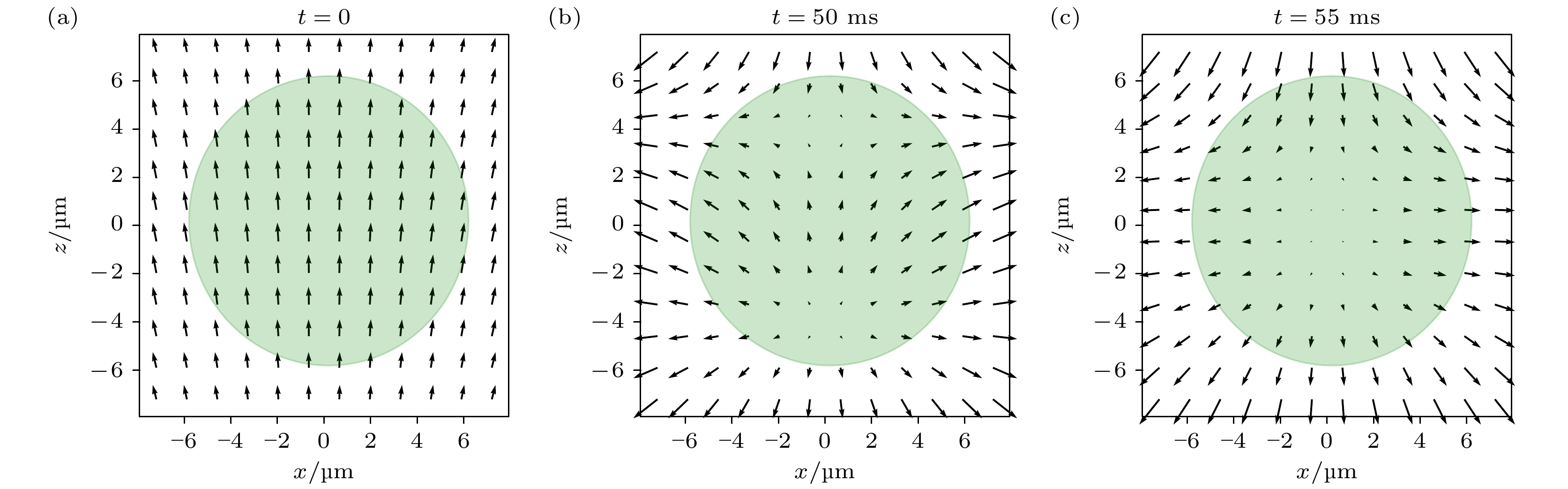
图 1 凝聚体处不同时刻的磁场在xoz平面的分布图. 箭头的方向和长度分别表示磁场的方向和大小. 绿色图案为凝聚体所在位置, 凝聚体的半径
${R_{{\rm{TF}}}}$ 可以通过托马斯-费米近似得到:${R_{{\rm{TF}}}} = 5 N{c_0}/(4 m{\omega ^2}) = 6\;{\rm{{\text{μ}} m}}$ , 其中各图分别对应时刻 (a) t = 0; (b) t = 50 ms; (c) t = 55 msFigure 1. Distributions of the magnetic field at xoz plane for different timesaround the condensation. Direction and length of arrows indicate the direction and size of the magnetic field. The green pattern indicates the condensation, radius of which is determined by Thomas-Fermi approximation, i.e.,
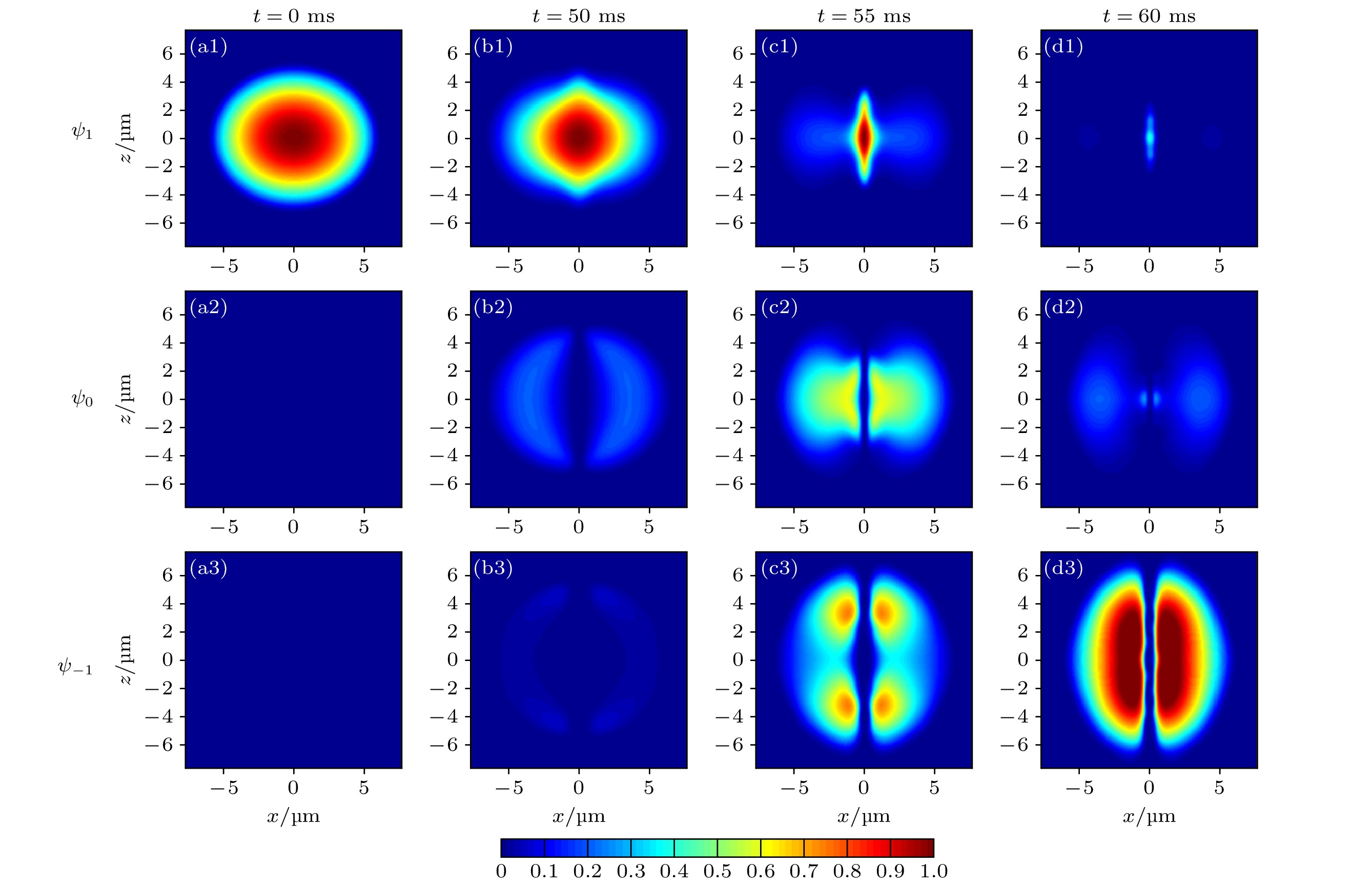
${R_{{\rm{TF}}}} = 5 N{c_0}/(4 m{\omega ^2}) = 6\;{\rm{{\text{μ}} m}}$ . (a) t = 0; (b) t = 50 ms; (c) t = 55 ms.
图 2 不同时刻凝聚体各个组分密度在xoz平面的分布图, 其中各图分别对应时刻 (a) t = 0; (b) t = 50 ms; (c) t = 55 ms; (d) t = 60 ms
Figure 2. Distributions of density of the condensation at xoz-plane for different times: (a) t = 0; (b) t = 50 ms; (c) t = 55 ms; (d) t = 60 ms.
图 3 第一行是不同时刻涡度场在xoz平面的分布图. 第二行是归一化的涡旋场, 只保留了涡旋场的方向 (a), (b) t = 50 ms; (c), (d) t = 55 ms; (e), (f) t = 60 ms
Figure 3. First row is the distributions of vorticity at xoz-plane for different times. Second row is the corresponding normalized field. (a), (b) t = 50 ms; (c), (d) t = 55 ms; (e), (f) t = 60 ms.
-
[1] Milton K A 2006 Rep. Prog. Phys. 69 1637
Google Scholar
[2] Vilenkin A, Shellard E P S 1994 Cosmic Strings and Other Topological Defects (Britain: Cambridge University Press) pp397−399
[3] Guth A H 1981 Phys. Rev. D 23 347
Google Scholar
[4] Dirac P A 1931 Proc. R. Soc. Lond. A 133 60
Google Scholar
[5] Konstantin Tiurev 2017 Quantum Knots and Monopoles (Finland: School of Science) p19
[6] Blaha S 1976 Phys. Rev. Lett. 36 874
Google Scholar
[7] Salomaa M M 1987 Nature 326 367
Google Scholar
[8] Volovik G E 2009 The Universe in a Helium Droplet (Britain: Oxford University Press) p214
[9] Castelnovo C, Moessner R, Sondhi S L 2008 Nature 451 42
Google Scholar
[10] Morris D J, Tennant D A, Grigera S A, Klemke B, Castelnovo C, Moessner R, Czternasty C, Meissner M, Rule K C, Hoffmann J U, Kiefer K, Gerischer S, Slobinsky D, Perry R S 2009 Science 326 411
Google Scholar
[11] Chuang I L, Durrer R, Turok N, Yurke B 1991 Science 251 1336
Google Scholar
[12] Milde P, Köhler D, Seidel J, Eng L M, Bauer A, Chacon A, Kindervate J, Mühlbauer S, Pfleiderer C, Buhrandt S, Schütte C, Rosch A 2013 Science 340 1076
Google Scholar
[13] Choi J, Kang S, Seo S W, Kwon W J, Shin Y 2013 Phys. Rev. Lett. 111 245301
Google Scholar
[14] Choi J, Kwon W J, Shin Y 2012 Phys. Rev. Lett. 108 035301
Google Scholar
[15] Leanhardt A E, Görlitz A, Chikkatur A P, Kielpinski D, Shin Y, Pritchard D E, Ketterle W 2002 Phys. Rev. Lett. 89 190403
Google Scholar
[16] Leanhardt A E, Shin Y, Kielpinski D, Pritchard D E, Ketterle W 2003 Phys. Rev. Lett. 90 140403
Google Scholar
[17] Ogawa S, Möttönen M, Nakahara M, Ohmi T, Shimada H 2002 Phys. Rev. A 66 013617
Google Scholar
[18] Isoshima T, Nakahara M, Ohmi T, Machida K 2000 Phys. Rev. A 61 063610
Google Scholar
[19] 石康杰 1983 32 1426
Google Scholar
Shi K J 1983 Acta Phys. Sin. 32 1426
Google Scholar
[20] 曾伦武, 宋润霞 2012 61 117302
Google Scholar
Zeng L W, Song R X 2012 Acta Phys. Sin. 61 117302
Google Scholar
[21] 胡国琦, 李康 2002 51 1208
Google Scholar
Hu G Q, Li K 2002 Acta Phys. Sin. 51 1208
Google Scholar
[22] Savage C M, Ruostekoski J 2003 Phys. Rev. A 68 043604
Google Scholar
[23] Ray M W, Ruokokoski E, Kandel S, Möttönen M, Hall D S 2014 Nature 505 657
Google Scholar
[24] Martikainen J P, Collin A, Suominen K A 2002 Phys. Rev. Lett. 88 090404
Google Scholar
[25] Pietilä V, Möttönen M 2009 Phys. Rev. Lett. 103 030401
Google Scholar
[26] Zhong F, Nagaosa N, Takahashi K S, Asamitsu A, Mathieu R, Ogasawara T, Yamada H, Kawasaki M, Tokura Y, Terakura K 2003 Science 302 92
Google Scholar
[27] Pietilä V, Möttönen M 2009 Phys. Rev. Lett. 102 080403
Google Scholar
[28] Stoof H T C, Vliegen E, Khawaja U A 2001 Phys. Rev. Lett. 87 120407
Google Scholar
[29] Jaubert L D C, Holdsworth P C W 2009 Nature Phys. 5 258
Google Scholar
[30] Qi X L, Li R D, Zang J D, Zhang S C 2009 Science 323 1184
Google Scholar
[31] Ohmi T, Machida K 1998 J. Phys. Soc. Jpn. 67 1822
Google Scholar
[32] Ho T L 1998 Phys. Rev. Lett. 81 742
Google Scholar
[33] Luo H B, Li L, Liu W M 2019 Sci. Rep. 9 18804
Google Scholar
DownLoad:
Catalog
Metrics
- Abstract views: 4771
- PDF Downloads: 90
- Cited By: 0
