-
数值研究了具有三体相互作用的均匀介质界面和半无限雅克比椭圆正弦势下准一维玻色-爱因斯坦凝聚体(Bose-Einstein condensate, BEC)中的表面带隙孤子及其稳定性. 在平均场近似下, 其动力学行为可用3次-5次Gross-Pitaevskii方程描述. 首先用牛顿-共轭梯度法寻找表面带隙孤子, 发现表面亮孤子仅当化学势小于0时才可于带隙内激发, 但表面扭结孤子和气泡孤子既可存在于带隙中也可存在于能带中. 然后采用线性稳定性分析和非线性动力学演化研究了孤子的稳定性, 结果表明三体相互作用会明显影响表面亮孤子的稳定性, 表面扭结孤子既有稳定的也有不稳定的, 但表面气泡孤子均不稳定.
-
关键词:
- 玻色-爱因斯坦凝聚体 /
- 表面带隙孤子 /
- 三体相互作用 /
- 牛顿共轭梯度法
The dynamical stability properties of surface gap solitons in quasi-one-dimensional Bose-Einstein condensate loaded in the interface between uniform media and a semi-infifinite Jacobian elliptic sine potential with three-body interactions are investigated numerically. Under the mean-fifield approximation, the dynamical behaviors can be well-described by the nonlinear cubic-quintic Gross-Pitaevskii equation. Firstly, many kinds of surface gap solitons, including the surface bright solitons, surface kink solitons and surface bubble solitons, are obtained numerically by the Newton-conjugate gradient method. The surface bright solitons can be excited in the gap only for the case that the chemical potential is negative and their power is beyond a threshold value. All of them are not bifurcated from the Bloch band. A class of surface solitons with new structures, named the surface dark solitons, can be formed when the three-body interactions are taken into account. The surface dark solitons can exist not only in gap but also in band. The numerical results indicate that the amplitude of the surface gap solitons decreases as the three-body interaction strength increases. Both linear stability analysis and nonlinear dynamical evolution methods are applied to investigate the stability properties of surface gap solitons. For surface bright solitons in the semi-infinite gap, there is a critical value when the chemical potential is given. The surface bright solitons become linearly stable as the three-body interaction exceeds the critical value, or they are linearly unstable. Therefore, the three-body interaction strength plays an important role on the stability of surface gap solitons. One can change the dynamical behaviors of surface gap solitons by adjusting the three-body interaction strength in experiments. Numerical results also show that both stable and unstable surface kink solitons exist. However, all the surface bubble solitons are unstable.-
Keywords:
- Bose-Einstein condensate /
- surface gap soliton /
- three-body interaction /
- Newton-conjugate gradient method
[1] Ketterle W 2002 Rev. Mod. Phys. 74 1131
Google Scholar
[2] Choi D, Qian N 1999 Phys. Rev. Lett. 82 2002
Google Scholar
[3] Eiermann B, Anker T, Albiez M, Taglieber M, Treutlein P, Marzlin K P, Oberthaler M K 2004 Phys. Rev. Lett. 92 230401
Google Scholar
[4] Hagley E W, Deng L, Kozuma M, Wen J, Helmerson K, Rolston S L, Phillips W D 1999 Science 283 1706
Google Scholar
[5] Dalfovo F, Giorgini S, Pitaevskii L P, Stringari S 1999 Rev. Mod. Phys. 71 463
Google Scholar
[6] Saito H, Ueda M 2001 Phy. Rev. Lett. 86 1406
Google Scholar
[7] Filho V S, Gammal A, Frederico T, Tomio L 2000 Phys. Rev. A 62 033605
Google Scholar
[8] Wang D S, Zhang D J, Yang J K 2010 J. Math. Phys. 51 023510
Google Scholar
[9] Tsatsos M C, Tavares P E S, Cidrim A, Fritsch A R, Caracanhas M A, Dos Santos F E A, Barenghi C F, Bagnato V S 2016 Phys. Rep. 622 1
Google Scholar
[10] Villois A, Krstulovic G, Proment D, Salman H 2016 J. Phys. A: Math. Theor. 49 415502
Google Scholar
[11] Wang D S, Xu L, Xuan Z 2022 J. Nonlinear. Sci. 32 3
Google Scholar
[12] 唐娜, 杨雪滢, 宋琳, 张娟, 李晓霖, 周志坤, 石玉仁 2020 69 010301
Google Scholar
Tang N, Yang X Y, Song L, Zhang J, Li X L, Zhou Z K, Shi Y R 2020 Acta Phys. Sin. 69 010301
Google Scholar
[13] Abdullaev F K, Salerno M 2005 Phys. Rev. A 72 033617
Google Scholar
[14] Will S, Best T, Schneider U, Hackermuller L, Luehmann D S, Bloch I 2010 Nature 465 197
Google Scholar
[15] Daley A J, Simon J 2013 Phys. Rev. A 89 95
Google Scholar
[16] Inouye S, Andrews M, Stenger J, Miesner H J, Ketterle W 1998 Nature 392 151
Google Scholar
[17] Eddy T, Paolo T, Mahir H, Arthur K 1999 Phys. Rep. 315 199
Google Scholar
[18] Tang N, Yang X Y, Feng W X, Song L, Li X L, Zhou Z K, Wang D S, Shi Y R 2019 Phys.A 528 121344
Google Scholar
[19] Strecker K E, Partridge G B, Truscott A G 2002 Nature 417 150
Google Scholar
[20] Chen Y J, Tran H T 1992 Optics Lett. 17 580
Google Scholar
[21] 王力, 刘静思, 李吉, 周晓林, 陈向荣, 刘超飞, 刘伍明 2020 69 010303
Google Scholar
Wang L, Liu J S, Li J, Zhou X L, Chen X R, Liu C F, Liu W M 2020 Acta Phys. Sin. 69 010303
Google Scholar
[22] Madison K W, Chevy F, Wohlleben W, Dalibard J 2000 Phys. Rev. Lett. 84 806
Google Scholar
[23] Makris K G, Suntsov S, Christodoulides D N, Stegeman G I, Hache A 2005 Optics Lett. 30 2466
Google Scholar
[24] Monkhorst H J, Pack J D 1976 Phys. Rev. B 13 5188
Google Scholar
[25] Stegeman G I, Wright E M 1988 J. Lightwave. Technol. 6 953
Google Scholar
[26] Mihalache D, Mazilu D, Bertolotti M, Sibilia C 1988 J. Opt. Soc. Am. B 5 565
Google Scholar
[27] Kawata S, Koyuncu M, Guvenç A, Baser KHC, Ozek T, Kurucu S, Koyuncu M, Guvenç A 2001 Opt. Laser. Eng. 38 604
Google Scholar
[28] Nikitov S A, Wallis R F 1994 Phys. Rev. B 50 998
Google Scholar
[29] Chen S L, Wang L X, Wen L, Dai C Q, Liu J K, Zhang X F 2021 Optik 247 167932
Google Scholar
[30] Kartashov Y V, Vysloukh V A, Torner L 2006 Phys. Rev. Lett. 96 073901
Google Scholar
[31] Wang X, Bezryadina A, Chen Z, Makris K G, Christodoulides D N, Stegeman G I 2007 Phys. Rev. Lett. 12 123903
Google Scholar
[32] Rosberg C R, Neshev D N, Krolikowski W, Mitchell A, Kivshar Y S 2006 Phys. Rev. Lett. 97 083901
Google Scholar
[33] Sabari S, Porsezian K, Murali R 2015 Phys. Rev. A 379 299
Google Scholar
[34] Bulgac A 2002 Phys. Rev. Lett. 89 050402
Google Scholar
[35] Braaten E, Hammer H W, Mehen T 2002 Phys. Rev. Lett. 88 040401
Google Scholar
[36] Bao W, Liu J G 2007 Chem. J. Chinese. U. 35 1546
Google Scholar
[37] Zhou Y S, Meng H J, Zhang J, Li X L, Ren X P, Wan X H, Zhou Z K, Wang J, Fan X B, Shi Y R 2021 Sci. Rep. 11 11382
Google Scholar
[38] Kostov N A, Enolśkii V Z, Gerdjikov V S, Konotop V V, Salerno M 2004 Phys. Rev. E 70 056617
Google Scholar
[39] Wang D L, Yan X H, Liu W M 2008 Phys. Rev. E 78 026606
Google Scholar
[40] Yang J K 2010 Nonlinear Waves in Integrable and Nonintegrable Systems (Vol. 1) (Philadelphia: SIAM) pp269–283
[41] Nascimbene S, Goldman N, Cooper N R, Dalibard J 2015 Phys. Rev. Lett. 115 140401
Google Scholar
[42] Yang J K 2009 J. Comput. Phys. 228 7007
Google Scholar
[43] Jing X, Tian Z, Huang C, Dong L 2018 Opt. Express. 26 2650
Google Scholar
[44] Zuccher S, Caliari M, Baggaley A W, Barenghi C F 2012 Phys. Fluids 24 125108
Google Scholar
[45] Allen A J, Zuccher S, Caliari M, Proukakis N P, Parker N G, Barenghi C F 2014 Phys. Rev. A 90 013601
Google Scholar
[46] Barashenkov I V, Gocheva A D, Makhankov V G, Puzynin I 1989 Phys. D 34 240
Google Scholar
-
图 1
$ q = 0, 0.8 $ 和$ 0.99 $ 时$ V(x) $ 的图像. 子图显示了$V(x) $ $ (x\geqslant 0)$ 的周期随q的变化$ (V_0=-2) $ Fig. 1. Profiles of
$ V(x) $ for$ q = 0, 0.8 $ and$0.99 \;(V_0=-2)$ . The sub-plot displays the period of$V(x) (x\geqslant0)$ versus q.
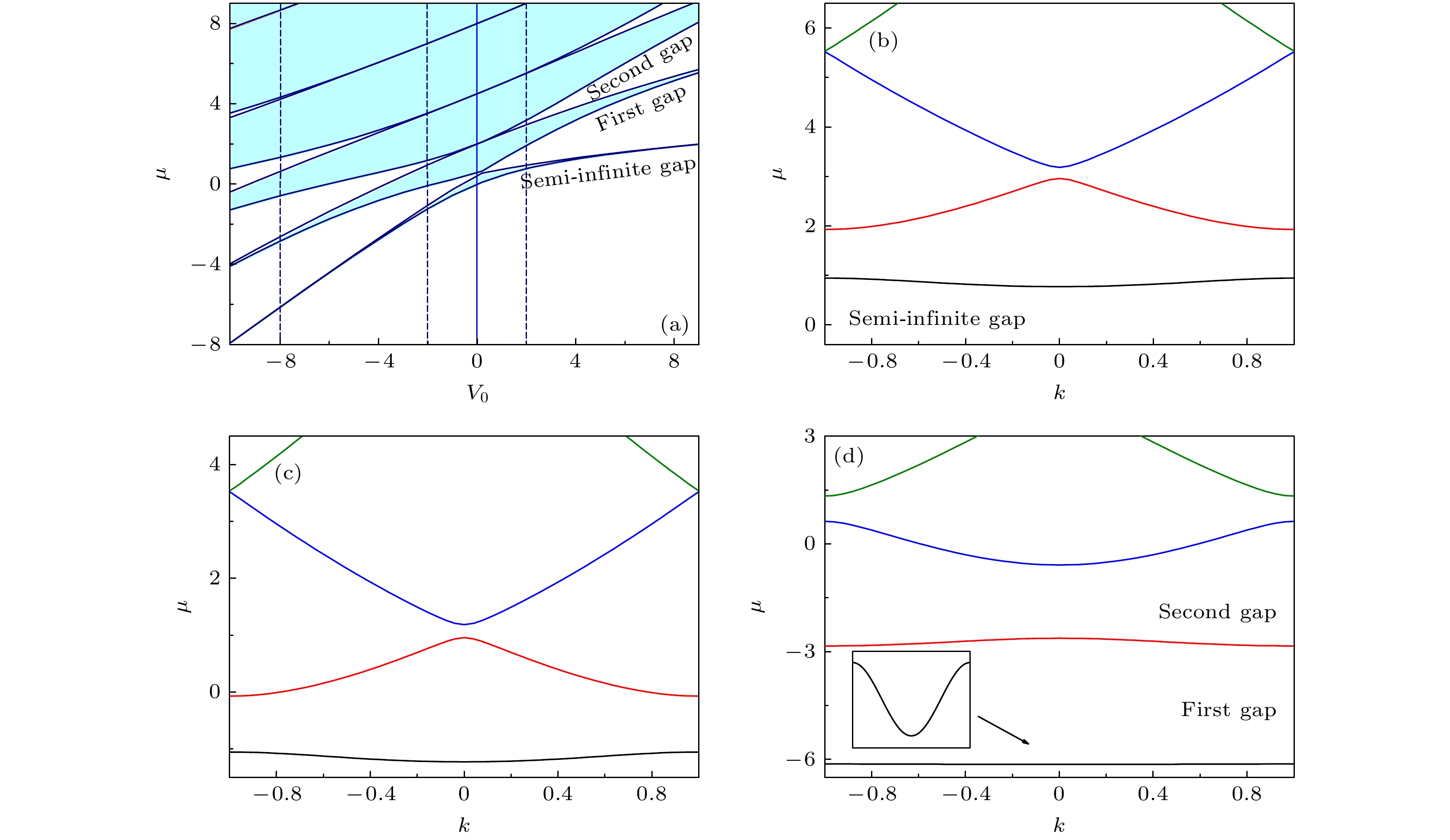
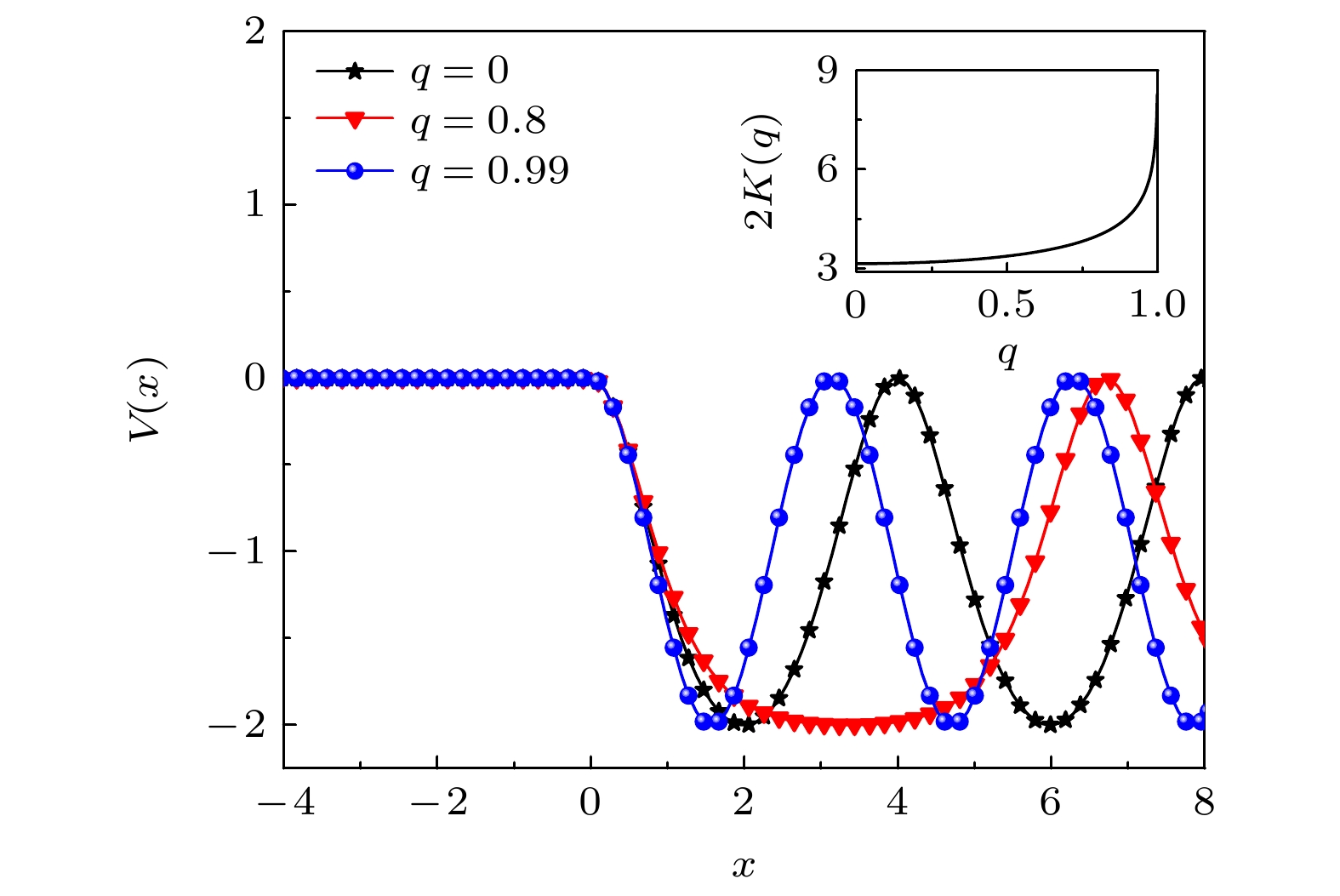
图 2 (a) 带隙结构随
$ V_0 $ 的变化($ q=0 $ ). 阴影区域代表能带, 空白区域表示带隙, 垂直虚线指示图(b)—(d)中用到的$ V_0 $ 值. 蓝色实线处为$ V_0=0 $ . (b)$ V_0 = 2 $ . (c)$ V_0 = -2 $ . (d)$ V_0 = -8 $ Fig. 2. Profiles of band-gap structures versus
$ V_0 $ ($ q=0 $ ). Bands are marked with the shaded regions, gaps are shown as blank. The vertical dashed lines identify the values that will be used in panel (b)–(d). (b)$ V_0= 2 $ ; (c)$ V_0= -2 $ ; (d)$ V_0= -8 $ .
图 3 不同三体相互作用强度
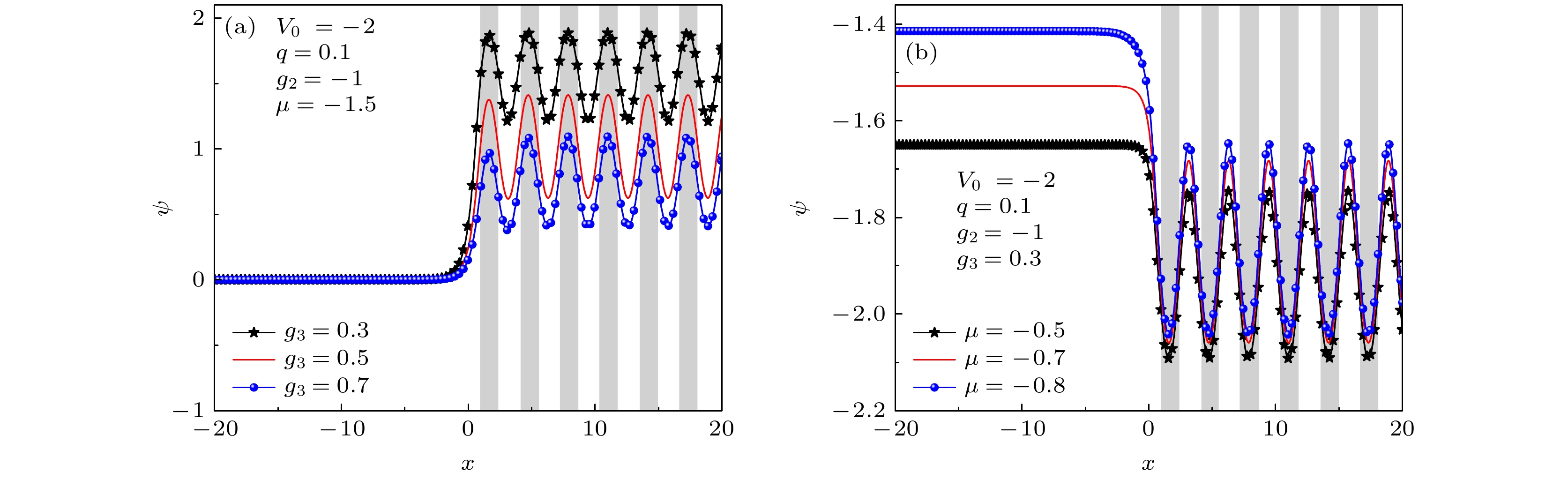
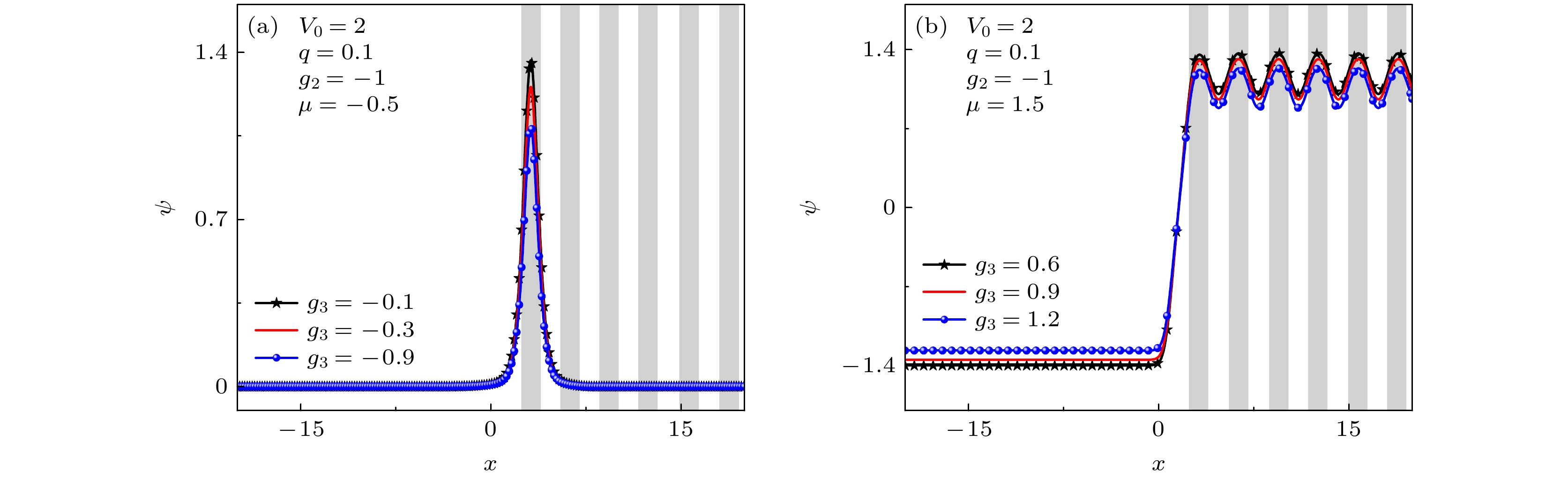
$ g_3 $ 时的表面带隙孤子 (a), (b) 半无限带隙中; (c), (d) 第一带隙中. 阴影区域表示外势$ V(x) $ 的低处Fig. 3. Profiles of surface gap solitons under different three-body interaction strength
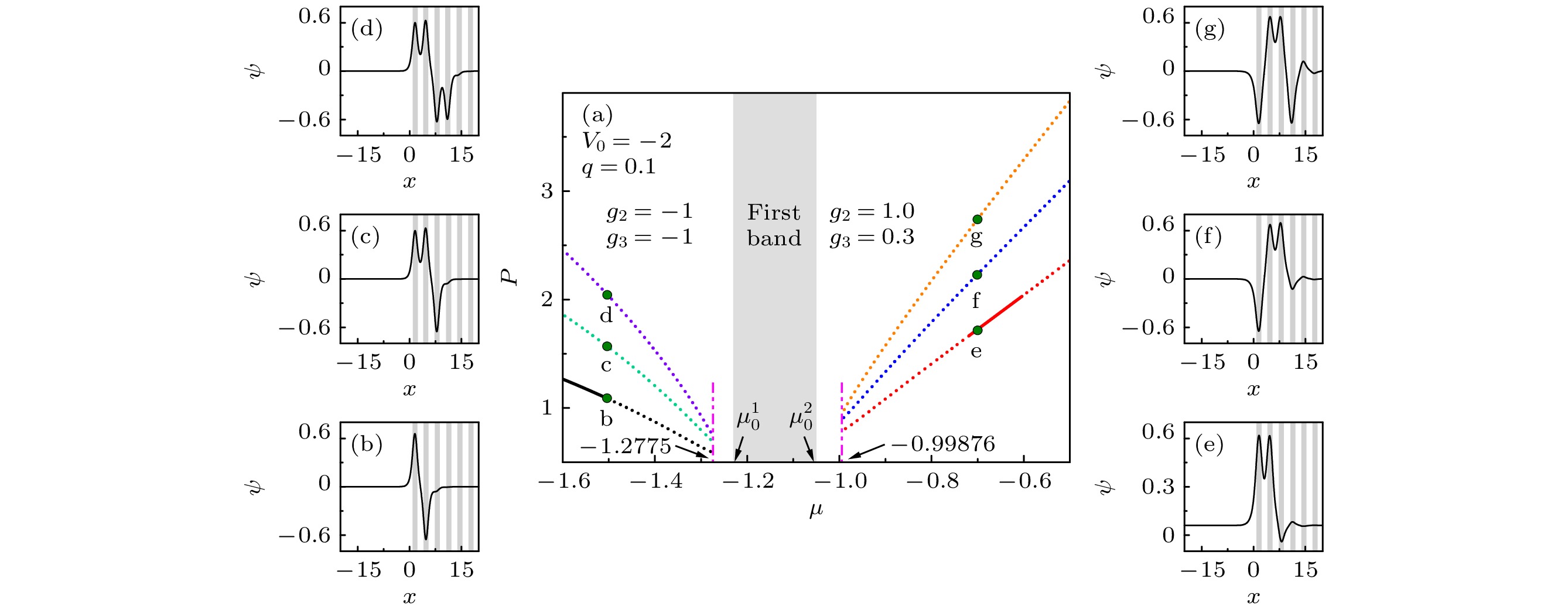
$ g_3 $ : (a), (b) In the semi-infinite gap; (c), (d) in the first gap. Shaded regions represent lattice sites, i.e., regions of low potential values of$ V(x) $ .
图 4 (a) 表面带隙孤子粒子数随化学势的变化. 实线表示稳定分支, 虚线表示不稳定分支. 图(b)—(g)分别表示图(a)中标记点处对应的孤子波形. 第一布洛赫带的边缘分别是
$ \mu_0^1\approx-1.22757 $ 和$ \mu_0^2\approx -1.05512 $ Fig. 4. (a) Power curves of surface gap solitons, which are not bifurcated from the first band edge. The dashed line are unstable branches, while the solid lines are stable ones. Soliton profiles at the marked points in panel (a) are shown in panel (b)–(g). The edges of the first Bloch band are
$ \mu_0^1\approx -1.22757 $ and$ \mu_0^2\approx -1.05512 $ .
图 5 不同参数下表面扭结孤子的波形 (a) 半无界带隙中; (b) 第一带隙中. 阴影区域表示外势
$ V(x) $ 低处Fig. 5. Profiles of surface kink solitons with different parameters. (a) In the semi-infinite gap; (b) in the first gap. Shaded regions represent lattice sites, i.e., regions of low potential values of
$ V(x) $ .
图 6 不同非线性相互作用强度
$ g_2 $ 和$ g_3 $ 下表面扭结孤子振幅随化学势μ 的变化 ($ q=0.1 $ ). 子图为标记点处孤子波形, 阴影区域表示外势$ V(x) $ 低处. 黑色圆点为相变点Fig. 6. Amplitude of surface kinks versus the chemical potential μ under different nonlinear interaction strength
$ g_2 $ and$ g_3 $ . The profiles of solitons at the marked points${P}_1, {P}_2, {P}_3$ are shown in the subplots.
图 7 表面亮孤子的线性稳定性谱 (a), (b) 半无限带隙中; (c), (d) 第一带隙中. 子图为对应波函数
Fig. 7. Linear stability spectrum of surface gap solitons: (a), (b) In the semi-infinite gap; (c), (d) in the first gap. The sub-plots are the corresponding wave functions.
图 8 不同化学势μ下表面带隙孤子扰动最大增长率
$\lambda_{\rm{m}}$ 随三体相互作用强度$ g_3 $ 的变化. 表面带隙孤子的波形如图4(b), (e)所示 (a) 半无限带隙中; (b) 第一带隙中Fig. 8. Maximum growth rate of perturbation
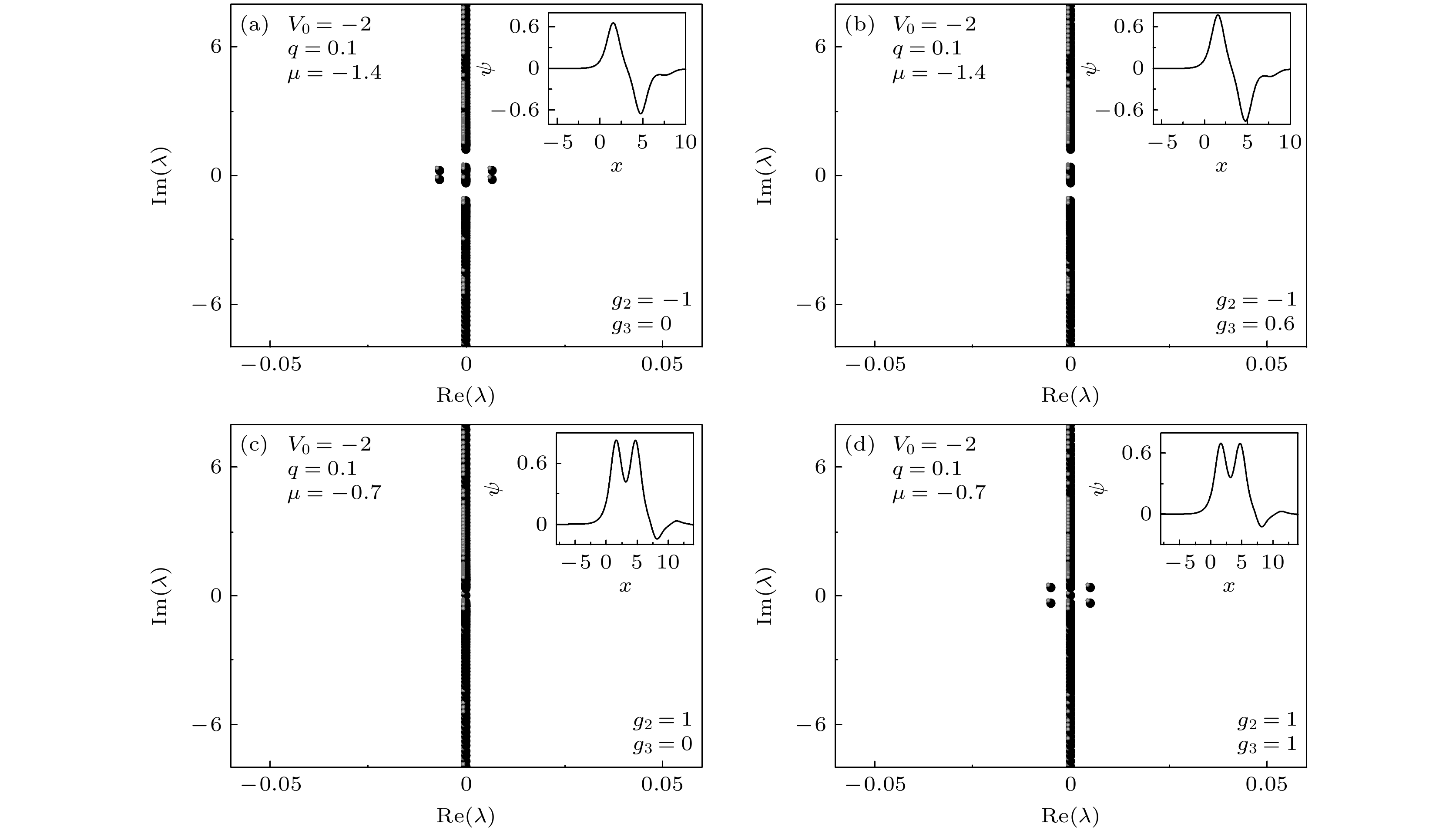
$\lambda_{\rm{m}}$ for the surface gap solitons versus the three-body interaction strength$ g_3 $ under different chemical potential μ. The profiles of surface gap solitons are similar as those in Figs. 4(b), (e): (a) In the semi-infinite gap; (b) in the first gap.
图 9 表面亮孤子非线性动力学演化等值线图 (a), (b) 半无限带隙中; (c), (d) 第一带隙中
Fig. 9. Contour plots of
$\left|\varPsi(x, t)\right|$ perturbed for surface bright solitons: (a), (b) In the semi-infinite gap; (c), (d) in the first gap.
图 10 (a) 表面扭结孤子的线性稳定性谱, 子图为相应波函数; (b) 表面扭结孤子非线性动力学演化的等值线图
Fig. 10. (a) Linear stability spectrum for the surface kink soliton, and the inset is the corresponding wave function; (b) contour plots of
$|\varPsi(x, t)|$ for the surface kink soliton.
图 11 (a), (c) 表面气泡孤子和表面扭结孤子的线性稳定性谱, 子图为相应波函数. (b), (d) 表面气泡孤子和表面扭结孤子非线性动力学演化的等值线图
Fig. 11. (a), (c) Linear stability spectra for the surface bubble and kink solitons. The insets are the corresponding wave functions. (b) Contour plots of
$\left|\varPsi(x, t)\right|$ for the surface bubble and kink solitons.
图 12 不同化学势μ下表面带隙孤子扰动最大增长率
$\lambda_{\rm{m}}$ 随外势模数q的变化 (a) 表面亮孤子, 波形见图4(e); (b) 表面气泡孤子, 波形见图11(a)Fig. 12. Maximum growth rate of perturbation
$\lambda_{\rm{m}}$ for the surface gap solitons versus q under different chemical potential μ: (a) For surface bright solitons, and the profiles are similar as that shown in Fig. 4(e); (b) for surface bubble solitons, and the profiles are similar as that shown in Fig. 11(a).
图 13
$ V_0=2 $ 时的表面亮孤子和表面扭结孤子 (a) 半无界带隙中; (b) 第一带隙中. 阴影区域表示外势$ V(x) $ 低处Fig. 13. Profiles of surface bright and kink solitons when
$ V_0=2 $ : (a) In the semi-infinite gap; (b) in the first gap. Shaded regions represent lattice sites, i.e., regions of low potential values of$ V(x) $ . -
[1] Ketterle W 2002 Rev. Mod. Phys. 74 1131
Google Scholar
[2] Choi D, Qian N 1999 Phys. Rev. Lett. 82 2002
Google Scholar
[3] Eiermann B, Anker T, Albiez M, Taglieber M, Treutlein P, Marzlin K P, Oberthaler M K 2004 Phys. Rev. Lett. 92 230401
Google Scholar
[4] Hagley E W, Deng L, Kozuma M, Wen J, Helmerson K, Rolston S L, Phillips W D 1999 Science 283 1706
Google Scholar
[5] Dalfovo F, Giorgini S, Pitaevskii L P, Stringari S 1999 Rev. Mod. Phys. 71 463
Google Scholar
[6] Saito H, Ueda M 2001 Phy. Rev. Lett. 86 1406
Google Scholar
[7] Filho V S, Gammal A, Frederico T, Tomio L 2000 Phys. Rev. A 62 033605
Google Scholar
[8] Wang D S, Zhang D J, Yang J K 2010 J. Math. Phys. 51 023510
Google Scholar
[9] Tsatsos M C, Tavares P E S, Cidrim A, Fritsch A R, Caracanhas M A, Dos Santos F E A, Barenghi C F, Bagnato V S 2016 Phys. Rep. 622 1
Google Scholar
[10] Villois A, Krstulovic G, Proment D, Salman H 2016 J. Phys. A: Math. Theor. 49 415502
Google Scholar
[11] Wang D S, Xu L, Xuan Z 2022 J. Nonlinear. Sci. 32 3
Google Scholar
[12] 唐娜, 杨雪滢, 宋琳, 张娟, 李晓霖, 周志坤, 石玉仁 2020 69 010301
Google Scholar
Tang N, Yang X Y, Song L, Zhang J, Li X L, Zhou Z K, Shi Y R 2020 Acta Phys. Sin. 69 010301
Google Scholar
[13] Abdullaev F K, Salerno M 2005 Phys. Rev. A 72 033617
Google Scholar
[14] Will S, Best T, Schneider U, Hackermuller L, Luehmann D S, Bloch I 2010 Nature 465 197
Google Scholar
[15] Daley A J, Simon J 2013 Phys. Rev. A 89 95
Google Scholar
[16] Inouye S, Andrews M, Stenger J, Miesner H J, Ketterle W 1998 Nature 392 151
Google Scholar
[17] Eddy T, Paolo T, Mahir H, Arthur K 1999 Phys. Rep. 315 199
Google Scholar
[18] Tang N, Yang X Y, Feng W X, Song L, Li X L, Zhou Z K, Wang D S, Shi Y R 2019 Phys.A 528 121344
Google Scholar
[19] Strecker K E, Partridge G B, Truscott A G 2002 Nature 417 150
Google Scholar
[20] Chen Y J, Tran H T 1992 Optics Lett. 17 580
Google Scholar
[21] 王力, 刘静思, 李吉, 周晓林, 陈向荣, 刘超飞, 刘伍明 2020 69 010303
Google Scholar
Wang L, Liu J S, Li J, Zhou X L, Chen X R, Liu C F, Liu W M 2020 Acta Phys. Sin. 69 010303
Google Scholar
[22] Madison K W, Chevy F, Wohlleben W, Dalibard J 2000 Phys. Rev. Lett. 84 806
Google Scholar
[23] Makris K G, Suntsov S, Christodoulides D N, Stegeman G I, Hache A 2005 Optics Lett. 30 2466
Google Scholar
[24] Monkhorst H J, Pack J D 1976 Phys. Rev. B 13 5188
Google Scholar
[25] Stegeman G I, Wright E M 1988 J. Lightwave. Technol. 6 953
Google Scholar
[26] Mihalache D, Mazilu D, Bertolotti M, Sibilia C 1988 J. Opt. Soc. Am. B 5 565
Google Scholar
[27] Kawata S, Koyuncu M, Guvenç A, Baser KHC, Ozek T, Kurucu S, Koyuncu M, Guvenç A 2001 Opt. Laser. Eng. 38 604
Google Scholar
[28] Nikitov S A, Wallis R F 1994 Phys. Rev. B 50 998
Google Scholar
[29] Chen S L, Wang L X, Wen L, Dai C Q, Liu J K, Zhang X F 2021 Optik 247 167932
Google Scholar
[30] Kartashov Y V, Vysloukh V A, Torner L 2006 Phys. Rev. Lett. 96 073901
Google Scholar
[31] Wang X, Bezryadina A, Chen Z, Makris K G, Christodoulides D N, Stegeman G I 2007 Phys. Rev. Lett. 12 123903
Google Scholar
[32] Rosberg C R, Neshev D N, Krolikowski W, Mitchell A, Kivshar Y S 2006 Phys. Rev. Lett. 97 083901
Google Scholar
[33] Sabari S, Porsezian K, Murali R 2015 Phys. Rev. A 379 299
Google Scholar
[34] Bulgac A 2002 Phys. Rev. Lett. 89 050402
Google Scholar
[35] Braaten E, Hammer H W, Mehen T 2002 Phys. Rev. Lett. 88 040401
Google Scholar
[36] Bao W, Liu J G 2007 Chem. J. Chinese. U. 35 1546
Google Scholar
[37] Zhou Y S, Meng H J, Zhang J, Li X L, Ren X P, Wan X H, Zhou Z K, Wang J, Fan X B, Shi Y R 2021 Sci. Rep. 11 11382
Google Scholar
[38] Kostov N A, Enolśkii V Z, Gerdjikov V S, Konotop V V, Salerno M 2004 Phys. Rev. E 70 056617
Google Scholar
[39] Wang D L, Yan X H, Liu W M 2008 Phys. Rev. E 78 026606
Google Scholar
[40] Yang J K 2010 Nonlinear Waves in Integrable and Nonintegrable Systems (Vol. 1) (Philadelphia: SIAM) pp269–283
[41] Nascimbene S, Goldman N, Cooper N R, Dalibard J 2015 Phys. Rev. Lett. 115 140401
Google Scholar
[42] Yang J K 2009 J. Comput. Phys. 228 7007
Google Scholar
[43] Jing X, Tian Z, Huang C, Dong L 2018 Opt. Express. 26 2650
Google Scholar
[44] Zuccher S, Caliari M, Baggaley A W, Barenghi C F 2012 Phys. Fluids 24 125108
Google Scholar
[45] Allen A J, Zuccher S, Caliari M, Proukakis N P, Parker N G, Barenghi C F 2014 Phys. Rev. A 90 013601
Google Scholar
[46] Barashenkov I V, Gocheva A D, Makhankov V G, Puzynin I 1989 Phys. D 34 240
Google Scholar
下载:
计量
- 文章访问数: 3330
- PDF下载量: 127
- 被引次数: 0
