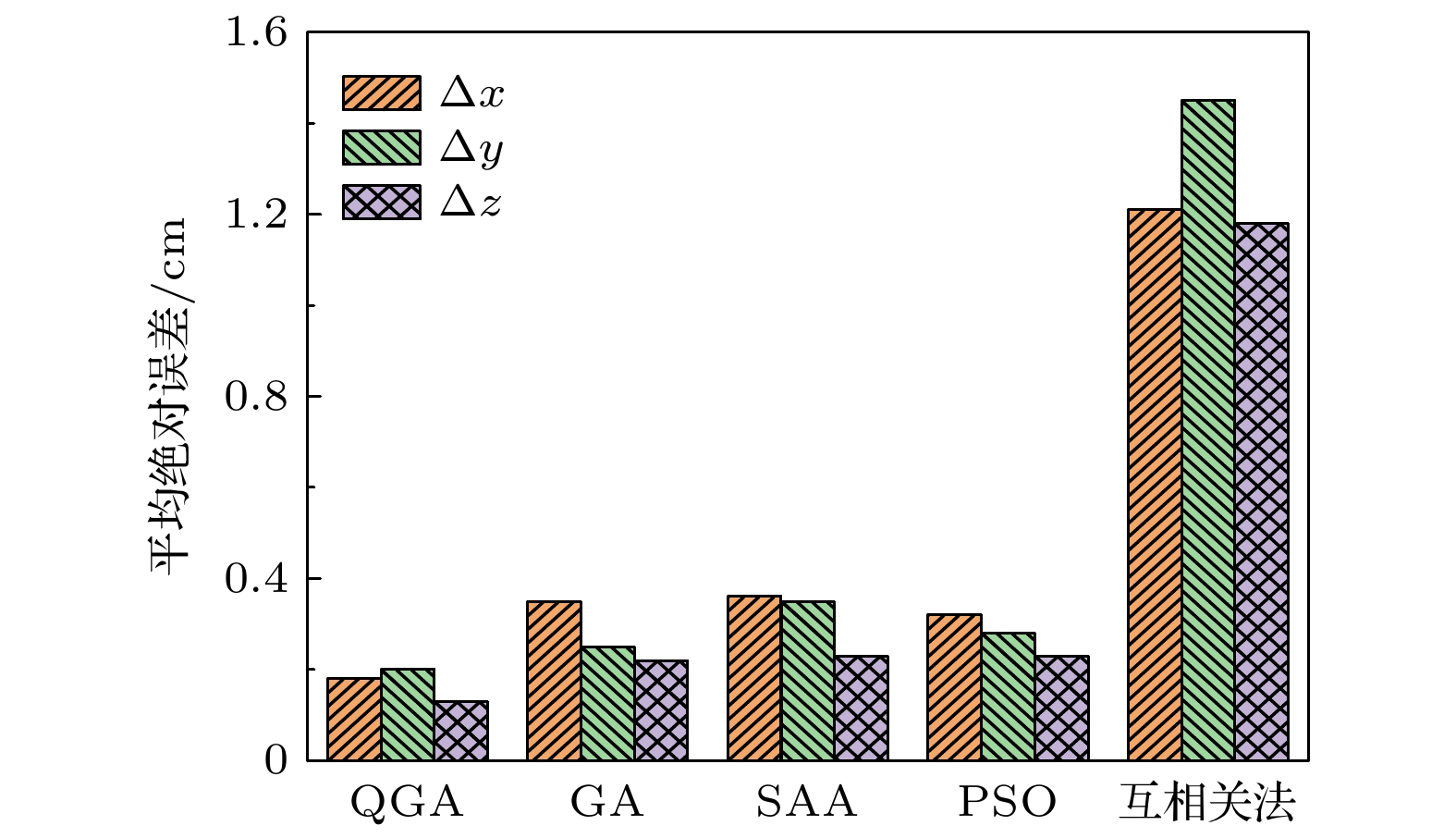
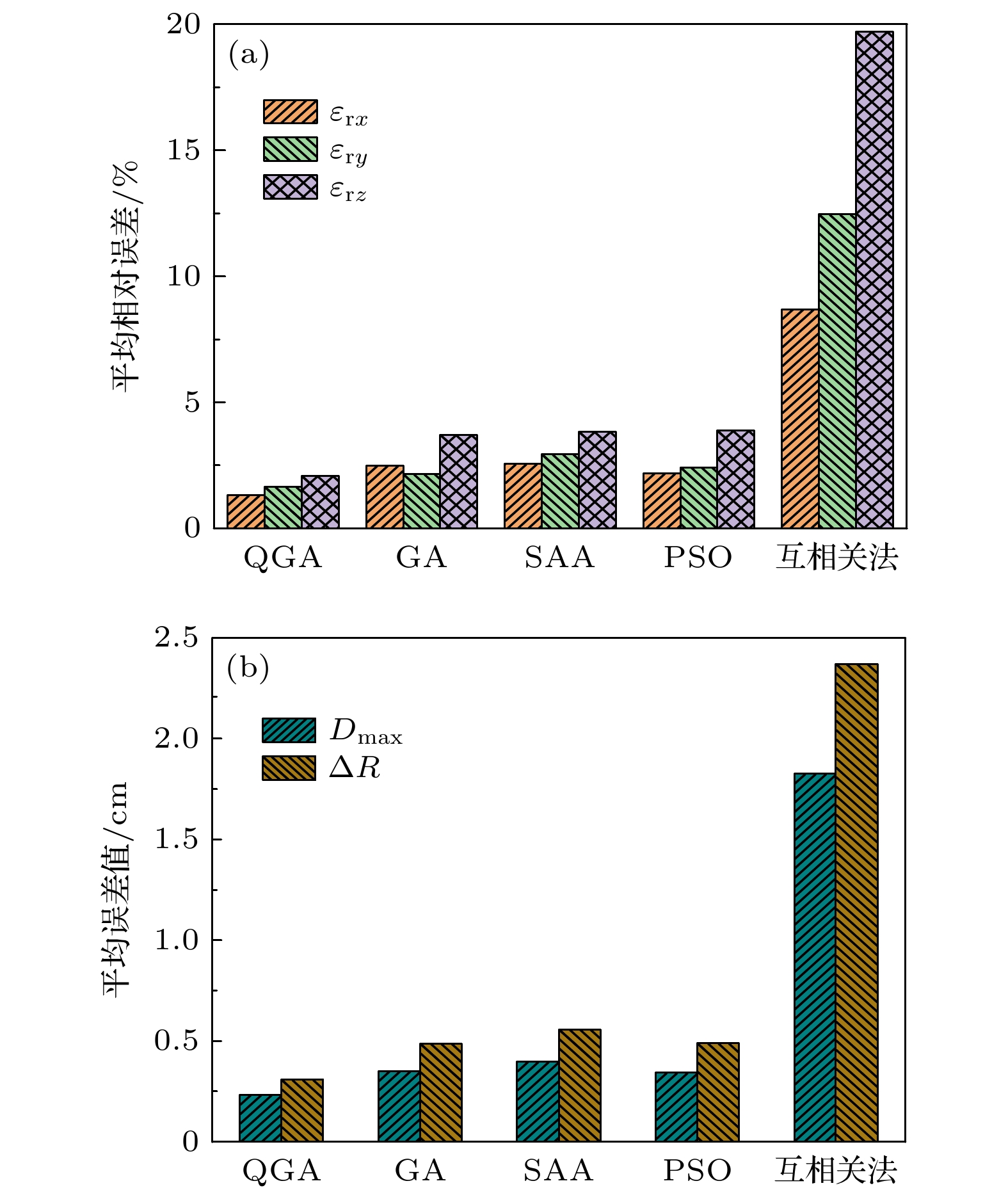
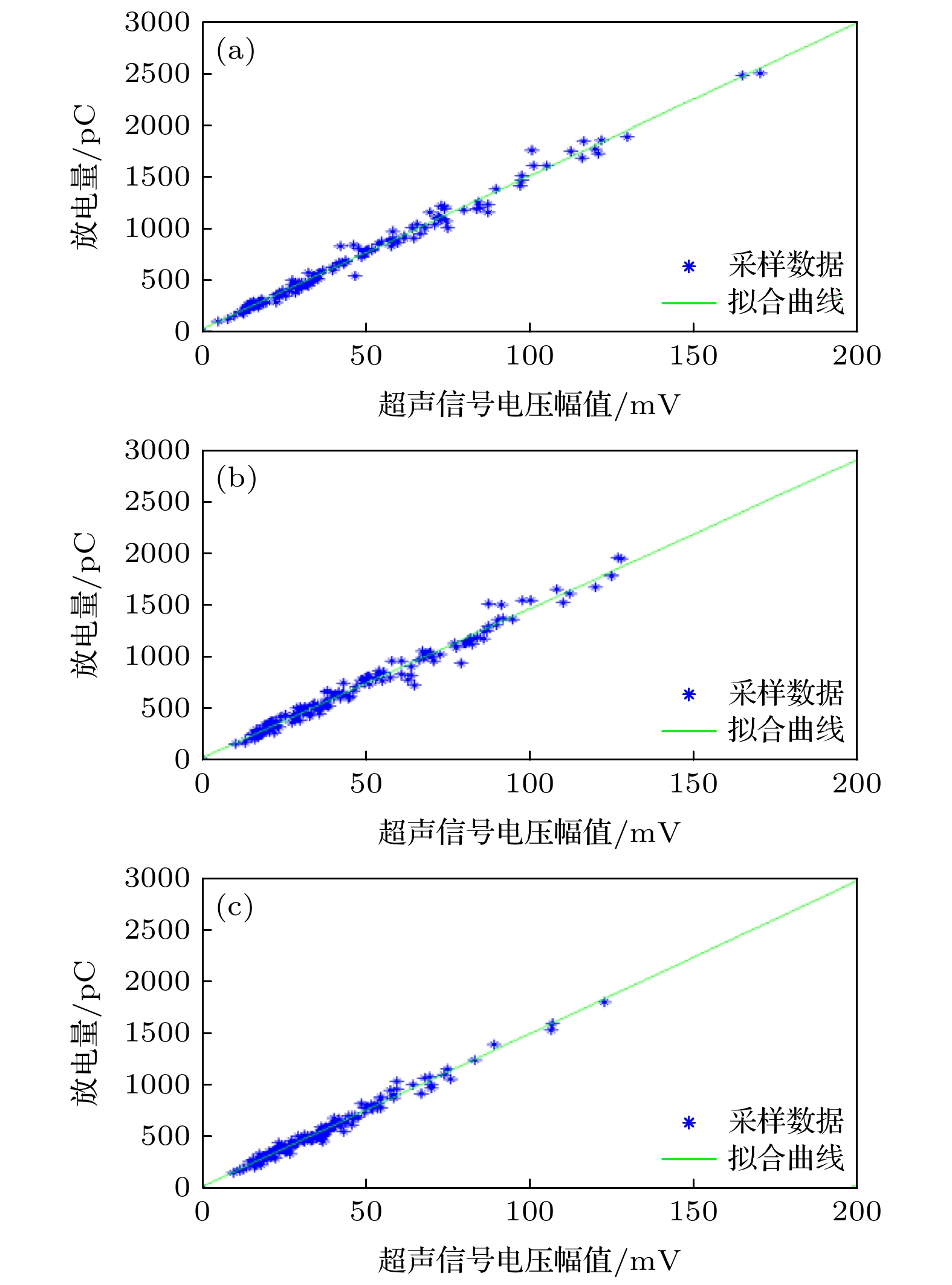
-
In the insulation system of power equipment, the partial discharge (PD) of short period does not cause the insulation to produce the penetrating breakdown, however the long-term PD of is one of the important causes of local deterioration, and even breakdown in dielectric. Therefore, it is very important to study the location of PD source and the calibration of discharge intensity. To achieve this, in this paper we take the needle-plate discharge model for example and go through the following steps respectively. Firstly, combined with the positive correlation between the ultrasonic signal and the apparent discharge magnitude in the process of PD, the ultrasonic method to detect partial discharge can be implemented. Then, based on the principle of time difference of arrival method (TDOAM), the accuracy of location is analyzed by using quantum genetic algorithm (QGA), genetic algorithm (GA), simulated annealing algorithm (SAA), particle swarm optimization (PSO) and generalized cross correlation method (GCC), respectively. And thus, starting from the study of the attenuation effect of sound pressure caused by the propagation loss, reflection and refraction of acoustic wave, the calibration model of PD intensity is established for the first time after determining the location of PD source with high precision. Some important findings are extracted from simulations and experimental results. First, the localization algorithm of PD source with high precision is observed. The localization of PD source by means of QGA is the most accurate, with maximum deviation of (0.27 ± 0.13) cm. Comparing with GA, SAA, PSO and GCC, the accuracy of location is improved by 33.57%, 41.51%, 32.11% and 87.26%, respectively. Second, due to the attenuation effect of sound pressure, when the measured voltage amplitude of ultrasonic signal is the same, the apparent discharge magnitude of PD source gradually increases with the test distance increasing. When the test distance is 37.80 cm, the apparent discharge magnitude of PD source is 633.83 pC, which increases by 28.51% compared with 7.00 cm. Moreover, simulation results and measurement results are compared with each other and they are well consistent. The discharge curve almost coincides with the calibration fitting curve of PD source when the test distance is 7.00 cm. Finally, it is concluded that the discharge intensity calibration model of PD source is accurate, which is of great significance in evaluating the extent of insulation damage.
-
Keywords:
- partial discharge /
- localization of ultrasonic method /
- discharge intensity /
- mathematical model
[1] 李丹, 胡海云 2014 63 117701
Google Scholar
Li D, Hu H Y 2014 Acta Phys. Sin. 63 117701
Google Scholar
[2] Lü Z P, Rowland S M, Chen S Y, Zheng H L 2018 IEEE Trans. Dielectr. Electr. Insul. 25 1999
Google Scholar
[3] 赵法强, 唐明, 郭飞飞 2020 电线电缆 63 20
Google Scholar
Zhao F Q, Tang M, Guo F F 2020 Electric Wire & Cable 63 20
Google Scholar
[4] Romano P, Presti G, Imburgia A, Candela R 2018 IEEE Electr. Insul. M. 34 32
Google Scholar
[5] 李军浩, 韩旭涛, 刘泽辉, 李彦明 2015 高电压技术 41 2583
Google Scholar
Li J H, Han X T, Liu Z H, Li Y M 2015 High Voltage Eng. 41 2583
Google Scholar
[6] Heredia L C C, Mor A R 2019 Int. J. Electr. Power Energy Syst. 107 224
Google Scholar
[7] Callender G, Golosnoy I O, Rapisarda P, Lewin P L 2018 J. Phys. D: Appl. Phys. 51 125601
Google Scholar
[8] 杜劲超, 陈伟根, 张知先, 杨贤 2020 高电压技术 46 2185
Google Scholar
Du J C, Chen W G, Zhang Z X, Yang X 2020 High Voltage Eng. 46 2185
Google Scholar
[9] 夏睿, 谭笑, 陈杰, 刘洋, 胡丽斌, 李陈莹, 王伟 2020 绝缘材料 53 95
Google Scholar
Xia R, Tan X, Chen J, Liu J, Hu L B, Li C Y, Wang W 2020 Insulating Mater. 53 95
Google Scholar
[10] 曾喆昭, 周勇, 胡凯 2015 64 070505
Google Scholar
Zeng Z Z, Zhou Y, Hu K 2015 Acta Phys. Sin. 64 070505
Google Scholar
[11] 张若兵, 金森, 杜钢 2020 高电压技术 46 273
Google Scholar
Zhang R B, Jin S, Du G 2020 High Voltage Eng. 46 273
Google Scholar
[12] Ahmed Z, Hussain G A, Lehtonen M, Varacka L, Kudelcik J 2016 17 th International Scientific Conference on Electric Power Engineering Prague, Czech Republic, May 16-18, 2016 p1
[13] Iorkyase E T, Tachtatzis C, Atkinson R C, Glover I A 2015 Loughborough Antennas & Propagation Conference UK, Loughborough, November 2−3, 2015 p1
[14] 卢毅, 楼樟达 1999 电工技术学报 14 51
Google Scholar
Lu Y, Lou Z D 1999 Trans. Chin. Electrotech. Soc. 14 51
Google Scholar
[15] Li Y Q, Lu F C, Xie H L, Yin M 2004 International Conference on Power System Technology Singapore, Singapore, November 21–24, 2004 p1371
[16] 吴治国 2007 硕士学位论文 (武汉: 华中科技大学)
Wu Z G 2007 M. S. Thesis (Wuhan: Huazhong University of Science & Technology) (in Chinese)
[17] Veloso G F C, da Silva L E B, Noronha I, Lambert-Torres G 2008 IEEE International Symposium on Industrial Electronics Cambridge, UK, June 30–July 2, 2008 p1003
[18] Tang L J, Luo R C, Deng M, Su J 2008 IEEE Trans. Dielectr. Electr. Insul. 15 492
Google Scholar
[19] 张丽君, 谢庆, 李菱, 律方成 2012 高压电器 48 30
Google Scholar
Zhang L J, Xie Q, Li L, Lv F C 2012 High Voltage Apparatus 48 30
Google Scholar
[20] 谢庆, 律方成, 李燕青, 黄华平, 李宁远, 谭向宇 2014 电工技术学报 26 217
Google Scholar
Xie Q, Lv F C, Li Y Q, Huang H P, Li N Y, Tan X Y 2014 Trans. Chin. Electrotech.l Soc. 26 217
Google Scholar
[21] 瞿磊 2020 硕士学位论文 (上海: 上海电机学院)
Qu L 2020 M. S. Thesis (Shanghai: Shanghai Dian Ji university) (in Chinese)
[22] Zhu Y C, Zhou L, Xu H S 2020 Neural Comput. Appl. 32 1775
Google Scholar
[23] Zhu M X, Wang Y B, Liu Q, Zhang J N, Deng J B, Zhang G J, Shao X J, He W L 2017 IEEE Trans. Dielectr. Electr. Insul. 24 157
Google Scholar
[24] 张磊祺, 盛博杰, 姜伟, 周文俊, 田智, 唐泽洋 2015 高电压技术 41 1204
Google Scholar
Zhang L Q, Sheng B J, Jiang W, Zhou W J, Tian Z, Tang Z Y 2015 High Voltage Eng. 41 1204
Google Scholar
[25] 吴勇峰, 黄绍平, 金国彬 2013 62 130505
Google Scholar
Wu Y F, Huang S P, Jin G B 2013 Acta Phys. Sin. 62 130505
Google Scholar
[26] 杜锦阳 2013 硕士学位论文 (哈尔滨: 哈尔滨理工大学)
Du J Y 2013 M. S. Thesis (Harbin: Harbin University of Science and Technology) (in Chinese)
[27] 芦翔 2017 硕士学位论文 (哈尔滨: 哈尔滨理工大学)
Lu X 2017 M. S. Thesis (Harbin: Harbin University of Science and Technology) (in Chinese)
[28] Morshuis P H F 2005 IEEE Trans. Dielectr. Eectrl. Insul. 12 905
Google Scholar
[29] Liu H L 2016 Appl. Acoust. 102 71
Google Scholar
[30] Zhu M X, Li J C, Chang D G, Zhang G J, Chen J M 2018 Energies 11 1813
Google Scholar
[31] Smith J S, Baginski M E 2019 IEEE Trans. Antennas Propag. 67 2934
Google Scholar
[32] Xiao Z K, Xu C G, Xiao D G, Liu F, Yin M 2017 Exp. Tech. 41 389
Google Scholar
[33] Gao S G, Zhang Y, Xie Q, Kan Y Q, Li S, Liu D, Lv F C 2017 Energies 10 593
Google Scholar
[34] Xie Q, Li T, Tao J H, Liu X Y, Liu D, Xu Y Q 2016 IET Radar Sonar Nav. 10 166
Google Scholar
[35] 孙才新, 罗兵, 赵文麒, 赵贤正 1997 仪器仪表学报 18 453
Google Scholar
Sun C X, Luo B, Zhao W Q, Zhao X Z 1997 Chin. J. Sci. Instrum. 18 453
Google Scholar
-
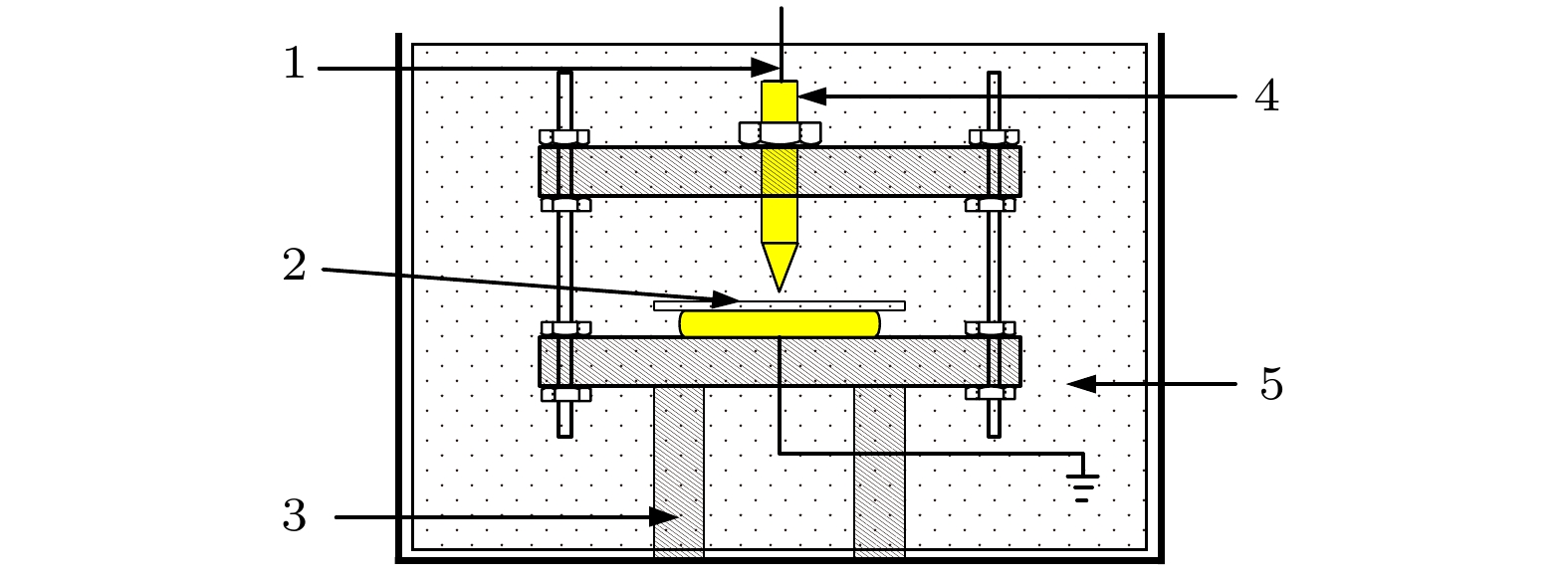
图 1 超声波检测试验系统电路图(T1, 隔离变压器; T2, 调压器; C1, L1, 低压低通π型滤波器; T3, 高压实验变压器; C2, L2, 高压低通滤波器; CK, 耦合电容器; Zin, 检测阻抗; T, 油箱; S, 压电传感器; AMP, 前置放大器; DAQ, 数据采集卡)
Figure 1. Test system schematic diagram of ultrasonic testing (T1, isolating transformer; T2, voltage regulator; C1, L1, low-voltage low-pass π filter; T3, high voltage test transformer; C2, L2, high-voltage low-pass filter; CK, coupling capacitor; Zin, detection impedance; T, Tank; S, piezoelectric sensor; AMP, preamplifier; DAQ, data acquisition card).
图 2 针-板放电模型结构示意图(1, 高压引线; 2, 聚乙烯试验板; 3, 聚四氟乙烯支架; 4, 铜电极; 5, 电缆油)
Figure 2. Schematic diagram of needle-plate discharge model (1, high voltage wire; 2, polyethylene sample; 3, support frame of polytetrafluoroethylene; 4, copper electrode; 5, cable oil).
图 3 油箱中放电源及超声波传感器的位置图
Figure 3. Location illustration of PD source and ultrasonic sensors in the oil tank.
图 4 TDOAM中的超声时差示意图
Figure 4. Schematic diagram of ultrasonic time difference in TDOAM.
图 5 脉冲电流法的校正曲线
Figure 5. Calibration curve of pulse current method.
图 6 不同算法下局部放电定位的平均绝对误差变化
Figure 6. Average absolute errors of PD location under different algorithms.
图 7 不同算法下局部放电定位的平均误差变化 (a) 平均绝对误差; (b) 平均最大偏差和综合误差
Figure 7. Average errors of PD location under different algorithms: (a) εrx, εry and εrz; (b) Dmax and ΔR.
图 8 不同绝缘纸厚度的电压幅值与放电量拟合曲线 (a) 2 mm; (b) 3 mm; (c) 4 mm
Figure 8. Fitting curves of voltage amplitude and discharge amplitudes at different thickness of insulating papers: (a) 2 mm; (b) 3 mm; (c) 4 mm.
图 9 不同测量距离下视在放电量与电压的关系
Figure 9. Relationship between apparent charge and voltage at different measuring distances.
表 1 局部放电的超声定位精度比较
Table 1. Comparison of ultrasonic location accuracy of PD.
使用算法 研究对象 综合距离误差ΔR/cm 最大偏差Dmax/cm 广义互相关算法 油箱体内 3.9 4.4 时延法 变压器绝缘 0.8 0.6 基于高斯-牛顿迭代的等值声速修正算法 1.7 1.6 粒子群优化算法 2.2 1.9 遗传算法 1.8 2.0 多平台测向与全局搜索的阵列定位的结合 三电容放电管模型 7.8 6.0 基于测向线公垂线中点的局部放电相控超声几何定位算法 13.9 10.3 Chan算法 电缆绝缘 9.0 12.0 
DownLoad: CSV
表 2 QGA的程序过程
Table 2. Procedures of QGA.
过程 程序 种群初
始化$Q\left( t \right) = \left| { {\psi _{q_j^0} } } \right\rangle = \displaystyle\sum\limits_{k = 1}^{ {2^m} } {\dfrac{1}{ {\sqrt { {2^m} } } }\left| { {S_k} } \right\rangle }$ 预设进
化条件Cmax, t, N, Pmax, Pc 算法
实现For t = 1, 2, 3, ···, Cmax for i = 1, 2, ···, N ${P_i} = {f_i}\Big/\sum\limits_{i = 1}^N { {f_i} }$ $\quad P(t) = \left\{ {p_1^t, p_2^t, \cdots, p_n^t} \right\},$ ${P_c} \!=\! \left\{\!\!\!\! \begin{array}{l}\dfrac{ { { {P_{c\max} } + {P_{\min} } } } }{ {1 \!+\! \exp\left\{ {A\left[ {\dfrac{ {2(f-f')} }{ { {f_{\max} } - {f_{\rm{avg} } } } } } \right]} \right\} } } \!+\! {P_{c\min} }, ~{f \!\geqslant\! {f_{\rm{avg} } } } \\ {P_{c\max} }, \qquad\quad\qquad\qquad\quad\qquad\qquad{f \!\leqslant\! {f_{\rm{avg} } } } \end{array} \right.$ ${P_m} \!=\! \left\{\!\!\!\! \begin{array}{l} \dfrac{ { { {P_{m\max} } - {P_{\min} } } } }{ {1 \!+\! \exp\left\{ {A\left[ {\dfrac{ {2( {f'' - f'})} }{ { {f_{\max} } - {f_{\rm{avg} } } } } } \right]} \right\} } } \!+\! {P_{m\min} }, ~~{f'' \geqslant {f_{\rm{avg} } } } \\ {P_{m\max} },\;\;\; \qquad\quad\qquad\qquad\qquad\qquad\quad{f'' \leqslant {f_{\rm{avg} } } } \end{array} \right.$ ${F_{t + 1} }({U({x, y, z, {v_{\rm{e} } }})}) \!=\! {C_{t\max} } \!-\! {U_t}( {x, y, z, {v_{\rm{e} } }})$ $X_i \;\& \; x_{ {\rm best}, i}\; \& \; f(x) > f(x_{ {\rm best}, i}) \; \& \; \Delta \theta_i$ S(αi, βi); end end S(αi, βi); P(t); X;
DownLoad: CSV
表 3 量子旋转门的调整策略
Table 3. Adjustment strategies of quantum rotation gates.
xi xbest,i f (x) > f (xbest,i) Δθi S(αi, βi) αi βi > 0 αi βi < 0 αi = 0 βi = 0 0 0 false 0 0 0 0 0 0 0 true 0 0 0 0 0 0 1 false 0.01π +1 –1 0 ± 1 0 1 true 0.01π –1 +1 ± 1 0 1 0 false 0.01π –1 +1 ± 1 0 1 0 true 0.01π +1 –1 0 ± 1 1 1 false 0 0 0 0 0 1 1 true 0 0 0 0 0
DownLoad: CSV
表 4 局部放电定位的算法参数
Table 4. Algorithm parameters of PD localization.
算法 参数 数值 QGA 群体数量 40 最大遗传次数 200 GA 群体数量 40 最大遗传次数 200 重组概率 0.9 变异概率 0.01 SAA 初始温度 10 最终温度 0.0001 衰减系数 0.8 冷却新状态迭代次数 1000 PSO 种群大小 40 学习因子 2 初始惯性权值 0.9 原始粒子群 1 迭代次数 100
DownLoad: CSV
表 5 不同算法的局部放电定位
Table 5. The PD location of different algorithms.
算法 位置 实验组1 (12, 14, 6) cm 实验组2 (14, 10, 6) cm 实验组3 (15, 11, 6) cm 实验组4 (16, 12, 6) cm QGA (11.79, 13.61, 5.78) (13.78, 9.88, 6.06) (14.88, 10.86, 5.90) (15.82, 11.84, 5.88) GA (12.33, 14.24, 5.73) (13.62, 10.22, 6.16) (14.65, 11.24, 6.22) (16.34, 12.30, 6.24) SAA (11.58, 13.41, 5.78) (13.66, 10.32, 6.24) (15.34, 11.22, 6.20) (16.32, 12.28, 6.26) PSO (12.12, 14.21, 6.15) (14.32, 9.72, 5.84) (15.42, 11.28, 6.30) (16.42, 12.34, 6.32) GCC (13.38, 15.06, 7.42) (15.51, 9.62, 6.94) (15.71, 8.32, 7.24) (14.76, 10.31, 7.13)
DownLoad: CSV
表 6 系统灵敏度和相关系数的变化
Table 6. Change of system sensitivity and correlation coefficients.
电缆纸厚度/mm 系统灵敏度 相关系数 2 14.91 0.99 3 14.37 0.99 4 14.84 0.99
DownLoad: CSV
表 7 局部放电的线性系数
Table 7. Linear coefficients of PD.
线性系数 K0 K1 K2 K3 K4 数值 5.01 2.98 2.93 2.86 2.95
DownLoad: CSV
-
[1] 李丹, 胡海云 2014 63 117701
Google Scholar
Li D, Hu H Y 2014 Acta Phys. Sin. 63 117701
Google Scholar
[2] Lü Z P, Rowland S M, Chen S Y, Zheng H L 2018 IEEE Trans. Dielectr. Electr. Insul. 25 1999
Google Scholar
[3] 赵法强, 唐明, 郭飞飞 2020 电线电缆 63 20
Google Scholar
Zhao F Q, Tang M, Guo F F 2020 Electric Wire & Cable 63 20
Google Scholar
[4] Romano P, Presti G, Imburgia A, Candela R 2018 IEEE Electr. Insul. M. 34 32
Google Scholar
[5] 李军浩, 韩旭涛, 刘泽辉, 李彦明 2015 高电压技术 41 2583
Google Scholar
Li J H, Han X T, Liu Z H, Li Y M 2015 High Voltage Eng. 41 2583
Google Scholar
[6] Heredia L C C, Mor A R 2019 Int. J. Electr. Power Energy Syst. 107 224
Google Scholar
[7] Callender G, Golosnoy I O, Rapisarda P, Lewin P L 2018 J. Phys. D: Appl. Phys. 51 125601
Google Scholar
[8] 杜劲超, 陈伟根, 张知先, 杨贤 2020 高电压技术 46 2185
Google Scholar
Du J C, Chen W G, Zhang Z X, Yang X 2020 High Voltage Eng. 46 2185
Google Scholar
[9] 夏睿, 谭笑, 陈杰, 刘洋, 胡丽斌, 李陈莹, 王伟 2020 绝缘材料 53 95
Google Scholar
Xia R, Tan X, Chen J, Liu J, Hu L B, Li C Y, Wang W 2020 Insulating Mater. 53 95
Google Scholar
[10] 曾喆昭, 周勇, 胡凯 2015 64 070505
Google Scholar
Zeng Z Z, Zhou Y, Hu K 2015 Acta Phys. Sin. 64 070505
Google Scholar
[11] 张若兵, 金森, 杜钢 2020 高电压技术 46 273
Google Scholar
Zhang R B, Jin S, Du G 2020 High Voltage Eng. 46 273
Google Scholar
[12] Ahmed Z, Hussain G A, Lehtonen M, Varacka L, Kudelcik J 2016 17 th International Scientific Conference on Electric Power Engineering Prague, Czech Republic, May 16-18, 2016 p1
[13] Iorkyase E T, Tachtatzis C, Atkinson R C, Glover I A 2015 Loughborough Antennas & Propagation Conference UK, Loughborough, November 2−3, 2015 p1
[14] 卢毅, 楼樟达 1999 电工技术学报 14 51
Google Scholar
Lu Y, Lou Z D 1999 Trans. Chin. Electrotech. Soc. 14 51
Google Scholar
[15] Li Y Q, Lu F C, Xie H L, Yin M 2004 International Conference on Power System Technology Singapore, Singapore, November 21–24, 2004 p1371
[16] 吴治国 2007 硕士学位论文 (武汉: 华中科技大学)
Wu Z G 2007 M. S. Thesis (Wuhan: Huazhong University of Science & Technology) (in Chinese)
[17] Veloso G F C, da Silva L E B, Noronha I, Lambert-Torres G 2008 IEEE International Symposium on Industrial Electronics Cambridge, UK, June 30–July 2, 2008 p1003
[18] Tang L J, Luo R C, Deng M, Su J 2008 IEEE Trans. Dielectr. Electr. Insul. 15 492
Google Scholar
[19] 张丽君, 谢庆, 李菱, 律方成 2012 高压电器 48 30
Google Scholar
Zhang L J, Xie Q, Li L, Lv F C 2012 High Voltage Apparatus 48 30
Google Scholar
[20] 谢庆, 律方成, 李燕青, 黄华平, 李宁远, 谭向宇 2014 电工技术学报 26 217
Google Scholar
Xie Q, Lv F C, Li Y Q, Huang H P, Li N Y, Tan X Y 2014 Trans. Chin. Electrotech.l Soc. 26 217
Google Scholar
[21] 瞿磊 2020 硕士学位论文 (上海: 上海电机学院)
Qu L 2020 M. S. Thesis (Shanghai: Shanghai Dian Ji university) (in Chinese)
[22] Zhu Y C, Zhou L, Xu H S 2020 Neural Comput. Appl. 32 1775
Google Scholar
[23] Zhu M X, Wang Y B, Liu Q, Zhang J N, Deng J B, Zhang G J, Shao X J, He W L 2017 IEEE Trans. Dielectr. Electr. Insul. 24 157
Google Scholar
[24] 张磊祺, 盛博杰, 姜伟, 周文俊, 田智, 唐泽洋 2015 高电压技术 41 1204
Google Scholar
Zhang L Q, Sheng B J, Jiang W, Zhou W J, Tian Z, Tang Z Y 2015 High Voltage Eng. 41 1204
Google Scholar
[25] 吴勇峰, 黄绍平, 金国彬 2013 62 130505
Google Scholar
Wu Y F, Huang S P, Jin G B 2013 Acta Phys. Sin. 62 130505
Google Scholar
[26] 杜锦阳 2013 硕士学位论文 (哈尔滨: 哈尔滨理工大学)
Du J Y 2013 M. S. Thesis (Harbin: Harbin University of Science and Technology) (in Chinese)
[27] 芦翔 2017 硕士学位论文 (哈尔滨: 哈尔滨理工大学)
Lu X 2017 M. S. Thesis (Harbin: Harbin University of Science and Technology) (in Chinese)
[28] Morshuis P H F 2005 IEEE Trans. Dielectr. Eectrl. Insul. 12 905
Google Scholar
[29] Liu H L 2016 Appl. Acoust. 102 71
Google Scholar
[30] Zhu M X, Li J C, Chang D G, Zhang G J, Chen J M 2018 Energies 11 1813
Google Scholar
[31] Smith J S, Baginski M E 2019 IEEE Trans. Antennas Propag. 67 2934
Google Scholar
[32] Xiao Z K, Xu C G, Xiao D G, Liu F, Yin M 2017 Exp. Tech. 41 389
Google Scholar
[33] Gao S G, Zhang Y, Xie Q, Kan Y Q, Li S, Liu D, Lv F C 2017 Energies 10 593
Google Scholar
[34] Xie Q, Li T, Tao J H, Liu X Y, Liu D, Xu Y Q 2016 IET Radar Sonar Nav. 10 166
Google Scholar
[35] 孙才新, 罗兵, 赵文麒, 赵贤正 1997 仪器仪表学报 18 453
Google Scholar
Sun C X, Luo B, Zhao W Q, Zhao X Z 1997 Chin. J. Sci. Instrum. 18 453
Google Scholar
DownLoad:
Catalog
Metrics
- Abstract views: 5922
- PDF Downloads: 89
- Cited By: 0
