-
General Gauss-Bonnet gravity with a cosmological constant allows two anti-de Sitter (AdS) spacetimes to be taken as its vacuum solutions. It is found that there is a critical point in the parameter space where the two AdS vacuums coalesce into one, which is very different from the general Gauss-Bonnet gravity. Susskind’s team proposed a Complexity/Action duality based on AdS/CFT duality, which provides a new method of studying the complexity of black holes. Fan and Liang (Fan Z Y, Liang H Z 2019 Phys. Rev. D 100 086016) gave the formula of the evolution of complexity for general higher derivative gravity, and discussed the complexity evolution of the neutral planar Gauss-Bonnet-AdS black holes in detail by the numerical method. With the method of studying the complexity of general higher derivative gravity proposed by Fan and Liang (2019), we investigate the complexity evolution of critical neutral Gauss-Bonnet-AdS black holes, and compare these results with the results of the general neutral Gauss-Bonnet-AdS black holes, showing that the overall regularities of the evolution of the complexity of these two objects are consistent, and their main difference lies in the dimensionless critical time. As for the five-dimensional critical neutral Gauss-Bonnet-AdS black holes, when the event horizon of the black holes is flat or spherical, the dimensionless critical times of black holes with different sizes are identical, all reaching their minimum values. While in the higher dimensional cases, the differences in dimensionless critical time among spherically symmetric critical neutral Gauss-Bonnet-AdS black holes with different sizes are obviously less than those of general ones. These differences are probably related to the criticality of the neutral Gauss-Bonnet-AdS black holes.
-
Keywords:
- black holes /
- criticality /
- complexity /
- evolution
[1] ’t Hooft G 1993 arXiv: gr-qc/9310026
[2] Susskind L 1995 J. Math. Phys. 36 6377
Google Scholar
[3] Maldacena J M 1998 Adv. Theor. Math. Phys. 2 231
Google Scholar
[4] Witten E 1998 Adv. Theor. Math. Phys. 2 253
Google Scholar
[5] Gubser S S, Klebanov I R, Polyakov A M 1998 Phys. Lett. B 428 105
Google Scholar
[6] Susskind L 2016 Fortsch. Phys. 64 24
Google Scholar
[7] Susskind L 2016 Fortsch. Phys. 64 44
Google Scholar
[8] Stanford D, Susskind L 2014 Phys. Rev. D 90 126007
Google Scholar
[9] Brown A R, Roberts D A, Susskind L, Swingle B, Zhao Y 2016 Phys. Rev. Lett 116 191301
Google Scholar
[10] Brown A R, Roberts D A, Susskind L, Swingle B, Zhao Y 2016 Phys. Rev. D 93 086006
Google Scholar
[11] Fan Z Y, Liang H Z 2019 Phys. Rev. D 100 086016
Google Scholar
[12] 梁华志, 张靖仪 2020 湖南文理学院学报 (自然科学版) 32 26
Google Scholar
Liang H Z, Zhang J Y 2020 J. Hunan Univ. Arts Sci. (Science and Technology) 32 26
Google Scholar
[13] Mahapatra S, Roy P 2018 J. High Energy Phys. 2018 138
Google Scholar
[14] Chapman S, Marrochio H, Myers R C 2017 J. High Energy Phys. 2017 62
Google Scholar
[15] Carmi D, Myers R C, Rath P 2017 J. High Energy Phys. 2017 118
Google Scholar
[16] Yang R Q, Niu C, Kim K Y 2017 J. High Energy Phys. 2017 42
Google Scholar
[17] Yang R Q 2017 Phys. Rev. D 95 086017
Google Scholar
[18] Chapman S, Marrochio H, Myers R C 2018 J. High Energy Phys. 2018 46
Google Scholar
[19] Chapman S, Marrochio H, Myers R C 2018 J. High Energy Phys. 2018 114
Google Scholar
[20] Moosa M 2018 J. High Energy Phys. 2018 31
Google Scholar
[21] Alishahiha M, Astaneh A F, Mozaffar M R M, Mollabashi A 2018 J. High Energy Phys. 2018 42
Google Scholar
[22] An Y S, Peng R H 2018 Phys. Rev. D 97 066022
Google Scholar
[23] Jiang J 2018 Phys. Rev. D 98 086018
Google Scholar
[24] Yang R Q, Niu C, Zhang C Y, Kim K Y 2018 J. High Energy Phys. 2018 82
[25] Yang R, Jeong H S, Niu C, Kim K Y 2019 J. High Energy Phys. 2019 146
Google Scholar
[26] Cai R G, Ruan S M, Wang S J, Yang R Q, Peng R H 2016 J. High Energy Phys. 2016 161
Google Scholar
[27] Lehner L, Myers R C, Poisson E, Sorkin R D 2016 Phys. Rev. D 94 084046
Google Scholar
[28] Huang H, Feng X H, Lu H 2017 Phys. Lett. B 769 357
Google Scholar
[29] Cano P A, Hennigar R A, Marrochio H 2018 Phys. Rev. Lett. 121 121602
Google Scholar
[30] Jiang J, Zhang H 2019 Phys. Rev. D 99 086005
Google Scholar
[31] Feng X H, Liu H S 2019 Eur. Phys. J. C 79 40
Google Scholar
[32] Alishahiha M, Astaneh A F, Naseh A, Vahidinia M H 2017 J. High Energy Phys. 2017 9
Google Scholar
[33] Carmi D, Chapman S, Marrochio H, Myers R C, Sugishita S 2017 J. High Energy Phys. 2017 188
Google Scholar
[34] Jiang J, Ge B X 2019 Phys. Rev. D 99 126006
Google Scholar
[35] Moosa M 2018 Phys. Rev. D 97 106016
Google Scholar
[36] Fan Z Y, Chen B, Lü H 2016 Eur. Phys. J. C 76 542
Google Scholar
[37] Haking S W, Page D N 1983 Commun. Math. Phys. 87 577
Google Scholar
[38] 刘显明, 雷焱林, 陈丽, 韩成 2015 湖北民族学院学报(自然科学版) 33 1
Google Scholar
Liu X M, Lei Y L, Chen L, Han C 2015 J. Hubei Univ. Nationalities (Nat. Sci. Ed.) 33 1
Google Scholar
[39] Brigante M, Liu H, Myers R C, Shenker S, Yaida S 2008 Phys. Rev. D 77 126006
Google Scholar
[40] Brigante M, Liu H, Myers R C, Shenker S, Yaida S 2008 Phys. Rev. Lett. 100 191601
Google Scholar
[41] Buchel A, Myers R C 2009 J. High Energy Phys. 2009 8
Google Scholar
[42] Camanho X O, Edelstein J D 2010 J. High Energy Phys. 2010 7
Google Scholar
[43] Wald R M 1993 Phys. Rev. D 48 3427
Google Scholar
[44] Iyer V, Wald R M 1994 Phys. Rev. D 50 846
Google Scholar
[45] Fan Z Y, Lü H 2015 Phys. Rev. D 91 064009
Google Scholar
-
图 1 一般的中性双边AdS黑洞Wheeler-Dewitt片
Figure 1. The Wheeler-DeWitt patch for a general neutral two-sided AdS black hole.
图 2 临界中性Gauss-Bonnet-AdS黑洞的复杂度演化图 (a)
$D = 5, \quad k = 0$ ; (b)$D = 5, \quad k = 1$ ; (c)$D = 6, \quad k = 0$ ; (d)$D = 6, \quad k = 1$ ; (e)$D = 7, \quad k = 0$ ; (f)$D = 7, \quad k = 1$ Figure 2. Complexity evolution diagram of the critical neutral Gauss-Bonnet-AdS black holes: (a)
$D = 5, \quad k = 0$ ; (b)$D = 5, \quad k = 1$ ; (c)$D = 6, \quad k = 0$ ; (d)$D = 6, \quad k = 1$ ; (e)$D = 7, \quad k = 0$ ; (f)$D = 7, \quad k = 1$ .
图 3 临界中性Gauss-Bonnet-AdS黑洞的复杂度微分图 (a)
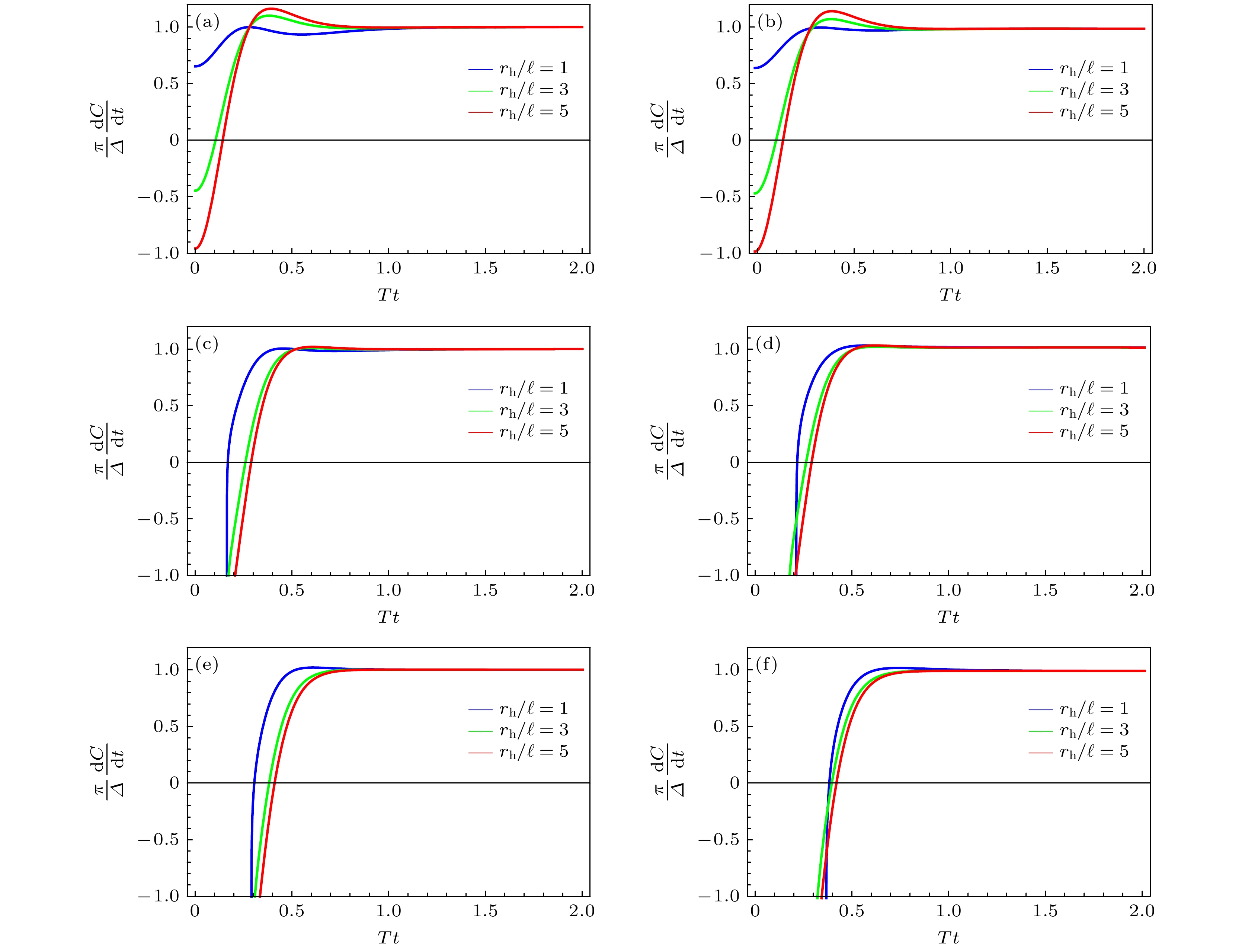
$D = 5, \quad k = 0$ ; (b)$D = 5, \quad k = 1$ ; (c)$D = 6, \quad k = 0$ ; (d)$D = 6, \quad k = 1$ ; (e)$D = 7, \quad k = 0$ ; (f)$D = 7, \quad k = 1$ Figure 3. Complexity difference diagram of the critical neutral Gauss-Bonnet-AdS black holes: (a)
$D = 5, \quad k = 0$ ; (b)$D = 5, \quad k = 1$ ; (c)$D = 6, \quad k = 0$ ; (d)$D = 6, \quad k = 1$ ; (e)$D = 7, \quad k = 0$ ; (f)$D = 7, \quad k = 1$ .表 1
$k = 0$ 时, 临界中性Gauss-Bonnet-AdS黑洞无量纲的临界时间$T{t_{\rm{c}}}$ ($\lambda = 0.05$ )Table 1. Dimensionless critical time
$T{t_{\rm{c}}}$ of critical neutral Gauss-Bonnet-AdS black holes ($\lambda = 0.05$ ) for$k = 0$ .维度 $T{t_{\rm{c} } }\,({r_{\rm{h} } }/\ell = 1)$ $T{t_{\rm{c} } }\,({r_{\rm{h} } }/\ell = 3)$ $T{t_{\rm{c} } }\,({r_{\rm{h} } }/\ell = 5)$ $D = 5$ 0 0 0 $D = 6$ 0.162460 0.162460 0.162460 $D = 7$ 0.288675 0.288675 0.288675 $D = 8$ 0.398736 0.398736 0.398736 
DownLoad: CSV
表 2
$k = 1$ 时, 临界中性Gauss-Bonnet-AdS黑洞无量纲的临界时间$T{t_{\rm{c}}}$ ($\lambda = 0.05$ )Table 2. Dimensionless critical time
$T{t_{\rm{c}}}$ of critical neutral Gauss-Bonnet-AdS black holes ($\lambda = 0.05$ ) for$k = 1$ .维度 $T{t_{\rm{c} } }\,({r_{\rm{h} } }/\ell = 1)$ $T{t_{\rm{c} } }\,({r_{\rm{h} } }/\ell = 3)$ $T{t_{\rm{c} } }\,({r_{\rm{h} } }/\ell = 5)$ $D = 5$ 0 0 0 $D = 6$ 0.209745 0.168224 0.164552 $D = 7$ 0.359752 0.297391 0.291841 $D = 8$ 0.490653 0.409981 0.402820
DownLoad: CSV
-
[1] ’t Hooft G 1993 arXiv: gr-qc/9310026
[2] Susskind L 1995 J. Math. Phys. 36 6377
Google Scholar
[3] Maldacena J M 1998 Adv. Theor. Math. Phys. 2 231
Google Scholar
[4] Witten E 1998 Adv. Theor. Math. Phys. 2 253
Google Scholar
[5] Gubser S S, Klebanov I R, Polyakov A M 1998 Phys. Lett. B 428 105
Google Scholar
[6] Susskind L 2016 Fortsch. Phys. 64 24
Google Scholar
[7] Susskind L 2016 Fortsch. Phys. 64 44
Google Scholar
[8] Stanford D, Susskind L 2014 Phys. Rev. D 90 126007
Google Scholar
[9] Brown A R, Roberts D A, Susskind L, Swingle B, Zhao Y 2016 Phys. Rev. Lett 116 191301
Google Scholar
[10] Brown A R, Roberts D A, Susskind L, Swingle B, Zhao Y 2016 Phys. Rev. D 93 086006
Google Scholar
[11] Fan Z Y, Liang H Z 2019 Phys. Rev. D 100 086016
Google Scholar
[12] 梁华志, 张靖仪 2020 湖南文理学院学报 (自然科学版) 32 26
Google Scholar
Liang H Z, Zhang J Y 2020 J. Hunan Univ. Arts Sci. (Science and Technology) 32 26
Google Scholar
[13] Mahapatra S, Roy P 2018 J. High Energy Phys. 2018 138
Google Scholar
[14] Chapman S, Marrochio H, Myers R C 2017 J. High Energy Phys. 2017 62
Google Scholar
[15] Carmi D, Myers R C, Rath P 2017 J. High Energy Phys. 2017 118
Google Scholar
[16] Yang R Q, Niu C, Kim K Y 2017 J. High Energy Phys. 2017 42
Google Scholar
[17] Yang R Q 2017 Phys. Rev. D 95 086017
Google Scholar
[18] Chapman S, Marrochio H, Myers R C 2018 J. High Energy Phys. 2018 46
Google Scholar
[19] Chapman S, Marrochio H, Myers R C 2018 J. High Energy Phys. 2018 114
Google Scholar
[20] Moosa M 2018 J. High Energy Phys. 2018 31
Google Scholar
[21] Alishahiha M, Astaneh A F, Mozaffar M R M, Mollabashi A 2018 J. High Energy Phys. 2018 42
Google Scholar
[22] An Y S, Peng R H 2018 Phys. Rev. D 97 066022
Google Scholar
[23] Jiang J 2018 Phys. Rev. D 98 086018
Google Scholar
[24] Yang R Q, Niu C, Zhang C Y, Kim K Y 2018 J. High Energy Phys. 2018 82
[25] Yang R, Jeong H S, Niu C, Kim K Y 2019 J. High Energy Phys. 2019 146
Google Scholar
[26] Cai R G, Ruan S M, Wang S J, Yang R Q, Peng R H 2016 J. High Energy Phys. 2016 161
Google Scholar
[27] Lehner L, Myers R C, Poisson E, Sorkin R D 2016 Phys. Rev. D 94 084046
Google Scholar
[28] Huang H, Feng X H, Lu H 2017 Phys. Lett. B 769 357
Google Scholar
[29] Cano P A, Hennigar R A, Marrochio H 2018 Phys. Rev. Lett. 121 121602
Google Scholar
[30] Jiang J, Zhang H 2019 Phys. Rev. D 99 086005
Google Scholar
[31] Feng X H, Liu H S 2019 Eur. Phys. J. C 79 40
Google Scholar
[32] Alishahiha M, Astaneh A F, Naseh A, Vahidinia M H 2017 J. High Energy Phys. 2017 9
Google Scholar
[33] Carmi D, Chapman S, Marrochio H, Myers R C, Sugishita S 2017 J. High Energy Phys. 2017 188
Google Scholar
[34] Jiang J, Ge B X 2019 Phys. Rev. D 99 126006
Google Scholar
[35] Moosa M 2018 Phys. Rev. D 97 106016
Google Scholar
[36] Fan Z Y, Chen B, Lü H 2016 Eur. Phys. J. C 76 542
Google Scholar
[37] Haking S W, Page D N 1983 Commun. Math. Phys. 87 577
Google Scholar
[38] 刘显明, 雷焱林, 陈丽, 韩成 2015 湖北民族学院学报(自然科学版) 33 1
Google Scholar
Liu X M, Lei Y L, Chen L, Han C 2015 J. Hubei Univ. Nationalities (Nat. Sci. Ed.) 33 1
Google Scholar
[39] Brigante M, Liu H, Myers R C, Shenker S, Yaida S 2008 Phys. Rev. D 77 126006
Google Scholar
[40] Brigante M, Liu H, Myers R C, Shenker S, Yaida S 2008 Phys. Rev. Lett. 100 191601
Google Scholar
[41] Buchel A, Myers R C 2009 J. High Energy Phys. 2009 8
Google Scholar
[42] Camanho X O, Edelstein J D 2010 J. High Energy Phys. 2010 7
Google Scholar
[43] Wald R M 1993 Phys. Rev. D 48 3427
Google Scholar
[44] Iyer V, Wald R M 1994 Phys. Rev. D 50 846
Google Scholar
[45] Fan Z Y, Lü H 2015 Phys. Rev. D 91 064009
Google Scholar
DownLoad:
Catalog
Metrics
- Abstract views: 5179
- PDF Downloads: 69
- Cited By: 0
