Method of accelerating convergence for gas kinetic algorithm based on digital constitutive relation of macroscopic equations

Pi Xing-Cai; Zhu Lian-Hua; Li Zhi-Hui; Peng Ao-Ping; Zhang Yong-Hao

doi:10.7498/aps.69.20200602

Abstract

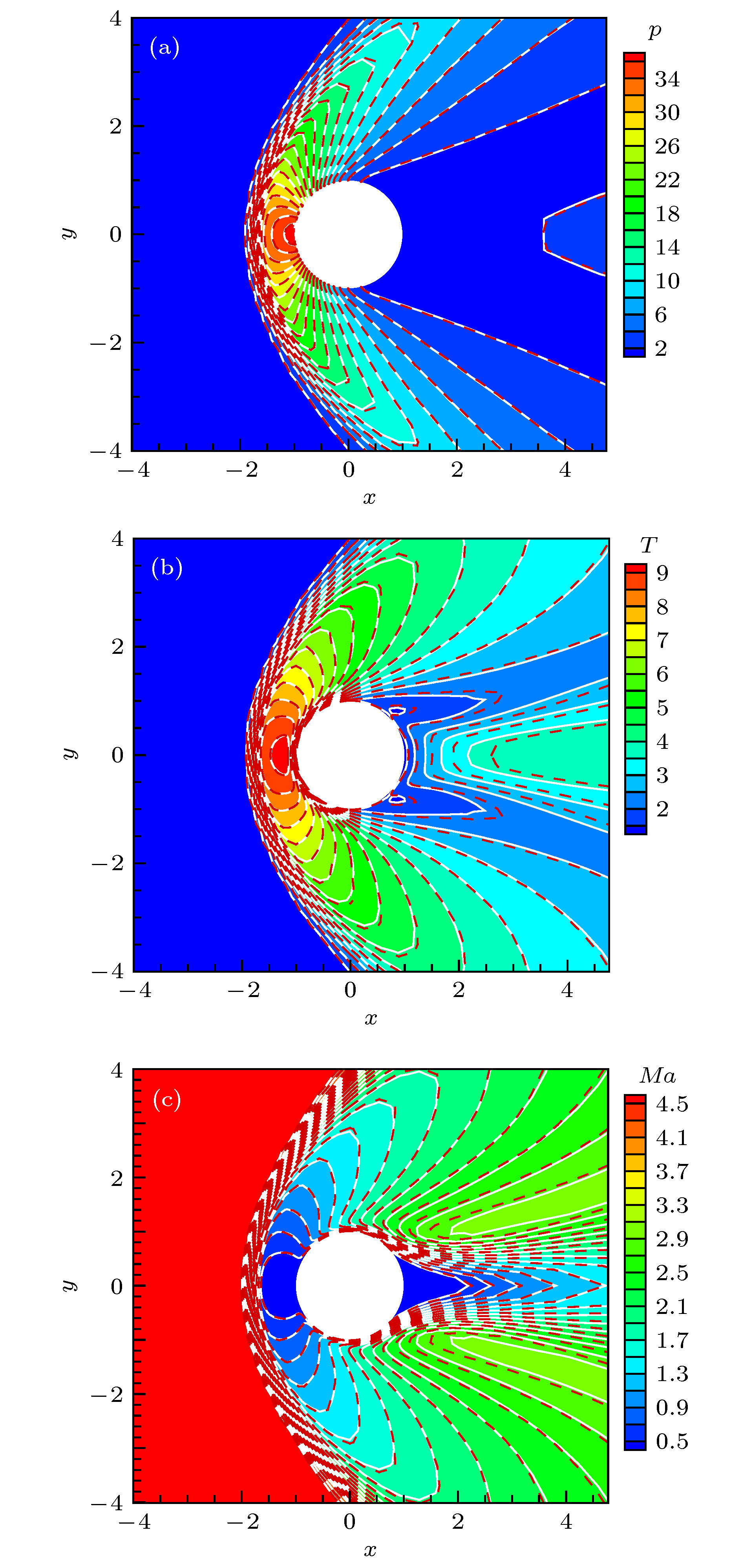
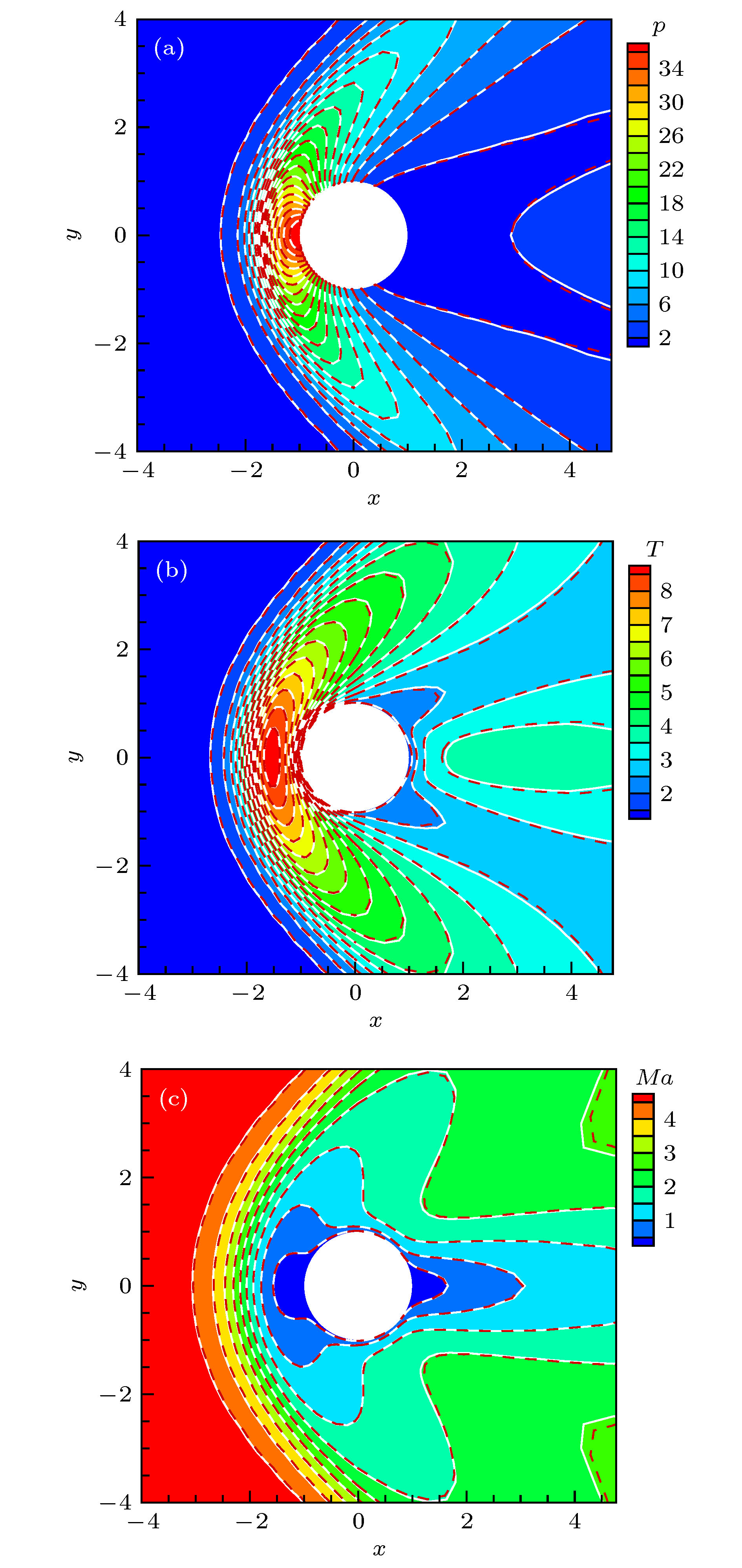
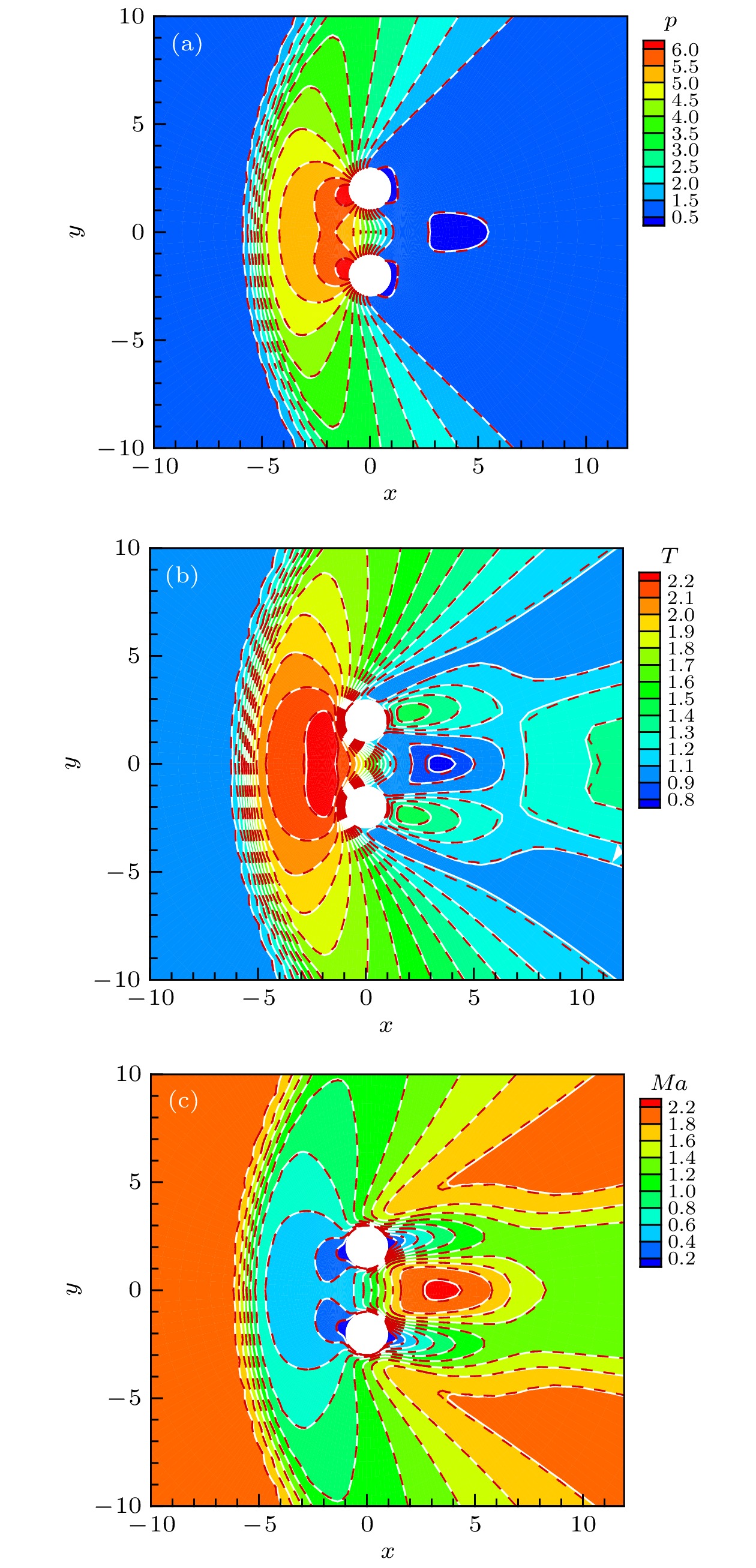
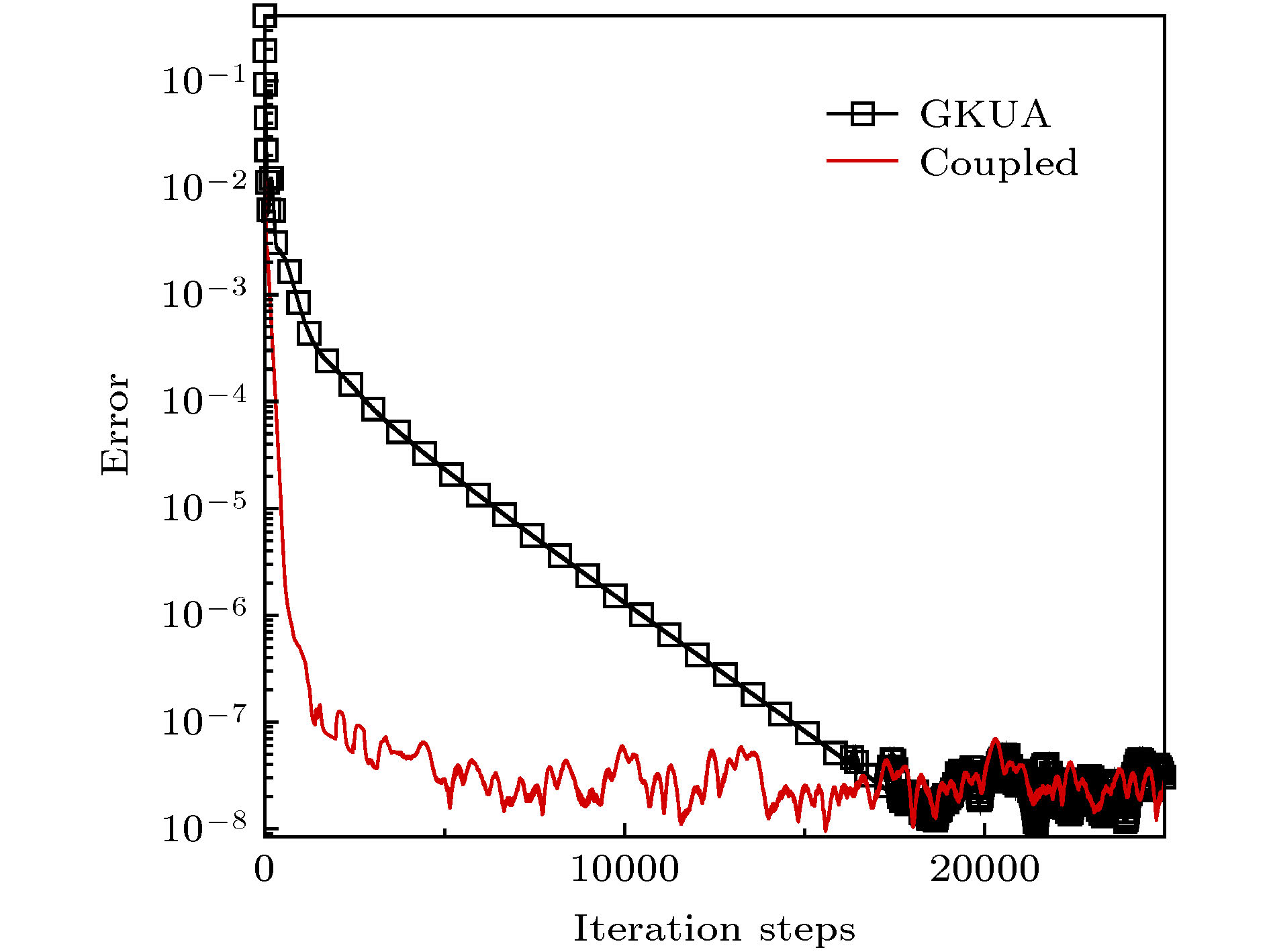
In the simulation of complex multi-scale flows covering various flow regimes, the computational efficiency of gas kinetic method by which the evolution equation of velocity distribution function is solved directly is the key to engineering applications. In order to accelerate simulation for steady flows, a gas kinetic algorithm accelerated by utilizing the macroscopic conservative equations with a digital constitutive relation is developed. In this algorithm, the contribution of the high-order terms of stress and heat flux in macroscopic conservative equations is determined by the gas kinetic solution. Meanwhile, the solution of the macroscopic conservative equations provides the macroscopic quantities for the equilibrium distribution function in the Boltzmann model equation, where a fully implicit scheme to solve the Boltzmann model equation is developed. Extensive validations are performed for the cavity flow, the supersonic flow around the cylinder, and the interactive rarefied flow around two side-by-side cylinders. The results from the above method are in good agreement with the results from the conventional gas kinetic unified algorithm and the direct simulation Monte Carlo method. It can be concluded that the nonlinear constitutive relation of rarefied flow can be well captured by the present method. And the ability of this method to simulate complex flows such as shock wave, strong wall shear and flow separation is demonstrated. Furthermore, the present method has shown to be much faster than the conventional gas kinetic unified algorithm, especially for the low-Kn flows. As the value of Kn increases, the acceleration rate decreases, because the effect of flow convection becomes weak. Meanwhile, more effort is needed to reduce inner loop iterations to improve its efficiency.

Keywords:

Authors and contacts

1.
Hypervelocity Aerodynamics Institute, China Aerodynamics Research and Development Center, Mianyang 621000, China
2.
James Weir Fluids Laboratory, Department of Mechanical and Aerospace Engineering, University of Strathclyde, Glasgow G1 1XJ, UK
3.
National Laboratory for Computational Fluid Dynamics, Beijing 100191, China

Corresponding author: Li Zhi-Hui, zhli0097@x263.net

Funds: Project supported by the Young Scientists Fund of the National Natural Science Foundation of China (Grant No. 11902339)

FullText HTML

References

[1]	Cercignani C 1988 The Boltzmann Equation and its Applications (New York: Springer) pp40−103
[2]	Kremer G M 2010 An Introduction to the Boltzmann Equation and Transport Processes in Gases (Berlin: Springer) pp37−80
[3]	Shakhov E M 1968 Fluid Dyn. 3 95
[4]	Brull S, Schneider J 2009 Cont. Mech. Thermodyn. 20 489 Google Scholar
[5]	Broadwell J 1964 J. Fluid Mech. 19 401 Google Scholar
[6]	Huang A B, Huang P F, Giddens D P, Srinivasan R 1973 Phys. Fluids 16 814 Google Scholar
[7]	李志辉 2001 博士学位论文 (绵阳: 中国空气动力研究与发展中心) Li Z H 2001 Ph. D. Dissertation (Mianyang: China Aerodynamics Research and Development Center) (in Chinese)
[8]	Li Z H, Zhang H X 2004 J. Comput. Phys. 223 708
[9]	Li Z H, Zhang H X 2008 Int. J. Comput. Fluid Dyn. 22 623 Google Scholar
[10]	Li Z H, Zhang H X 2009 J. Comput. Phys. 228 1116 Google Scholar
[11]	Xu K, Huang J C 2010 J. Comput. Phys. 229 7747 Google Scholar
[12]	Jin S, Wang L 2013 SIAM J. Sci. Comput. 35 799 Google Scholar
[13]	Jin S 1999 SIAM J. Sci. Comput. 21 441 Google Scholar
[14]	Gu X J, Emerson D R 2011 Microfluid. Nanofluid. 10 389 Google Scholar
[15]	许爱国, 张广财, 李英骏, 李华 2014 物理学进展 34 136 Google Scholar Xu A G, Zhang G C, Li Y J, Li H 2014 Prog. Phys. 34 136 Google Scholar
[16]	许爱国, 张广财, 应阳君 2015 64 184701 Google Scholar Xu A G, Zhang G C, Ying Y J 2015 Acta Phys. Sin. 64 184701 Google Scholar
[17]	Li Z H, Peng A P, Zhang H X, Yang J Y 2015 Prog. Aerosp. Sci. 74 81 Google Scholar
[18]	Li Z H, Peng A P, Ma Q, Dang L N, Tang X W, Sun X Z 2019 Adv. Aerodyn. 1 1 Google Scholar
[19]	彭傲平 2017 博士学位论文 (绵阳: 中国空气动力研究与发展中心) Peng A P 2017 Ph. D. Dissertation (Mianyang: China Aerodynamics Research and Development Center) (in Chinese)
[20]	李志辉, 梁杰, 李中华, 李海燕, 吴俊林, 戴金雯, 唐志共 2018 空气动力学学报 36 826 Google Scholar Li Z H, Liang J, Li Z H, Li H Y, Wu J L, Dai J W, Tang Z G 2018 Acta Aerodynam. Sin. 36 826 Google Scholar
[21]	吴俊林 2018博士学位论文 (绵阳: 中国空气动力研究与发展中心) Wu J L 2018 Ph. D. Dissertation (Mianyang: China Aerodynamics Research and Development Center) (in Chinese)
[22]	Mieussens L 2000 J. Comput. Phys. 162 429 Google Scholar
[23]	Chen S Z, Xu K, Lee C B, Cai Q D 2012 J. Comput. Phys. 231 6643 Google Scholar
[24]	江定武 2016 博士学位论文 (绵阳: 中国空气动力研究与发展中心) Jiang D W 2016 Ph. D. Dissertation (Mianyang: China Aerodynamics Research and Development Center) (in Chinese)
[25]	Li Z H, Bi L, Tang Z G 2009 Appl. Math. Mech.-Engl. 30 889 Google Scholar
[26]	Peng A P, Li Z H, Wu J L, Jiang X Y 2016 J. Comput. Phys. 327 919 Google Scholar
[27]	Hu W Q, Li Z H 2018 Comput. Math. Appl. 75 4179 Google Scholar
[28]	Rovenskaya O, Croce G 2014 Vacuum 109 266 Google Scholar
[29]	Valougeorgis D, Naris S 2003 SIAM J. Sci. Comput. 25 534 Google Scholar
[30]	Zhu Y J, Zhong C W, Xu K 2017 Phys. Fluids 29 096102 Google Scholar
[31]	Zhu Y J, Zhong C W, Xu K 2016 J. Comput. Phys. 315 16 Google Scholar
[32]	Jin S, Slemrod M 2001 J. Stat. Phys. 103 1009 Google Scholar
[33]	Struchtrup H, Torrilbon M 2003 Phys. Fluids 15 2668 Google Scholar
[34]	Xiao H, Tang K 2017 Sci. Rep. 7 13108 Google Scholar
[35]	Myong R S 2001 J. Comput. Phys. 168 47 Google Scholar
[36]	陈伟芳, 赵文文 2017 稀薄气体动力学矩方法及数值模拟 (北京: 科学出版社) 第1—16页 Chen W F, Zhao W W 2017 Moment Method and Numerical Simulation on Rarefied Gas Dynamics (Beijing: Science Press) pp1–16 (in Chinese)
[37]	Su W, Zhu L H, Wang P, Zhang Y H, Wu L 2020 J. Comput. Phys. 407 109245 Google Scholar
[38]	Adams M L, Larsen E W 2002 Prog. Nucl. Energy 40 3 Google Scholar
[39]	Zhu L H, Pi X C, Su W, Li Z H, Zhang Y H, Wu L 2020 arXiv: 2004.10530 v [physics. comp-ph]
[40]	Guo Z L, Xu K, Wang R J 2013 Phys. Rev. E 88 033305 Google Scholar
[41]	Guo Z L, Wang R J, Xu K 2015 Phys. Rev. E 91 033313 Google Scholar
[42]	Li X L http://pan.baidu.com/s/1 slfC5 Yl [2020-6-6]
[43]	Kudryavtsev A N, Shershnev A A 2013 J. Sci. Comput. 57 42 Google Scholar
[44]	沈青 2003 稀薄气体动力学 (北京: 国防工业出版社) 第105−110页 Shen Q 2003 Rarefied Gas Dynamics (Beijing: National Defense Industry Press) pp105−110 (in Chinese)
[45]	Yang L M, Chen Z, Shu C, Yang W M, Wu J, Zhang L Q 2018 Phys. Rev. E 98 063313 Google Scholar
[46]	Bird G A 2005 Proceedings of the 24th International Symposium on Rarefied Gas Dynamics Bari, Italy, July 10−16, 2004 p541
[47]	Zhu L H, Guo Z L, Xu K 2016 Comput. Fluids 127 211 Google Scholar

Cited By

图 1 方腔流温度分布计算结果　(a) Kn = 1 ; (b) Kn = 0.075; (c) Kn = 0.01 (GKUA: 彩色背景及黑色实线; Coupled: 红色虚线)

Figure 1. Temperature distribution in cavity flow: (a) Kn = 1; (b) Kn = 0.075; (c) Kn = 0.01 (GKUA: coloured background and black solid lines; Coupled: red dashed lines).

DownLoad: Full-Size Img PowerPoint

图 2 方腔中心线上的速度场　(a) Kn = 1; (b) Kn = 0.075; (c) Kn = 0.01

Figure 2. Velocity profiles at the central lines of the cavity: (a) Kn = 1; (b) Kn = 0.075; (c) Kn = 0.01.

DownLoad: Full-Size Img PowerPoint

图 3 耦合加速收敛方法与常规GKUA的计算收敛历史

Figure 3. The convergence history between coupled acceleration method and the conventional GKUA.

DownLoad: Full-Size Img PowerPoint

图 4 Kn = 0.01圆柱绕流流场对比　(a) 压力; (b) 温度; (c) 马赫数 (GKUA: 彩色背景及白实线; Coupled: 红色虚线)

Figure 4. (a) Pressure, (b) temperature, (c) Mach number distribution around cylinder for Kn = 0.01 (GKUA: coloured background and white solid lines; Coupled: red dash lines).

DownLoad: Full-Size Img PowerPoint

图 5 Kn = 0.1圆柱绕流流场对比　(a) 压力; (b) 温度; (c) 马赫数(GKUA: 彩色背景及白实线; Coupled: 红色虚线)

Figure 5. (a) Pressure, (b) temperature, (c) Mach number distribution around cylinder for Kn = 0.1 (GKUA: coloured background and white solid lines; Coupled: red dash lines).

DownLoad: Full-Size Img PowerPoint

图 6 圆柱壁面的　(a) 压力, (b) 热流, (c) 剪切应力

Figure 6. (a) Pressure, (b) heat flux, and (c) shear stress profile along the wall surface of cylinder.

DownLoad: Full-Size Img PowerPoint

图 7 耦合加速收敛方法与常规GKUA的超声速圆柱绕流计算收敛情况对比

Figure 7. Comparison of the convergence history of supersonic flow around the cylinder between the coupled acceleration method and the conventional GKUA.

DownLoad: Full-Size Img PowerPoint

图 8 并列双圆柱多块网格布局

Figure 8. The multi-blocks mesh layout for two side-by-side cylinders.

DownLoad: Full-Size Img PowerPoint

图 9 并列双圆柱绕流流场对比　(a) 压力; (b) 温度; (c) 马赫数(GKUA: 彩色背景及白实线; Coupled: 红色虚线)

Figure 9. (a) Pressure, (b) temperature, (c) Mach number field for two side-by-side cylinders (GKUA: coloured background and white solid lines; Coupled: red dash lines).

DownLoad: Full-Size Img PowerPoint

图 10 上圆柱壁面的　(a) 压力, (b) 热流, (c) 剪切应力

Figure 10. (a) Pressure, (b) heat flux, and (c) shear stress profile along the surface of upper cylinder.

DownLoad: Full-Size Img PowerPoint

图 11 耦合加速收敛方法与常规GKUA的并列双圆柱超声速绕流计算收敛情况对比

Figure 11. Comparison of the convergence history of supersonic flow around two side-by-side cylinders between the coupled acceleration method and the conventional GKUA.

DownLoad: Full-Size Img PowerPoint

表 1 耦合加速收敛方法与常规GKUA的收敛情况对比

Table 1. Convergence comparison between the conventional GKUA and the coupled acceleration method.

Kn 迭代步数(收敛标准: 10^–7) 加速比
GKUA Coupled

0.010 8000 170 47.00
0.075 2300 300 7.60
1.000 1200 1100 1.09

DownLoad: CSV

map

[1]	Cercignani C 1988 The Boltzmann Equation and its Applications (New York: Springer) pp40−103
[2]	Kremer G M 2010 An Introduction to the Boltzmann Equation and Transport Processes in Gases (Berlin: Springer) pp37−80
[3]	Shakhov E M 1968 Fluid Dyn. 3 95
[4]	Brull S, Schneider J 2009 Cont. Mech. Thermodyn. 20 489 Google Scholar
[5]	Broadwell J 1964 J. Fluid Mech. 19 401 Google Scholar
[6]	Huang A B, Huang P F, Giddens D P, Srinivasan R 1973 Phys. Fluids 16 814 Google Scholar
[7]	李志辉 2001 博士学位论文 (绵阳: 中国空气动力研究与发展中心) Li Z H 2001 Ph. D. Dissertation (Mianyang: China Aerodynamics Research and Development Center) (in Chinese)
[8]	Li Z H, Zhang H X 2004 J. Comput. Phys. 223 708
[9]	Li Z H, Zhang H X 2008 Int. J. Comput. Fluid Dyn. 22 623 Google Scholar
[10]	Li Z H, Zhang H X 2009 J. Comput. Phys. 228 1116 Google Scholar
[11]	Xu K, Huang J C 2010 J. Comput. Phys. 229 7747 Google Scholar
[12]	Jin S, Wang L 2013 SIAM J. Sci. Comput. 35 799 Google Scholar
[13]	Jin S 1999 SIAM J. Sci. Comput. 21 441 Google Scholar
[14]	Gu X J, Emerson D R 2011 Microfluid. Nanofluid. 10 389 Google Scholar
[15]	许爱国, 张广财, 李英骏, 李华 2014 物理学进展 34 136 Google Scholar Xu A G, Zhang G C, Li Y J, Li H 2014 Prog. Phys. 34 136 Google Scholar
[16]	许爱国, 张广财, 应阳君 2015 64 184701 Google Scholar Xu A G, Zhang G C, Ying Y J 2015 Acta Phys. Sin. 64 184701 Google Scholar
[17]	Li Z H, Peng A P, Zhang H X, Yang J Y 2015 Prog. Aerosp. Sci. 74 81 Google Scholar
[18]	Li Z H, Peng A P, Ma Q, Dang L N, Tang X W, Sun X Z 2019 Adv. Aerodyn. 1 1 Google Scholar
[19]	彭傲平 2017 博士学位论文 (绵阳: 中国空气动力研究与发展中心) Peng A P 2017 Ph. D. Dissertation (Mianyang: China Aerodynamics Research and Development Center) (in Chinese)
[20]	李志辉, 梁杰, 李中华, 李海燕, 吴俊林, 戴金雯, 唐志共 2018 空气动力学学报 36 826 Google Scholar Li Z H, Liang J, Li Z H, Li H Y, Wu J L, Dai J W, Tang Z G 2018 Acta Aerodynam. Sin. 36 826 Google Scholar
[21]	吴俊林 2018博士学位论文 (绵阳: 中国空气动力研究与发展中心) Wu J L 2018 Ph. D. Dissertation (Mianyang: China Aerodynamics Research and Development Center) (in Chinese)
[22]	Mieussens L 2000 J. Comput. Phys. 162 429 Google Scholar
[23]	Chen S Z, Xu K, Lee C B, Cai Q D 2012 J. Comput. Phys. 231 6643 Google Scholar
[24]	江定武 2016 博士学位论文 (绵阳: 中国空气动力研究与发展中心) Jiang D W 2016 Ph. D. Dissertation (Mianyang: China Aerodynamics Research and Development Center) (in Chinese)
[25]	Li Z H, Bi L, Tang Z G 2009 Appl. Math. Mech.-Engl. 30 889 Google Scholar
[26]	Peng A P, Li Z H, Wu J L, Jiang X Y 2016 J. Comput. Phys. 327 919 Google Scholar
[27]	Hu W Q, Li Z H 2018 Comput. Math. Appl. 75 4179 Google Scholar
[28]	Rovenskaya O, Croce G 2014 Vacuum 109 266 Google Scholar
[29]	Valougeorgis D, Naris S 2003 SIAM J. Sci. Comput. 25 534 Google Scholar
[30]	Zhu Y J, Zhong C W, Xu K 2017 Phys. Fluids 29 096102 Google Scholar
[31]	Zhu Y J, Zhong C W, Xu K 2016 J. Comput. Phys. 315 16 Google Scholar
[32]	Jin S, Slemrod M 2001 J. Stat. Phys. 103 1009 Google Scholar
[33]	Struchtrup H, Torrilbon M 2003 Phys. Fluids 15 2668 Google Scholar
[34]	Xiao H, Tang K 2017 Sci. Rep. 7 13108 Google Scholar
[35]	Myong R S 2001 J. Comput. Phys. 168 47 Google Scholar
[36]	陈伟芳, 赵文文 2017 稀薄气体动力学矩方法及数值模拟 (北京: 科学出版社) 第1—16页 Chen W F, Zhao W W 2017 Moment Method and Numerical Simulation on Rarefied Gas Dynamics (Beijing: Science Press) pp1–16 (in Chinese)
[37]	Su W, Zhu L H, Wang P, Zhang Y H, Wu L 2020 J. Comput. Phys. 407 109245 Google Scholar
[38]	Adams M L, Larsen E W 2002 Prog. Nucl. Energy 40 3 Google Scholar
[39]	Zhu L H, Pi X C, Su W, Li Z H, Zhang Y H, Wu L 2020 arXiv: 2004.10530 v [physics. comp-ph]
[40]	Guo Z L, Xu K, Wang R J 2013 Phys. Rev. E 88 033305 Google Scholar
[41]	Guo Z L, Wang R J, Xu K 2015 Phys. Rev. E 91 033313 Google Scholar
[42]	Li X L http://pan.baidu.com/s/1 slfC5 Yl [2020-6-6]
[43]	Kudryavtsev A N, Shershnev A A 2013 J. Sci. Comput. 57 42 Google Scholar
[44]	沈青 2003 稀薄气体动力学 (北京: 国防工业出版社) 第105−110页 Shen Q 2003 Rarefied Gas Dynamics (Beijing: National Defense Industry Press) pp105−110 (in Chinese)
[45]	Yang L M, Chen Z, Shu C, Yang W M, Wu J, Zhang L Q 2018 Phys. Rev. E 98 063313 Google Scholar
[46]	Bird G A 2005 Proceedings of the 24th International Symposium on Rarefied Gas Dynamics Bari, Italy, July 10−16, 2004 p541
[47]	Zhu L H, Guo Z L, Xu K 2016 Comput. Fluids 127 211 Google Scholar

[1]	Cao Zhen, Hao Da-Peng, Tang Gang, Xun Zhi-Peng, Xia Hui. Influence of cluster shaped defects on fracture process of fiber bundle. Acta Physica Sinica, 2021, 70(20): 204602. doi: 10.7498/aps.70.20210310
[2]	Wang Qiang, Guo Li-Xin. Composite electromagnetic scattering from a ship located on one-dimensional sea surface with time-domain hybrid method. Acta Physica Sinica, 2017, 66(18): 180301. doi: 10.7498/aps.66.180301
[3]	Wu Xiao-Di, Liu Hua-Ping, Chen Fu. A method combined immersed boundary with multi-relaxation-time lattice Boltzmann flux solver for fluid-structure interaction. Acta Physica Sinica, 2017, 66(22): 224702. doi: 10.7498/aps.66.224702
[4]	Peng Ao-Ping, Li Zhi-Hui, Wu Jun-Lin, Jiang Xin-Yu. Validation and analysis of gas-kinetic unified algorithm for solving Boltzmann model equation with vibrational energy excitation. Acta Physica Sinica, 2017, 66(20): 204703. doi: 10.7498/aps.66.204703
[5]	Xing Hong-Yan, Zhang Qiang, Xu Wei. Hybrid algorithm for weak signal detection in chaotic sea clutter. Acta Physica Sinica, 2015, 64(4): 040506. doi: 10.7498/aps.64.040506
[6]	Xu Xin-He, Liu Ying, Gan Yue-Hong, Liu Wen-Miao. A method of retrieving the constitutive parameter matrix of magnetoelectric coupling metamaterial. Acta Physica Sinica, 2015, 64(4): 044101. doi: 10.7498/aps.64.044101
[7]	Cao Bei, Luo Xiu-Juan, Si Qing-Dan, Zeng Zhi-Hong. Four-phase closure algorithm for coherent field imaging. Acta Physica Sinica, 2015, 64(5): 054204. doi: 10.7498/aps.64.054204
[8]	Li Zhi-Hui, Peng Ao-Ping, Fang Fang, Li Si-Xin, Zhang Shun-Yu. Gas-kinetic unified algorithm for hypersonic aerothermodynamics covering various flow regimes solving Boltzmann model equation. Acta Physica Sinica, 2015, 64(22): 224703. doi: 10.7498/aps.64.224703
[9]	Chen Yan-Pei, Pierre Evesque, Hou Mei-Ying. Experimental study on the local equation of state for vibrated granular gases. Acta Physica Sinica, 2013, 62(16): 164503. doi: 10.7498/aps.62.164503
[10]	Tao Wei-Jun, Huan Shi. Study on Lagrangian analysis for solving the stress gradually along the time. Acta Physica Sinica, 2012, 61(20): 200703. doi: 10.7498/aps.61.200703
[11]	Pan Hao, Hu Xiao-Mian, Wu Zi-Hui, Dai Cheng-Da, Wu Qiang. Numerical study of shock-induced phase transformation of cerium under low pressure. Acta Physica Sinica, 2012, 61(20): 206401. doi: 10.7498/aps.61.206401
[12]	Guo Li-Xin, Qin San-Tuan, Gong Shu-Xi, Dai Shao-Yu. A hybrid algorithm for the transient scattering from a two-dimensional conductor target above a randomly rough surface. Acta Physica Sinica, 2011, 60(7): 074217. doi: 10.7498/aps.60.074217
[13]	Gan Tian, Feng Shao-Tong, Nie Shou-Ping, Zhu Zhu-Qing. Image fusion algorithm based on block-DCT in wavelet domain. Acta Physica Sinica, 2011, 60(11): 114205. doi: 10.7498/aps.60.114205
[14]	Liu Wen-Long, Pang Shuang-Jie, Zhang Ji-Feng. A fast algorithm with convergence for generalized predictive function control of Hnon chaotic system. Acta Physica Sinica, 2011, 60(11): 110505. doi: 10.7498/aps.60.110505
[15]	Liang Yu, Guo Li-Xin, Wang Rui. Investigation on the reconstruction of roughsurface with hybrid method. Acta Physica Sinica, 2011, 60(3): 034102. doi: 10.7498/aps.60.034102
[16]	Gong Jian-Qiang, Liang Chang-Hong. Extraction algorithm for retrieving the effective constitutive parameters of metamaterials based on TE10 rectangular waveguide. Acta Physica Sinica, 2011, 60(5): 059204. doi: 10.7498/aps.60.059204
[17]	Fang Wei, Sun Jun, Xie Zhen-Ping, Xu Wen-Bo. Convergence analysis of quantum-behaved particle swarm optimization algorithm and study on its control parameter. Acta Physica Sinica, 2010, 59(6): 3686-3694. doi: 10.7498/aps.59.3686
[18]	Lan Xu-Dong. Breakdown parameter in hybrid method. Acta Physica Sinica, 2009, 58(12): 8415-8418. doi: 10.7498/aps.58.8415
[19]	Ye Hong-Xia, Jin Ya-Qiu. A hybrid analytical-numerical algorithm for scattering from a 3-D target above a randomly rough surface. Acta Physica Sinica, 2008, 57(2): 839-846. doi: 10.7498/aps.57.839
[20]	Wang Rui, Guo Li-Xin, Qin San-Tuan, Wu Zhen-Sen. Hybrid method for investigation of electromagnetic scattering interaction between the conducting target and rough sea surface. Acta Physica Sinica, 2008, 57(6): 3473-3480. doi: 10.7498/aps.57.3473

Catalog

Vol. 69, Issue 20 - 2020-10-20

Metrics

Abstract views: 7132
PDF Downloads: 82
Cited By: 0

姓名
邮箱
手机号码
标题
留言内容
验证码

Search

Article

留言板