-
Proton radiography is a widely used method to diagnose the electromagnetic field of plasma. When protons pass through the electromagnetic field of plasma, they are deflected by Lorentz force and redistributed on the recorder. How to reconstruct electromagnetic field from the experimental result is an open problem. In this paper, we take the laser-driven capacitor-coil target for example to introduce and compare particle tracing and flux analysis, which are two widely used methods in proton radiography experiment to reconstruct the magnetic field. The capacitor-coil target is an important method to generate strong magnetic field in laser plasma experiment, where the strong current flows in the coil and its producing magnetic field may be larger than kilotesla. Firstly, the theoretical magnetic fields of capacitor-coil target are calculated with current being 10 kA and 50 kA. Secondly, the Geant4 is used to simulate the proton radiographs, where protons with 7.5 MeV pass through the target and the theoretical magnetic field is recorded. Thirdly, the theoretical proton radiographs are analyzed by the flux analysis method, and two magnetic fields are reconstructed. Finally, the theoretical magnetic fields are compared with the reconstructed ones, and the advantages and disadvantages of these two methods are analyzed. Particle tracing rebuilds the geometry distribution of proton source, plasma magnetic field and recorder in experiment, and it needs few assumptions. However, it strongly relies on accurate calculation of theoretical magnetic field and proton trajectory, and it requires to change the magnetic field over and over to achieve a closest result to the experimental proton radiograph. Meanwhile, particle tracing method consumes a lot of computation sources. The flux analysis directly reconstructs the magnetic field from experimental proton radiograph. However, it is only applicable to the case of weak magnetic field, and the error becomes larger for the case of stronger magnetic field. A dimensionless parameter μ is used to estimate the deflection of proton in the magnetic field, which measures the amount of deflection per unit length in the interaction region. The flux analysis method is applicable to the
$\mu\ll 1$ regime. Additionally, the target may absorb the proton when the energy of proton is low and produces shadow on the proton radiograph, which leads to some difference between the original magnetic field and the reconstructed result.[1] Mackinnon A J, Patel P K, Town R P, et al. 2004 Rev. Sci. Instrum. 75 3531
Google Scholar
[2] Mackinnon A J, Patel P K, Borghesi M, et al. 2006 Phys. Rev. Lett. 97 045001
Google Scholar
[3] Li C K, Seguin F H, Frenje J A, et al. 2006 Phys. Rev. Lett. 97 135003
Google Scholar
[4] Rygg J R, Seguin F H, Li C K, et al. 2008 Science 319 1223
Google Scholar
[5] Romagnani L, Bulanov S V, Borghesi M, Audebert P, Gauthier J C, Lowenbruck K, MacKinnon A J, Patel P, Pretzler G, Toncian T, Willi O 2008 Phys. Rev. Lett. 101 025004
Google Scholar
[6] Huntington C M, Fiuza F, Ross J S, et al. 2015 Nat. Phys. 11 173
Google Scholar
[7] Hatchett S P, Brown C G, Cowan T E, et al. 2000 Phys. Plasmas 7 2076
Google Scholar
[8] Snavely R A, Key M H, Hatchett S P, et al. 2000 Phys. Rev. Lett. 85 2945
Google Scholar
[9] Maksimchuk A, Gu S, Flippo K, Umstadter D, Bychenkov A Yu 2000 Phys. Rev. Lett. 84 4108
Google Scholar
[10] Clark E L, Krushelnick K, Davies J R, Zepf M, Tatarakis M, Beg F N, Machacek A, Norreys P A, Santala M I, Watts I, Dangor A E 2000 Phys. Rev. Lett., 84 670
Google Scholar
[11] Roth M, Schollmeier M 2017 arXiv:1705.10569
[12] Li C K, Sguin F H, Frenje J A, et al. 2006 Rev. Sci. Instrum. 77 10E
[13] Manuel M J, Zylstra A B, Rinderknecht H G, Casey D T, Rosenberg M J, Sinenian N, Li C K, Frenje J A, Séguin F H, Petrasso R D 2012 Rev. Sci. Instrum. 83 063506
Google Scholar
[14] Levy M C, Ryutov D D, Wilks S C, Ross J S, Huntington C M, Fiuza F, Martinez D A, Kugland N L, Baring M G, Park H S 2015 Rev. Sci. Instrum. 86 033302
Google Scholar
[15] Zhang C J, Hua J F, Wan Y, Pai C H, Guo B, Zhang J, Ma Y, Li F, Wu Y P, Chu H H, Gu Y Q, Xu X L, Mori W B, Joshi C, Wang J, Lu W 2017 Phys. Rev. Lett. 119 064801
Google Scholar
[16] Kugland N L, Ryutov D D, Plechaty C, Ross J S, Park H S 2012 Rev. Sci. Instrum. 83 101301
Google Scholar
[17] Graziani C, Tzeferacos P, Lamb D Q, Li C K 2017 Rev. Sci. Instrum. 88 123507
Google Scholar
[18] Bott A F A, Graziani C, Tzeferacos P, White T G, Lamb D Q, Gregori G, Schekochihin A A 2017 J. Plasma Phys. 83 905830614
Google Scholar
[19] 杜报, 蔡洪波, 张文帅, 陈京, 邹士阳, 朱少平 2019 68 185205
Google Scholar
Du B, Cai H B, Zhang W S, Zou S Y, Chen J, Zhu S P 2019 Acta Phys. Sin. 68 185205
Google Scholar
[20] Du B, Cai H B, Zhang W S, Tian J M, Zhang E H, Zou S Y, Chen J, Zhu S P 2019 Plasma Phys. Control. Fusion 62 025017
[21] Daido H, Miki F, Mima K, Fujita M, Sawai K, Fujita H, Kitagawa Y, Nakai S, Yamanaka C 1986 Phys. Rev. Lett. 56 846
Google Scholar
[22] Courtois C, Ash A D, Chambers D M, Grundy R A, Woolsey N C 2005 J. Appl. Phys. 98 054913
Google Scholar
[23] Fujioka S, Zhang Z, Ishihara K, Shigemori K, Hironaka Y, Johzaki T, Sunahara A, Yamamoto N, Nakashima H, Watanabe T, Shiraga H, Nishimura H, Azechi H 2013 Sci. Rep. 3 1170
Google Scholar
[24] Pei X X, Zhong J Y, Sakawa Y, et al. 2016 Phys. Plasmas 23 032125
Google Scholar
[25] Yuan X X, Zhong J Y, Zhang Z, et al. 2018 Plasma Phys. Control. Fusion 60 065009
Google Scholar
[26] Pia M G 2003 Nucl. Phys. B Proc. Suppl. 125 60
Google Scholar
[27] Allison J, Amako K, Apostolakis J, et al. 2006 IEEE Trans. Nucl. Sci. 53 270
Google Scholar
[28] Allison J, Amako K, Apostolakis J, et al. 2016 Nucl. Instrum. Methods Phys. Res., Sect. A 835 186
Google Scholar
[29] McGuire E J 1991 J. Appl. Phys. 70 7213
Google Scholar
-
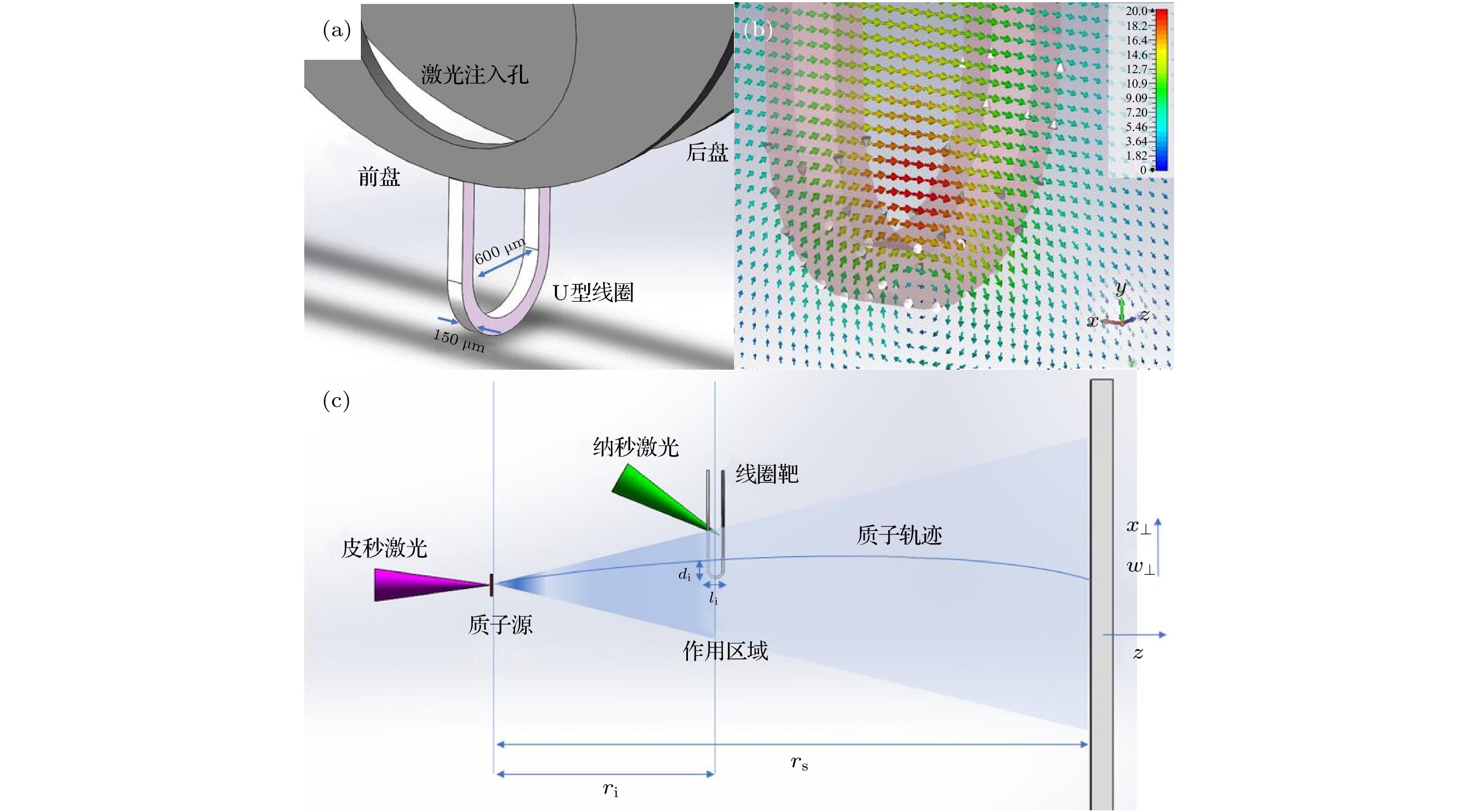
图 1 (a)电容线圈靶构造; (b)电容线圈靶磁场的分布示意图, 粉红色半透明区域为靶结构, 白色箭头标示了电流方向, 彩色箭头为X-Y平面的磁场结构; (c) 质子成像技术实验设置
Figure 1. (a) Configuration of capacitor-coil target; (b) schematic of magnetic field of capacitor-coil target. Pink-semitransparent is the coil, white arrows indicate the current direction, and colorful arrows indicate the magnetic field in X-Y plane; (c) experimental setup of proton radiography.
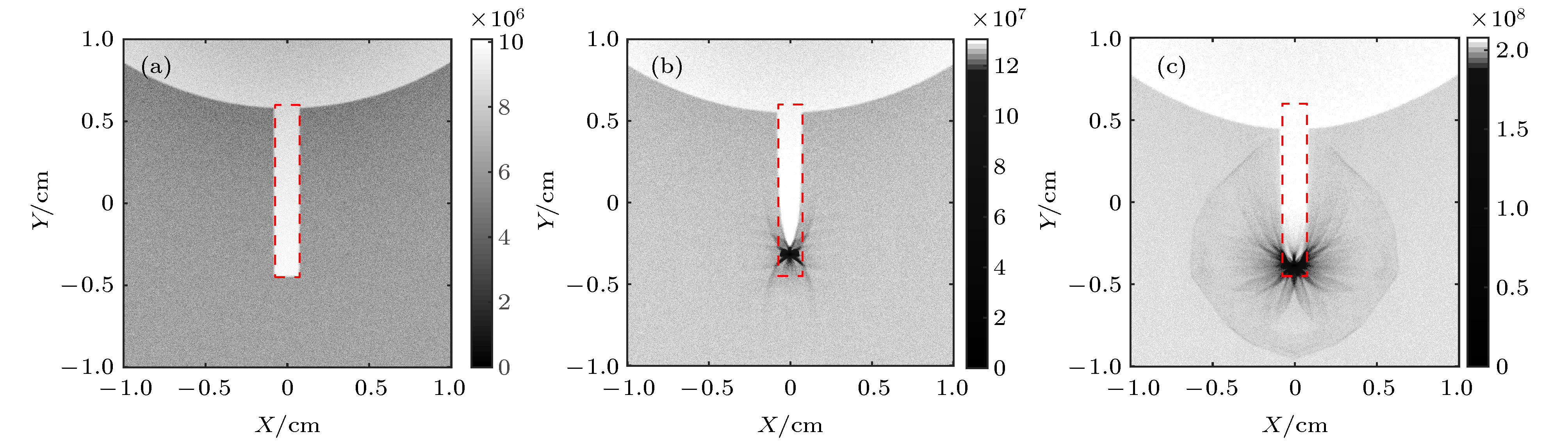
图 2 Geant4模拟结果, 图片中的坐标为放大10倍的成像板处的坐标 (a)线圈电流I = 0的静态结果; (b)线圈电流I = 10 kA的结果; (c)线圈电流I = 50 kA的结果. 红色虚线是线圈阴影的位置
Figure 2. Simulation results of Geant4, the coordinates are adjusted at the position of detector: (a) Coil current I = 0; (b) coil current I = 10 kA; (c) coil current I = 50 kA. The red dash regions are the position of the shadow of the coils
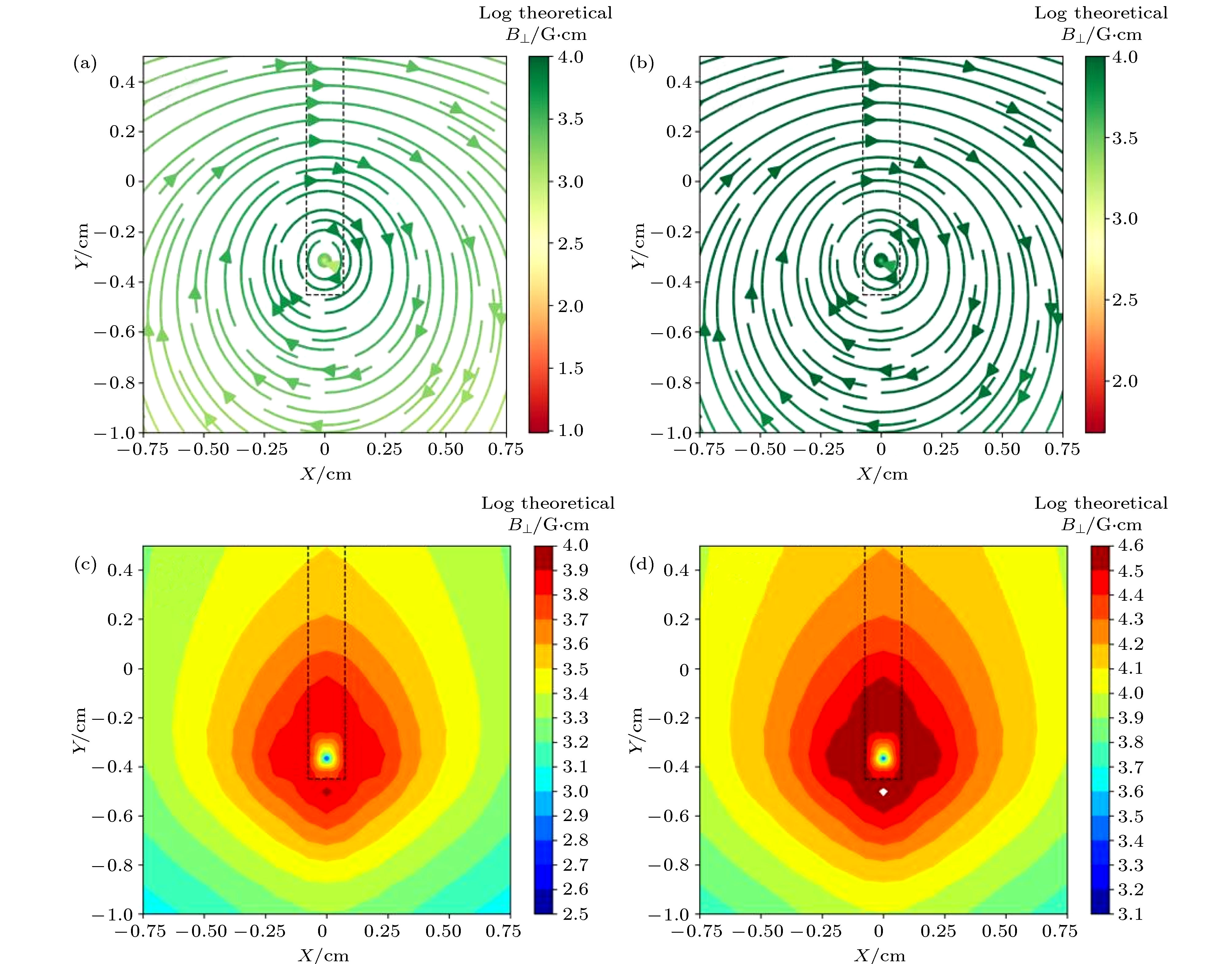
图 3 (a) I = 10 kA的理论磁场结构分布; (b) I = 50 kA 的理论磁场结构分布; (c) I = 10 kA 的理论磁感应强度分布; (d) I = 50 kA的理论磁感应强度分布. 黑色虚线是线圈阴影的位置. 图片中的坐标为放大10 倍后成像板处的坐标
Figure 3. (a) Theoretical magnetic strength for I = 10 kA; (b) theoretical magnetic strength for I = 50 kA; (c) theoretical magnetic configuration for I = 10 kA; (d) theoretical magnetic configuration for I = 50 kA. The black dash regions are the position of the shadow of the coils. The coordinates are adjusted at the position of detector
图 4 (a) I = 10 kA的理论重构结构分布; (b) I = 50 kA 的重构磁场结构分布; (c) I = 10 kA 的重构磁感应强度分布; (d) I = 50 kA的理论重构强度分布. 黑色虚线是线圈阴影的位置. 图片中的坐标为放大10 倍后成像板处的坐标
Figure 4. (a) Reconstructed magnetic strength for I = 10 kA; (b) reconstructed magnetic strength for I = 50 kA; (c) reconstructed magnetic configuration for I = 10 kA; (d) reconstructed magnetic configuration for I = 50 kA. The black dash regions are the position of the shadow of the coils. The coordinates are adjusted at the position of detector
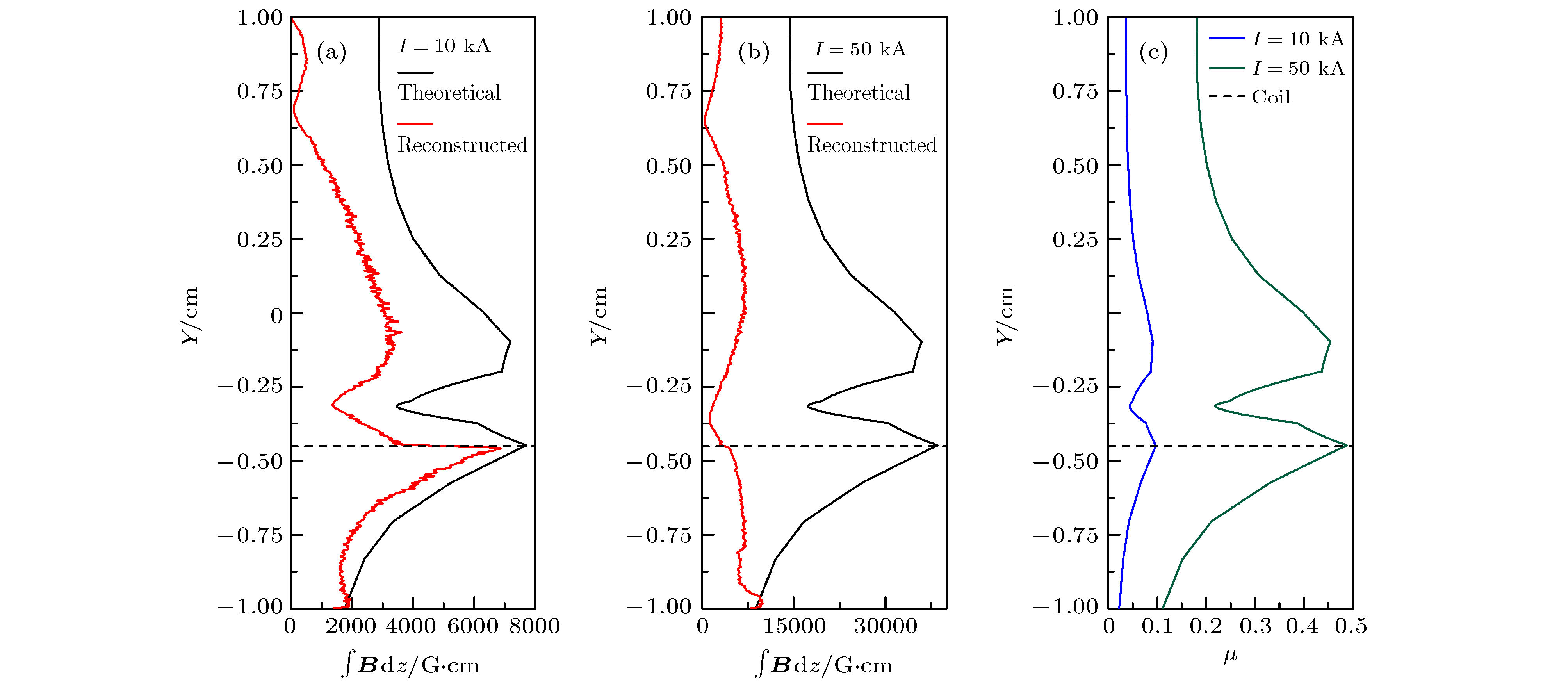
图 5 (a) I = 10 kA, 沿Y方向的理论磁场和重构磁场在–0.15 cm < X < 0.15 cm 区域平均值的对比; (b) I = 50 kA, 沿Y方向的理论磁场和重构磁场在–0.15 cm < X < 0.15 cm 区域平均值的对比. (a)和(b)中黑色实线是理论值, 红色实线是重构值, 黑色虚线是线圈顶端对应的位置; (c)两种情况下沿Y 方向μ值的对比, 蓝色实线为I = 10 kA的结果, 绿色实线为I = 50 kA 的结果
Figure 5. (a) Comparison between the mean theoretical and the mean reconstructed magnetic field for the I = 10 kA case in the region of –0.15 cm < X < 0.15 cm along Y direction; (b) comparison between the mean theoretical and the mean reconstructed magnetic field for the I = 50 kA case in the region of –0.15 cm < X < 0.15 cm along Y direction. The black solid lines are the theoretical results. The red solid lines are the reconstructed line. The black dash lines are the position of the tips of the coils; (c) comparison of μ value along the Y direction between the I = 10 kA and I = 50 kA cases
图 6 黑色实线和散点是电流强度与圆弧顶点处磁感应强度的关系. 不同颜色的实线和散点分别是质子能量为1, 4, 7.5 和10 MeV时实验设置中相应的μ值
Figure 6. Black solid line and scatters are the relation between current strength and the magnetic flux density at the top of the nickel coil. The colorful solid line and scatters are the corresponding μ values when proton energy is 1, 4, 7.5 and 10 MeV, respectively
-
[1] Mackinnon A J, Patel P K, Town R P, et al. 2004 Rev. Sci. Instrum. 75 3531
Google Scholar
[2] Mackinnon A J, Patel P K, Borghesi M, et al. 2006 Phys. Rev. Lett. 97 045001
Google Scholar
[3] Li C K, Seguin F H, Frenje J A, et al. 2006 Phys. Rev. Lett. 97 135003
Google Scholar
[4] Rygg J R, Seguin F H, Li C K, et al. 2008 Science 319 1223
Google Scholar
[5] Romagnani L, Bulanov S V, Borghesi M, Audebert P, Gauthier J C, Lowenbruck K, MacKinnon A J, Patel P, Pretzler G, Toncian T, Willi O 2008 Phys. Rev. Lett. 101 025004
Google Scholar
[6] Huntington C M, Fiuza F, Ross J S, et al. 2015 Nat. Phys. 11 173
Google Scholar
[7] Hatchett S P, Brown C G, Cowan T E, et al. 2000 Phys. Plasmas 7 2076
Google Scholar
[8] Snavely R A, Key M H, Hatchett S P, et al. 2000 Phys. Rev. Lett. 85 2945
Google Scholar
[9] Maksimchuk A, Gu S, Flippo K, Umstadter D, Bychenkov A Yu 2000 Phys. Rev. Lett. 84 4108
Google Scholar
[10] Clark E L, Krushelnick K, Davies J R, Zepf M, Tatarakis M, Beg F N, Machacek A, Norreys P A, Santala M I, Watts I, Dangor A E 2000 Phys. Rev. Lett., 84 670
Google Scholar
[11] Roth M, Schollmeier M 2017 arXiv:1705.10569
[12] Li C K, Sguin F H, Frenje J A, et al. 2006 Rev. Sci. Instrum. 77 10E
[13] Manuel M J, Zylstra A B, Rinderknecht H G, Casey D T, Rosenberg M J, Sinenian N, Li C K, Frenje J A, Séguin F H, Petrasso R D 2012 Rev. Sci. Instrum. 83 063506
Google Scholar
[14] Levy M C, Ryutov D D, Wilks S C, Ross J S, Huntington C M, Fiuza F, Martinez D A, Kugland N L, Baring M G, Park H S 2015 Rev. Sci. Instrum. 86 033302
Google Scholar
[15] Zhang C J, Hua J F, Wan Y, Pai C H, Guo B, Zhang J, Ma Y, Li F, Wu Y P, Chu H H, Gu Y Q, Xu X L, Mori W B, Joshi C, Wang J, Lu W 2017 Phys. Rev. Lett. 119 064801
Google Scholar
[16] Kugland N L, Ryutov D D, Plechaty C, Ross J S, Park H S 2012 Rev. Sci. Instrum. 83 101301
Google Scholar
[17] Graziani C, Tzeferacos P, Lamb D Q, Li C K 2017 Rev. Sci. Instrum. 88 123507
Google Scholar
[18] Bott A F A, Graziani C, Tzeferacos P, White T G, Lamb D Q, Gregori G, Schekochihin A A 2017 J. Plasma Phys. 83 905830614
Google Scholar
[19] 杜报, 蔡洪波, 张文帅, 陈京, 邹士阳, 朱少平 2019 68 185205
Google Scholar
Du B, Cai H B, Zhang W S, Zou S Y, Chen J, Zhu S P 2019 Acta Phys. Sin. 68 185205
Google Scholar
[20] Du B, Cai H B, Zhang W S, Tian J M, Zhang E H, Zou S Y, Chen J, Zhu S P 2019 Plasma Phys. Control. Fusion 62 025017
[21] Daido H, Miki F, Mima K, Fujita M, Sawai K, Fujita H, Kitagawa Y, Nakai S, Yamanaka C 1986 Phys. Rev. Lett. 56 846
Google Scholar
[22] Courtois C, Ash A D, Chambers D M, Grundy R A, Woolsey N C 2005 J. Appl. Phys. 98 054913
Google Scholar
[23] Fujioka S, Zhang Z, Ishihara K, Shigemori K, Hironaka Y, Johzaki T, Sunahara A, Yamamoto N, Nakashima H, Watanabe T, Shiraga H, Nishimura H, Azechi H 2013 Sci. Rep. 3 1170
Google Scholar
[24] Pei X X, Zhong J Y, Sakawa Y, et al. 2016 Phys. Plasmas 23 032125
Google Scholar
[25] Yuan X X, Zhong J Y, Zhang Z, et al. 2018 Plasma Phys. Control. Fusion 60 065009
Google Scholar
[26] Pia M G 2003 Nucl. Phys. B Proc. Suppl. 125 60
Google Scholar
[27] Allison J, Amako K, Apostolakis J, et al. 2006 IEEE Trans. Nucl. Sci. 53 270
Google Scholar
[28] Allison J, Amako K, Apostolakis J, et al. 2016 Nucl. Instrum. Methods Phys. Res., Sect. A 835 186
Google Scholar
[29] McGuire E J 1991 J. Appl. Phys. 70 7213
Google Scholar
DownLoad:
Catalog
Metrics
- Abstract views: 6055
- PDF Downloads: 74
- Cited By: 0
