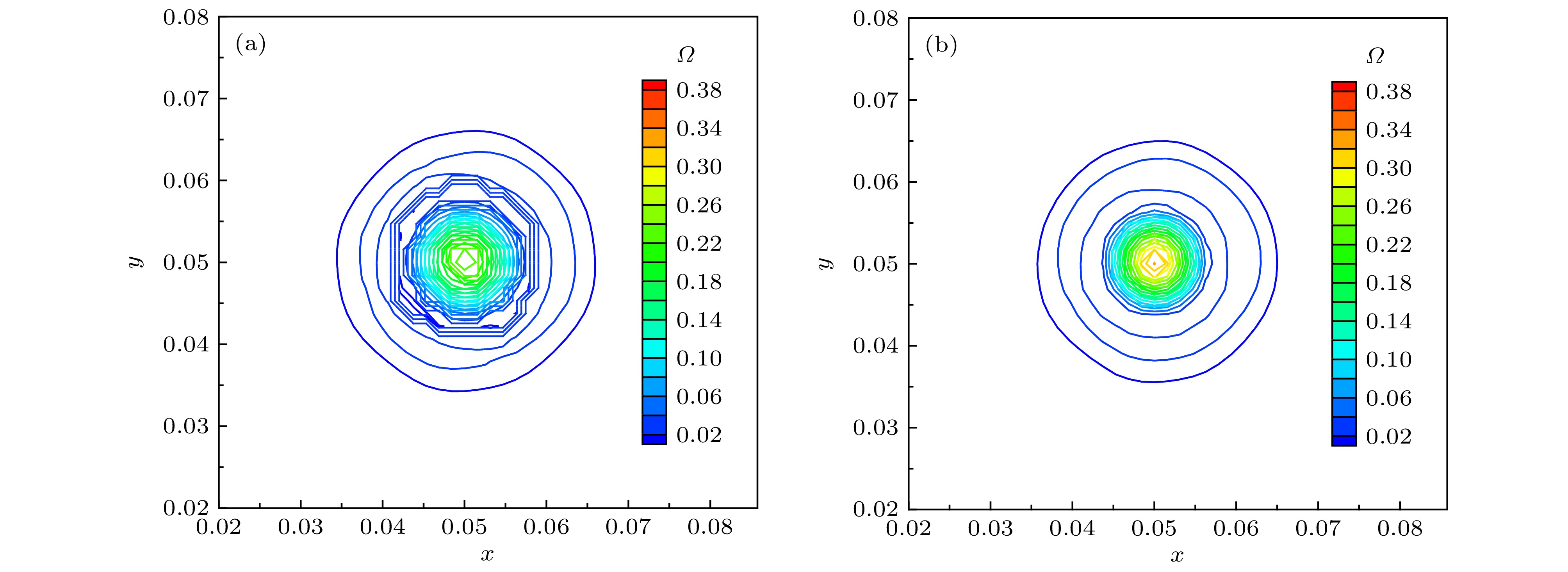
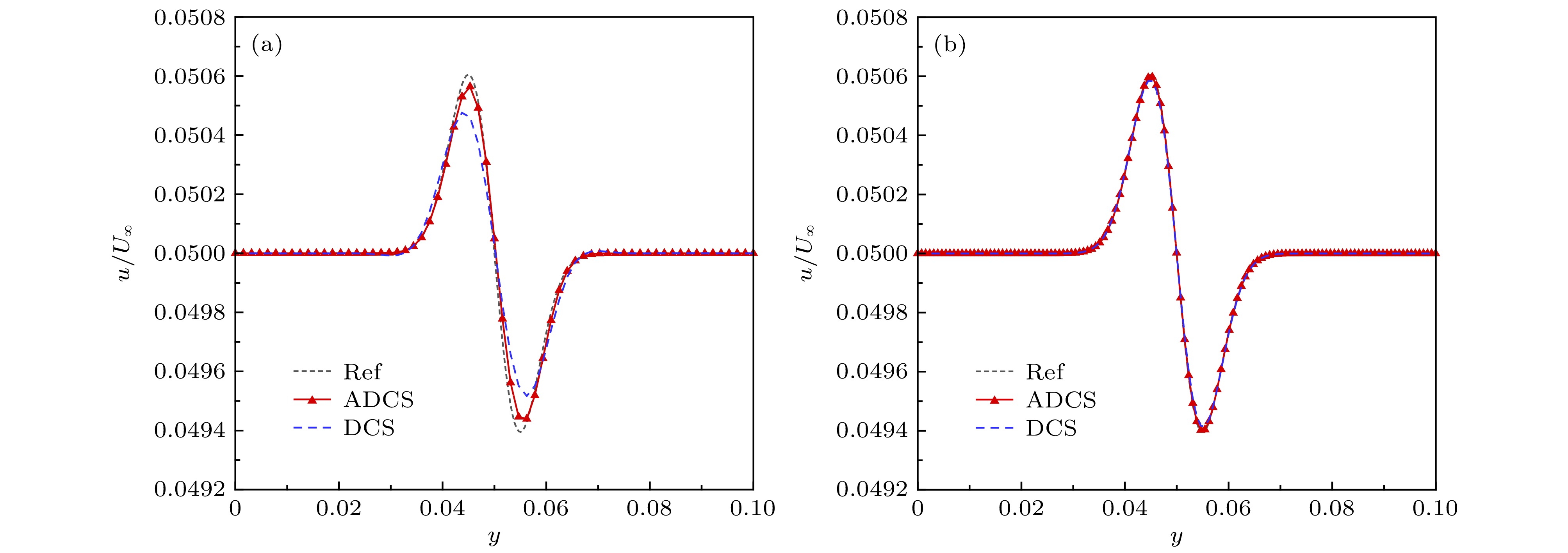
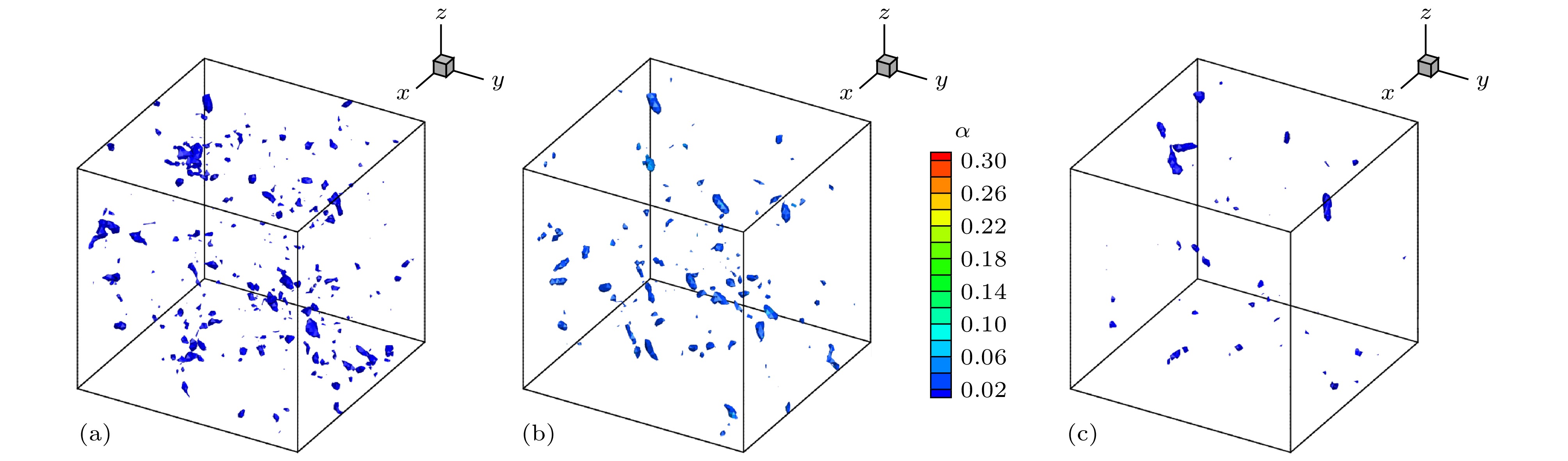
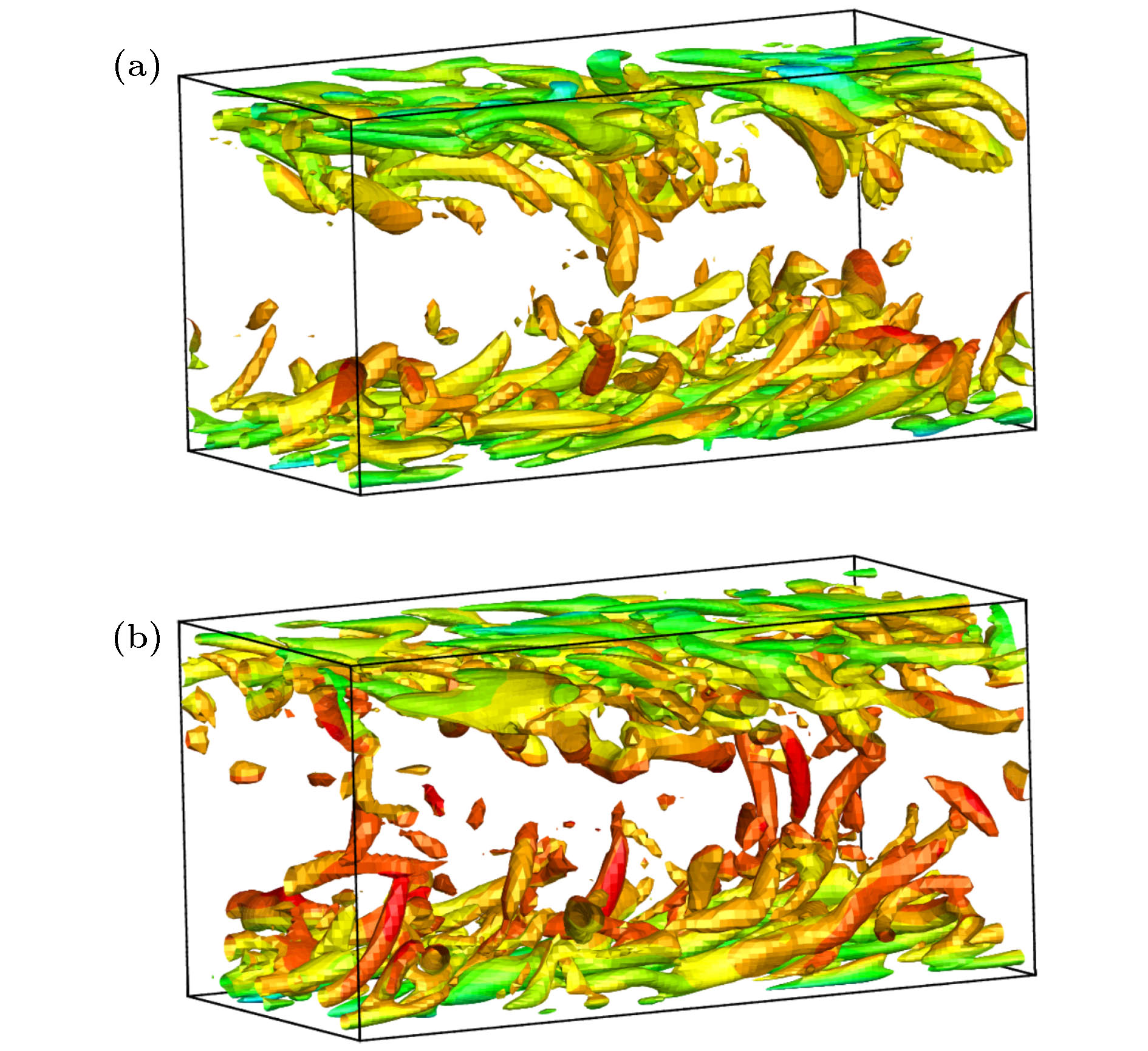
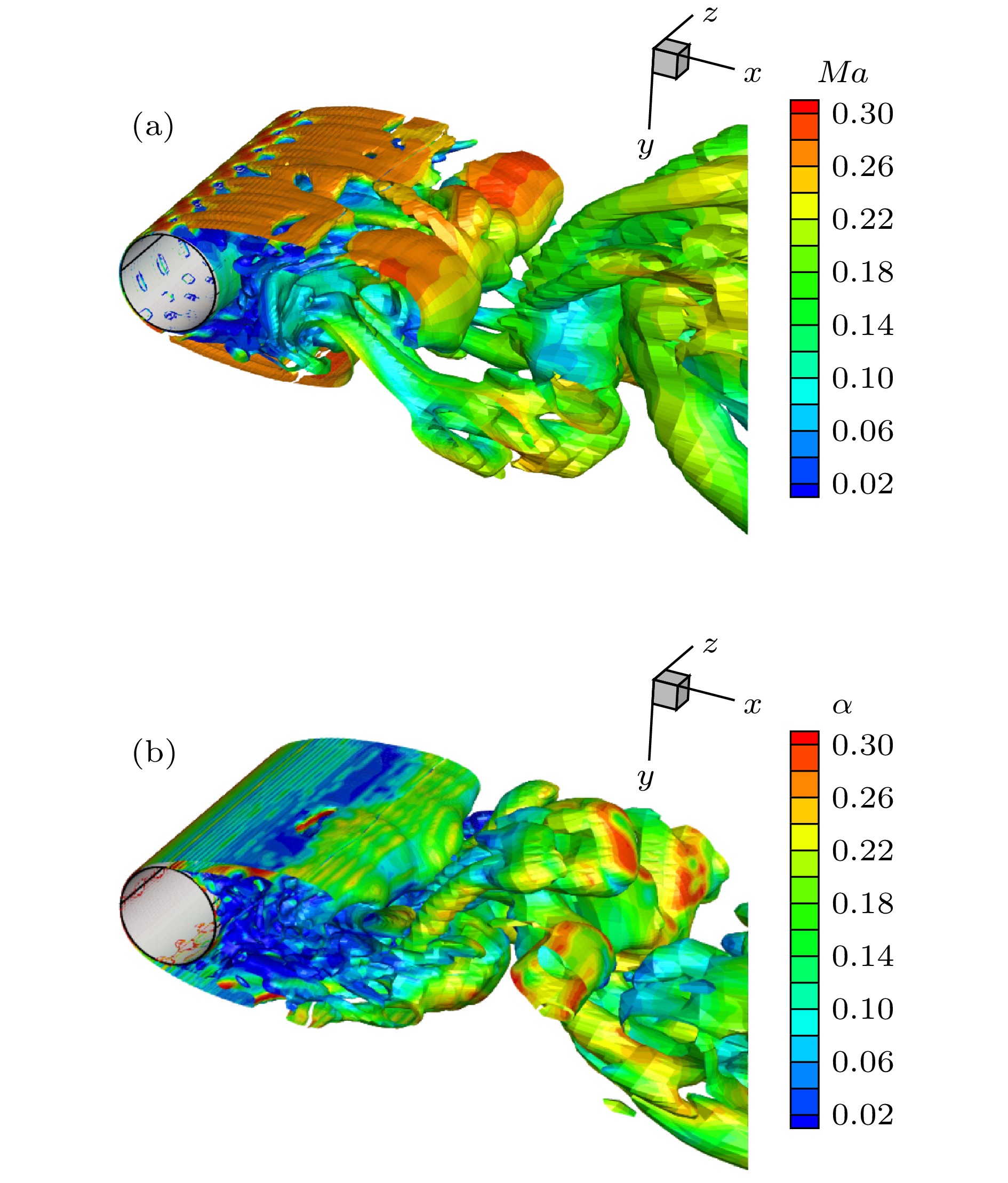
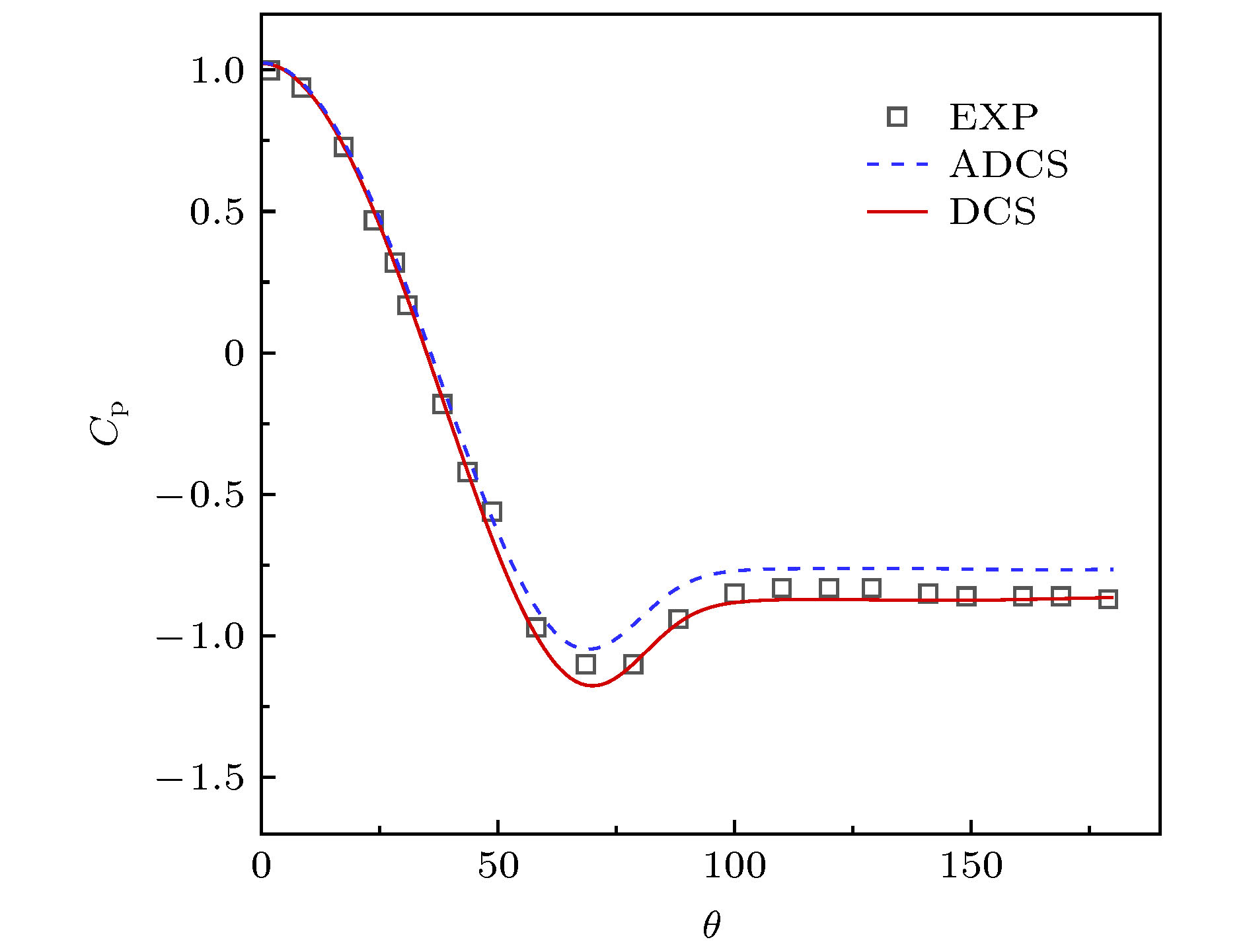
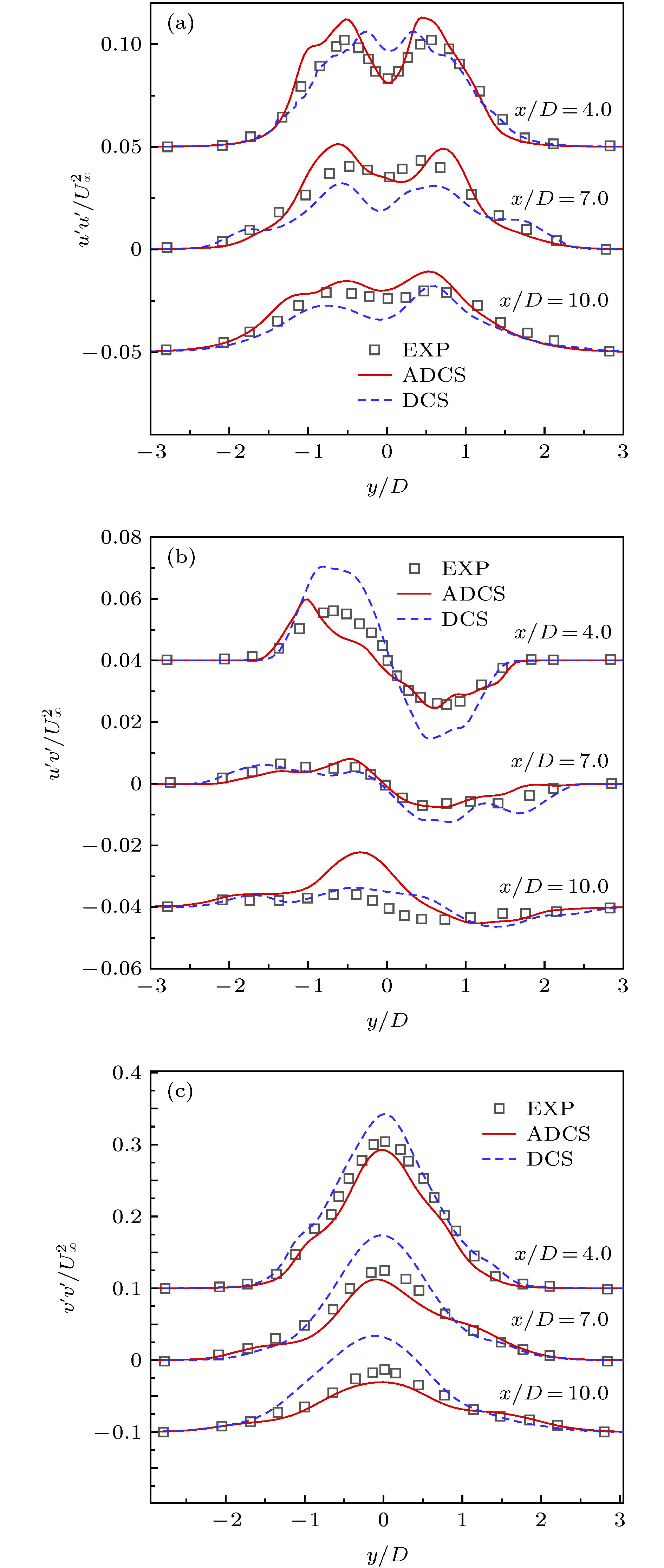
-
Separate flow is a typical complex turbulent phenomenon. The full development of small-scaled structures is of great importance for accurate numerical simulation. However, these small-scaled structures can be easily damped by the inherent dissipation of numerical method. Therefore, based on the 5th-order dissipative compact scheme (DCS), we propose an adaptive dissipative compact scheme (ADCS), which can adjust the numerical dissipation with self-adaptive capability by incorporating a flow related adjusting parameter. Combining with the delay detached eddy simulation (DDES), the ADCS can reduce the influence of numerical dissipation in LES region to enhance the ability to discern small-scaled structures, and restore the normal dissipation level in the RANS region to keep numerical stability. In the process of numerical simulation, firstly, the approximate dispersion relation (ADR) is obtained, it shows that the ADCS method can effectively reduce the influence of dissipation in the high wave number region, without contaminating the dispersive performance, which is conducive to enhancing the resolution of turbulent structures. Secondly, the advection of vortical structure is simulated. Compared with DCS, the ADCS can reach the theoretical accuracy in an efficient way and acquire more advanced resolution of vortical structure even on a relatively coarse mesh scale, which proves that the ADCS reduces the negative influence of dissipation on vortical structure. The third case is the decay of isotropic turbulence. The energy spectral curves stay close to the reference before cut-off number, showing that more small-scaled structures can be distinguished by the ADCS method, and most of the vortical dominated regions are solved at a near-minimum level. The forth case is the plate channel turbulent flow. Both of DCS method and ADCS method give acceptable results. The ADCS method is performed with optimal dissipation in the near-wall region and reduces the dissipative level in the vortex dominated region, and it is also exhibited that the ADCS method can maintain the stability for flow with high gradient and avoid divergence. Finally, the sub-critical Re = 3900circular cylinder is simulated, and the fully separate flow is developed in the wake. The turbulent fluctuation near the wall is sensitive to the effect of numerical dissipation. The contour of flow field shows that the ADCS method obtains more small-scale structures. As for the pressure coefficient and mean velocity, the ADCS method shows an acceptable accuracy. Considering the Reynolds stress profile, which can be easily affected by the dissipation, the ADCS exhibits more accurate results than the traditional DCS method. Generally, the ADCS method can reduce the influence of dissipation and is beneficial to acquiring more accurate results in separate flow.
-
Keywords:
- separated flow /
- delayed-detached eddy simulation /
- adaptive dissipative method /
- dissipative compact scheme
[1] Cummingsa R M, Forsytheb J R, Mortonb S A 2003 Prog. Aerosp. Sci 39 369
Google Scholar
[2] Tucker P 2016 Appl. Math. Comput. 272 582
[3] 王光学, 王圣业, 葛明明, 邓小刚 2018 67 194701
Google Scholar
Wang G X, Wang S Y, Ge M M, Deng X G 2018 Acta Phys. Sin. 67 194701
Google Scholar
[4] 葛明明, 王圣业, 王光学, 邓小刚 2019 68 204702
Google Scholar
Ge M M, Wang S Y, Wang G X, Deng X G 2019 Acta Phys. Sin. 68 204702
Google Scholar
[5] Travin A, Shur M, Strelets M, Spalart P R 2002 Adv. LES Complex. Flow 65 239
[6] Jiang G S 1996 J. Comput. Phys. 126 202
Google Scholar
[7] Henrick A K, Aslam T D, Powers J M 2005 J. Comput. Phys. 207 542
Google Scholar
[8] Borges R, Carmona M, Costa B, Don W S 2008 J. Comput. Phys. 227 3191
Google Scholar
[9] Martín M P, Taylor E M, Wu M, Weirs V G 2006 J. Comput. Phys. 220 270
Google Scholar
[10] Hu X Y, Wang Q, Adams N A 2010 J. Comput. Phys. 229 8952
Google Scholar
[11] Wong M L, Lele S K 2017 J. Comput. Phys. 339 179
Google Scholar
[12] Adams N A, Shariff K 1996 J. Comput. Phys. 127 27
Google Scholar
[13] Pirozzoli S 2002 J. Comput. Phys. 178 81
Google Scholar
[14] Shahbazi K, Nathan A, Oscar P B, Jan S H 2011 J. Comput. Phys. 230 8779
Google Scholar
[15] Meitz H L, Fasel H F 2000 J. Comput. Phys. 157 371
Google Scholar
[16] Lele S K 1992 J. Comput. Phys. 103 16
Google Scholar
[17] Deng X, Shen C 1996 AIAA 27th Fluid Dynamics Conference, New Orleans, USA, June 17–20, 1996
[18] Chaouat, Bruno 2017 Flow Turbul. Combust. 99 279
Google Scholar
[19] Xiao Z, Fu S 2009 Acta Mech. Sin. 25 471
Google Scholar
[20] Mary I, Sagaut P 2002 AIAA 40 1139
Google Scholar
[21] Anderson N, Eriksson L E, Davidson L 2005 AIAA 43 1899
Google Scholar
[22] Bui T T 2000 Comput. Fluids 29 877
Google Scholar
[23] Qin N, Xia H 2008 Proc. Inst. Mech. Eng. I 222 373
[24] Yoon S, Barnhardt M, Candler G 48th AIAA Aerospace Science Meeting, Orlando, USA, January 4–7, 2010 p1573
[25] Mockett C 2009 Ph. D. Dissertation (Berlin: Technische Universitat Berlin)
[26] Tajallipour N, Babaee Owlam B, Paraschivoiu M 2009 J. Aircraft 46 915
Google Scholar
[27] Xiao Z, Jian L, Huang J, Song F 2012 AIAA 50 1119
Google Scholar
[28] Spalart P R, Jou W H, Strelets M, Allmaras S R 1997 Adv. In DNS/LES (Columbus: Greyden Press) pp137–149
[29] Strelets M 2001 39th AIAA Aerospace Sciences Meeting and Exhibit Reno, NV, January 8–11, 2001 pA01-16694
[30] Spalart P R, Deck S, Shur M L, Squires K D, Strelets M K, Travin A 2006 Theor. Comput. Fluid Dyn. 20 181
Google Scholar
[31] Pirozzoli S 2006 J. Comput. Phys. 219 489
Google Scholar
[32] Wang Z J, Fidkowski K, Abgrall R, Bassi F, Caraeni D, Cary A, Deconinck H, Hartmann R, Hillewaert K, Huynh H T 2013 Int. J. Numer. Methods Fluids 72 811
Google Scholar
[33] Kroll N, Bieler H, Deconinck H, Couaillier V, Ven H v d, Sorensen K 2010 ADIGMA A European Initiative on the Development of Adaptive Higher-order Variational Methods for Aerospace Applications (Berlin: Springer) pp1–10
[34] Comte-Bellot G, Corrsin S 1971 J. Fluid. Mech. 48 273
Google Scholar
[35] Bunge U, Mockett C, Thiele F 2007 Aerosp. Sci. Technol. 11 376
Google Scholar
[36] Pope S B 2000 Turbulent Flows (Cambridge: Cambridge University Press) pp264–288
[37] Kravchenko, P M 2000 Phys. Fluids 12 403
Google Scholar
[38] Parnaudeau P, Carlier J, Heitz D, Lamballais E 2008 Phys. Fluids 20 261
-
图 1 耗散色散特性分析 (a) 耗散特性; (b) 色散特性
Figure 1. Analysis of dissipation and dispersion: (a) Dissipation; (b) dispersion
图 2
$ L_2 $ 误差变化曲线 (a)随网格尺度$ h $ ; (b)随CPU 时间Figure 2. The curve of
$ L_2 $ error (a) vs. mesh scale$ h $ ; (b) vs. CPU time
图 3
$ 64^2 $ 网格下涡结构等值线图 (a) DCS; (b) ADCSFigure 3. Vorticity magnitude contour of
$ 64^2 $ grid: (a) DCS; (b) ADCS
图 4
$ 128^2 $ 网格下涡结构等值线图 (a) DCS; (b) ADCSFigure 4. Vorticity magnitude contour of
$ 128^2 $ grid: (a) DCS; (b) ADCS
图 5 中心线处水平速度型比较 (a)
$ 64^2 $ 网格; (b)$ 128^2 $ 网格Figure 5. Comparison of u velocity profile at centerline: (a) 642; (b)
$ 128^2 $ 
图 6 不同时刻能量谱曲线 (a)
$ U_0 t/L = 98 $ ; (b)$ U_0 t/L = $ 171Figure 6. Comparison of energy-spectral: (a)
$ U_0 t/L = 98 $ ; (b)$ U_0 t/L = 171 $ 
图 7
$ U_0 t/L = 98 $ 处$ Q $ 等值面云图 (a) ADCS$ (\alpha_{\rm {min}}) $ ; (b) ADCS; (c) DCSFigure 7.
$ Q $ -criterion iso-surface at$ U_0 t/L = 98 $ : (a) ADCS$ (\alpha_{\rm {min}}) $ ; (b) ADCS; (c) DCS
图 8
$ U_0 t/L = 171 $ 处$ Q $ 等值面云图 (a) ADCS$ (\alpha_{\rm {min}}) $ ; (b) ADCS; (c) DCSFigure 8.
$ Q $ - criterion iso-surface at$ U_0 t/L = 171 $ : (a) ADCS$ (\alpha_{\rm {min}}) $ ; (b) ADCS; (c) DCS
图 9
$ Re_\tau = 180 $ 条件下$ u^+ $ 和$ 20 f_{\rm d} $ 分布曲线Figure 9.
$ u^+ $ and$ 20 f_{\rm d} $ curves at$ Re_\tau = 180 $ 
图 10
$ Re_\tau = 180 $ 条件下$ Q $ 等值面 (a) DCS; (b) ADCSFigure 10.
$ Q $ criterion iso-surface at$ Re_\tau = 180 $ : (a) DCS; (b) ADCS
图 11
$ Re_\tau = 180 $ 条件下ADCS$ f_{\rm d}$ 和$ \alpha $ 分布 (a)$ f_{\rm d} $ ; (b)$ \alpha $ Figure 11. The contour of
$ f_{\rm d} $ and$ \alpha $ of ADCS at$ Re_\tau = 180 $ : (a)$ f_{\rm d} $ ; (b)$ \alpha $ 
图 12
$ y = 0.1 H $ 处$ y $ 方向涡量分布云图 (a) DCS; (b) ADCSFigure 12. The contour of vorticity y at
$ y = 0.1 H $ : (a) DCS; (b) ADCS
图 13 圆柱尾流
$ Q $ 等值面云图 (a) DCS; (b) ADCSFigure 13.
$ Q $ criterion at the wake of circular cylinder: (a) DCS; (b) ADCS
图 14 圆柱表面压力系数分布曲线
Figure 14.
$ C_{\rm p} $ around the circular cylinder
图 15
$ y = 0 $ 处水平速度分布曲线Figure 15. u velocity profile at
$ y = 0 $ 
图 16
$ x/D = 1.06, 1.54, 2.02 $ 三个站位时均速度分布 (a)$ u $ ; (b)$ v $ Figure 16. Mean velocity profile at
$ x/D = 1.06, 1.54, 2.02 $ : (a)$ u $ ; (b)$ v $ 
图 19
$ x/D = 4.0, 7.0, 10.0 $ 三个站位雷诺应力分布 (a)$ u'u' $ ; (b)$ u'v' $ ; (c)$ v'v' $ Figure 19. Reynolds stress profile at
$ x/D = 4.0, 7.0, 10.0 $ : (a)$ u'u' $ ; (b)$ u'v' $ ; (c)$ v'v' $ 
图 17
$ x/D = 1.06, 1.54, 2.02 $ 三个站位雷诺应力分布 (a)$ u'u' $ ; (b)$ u'v' $ ; (c)$ v'v' $ Figure 17. Reynolds stress profile at
$ x/D = 1.06, 1.54, 2.02 $ : (a)$ u'u' $ ; (b)$ u'v' $ ; (c)$ v'v' $ 
图 18
$ x/D = 4.0, 7.0, 10.0 $ 三个站位时均速度分布 (a)$ u $ ; (b)$ v $ Figure 18. Mean velocity profile at
$ x/D = 4.0, 7.0, 10.0 $ : (a)$ u $ ; (b)$ v $ 表 1
$ L_2 $ 误差和计算精度比较Table 1. Comparison of
$ L_2 $ error and accuracy of order网格 ADCS DCS $ L_2 $误差 精度 $ L_2 $误差 精度 $ 32^2 $ 5.91520$ \times 10^{-9} $ — 5.49050$ \times 10^{-9} $ — $ 48^2 $ 4.14450$ \times 10^{-9} $ 0.87 3.84780$ \times 10^{-9} $ 0.88 $ 64^2 $ 2.33030$ \times 10^{-9} $ 2.01 2.06870$ \times 10^{-9} $ 2.16 $ 96^2 $ 2.59250$ \times 10^{-10} $ 5.42 5.15010$ \times 10^{-10} $ 3.43 $ 128^2 $ 5.39380$ \times 10^{-11} $ 5.46 1.26630$\times 10^{-10}$ 4.88 
DownLoad: CSV
-
[1] Cummingsa R M, Forsytheb J R, Mortonb S A 2003 Prog. Aerosp. Sci 39 369
Google Scholar
[2] Tucker P 2016 Appl. Math. Comput. 272 582
[3] 王光学, 王圣业, 葛明明, 邓小刚 2018 67 194701
Google Scholar
Wang G X, Wang S Y, Ge M M, Deng X G 2018 Acta Phys. Sin. 67 194701
Google Scholar
[4] 葛明明, 王圣业, 王光学, 邓小刚 2019 68 204702
Google Scholar
Ge M M, Wang S Y, Wang G X, Deng X G 2019 Acta Phys. Sin. 68 204702
Google Scholar
[5] Travin A, Shur M, Strelets M, Spalart P R 2002 Adv. LES Complex. Flow 65 239
[6] Jiang G S 1996 J. Comput. Phys. 126 202
Google Scholar
[7] Henrick A K, Aslam T D, Powers J M 2005 J. Comput. Phys. 207 542
Google Scholar
[8] Borges R, Carmona M, Costa B, Don W S 2008 J. Comput. Phys. 227 3191
Google Scholar
[9] Martín M P, Taylor E M, Wu M, Weirs V G 2006 J. Comput. Phys. 220 270
Google Scholar
[10] Hu X Y, Wang Q, Adams N A 2010 J. Comput. Phys. 229 8952
Google Scholar
[11] Wong M L, Lele S K 2017 J. Comput. Phys. 339 179
Google Scholar
[12] Adams N A, Shariff K 1996 J. Comput. Phys. 127 27
Google Scholar
[13] Pirozzoli S 2002 J. Comput. Phys. 178 81
Google Scholar
[14] Shahbazi K, Nathan A, Oscar P B, Jan S H 2011 J. Comput. Phys. 230 8779
Google Scholar
[15] Meitz H L, Fasel H F 2000 J. Comput. Phys. 157 371
Google Scholar
[16] Lele S K 1992 J. Comput. Phys. 103 16
Google Scholar
[17] Deng X, Shen C 1996 AIAA 27th Fluid Dynamics Conference, New Orleans, USA, June 17–20, 1996
[18] Chaouat, Bruno 2017 Flow Turbul. Combust. 99 279
Google Scholar
[19] Xiao Z, Fu S 2009 Acta Mech. Sin. 25 471
Google Scholar
[20] Mary I, Sagaut P 2002 AIAA 40 1139
Google Scholar
[21] Anderson N, Eriksson L E, Davidson L 2005 AIAA 43 1899
Google Scholar
[22] Bui T T 2000 Comput. Fluids 29 877
Google Scholar
[23] Qin N, Xia H 2008 Proc. Inst. Mech. Eng. I 222 373
[24] Yoon S, Barnhardt M, Candler G 48th AIAA Aerospace Science Meeting, Orlando, USA, January 4–7, 2010 p1573
[25] Mockett C 2009 Ph. D. Dissertation (Berlin: Technische Universitat Berlin)
[26] Tajallipour N, Babaee Owlam B, Paraschivoiu M 2009 J. Aircraft 46 915
Google Scholar
[27] Xiao Z, Jian L, Huang J, Song F 2012 AIAA 50 1119
Google Scholar
[28] Spalart P R, Jou W H, Strelets M, Allmaras S R 1997 Adv. In DNS/LES (Columbus: Greyden Press) pp137–149
[29] Strelets M 2001 39th AIAA Aerospace Sciences Meeting and Exhibit Reno, NV, January 8–11, 2001 pA01-16694
[30] Spalart P R, Deck S, Shur M L, Squires K D, Strelets M K, Travin A 2006 Theor. Comput. Fluid Dyn. 20 181
Google Scholar
[31] Pirozzoli S 2006 J. Comput. Phys. 219 489
Google Scholar
[32] Wang Z J, Fidkowski K, Abgrall R, Bassi F, Caraeni D, Cary A, Deconinck H, Hartmann R, Hillewaert K, Huynh H T 2013 Int. J. Numer. Methods Fluids 72 811
Google Scholar
[33] Kroll N, Bieler H, Deconinck H, Couaillier V, Ven H v d, Sorensen K 2010 ADIGMA A European Initiative on the Development of Adaptive Higher-order Variational Methods for Aerospace Applications (Berlin: Springer) pp1–10
[34] Comte-Bellot G, Corrsin S 1971 J. Fluid. Mech. 48 273
Google Scholar
[35] Bunge U, Mockett C, Thiele F 2007 Aerosp. Sci. Technol. 11 376
Google Scholar
[36] Pope S B 2000 Turbulent Flows (Cambridge: Cambridge University Press) pp264–288
[37] Kravchenko, P M 2000 Phys. Fluids 12 403
Google Scholar
[38] Parnaudeau P, Carlier J, Heitz D, Lamballais E 2008 Phys. Fluids 20 261
DownLoad:
Catalog
Metrics
- Abstract views: 6012
- PDF Downloads: 82
- Cited By: 0
