-
在二维空间内, 考虑周期性边界条件, 提出了一种用时间延迟反馈分离混合手征活性粒子的新方法. 当系统引入时间延迟反馈时, 手征活性粒子动力学特征发生明显改变. 通过调节外加时间延迟反馈的强度和反馈时间可以控制逆时针旋转(counterclockwise, CCW)粒子扩散受到顺时针旋转(clockwise, CW)粒子扩散的影响程度. 当时间延迟反馈强度和反馈时间较大且系统参数取最优值时, CCW粒子加快旋转角速度, 扩散完全由粒子相互作用决定, 而CW粒子的扩散由自身参数和粒子相互作用共同决定, 在此情况下, CCW粒子容易聚集形成团簇, 而CW粒子加快扩散, 混合手征活性粒子实现分离.Considering the periodic boundary conditions, a new prescription for separating binary mixtures of chiral active particles by time-delayed feedback in a two-dimensional square box is proposed. We investigate the angular velocity, the feedback intensity, the delayed time, the rotational diffusion coefficient, the self-propelled speed and the packing fraction as functions of the effective diffusion coefficient and the separation coefficient numerically by the extensive Brownian dynamics simulations. It is found that mixed chiral active particles be separated without time-delayed feedback, but the dynamics of chiral active particles are different obviously and mixed chiral particles can be separated when the time-delayed feedback is introduced. The particle configuration (mixing or demixing) is determined by the dominant factor of particles’ diffusion. We can control the extent to which the diffusion of counterclockwise (CCW) active particles is affected by the diffusion of clockwise (CW) active particles adjusting the strength and the delayed time of the feedback. The response to the feedback for different chiral particles show different behaviors under different system parameters. When the feedback intensity is strong and the delayed time is long enough, the angular velocity of counterclockwise particles is accelerated and the diffusion of which is dominated by the interactions between particles completely. However, the angular speed of clockwise particles change little and the diffusion of which is determined by its parameters and particle interactions jointly. In this case, the counterclockwise particles aggregate to form clusters easily, and the clockwise particles diffuse quickly, therefore, the mixed chirality active particles are separated. When the feedback intensity is weak and the delayed time is short, the chirality difference between different chiral particles modulated by the feedback is smaller than the former case. The diffusions of counterclockwise particles and clockwise particles are both determined by their parameters and particle interactions, and the particles are mixed. Our findings provide novel strategies for the experimental pursuit of separating mixed chiral active particles and could be applied practically in many biological circle swimmers, such as autochemotactic particles, the bacteria in an external light field and sperm cells with vortex motion.
-
Keywords:
- active particles /
- diffusion /
- time-delayed feedback /
- particle separation
[1] Bechinger C, Di Leonardo R, Löwen H, Reichhardt C, Volpe G 2016 Rev. Mod. Phys. 88 045006
Google Scholar
[2] Chen C, Liu S, Shi X, Chate H, Wu Y 2017 Nature 542 210
Google Scholar
[3] Reichhardt C J O, Reichhardt C 2017 Annu. Rev. Condens. Matter Phys. 8 51
Google Scholar
[4] Reichhardt C J O, Reichhardt C 2017 Nat. Phys. 13 10
Google Scholar
[5] 夏益祺, 谌庄琳, 郭永坤 2019 68 161101
Google Scholar
Xia Y Q, Zhan Z L, Guo Y K 2019 Acta Phys. Sin. 68 161101
Google Scholar
[6] 张红, 宗奕吾, 杨明成, 赵坤 2019 68 134702
Google Scholar
Zhang H, Zong Y W, Yang M C, Zhao K 2019 Acta Phys. Sin. 68 134702
Google Scholar
[7] Vale R D, Milligan R A 2000 Science 288 88
Google Scholar
[8] Leptos K C, Guasto J S, Gollub J P, Pesci A I, Goldstein R E 2009 Phys. Rev. Lett. 103 198103
Google Scholar
[9] Howse J, Jones R, Ryan A, Gough T, Vafabakhsh R, Golestanian R 2007 Phys. Rev. Lett. 99 048102
Google Scholar
[10] van Teeffelen S, Löwen H 2008 Phys. Rev. E 78 020101(R
Google Scholar
[11] Tjhung E, Cates M E, Marenduzzo D 2017 Proc. Natl. Acad. Sci. 114 4631
Google Scholar
[12] Friedrich B M, Jülicher F 2007 Proc. Natl. Acad. Sci. 104 13256
Google Scholar
[13] Leonardo R D, Dell'Arciprete D, Angelani L, Iebba V 2011 Phys. Rev. Lett. 106 038101
Google Scholar
[14] Shenoy V B, Tambe D T, Prasad A, Theriot J A 2007 Proc. Natl. Acad. Sci. 104 8229
Google Scholar
[15] Von Lospichl B, Klapp S H L 2018 Phys. Rev. E 98 042605
Google Scholar
[16] Lopez B J, Kuwada N J, Craig E M, Long B R, Linke H 2008 Phys. Rev. Lett. 101 220601
Google Scholar
[17] Gernert R, Klapp S H L 2015 Phys. Rev. E 92 022132
Google Scholar
[18] Popli P, Ganguly S, Sengupta S 2018 Soft Matter 14 104
Google Scholar
[19] Yang Y, Bevan M A 2018 ACS Nano 12 10712
Google Scholar
[20] Blickle V, Bechinger C 2011 Nat. Phys. 8 143
Google Scholar
[21] Hanes R D L, Jenkins M C, Egelhaaf S U 2009 Rev. Sci. Instrum. 80 083703
Google Scholar
[22] Evers F, Hanes R D L, Zunke C, Capellmann R F, Bewerunge J, Dalle-Ferrier C, Jenkins M C, Ladadwa I, Heuer A, Castaneda-Priego R, Egelhaaf S U 2013 Eur. Phys. J. Spec. Top. 222 2995
Google Scholar
[23] Bewerunge J, Egelhaaf S U 2016 Phys. Rev. A 93 013806
Google Scholar
[24] Bäuerle T, Fischer A, Speck T, Bechinger C 2018 Nat. Commun. 9 3232
Google Scholar
[25] Jones P, Marag O, Volpe G 2015 Optical Tweezers: Principles and Applications (Cambridge: Cambridge University Press)
[26] Nishizawa K, Bremerich M, Ayade H, Schmidt C F, Ariga T, Mizuno D 2017 Sci. Adv. 3 e1700318
Google Scholar
[27] Leyman M, Ogemark F, Wehr J, Volpe G 2018 Phys. Rev. E 98 052606
Google Scholar
[28] Lavergne F A, Wendehenne H, Bäuerle T, Bechinger C 2019 Science 364 70
Google Scholar
[29] Adler J 1966 Science 153 708
Google Scholar
[30] Couzin I D, Franks N R 2003 Proc. R. Soc. London, Ser. B 270 139
Google Scholar
[31] Jin C, Hokmabad B V, Baldwin K A, Maass C C 2018 J. Phys. Condens. Matter 30 054003
Google Scholar
[32] Volpe G, Gigan S, Volpe G 2014 Am. J. Phys. 82 659
Google Scholar
[33] Kumari S, Nunes A S, Araújo N A M, Margarida M Telo da Gama 2017 J. Chem. Phys. 147 174702
Google Scholar
[34] Maggi C, Lepore A, Solari J, Rizzo A, Di Leonardo R 2013 Soft Matter 9 10885
Google Scholar
[35] Berdakin I, Jeyaram Y, Moshchalkov V V, Venken L, Dierckx S, Vanderleyden S J, Sil-hanek A V, Condat C A, Marconi V I 2013 Phys. Rev. E 87 052702
Google Scholar
[36] Yang W, Misko V R, Nelissen K, Kong M, Peeters F M 2012 Soft Matter 8 5175
Google Scholar
[37] Weber S N, Weber C A, Frey E 2016 Phys. Rev. Lett. 116 058301
Google Scholar
[38] Costanzo A, Elgeti J, Auth T, Gompper G, Ripoll M 2014 EPL 107 36003
Google Scholar
[39] Stenhammar J, Wittkowski R, Marenduzzo D, et al. 2015 Phys. Rev. Lett. 114 018301
Google Scholar
[40] Ma Z, Lei Q, Ni R 2017 Soft Matter 13 8940
Google Scholar
[41] McCandlish S R, Baskaran A, Hagan M F 2012 Soft Matter 8 2527
Google Scholar
[42] Smrek J, Kremer K 2017 Phys. Rev. Lett. 118 098002
Google Scholar
[43] Harder J, Cacciuto A 2018 Phys. Rev. E 97 022603
Google Scholar
[44] Nourhani A, Crespi V H, Lammert P E 2015 Phys. Rev. Lett. 115 118101
Google Scholar
[45] Mijalkov M, Volpe G 2013 Soft Matter 9 6376
Google Scholar
[46] Scholz C, Engel M, Pöschel T 2018 Nat. Commun. 9 1
Google Scholar
[47] Chen Q, Ai B 2015 J. Chem. Phys. 143 104113
Google Scholar
[48] Ai B, Shao Z, Zhong W 2018 Soft Matter 14 4388
Google Scholar
[49] Wysocki A, Winkler R G, Gompper G 2016 New J. Phys. 18 123030
Google Scholar
[50] Dolai P, Simha A, Mishra S 2018 Soft Matter 14 6137
Google Scholar
[51] Ai B 2016 Sci. Rep. 6 1
Google Scholar
[52] Nguyen N H P, Klotsa D, Engel M, Glotzer S C 2014 Phys. Rev. Lett. 112 075701
Google Scholar
[53] Agrawal A, Babu S B 2018 Phys. Rev. E 97 020401(R
Google Scholar
[54] Ai B, He Y, Zhong W 2015 Soft Matter 11 3852
Google Scholar
[55] Reichhardt C, Reichhardt C J O 2013 Phys. Rev. E 88 042306
Google Scholar
[56] DiLuzio W R, Turner L, Mayer M, Garstecki P, Weibel D B, Berg H C, Whitesides G M 2005 Nature 435 1271
Google Scholar
[57] Shin J, Cherstvy A G, Metzler R 2014 New J. Phys. 16 053047
Google Scholar
[58] Di Leonardo R, Dell’Arciprete D 2011 Physical Review Letters 106 038101
[59] Cẽbers A 2011 J. Magn. Magn. Mater. 323 279
Google Scholar
[60] Hennig D 2009 Phys. Rev. E 79 041114
Google Scholar
[61] Yang X, Manning M L, Marchetti M C 2014 Soft Matter 10 6477
Google Scholar
[62] Cates M E, Tailleur J 2015 Annu. Rev. Condens. Matter Phys. 6 219
Google Scholar
-
图 1 时间延迟反馈示意图. 当
$ \tau = 0 $ 时,$ {{\varOmega}}(t) = K_{\rm {fb}} $ ; 当$ \tau\rightarrow\infty $ 且$\theta({t}\!-\!\tau ) > \theta(t)$ 时,$ {{\varOmega}}(t) = 0 $ ; 当$ \tau\rightarrow\infty $ 且$\theta({t}\!-\!\tau ) < \theta(t)$ 时,$ {{\varOmega}}(t) = 2 K_{\rm {fb}} $ Fig. 1. Schematic diagram of time-delayed feedback. When
$ \tau = 0 $ ,$ {{\varOmega}}(t) = K_{\rm {fb}} $ ; when$ \tau\rightarrow\infty $ and$ \theta({t}-\tau ) > \theta(t) $ ,$ {{\varOmega}}(t) = 0 $ ; when$ \tau\rightarrow\infty $ and$ \theta({t}-\tau ) < \theta(t) $ ,${{\varOmega}}(t) = 2 K_{\rm {fb}}$ .
图 2 CCW粒子(红色)和CW粒子(蓝色)的混合物分布 (a)
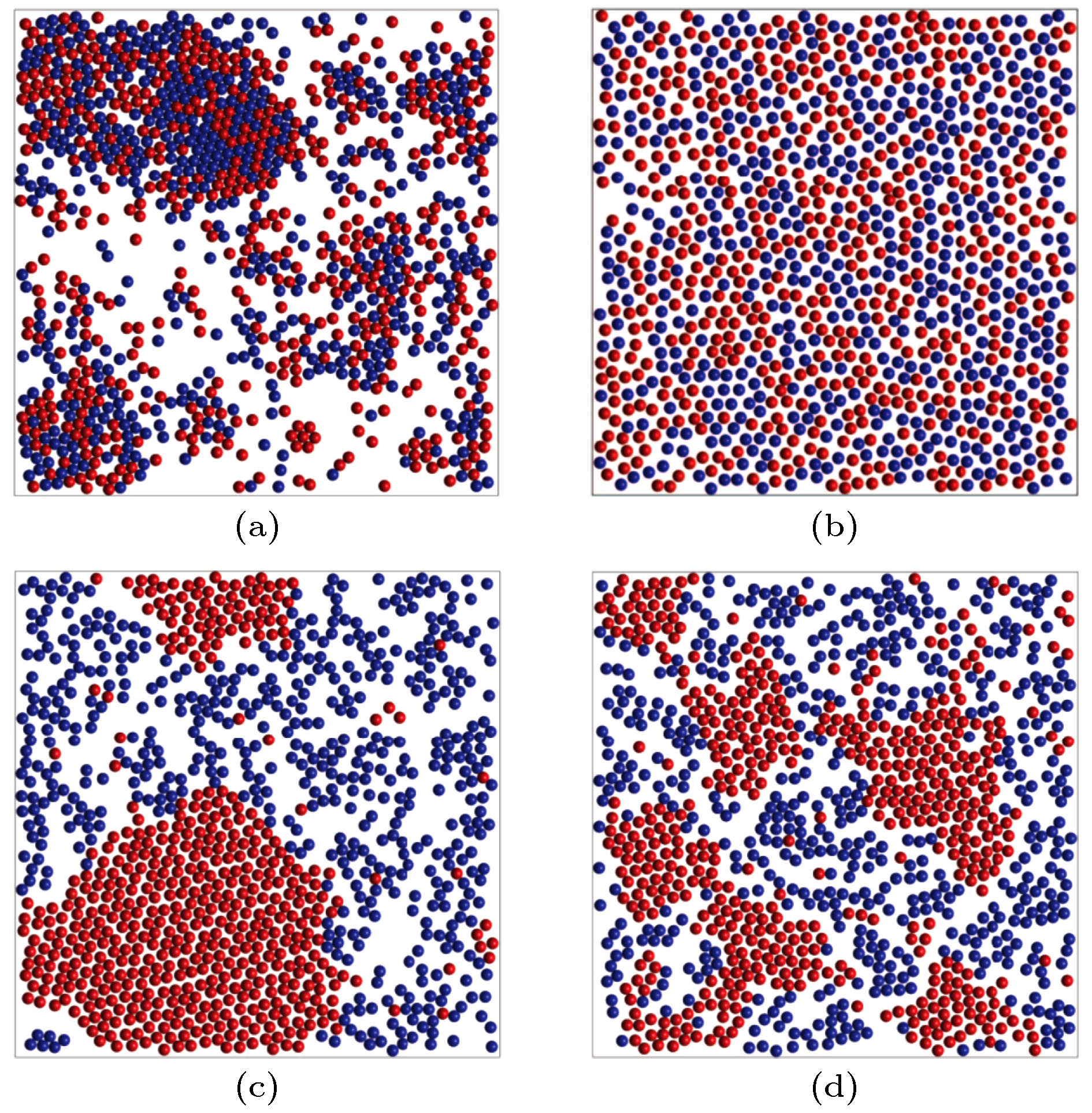
$K_{\rm {fb}} = 0, ~\omega = 0$ ; (b)$K_{\rm {fb}} = 10.0, ~ \tau = 10.0, ~\omega = 0$ ; (c)$K_{\rm {fb}} \!=\! 10.0, \tau \!=\! 10.0, \omega \!=\! 2.2$ ; (d)$K_{\rm {fb}} = 10.0,~ \tau = 10.0, ~\omega = 4.2$ . 其他参数设置为$ v_0 = 2.5 $ ,$D_{\theta} = 0.001$ ,$ \phi = 0.5 $ Fig. 2. The snapshots of mixture of CCW particles (red) and CW particles (blue): (a)
$ K_{\rm {fb}} = 0, \omega = 0 $ ; (b)$K_{\rm {fb}} = 10.0, \tau = 10.0, \omega = 0$ ; (c)$ K_{\rm {fb}} = 10.0, \tau = 10.0, \omega = 2.2 $ ; (d)$ K_{\rm {fb}} = 10.0, \tau = 10.0, \omega = 4.2 $ . The other parameters are$ v_0 = 2.5 $ ,$ D_{\theta} = 0.001 $ , and$ \phi = 0.5 $ .
图 3 (a) CW粒子和CCW粒子的最大团簇粒子数占各自总粒子数的比例P随角速度
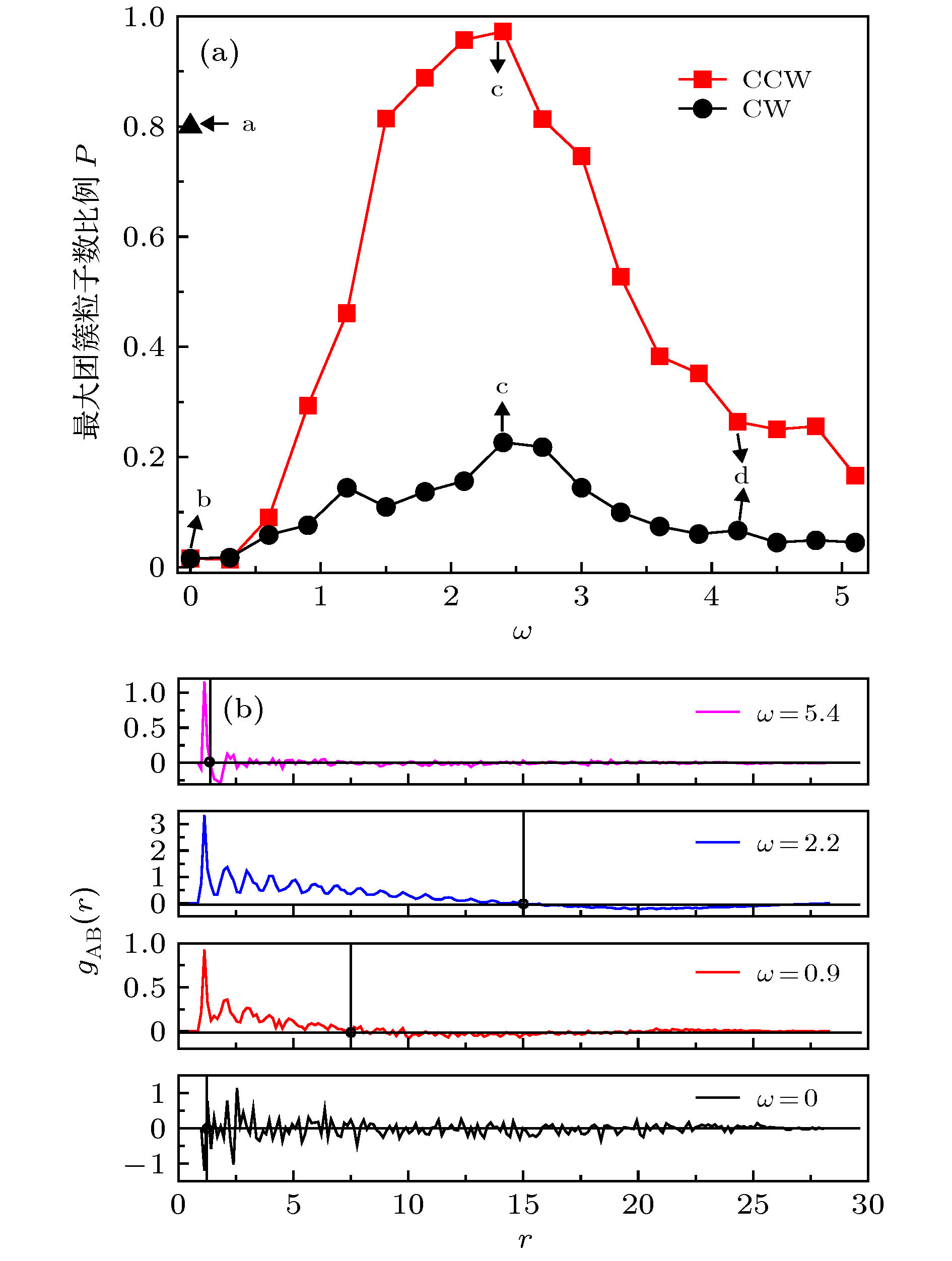
$ \omega $ 的变化. 图中a, b, c, d四点的构型图分别对应图2(a), 图2(b), 图2(c), 图2(d); (b)在不同$ \omega $ 下,$ t = 2\times10^4 $ 时, 相对径向分布函数$ g_{\rm {AB}}(r) $ . 图中标注的圆圈为第一个零根, 代表单种粒子的团簇尺寸. 其他参数设置为$ v_0 = 2.5 $ ,$ D_{\theta} = 0.001 $ ,$ \phi = 0.5 $ ,$ K_{\rm {fb}} = 10.0 $ ,$ \tau = 10.0 $ Fig. 3. (a) The ratio of the particle number in maximum cluster of CW particles and CCW particles to the total number of particles respectively as a function of
$ \omega $ . The points a, b, c, d are corresponding to Fig. 2(a),Fig. 2(b),Fig. 2(c),Fig. 2(d), respectively; (b) relative radial distribution function$ g_{\rm {AB}}(r) $ for different value of$ \omega $ at$ t = 2\times10^4 $ . The first non-trivial root (marked by circles) denotes the cluster size of the single particle species. The other parameters are$ v_0 = 2.5 $ ,$ D_{\theta} = 0.001 $ ,$ \phi = 0.5 $ ,$ K_{\rm {fb}} = 10.0 $ , and$ \tau = 10.0 $ .
图 4 (a)在不同
$ K_{\rm {fb}} $ 和$ \tau $ 值下, CCW粒子和CW粒子的有效扩散系数D随角频率$ \omega $ 的变化; (b)在不同$ K_{\rm {fb}} $ 和$ \tau $ 下, 分离系数S随角频率$ \omega $ 的变化. 其他参数设置为$ v_0 = 2.5 $ ,$ D_{\theta} = 0.001 $ ,$ \phi = 0.5 $ Fig. 4. (a) The effective diffusion coefficient D of CCW and CW particles as a function of
$ \omega $ for different$ K_{\rm {fb}} $ and$ \tau $ ; (b) the separation coefficient S as a function of$ \omega $ for different$ K_{\rm {fb}} $ and$ \tau $ . The other parameters are$ v_0 = 2.5 $ ,$ D_{\theta} = 0.001 $ , and$ \phi = 0.5 $ .
图 10 (a)在不同填充率
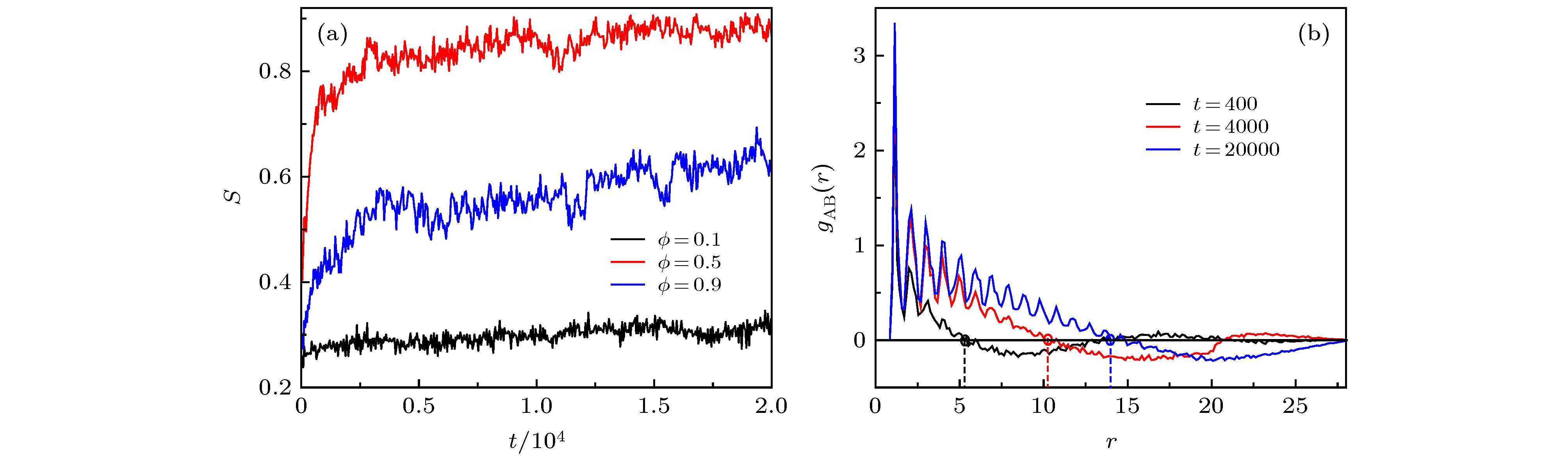
$ \phi $ 下, 分离系数S随时间t的变化; (b)在不同时间t下,$ \phi = 0.5 $ 时, 相对径向分布函数$ g_{\rm {AB}}(r) $ . 图中标注的圆圈为第一个零根, 代表单种粒子的团簇尺寸. 其他参数设置为$ v_0 = 2.5 $ ,$ D_{\theta} = 0.001 $ ,$ \omega = 2.1 $ ,$ K_{\rm {fb}} = 10.0 $ ,$ \tau = 10.0 $ Fig. 10. (a) The separation S as a function of t for different
$ \phi $ ; (b) the relative radial distribution function$ g_{\rm {AB}}(r) $ for different t at$ \phi = 0.5 $ . The first non-trivial root (marked by circles) denotes the cluster size of the single particle species. The other parameters are$ v_0 = 2.5 $ ,$ D_{\theta} = 0.001 $ ,$ \omega = 2.1 $ ,$ K_{\rm {fb}} = 10.0 $ , and$ \tau = 10.0 $ .
图 5 在 (a)
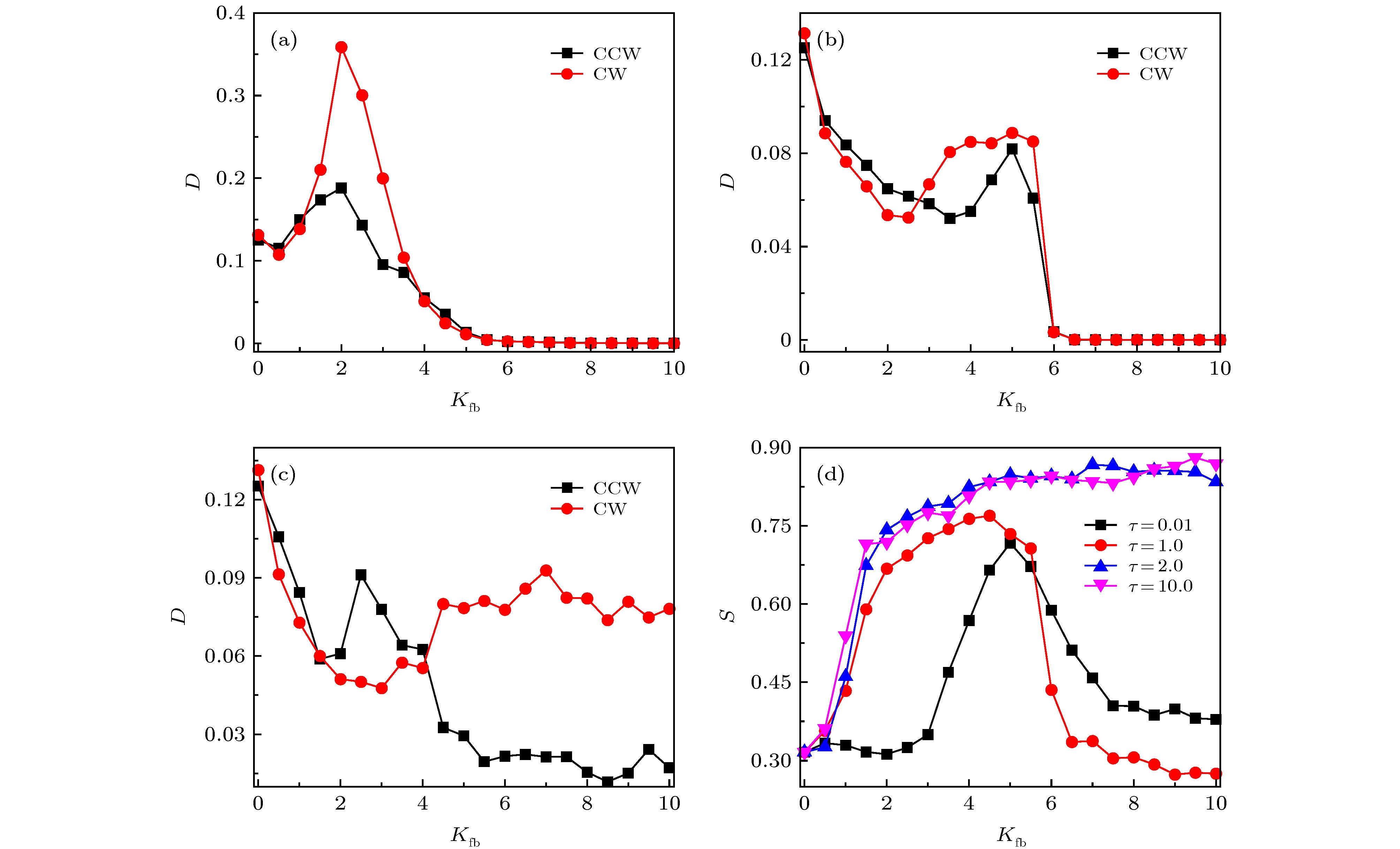
$ \tau = 0.01 $ , (b)$ \tau = 1.0 $ , (c)$ \tau = 10.0 $ 时, CCW粒子和CW粒子的有效扩散系数D随反馈强度$ K_{\rm {fb}} $ 的变化; (d)在不同$ \tau $ 下, 分离系数S随反馈强度$ K_{\rm {fb}} $ 的变化. 其他参数设置为$ \omega = 2.1 $ ,$ v_0 = 2.5 $ ,$ D_{\theta} = 0.001 $ ,$ \phi = 0.5 $ Fig. 5. The effective diffusion coefficient D of CCW and CW particles as a function of
$ K_{\rm {fb}} $ at (a)$ \tau = 0.01 $ , (b)$ \tau = 1.0 $ , and (c)$ \tau = 10.0 $ ; (d) the separation coefficient S as a function of$ K_{\rm {fb}} $ for different$ \tau $ . The other parameters are$ \omega = 2.1 $ ,$ v_0 = 2.5 $ ,$ D_{\theta} = 0.001 $ , and$ \phi = 0.5 $ .
图 6 在(a)
$ K_{\rm {fb}} = 1.0 $ , (b)$ K_{\rm {fb}} = 2.5 $ , (c)$ K_{\rm {fb}} = 10.0 $ 时, CCW粒子和CW粒子的有效扩散系数D随反馈时间$ \tau $ 的变化; (d) 在不同$ K_{\rm {fb}} $ 下, 分离系数S随反馈时间$ \tau $ 的变化. 其他参数设置为$ \omega = 2.1 $ ,$ v_0 = 2.5 $ ,$ D_{\theta} = 0.001 $ ,$ \phi = 0.5 $ Fig. 6. The effective diffusion coefficient D of CCW and CW particles as a function of
$ \tau $ at (a)$ K_{\rm {fb}} = 1.0 $ , (b)$ K_{\rm {fb}} = 2.5 $ , and (c)$ K_{\rm {fb}} = 10.0 $ ; (d) the separation coefficient S as a function of$ \tau $ for different$ K_{\rm {fb}} $ . The other parameters are$ \omega = 2.1 $ ,$ v_0 = 2.5 $ ,$ D_{\theta} = 0.001 $ , and$ \phi = 0.5 $ .
图 7 在(a)
$ K_{\rm {fb}} = 0.0 $ , (b)$ K_{\rm {fb}} = 2.5, \tau = 1.0 $ , (c)$ K_{\rm {fb}} = 10.0, \tau = 10.0 $ 时, CCW粒子和CW粒子的有效扩散系数D随转动扩散系数$ D_{\theta} $ 的变化; (d) 在不同$ K_{\rm {fb}} $ 和$ \tau $ 下, 分离系数S随转动扩散系数$ D_{\theta} $ 的变化. 其他参数设置为$ \omega = 2.1 $ ,$ v_0 = 2.5 $ ,$ \phi = 0.5 $ Fig. 7. The effective diffusion coefficient D of CCW and CW particles as a function of
$ D_{\theta} $ at (a)$ K_{\rm {fb}} = 0.0 $ , (b)$K_{\rm {fb}} = 2.5, \tau = 1.0$ , and (c)$ K_{\rm {fb}} = 10.0, \tau = 10.0 $ ; (d) the separation coefficient S as a function of$ D_{\theta} $ for different$ K_{\rm {fb}} $ and$ \tau $ . The other parameters are$ \omega = 2.1 $ ,$ v_0 = 2.5 $ , and$ \phi = 0.5 $ .
图 8 (a)在
$ K_{\rm {fb}} = 10.0 $ ,$ \tau = 10.0 $ 时, 不同自驱动速度$ v_0 $ 下, 均方位移MSD$ = \left\langle{{{\left| {\Delta {{{r}}_i}(t)} \right|}^2}}\right\rangle $ 随时间t的变化; (b)在不同$ K_{\rm {fb}} $ 和$ \tau $ 下, 分离系数S随自驱动速度$ v_0 $ 的变化. 其他参数设置为$ \omega = 2.1 $ ,$ D_{\theta} = 0.001 $ ,$ \phi = 0.5 $ Fig. 8. (a) The mean square displacement MSD
$ = \left\langle{{{\left| {\Delta {{{r}}_i}(t)} \right|}^2}}\right\rangle $ as a function of t for different$ v_0 $ at$ K_{\rm {fb}} = 10.0 $ and$ \tau = 10.0 $ ; (b) the separation coefficient S as a function of$ v_0 $ for different$ K_{\rm {fb}} $ and$ \tau $ . The other parameters are$ \omega = 2.1 $ ,$ D_{\theta} = 0.001 $ , and$ \phi = 0.5 $ .
图 9 (a) CCW粒子和CW粒子的有效扩散系数D随填充率
$ \phi $ 的变化; (b) 分离系数S随填充率$ \phi $ 的变化. 其他参数设置为$ v_0 = 2.5 $ ,$ D_{\theta} = 0.001 $ ,$ \omega = 2.1 $ ,$ K_{\rm {fb}} = 10.0 $ ,$ \tau = 10.0 $ Fig. 9. (a) The effective diffusion coefficient D of CCW and CW particles as a function of
$ \phi $ ; (b) the separation coefficient S as a function of$ \phi $ . The other parameters are$ v_0 = 2.5 $ ,$ D_{\theta} = 0.001 $ ,$ \omega = 2.1 $ ,$ K_{\rm {fb}} = 10.0 $ , and$ \tau = 10.0 $ . -
[1] Bechinger C, Di Leonardo R, Löwen H, Reichhardt C, Volpe G 2016 Rev. Mod. Phys. 88 045006
Google Scholar
[2] Chen C, Liu S, Shi X, Chate H, Wu Y 2017 Nature 542 210
Google Scholar
[3] Reichhardt C J O, Reichhardt C 2017 Annu. Rev. Condens. Matter Phys. 8 51
Google Scholar
[4] Reichhardt C J O, Reichhardt C 2017 Nat. Phys. 13 10
Google Scholar
[5] 夏益祺, 谌庄琳, 郭永坤 2019 68 161101
Google Scholar
Xia Y Q, Zhan Z L, Guo Y K 2019 Acta Phys. Sin. 68 161101
Google Scholar
[6] 张红, 宗奕吾, 杨明成, 赵坤 2019 68 134702
Google Scholar
Zhang H, Zong Y W, Yang M C, Zhao K 2019 Acta Phys. Sin. 68 134702
Google Scholar
[7] Vale R D, Milligan R A 2000 Science 288 88
Google Scholar
[8] Leptos K C, Guasto J S, Gollub J P, Pesci A I, Goldstein R E 2009 Phys. Rev. Lett. 103 198103
Google Scholar
[9] Howse J, Jones R, Ryan A, Gough T, Vafabakhsh R, Golestanian R 2007 Phys. Rev. Lett. 99 048102
Google Scholar
[10] van Teeffelen S, Löwen H 2008 Phys. Rev. E 78 020101(R
Google Scholar
[11] Tjhung E, Cates M E, Marenduzzo D 2017 Proc. Natl. Acad. Sci. 114 4631
Google Scholar
[12] Friedrich B M, Jülicher F 2007 Proc. Natl. Acad. Sci. 104 13256
Google Scholar
[13] Leonardo R D, Dell'Arciprete D, Angelani L, Iebba V 2011 Phys. Rev. Lett. 106 038101
Google Scholar
[14] Shenoy V B, Tambe D T, Prasad A, Theriot J A 2007 Proc. Natl. Acad. Sci. 104 8229
Google Scholar
[15] Von Lospichl B, Klapp S H L 2018 Phys. Rev. E 98 042605
Google Scholar
[16] Lopez B J, Kuwada N J, Craig E M, Long B R, Linke H 2008 Phys. Rev. Lett. 101 220601
Google Scholar
[17] Gernert R, Klapp S H L 2015 Phys. Rev. E 92 022132
Google Scholar
[18] Popli P, Ganguly S, Sengupta S 2018 Soft Matter 14 104
Google Scholar
[19] Yang Y, Bevan M A 2018 ACS Nano 12 10712
Google Scholar
[20] Blickle V, Bechinger C 2011 Nat. Phys. 8 143
Google Scholar
[21] Hanes R D L, Jenkins M C, Egelhaaf S U 2009 Rev. Sci. Instrum. 80 083703
Google Scholar
[22] Evers F, Hanes R D L, Zunke C, Capellmann R F, Bewerunge J, Dalle-Ferrier C, Jenkins M C, Ladadwa I, Heuer A, Castaneda-Priego R, Egelhaaf S U 2013 Eur. Phys. J. Spec. Top. 222 2995
Google Scholar
[23] Bewerunge J, Egelhaaf S U 2016 Phys. Rev. A 93 013806
Google Scholar
[24] Bäuerle T, Fischer A, Speck T, Bechinger C 2018 Nat. Commun. 9 3232
Google Scholar
[25] Jones P, Marag O, Volpe G 2015 Optical Tweezers: Principles and Applications (Cambridge: Cambridge University Press)
[26] Nishizawa K, Bremerich M, Ayade H, Schmidt C F, Ariga T, Mizuno D 2017 Sci. Adv. 3 e1700318
Google Scholar
[27] Leyman M, Ogemark F, Wehr J, Volpe G 2018 Phys. Rev. E 98 052606
Google Scholar
[28] Lavergne F A, Wendehenne H, Bäuerle T, Bechinger C 2019 Science 364 70
Google Scholar
[29] Adler J 1966 Science 153 708
Google Scholar
[30] Couzin I D, Franks N R 2003 Proc. R. Soc. London, Ser. B 270 139
Google Scholar
[31] Jin C, Hokmabad B V, Baldwin K A, Maass C C 2018 J. Phys. Condens. Matter 30 054003
Google Scholar
[32] Volpe G, Gigan S, Volpe G 2014 Am. J. Phys. 82 659
Google Scholar
[33] Kumari S, Nunes A S, Araújo N A M, Margarida M Telo da Gama 2017 J. Chem. Phys. 147 174702
Google Scholar
[34] Maggi C, Lepore A, Solari J, Rizzo A, Di Leonardo R 2013 Soft Matter 9 10885
Google Scholar
[35] Berdakin I, Jeyaram Y, Moshchalkov V V, Venken L, Dierckx S, Vanderleyden S J, Sil-hanek A V, Condat C A, Marconi V I 2013 Phys. Rev. E 87 052702
Google Scholar
[36] Yang W, Misko V R, Nelissen K, Kong M, Peeters F M 2012 Soft Matter 8 5175
Google Scholar
[37] Weber S N, Weber C A, Frey E 2016 Phys. Rev. Lett. 116 058301
Google Scholar
[38] Costanzo A, Elgeti J, Auth T, Gompper G, Ripoll M 2014 EPL 107 36003
Google Scholar
[39] Stenhammar J, Wittkowski R, Marenduzzo D, et al. 2015 Phys. Rev. Lett. 114 018301
Google Scholar
[40] Ma Z, Lei Q, Ni R 2017 Soft Matter 13 8940
Google Scholar
[41] McCandlish S R, Baskaran A, Hagan M F 2012 Soft Matter 8 2527
Google Scholar
[42] Smrek J, Kremer K 2017 Phys. Rev. Lett. 118 098002
Google Scholar
[43] Harder J, Cacciuto A 2018 Phys. Rev. E 97 022603
Google Scholar
[44] Nourhani A, Crespi V H, Lammert P E 2015 Phys. Rev. Lett. 115 118101
Google Scholar
[45] Mijalkov M, Volpe G 2013 Soft Matter 9 6376
Google Scholar
[46] Scholz C, Engel M, Pöschel T 2018 Nat. Commun. 9 1
Google Scholar
[47] Chen Q, Ai B 2015 J. Chem. Phys. 143 104113
Google Scholar
[48] Ai B, Shao Z, Zhong W 2018 Soft Matter 14 4388
Google Scholar
[49] Wysocki A, Winkler R G, Gompper G 2016 New J. Phys. 18 123030
Google Scholar
[50] Dolai P, Simha A, Mishra S 2018 Soft Matter 14 6137
Google Scholar
[51] Ai B 2016 Sci. Rep. 6 1
Google Scholar
[52] Nguyen N H P, Klotsa D, Engel M, Glotzer S C 2014 Phys. Rev. Lett. 112 075701
Google Scholar
[53] Agrawal A, Babu S B 2018 Phys. Rev. E 97 020401(R
Google Scholar
[54] Ai B, He Y, Zhong W 2015 Soft Matter 11 3852
Google Scholar
[55] Reichhardt C, Reichhardt C J O 2013 Phys. Rev. E 88 042306
Google Scholar
[56] DiLuzio W R, Turner L, Mayer M, Garstecki P, Weibel D B, Berg H C, Whitesides G M 2005 Nature 435 1271
Google Scholar
[57] Shin J, Cherstvy A G, Metzler R 2014 New J. Phys. 16 053047
Google Scholar
[58] Di Leonardo R, Dell’Arciprete D 2011 Physical Review Letters 106 038101
[59] Cẽbers A 2011 J. Magn. Magn. Mater. 323 279
Google Scholar
[60] Hennig D 2009 Phys. Rev. E 79 041114
Google Scholar
[61] Yang X, Manning M L, Marchetti M C 2014 Soft Matter 10 6477
Google Scholar
[62] Cates M E, Tailleur J 2015 Annu. Rev. Condens. Matter Phys. 6 219
Google Scholar
下载:
计量
- 文章访问数: 6267
- PDF下载量: 94
- 被引次数: 0
