Problems and challenges of power-electronic-based power system stability: A case study of transient stability comparison

Yang Zi-Qian; Ma Rui; Cheng Shi-Jie; Zhan Meng

doi:10.7498/aps.69.20191954

Abstract

With the development of power electronic technology and requirement for clean energy, the traditional power systems which are dominated by synchronous generators are gradually changing into the power-electronic-based power systems with diversified power electronic equipment. The power systems are facing a great revolution in their primary equipment, and this has not happened in the past one hundred years. In recent years, with great increasing penetration of power electronic devices into power grids, the large-scale blackouts caused by power electronic devices have been reported, which seriously threatens the safe and stable operation of power systems. Under the above background, in this paper we first introduce several methods of analyzing the traditional power system transient stability from the equal area criterion for the single machine infinite bus system to several Lyapunov function based direct methods for multi-machine systems. Then we introduce some of our recent work on the nonlinear modeling and analysis of a key component of power-electronic-based power systems, voltage source converter (VSC), and propose a multiple machine system model including power electronic equipment and traditional synchronous machines. Finally, we illustrate the transient characteristics of the power electronic devices, and summarize the basic problems and challenges for the transient stability of power-electronic-based power systems. We hope that these basic problems in power-electronic-based power system dynamics including nonlinearity, multi-time-scale, and complexity could arouse the general interest of researchers in the fields of complex systems and statistical mechanics.

Keywords:

power-electronic-based power system dynamics /
transient stability analysis /
grid-connected converter /
complex system dynamics

Authors and contacts

State Key Laboratory of Advanced Electromagnetic Engineering and Technology, Hubei Electric Power Security and High Efficiency Key Laboratory, School of Electrical and Electronic Engineering, Huazhong University of Science and Technology, Wuhan 430074, China

Corresponding author: Zhan Meng, zhanmeng@hust.edu.cn

Funds: Project supported by the National Key Research and Development Program of China (Grant No. 2017YFB0902000), Science and Technology Project of State Grid (Grant No. SGXJ0000KXJS1700841) and the Funds for International Cooperation and Exchange of the National Natural Science Foundation of China (Grant No. 11861131011)

FullText HTML : translate this paragraph

References

[1]	周孝信, 陈树勇, 鲁宗相, 黄彦浩, 马士聪, 赵强 2018 电机工程学报 38 1893 Google Scholar Zhou X X, Chen S Y, Lu Z X, Huang Y H, Ma S C 2018 Proceedings of the CSEE 38 1893 Google Scholar
[2]	袁小明, 程时杰, 胡家兵 2016 电机工程学报 36 5145 Google Scholar Yuan X M, Cheng S J, Hu J B 2016 Proceedings of the CSEE 36 5145 Google Scholar
[3]	胡家兵, 袁小明, 程时杰 2019 电机工程学报 39 5457 Google Scholar Hu J B, Yuan X M, Cheng S J 2019 Proceedings of the CSEE 39 5457 Google Scholar
[4]	Biaabjerg F, Ma K 2013 IEEE J. Emerging Sel. Top. Power Electron. 1 139 Google Scholar
[5]	Biaabjerg F, Teodorescu R, Liserre M, Timbus A V 2006 IEEE Trans. Ind. Electron. 53 1398
[6]	National Grid ESO LFDD 09/08/2019 Incident Report https://www.nationalgrideso.com/document/152346/download [2019-11-10]
[7]	Kundur P, Balu N J, Lauby M G 1994 Power System Stability and Control (Vol. 1) (New York: McGraw-hill) p827
[8]	Anderson P M, Fouad A A 2002 Power System Control and Stability (Vol. 2) (Boloken: John Wiley & Sons) p13
[9]	傅书逷, 倪以信, 薛禹胜 1999 直接法稳定分析(北京: 中国电力出版社) 第25页 Fu S T, Ni Y Y, Xue Y S 1999 Direct Method Stability Analysis (Vol. 1) (Beijing: China Electric Power Press) p25 (in Chinese)
[10]	刘笙, 陈陈 2014 电力系统暂态稳定的能量函数分析: 网络结构保持模型(北京: 科学出版社) 第75页 Liu S, Chen C 2014 Energy Function Analysis of Power Aystem Transient Atability: Network Structure Maintenance Model (Vol. 1) (Beijing: Science Press) p75 (in Chinese)
[11]	Chiang H D 2010 Direct Methods for Stability Analysis of Electric Power Systems (Vol. 1) (Beijing: Science Press) p60
[12]	Kakimoto N, Ohsawa Y, Hayashi M 1978 Trans. IEE of Japan 98 62
[13]	Llamas A, Lopez J, Mili L, Phadke A, Thorp J 1995 IEEE Trans. Power Syst 10 210
[14]	Xue Y, Cutsem T V, Ribbens-Pavella V 1988 IEEE Trans. Power Syst. 3 400 Google Scholar
[15]	Kalcon G O, Adam G P, Anaya-Lara O, Lo S, Uhlen K 2012 IEEE Trans. Power Syst. 27 1818
[16]	Harnefors L, Bongiorno M, Lundberg S 2007 IEEE Trans. Ind. Electron. 54 3323 Google Scholar
[17]	Sun J 2011 IEEE Trans. Power Electron. 26 3075 Google Scholar
[18]	Rygg A, Molinas M, Zhang C, Cai X 2016 IEEE J. Emerging Sel. Top. Power Electron. 4 1383 Google Scholar
[19]	Huang Y, Yuan X, Hu J, Zhou P 2015 IEEE J. Emerging Sel. Top. Power Electron. 3 1193 Google Scholar
[20]	Yuan H, Yuan X, Hu J 2017 IEEE Trans. Power Syst. 32 3981 Google Scholar
[21]	Yang Z, Mei C, Chen S, Zhan M 2020 IEEE J. Emerging Sel. Top. Power Electron. (in press)Google Scholar
[22]	Kabalan M, Singh P, Niebur D 2016 IEEE Trans. Smart Grid 8 2287
[23]	Wu H, Wang X 2018 IEEE Trans. Ind. Electron. 66 6473
[24]	Huang L, Xin H, Wang Z, Zhang L, Wu K, Hu J 2017 IEEE Trans. Smart Grid 10 578
[25]	Huang M, Wong S C, Chi K T, Ruan X 2012 IEEE Trans. Circuits Syst. I, Reg. Papers 60 1062
[26]	Huang M, Peng Y, Chi K T, Liu Y, Sun J, Zha X 2017 IEEE Trans. Power Electron. 32 8868 Google Scholar
[27]	Zhang C, Cai X, Li Z, Rygg A, Molinas M 2017 IET Power Electron. 10 894 Google Scholar
[28]	Sun J, Wang G, Du X, Wang H 2018 IEEE Trans. Power Electron. 34 3025
[29]	Ying J, Yuan X X, Hu J B 2017 IEEE Trans. Energy Convers. 32 1502 Google Scholar
[30]	Vittal E, O’Malley M, Keane A 2010 IEEE Trans. Power Syst. 25 433
[31]	Gautam D, Vittal V, Harbour T 2009 IEEE Trans. Power Syst. 24 1426
[32]	Hu Q, Fu L, Ma F, Ji F 2019 IEEE Trans. Power Syst. 34 3220 Google Scholar
[33]	李明节, 于钊, 许涛, 贺静波, 王超, 谢小荣, 刘纯 2017 电网技术 41 1035 Google Scholar Li M J, Yu Z, Xu T, He J B, Wang C, Xie X X, Liu C 2017 Proceedings of the CSEE 41 1035 Google Scholar
[34]	Menck P J, Heitzig J, Kurths J, Schellnhuber H J 2014 Nat.Commun. 5 3969 Google Scholar
[35]	Schultz P, Heitzig J, Kurths J 2014 New J.Phys. 16 125001 Google Scholar
[36]	Rohden M, Sorge A, Timme M, Witthaut D 2012 Phys. Rev. Lett. 109 064101 Google Scholar
[37]	Schafer B, Witthaut D, Timme M, Latora V 2018 Nat. Commun. 9 1975 Google Scholar
[38]	Motter A E, Myers S A, Anghel M, Nishikawa T 2013 Nat. Phys. 9 191 Google Scholar
[39]	Yang Y, Nishikawa T, Motter A E 2017 Science 358 3184 Google Scholar
[40]	Dorfler F, Chertkov M, Bullo F 2013 PNAS 110 2005 Google Scholar
[41]	Grob D, Arghir C, Dorfler F 2018 Automatica 90 248 Google Scholar
[42]	Carareto R, Baptista M S, Grebogi C 2013 Commun. Nonlinear Sci. Numer. Simul. 18 1035 Google Scholar
[43]	Ma J, Sun Y, Yuan X, Kurths J, Zhan M 2016 PLoS ONE 11 e0165943 Google Scholar
[44]	Sun Y, Kurths J, and Zhan M 2017 CHAOS 27 083116 Google Scholar
[45]	Y Sun, J Ma, J Kurths, M Zhan 2018 Proc. R. Soc. London, Ser. A 474 20170733 Google Scholar
[46]	M He, W He, J Hu, X Yuan, M Zhan 2019 Nonlinear Dynamics 95 1965 Google Scholar
[47]	Q Yue, J Yu, Zhan M 2019 IET RPG 2019 International Conference on Renewable Power Generation Shanghai, China, October 24–25, 2019 p294
[48]	Qiu Q, Ma R, Kurths J, Zhan M 2020 Chaos 30 013110 Google Scholar
[49]	Yang Z Q, Ma R, Chen S, Zhan M 2020 IEEE J. Emerging. Sel. Top. Power Electron. (in press)Google Scholar
[50]	Ma R, Yang Z, Cheng S, Zhan M 2020 Sustained Oscillations and Bifurcations in Three-phase VSC Tied to AC Gird (submitted) IET Renewable Power Generation
[51]	Strogatz S H 2018 Nonlinear Dynamics and Chaos: with Applications to Physics, Biology, Chemistry, and Engineering (Vol. 2) (Boulder: Westview Press) p241
[52]	Kuehn C 2015 Multiple Time Scale Dynamics (Vol. 1) (Berlin: Springer International Publishing) p53

Cited By

图 1 电力电子化电力系统示意图

Figure 1. Schematic diagram of power electronic dominated power systems

DownLoad: Full-Size Img PowerPoint

图 2 一台同步发电机经变压器升压后串联双回线路接入无穷大电网的示意图

Figure 2. Schematic show for a single-machine-infinite-bus (SMIB) system

DownLoad: Full-Size Img PowerPoint

图 3 系统的功率特性曲线^[7]

Figure 3. Power-angle relationship^[7].

DownLoad: Full-Size Img PowerPoint

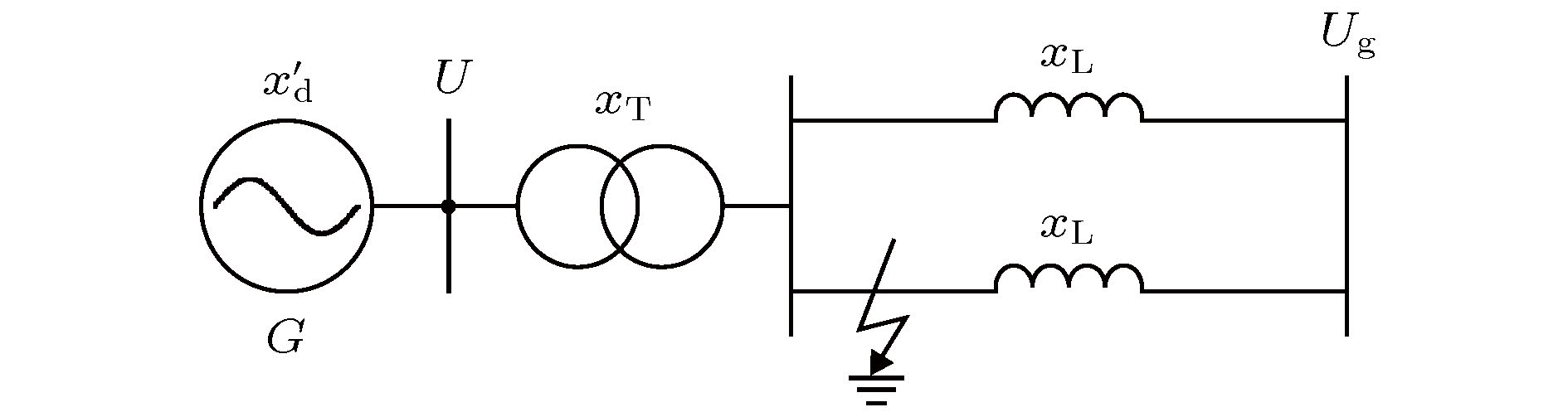
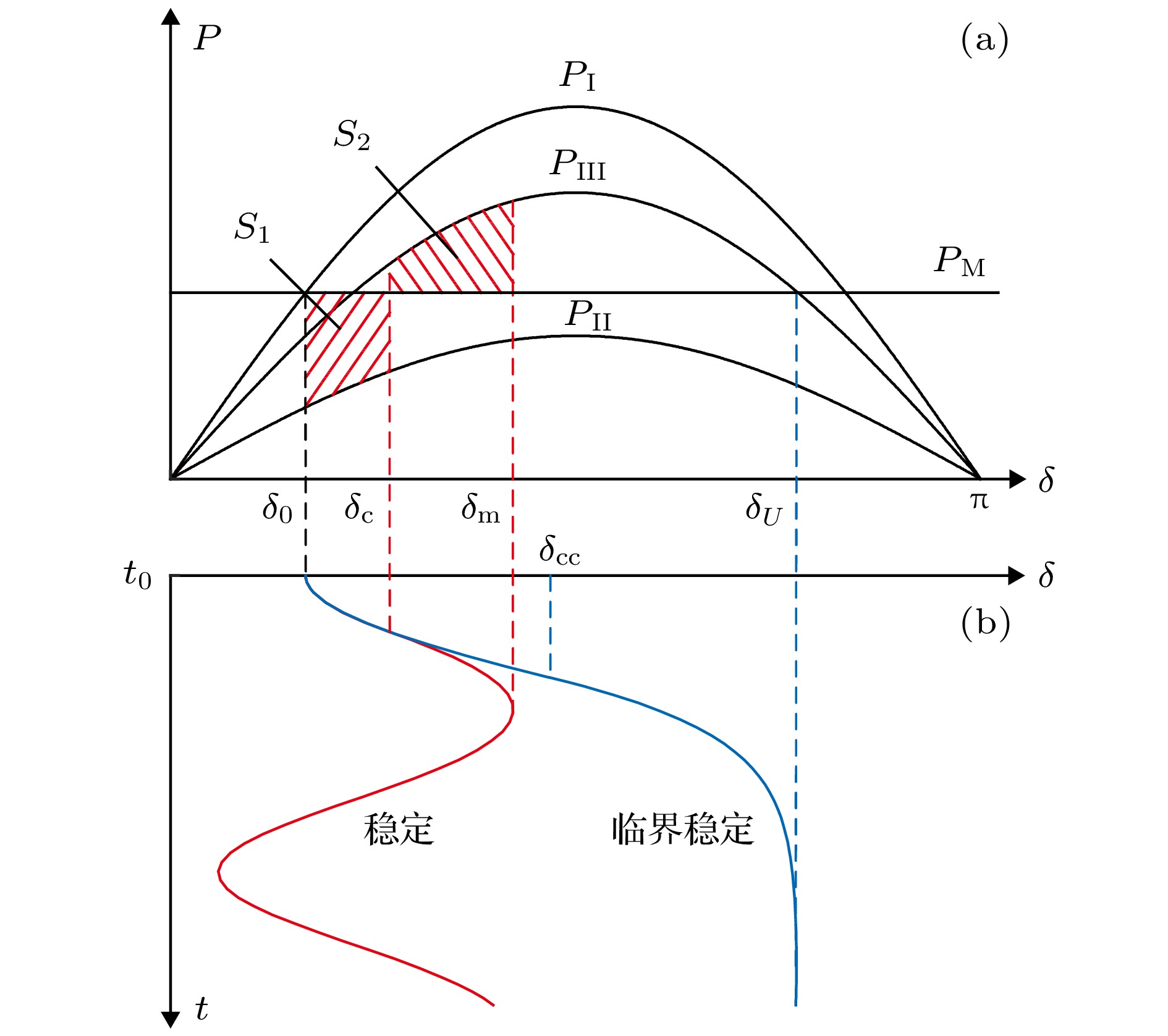
图 4 (a) 简单系统在故障前、故障中、故障后的三条不同功率特性曲线; (b) 暂态稳定(红色曲线)和临界稳定(蓝色曲线)情况下的功角的时域波形^[9]

Figure 4. (a) Power-angle relationships for three different states of before-fault ($ P_{\rm {I}} $), during-fault ($ P_{\rm {II}} $), and post-fault ($ P_{\rm {III}} $); (b) time-domain responses of the power angle when the system are stable (red curve) and critical stable (blue curve), respectively^[9]

DownLoad: Full-Size Img PowerPoint

图 5 (a)势能函数曲线；(b)不同状态下的轨迹^[10]

Figure 5. (a) Potential energy function curve; (b) trajectories in state space corresponding different states: stable, critically stable, and unstable^[10].

DownLoad: Full-Size Img PowerPoint

图 6 VSC单机并网系统控制框图

Figure 6. Schematic show of a grid-connected VSC system and its controllers

DownLoad: Full-Size Img PowerPoint

图 7 VSC电压时间尺度模型系统控制框图

Figure 7. Schematic show of the control diagram of the VSC system within the voltage timescale

DownLoad: Full-Size Img PowerPoint

图 8 参数$ U_{\rm {g}} $变化时的分岔图(包含亚临界霍普夫分岔和广义鞍结点分岔). 小图中显示$ U_{\rm {g}} $减小时经过霍普夫分岔点的特征根轨迹

Figure 8. Bifurcation diagram with the variation of $ U_{\rm {g}} $ including a sub-critical Hopf bifurcation and a generalized saddle-node bifurcation. The sub-figure shows the eigenvalue traces when $ U_{\rm {g}} $ decreases and passes through the Hopf bifurcation point

DownLoad: Full-Size Img PowerPoint

图 9 VSC电压时间尺度模型与详细模型在暂态故障后的响应对比

Figure 9. Response comparison between the voltage timescale VSC system and the detailed VSC system after transient fault

DownLoad: Full-Size Img PowerPoint

图 10 (a)VSC与同步机多机耦合系统和(b)其微分代数方程组中变量传递关系

Figure 10. (a) A multi-machine power system with VSC devices and synchronous generators and (b) its variable relations in differential algebraic equations

DownLoad: Full-Size Img PowerPoint

表 1 电力电子化系统与传统电力系统暂态问题初步比较

Table 1. Comparison of transient problems between Power-electronic-based power systems and traditional power systems

	复杂性	时间尺度	系统阶数
传统电力系统	非线性项较少且单一	机电与电磁时间尺度较好分离	同步机二阶模型
电力电子化电力系统	非线性项分布广泛且复杂	多时间尺度间强耦合	装备多样化且高阶

DownLoad: CSV

map

[1]	周孝信, 陈树勇, 鲁宗相, 黄彦浩, 马士聪, 赵强 2018 电机工程学报 38 1893 Google Scholar Zhou X X, Chen S Y, Lu Z X, Huang Y H, Ma S C 2018 Proceedings of the CSEE 38 1893 Google Scholar
[2]	袁小明, 程时杰, 胡家兵 2016 电机工程学报 36 5145 Google Scholar Yuan X M, Cheng S J, Hu J B 2016 Proceedings of the CSEE 36 5145 Google Scholar
[3]	胡家兵, 袁小明, 程时杰 2019 电机工程学报 39 5457 Google Scholar Hu J B, Yuan X M, Cheng S J 2019 Proceedings of the CSEE 39 5457 Google Scholar
[4]	Biaabjerg F, Ma K 2013 IEEE J. Emerging Sel. Top. Power Electron. 1 139 Google Scholar
[5]	Biaabjerg F, Teodorescu R, Liserre M, Timbus A V 2006 IEEE Trans. Ind. Electron. 53 1398
[6]	National Grid ESO LFDD 09/08/2019 Incident Report https://www.nationalgrideso.com/document/152346/download [2019-11-10]
[7]	Kundur P, Balu N J, Lauby M G 1994 Power System Stability and Control (Vol. 1) (New York: McGraw-hill) p827
[8]	Anderson P M, Fouad A A 2002 Power System Control and Stability (Vol. 2) (Boloken: John Wiley & Sons) p13
[9]	傅书逷, 倪以信, 薛禹胜 1999 直接法稳定分析(北京: 中国电力出版社) 第25页 Fu S T, Ni Y Y, Xue Y S 1999 Direct Method Stability Analysis (Vol. 1) (Beijing: China Electric Power Press) p25 (in Chinese)
[10]	刘笙, 陈陈 2014 电力系统暂态稳定的能量函数分析: 网络结构保持模型(北京: 科学出版社) 第75页 Liu S, Chen C 2014 Energy Function Analysis of Power Aystem Transient Atability: Network Structure Maintenance Model (Vol. 1) (Beijing: Science Press) p75 (in Chinese)
[11]	Chiang H D 2010 Direct Methods for Stability Analysis of Electric Power Systems (Vol. 1) (Beijing: Science Press) p60
[12]	Kakimoto N, Ohsawa Y, Hayashi M 1978 Trans. IEE of Japan 98 62
[13]	Llamas A, Lopez J, Mili L, Phadke A, Thorp J 1995 IEEE Trans. Power Syst 10 210
[14]	Xue Y, Cutsem T V, Ribbens-Pavella V 1988 IEEE Trans. Power Syst. 3 400 Google Scholar
[15]	Kalcon G O, Adam G P, Anaya-Lara O, Lo S, Uhlen K 2012 IEEE Trans. Power Syst. 27 1818
[16]	Harnefors L, Bongiorno M, Lundberg S 2007 IEEE Trans. Ind. Electron. 54 3323 Google Scholar
[17]	Sun J 2011 IEEE Trans. Power Electron. 26 3075 Google Scholar
[18]	Rygg A, Molinas M, Zhang C, Cai X 2016 IEEE J. Emerging Sel. Top. Power Electron. 4 1383 Google Scholar
[19]	Huang Y, Yuan X, Hu J, Zhou P 2015 IEEE J. Emerging Sel. Top. Power Electron. 3 1193 Google Scholar
[20]	Yuan H, Yuan X, Hu J 2017 IEEE Trans. Power Syst. 32 3981 Google Scholar
[21]	Yang Z, Mei C, Chen S, Zhan M 2020 IEEE J. Emerging Sel. Top. Power Electron. (in press)Google Scholar
[22]	Kabalan M, Singh P, Niebur D 2016 IEEE Trans. Smart Grid 8 2287
[23]	Wu H, Wang X 2018 IEEE Trans. Ind. Electron. 66 6473
[24]	Huang L, Xin H, Wang Z, Zhang L, Wu K, Hu J 2017 IEEE Trans. Smart Grid 10 578
[25]	Huang M, Wong S C, Chi K T, Ruan X 2012 IEEE Trans. Circuits Syst. I, Reg. Papers 60 1062
[26]	Huang M, Peng Y, Chi K T, Liu Y, Sun J, Zha X 2017 IEEE Trans. Power Electron. 32 8868 Google Scholar
[27]	Zhang C, Cai X, Li Z, Rygg A, Molinas M 2017 IET Power Electron. 10 894 Google Scholar
[28]	Sun J, Wang G, Du X, Wang H 2018 IEEE Trans. Power Electron. 34 3025
[29]	Ying J, Yuan X X, Hu J B 2017 IEEE Trans. Energy Convers. 32 1502 Google Scholar
[30]	Vittal E, O’Malley M, Keane A 2010 IEEE Trans. Power Syst. 25 433
[31]	Gautam D, Vittal V, Harbour T 2009 IEEE Trans. Power Syst. 24 1426
[32]	Hu Q, Fu L, Ma F, Ji F 2019 IEEE Trans. Power Syst. 34 3220 Google Scholar
[33]	李明节, 于钊, 许涛, 贺静波, 王超, 谢小荣, 刘纯 2017 电网技术 41 1035 Google Scholar Li M J, Yu Z, Xu T, He J B, Wang C, Xie X X, Liu C 2017 Proceedings of the CSEE 41 1035 Google Scholar
[34]	Menck P J, Heitzig J, Kurths J, Schellnhuber H J 2014 Nat.Commun. 5 3969 Google Scholar
[35]	Schultz P, Heitzig J, Kurths J 2014 New J.Phys. 16 125001 Google Scholar
[36]	Rohden M, Sorge A, Timme M, Witthaut D 2012 Phys. Rev. Lett. 109 064101 Google Scholar
[37]	Schafer B, Witthaut D, Timme M, Latora V 2018 Nat. Commun. 9 1975 Google Scholar
[38]	Motter A E, Myers S A, Anghel M, Nishikawa T 2013 Nat. Phys. 9 191 Google Scholar
[39]	Yang Y, Nishikawa T, Motter A E 2017 Science 358 3184 Google Scholar
[40]	Dorfler F, Chertkov M, Bullo F 2013 PNAS 110 2005 Google Scholar
[41]	Grob D, Arghir C, Dorfler F 2018 Automatica 90 248 Google Scholar
[42]	Carareto R, Baptista M S, Grebogi C 2013 Commun. Nonlinear Sci. Numer. Simul. 18 1035 Google Scholar
[43]	Ma J, Sun Y, Yuan X, Kurths J, Zhan M 2016 PLoS ONE 11 e0165943 Google Scholar
[44]	Sun Y, Kurths J, and Zhan M 2017 CHAOS 27 083116 Google Scholar
[45]	Y Sun, J Ma, J Kurths, M Zhan 2018 Proc. R. Soc. London, Ser. A 474 20170733 Google Scholar
[46]	M He, W He, J Hu, X Yuan, M Zhan 2019 Nonlinear Dynamics 95 1965 Google Scholar
[47]	Q Yue, J Yu, Zhan M 2019 IET RPG 2019 International Conference on Renewable Power Generation Shanghai, China, October 24–25, 2019 p294
[48]	Qiu Q, Ma R, Kurths J, Zhan M 2020 Chaos 30 013110 Google Scholar
[49]	Yang Z Q, Ma R, Chen S, Zhan M 2020 IEEE J. Emerging. Sel. Top. Power Electron. (in press)Google Scholar
[50]	Ma R, Yang Z, Cheng S, Zhan M 2020 Sustained Oscillations and Bifurcations in Three-phase VSC Tied to AC Gird (submitted) IET Renewable Power Generation
[51]	Strogatz S H 2018 Nonlinear Dynamics and Chaos: with Applications to Physics, Biology, Chemistry, and Engineering (Vol. 2) (Boulder: Westview Press) p241
[52]	Kuehn C 2015 Multiple Time Scale Dynamics (Vol. 1) (Berlin: Springer International Publishing) p53

[1]	Wang Jian-Hai, Qian Jian-Qiang, Dou Zhi-Peng, Lin Rui, Xu Ze-Yu, Cheng Peng, Wang Cheng, Li Lei, Li Ying-Zi. Wavelet transform based method of measuring multi-frequency electrostatic force microscopy dynamic process. Acta Physica Sinica, 2022, 71(9): 096801. doi: 10.7498/aps.71.20212095
[2]	Zhang Hai-Feng, Wang Wen-Xu. Complex system reconstruction. Acta Physica Sinica, 2020, 69(8): 088906. doi: 10.7498/aps.69.20200001
[3]	Min Fu-Hong, Ma Mei-Ling, Zhai Wei, Wang En-Rong. Chaotic control of the interconnected power system based on the relay characteristic function. Acta Physica Sinica, 2014, 63(5): 050504. doi: 10.7498/aps.63.050504
[4]	Ni Jun-Kang, Liu Chong-Xin, Pang Xia. Fuzzy fast terminal sliding mode controller using an equivalent control for chaotic oscillation in power system. Acta Physica Sinica, 2013, 62(19): 190507. doi: 10.7498/aps.62.190507
[5]	Zhang Xi, Bao Bo-Cheng, Wang Jin-Ping, Ma Zheng-Hua, Xu Jian-Ping. Stability analysis of equivalent series resistance of output capacitor in fixed off-time controlled Buck converter. Acta Physica Sinica, 2012, 61(16): 160503. doi: 10.7498/aps.61.160503
[6]	Ding Yi-Min, Yang Chang-Ping. The network model of mobile agents with the human mobility. Acta Physica Sinica, 2012, 61(23): 238901. doi: 10.7498/aps.61.238901
[7]	Yang Bin-Xin, Ouyang Jie, Li Xue-Juan. Dynamic simulation of fiber orientation in mold filling process in a complex cavity. Acta Physica Sinica, 2012, 61(4): 044701. doi: 10.7498/aps.61.044701
[8]	Xie Fan, Yang Ru, Zhang Bo. Analysis of weight Lempel-Ziv complexity in piecewise smooth systems of DC-DC switching converters. Acta Physica Sinica, 2012, 61(11): 110504. doi: 10.7498/aps.61.110504
[9]	Zhou Guo-Hua, Xu Jian-Ping, Bao Bo-Cheng, Wang Jin-Ping, Jin Yan-Yan. Complex subharmonic oscillation phenomenon of peak current controlled buck converter with current source load. Acta Physica Sinica, 2011, 60(1): 010503. doi: 10.7498/aps.60.010503
[10]	Cheng Wei-Bin, Kang Si-Min, Wang Yue-Long, Tang Nan, Guo Ying-Na, Huo Ai-Qing. Fast-scale instability and dynamic parameter resonance of power factor correction Boost converter. Acta Physica Sinica, 2011, 60(2): 020506. doi: 10.7498/aps.60.020506
[11]	Yang Ru, Zhang Bo, Zhao Shou-Bai, Lao Yu-Jin. Arithmetic complexity of discrete map of converter based on symbol time series. Acta Physica Sinica, 2010, 59(6): 3756-3762. doi: 10.7498/aps.59.3756
[12]	Zhang Bo, Xie Fan, Yang Ru. Study on border collision and bifurcation of two-dimensional piecewise smooth systems in current mode controlled Buck converter. Acta Physica Sinica, 2010, 59(12): 8393-8406. doi: 10.7498/aps.59.8393
[13]	Zhang Yuan, Zhang Hao, Ma Xi-Kui. Intermediate-scale instability in one-cycle controlled Cuk power factor correction converter. Acta Physica Sinica, 2010, 59(12): 8432-8443. doi: 10.7498/aps.59.8432
[14]	Gao Yang, Li Li-Xiang, Peng Hai-Peng, Yang Yi-Xian, Zhang Xiao-Hong. Adaptive synchronization in united complex dynamical network with multi-links. Acta Physica Sinica, 2008, 57(4): 2081-2091. doi: 10.7498/aps.57.2081
[15]	Gao Yang, Li Li-Xiang, Peng Hai-Peng, Yang Yi-Xian, Zhang Xiao-Hong. Stability analysis of complex networks with multi-links. Acta Physica Sinica, 2008, 57(3): 1444-1452. doi: 10.7498/aps.57.1444
[16]	Yang Ru, Zhang Bo, Qiu Dong-Yuan. Chaotic point process description of converter discrete subsystem and EMI suppression. Acta Physica Sinica, 2008, 57(3): 1389-1397. doi: 10.7498/aps.57.1389
[17]	Wang Ling-Tao, Ma Xi-Kui, Zou Jian-Long, Yang Mei. Study of complex behavior in a time-delayed van der Pol’s electromagnetic system (Ⅱ)——Pattern dynamics in spatiotemporal chaos. Acta Physica Sinica, 2006, 55(11): 5657-5666. doi: 10.7498/aps.55.5657
[18]	Zhao Yi-Bo, Luo Xiao-Shu, Fang Jin-Qing, Wang Bing-Hong. Study on stability of the voltage-mode DC-DC converters. Acta Physica Sinica, 2005, 54(11): 5022-5026. doi: 10.7498/aps.54.5022
[19]	XIMEN JI-YE, LI YU. DYNAMIC ABERRATION CORRECTION IN A COMBINED SCANNING ELECTRON BEAM SYSTEM. Acta Physica Sinica, 1982, 31(12): 37-43. doi: 10.7498/aps.31.37
[20]	S. T. BOW. GRAPHICAL ANALYSIS OF THE NONLINEAR POWER SYSTEM OSCILLATION. Acta Physica Sinica, 1962, 18(8): 411-421. doi: 10.7498/aps.18.411

Catalog

Vol. 69, Issue 8 - 2020-04-20

Metrics

Abstract views: 17044
PDF Downloads: 517
Cited By: 0

姓名
邮箱
手机号码
标题
留言内容
验证码

Search

Article

留言板