-
Nonlinear acoustics is an important branch of acoustics and has important applications in some areas, such as high-intensity focused ultrasound, ultrasonic suspension, acoustic cavitation, acoustic harmonic imaging, and parametric emission array. The solving of nonlinear equations in these fields is very important. Regarding the solution of the wave equation of a nonlinear acoustic system, the methods used at this stage generally include complete numerical calculation method, strict analytical method, and perturbation method. 1) For the complete numerical calculation method, it covers the finite element method and the finite difference method. The physical meaning of the solution obtained by this kind of method is not clear, and it is difficult to reveal the physical nature of nonlinear event. And in many cases it will lead to the numerical divergence problems, and it is not suitable for all nonlinear problems. 2) For the strict analytical method, it can only deal with nonlinear acoustic problems of very few systems, such as the propagation of nonlinear acoustic waves in an ideal fluid. 3) For perturbation method, its advantage is that the method is simple and the physical meaning of the solution is clear, but it is only suitable for dealing with nonlinear effects at low sound intensity. And it takes into consideration only the effect of low-order harmonics on higher-order harmonics, with ignoring its reaction, so it does not satisfy the law of conservation of energy. In this paper, we propose a new, semi-analytical numerical iterative method of solving nonlinear wave equations. It is a form of expanding the sound field into a Fourier series in the frequency domain, realizing the separation of time variables from space coordinates. Then, according to the specific requirements for the calculation accuracy, the high frequency harmonics are cut off to solve the equation. Compared with the results from the complete numerical methods (such as finite element method and finite difference method), the solution from this iterative method has a very clear physical meaning. That is, its solution is a combination of harmonics of all orders. Compared with the perturbation method, it can consider the interaction of various harmonics and can satisfy the law of conservation of energy (provided that the system has no dissipation). It is used to study the propagation properties of nonlinear acoustic waves in liquids. The results show that the iterative method is also applicable in the range of sound intensity where the perturbation method is applicable. In a wide range of sound intensity where the perturbation method is unapplicable, the iterative method is still applicable and satisfies the law of conservation of energy (provided that the system has no dissipation). It is unapplicable only if the sound intensity is extremely loud and strong. And when more high-order harmonics are involved, the calculation time by using the numerical method proposed in this paper does not increase sharply. -
Keywords:
- nonlinear acoustics /
- numerical iterative method /
- energy flow density
[1] 叶欣, 费兴波 2004 国外医学: 肿瘤学分册 31 38
Ye X, Fei X B 2004 Foreign Med. Sci. Cancer Section 31 38
[2] 李发琪, 王智彪, 杜永洪, 许贵安, 文爽, 白晋, 伍烽, 王芷龙 2003 中国生物医学工程学报 22 321
Google Scholar
Li F Q, Wang Z B, Du Y H, Xu G A, Wen S, Bai J, Wu F, Wang Z L 2003 Chin. Biological Eng. 22 321
Google Scholar
[3] 祝宝让, 刁立岩, 李静, 刘滢, 范燕娜, 杨武威 2019 中国超声医学杂志 35 817
Google Scholar
Zhu B R, Diao L Y, Li J, Liu Y, Fan Y N, Yang W W 2019 Chin. J. Ultrasound in Med. 35 817
Google Scholar
[4] 杨竹,曹友德, 胡丽娜, 王智彪 2003 临床超声医学杂志 6 33
Google Scholar
Yang Z, Cao Y D, Hu L N, Wang Z B 2003 J. Ultras. Clin. Med. 6 33
Google Scholar
[5] 秦修培, 耿德路, 洪振宇, 魏炳波 2017 66 124301
Google Scholar
Qin X P, Gen D L, Hong Z Y, Wei B B 2017 Acta Phys. Sin. 66 124301
Google Scholar
[6] Tait A, Glynne-Jones P, Hill A R, Smart D E, Blume C, Hammarstrom B, Fisher A L, Grossel M C, Swindle E J, Hill M, Davies D E 2019 Sci. Rep. 9 9789
Google Scholar
[7] Morris R H, Dey E R, Axford D, Newton M L, Beale J H, Docker P T 2019 Sci. Rep. 9 12431
Google Scholar
[8] 陈伟中 2014 声空化物理 (北京: 科学出版社) 第371−421页
Chen W Z 2014 Acoustic Cavitation Physics (Beijing: Science Press) pp371−421 (in Chinese)
[9] Burns P N, Simpson D H, Averkiou A 2000 Ultrasound Med. Biol. 26 19
Google Scholar
[10] Tranquart F, Greniek N, Eder V 1999 Ultrasound Med. Biol. 25 889
Google Scholar
[11] Gan W S 2012 Appl. Acoust. 73 1209
Google Scholar
[12] 吴培荣, 李颂文 2010 声学技术 29 41
Wu P R, Li S W 2010 Tech. Acoust. 29 41
[13] Enflo B O, Hedberg C M 2004 Theory of Nonlinear Acoustics in Fluids (New York: Kluwer Academic Publishers) pp53−112
[14] Rosing T D 2007 Springer Handbook of Acoustics (New York: Springer Science Business Media) p260
[15] Beyer R T 1969 Physical Ultrasonics (New York: Academic Press) pp202—240
[16] Michelle G, Bengt F, Tobin A, Driscoll 2000 SIAM J. Numer. Anal. 38 718
Google Scholar
[17] Campos-Pozuelo C, Dubus B, Gallego-Juráez J A 1999 J. Acoust. Soc. Am. 106 91
Google Scholar
[18] 钱祖文 2009 非线性声学 (北京: 科学出版社) 第57−72页
Qian Z W 2009 Nonlinear Acoustics (Beijing: Science Press) pp57−72 (in Chinese)
[19] Blackstock D T 1966 J. Acoust. Soc. Am. 39 1019
[20] 张世功, 吴先梅, 张碧星, 安志武 2016 65 104301
Google Scholar
Zhang S G, Wu X M, Zhang B X, An Z W 2016 Acta Phys. Sin. 65 104301
Google Scholar
[21] 吴先梅, 吕文瀚, 陈家熠 2017 声学技术 36 57
Wu X M, Lv W H, Zhang J Y 2017 Tech. Acoust. 36 57
[22] Qian Z W 2014 Chin. Phys. B. 23 064301
Google Scholar
[23] 钱祖文 2009 非线性声学 (北京: 科学出版社) 第19−22页
Qian Z W 2009 Nonlinear Acoustics (Beijing: Science Press) pp19−22 (in Chinese)
[24] Kim J Y, Laurence J J, Qu J M 2006 J. Acoust. Soc. Am. 120 1266
-
图 1 能量守恒的破坏程度、二次谐波的相对能流和三次谐波的相对能流随入射波能流的变化
Figure 1. Damage degree of energy conservation, the relative energy flow of the second harmonic, and the relative energy flow of the third harmonic with incident wave energy flow.
图 2 各阶谐波的相对能流随入射波能流的变化
Figure 2. Relation between relative energy of each order of harmonics and incident wave energy.
图 3 入射波能流不同时二阶谐波的相对能流随迭代次数的变化
Figure 3. Relative energy flow of the second harmonic varies with the number of iterations under different incident wave energy flow.
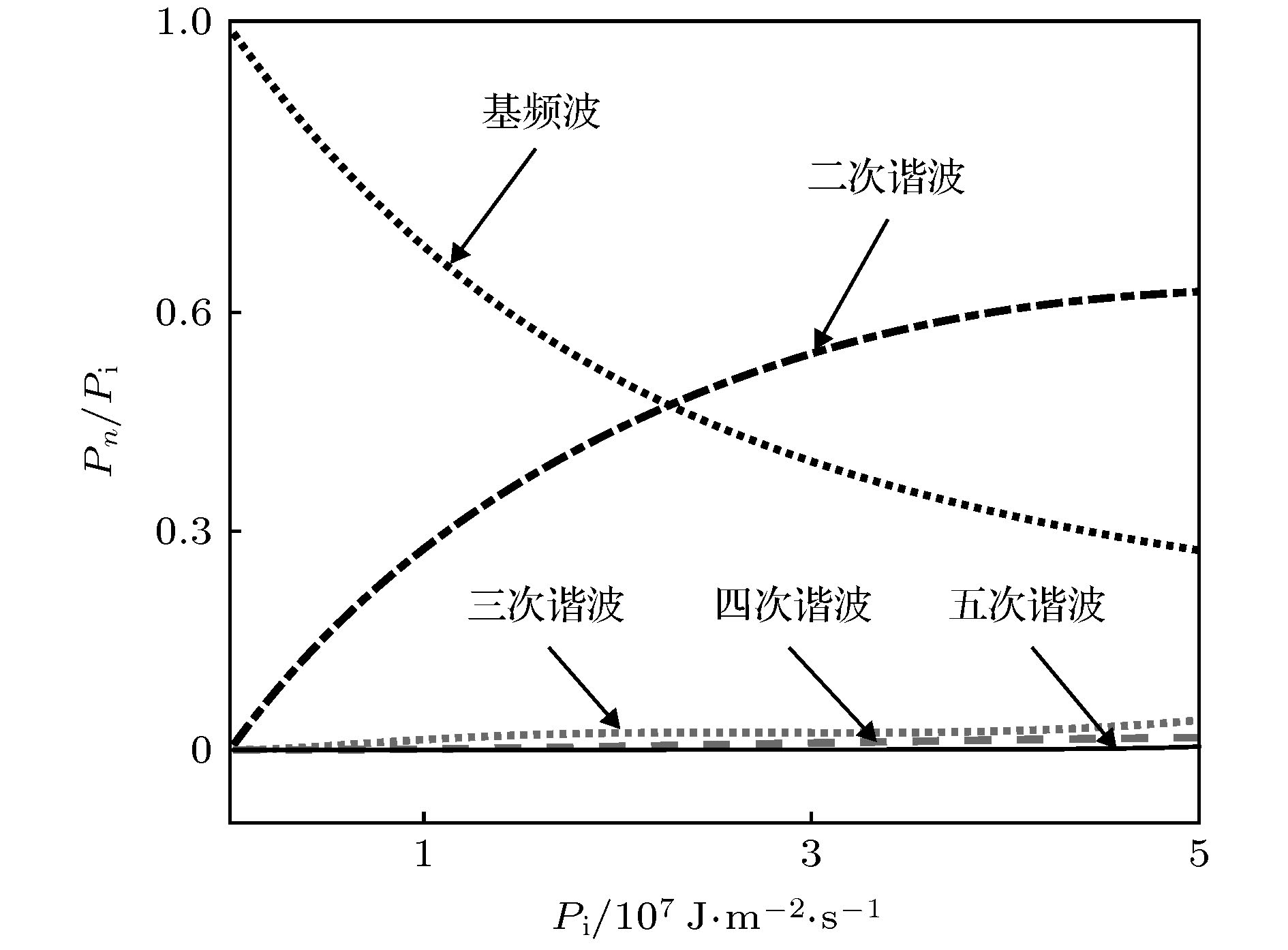
图 4 黏度不同的情况下, 各阶谐波的能流随入射波能流的变化(图中曲线的黏度分别是
$1 \times {10^{ - 6}}$ ,$6 \times {10^{ - 1}}$ 和$10 \times {10^{ - 1}}$ Pa/s, 箭头表示黏度减小的方向)Figure 4. Relation of relative energy flow of each order of harmonics with incident wave energy flow under different viscosity. Viscosites for different curves are
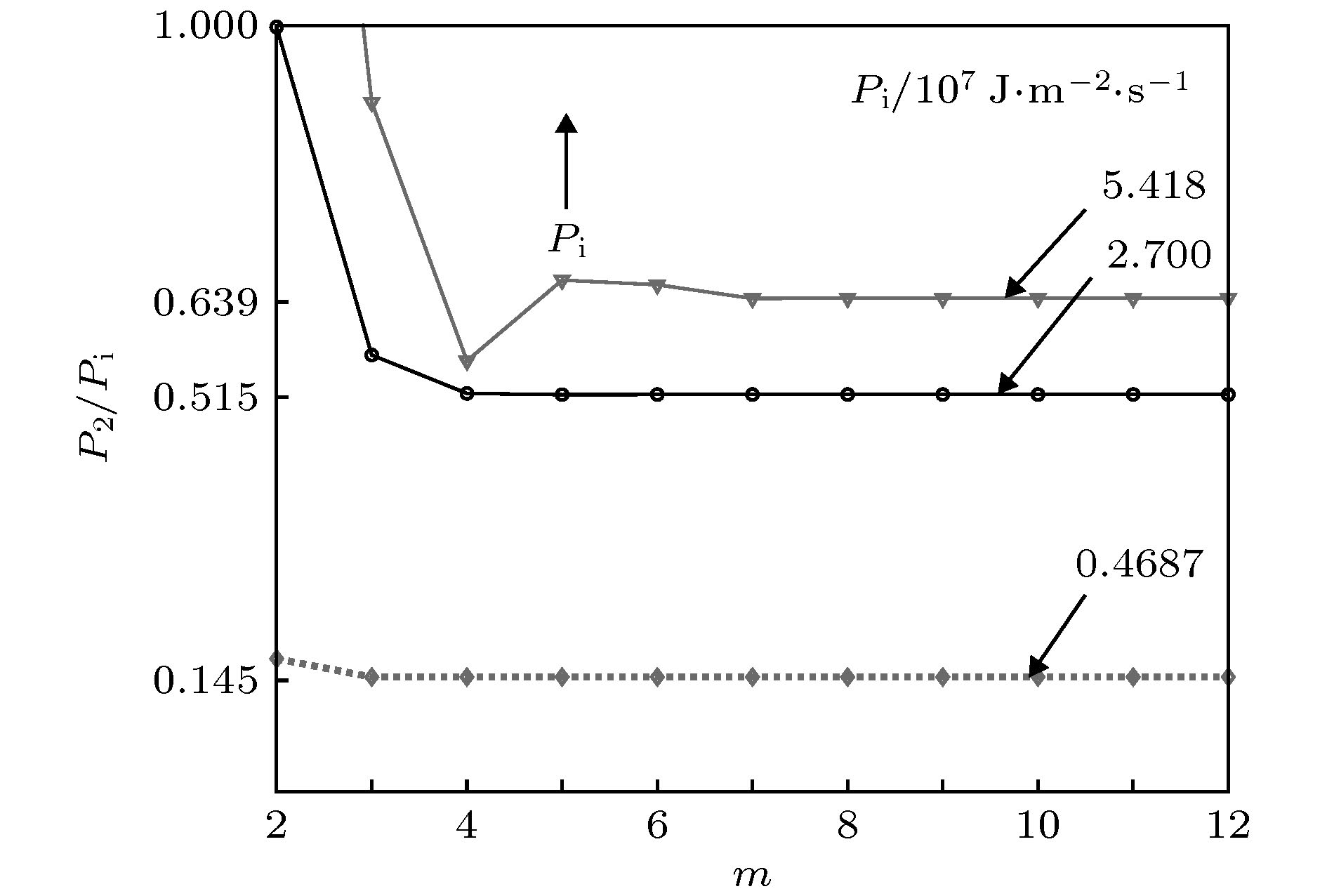
$1 \times {10^{ - 6}}$ ,$6 \times {10^{ - 1}}$ ,$10 \times {10^{ - 1}}$ Pa/s, respectively. Arrows indicate the direction of decreasing viscosity.
图 5 黏度不同的情况下, 各阶谐波的相对能流随角频率的变化(图中曲线的黏度分别是
$1 \times {10^{ - 6}}$ 和$1 \times {10^{ - 1}}$ Pa/s, 箭头表示黏度减小的方向)Figure 5. Relative energy flow varies with angular frequency under different visco-sity. Viscosites for different curves are
$1 \times {10^{ - 6}}$ and$1 \times {10^{ - 1}}$ Pa/s, respectively. Arrows indicate the direction of decreasing viscosity. -
[1] 叶欣, 费兴波 2004 国外医学: 肿瘤学分册 31 38
Ye X, Fei X B 2004 Foreign Med. Sci. Cancer Section 31 38
[2] 李发琪, 王智彪, 杜永洪, 许贵安, 文爽, 白晋, 伍烽, 王芷龙 2003 中国生物医学工程学报 22 321
Google Scholar
Li F Q, Wang Z B, Du Y H, Xu G A, Wen S, Bai J, Wu F, Wang Z L 2003 Chin. Biological Eng. 22 321
Google Scholar
[3] 祝宝让, 刁立岩, 李静, 刘滢, 范燕娜, 杨武威 2019 中国超声医学杂志 35 817
Google Scholar
Zhu B R, Diao L Y, Li J, Liu Y, Fan Y N, Yang W W 2019 Chin. J. Ultrasound in Med. 35 817
Google Scholar
[4] 杨竹,曹友德, 胡丽娜, 王智彪 2003 临床超声医学杂志 6 33
Google Scholar
Yang Z, Cao Y D, Hu L N, Wang Z B 2003 J. Ultras. Clin. Med. 6 33
Google Scholar
[5] 秦修培, 耿德路, 洪振宇, 魏炳波 2017 66 124301
Google Scholar
Qin X P, Gen D L, Hong Z Y, Wei B B 2017 Acta Phys. Sin. 66 124301
Google Scholar
[6] Tait A, Glynne-Jones P, Hill A R, Smart D E, Blume C, Hammarstrom B, Fisher A L, Grossel M C, Swindle E J, Hill M, Davies D E 2019 Sci. Rep. 9 9789
Google Scholar
[7] Morris R H, Dey E R, Axford D, Newton M L, Beale J H, Docker P T 2019 Sci. Rep. 9 12431
Google Scholar
[8] 陈伟中 2014 声空化物理 (北京: 科学出版社) 第371−421页
Chen W Z 2014 Acoustic Cavitation Physics (Beijing: Science Press) pp371−421 (in Chinese)
[9] Burns P N, Simpson D H, Averkiou A 2000 Ultrasound Med. Biol. 26 19
Google Scholar
[10] Tranquart F, Greniek N, Eder V 1999 Ultrasound Med. Biol. 25 889
Google Scholar
[11] Gan W S 2012 Appl. Acoust. 73 1209
Google Scholar
[12] 吴培荣, 李颂文 2010 声学技术 29 41
Wu P R, Li S W 2010 Tech. Acoust. 29 41
[13] Enflo B O, Hedberg C M 2004 Theory of Nonlinear Acoustics in Fluids (New York: Kluwer Academic Publishers) pp53−112
[14] Rosing T D 2007 Springer Handbook of Acoustics (New York: Springer Science Business Media) p260
[15] Beyer R T 1969 Physical Ultrasonics (New York: Academic Press) pp202—240
[16] Michelle G, Bengt F, Tobin A, Driscoll 2000 SIAM J. Numer. Anal. 38 718
Google Scholar
[17] Campos-Pozuelo C, Dubus B, Gallego-Juráez J A 1999 J. Acoust. Soc. Am. 106 91
Google Scholar
[18] 钱祖文 2009 非线性声学 (北京: 科学出版社) 第57−72页
Qian Z W 2009 Nonlinear Acoustics (Beijing: Science Press) pp57−72 (in Chinese)
[19] Blackstock D T 1966 J. Acoust. Soc. Am. 39 1019
[20] 张世功, 吴先梅, 张碧星, 安志武 2016 65 104301
Google Scholar
Zhang S G, Wu X M, Zhang B X, An Z W 2016 Acta Phys. Sin. 65 104301
Google Scholar
[21] 吴先梅, 吕文瀚, 陈家熠 2017 声学技术 36 57
Wu X M, Lv W H, Zhang J Y 2017 Tech. Acoust. 36 57
[22] Qian Z W 2014 Chin. Phys. B. 23 064301
Google Scholar
[23] 钱祖文 2009 非线性声学 (北京: 科学出版社) 第19−22页
Qian Z W 2009 Nonlinear Acoustics (Beijing: Science Press) pp19−22 (in Chinese)
[24] Kim J Y, Laurence J J, Qu J M 2006 J. Acoust. Soc. Am. 120 1266
DownLoad:
Catalog
Metrics
- Abstract views: 8283
- PDF Downloads: 134
- Cited By: 0
