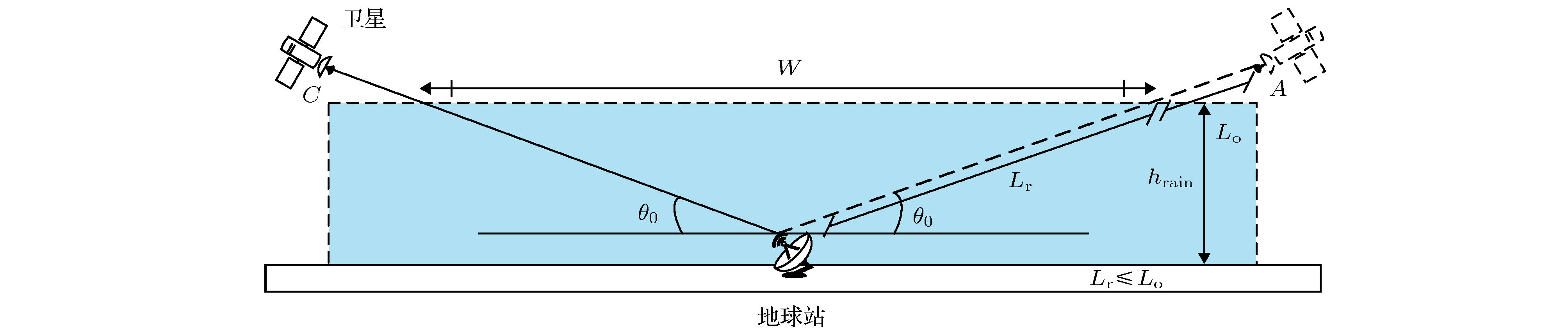
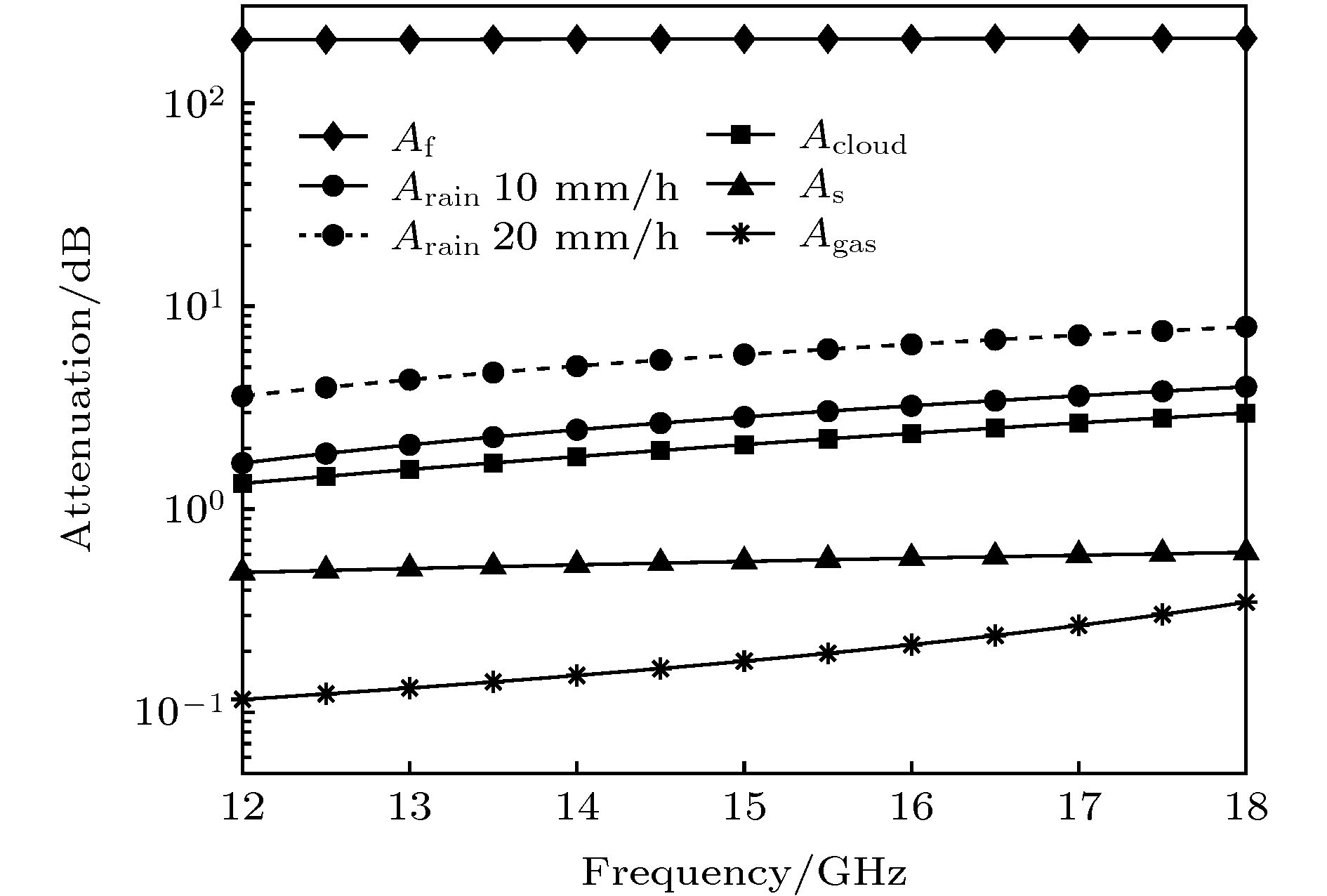
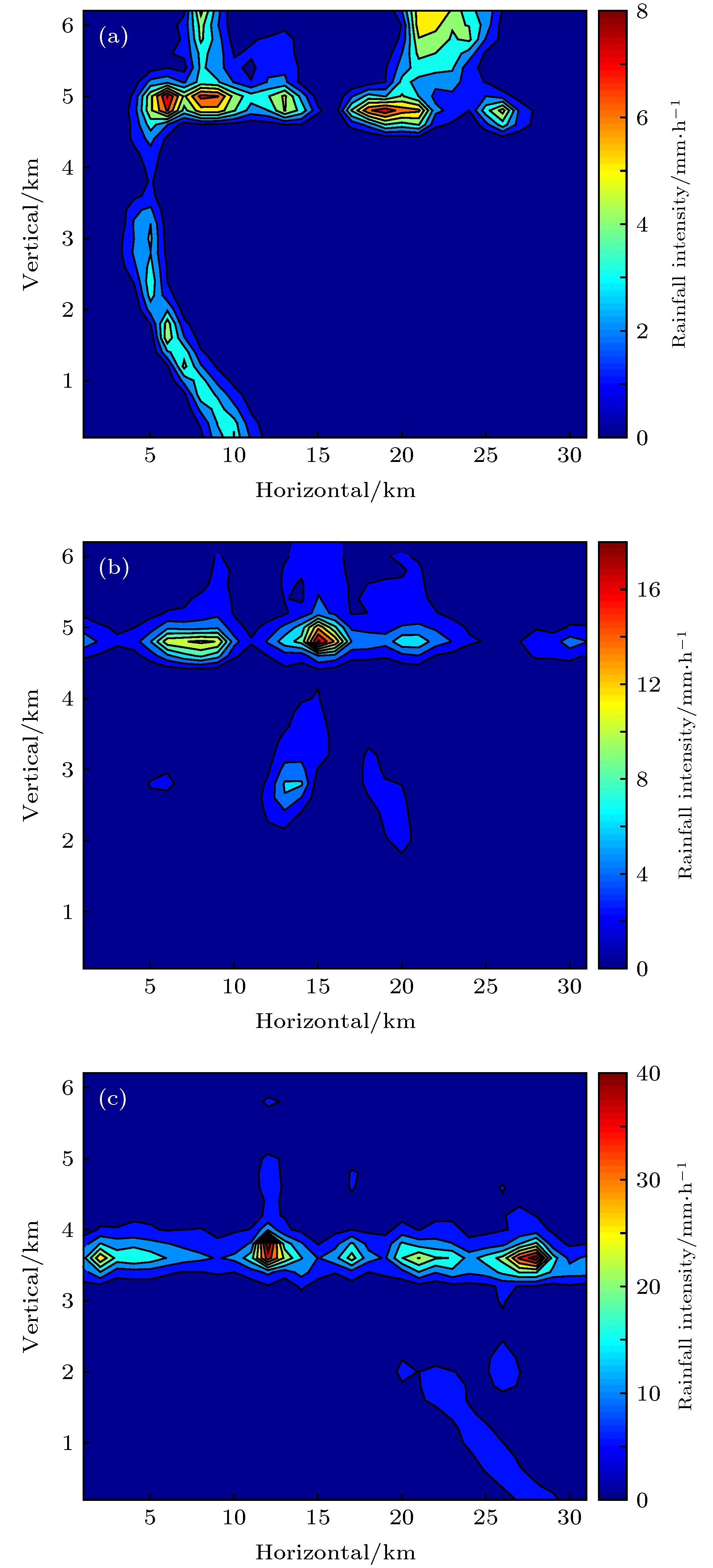
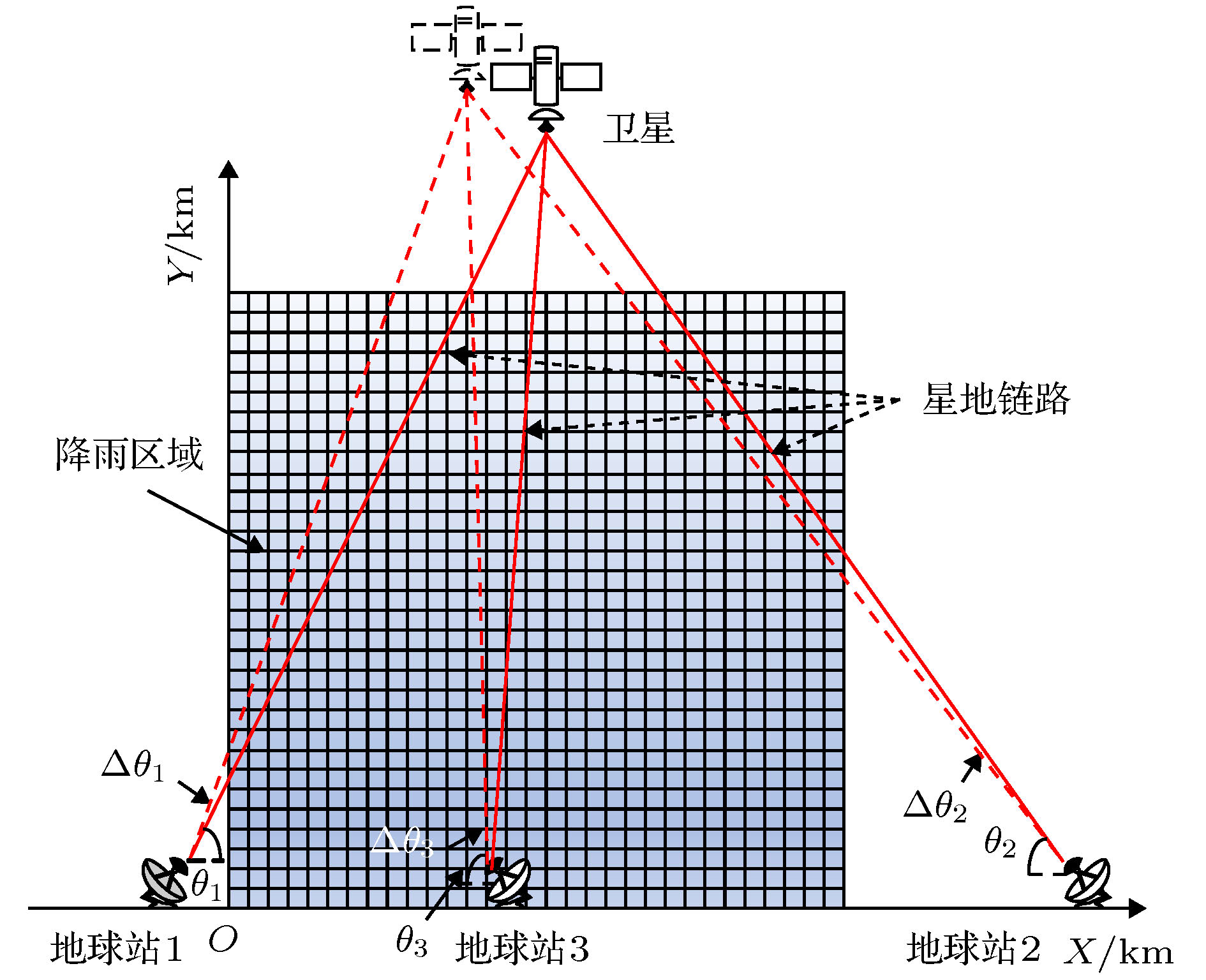
-
The accurate measurement of rain intensity and its distribution in vertical direction can not only help to understand the process of rainfall development, but also play an important role in human life such as agriculture, weather forecasting, water resources management, and natural disaster warning. According to the analysis of the geometric structure of earth-space link and propagation model of electromagnetic wave in atmosphere, in this paper we propose a method to reconstruct two-dimensional(2D) vertical rainfall field by using earth-space links. Firstly, the measured data of micro rain radar (MRR) from Nanjing are used to generate three real vertical rainfall fields which are marked as I, II and III respectively. Secondly, based on the analysis of the earth-space link’s geometry and the effect of signal attenuation from other factors such as scintillation, atmosphere gas and cloud, the vertical rainfall field inversion model is established. According to the power-law relationship between rain intensity and rain attenuation, which is given by International Telecommunication Union (ITU), the simultaneous algebraic reconstruction technique (SART) is used to inverse the vertical rainfall field. Then, one earth station which can receive a 17 GHz signal from satellite is employed to detect the vertical rainfall field. However, the simulation results show that it is difficult for one earth station to achieve the inversion of rainfall field, and that the correlation coefficients between rainfall fields and inversed fields are 0.556, 0.504 and 0.364 respectively. Based on the result, two earth stations are jointly used. In this simulation, the result shows that after 500 iterations the correlation coefficients all increase above 0.98, and the average biases between rainfall field I, II, III and their inversed fields are 0.122, 0.159 and 0.537 mm/h, respectively. Meanwhile, the Euclidean distances decrease to 0.246, 0.235 and 0.812 mm/h, and the relative errors of entropy are both less than 2%. It can be seen from the inversion fields that the vertical distribution of rain rate is close to that of the real field, which suggests that the method proposed in this paper can basically achieve the inversion of vertical rainfall field by using earth-space links. In addition, with the combined detection of three earth stations the accuracy of the inversion results is significantly improved. The correlation coefficients are all close to 1 and the mean deviations are all on the order of 10–12 mm/h, indicating that the 2D vertical rainfall fields are accurately reconstructed. In the near future, the satellite constellation system will be globally deployed, which can promote the applications of our method in areas, such as plateaus, mountains and islands, where there exist no traditional observation data, serving as a supplement to existing precipitation measurements.
-
Keywords:
- earth-space link /
- vertical precipitation field /
- rain attenuation /
- simultaneous algebraic reconstruction technique
[1] Giuli D, Toccafondi A, Gentili G B, Freni A 1991 J. Appl. Meteoro 30 1323
Google Scholar
[2] Messer H, Zinevich A, Alpert P 2006 Science 312 713
Google Scholar
[3] Rahimi A 2003 J Geophys Res 108 8
[4] Rafael F, Roger H 2002 IEEE T Geosci Remote 40 760
Google Scholar
[5] Rahimi A, Holt A, Upton G, Krämer S, Redder A, Verworn H-R 2006 B Am Meteorol Soc 23 395
[6] Fencl M, Rieckermann J, Schleiss M, Stransky D, Bares V 2013 Water Sci Technol 68 1810
Google Scholar
[7] Fencl M, Dohnal M, Rieckermann J, Bareš V 2017 Hydrol Earth Syst Sc 21 617
Google Scholar
[8] 高太长 2013 气象水文装备 24 1
Gao T C 2013 Meteol. Hydrol 24 1
[9] 高太长, 宋堃, 刘西川, 印敏, 刘磊, 姜世太 2015 64 174301
Google Scholar
Gao T C, Song K, Liu X C, Yin M, Liu L, Jiang S T 2015 Acta Phys. Sin. 64 174301
Google Scholar
[10] 姜世太, 高太长, 刘西川, 刘磊, 刘志田 2013 62 154303
Google Scholar
Jiang S T, Gao T C, Liu X C, Liu L, Liu Z T 2013 Acta Phys. Sin. 62 154303
Google Scholar
[11] 宋堃, 高太长, 刘西川, 印敏, 薛杨 2015 64 244301
Google Scholar
Song K, Gao T C, Liu X C, Yin M, Xue Y 2015 Acta Phys. Sin. 64 244301
Google Scholar
[12] 宋堃, 高太长, 刘西川, 印敏, 薛杨 2017 66 154301
Google Scholar
Song K, Gao T C, Liu X C, Yin M, Xue Y 2017 Acta Phys. Sin. 66 154301
Google Scholar
[13] 肖永伟, 孙晨华, 赵伟松 2018 国际太空 11 24
Google Scholar
Xiao Y W, Sun C H, Zhao W S 2018 Space Int. 11 24
Google Scholar
[14] 李黄 2006 遥感学报 10 568
Google Scholar
Li H 2006 Journal of J Remote Sens. 10 568
Google Scholar
[15] Arslan C H, Aydin K, Urbina J, Dyrud L P 2014 IEEE Geoscience and Remote Sensing Symposium, Quebec City, July 13–18, 2014 p4111
[16] François M, Laurent B, Cécile M 2015 J Atmos Ocean Tech 32 1709
Google Scholar
[17] Adirosi E, Facheris L 2018 2 nd URSI Atlantic Radio Science Meeting, Meloneras, 28 May–1 June, 2018 p1
[18] International Telecommunication Union 2017 Rec. ITU-R p618−13
[19] 宗蓉 2013 博士学位论文 (南京: 南京信息工程大学)
[20] International Telecommunication Union 2005 Rec. ITU-R p838-3
[21] 杨富强, 张定华, 黄魁东, 王鹍, 徐哲 2014 63 058701
Google Scholar
Yang F Q, Zhang D H, Huang K D, Wang K, Xu Z 2014 Acta Phys. Sin. 63 058701
Google Scholar
[22] Kaczmarz S 1993 Int J Control 57 1269
Google Scholar
[23] Hansen, Christian P, Hansen S, Maria 2012 J Comput Appl Math 236 2167
Google Scholar
[24] Andersen A H, Kak A C 1984 Ultrasonic Imaging 6 81
Google Scholar
-
图 1 星地链路几何结构
Figure 1. Geometry of earth-space link.
图 2 星地链路探测垂直降雨场
Figure 2. The detection of vertical rainfall field with earth-space link.
图 3 星地链路闪烁衰减、云致衰减、气体衰减、雨强为10 mm/h和20 mm/h的雨致衰减
Figure 3. Scintillation attenuation, cloud attenuation, gas attenuation and rain attenuation with 10 mm/h and 20 mm/h rain rate in earth space link.
图 4 计算星地链路降雨衰减简易图
Figure 4. The sketch of calculation of earth-space link rain attenuation.
图 5 幂律系数随仰角的变化
Figure 5. The change of power law coefficients with elevation.
图 6 反演算法流程图
Figure 6. The flow chart of vertical rainfall field inversion method.
图 7 基于MRR实测资料构建的垂直降雨场 (a) 降雨场I; (b) 降雨场II; (c) 降雨场III
Figure 7. Vertical rainfall field derived from the data of MRR: (a) rainfall field I; (b) rainfall field II; (c) rainfall field III.
图 8 降雨场网格化和星地链路探测示意图
Figure 8. Sketch of grid for rainfall field and detection of earth-space links.
图 9 垂直降雨场反演效果图 (a) 单地球站反演降雨场I; (b) 单地球站反演降雨场II; (c) 单地球站反演降雨场III; (d) 双地球站反演降雨场I; (e) 双地球站反演降雨场II; (f) 双地球站反演降雨场III; (g) 三地球站反演降雨场I; (h) 三地球站反演降雨场II; (i) 三地球站反演降雨场III
Figure 9. Inversed vertical rainfall field: (a) Inversed field I with one earth station; (b) inversed field II with one earth station; (c) inversed field III with one earth station; (d) inversed field I with two earth stations; (e) inversed field II with two earth stations; (f) inversed field III with two earth stations; (g) inversed field I with three earth stations; (h) inversed field II with three earth stations; (i) inversed field III with three earth stations.
图 10 欧氏距离随迭代次数的变化情况 (a) 单地球站反演降雨场I; (b) 单地球站反演降雨场II; (c) 单地球站反演降雨场III; (d) 双地球站反演降雨场I; (e) 双地球站反演降雨场II; (f) 双地球站反演降雨场III;(g) 三地球站反演降雨场I; (h) 三地球站反演降雨场II; (i) 三地球站反演降雨场III
Figure 10. The change of Euclidean distance with iterations: (a) Inversed field I with one earth station; (b) inversed field II with one earth station; (c) inversed field III with one earth station;(d) inversed field I with two earth stations; (e) inversed field II with two earth stations; (f) inversed field III with two earth stations;(g) inversed field I with three earth stations; (h) inversed field II with three earth stations; (i) inversed field III with three earth stations.
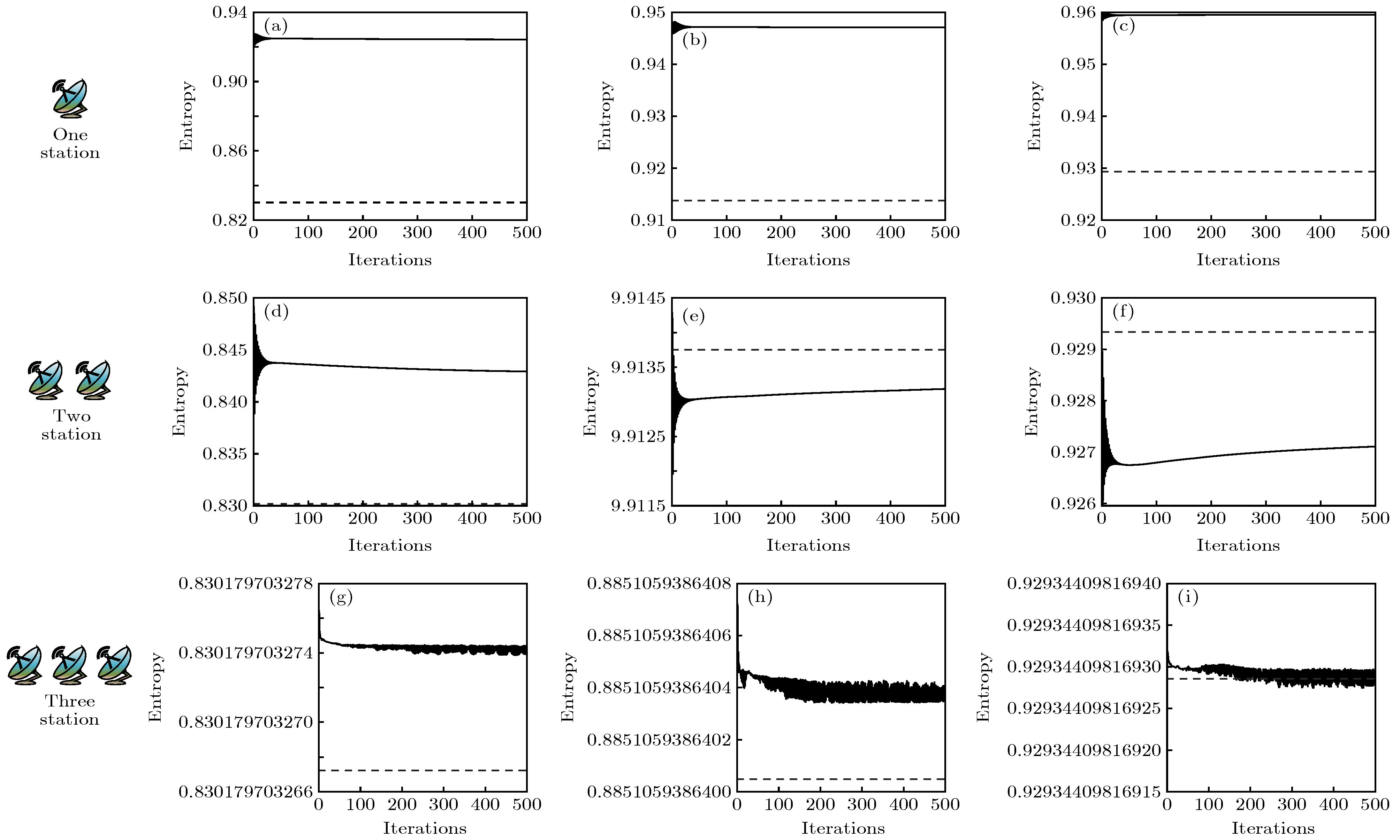
图 11 欧氏距离随迭代次数的变化情况 (a) 单地球站反演降雨场I; (b) 单地球站反演降雨场II; (c) 单地球站反演降雨场III; (d) 双地球站反演降雨场I; (e) 双地球站反演降雨场II; (f) 双地球站反演降雨场III; (g) 三地球站反演降雨场I; (h) 三地球站反演降雨场II; (i) 三地球站反演降雨场III
Figure 11. The change of entropy with iterations: (a) inversed field I with one earth station; (b) inversed field II with one earth station; (c) inversed field III with one earth station; (d) inversed field I with two earth stations; (e) inversed field II with two earth stations; (f) inversed field III with two earth stations; (g) inversed field I with three earth stations; (h) inversed field II with three earth stations; (i) inversed field III with three earth stations.
表 1 星地链路参数
Table 1. Parameters of earth-space link.
地球站 频率/ GHz 极化方式 Δθ/(°) θMin/(°) C/dB 1 17 垂直 0.1 0.091 105 2 17 垂直 0.1 0.065 105 3 17 垂直 0.1 1.00 105 
DownLoad: CSV
-
[1] Giuli D, Toccafondi A, Gentili G B, Freni A 1991 J. Appl. Meteoro 30 1323
Google Scholar
[2] Messer H, Zinevich A, Alpert P 2006 Science 312 713
Google Scholar
[3] Rahimi A 2003 J Geophys Res 108 8
[4] Rafael F, Roger H 2002 IEEE T Geosci Remote 40 760
Google Scholar
[5] Rahimi A, Holt A, Upton G, Krämer S, Redder A, Verworn H-R 2006 B Am Meteorol Soc 23 395
[6] Fencl M, Rieckermann J, Schleiss M, Stransky D, Bares V 2013 Water Sci Technol 68 1810
Google Scholar
[7] Fencl M, Dohnal M, Rieckermann J, Bareš V 2017 Hydrol Earth Syst Sc 21 617
Google Scholar
[8] 高太长 2013 气象水文装备 24 1
Gao T C 2013 Meteol. Hydrol 24 1
[9] 高太长, 宋堃, 刘西川, 印敏, 刘磊, 姜世太 2015 64 174301
Google Scholar
Gao T C, Song K, Liu X C, Yin M, Liu L, Jiang S T 2015 Acta Phys. Sin. 64 174301
Google Scholar
[10] 姜世太, 高太长, 刘西川, 刘磊, 刘志田 2013 62 154303
Google Scholar
Jiang S T, Gao T C, Liu X C, Liu L, Liu Z T 2013 Acta Phys. Sin. 62 154303
Google Scholar
[11] 宋堃, 高太长, 刘西川, 印敏, 薛杨 2015 64 244301
Google Scholar
Song K, Gao T C, Liu X C, Yin M, Xue Y 2015 Acta Phys. Sin. 64 244301
Google Scholar
[12] 宋堃, 高太长, 刘西川, 印敏, 薛杨 2017 66 154301
Google Scholar
Song K, Gao T C, Liu X C, Yin M, Xue Y 2017 Acta Phys. Sin. 66 154301
Google Scholar
[13] 肖永伟, 孙晨华, 赵伟松 2018 国际太空 11 24
Google Scholar
Xiao Y W, Sun C H, Zhao W S 2018 Space Int. 11 24
Google Scholar
[14] 李黄 2006 遥感学报 10 568
Google Scholar
Li H 2006 Journal of J Remote Sens. 10 568
Google Scholar
[15] Arslan C H, Aydin K, Urbina J, Dyrud L P 2014 IEEE Geoscience and Remote Sensing Symposium, Quebec City, July 13–18, 2014 p4111
[16] François M, Laurent B, Cécile M 2015 J Atmos Ocean Tech 32 1709
Google Scholar
[17] Adirosi E, Facheris L 2018 2 nd URSI Atlantic Radio Science Meeting, Meloneras, 28 May–1 June, 2018 p1
[18] International Telecommunication Union 2017 Rec. ITU-R p618−13
[19] 宗蓉 2013 博士学位论文 (南京: 南京信息工程大学)
[20] International Telecommunication Union 2005 Rec. ITU-R p838-3
[21] 杨富强, 张定华, 黄魁东, 王鹍, 徐哲 2014 63 058701
Google Scholar
Yang F Q, Zhang D H, Huang K D, Wang K, Xu Z 2014 Acta Phys. Sin. 63 058701
Google Scholar
[22] Kaczmarz S 1993 Int J Control 57 1269
Google Scholar
[23] Hansen, Christian P, Hansen S, Maria 2012 J Comput Appl Math 236 2167
Google Scholar
[24] Andersen A H, Kak A C 1984 Ultrasonic Imaging 6 81
Google Scholar
DownLoad:
Catalog
Metrics
- Abstract views: 7810
- PDF Downloads: 46
- Cited By: 0
