Time domain hybrid method for coupling analysis of multi-conductor transmission lines on the lossy dielectric layer excited by ambient wave

Ye Zhi-Hong; Zhang Jie; Zhou Jian-Jian; Gou Dan

doi:10.7498/aps.69.20191214

Abstract

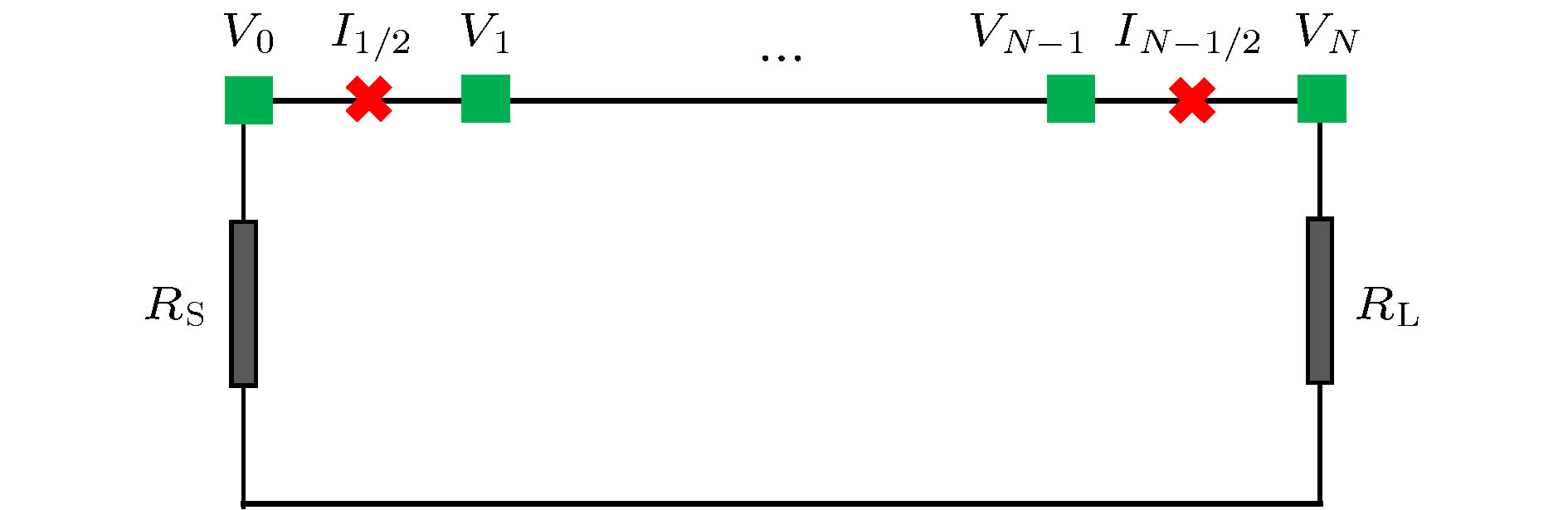
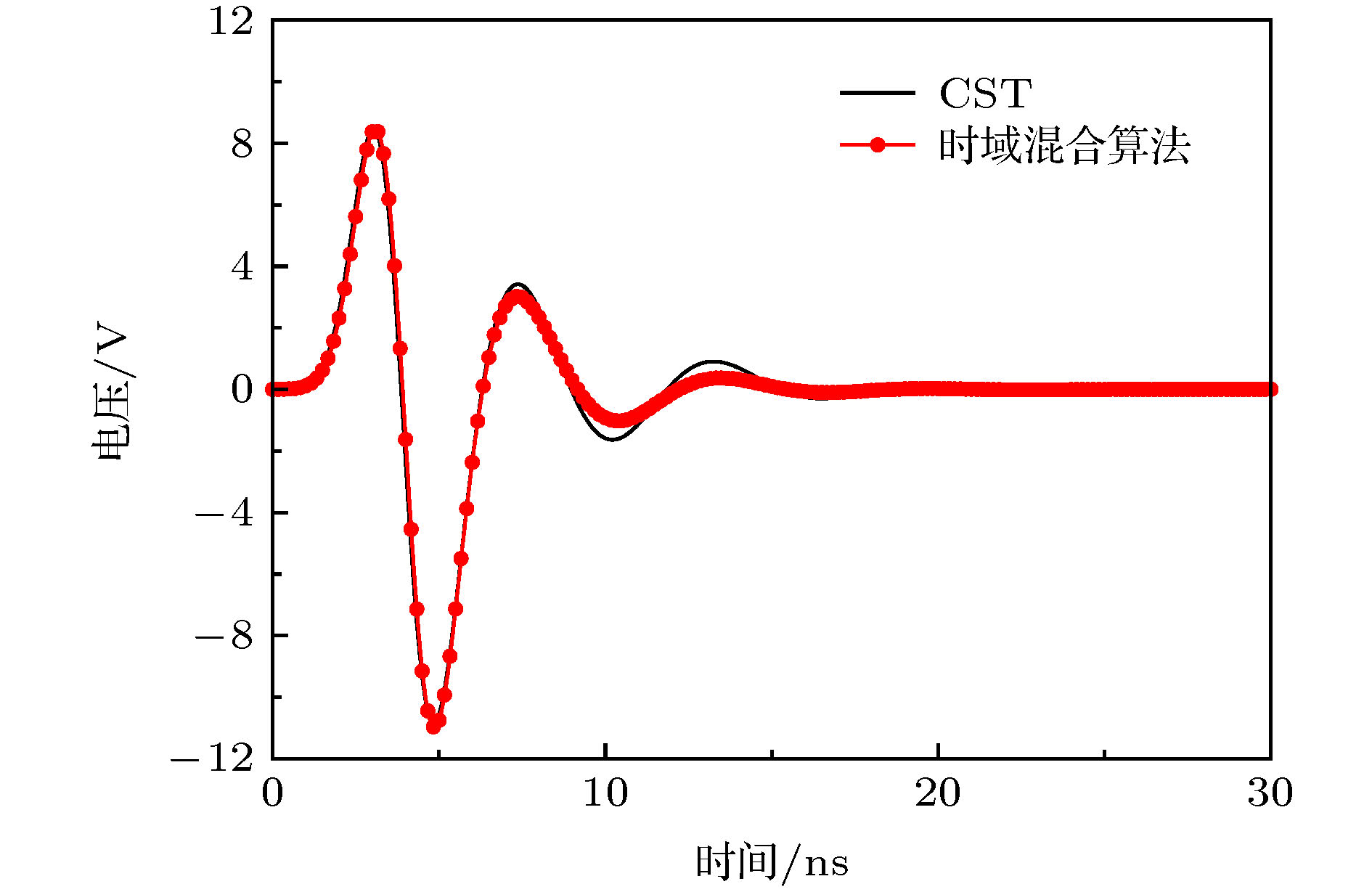
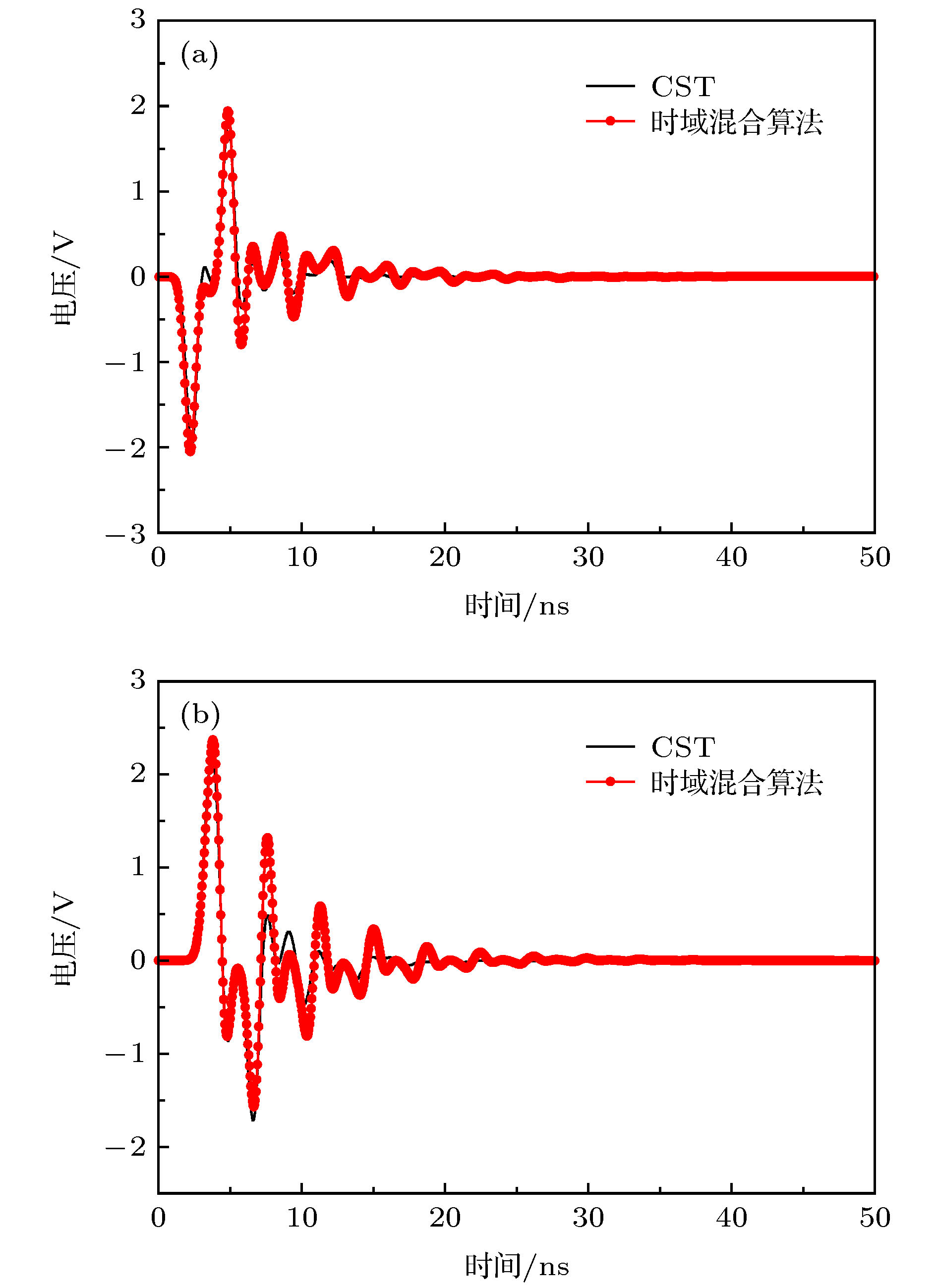
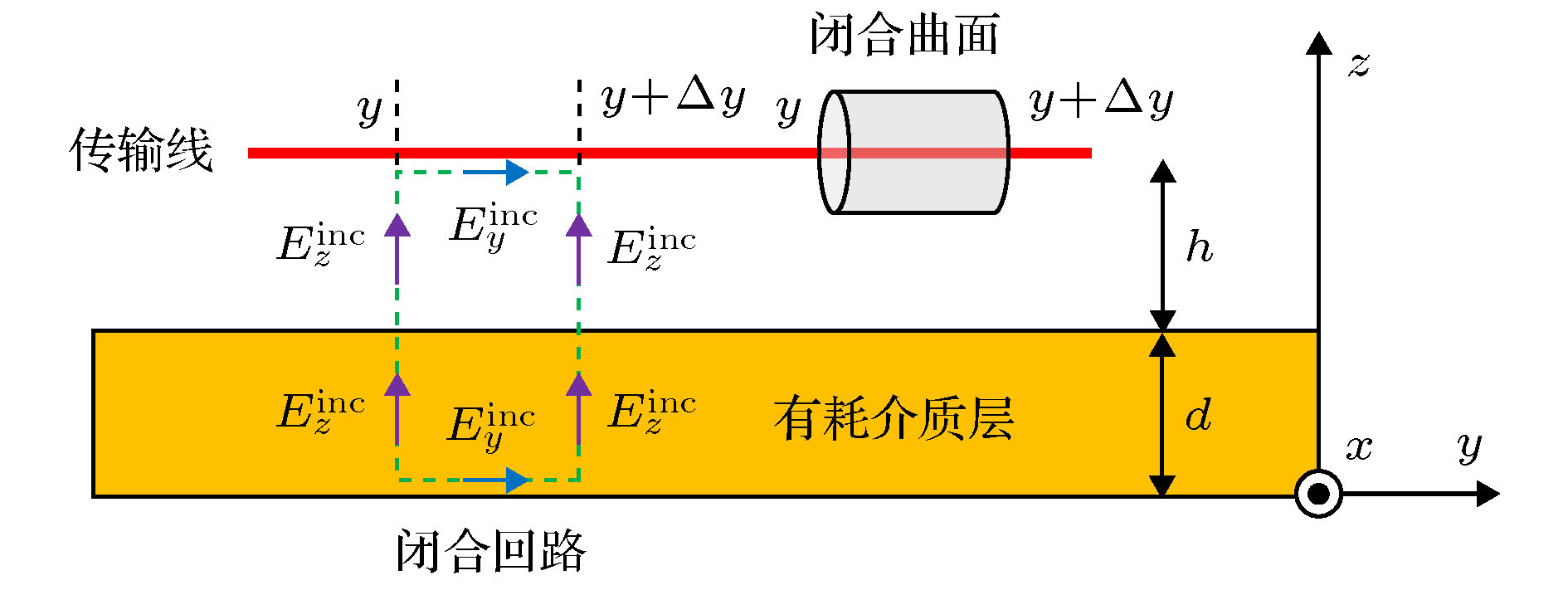
At present, numerical methods applied to the coupling analysis of transmission lines on the lossy dielectric layer excited by ambient wave are still rare in the literature. As a temptation to fill this gap, a novel time domain hybrid method is proposed, in which the modified transmission line (TL) equations, finite-difference time-domain (FDTD) method, and some interpolation schemes are organically combined together. It can overcome the difficulty in building the coupling model of ambient wave to transmission lines on the lossy dielectric layer greatly. In this method, the modified transmission line (TL) equations suitable for the coupling analysis of multi-conductor transmission lines (MTLs) on the lossy dielectric layer are derived from the traditional TL equations firstly. Compared with the traditional TL equations, the electromagnetic fields in the lossy dielectric layer are introduced into the equivalent distribution sources of modified TL equations. Generally, the precision of TL equations is dependent on the accuracy of equivalent distribution sources, which are obtained from the incident electric fields parallel and perpendicular to the MTLs. Therefore, the FDTD method is utilized to model the structure of lossy dielectric layer to calculate the electromagnetic field distribution surrounding the MTLs and in the dielectric layer. Since the heights and distances of MTLs can be arbitrary values, the electric fields parallel and perpendicular to the MTLs cannot be obtained from the electric fields on the edges of FDTD grids directly, which should be computed via some interpolation schemes. Then the modified TL equations are established, which should be solved by the central difference scheme of FDTD method to obtain the voltages and currents on the MTLs and terminal loads. The significant feature of this proposed method is that it can realize the synchronous calculations of electromagnetic field radiation and transient responses on the MTLs. Finally, numerical simulations of single and multiconductor transmission lines on the lossy dielectric layer excited by ambient wave at different incident angles are employed to exhibit the accuracy and efficiency of the proposed method by comparing with the simulation software CST. Because the structures of MTLs do not need to be meshed, the proposed method outperforms the simulation software CST in both memory usage and computation time.

Keywords:

Authors and contacts

School of Communication and Information Engineering, Chongqing University of Posts and Communications, Chongqing 400065, China

Corresponding author: Ye Zhi-Hong, yezh@cqupt.edu.cn

FullText HTML

References

[1]	Holland R, Simpson L 1981 IEEE Trans. Electromagn. Compat. 23 88 Google Scholar
[2]	Berenger J P 2000 IEEE Trans. Electromagn. Compat. 42 257 Google Scholar
[3]	魏兵, 李小勇, 王飞 2009 58 6174 Google Scholar Wei B, Li X Y, Wang F 2009 Acta Phys. Sin. 58 6174 Google Scholar
[4]	He X B, Wei B, Fan K H, Li Y W, Wei X L 2019 Chin. Phys. B 28 074102 Google Scholar
[5]	Agrawal A K, Harold J P, Shyam H G 1980 IEEE Trans. Electromagn. Compat. 22 119 Google Scholar
[6]	王庆国, 周星, 李许东 2012 高电压技术 38 2205 Google Scholar Wang Q G, Zhou X, Li X 2012 High Voltage Eng. 38 2205 Google Scholar
[7]	Xu Q X, Xie Y Z 2015 7th Asia-Pacific Conference on Environmental Electromagnetics, Hangzhou, China, November 4−7, 2015 p411
[8]	Du J K, Hwang S M, Ahn J W, Yook J G 2013 IEEE Trans. Microw. Theory Tech. 61 3514 Google Scholar
[9]	罗静雯, 杜平安, 任丹, 聂宝林 2015 64 010701 Google Scholar Luo J W, Du P A, Ren D, Nie B L 2015 Acta Phys. Sin. 64 010701 Google Scholar
[10]	阚勇, 闫丽萍, 赵翔, 周海京, 刘强, 黄卡玛 2016 65 030702 Google Scholar Kan Y, Yan L P, Zhao X, Zhou H J, Liu Q, Huang K M 2016 Acta Phys. Sin. 65 030702 Google Scholar
[11]	Ni G Y, Yan L, Yuan N C 2008 Chin. Phys. B 17 3629 Google Scholar
[12]	Paul C R 1994 IEEE Trans. Electromagn. Compat. 36 342 Google Scholar
[13]	Erdin I, Dounavis A, Achar R 2001 IEEE Trans. Electromagn. Compat. 43 485 Google Scholar
[14]	Xie H Y, Wang J G, Fan R Y, Liu Y N 2009 IEEE Trans. Electromagn. Compat. 51 811 Google Scholar
[15]	Xie H Y, Wang J G, Fan R Y, Liu Y N 2010 IEEE Trans. Electromagn. Compat. 52 215 Google Scholar
[16]	Xie H Y, Wang J G, Li Y, Xia H F 2014 IEEE Trans. Electromagn. Compat. 56 1623 Google Scholar
[17]	Xie H Y, Li Y, Qiao H L, Wang J G 2016 IEEE Trans. Electromagn. Compat. 58 581 Google Scholar
[18]	Ye Z H, Xiong X Z, Liao C, Li Y 2015 Prog. Electromagn. Res. M 42 85 Google Scholar
[19]	Ye Z H, Liao C, Xiong X Z, Zhang M 2016 IEEE Trans. Electromagn. Compat. 58 964 Google Scholar
[20]	Ye Z H, Liao C, Xiong X Z, Zhang M 2017 IEEE Trans. Electromagn. Compat. 59 1211 Google Scholar
[21]	赵晓辉, 蔡理, 张鹏 2013 62 130506 Google Scholar Zhao X H, Cai L, Zhang P 2013 Acta Phys. Sin. 62 130506 Google Scholar
[22]	吴振军, 王丽芳, 廖承林 2009 58 6146 Google Scholar Wu Z J, Wang L F, Liao C L 2009 Acta Phys. Sin. 58 6146 Google Scholar
[23]	Tesche F M, Ianoz M V, Karlsson T 1997 EMC Analysis Methods and Computational Models (New York: Wiley) p451
[24]	Chen J, Wang J G 2007 IEEE Trans. Electromagn. Compat. 49 354 Google Scholar
[25]	Chen J, Wang J G 2013 IEEE Trans. Electromagn. Compat. 55 1239 Google Scholar

Cited By

图 1 闭合回路和闭合曲面的选取

Figure 1. Selections of closed loop and surface.

DownLoad: Full-Size Img PowerPoint

图 2 多导体传输线的横截面几何结构

Figure 2. Cross section geometry of multi-conductor transmission lines.

DownLoad: Full-Size Img PowerPoint

图 3 多导线沿线和垂直电场分量的插值示意图

Figure 3. Interpolation schemes of the electric fields along and perpendicular to the multi-conductor transmission lines.

DownLoad: Full-Size Img PowerPoint

图 4 传输线的FDTD网格划分

Figure 4. FDTD grid division of transmission lines.

DownLoad: Full-Size Img PowerPoint

图 5 有耗介质层上单导线的电磁耦合模型

Figure 5. Coupling model of single transmission line on the lossy dielectric layer.

DownLoad: Full-Size Img PowerPoint

图 6 负载R₂上的电压响应

Figure 6. Voltages on the load R₂ computed by the two methods

DownLoad: Full-Size Img PowerPoint

图 7 有耗介质层上多导体传输线的电磁耦合模型

Figure 7. Coupling model of multi-conductor transmission lines on the lossy dielectric layer.

DownLoad: Full-Size Img PowerPoint

图 8 入射波垂直照射下的多导线端接负载的电压响应 (a)负载R₁上的电压; (b)负载R₇上的电压

Figure 8. Voltages on the terminal loads of multi-conductor transmission lines under the condition of ambient wave perpendicular to the multi-conductor transmission lines: (a) Voltages on R₁; (b) voltages on R₇.

DownLoad: Full-Size Img PowerPoint

图 9 入射波斜照射下的多导线端接负载的电压响应　(a)负载R₁上的电压; (b)负载R₇上的电压

Figure 9. Voltages on the terminal loads of multi-conductor transmission lines under the condition of ambient wave oblique to the multi-conductor transmission lines: (a) Voltages on R₁; (b) voltages on R₇.

DownLoad: Full-Size Img PowerPoint

表 1 两种方法计算算例1时所需内存和时间对比

Table 1. Memories and computation time needed by the two methods for the first example.

方法内存/MB 计算时间/min

CST 63 19
时域混合算法 34 10

DownLoad: CSV

表 2 两种方法计算算例2时所需内存和时间对比

Table 2. Memories and computation time needed by the two methods for the second example.

方法内存/MB 计算时间/min

CST 217 64
时域混合算法 78 15

DownLoad: CSV

map

[1]	Holland R, Simpson L 1981 IEEE Trans. Electromagn. Compat. 23 88 Google Scholar
[2]	Berenger J P 2000 IEEE Trans. Electromagn. Compat. 42 257 Google Scholar
[3]	魏兵, 李小勇, 王飞 2009 58 6174 Google Scholar Wei B, Li X Y, Wang F 2009 Acta Phys. Sin. 58 6174 Google Scholar
[4]	He X B, Wei B, Fan K H, Li Y W, Wei X L 2019 Chin. Phys. B 28 074102 Google Scholar
[5]	Agrawal A K, Harold J P, Shyam H G 1980 IEEE Trans. Electromagn. Compat. 22 119 Google Scholar
[6]	王庆国, 周星, 李许东 2012 高电压技术 38 2205 Google Scholar Wang Q G, Zhou X, Li X 2012 High Voltage Eng. 38 2205 Google Scholar
[7]	Xu Q X, Xie Y Z 2015 7th Asia-Pacific Conference on Environmental Electromagnetics, Hangzhou, China, November 4−7, 2015 p411
[8]	Du J K, Hwang S M, Ahn J W, Yook J G 2013 IEEE Trans. Microw. Theory Tech. 61 3514 Google Scholar
[9]	罗静雯, 杜平安, 任丹, 聂宝林 2015 64 010701 Google Scholar Luo J W, Du P A, Ren D, Nie B L 2015 Acta Phys. Sin. 64 010701 Google Scholar
[10]	阚勇, 闫丽萍, 赵翔, 周海京, 刘强, 黄卡玛 2016 65 030702 Google Scholar Kan Y, Yan L P, Zhao X, Zhou H J, Liu Q, Huang K M 2016 Acta Phys. Sin. 65 030702 Google Scholar
[11]	Ni G Y, Yan L, Yuan N C 2008 Chin. Phys. B 17 3629 Google Scholar
[12]	Paul C R 1994 IEEE Trans. Electromagn. Compat. 36 342 Google Scholar
[13]	Erdin I, Dounavis A, Achar R 2001 IEEE Trans. Electromagn. Compat. 43 485 Google Scholar
[14]	Xie H Y, Wang J G, Fan R Y, Liu Y N 2009 IEEE Trans. Electromagn. Compat. 51 811 Google Scholar
[15]	Xie H Y, Wang J G, Fan R Y, Liu Y N 2010 IEEE Trans. Electromagn. Compat. 52 215 Google Scholar
[16]	Xie H Y, Wang J G, Li Y, Xia H F 2014 IEEE Trans. Electromagn. Compat. 56 1623 Google Scholar
[17]	Xie H Y, Li Y, Qiao H L, Wang J G 2016 IEEE Trans. Electromagn. Compat. 58 581 Google Scholar
[18]	Ye Z H, Xiong X Z, Liao C, Li Y 2015 Prog. Electromagn. Res. M 42 85 Google Scholar
[19]	Ye Z H, Liao C, Xiong X Z, Zhang M 2016 IEEE Trans. Electromagn. Compat. 58 964 Google Scholar
[20]	Ye Z H, Liao C, Xiong X Z, Zhang M 2017 IEEE Trans. Electromagn. Compat. 59 1211 Google Scholar
[21]	赵晓辉, 蔡理, 张鹏 2013 62 130506 Google Scholar Zhao X H, Cai L, Zhang P 2013 Acta Phys. Sin. 62 130506 Google Scholar
[22]	吴振军, 王丽芳, 廖承林 2009 58 6146 Google Scholar Wu Z J, Wang L F, Liao C L 2009 Acta Phys. Sin. 58 6146 Google Scholar
[23]	Tesche F M, Ianoz M V, Karlsson T 1997 EMC Analysis Methods and Computational Models (New York: Wiley) p451
[24]	Chen J, Wang J G 2007 IEEE Trans. Electromagn. Compat. 49 354 Google Scholar
[25]	Chen J, Wang J G 2013 IEEE Trans. Electromagn. Compat. 55 1239 Google Scholar

Catalog

Vol. 69, Issue 6 - 2020-03-20

Metrics

Abstract views: 7603
PDF Downloads: 106
Cited By: 0

姓名
邮箱
手机号码
标题
留言内容
验证码

Search

Article

留言板