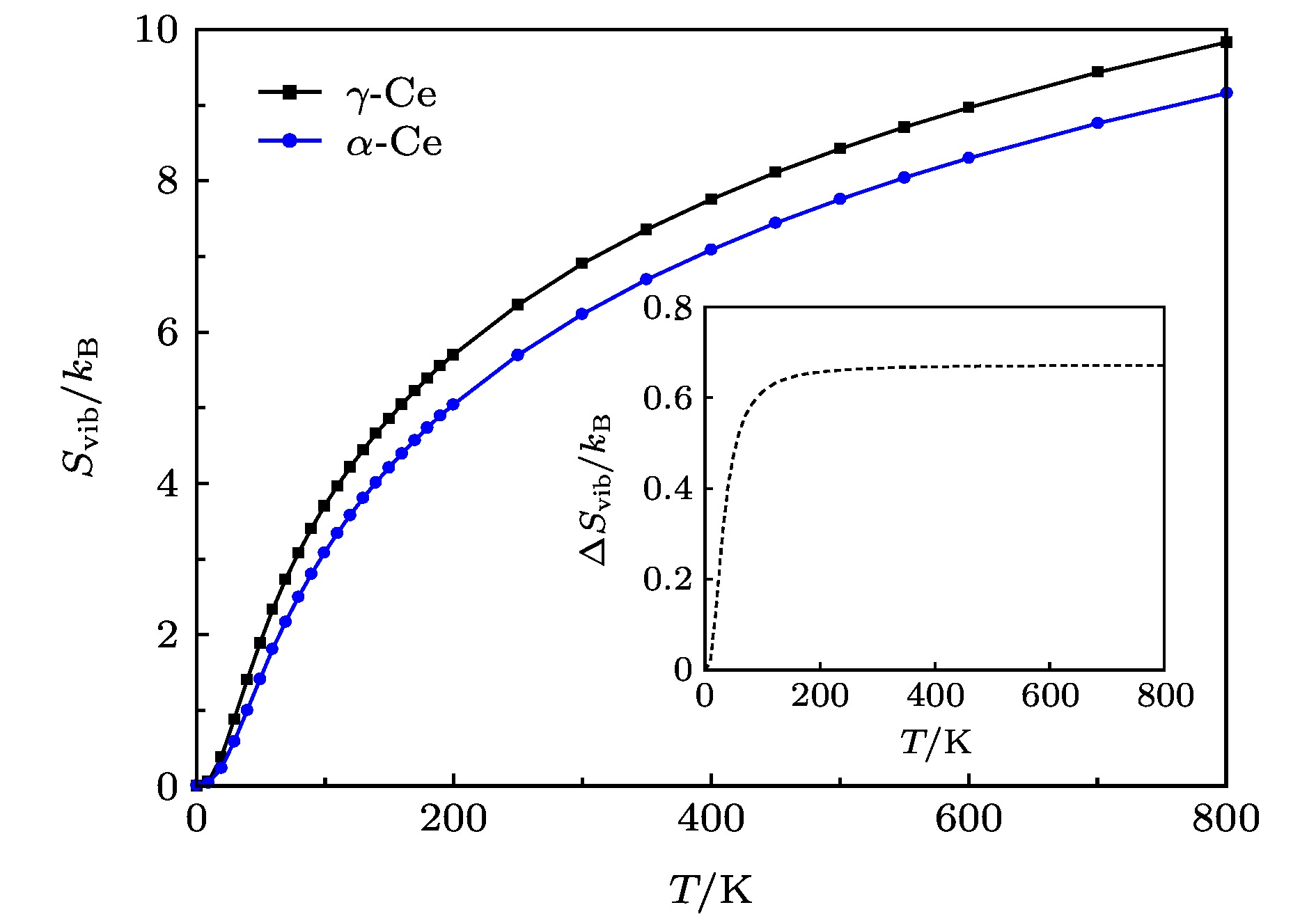
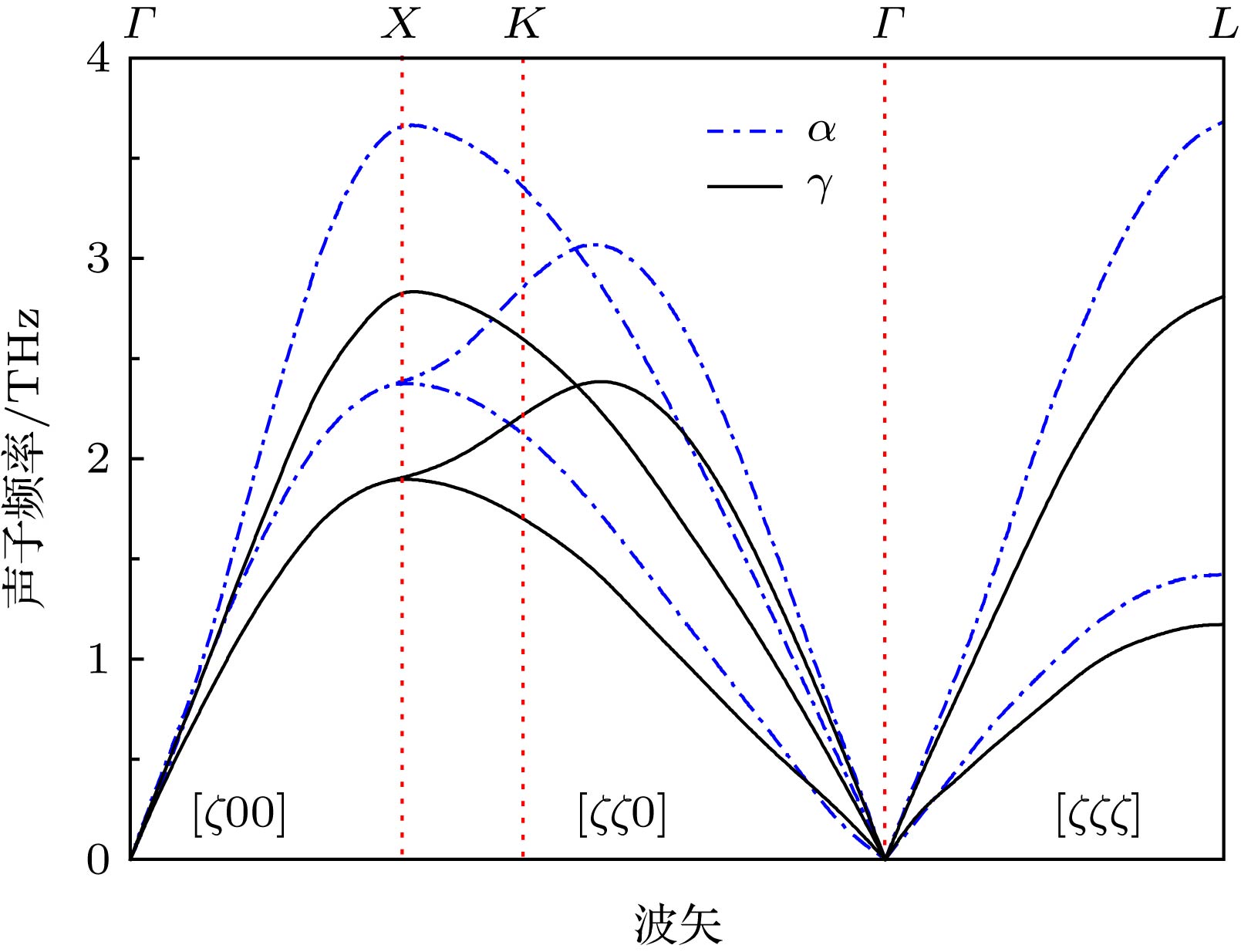
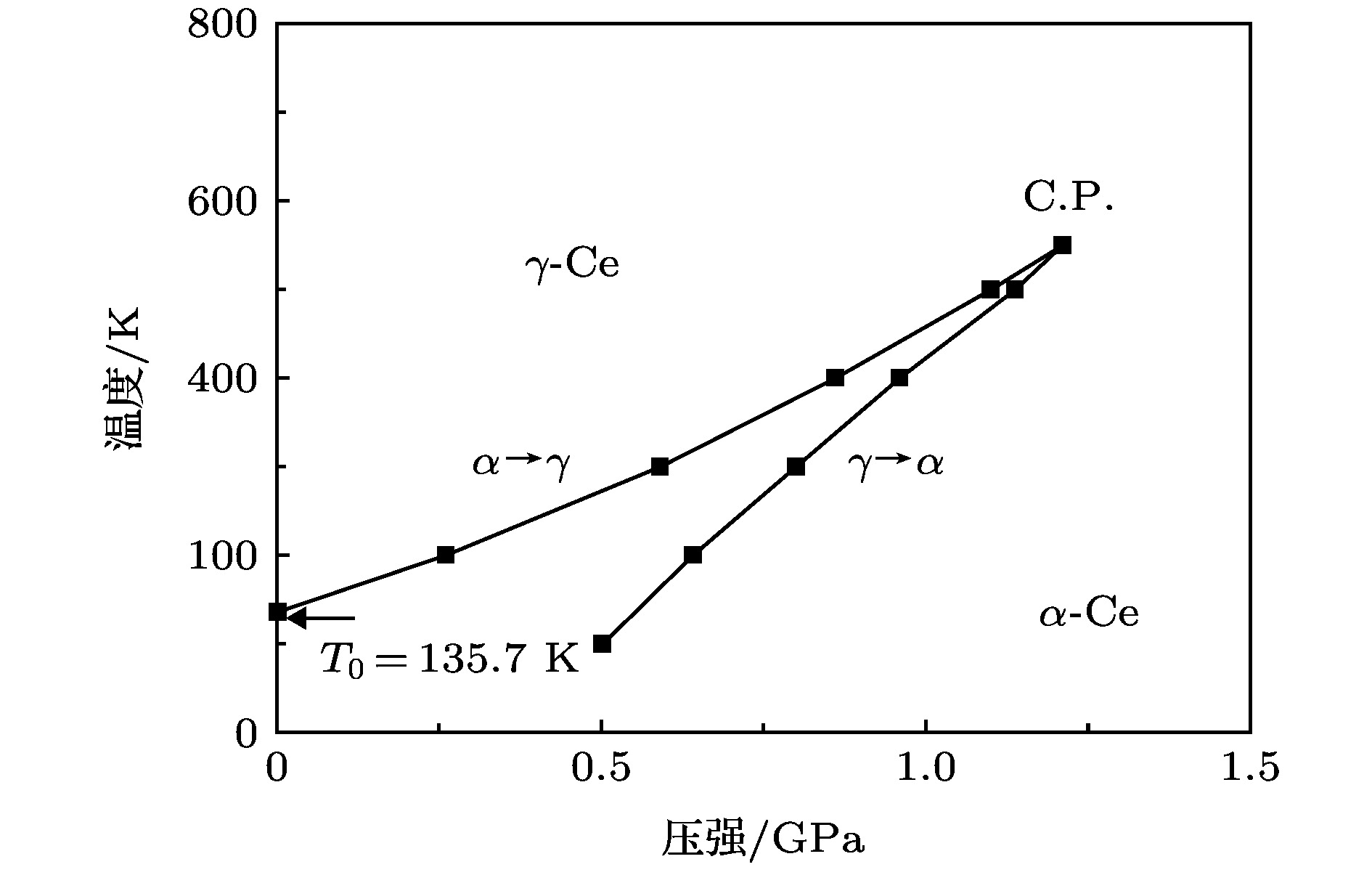
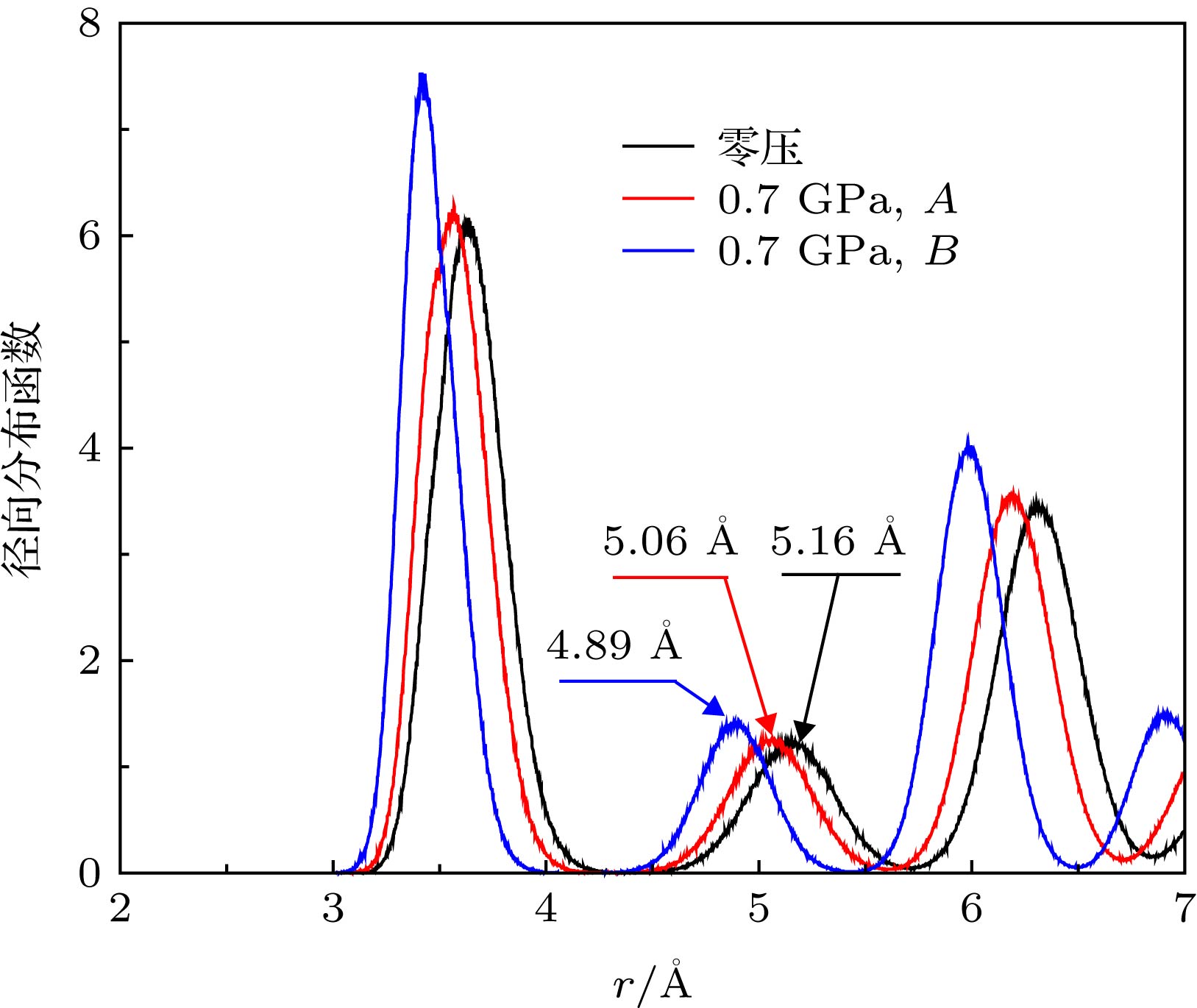
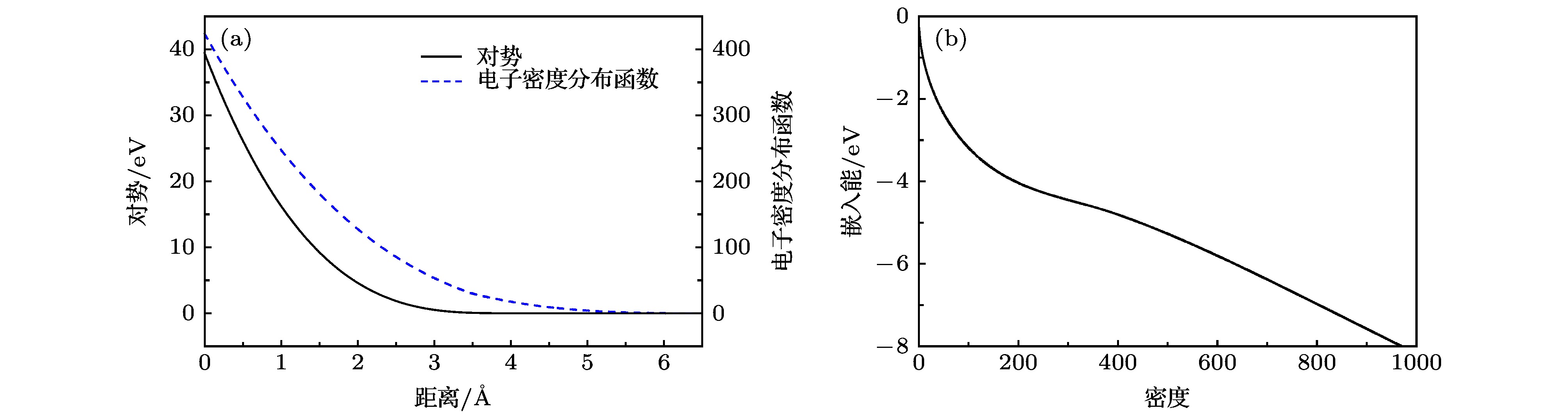
-
Ce is a rare earth element in the periodic table. In the range of low temperature and low pressure, there are two face-centered-cubic (FCC) phases (α-Ce and γ-Ce) and a double-hexagonal-close-packed phase (β-Ce) for metallic Ce. At ambient temperature and about 0.7 GPa pressure, Ce undergoes γ→α phase transition with a volume shrink of 14%–17% discontinuously. In this paper, an embedded-atom method (EAM) potential compatible for α-Ce and γ-Ce was developed. This EAM potential has been employed to study several basic properties of cerium in these two FCC phases, such as equilibrium lattice constants, cohesive energies, and elastic constants. These results showed good accordance with experiments and first principle calculations. The lattice defects have been studied with the formation energy calculations of vacancies, interstitials, surfaces, stacking faults, and twinning defects in α-Ce and γ-Ce lattice. The lattice dynamics of α-Ce and γ-Ce have been analyzed using our EAM potential. The lattice vibrational entropy was calculated and plotted as functions of temperature for each phases. The vibrational entropy change across the α-γ phase transition showed to be ~0.67 kB per atom at ambient temperature. Using molecular dynamics simulation with our EAM potential, several isotherms and radial distribution functions were calculated. These isotherms and radial distribution functions demonstrate a first order phase transition between two FCC structures, corresponding to α-Ce and γ-Ce, with a critical point sets at Tc≈550 K and Pc≈1.21 GPa. Thus the newly developed EAM potential could provide a reasonable description of FCC Ce and its α-γ phase transition within the scale of classical molecular dynamics simulation.
-
Keywords:
- interatomic potential /
- embedded-atom method /
- isomorphic phase transition /
- cerium
[1] 郑海冰 2017 硕士学位论文 (哈尔滨: 哈尔滨工业大学
Zheng H B 2017 M. S. Thesis (Harbin: Harbin Institute of Technoloty) (in Chinese)
[2] 金铭 2018 硕士学位论文 (哈尔滨: 哈尔滨工业大学
Jin M 2018 M. S. Thesis (Harbin: Harbin Institute of Technoloty) (in Chinese)
[3] 林河成 2005 中国有色冶金 3 31
Google Scholar
Lin H C 2005 China Nonferrous Metallurgy 3 31
Google Scholar
[4] Koskenmaki D C, Gschneidner K A 1978 Handbook on the Physics and Chemistry of Rare Earths (Vol. 1) (Amsterdam: Elsevier North-Holland) pp337–377
[5] 潘昊, 胡晓棉, 吴子辉, 戴诚达, 吴强 2012 61 206401
Google Scholar
Pan H, Hu X M, Wu Z H, Dai C D, Wu Q 2012 Acta Phys. Sin. 61 206401
Google Scholar
[6] Wang Y, Jr Hector L G, Zhang H, Shang S L, Chen L Q, Liu Z K 2008 Phys. Rev. B 78 104113
Google Scholar
[7] Decremps F, Belhadi L, Farber D L, Moore K T, Occelli F, Gauthier M, Polian A, Antonangeli D, Aracne-Ruddle C M, Amadon B 2011 Phys. Rev. Lett. 106 065701
[8] Lipp M J, Jackson D, Cynn H, Aracne C, Evans W J, McMahan A K 2008 Phys. Rev. Lett. 101 165703
Google Scholar
[9] Johansson B 1974 Philos. Mag. 30 469
Google Scholar
[10] Allen J W, Martin R M 1982 Phys. Rev. Lett. 49 1106
Google Scholar
[11] Casadei M, Ren X, Rinke P, Rubio A, Scheffler M 2016 Phys. Rev. B 93 075153
Google Scholar
[12] Amadon B, Biermann S, Georges A, Aryasetiawan F 2006 Phys. Rev. Lett. 96 066402
Google Scholar
[13] Jeong I K, Darling T W, Graf M J, Proffen T, Heffner R H, Lee Y, Vogt T, Jorgensen J D 2004 Phys. Rev. Lett. 92 105702
Google Scholar
[14] El'kin V M, Kozlov E A, Kakshina E V, Moreva Y S 2006 Phys. Met. Metall. 101 208
Google Scholar
[15] El'kin V M, Mikhaylov V N, Petrovtsev A V, Cherne F J 2011 Phys. Rev. B 84 094120
Google Scholar
[16] Yelkin V M, Kozlov E A, Kakshina E V, Moreva Y S 2006 Shock Compression of Condensed Matter–2005 Baltimore, Maryland 31 July–5 August, 2005 pp77–80
[17] Casadei M, Ren X, Rinke P, Rubio A, Scheffler M 2012 Phys. Rev. Lett. 109 146402
Google Scholar
[18] Huang L, Chen CA 2007 J. Phys.Condens. Matter 19 476206
Google Scholar
[19] Krisch M, Farber D L, Xu R, Antonangeli D, Aracne C M, Beraud A, Chiang T-C, Zarestky J, Kim D Y, Isaev E I, Ahuja R, Johansson B 2011 Proc. Natl. Acad. Sci. U.S.A. 108 9342
Google Scholar
[20] Singh N, Singh S P 1990 Phys. Rev. B 42 1652
Google Scholar
[21] Hachiya K, Ito Y 1999 J. Phys. Condens. Matter 11 6543
Google Scholar
[22] Sheng H W, Kramer M J, Cadien A, Fujita T, Chen M W 2011 Phys. Rev. B 83 134118
Google Scholar
[23] Fu J, Zhao J 2013 Modell. Simul. Mater. Sci. Eng. 21 065003
Google Scholar
[24] Voter A F, Chen S P 1986 MRS Proceedings 82 175
Google Scholar
[25] Dupont V, Chen S P, Germann T C 2010 EPJ Web of Conferences Paris, France, May 24–28, 2010 p00009
[26] Dupont V, Germann T C 2010 APS March Meeting Portland, Oregon, March 15–19, 2010 W30.00007
[27] Rose J H, Smith J R, Guinea F, Ferrante J 1984 Phys. Rev. B 29 2963
[28] Duff A I, Finnis M W, Maugis P, Thijsse B J, Sluiter M H F 2015 Comput. Phys. Commun. 196 439
Google Scholar
[29] Plimpton S 1995 J. Comput. Phys. 117 1
Google Scholar
[30] Eriksson O, Brooks M S S, Johansson B 1990 Phys. Rev. B 41 7311
Google Scholar
[31] Greiner J D, McMasters O D, Smith J F 1980 Scr. Metall. 14 989
Google Scholar
[32] Staun Olsen J, Gerward L, Dancausse J P, Gering E 1993 Physica B 190 92
Google Scholar
[33] Voronov F F, Goncharova V A, Stal'gorova O V 1979 Soviet Phys. JETP 49 687
[34] Söderlind P, Eriksson O, Wills J M, Boring A M 1993 Phys. Rev. B 48 9306
Google Scholar
[35] Korzhavyi P A, Abrikosov I A, Johansson B, Ruban A V, Skriver H L 1999 Phys. Rev. B 59 11693
Google Scholar
[36] Press W H, Teukolsky S A, Vetterling W T, Flannery B P 2007 Numerical Recipes: The Art of Scientific Computing (3rd Ed.) (New York: Cambridge University Press) pp487–562
[37] Östlin A, Di Marco I, Locht I L M, Lashley J C, Vitos L 2016 Phys. Rev. B 93 094103
Google Scholar
[38] van Swygenhoven H, Derlet P M, Frøseth A G 2004 Nat. Mater. 3 399
Google Scholar
[39] Hai S, Tadmor E B 2003 Acta Mater. 51 117
Google Scholar
[40] Tadmor E, Hai S 2003 J. Mech. Phys. Solids 51 765
Google Scholar
[41] Stassis C, Gould T, McMasters O D, Gschneidner K A, Nicklow R M 1979 Phys. Rev. B 19 5746
Google Scholar
-
图 1 Ce的EAM势 (a)对势函数和电子密度分布函数; (b)嵌入能函数
Figure 1. EAM potential for Ce: (a) The pair function Φ(rij) and the density function f(rij); (b) the embedded function F(ρ).
图 2 由本文EAM势得出的面心立方Ce的冷能曲线
Figure 2. The cold energy of fcc Ce calculated with the newly developed EAM potential.
图 3 面心立方Ce中的广义层错能和广义孪晶能 (a) α-Ce; (b) γ-Ce
Figure 3. Generalized stacking fault energy and generalized twining fault energy curve for (a) α-Ce and (b) γ-Ce.
图 4 面心立方Ce的声子态密度
Figure 4. Phonon density of states for FCC Ce.
图 5 α-Ce和γ-Ce两相的晶格振动熵Svib以及熵差ΔSvib (右下插图)随温度T的变化
Figure 5. The vibrational entropy Svib and its change ΔSvib between two phases (the inset) plotted as functions of temperature.
图 6 面心立方Ce的声子色散谱
Figure 6. Phonon dispersion relations for FCC Ce.
图 7 面心立方Ce的等温线 (a) NPT增压; (b) NPT减压; (c) NVT
Figure 7. Isotherms of FCC Ce: (a) NPT, pressure increased; (b) NPT, pressure decreased; (c) NVT.
图 8 Ce的γ→α和α→γ相变路径
Figure 8. The path of Ce γ→α and α→γ phase transition.
表 1 面心立方Ce的基本性质的EAM计算值与实验和第一性原理结果的比较
Table 1. EAM predicted properties of Ce lattice in comparison with experimental and ab initiodata.
γ-Ce α-Ce 实验 第一性原理 本文EAM 实验 第一性原理 本文EAM a0/Å 5.16[4] 5.22[11] 5.14 4.84[4] 4.90[30] 4.63[11] 4.81 Ecoh/eV 4.32[4] 4.35[11] 4.32 4.3[11] 3.76[11] 4.3255 体弹模量/GPa 18.18[31] 28.3[11] 16.78 35.0[32], 16.94[33] 37.0[34] 37.00 c11 /GPa 26.01[31] 23.06 52.9[34] 59.77 c12 /GPa 14.26[31] 13.64 29.1[34] 25.62 c44 /GPa 17.30[31] 17.64 44.6[34] 49.98 剪切模量/GPa 12.73[31] 12.47 17.26[33] 36.82 
DownLoad: CSV
表 2 γ-Ce and α-Ce中晶体缺陷的形成能
Table 2. Calculated formation energy of lattice defectsin γ-Ce and α-Ce.
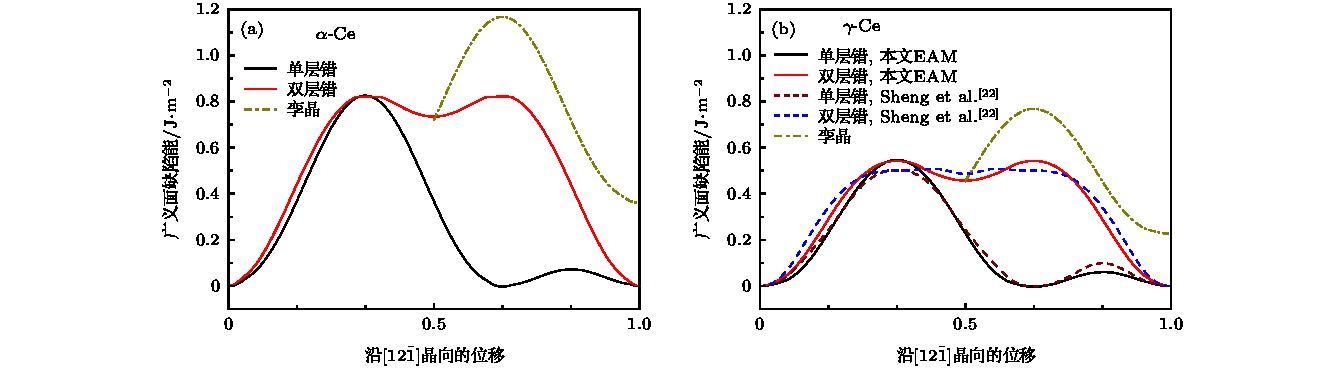
γ-Ce α-Ce 之前的结果 本文EAM 之前的结果 本文EAM Eif/eV 3.3[22] 1.93 2.97 Evf/eV 0.75[22], 2.02[23] 0.85 1.15 γ(100)/mJ·m–2 697[22], 2140[23] 391 308 γ(110)/mJ·m–2 797[22], 2220[23] 442 390 γ(111)/mJ·m–2 586[22], 2190[23] 297 195 γssf/mJ·m–2 486[22],58[37], 16[37], –0.2[37] 457 301[37], 311[37], 369[37] 734 γusf/mJ·m–2 501[22] 543 822 γutf/mJ·m–2 12[22] 768 1167
DownLoad: CSV
-
[1] 郑海冰 2017 硕士学位论文 (哈尔滨: 哈尔滨工业大学
Zheng H B 2017 M. S. Thesis (Harbin: Harbin Institute of Technoloty) (in Chinese)
[2] 金铭 2018 硕士学位论文 (哈尔滨: 哈尔滨工业大学
Jin M 2018 M. S. Thesis (Harbin: Harbin Institute of Technoloty) (in Chinese)
[3] 林河成 2005 中国有色冶金 3 31
Google Scholar
Lin H C 2005 China Nonferrous Metallurgy 3 31
Google Scholar
[4] Koskenmaki D C, Gschneidner K A 1978 Handbook on the Physics and Chemistry of Rare Earths (Vol. 1) (Amsterdam: Elsevier North-Holland) pp337–377
[5] 潘昊, 胡晓棉, 吴子辉, 戴诚达, 吴强 2012 61 206401
Google Scholar
Pan H, Hu X M, Wu Z H, Dai C D, Wu Q 2012 Acta Phys. Sin. 61 206401
Google Scholar
[6] Wang Y, Jr Hector L G, Zhang H, Shang S L, Chen L Q, Liu Z K 2008 Phys. Rev. B 78 104113
Google Scholar
[7] Decremps F, Belhadi L, Farber D L, Moore K T, Occelli F, Gauthier M, Polian A, Antonangeli D, Aracne-Ruddle C M, Amadon B 2011 Phys. Rev. Lett. 106 065701
[8] Lipp M J, Jackson D, Cynn H, Aracne C, Evans W J, McMahan A K 2008 Phys. Rev. Lett. 101 165703
Google Scholar
[9] Johansson B 1974 Philos. Mag. 30 469
Google Scholar
[10] Allen J W, Martin R M 1982 Phys. Rev. Lett. 49 1106
Google Scholar
[11] Casadei M, Ren X, Rinke P, Rubio A, Scheffler M 2016 Phys. Rev. B 93 075153
Google Scholar
[12] Amadon B, Biermann S, Georges A, Aryasetiawan F 2006 Phys. Rev. Lett. 96 066402
Google Scholar
[13] Jeong I K, Darling T W, Graf M J, Proffen T, Heffner R H, Lee Y, Vogt T, Jorgensen J D 2004 Phys. Rev. Lett. 92 105702
Google Scholar
[14] El'kin V M, Kozlov E A, Kakshina E V, Moreva Y S 2006 Phys. Met. Metall. 101 208
Google Scholar
[15] El'kin V M, Mikhaylov V N, Petrovtsev A V, Cherne F J 2011 Phys. Rev. B 84 094120
Google Scholar
[16] Yelkin V M, Kozlov E A, Kakshina E V, Moreva Y S 2006 Shock Compression of Condensed Matter–2005 Baltimore, Maryland 31 July–5 August, 2005 pp77–80
[17] Casadei M, Ren X, Rinke P, Rubio A, Scheffler M 2012 Phys. Rev. Lett. 109 146402
Google Scholar
[18] Huang L, Chen CA 2007 J. Phys.Condens. Matter 19 476206
Google Scholar
[19] Krisch M, Farber D L, Xu R, Antonangeli D, Aracne C M, Beraud A, Chiang T-C, Zarestky J, Kim D Y, Isaev E I, Ahuja R, Johansson B 2011 Proc. Natl. Acad. Sci. U.S.A. 108 9342
Google Scholar
[20] Singh N, Singh S P 1990 Phys. Rev. B 42 1652
Google Scholar
[21] Hachiya K, Ito Y 1999 J. Phys. Condens. Matter 11 6543
Google Scholar
[22] Sheng H W, Kramer M J, Cadien A, Fujita T, Chen M W 2011 Phys. Rev. B 83 134118
Google Scholar
[23] Fu J, Zhao J 2013 Modell. Simul. Mater. Sci. Eng. 21 065003
Google Scholar
[24] Voter A F, Chen S P 1986 MRS Proceedings 82 175
Google Scholar
[25] Dupont V, Chen S P, Germann T C 2010 EPJ Web of Conferences Paris, France, May 24–28, 2010 p00009
[26] Dupont V, Germann T C 2010 APS March Meeting Portland, Oregon, March 15–19, 2010 W30.00007
[27] Rose J H, Smith J R, Guinea F, Ferrante J 1984 Phys. Rev. B 29 2963
[28] Duff A I, Finnis M W, Maugis P, Thijsse B J, Sluiter M H F 2015 Comput. Phys. Commun. 196 439
Google Scholar
[29] Plimpton S 1995 J. Comput. Phys. 117 1
Google Scholar
[30] Eriksson O, Brooks M S S, Johansson B 1990 Phys. Rev. B 41 7311
Google Scholar
[31] Greiner J D, McMasters O D, Smith J F 1980 Scr. Metall. 14 989
Google Scholar
[32] Staun Olsen J, Gerward L, Dancausse J P, Gering E 1993 Physica B 190 92
Google Scholar
[33] Voronov F F, Goncharova V A, Stal'gorova O V 1979 Soviet Phys. JETP 49 687
[34] Söderlind P, Eriksson O, Wills J M, Boring A M 1993 Phys. Rev. B 48 9306
Google Scholar
[35] Korzhavyi P A, Abrikosov I A, Johansson B, Ruban A V, Skriver H L 1999 Phys. Rev. B 59 11693
Google Scholar
[36] Press W H, Teukolsky S A, Vetterling W T, Flannery B P 2007 Numerical Recipes: The Art of Scientific Computing (3rd Ed.) (New York: Cambridge University Press) pp487–562
[37] Östlin A, Di Marco I, Locht I L M, Lashley J C, Vitos L 2016 Phys. Rev. B 93 094103
Google Scholar
[38] van Swygenhoven H, Derlet P M, Frøseth A G 2004 Nat. Mater. 3 399
Google Scholar
[39] Hai S, Tadmor E B 2003 Acta Mater. 51 117
Google Scholar
[40] Tadmor E, Hai S 2003 J. Mech. Phys. Solids 51 765
Google Scholar
[41] Stassis C, Gould T, McMasters O D, Gschneidner K A, Nicklow R M 1979 Phys. Rev. B 19 5746
Google Scholar
DownLoad:
Catalog
Metrics
- Abstract views: 11413
- PDF Downloads: 160
- Cited By: 0
