Explanation to negative feedback induced-enhancement of neural electronic activities with phase response curve

Ding Xue-Li; Jia Bing; Li Yu-Ye

doi:10.7498/aps.68.20190197

Abstract

It has been found in many experimental and theoretical studies that autapse regulates the electrical activities of single neurons and the spatiotemporal behaviors of neuronal networks through feedback or coupling currents to achieve physiological functions. In the present paper, the effect of inhibitory self-feedback on spiking patterns near Hopf bifurcation point is studied in the deterministic Morris-Lecar model and the stochastic Morris-Lecar model, and the dynamical mechanism is acquired with the phase response curve (PRC) of spiking to the inhibitory square pulse current stimulation. The inhibitory self-feedback current with a suitable time-delay can induce the spiking frequency to increase, which is different from the traditional viewpoint that the inhibitory stimulations often induce the firing frequency to decrease. For the remained time delays, spiking frequency decreases. Furthermore, the changes of spiking frequency, induced by the inhibitory self-feedback current, can be well explained with the dynamical responses of the spiking pattern of a single neuron without autapse to an inhibitory square pulse current stimulation. For the spiking pattern of a neuron without autapse, when an inhibitory square pulse stimulation current resembling to the inhibitory self-feedback current is applied at some suitable phases after an action potential/spike, the phase of the action potential/spike following the square pulse current advances, which leads the interspike intervals (ISIs) to decrease and firing frequency to increase. For the remained stimulation phases of the inhibitory pulse current, the response phase of the following action potential/spike delays. Therefore, the PRC of the action potential/spike shows the characteristics of type-II excitability corresponding to Hopf bifurcation. The stimulation phase of the inhibitory square pulse current that can induce the spiking frequency of single neurons to increase corresponds to the time delay of inhibitory self-feedback that can enhance firing frequency, which shows that the type-II PRC is the cause that the inhibitory self-feedback can induce the spiking frequency to increase. Finally, when noise is introduced into the ML model with inhibitory self-feedback, the coefficient of variation (CV) of the ISIs is smaller for the longer time delay of the self-feedback or the stronger coupling strength of the autapse, that is, the spike-timing precision is improved for the smaller CV of ISIs. Such a result is consistent with the experimental result that slow inhibitory autapse can enhance spike-timing precision. The results present a novel phenomenon that negative self-feedback can enhance the response of the system and the corresponding nonlinear dynamical mechanism, i.e. the PRC, provide a new method of regulating the neural electrical activities, and are helpful in understanding the potential function of inhibitory autapse.

Keywords:

Authors and contacts

1.
Department of Basic Education, Fuyang Institute of Technology, Fuyang 236031, China
2.
Department of Physiology and Biophysics, School of Life Sciences, Fudan University, Shanghai 200438, China
3.
School of Mathematics and Statistics, Chifeng University, Chifeng 024000, China

Corresponding author: Jia Bing, jiabing427@163.com

Funds: Project supported by the National Natural Science Foundation of China (Grant Nos. 11402055, 11762001) and the Natural Science Foundation of the Higher Education Institutions of Anhui Province, China (Grant No. KJ2018A0739)

FullText HTML : translate this paragraph

References

[1]	Gu H G, Pan B B, Chen G R, Duan L X 2014 Nonlinear Dyn. 78 391 Google Scholar
[2]	Gu H G, Chen S G 2014 Sci. China: Technol. Sci. 57 864 Google Scholar
[3]	Gu H G, Chen S G, Li Y Y 2015 Chin. Phys. B 24 050505 Google Scholar
[4]	Izhikevich E M 2000 Int. J. Bifurcat. Chaos 10 1171 Google Scholar
[5]	Tateno T, Pakdaman K 2004 Chaos 14 511 Google Scholar
[6]	Tateno T, Harsch A, Robinson H P C 2004 J. Neurophysiol. 92 2283 Google Scholar
[7]	Ermentrout B 1996 Neural Comput. 8 979 Google Scholar
[8]	Gutkin B S, Ermentrout G B, Reyes A D 2005 J. Neurophysiol. 94 1623 Google Scholar
[9]	Stiefel K M, Gutkin B S, Sejnowski T J 2009 J. Comput. Neurosci. 26 289 Google Scholar
[10]	谢勇, 程建慧 2017 66 090501 Google Scholar Xie Y, Cheng J H 2017 Acta Phys. Sin. 66 090501 Google Scholar
[11]	van der Loos H, Glaser E M 1972 Brain Res. 48 355 Google Scholar
[12]	Pouzat C, Marty A 1998 J. Physiol. 509 777 Google Scholar
[13]	Tamas G, Buhl E H, Somogyi P 1997 J. Neurosci. 17 6352 Google Scholar
[14]	Saada R, Miller N, Hurwitz I, Susswein A J 2009 Curr. Biol. 19 479 Google Scholar
[15]	Bacci A, Huguenard J R 2006 Neuron 49 119 Google Scholar
[16]	Bacci A, Huguenard J R, Prince D A 2003 J. Neurosci. 23 859 Google Scholar
[17]	Hájos N, Pálhalmi J, Mann E O, Németh B, Paulsen O, Freund T F 2004 J. Neurosci. 24 9127 Google Scholar
[18]	Vida I, Bartos M, Jonas P 2006 Neuron 49 107 Google Scholar
[19]	Zhao Z G, Li L, Gu H G 2018 Front. Cell. Neurosci. 12 62
[20]	Zhao Z G, Jia B, Gu H G 2016 Nonlinear Dyn. 86 1549 Google Scholar
[21]	Wang H T, Ma J, Chen Y L, Chen Y 2014 Commun. Nonlinear Sci. Numer. Simul. 19 3242 Google Scholar
[22]	Wang H T, Wang L F, Chen Y L, Chen Y 2014 Chaos 24 033122 Google Scholar
[23]	Zhao Z G, Gu H G 2017 Sci. Rep. 7 6760 Google Scholar
[24]	Han F, Gu X C, Wang Z J, Fan H, Cao J F, Lu Q S 2018 Chaos 28 106324 Google Scholar
[25]	Dodla R, Svirskis G, Rinzel J 2006 J. Neurophysiol. 95 2664 Google Scholar
[26]	Dodla R, Rinzel J 2006 Phys. Rev. E 73 010903 Google Scholar
[27]	丁学利, 李玉叶 2016 65 210502 Google Scholar Ding X L, Li Y Y 2016 Acta Phys. Sin. 65 210502 Google Scholar
[28]	Qin H X, Ma J, Wang C N, Wu Y 2014 PloS One 9 e100849 Google Scholar
[29]	Wu Y A, Gong Y B, Wang Q 2015 Chaos 25 043113 Google Scholar
[30]	Yilmaz E, Baysal V, Perc M, Ozer M 2016 Sci. China: Technol. Sci. 59 364 Google Scholar
[31]	Elson R C, Selverston A I, Abarbanel H D I, Rabinovich M I 2002 J. Neurophysiol. 88 1166 Google Scholar
[32]	Prinz A A, Abbott L F, Marder E 2004 Trends Neurosci. 27 218 Google Scholar
[33]	Blitz D M, Nusbaum M P 2012 J. Neurosci. 32 9182 Google Scholar
[34]	Hashemi M, Valizadeh A, Azizi Y 2012 Phys. Rev. E 85 021917 Google Scholar
[35]	Gu H G, Zhao Z G 2015 PloS One 10 e0138593 Google Scholar
[36]	Jia B, Wu Y C, He D, Guo B H, Xue L 2018 Nonlinear Dyn. 93 1599 Google Scholar
[37]	曹奔, 关利南, 古华光 2018 67 240502 Google Scholar Cao B, Guan L N, Gu H G 2018 Acta Phys. Sin. 67 240502 Google Scholar
[38]	Achuthan S, Canavier C C 2009 J. Neurosci. 29 5218 Google Scholar
[39]	Goldberg J A, Atherton J F, Surmeier D J 2013 J. Neurophysiol. 110 2497 Google Scholar
[40]	Smeal R M, Ermentrout G B, White J A 2010 Philos. Trans. R. Soc. Lond. B: Biol. Sci. 365 2407 Google Scholar

Cited By

图 1 当I = 45.5 µA·cm^–2, 方波脉冲幅值A = 1.65 µA·cm^–2, 宽度d = 4.4 ms时, ML模型的放电序列和PRC　(a) 方波脉冲刺激电流(短划线)、没有方波脉冲的放电(点线)和有方波脉冲的放电(实线); (b) PRC

Figure 1. Spiketrains and PRC of the ML model when I = 45.5 µA·cm^–2, A = 1.65 µA·cm^–2, and d = 4.4 ms: (a) Square pulse disturbance current (dashed line), and spike trains without (dotted line) and with square pulse disturbance (solid line); (b) PRC.

DownLoad: Full-Size Img PowerPoint

图 2 (a) ML模型随I的平衡点分岔; (b) 当I = 45.5 µA·cm^–2时, ML模型的放电序列图; (c) 当I = 44 µA·cm^–2时, ML模型处于静息状态; (d) ISIs和频率随I的变化(实线表示ISIs, 虚线表示频率)

Figure 2. (a) Bifurcation of ML model with respect to I; (b) spike trains of ML model when I = 45.5 µA·cm^–2; (c) resting state of ML model when I = 44 µA·cm^–2; (d) the changes of ISIs (solid line) and frequency (dashed line) with respect to I.

DownLoad: Full-Size Img PowerPoint

图 3 当I = 45.5 µA·cm^–2时, 负向方波脉冲电流(虚线)作用在不同相位的放电序列(实线)和无方波脉冲作用的放电序列(红色的点线)　(a) t_s = 22 ms, A = –0.6 µA·cm^–2, d = 4.9 ms; (b) t_s = 22 ms, A = –1.65 µA·cm^–2, d = 4.8 ms; (c) t_s = 40 ms, A = –0.6 µA·cm^–2, d = 4.9 ms; (d) t_s = 40 ms, A = –1.65 µA·cm^–2, d = 4.8 ms

Figure 3. Spike trains induced by square pulse current applied at different phases when I = 45.5 µA·cm^–2. The spike trains (solid line) influenced by negative square pulse current (dashed line) and the trains (red dotted line) without negative square pulse current. (a) t_s = 22 ms, A = –0.6 µA·cm^–2, d = 4.9 ms; (b) t_s = 22 ms, A = –1.65 µA·cm^–2, d = 4.8 ms; (c) t_s = 40 ms, A = –0.6 µA·cm^–2, d = 4.9 ms; (d) t_s = 40 ms, A = –1.65 µA·cm^–2, d = 4.8 ms.

DownLoad: Full-Size Img PowerPoint

图 4 当I = 45.5 µA·cm^–2时, ML模型在Hopf分岔点附近的负向脉冲刺激诱发的PRC　(a) A = –0.6 µA·cm^–2, d = 4.9 ms; (b) A = –1.65 µA·cm^–2, d = 4.8 ms

Figure 4. PRC induced by negative square pulse current near the Hopf bifurcation point in the ML model when I = 45.5 µA·cm^–2: (a) A = –0.6 µA·cm^–2, d = 4.9 ms; (b) A = –1.65 µA·cm^–2, d = 4.8 ms.

DownLoad: Full-Size Img PowerPoint

图 5 当I = 45.5 µA·cm^–2, g_aut = 0.04 mS·cm^–2, 具有抑制性自突触ML模型的放电模式(实线)与抑制性自突触电流(短划线) (a) τ = 0 mS; (b) τ = 10 mS; (c) τ =20 mS; (d) τ = 30 mS; (e) τ = 40 mS; (f) τ =50 mS

Figure 5. Inhibitory autapse current (dashed line) and spike trains (solid line) of the ML model with inhibitory autapse when I = 45.5 µA·cm^–2 and g_aut = 0.04 mS·cm^–2: (a) τ = 0 mS; (b) τ = 10 mS; (c) τ = 20 mS; (d) τ = 30 mS; (e) τ = 40 mS; (f) τ =50 mS.

DownLoad: Full-Size Img PowerPoint

图 6 不同耦合强度g_aut下归一化的ISIs (粗实线)和放电频率(细实线)随时滞τ的变化　(a) g_aut = 0.01 mS·cm^–2; (b) g_aut = 0.04 mS·cm^–2

Figure 6. Change of normalized ISIs (boldsolid line) and firing frequency (thin solid line) with respect to time delay τ: (a) g_aut = 0.01 mS·cm^–2; (b) g_aut = 0.04 mS·cm^–2.

DownLoad: Full-Size Img PowerPoint

图 7 当噪声强度D = 0.5 µA·cm^–2时, 平均ISIs对时滞τ和耦合强度g_aut的依赖关系

Figure 7. Dependence of average ISIs on time delay τ and coupling strength g_aut when D = 0.5 µA·cm^–2.

DownLoad: Full-Size Img PowerPoint

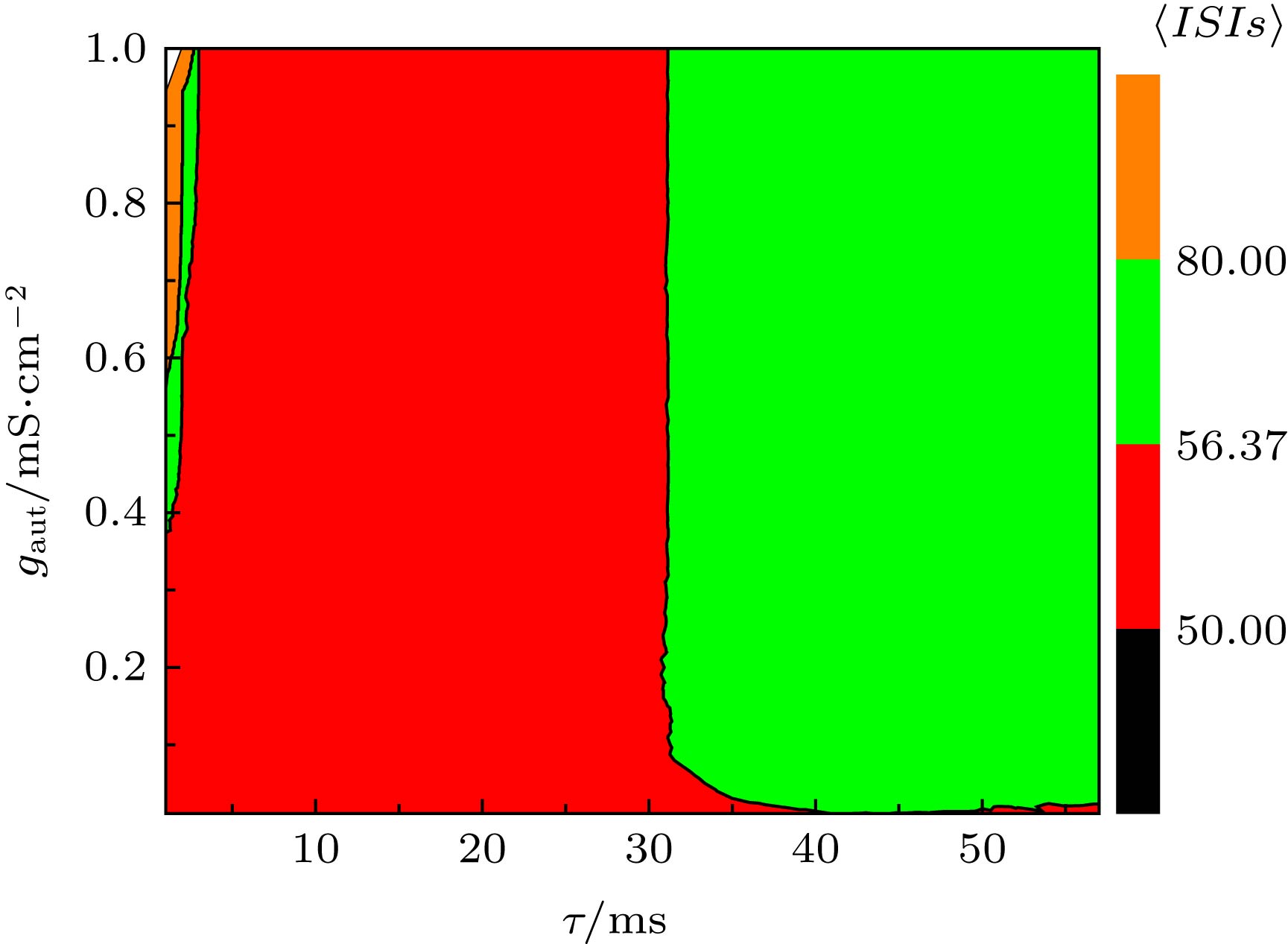
图 8 当I = 45.5 µA·cm^–2, D = 0.5 µA·cm^–2时, (a) ISIs的STD对时滞τ和耦合强度g_aut的依赖关系, (b) ISIs的CV对时滞τ和耦合强度g_aut的依赖关系

Figure 8. (a) Dependence of standard deviation of ISIs (STD) on time delay τ and coupling strength g_aut; (b) the dependence of coefficient of variation of ISIs (CV) on delay τ and coupling strength g_aut. The parameter values are I = 45.5 µA·cm^–2 and D = 0.5 µA·cm^–2.

DownLoad: Full-Size Img PowerPoint

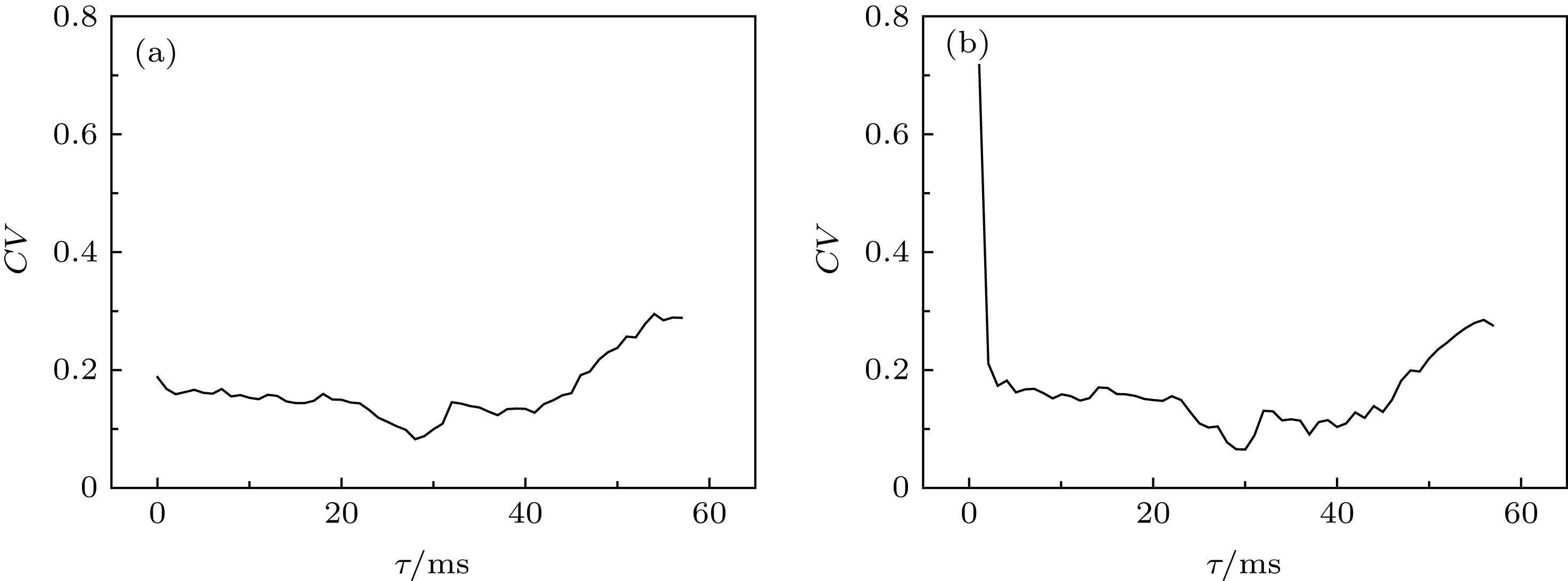
图 9 固定时滞τ在不同水平下, ISIs的CV随着耦合强度g_aut的变化　(a) τ = 27 ms; (b) τ = 30 ms; (c) τ = 40 ms; (d) τ = 46 ms

Figure 9. Changes of coefficient of variation (CV) of ISIs with respect to coupling strength g_aut when time delay τ is fixed at different values: (a) τ = 27 ms; (b) τ = 30 ms; (c) τ = 40 ms; (d) τ = 46 ms.

DownLoad: Full-Size Img PowerPoint

图 10 固定耦合强度g_aut在不同水平下, ISIs的变异系数CV随着时滞τ的变化　(a) g_aut = 0.31 mS·cm^–2; (b) g_aut = 0.61 mS·cm^–2

Figure 10. Changes of coefficient of variation (CV) of ISIs with respect to time delay τ when coupling strength g_aut is fixed at different levels: (a) g_aut = 0.31 mS·cm^–2; (b) g_aut = 0.61 mS·cm^–2.

DownLoad: Full-Size Img PowerPoint

图 11 当I = 45.5 µA·cm^–2, D = 0.5 µA·cm^–2, 耦合强度g_aut = 0.61 mS·cm^–2时, 时滞τ对神经元模型的精确放电的影响　(a) τ = 1 ms; (b) τ = 10 ms; (c) τ = 30 ms; (d) τ = 50 ms

Figure 11. Effect of time delay τ on spike-timing precision of neuron model when I = 45.5 µA·cm^–2, D = 0.5 µA·cm^–2, and g_aut = 0.61 mS·cm^–2: (a) τ = 1 ms; (b) τ = 10 ms; (c) τ = 30 ms; (d) τ = 50 ms.

DownLoad: Full-Size Img PowerPoint

map

[1]	Gu H G, Pan B B, Chen G R, Duan L X 2014 Nonlinear Dyn. 78 391 Google Scholar
[2]	Gu H G, Chen S G 2014 Sci. China: Technol. Sci. 57 864 Google Scholar
[3]	Gu H G, Chen S G, Li Y Y 2015 Chin. Phys. B 24 050505 Google Scholar
[4]	Izhikevich E M 2000 Int. J. Bifurcat. Chaos 10 1171 Google Scholar
[5]	Tateno T, Pakdaman K 2004 Chaos 14 511 Google Scholar
[6]	Tateno T, Harsch A, Robinson H P C 2004 J. Neurophysiol. 92 2283 Google Scholar
[7]	Ermentrout B 1996 Neural Comput. 8 979 Google Scholar
[8]	Gutkin B S, Ermentrout G B, Reyes A D 2005 J. Neurophysiol. 94 1623 Google Scholar
[9]	Stiefel K M, Gutkin B S, Sejnowski T J 2009 J. Comput. Neurosci. 26 289 Google Scholar
[10]	谢勇, 程建慧 2017 66 090501 Google Scholar Xie Y, Cheng J H 2017 Acta Phys. Sin. 66 090501 Google Scholar
[11]	van der Loos H, Glaser E M 1972 Brain Res. 48 355 Google Scholar
[12]	Pouzat C, Marty A 1998 J. Physiol. 509 777 Google Scholar
[13]	Tamas G, Buhl E H, Somogyi P 1997 J. Neurosci. 17 6352 Google Scholar
[14]	Saada R, Miller N, Hurwitz I, Susswein A J 2009 Curr. Biol. 19 479 Google Scholar
[15]	Bacci A, Huguenard J R 2006 Neuron 49 119 Google Scholar
[16]	Bacci A, Huguenard J R, Prince D A 2003 J. Neurosci. 23 859 Google Scholar
[17]	Hájos N, Pálhalmi J, Mann E O, Németh B, Paulsen O, Freund T F 2004 J. Neurosci. 24 9127 Google Scholar
[18]	Vida I, Bartos M, Jonas P 2006 Neuron 49 107 Google Scholar
[19]	Zhao Z G, Li L, Gu H G 2018 Front. Cell. Neurosci. 12 62
[20]	Zhao Z G, Jia B, Gu H G 2016 Nonlinear Dyn. 86 1549 Google Scholar
[21]	Wang H T, Ma J, Chen Y L, Chen Y 2014 Commun. Nonlinear Sci. Numer. Simul. 19 3242 Google Scholar
[22]	Wang H T, Wang L F, Chen Y L, Chen Y 2014 Chaos 24 033122 Google Scholar
[23]	Zhao Z G, Gu H G 2017 Sci. Rep. 7 6760 Google Scholar
[24]	Han F, Gu X C, Wang Z J, Fan H, Cao J F, Lu Q S 2018 Chaos 28 106324 Google Scholar
[25]	Dodla R, Svirskis G, Rinzel J 2006 J. Neurophysiol. 95 2664 Google Scholar
[26]	Dodla R, Rinzel J 2006 Phys. Rev. E 73 010903 Google Scholar
[27]	丁学利, 李玉叶 2016 65 210502 Google Scholar Ding X L, Li Y Y 2016 Acta Phys. Sin. 65 210502 Google Scholar
[28]	Qin H X, Ma J, Wang C N, Wu Y 2014 PloS One 9 e100849 Google Scholar
[29]	Wu Y A, Gong Y B, Wang Q 2015 Chaos 25 043113 Google Scholar
[30]	Yilmaz E, Baysal V, Perc M, Ozer M 2016 Sci. China: Technol. Sci. 59 364 Google Scholar
[31]	Elson R C, Selverston A I, Abarbanel H D I, Rabinovich M I 2002 J. Neurophysiol. 88 1166 Google Scholar
[32]	Prinz A A, Abbott L F, Marder E 2004 Trends Neurosci. 27 218 Google Scholar
[33]	Blitz D M, Nusbaum M P 2012 J. Neurosci. 32 9182 Google Scholar
[34]	Hashemi M, Valizadeh A, Azizi Y 2012 Phys. Rev. E 85 021917 Google Scholar
[35]	Gu H G, Zhao Z G 2015 PloS One 10 e0138593 Google Scholar
[36]	Jia B, Wu Y C, He D, Guo B H, Xue L 2018 Nonlinear Dyn. 93 1599 Google Scholar
[37]	曹奔, 关利南, 古华光 2018 67 240502 Google Scholar Cao B, Guan L N, Gu H G 2018 Acta Phys. Sin. 67 240502 Google Scholar
[38]	Achuthan S, Canavier C C 2009 J. Neurosci. 29 5218 Google Scholar
[39]	Goldberg J A, Atherton J F, Surmeier D J 2013 J. Neurophysiol. 110 2497 Google Scholar
[40]	Smeal R M, Ermentrout G B, White J A 2010 Philos. Trans. R. Soc. Lond. B: Biol. Sci. 365 2407 Google Scholar

[1]	Li Li, Zhao Zhi-Guo, Gu Hua-Guang. Suppression effects of excitatory and inhibitory self-feedbacks on neuronal spiking near Hopf bifurcation. Acta Physica Sinica, 2022, 71(5): 050504. doi: 10.7498/aps.71.20211829
[2]	Ding Xue-Li, Gu Hua-Guang, Jia Bing, Li Yu-Ye. Anticipated synchronization of electrical activity induced by inhibitory autapse in coupled Morris-Lecar neuron model. Acta Physica Sinica, 2021, 70(21): 218701. doi: 10.7498/aps.70.20210912
[3]	Xie Yong, Cheng Jian-Hui. A direct algorithm with square wave perturbation for calculating phase response curve. Acta Physica Sinica, 2017, 66(9): 090501. doi: 10.7498/aps.66.090501
[4]	Lu Jin-Bo, Hou Xiao-Rong, Luo Min. General robust stability controller design method for a class of hopf bifurcation systems. Acta Physica Sinica, 2016, 65(6): 060502. doi: 10.7498/aps.65.060502
[5]	Ding Xue-Li, Li Yu-Ye. Period-adding bifurcation of neural firings induced by inhibitory autapses with time-delay. Acta Physica Sinica, 2016, 65(21): 210502. doi: 10.7498/aps.65.210502
[6]	Zhang Wu-Fan, Zhao Qiang. Hopf bifurcation and chaos in the solar-forced El Niño /Southern Oscillation recharge oscillator model. Acta Physica Sinica, 2014, 63(21): 210201. doi: 10.7498/aps.63.210201
[7]	Zhang Ling-Mei, Zhang Jian-Wen, Wu Run-Heng. Anti-control of Hopf bifurcation in the new chaotic system with piecewise system and exponential system. Acta Physica Sinica, 2014, 63(16): 160505. doi: 10.7498/aps.63.160505
[8]	Ding Xue-Li, Li Yu-Ye. Phase noise induced single or double coherence resonances of neural firing. Acta Physica Sinica, 2014, 63(24): 248701. doi: 10.7498/aps.63.248701
[9]	Li Xiao-Jing, Chen Xuan-Qing, Yan Jing. Hopf bifurcation and the problem of periodic solutions in a recharge-discharge oscillator model for El Niño and southern oscillation with time delay. Acta Physica Sinica, 2013, 62(16): 160202. doi: 10.7498/aps.62.160202
[10]	Cui Yan, Liu Su-Hua, Ge Xiao-Ling. Amplitude control of limit cycle from Hopf bifurcation in the Langford system. Acta Physica Sinica, 2012, 61(10): 100202. doi: 10.7498/aps.61.100202
[11]	Zhao Hong-Yong, Chen Ling, Yu Xiao-Hong. Bifurcation and control of a class of inertial neuron networks. Acta Physica Sinica, 2011, 60(7): 070202. doi: 10.7498/aps.60.070202
[12]	Ma Shao-Juan. Hopf bifurcation in a kind of stochastic van der Pol system. Acta Physica Sinica, 2011, 60(1): 010502. doi: 10.7498/aps.60.010502
[13]	Wu Zhi-Qiang, Sun Li-Ming. Hopf bifurcation control of the Rössler system based on Washout filter controller. Acta Physica Sinica, 2011, 60(5): 050504. doi: 10.7498/aps.60.050504
[14]	Ma Wei, Wang Ming-Yu, Nie Hai-Long. Control of Hopf bifurcation in the one-cycle controlled Boost converter and its experimental implementation. Acta Physica Sinica, 2011, 60(10): 100202. doi: 10.7498/aps.60.100202
[15]	Zhang Li-Sen, Cai Li, Feng Chao-Wen. Hopf bifurcation and chaotification of Josephson junction with linear delayed feedback. Acta Physica Sinica, 2011, 60(6): 060306. doi: 10.7498/aps.60.060306
[16]	Liu Shuang, Liu Bin, Zhang Ye-Kuan, Wen Yan. Hopf bifurcation and stability of periodic solutions in a nonlinear relative rotation dynamical system with time delay. Acta Physica Sinica, 2010, 59(1): 38-43. doi: 10.7498/aps.59.38
[17]	Liu Hao-Ran, Liu Bin, Liu Shuang, Wen Yan. Hopf bifurcation control in a coupled nonlinear relative rotation dynamical system. Acta Physica Sinica, 2010, 59(8): 5223-5228. doi: 10.7498/aps.59.5223
[18]	Liu Shuang, Liu Bin, Shi Pei-Ming. Nonlinear feedback control of Hopf bifurcation in a relative rotation dynamical system. Acta Physica Sinica, 2009, 58(7): 4383-4389. doi: 10.7498/aps.58.4383
[19]	Wang Zuo-Lei. Stability and Hopf bifurcation of the simplified Lang-Kobayashi equation. Acta Physica Sinica, 2008, 57(8): 4771-4776. doi: 10.7498/aps.57.4771
[20]	Liu Su-Hua, Tang Jia-Shi. Anti-control of Hopf bifurcation at zero equilibrium of 4D Qi system. Acta Physica Sinica, 2008, 57(10): 6162-6168. doi: 10.7498/aps.57.6162

Catalog

Vol. 68, Issue 18 - 2019-09-20

Metrics

Abstract views: 8088
PDF Downloads: 76
Cited By: 0

姓名
邮箱
手机号码
标题
留言内容
验证码

Search

Article

留言板