-
Micro-structured targets have been widely used in the interaction between ultra-intense laser and target, aiming at improving the electron accelerating efficiency. In this paper, we perform two-dimensional particle-in-cell (PIC) simulations to study the interaction of the ultra-intense laser pulse with the micro-structured foam-attached target (the foam is composed of low density bubbles and high density interfaces between the bubbles). It is found that at the beginning of the laser-plasma interaction, the fast electrons accelerated at the front surface of the foam freely propagate into the target and drive a return current of cold background electrons. These cold background electrons are restricted to propagate along the interfaces between the bubbles in the foam due to the self-generated large sheath field. As a result, small current filaments are generated in the foam, which then leads to the generation of randomly distributed megagauss magnetic field in the foam layer. This quasistatic magnetic field then acts as an energy-selective " magnetic barrier”: the low-energy electrons are reflected back into the laser acceleration region while the high-energy electrons can penetrate through it. If the reflected electrons enter into the laser field with proper phases, they can be further accelerated to higher energy through cooperative actions of the ultra-intense laser pulse and the sheath field generated due to plasma expansion at the target surface. Our simulation results show that many of the laser accelerated low-energy electrons can be reflected back and accelerated several times until they gain enough energy to penetrate through the magnetic barrier. This is termed the " multiple acceleration mechanism”. Due to this mechanism, the electron acceleration efficiency in the foam-coated target with a thickness of several microns is significantly enhanced in comparison with that in the plane target. This enhancement in the electron acceleration efficiency will be beneficial to many important applications such as the fast ignition. Additionally, foam-coated targets with different bubble radii and layer thickness are also studied, and it is found that the yield of the high energy electrons increases with the radius of bubble size more efficiently than with the bubble thickness. In order to understand the physics more clearly, a single particle model is developed to analyze the simulation results.
-
Keywords:
- relativistic electron beam /
- ultra-intense laser /
- magnetic barrier /
- micro-structured target
[1] Ma Y Y, Sheng Z M, Li Y T, Chang W W, Yuan X H, Chen M, Chen H C, Zheng J, Zhang J 2006 Phys. Plasmas 13 110702
Google Scholar
[2] Kruer W L, Estabrook K 1985 Phys. Fluids 28 430
Google Scholar
[3] 孔青, 朱立俊, 王加祥, 霍裕昆 1999 48 650
Google Scholar
Kong Q, Zhu L J, Wang J X, Huo Y K 1999 Acta Phys. Sin. 48 650
Google Scholar
[4] Zhou C T, He X T 2007 Opt. Lett. 32 2444
Google Scholar
[5] Norreys P A, Zepf M, Moustaizis S, Fews A P, Zhang J, Lee P, Bakarezos M, Danson C N, Dyson A, Gibbon P, Loukakos P, Neely D, Walsh F N, Wark J S, Dangor A E 1996 Phys. Rev. Lett. 76 1832
Google Scholar
[6] Kodama R, Tanaka K, Sentoku Y, Matsushita T, Takahashi K, Kato Y, Fujita H, Kitagawa Y, Kanabe T, Yamanaka T, Mima K 2000 Phys. Rev. Lett. 84 674
Google Scholar
[7] Bastiani S, Rousse A, Geindre J P, Audebert P, Quoix C, Hamoniaux G, Antonetti A, Gauthier J C 1997 Phys. Rev. E 56 7179
Google Scholar
[8] Ruhl H, Sentoku Y, Mima K, Tanaka K A, Kodama R 1999 Phys. Rev. Lett. 82 743
Google Scholar
[9] Li C K, Séguin F H, Frenje J A, Rygg J R, Petrasso R D, Town R P J, Amendt P A, Hatchett S P, Landen O L, Mackinnon A J, Patel P K, Smalyuk V A, Sangster T C, Knauer J P 2006 Phys. Rev. Lett. 97 135003
Google Scholar
[10] Marshall F J, McKenty P W, Delettrez J A, Epstein R, Knauer J P, Smalyuk V A, Frenje J A, Li C K, Petrasso R D, Séguin F H, Mancini R C 2009 Phys. Rev. Lett. 102 185004
Google Scholar
[11] Tillman C, Persson A, Wahlstrom C G, Svanberg S, Herrlin K 1995 Appl. Phys. B 61 333
Google Scholar
[12] Tabak M, Hammer J, Glinsky M E, Kruer W L, Wilks S C, Wood-worth J, Campbell E M, Perry M D, Mason R J 1994 Phys. Plasmas 1 1626
Google Scholar
[13] Cai H B, Mima K, Zhou W M, Jozaki T, Nagatomo H, Sunahara A, Mason R J 2009 Phys. Rev. Lett. 102 245001
Google Scholar
[14] Chen L M, Kando M, Ma J, Kotaki H, Fukuda Y, Hayashi Y, Daito I, Homma T, Ogura K, Mori M, Pirozhkov A S, Koga J, Daido H, Bulanov S V, Kimura T, Tajima T, Kato Y 2007 Appl. Phys. Lett. 90 211501
Google Scholar
[15] 孙彦乾, 陈黎明, 张璐, 毛婧一, 刘峰, 李大章, 刘成, 李伟昌, 王兆华, 李英骏, 魏志义, 张杰 2012 61 075206
Google Scholar
Sun Y Q, Chen L M, Zhang L, Mao Q Y, Liu F, Li D Z, Liu C, Li W C, Wang Z H, Li Y J, Wei Z Y, Zhang J 2012 Acta Phys. Sin. 61 075206
Google Scholar
[16] Kulcsár G, AlMawlawi D, Budnik F W, Herman P R, Moskovits M, Zhao L, Marjoribanks R S 2000 Phys. Rev. Lett. 84 5049
Google Scholar
[17] Lei A L, Tanaka K A, Kodama R, Kumar G R, Nagai K, Norimatsu T, Yabuuchi T, Mima K 2006 Phys. Rev. Lett. 96 255006
Google Scholar
[18] Cao L H, Chen M, Zhao Z Q, Cai H B, Wu S Z, Gu Y Q 2011 Phys. Plasmas 18 054501
Google Scholar
[19] 余金清, 金晓林, 周维民, 李斌, 谷渝秋 2012 61 225202
Google Scholar
Yu J Q, Jin X L, Zhou W M, Li B, Gu Y Q 2012 Acta Phys. Sin. 61 225202
Google Scholar
[20] Wang W M, Sheng Z M, Zhang J 2008 Phys. Plasmas 15 030702
Google Scholar
[21] Hu G Y, Lei A L, Wang J W, Huang L G, Wang W T, Wang X, Xu Y, Shen B F, Liu J S, Yu W, Li R X, Xu Z Z 2010 Phys. Plasmas 17 083102
Google Scholar
[22] Tian Y, Liu J S, Wang W T, Wang C, Lu X M, Leng Y X, Liang X Y, Li R X, Xu Z Z 2014 Plasma Phys. Control. Fusion 56 075021
Google Scholar
[23] Wilks S C, Kruer W L 1997 IEEE J. Quantum Electron 33 1954
Google Scholar
[24] Wilks S C, Kruer W L, Tabak M, Langdon A B 1992 Phys. Rev. Lett. 69 1383
Google Scholar
[25] Sheng Z M, Mima K, Sentoku Y, Jovanović M S, Taguchi T, Zhang J, Meyer-ter-Vehn J 2002 Phys. Rev. Lett. 88 055004
Google Scholar
[26] Gibbon P 2005 Short Pulse Laser Interactions with Matter: An Introduction (London: Imperial College Press) pp31−33
[27] Landau B L, Lifshits E, Holbrow C H 1963 The Classical Theory of Fields (Oxford: Pergamon Press) p121
-
图 1 (a) 泡沫靶密度分布示意图(局部); (b) 75
$T_0$ 泡沫间隙的准静态电流(模拟窗口大小为$100\ \lambda_0 \times 16 \ \lambda_0$ ; 图中密度无量纲单位为$n_{\rm c}$ , 电流无量纲单位为$en_{\rm c}c$ )Figure 1. (a) Schematic diagram of initial plasma density (local); (b) current in the foam target at 75T0. The simulation window size is
$100\ \lambda_0 \times 16 \ \lambda_0$ . The units of plasma density and current are$n_{\rm c}$ , and$en_{\rm c}c$ , respectively
图 2 150
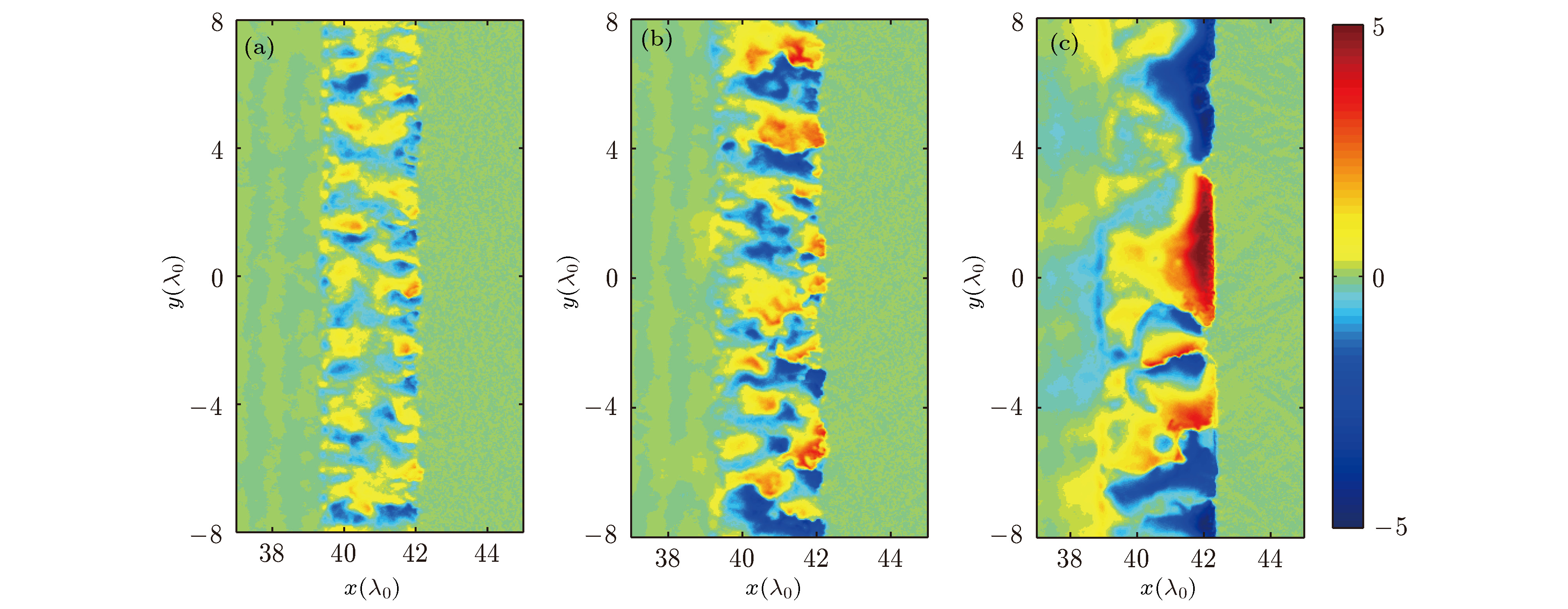
$T_0$ 的泡沫区磁场分布 (a) 泡沫孔径0.075$\lambda_0$ ; (b) 泡沫孔径0.15$\lambda_0$ ; (c) 泡沫孔径0.6$\lambda_0$ (磁场无量纲单位为$m_{\rm e}\omega c/e$ )Figure 2. Magnetic field distribution in foam region at 150
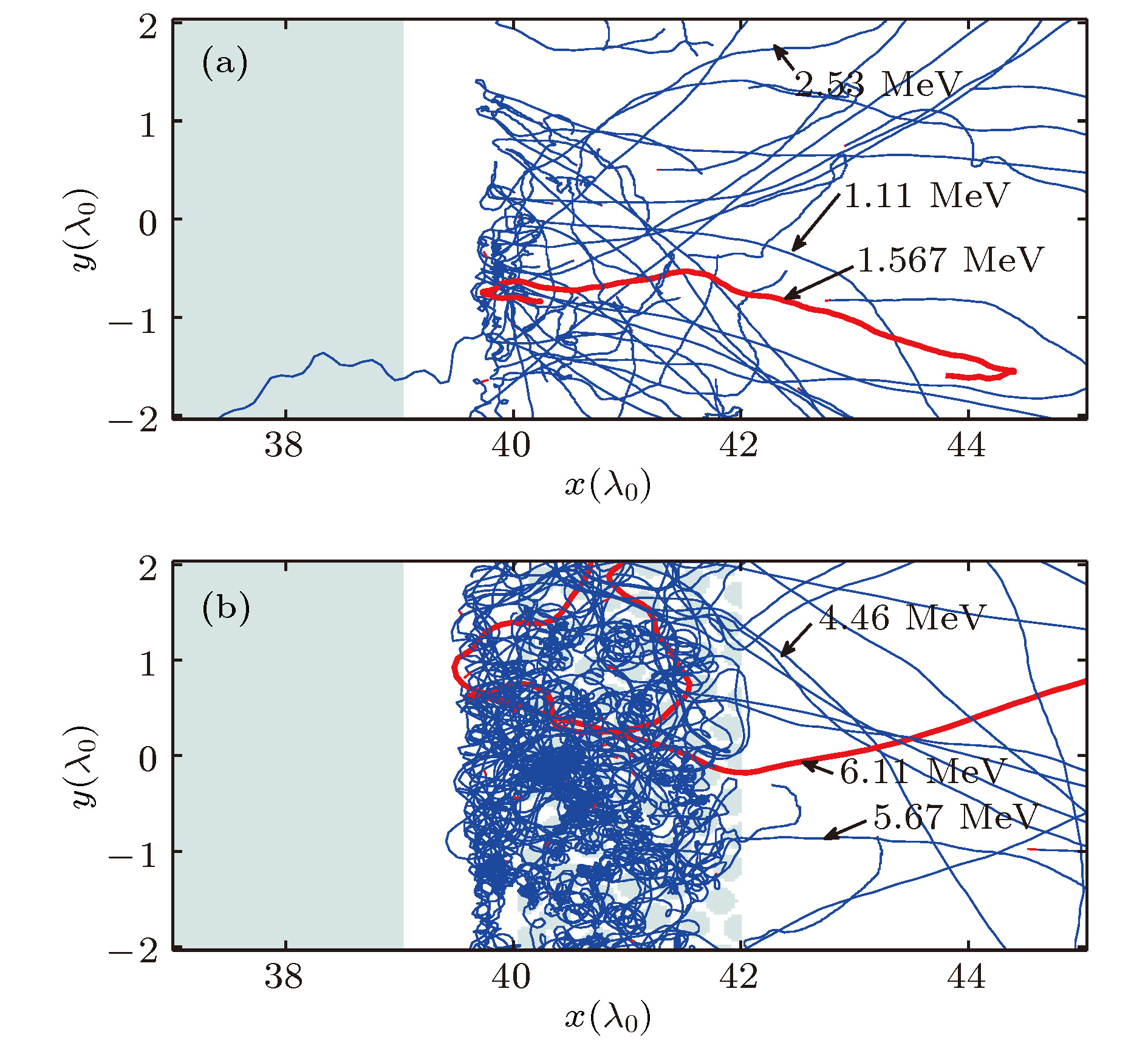
$T_0$ : (a) Bubble radius is 0.075$\lambda_0$ ; (b) bubble radius is 0.15$\lambda_0$ ; (c) bubble radius is 0.6$\lambda_0$ . The unit of magnetic field is$m_{\rm e}\omega c/e$ 
图 3 50个初始位置随机分布在靶前表面的电子的轨迹(a)平面靶; (b)泡沫靶; 图中标注数字为运动到靶后区域单个电子的动能, 红色线表示其中一个电子加速后的轨迹
Figure 3. Trajectory of 50 electrons whose initial positions randomly distributed on the front surface of the target: (a) Planar target; (b) foam target. The labeled number is the kinetic energy of the electrons moving to the area behind the target. The red line is the trajectory of one of the accelerated electrons
图 4 电子多次加速过程中的能量和位置随时间演化, 图中x = (40, 42)
$\lambda_0$ 黄色标记区域为泡沫靶区Figure 4. Evolution of electron energy and position with time in multiple acceleration of electron. Here, the x = (40, 42)
$\lambda_0$ region marked with yellow is the foam region
图 5 平面靶和不同孔径泡沫靶的电子能量密度空间分布 (a)平面靶; (b)泡沫孔径0.075
$\lambda_0$ ; (c)泡沫孔径0.15$\lambda_0$ ; (d)泡沫孔径0.6$\lambda_0$ ; 电子能量密度无量纲单位为$n_{\rm c}m_{\rm e}c^2$ Figure 5. Spatial distribution of electron energy density for (a) planar target, and bubble target with bubble size of (b) 0.075
$\lambda_0$ , (c) 0.15$\lambda_0$ , (d) 0.6$\lambda_0$ . The unit of electron energy density is$n_{\rm c}m_{\rm e}c^2$ 
图 6 (a)不同孔径泡沫靶的超热电子能谱; (b)不同厚度泡沫靶的超热电子能谱
Figure 6. (a) Electron energy spectra of foam targets with different bubble radii; (b) electron energy spectra of foam targets with different foam thicknesses
-
[1] Ma Y Y, Sheng Z M, Li Y T, Chang W W, Yuan X H, Chen M, Chen H C, Zheng J, Zhang J 2006 Phys. Plasmas 13 110702
Google Scholar
[2] Kruer W L, Estabrook K 1985 Phys. Fluids 28 430
Google Scholar
[3] 孔青, 朱立俊, 王加祥, 霍裕昆 1999 48 650
Google Scholar
Kong Q, Zhu L J, Wang J X, Huo Y K 1999 Acta Phys. Sin. 48 650
Google Scholar
[4] Zhou C T, He X T 2007 Opt. Lett. 32 2444
Google Scholar
[5] Norreys P A, Zepf M, Moustaizis S, Fews A P, Zhang J, Lee P, Bakarezos M, Danson C N, Dyson A, Gibbon P, Loukakos P, Neely D, Walsh F N, Wark J S, Dangor A E 1996 Phys. Rev. Lett. 76 1832
Google Scholar
[6] Kodama R, Tanaka K, Sentoku Y, Matsushita T, Takahashi K, Kato Y, Fujita H, Kitagawa Y, Kanabe T, Yamanaka T, Mima K 2000 Phys. Rev. Lett. 84 674
Google Scholar
[7] Bastiani S, Rousse A, Geindre J P, Audebert P, Quoix C, Hamoniaux G, Antonetti A, Gauthier J C 1997 Phys. Rev. E 56 7179
Google Scholar
[8] Ruhl H, Sentoku Y, Mima K, Tanaka K A, Kodama R 1999 Phys. Rev. Lett. 82 743
Google Scholar
[9] Li C K, Séguin F H, Frenje J A, Rygg J R, Petrasso R D, Town R P J, Amendt P A, Hatchett S P, Landen O L, Mackinnon A J, Patel P K, Smalyuk V A, Sangster T C, Knauer J P 2006 Phys. Rev. Lett. 97 135003
Google Scholar
[10] Marshall F J, McKenty P W, Delettrez J A, Epstein R, Knauer J P, Smalyuk V A, Frenje J A, Li C K, Petrasso R D, Séguin F H, Mancini R C 2009 Phys. Rev. Lett. 102 185004
Google Scholar
[11] Tillman C, Persson A, Wahlstrom C G, Svanberg S, Herrlin K 1995 Appl. Phys. B 61 333
Google Scholar
[12] Tabak M, Hammer J, Glinsky M E, Kruer W L, Wilks S C, Wood-worth J, Campbell E M, Perry M D, Mason R J 1994 Phys. Plasmas 1 1626
Google Scholar
[13] Cai H B, Mima K, Zhou W M, Jozaki T, Nagatomo H, Sunahara A, Mason R J 2009 Phys. Rev. Lett. 102 245001
Google Scholar
[14] Chen L M, Kando M, Ma J, Kotaki H, Fukuda Y, Hayashi Y, Daito I, Homma T, Ogura K, Mori M, Pirozhkov A S, Koga J, Daido H, Bulanov S V, Kimura T, Tajima T, Kato Y 2007 Appl. Phys. Lett. 90 211501
Google Scholar
[15] 孙彦乾, 陈黎明, 张璐, 毛婧一, 刘峰, 李大章, 刘成, 李伟昌, 王兆华, 李英骏, 魏志义, 张杰 2012 61 075206
Google Scholar
Sun Y Q, Chen L M, Zhang L, Mao Q Y, Liu F, Li D Z, Liu C, Li W C, Wang Z H, Li Y J, Wei Z Y, Zhang J 2012 Acta Phys. Sin. 61 075206
Google Scholar
[16] Kulcsár G, AlMawlawi D, Budnik F W, Herman P R, Moskovits M, Zhao L, Marjoribanks R S 2000 Phys. Rev. Lett. 84 5049
Google Scholar
[17] Lei A L, Tanaka K A, Kodama R, Kumar G R, Nagai K, Norimatsu T, Yabuuchi T, Mima K 2006 Phys. Rev. Lett. 96 255006
Google Scholar
[18] Cao L H, Chen M, Zhao Z Q, Cai H B, Wu S Z, Gu Y Q 2011 Phys. Plasmas 18 054501
Google Scholar
[19] 余金清, 金晓林, 周维民, 李斌, 谷渝秋 2012 61 225202
Google Scholar
Yu J Q, Jin X L, Zhou W M, Li B, Gu Y Q 2012 Acta Phys. Sin. 61 225202
Google Scholar
[20] Wang W M, Sheng Z M, Zhang J 2008 Phys. Plasmas 15 030702
Google Scholar
[21] Hu G Y, Lei A L, Wang J W, Huang L G, Wang W T, Wang X, Xu Y, Shen B F, Liu J S, Yu W, Li R X, Xu Z Z 2010 Phys. Plasmas 17 083102
Google Scholar
[22] Tian Y, Liu J S, Wang W T, Wang C, Lu X M, Leng Y X, Liang X Y, Li R X, Xu Z Z 2014 Plasma Phys. Control. Fusion 56 075021
Google Scholar
[23] Wilks S C, Kruer W L 1997 IEEE J. Quantum Electron 33 1954
Google Scholar
[24] Wilks S C, Kruer W L, Tabak M, Langdon A B 1992 Phys. Rev. Lett. 69 1383
Google Scholar
[25] Sheng Z M, Mima K, Sentoku Y, Jovanović M S, Taguchi T, Zhang J, Meyer-ter-Vehn J 2002 Phys. Rev. Lett. 88 055004
Google Scholar
[26] Gibbon P 2005 Short Pulse Laser Interactions with Matter: An Introduction (London: Imperial College Press) pp31−33
[27] Landau B L, Lifshits E, Holbrow C H 1963 The Classical Theory of Fields (Oxford: Pergamon Press) p121
DownLoad:
Catalog
Metrics
- Abstract views: 7570
- PDF Downloads: 90
- Cited By: 0
