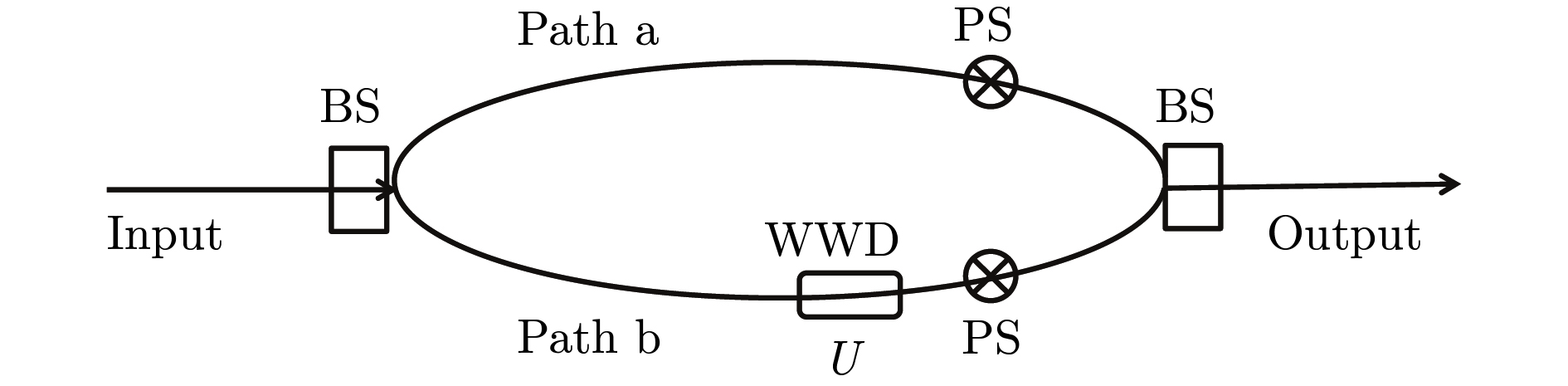
Coherence and information conservation and their applications in Mach-Zehnder interferometer

Fu Shuang-Shuang; Luo Shun-Long; Sun Yuan

doi:10.7498/aps.68.20181778

Abstract

Coherence and complementarity are two important themes in quantum mechanics, which have been widely and thoroughly investigated. Recently, with the rapid development of quantum information theory, various measures have been introduced for quantitatively studying the coherence and complementarity. However, most of these studies are independent of each other in that they focus on only one theme, for example, the wave-particle duality and Heisenberg uncertainty principle are usually regarded as manifestation of Bohr’s complementary principle, while coherence is a quantum feature closely related to quantum superposition. During the past few years, there has been a flurry of research interest in the study of quantum coherence from the quantum resource-theoretic point of view. In this paper, we establish two information conservation relations and employ them to characterize complementarity and quantum coherence. As an illustration of the main results, we discuss these two themes in the Mach-Zehnder interferometer. Our study reveals that these two quantum themes are closely related to each other. Our main results are listed as follows. Firstly, we establish two information conservation relations, one is based on " Bures distance versus fidelity” and the other based on " symmetry versus asymmetry”. Then we employ these information conservation relations to investigate coherence and complementarity. Specifically, we provide an explanation of the " Bures distance versus fidelity” trade-off relation from the information conservation perspective, establish the link between the information conservation relation and wave-particle duality, and derive the famous Englert inequality concerning " fringe visibility versus path distinguishability” from the information conservation relation. Furthermore, in the general framework of state-channel interaction, we derive " symmetry versus asymmetry” trade-off relation and explain it as an information conservation relation, reveal its intrinsic relations with coherence and complementarity. Lastly, we demonstrate that the two information conservation relations are closely interrelated, and we also discuss the coherence, decoherence and complementarity in the Mach-Zehnder interferometer, explicitly, we reveal that the Bures distance can be regarded as a lower bound of the asymmetry of state-channel interaction while fidelity is an upper bound of the symmetry of state-channel interaction. We expect that our information conservation relation can provide a unified framework for the study of coherence and complementarity.

Keywords:

Authors and contacts

1.
School of Mathematics and Physics, University of Science and Technology Beijing, Beijing 100083, China
2.
Academy of Mathematics and Systems Science, Chinese Academy of Sciences, Beijing 100190, China
3.
School of Mathematical Sciences, University of Chinese Academy of Sciences, Beijing 100049, China

Corresponding author: Luo Shun-Long, luosl@amt.ac.cn

Funds: Project supported by the Natural Science Foundation of Beijing, China (Grant No. 1174017), the Young Scientists Fund of the National Natural Science Foundation of China (Grant No. 11605006), the National Natural Science Foundation of China (Grant No. 11875317), the National Center for Mathematics and Interdisciplinary Sciences, Chinese Academy of Sciences, China (Grant No. Y029152K51), and the Key Laboratory of Random Complex Structures and Data Science, Chinese Academy of Sciences, China (Grant No. 2008DP173182).

FullText HTML

References

[1]	Bohr N 1937 Phil. Sci. 4 289 Google Scholar
[2]	Heisenberg W 1927 Zeit. Physik 43 172 Google Scholar
[3]	Heisenberg W 1930 The Physical Principles of the Quantum Theory (Chicago: The University of Chicago Press) pp13–39
[4]	Wootters W K, Zurek W H 1979 Phys. Rev. D 19 473 Google Scholar
[5]	Scully M O, Englert B G, Walther H 1991 Nature 351 111 Google Scholar
[6]	Mandel L 1991 Opt. Lett. 16 1882 Google Scholar
[7]	Jaeger G, Horne M A, Shimony A 1993 Phys. Rev. A 48 1023 Google Scholar
[8]	Englert B G 1996 Phys. Rev. Lett. 77 2154 Google Scholar
[9]	Busch P, Shilladay C 2006 Phys. Rep. 435 1 Google Scholar
[10]	Coles P J, Kaniewski J, Wehner S 2014 Nat. Commun. 5 5814 Google Scholar
[11]	Coles P J, Berta M, Tomamichel M, Wehner S 2017 Rev. Mod. Phys. 89 015002 Google Scholar
[12]	Jaeger G, Shimony A, Vaidmann L 1995 Phys. Rev. A 51 54 Google Scholar
[13]	Åberg J 2006 arXiv:quant-ph/0612146
[14]	Levi F, Mintert F 2014 New J. Phys. 16 033007 Google Scholar
[15]	Baumgratz T, Cramer M, Plenio M B 2014 Phys. Rev. Lett. 113 140401 Google Scholar
[16]	Girolami D 2014 Phys. Rev. Lett. 113 170401 Google Scholar
[17]	Streltsov A, Singh U, Dhar H S, Bera M N, Adesso G 2015 Phys. Rev. Lett. 115 020403 Google Scholar
[18]	Pires D P, Celeri L C, Soares-Pinto D O 2015 Phys. Rev. A 91 042330 Google Scholar
[19]	Yao Y, Xiao X, Ge L, Sun C P 2015 Phys. Rev. A 92 022112 Google Scholar
[20]	Winter A, Yang D 2016 Phys. Rev. Lett. 116 120404 Google Scholar
[21]	Ma J, Yadin B, Girolami D, Vedral V, Gu M 2016 Phys. Rev. Lett. 116 160407 Google Scholar
[22]	Chang L, Luo S, Sun Y 2017 Commun. Theor. Phys. 68 565 Google Scholar
[23]	Streltsov A, Adesso G, Plenio M B 2017 Rev. Mod. Phys. 89 041003 Google Scholar
[24]	Luo S, Sun Y 2017 Phys. Rev. A 96 022130 Google Scholar
[25]	Luo S, Sun Y 2017 Phys. Rev. A 96 022136 Google Scholar
[26]	Yao Y, Dong G H, Xiao X, Li M, Sun C P 2017 Phys. Rev. A 96 052322 Google Scholar
[27]	Zhao H, Yu C 2018 Sci. Rep. 8 299 Google Scholar
[28]	Jin Z X, Fei S M 2018 Phys. Rev. A 97 062342 Google Scholar
[29]	Horodecki M, Oppenheim J 2013 Nat. Commun. 4 2059 Google Scholar
[30]	Narasimhachar V, Gour G 2015 Nat. Commun. 6 7689 Google Scholar
[31]	Lloyd S 2011 J. Phys. Conf. Ser. 302 012037 Google Scholar
[32]	Marvian I, Spekkens R W 2014 Nat. Commun. 5 3821 Google Scholar
[33]	Marvian I, Spekkens R W 2016 Phys. Rev. A 94 052324 Google Scholar
[34]	Fang Y N, Dong G H, Zhou D L, Sun C P 2016 Commun. Theor. Phys. 65 423 Google Scholar
[35]	Yao Y, Dong G H., Xiao X, Sun C P 2016 Sci. Rep. 6 32010 Google Scholar
[36]	Bagan E, Bergou J A, Cottrell S S, Hillery M 2016 Phys. Rev. Lett. 116 160406 Google Scholar
[37]	Bera M N, Qureshi T, Siddiqui M A, Pati A K 2015 Phys. Rev. A 92 012118 Google Scholar
[38]	Hu M L, Hu X , Wang J C, Peng Yi, Zhang Y R, Fan H 2018 arXiv:1703.01852 [quant-ph]
[39]	Luo S, Sun Y 2018 Phys. Rev. A 98 012113 Google Scholar
[40]	Nielsen, M A, Chuang I L 2000 Quantum Computation and Quantum Information (10th Anniversary Edition) (New York: Cambridge University Press) pp60–111, 399–416
[41]	Bures D 1969 Trans. Amer. Math. Soc. 135 199-212 Google Scholar
[42]	Hubner M 1993 Phys. Lett. A 179 226 Google Scholar
[43]	Fuchs C A, Caves C M 1995 Open Sys. Inf. Dyn. 3 345 Google Scholar
[44]	Barnum H, Caves C M, Fuchs C A, Jozsa R, Schumacher B 1996 Phys. Rev. Lett. 76 2818 Google Scholar
[45]	Uhlmann A 2000 Phys. Rev. A 62 032307 Google Scholar
[46]	Dodd J L, Nielsen M A 2002 Phys. Rev. A 66 044301 Google Scholar
[47]	Luo S, Zhang Q 2004 Phys. Rev. A 69 032106 Google Scholar

Cited By

图 1 对称MZI (BS, 50 : 50分束器; PS, 相移器; WWD, 路径探测器)

Figure 1. A schematic sketch of the symmetric Mach-Zehnder interferometer. BS, 50:50 beam splitter; PS, phase shifter; WWD, which-way detector.

DownLoad: Full-Size Img PowerPoint

map

[1]	Bohr N 1937 Phil. Sci. 4 289 Google Scholar
[2]	Heisenberg W 1927 Zeit. Physik 43 172 Google Scholar
[3]	Heisenberg W 1930 The Physical Principles of the Quantum Theory (Chicago: The University of Chicago Press) pp13–39
[4]	Wootters W K, Zurek W H 1979 Phys. Rev. D 19 473 Google Scholar
[5]	Scully M O, Englert B G, Walther H 1991 Nature 351 111 Google Scholar
[6]	Mandel L 1991 Opt. Lett. 16 1882 Google Scholar
[7]	Jaeger G, Horne M A, Shimony A 1993 Phys. Rev. A 48 1023 Google Scholar
[8]	Englert B G 1996 Phys. Rev. Lett. 77 2154 Google Scholar
[9]	Busch P, Shilladay C 2006 Phys. Rep. 435 1 Google Scholar
[10]	Coles P J, Kaniewski J, Wehner S 2014 Nat. Commun. 5 5814 Google Scholar
[11]	Coles P J, Berta M, Tomamichel M, Wehner S 2017 Rev. Mod. Phys. 89 015002 Google Scholar
[12]	Jaeger G, Shimony A, Vaidmann L 1995 Phys. Rev. A 51 54 Google Scholar
[13]	Åberg J 2006 arXiv:quant-ph/0612146
[14]	Levi F, Mintert F 2014 New J. Phys. 16 033007 Google Scholar
[15]	Baumgratz T, Cramer M, Plenio M B 2014 Phys. Rev. Lett. 113 140401 Google Scholar
[16]	Girolami D 2014 Phys. Rev. Lett. 113 170401 Google Scholar
[17]	Streltsov A, Singh U, Dhar H S, Bera M N, Adesso G 2015 Phys. Rev. Lett. 115 020403 Google Scholar
[18]	Pires D P, Celeri L C, Soares-Pinto D O 2015 Phys. Rev. A 91 042330 Google Scholar
[19]	Yao Y, Xiao X, Ge L, Sun C P 2015 Phys. Rev. A 92 022112 Google Scholar
[20]	Winter A, Yang D 2016 Phys. Rev. Lett. 116 120404 Google Scholar
[21]	Ma J, Yadin B, Girolami D, Vedral V, Gu M 2016 Phys. Rev. Lett. 116 160407 Google Scholar
[22]	Chang L, Luo S, Sun Y 2017 Commun. Theor. Phys. 68 565 Google Scholar
[23]	Streltsov A, Adesso G, Plenio M B 2017 Rev. Mod. Phys. 89 041003 Google Scholar
[24]	Luo S, Sun Y 2017 Phys. Rev. A 96 022130 Google Scholar
[25]	Luo S, Sun Y 2017 Phys. Rev. A 96 022136 Google Scholar
[26]	Yao Y, Dong G H, Xiao X, Li M, Sun C P 2017 Phys. Rev. A 96 052322 Google Scholar
[27]	Zhao H, Yu C 2018 Sci. Rep. 8 299 Google Scholar
[28]	Jin Z X, Fei S M 2018 Phys. Rev. A 97 062342 Google Scholar
[29]	Horodecki M, Oppenheim J 2013 Nat. Commun. 4 2059 Google Scholar
[30]	Narasimhachar V, Gour G 2015 Nat. Commun. 6 7689 Google Scholar
[31]	Lloyd S 2011 J. Phys. Conf. Ser. 302 012037 Google Scholar
[32]	Marvian I, Spekkens R W 2014 Nat. Commun. 5 3821 Google Scholar
[33]	Marvian I, Spekkens R W 2016 Phys. Rev. A 94 052324 Google Scholar
[34]	Fang Y N, Dong G H, Zhou D L, Sun C P 2016 Commun. Theor. Phys. 65 423 Google Scholar
[35]	Yao Y, Dong G H., Xiao X, Sun C P 2016 Sci. Rep. 6 32010 Google Scholar
[36]	Bagan E, Bergou J A, Cottrell S S, Hillery M 2016 Phys. Rev. Lett. 116 160406 Google Scholar
[37]	Bera M N, Qureshi T, Siddiqui M A, Pati A K 2015 Phys. Rev. A 92 012118 Google Scholar
[38]	Hu M L, Hu X , Wang J C, Peng Yi, Zhang Y R, Fan H 2018 arXiv:1703.01852 [quant-ph]
[39]	Luo S, Sun Y 2018 Phys. Rev. A 98 012113 Google Scholar
[40]	Nielsen, M A, Chuang I L 2000 Quantum Computation and Quantum Information (10th Anniversary Edition) (New York: Cambridge University Press) pp60–111, 399–416
[41]	Bures D 1969 Trans. Amer. Math. Soc. 135 199-212 Google Scholar
[42]	Hubner M 1993 Phys. Lett. A 179 226 Google Scholar
[43]	Fuchs C A, Caves C M 1995 Open Sys. Inf. Dyn. 3 345 Google Scholar
[44]	Barnum H, Caves C M, Fuchs C A, Jozsa R, Schumacher B 1996 Phys. Rev. Lett. 76 2818 Google Scholar
[45]	Uhlmann A 2000 Phys. Rev. A 62 032307 Google Scholar
[46]	Dodd J L, Nielsen M A 2002 Phys. Rev. A 66 044301 Google Scholar
[47]	Luo S, Zhang Q 2004 Phys. Rev. A 69 032106 Google Scholar

[1]	Lü Xin. Coherence and path information. Acta Physica Sinica, 2020, 69(7): 070301. doi: 10.7498/aps.69.20191084
[2]	Cheng Jun-Ni. Mach-Zehnder interferometer based on fiber taper and fiber core mismatch for humidity sensing. Acta Physica Sinica, 2018, 67(2): 024212. doi: 10.7498/aps.67.20171677
[3]	Lan Bin, Feng Guo-Ying, Zhang Tao, Liang Jing-Chuan, Zhou Shou-Huan. A single-element interferometer for measuring parallelism and uniformity of transparent plate. Acta Physica Sinica, 2017, 66(6): 069501. doi: 10.7498/aps.66.069501
[4]	Qin Chen, Yu Hui, Ye Qiao-Bo, Wei Huan, Jiang Xiao-Qing. An improved Mach-Zehnder acousto-optic modulator on a silicon-on-insulator platform. Acta Physica Sinica, 2016, 65(1): 014304. doi: 10.7498/aps.65.014304
[5]	Tan Lin-Qiu, Hua Deng-Xin, Wang Li, Gao Fei, Di Hui-Ge. Wind velocity retrieval and field widening techniques of fringe-imaging Mach-Zehnder interferometer for Doppler lidar. Acta Physica Sinica, 2014, 63(22): 224205. doi: 10.7498/aps.63.224205
[6]	Li Cheng-Qiang, Wang Ting-Feng, Zhang He-Yong, Xie Jing-Jiang, Liu Li-Sheng, Guo Jin. Effect of source parameters on polarization characteristics of electromagnetic beam propagating in atmospheric turbulence. Acta Physica Sinica, 2014, 63(10): 104201. doi: 10.7498/aps.63.104201
[7]	Zhang Ying, Liu Lan-Qin, Wang Wen-Yi, Huang Wan-Qing, Geng Yuan-Chao, Xie Xu-Dong, Zhu Qi-Hua. Effect of laser coherent superposition in multi-pass amplification process. Acta Physica Sinica, 2014, 63(18): 184205. doi: 10.7498/aps.63.184205
[8]	Li Hui-Dong, Fu Hai-Wei, Shao Min, Zhao Na, Qiao Xue-Guang, Liu Ying-Gang, Li Yan, Yan Xu. In-fiber Mach-Zehnder interferometer based on fiber core etched air-bubble and core diameter mismatch for liquid refractive index sensing. Acta Physica Sinica, 2013, 62(21): 214209. doi: 10.7498/aps.62.214209
[9]	Yin Li-Mei, Zhang Wei-Gang, Xue Xiao-Lin, Bai Zhi-Yong, Wei Shi-Lei. Study on characteristics and fluid sensing of unparallel wall fiber micro-cavity Mach-Zehnder interferometer fabricated by femtosecond laser micromachining. Acta Physica Sinica, 2012, 61(17): 170701. doi: 10.7498/aps.61.170701
[10]	Cheng Zhi-Ming, Wu Feng-Tie, Fang Xiang, Fan Dan-Dan, Zhu Jian-Qiang. Multi-bottle beam generated by vaulted axicon. Acta Physica Sinica, 2012, 61(21): 214201. doi: 10.7498/aps.61.214201
[11]	Qi Xiao-Qing, Gao Chun-Qing. Experimental study of detecting orbital angular momentumstates of spiral phase beams. Acta Physica Sinica, 2011, 60(1): 014208. doi: 10.7498/aps.60.014208
[12]	Deng Yong, Meglinski Igor. Latest progress of Monte Carlo simulation of light transmission in tissues. Acta Physica Sinica, 2010, 59(2): 1396-1401. doi: 10.7498/aps.59.1396
[13]	Zheng Li-Ming, Wang Fa-Qiang, Liu Song-Hao. Pancharatnam phase in interaction model of light and phonon. Acta Physica Sinica, 2009, 58(5): 2884-2888. doi: 10.7498/aps.58.2884
[14]	Shang Ya-Na, Wang Dong, Yan Zhi-Hui, Wang Wen-Zhe, Jia Xiao-Jun, Peng Kun-Chi. Measurement of entangled state of light with non-degenerate frequency utilizing non-balanced fiber Mach-Zehnder interferometer. Acta Physica Sinica, 2008, 57(6): 3514-3518. doi: 10.7498/aps.57.3514
[15]	Zheng Wu-Di, Zhang Guo-Ping, Wang Chen, Sun Jin-Ren, Fang Zhi-Heng, Gu Yuan, Fu Si-Zu. Diagnosis of electron density in spot-focused CH plasma with X-ray Laser M-Z interferometer. Acta Physica Sinica, 2007, 56(7): 3984-3989. doi: 10.7498/aps.56.3984
[16]	Chai Lu, He Tie-Ying, Yang Sheng-Jie, Wang Qing-Yue, Zhang Zhi-Gang. Optimization of the parameters for a SPIDER. Acta Physica Sinica, 2004, 53(1): 114-118. doi: 10.7498/aps.53.114
[17]	Liu Ting-Ting, Wang Da-Wei, Lu Wei-Xin, Sun Quan, Yang Hong, Jiang Hong-Bing, Gong Qi-Huang. An experimental proof for the fifth-order harmonic generation by a coherent-controlled two-pulse optical field. Acta Physica Sinica, 2003, 52(4): 864-869. doi: 10.7498/aps.52.864
[18]	GUO HONG-XIA, CHEN YU-SHENG, ZHANG YI-MEN, ZHOU HUI, GONG JIAN-CHENG, HAN FU-BIN, GUAN YING, WU GUO-RONG. STUDY OF RELATIVE DOSE-ENHANCEMENT EFFECTS ON CMOS DEVICE IRRADIATED BY STEADY-STATE AND TRANSIENT PULSED X-RAYS. Acta Physica Sinica, 2001, 50(12): 2279-2283. doi: 10.7498/aps.50.2279
[19]	ZHUANG SONG-LIN, ZHENG QUAN. THE IRVERSE SOURCE PROBLEM IN PARTIALLY COH-ERENT OPTICAL INFORMATION PROCESSING. Acta Physica Sinica, 1985, 34(4): 439-446. doi: 10.7498/aps.34.439
[20]	THE LASER INTEEFEBENCE KESEARCH GROUP. THE STUDY OF θ-PINCH PLASMA USING A MACH-ZEHNDER INTERFEROMETER ILLUMINATED BY A GIANT PULSED RUBY LASER. Acta Physica Sinica, 1974, 23(1): 1-16. doi: 10.7498/aps.23.1

Catalog

Vol. 68, Issue 3 - 2019-02-05

Metrics

Abstract views: 8647
PDF Downloads: 151
Cited By: 0

姓名
邮箱
手机号码
标题
留言内容
验证码

Search

Article

留言板