Cellular automaton simulation of molten pool migration due to temperature gradient zone melting

Fang Hui; Xue Hua; Tang Qian-Yu; Zhang Qing-Yu; Pan Shi-Yan; Zhu Ming-Fang

doi:10.7498/aps.68.20181587

Abstract

Directional solidification is a common and important process in both scientific research and industrial practice. Owing to the presence of temperature gradients during directional solidification, local remelting and solidification in the mushy zone occurs, resulting in some typical phenomena such as temperature gradient zone melting (TGZM). The TGZM influences the solidifying microstructure and microsegregation significantly. In the present work, a two-dimensional (2D) cellular automaton (CA) model involving the mechanism of both solidification and melting is adopted to investigate the migration phenomena of molten liquid pools in the mushy zone due to the TGZM. The effect of pulling velocity, initial liquid pool position, temperature gradient, and alloy composition on the TGZM kinetics are studied. The simulation results are compared with the analytical predictions, and good agreement between two models is obtained. It is found that under a temperature gradient, the liquid pool always migrates towards the high temperature direction. When the pulling velocity is lower than the critical velocity, the liquid pool migrates through the liquidus into the bulk liquid and the time required for a liquid pool to reach the liquidus increases with pulling velocity increasing. On the other hand, when a pulling velocity higher than the critical value is adopted, the liquid pool moves towards the solidus and the time required for migrating liquid pool to reach the solidus decreases with pulling velocity increasing. For a given pulling velocity, the liquid pools located above the critical position move towards the liquidus, while the others gradually approach to the solidus. When a molten liquid pool migrates towards the liquidus, the migration velocity and liquid pool thickness are found to gradually increase, while the liquid pool composition decreases with time. Inversely, for the molten liquid pool that moves towards the solidus, the migration velocity and liquid pool thickness gradually decrease, while the liquid pool composition increases with time going by. The average migration velocity of liquid pool caused by the TGZM effect increases with temperature gradient increasing and alloy composition decreasing. The CA simulations provide an insight into the complicated interactions among the local temperature, solute distribution and diffusion, and the kinetics of local remelting and solidification in the TGZM process.

Keywords:

Authors and contacts

1.
Jiangsu Key Laboratory of Advanced Metallic Materials, School of Materials Science and Engineering, Southeast University, Nanjing 211189, China
2.
School of Materials Science and Engineering, Nanjing University of Science and Technology, Nanjing 210094, China

Corresponding author: Zhu Ming-Fang, zhumf@seu.edu.cn

Funds: Project supported by the National Natural Science Foundation of China (Grant Nos. 51371051, 51501091), the Fundamental Research Funds for the Central Universities of Ministry of Education of China (Grant No. 2242016K40008), and the Scientific Research Foundation of Graduate School of Southeast University, China (Grant No. YBJJ1627).

FullText HTML : translate this paragraph

References

[1]	Rettenmayr M 2009 Int. Mater. Rev. 54 1 Google Scholar
[2]	Pfann W G 1955 Trans. AIME 203 961
[3]	Tiller W A 1963 J. Appl. Phys. 34 2757 Google Scholar
[4]	Allen D J, Hunt J D 1976 Metall. Mater. Trans. A 7 767 Google Scholar
[5]	Kinoshita K, Arai Y, Inatomi Y, Tsukada T, Miyata H, Tanaka R 2016 J. Cryst. Growth 455 49 Google Scholar
[6]	Wang H, Li S, Li X, Zhong H 2017 J. Cryst. Growth 466 56 Google Scholar
[7]	Ma X, Yoshikawa T, Morita K 2014 Sci. Adv. Mater. 6 1697 Google Scholar
[8]	Shirzadi A A, Wallach E R 1999 Acta Mater. 47 3551 Google Scholar
[9]	Nguyen-Thi H, Reinhart G, Buffet A, Schenk T, Mangelinck-Noel N, Jung H, Bergeon N, Billia B, Hartwig J, Baruchel J 2008 J. Cryst. Growth 310 2906 Google Scholar
[10]	Buchmann M, Rettenmayr M 2005 J. Cryst. Growth 284 544 Google Scholar
[11]	Bösenberg U, Buchmann M, Rettenmayr M 2007 J. Cryst. Growth 304 281 Google Scholar
[12]	Löffler A, Reuther K, Engelhardt H, Liu D, Rettenmayr M 2015 Acta Mater. 91 34 Google Scholar
[13]	Liu D M, Li X Z, Su Y Q, Peng P, Luo L S, Guo J J, Fu H Z 2012 Acta Mater. 60 2679 Google Scholar
[14]	Liu D M, Li X Z, Su Y Q, Rettenmayr M, Guo J J, Fu H Z 2014 Appl. Phys. A 116 1821 Google Scholar
[15]	Pan S Y, Zhang Q Y, Zhu M F, Rettenmayr M 2015 Acta Mater. 86 229 Google Scholar
[16]	朱鸣芳, 汤倩玉, 张庆宇, 潘诗琰, 孙东科 2016 金属学报 52 1297 Google Scholar Zhu M F, Tang Q Y, Zhang Q Y, Pan S Y, Sun D K 2016 Acta Metall. Sin. 52 1297 Google Scholar
[17]	陈瑞, 许庆彦, 柳百成 2014 63 188102 Google Scholar Chen R, Xu Q Y, Liu B C 2014 Acta Phys. Sin . 63 188102 Google Scholar
[18]	张云鹏, 林鑫, 魏雷, 王猛, 彭东剑, 黄卫东 2012 61 228106 Google Scholar Zhang Y P, Lin X, Wei L, Wang M, Peng D J, Huang W D 2012 Acta Phys. Sin. 61 228106 Google Scholar
[19]	江鸿翔, 赵九洲 2011 金属学报 47 1099 Jiang H X, Zhao J Z 2011 Acta Metall. Sin. 47 1099
[20]	Zhu M F, Stefanescu D M 2007 Acta Mater. 55 1741 Google Scholar
[21]	Pan S, Zhu M 2010 Acta Mater. 58 340 Google Scholar
[22]	李强, 李殿中, 钱百年 2004 53 3477 Google Scholar Li Q, Li D Z, Qian B N 2004 Acta Phys. Sin. 53 3477 Google Scholar
[23]	Wei L, Lin X, Wang M, Huang W D 2015 Chin. Phys. B 24 078108 Google Scholar
[24]	Zhang Q Y, Fang H, Xue H, Pan S Y, Rettenmayr M, Zhu M F 2017 Sci. Rep. 7 17809 Google Scholar
[25]	朱鸣芳, 邢丽科, 方辉, 张庆宇, 汤倩玉, 潘诗琰 2018 金属学报 54 789 Google Scholar Zhu M F, Xing L K, Fang H, Zhang Q Y, Tang Q Y, Pan S Y 2018 Acta Metall. Sin. 54 789 Google Scholar
[26]	Zhang Q Y, Xue H, Tang Q Y, Pan S Y, Rettenmayr M, Zhu M F 2018 Comput. Mater. Sci. 146 20
[27]	Zhang Q Y, Fang H, Xue H, Tang Q Y, Pan S Y, Rettenmayr M, Zhu M F 2018 Scr. Mater. 151 28 Google Scholar
[28]	Farup I, Drezet J M, Rappaz M 2001 Acta Mater. 49 1261 Google Scholar

Cited By

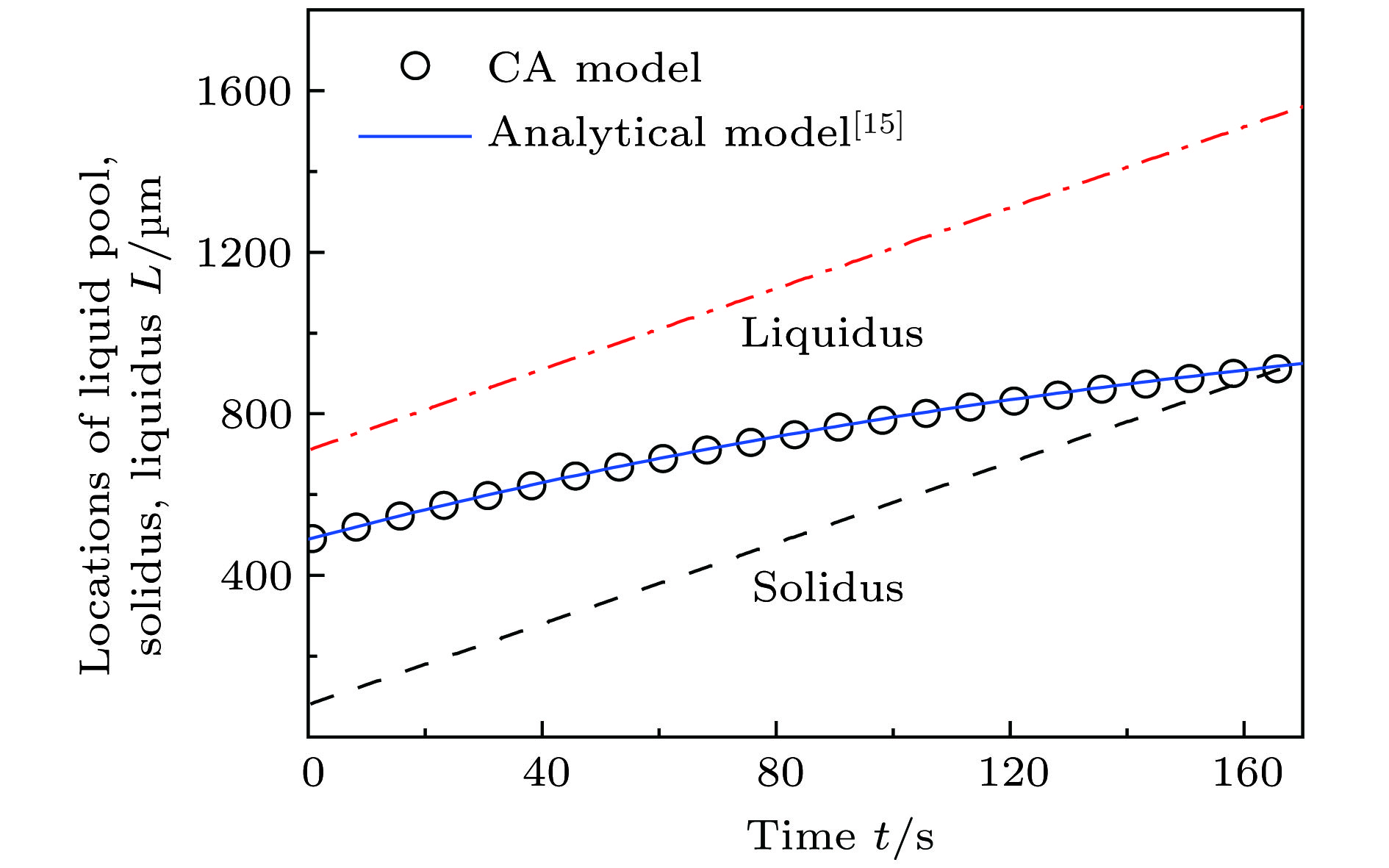
图 1 SCN–0.3 wt.% ACE合金在$\scriptstyle V_{\rm p}=0.6\;{\text{μ}}{\rm m/s}$($\scriptstyle {\tilde y_0} = 0.05$)和G = 12°C/mm条件下, 迁移熔池位置随时间变化的CA模拟结果与解析模型^[15]预测结果的比较

Figure 1. Comparison of the CA simulation with the analytical prediction^[15]regarding the time evolution of the location of a migrating liquid pool for a SCN–0.3 wt.% ACE alloy at $\scriptstyle V_{\rm p}=0.6\;{\text{μ}}{\rm m/s}$, $\scriptstyle{\tilde y_0} = 0.05$ and G = 12°C/mm.

DownLoad: Full-Size Img PowerPoint

图 2 SCN–0.3 wt.%ACE合金在$\scriptstyle V_{\rm p}=0.6\;{\text{μ}}{\rm m/s}$($\scriptstyle{\tilde y_0} = 0.05$)和G = 12 °C/mm条件下, (a)熔池迁移速度和(b)熔池成分随时间变化的CA模拟和解析模型^[15]预测结果的比较

Figure 2. Comparison of the CA simulation with the analytical prediction^[15] regarding the time evolution of (a) liquid pool velocity and (b) liquid pool composition for a SCN–0.3 wt.% ACE alloy at $\scriptstyle V_{\rm p}=0.6\;{\text{μ}}{\rm m/s}$, $\scriptstyle{\tilde y_0} = 0.05$ and G = 12°C/mm.

DownLoad: Full-Size Img PowerPoint

图 3 SCN–0.3 wt.% ACE合金在$\scriptstyle V_{\rm p}=5\;{\text{μ}}{\rm m/s}$($\scriptstyle{\tilde y_0} = 0.65$)和G = 12 °C/mm条件下, 迁移熔池位置随时间变化的CA模拟结果与解析模型^[15]预测结果的比较

Figure 3. Comparison of the CA simulation with the analytical prediction^[15] regarding the time evolution of the location of a migrating liquid pool for a SCN–0.3 wt.% ACE alloy at $\scriptstyle V_{\rm p}=5\;{\text{μ}}{\rm m/s}$, $\scriptstyle {\tilde y_0} = 0.65$ and G = 12 °C/mm.

DownLoad: Full-Size Img PowerPoint

图 4 SCN–0.3 wt.%ACE合金在$\scriptstyle V_{\rm p}=5\;{\text{μ}}{\rm m/s}$($\scriptstyle {\tilde y_0} = 0.65$)和G = 12°C/mm条件下, (a)熔池迁移速度和(b)熔池成分随时间变化的CA模拟和解析模型^[15]预测结果的比较

Figure 4. Comparison of the CA simulation with the analytical prediction^[15] regarding the time evolution of (a) liquid pool velocity and (b) liquid pool composition for a SCN–0.3 wt.% ACE alloy at $\scriptstyle V_{\rm p}=5\;{\text{μ}}{\rm m/s}$, $\scriptstyle {\tilde y_0} = 0.65$ and G = 12°C/mm.

DownLoad: Full-Size Img PowerPoint

图 5 SCN–0.3 wt.% ACE合金在G = 12 °C/mm条件下, (a) V_p < V_{p, cr}时熔池从初始位置($\scriptstyle {\tilde y_0} = 0.05$)迁移到移动的液相线所需时间t_l和(b) V_p > V_{p, cr}情况下熔池从初始位置($\scriptstyle {\tilde y_0} = 0.65$)迁移到移动的固相线所需时间t_s随抽拉速度变化的CA模拟与解析模型^[15]预测结果的比较

Figure 5. Comparison of the CA simulations with the analytical predictions ^[15] regarding the times required for a liquid pool to reach (a) the moving liquidus from $\scriptstyle{\tilde y_0} = 0.05$ at V_p < V_{p, cr} and (b) the moving solidus from $\scriptstyle{\tilde y_0} = 0.65$ at V_p > V_{p, cr} as a function of the pulling velocity for a SCN–0.3 wt.% ACE alloy at G = 12 °C/mm.

DownLoad: Full-Size Img PowerPoint

图 6 CA模拟的SCN–0.3 wt.% ACE合金在V_p = $ \scriptstyle 2.89\;{\text{μ}}{\rm m/s} $和G = 12°C/mm的条件下 (相应的临界位置$\scriptstyle{\tilde y_{0, {\rm{cr}}}}$ = 0.5), 5个不同初始位置的熔池的迁移演化过程 (a) 2 s; (b) 20 s; (c) 37 s. 5个熔池的无量纲初始位置分别为${\tilde y_0}$ = 0.08, 0.3, 0.5, 0.6和0.75. $\scriptstyle\widetilde y$为无量纲液滴位置, y为液滴位置

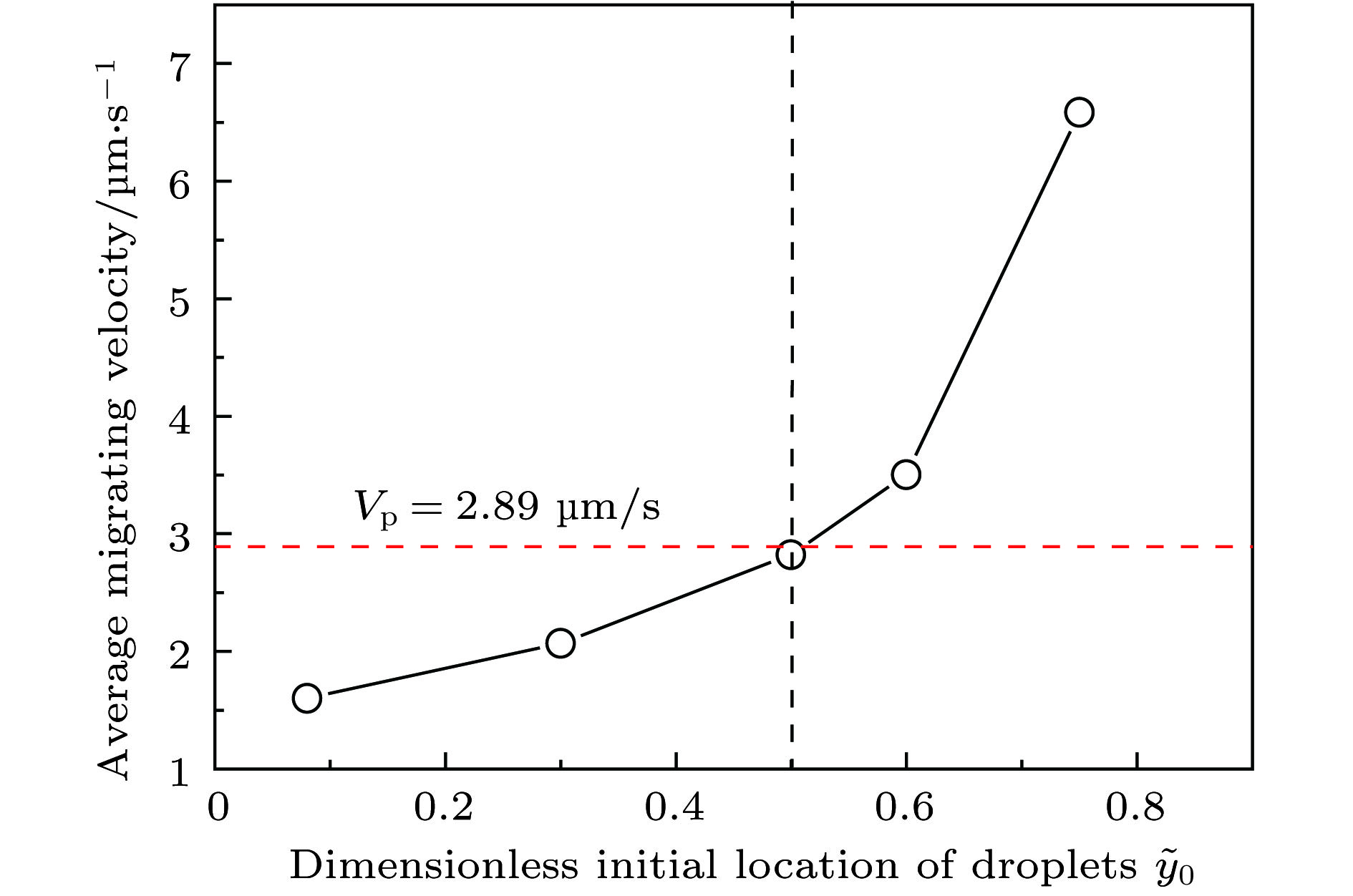
Figure 6. Simulated sequence of liquid pool migration for a SCN–0.3 wt.% ACE alloy at G = 12 °C/mm, $ \scriptstyle V_{\rm p}=2.89\;{\text{μ}}{\rm m/s} $ corresponding to $\scriptstyle {\tilde y_{0, {\rm{cr}}}}$ = 0.5: (a) 2 s; (b) 20 s; (c) 37 s. The dimensionless initial positions of the five liquid pools are $\scriptstyle {\tilde y_0}$ = 0.08, 0.3, 0.5, 0.6 and 0.75, respectively. $\scriptstyle \widetilde y$ is the dimensionless droplet position, y is the droplet position.

DownLoad: Full-Size Img PowerPoint

图 7 CA模拟的SCN–0.3 wt.% ACE合金在V_p = 2.89 ${\text{μ}}$m/s和G = 12°C/mm条件下(相应的临界位置${\tilde y_{0, {\rm{cr}}}}$ = 0.5), 平均迁移速度随无量纲初始熔池位置的变化

Figure 7. CA simulated average migrating velocity as a function of the dimensionless initial liquid pool position for a SCN–0.3 wt.% ACE alloy at G = 12°C/mm and V_p = 2.89 ${\text{μ}}$m/s, corresponding to ${\tilde y_{0, {\rm{cr}}}}$ = 0.5.

DownLoad: Full-Size Img PowerPoint

图 8 CA模拟的SCN–0.3 wt.% ACE合金在不同温度梯度条件下, 熔池迁移速度随时间的变化 (a) $ V_{\rm p} = 0.6 \;{\text{μ}}{\rm m/s}$, $ {\tilde y_0}$ = 0.3, V_p < V_{p, cr}; (b) $ V_{\rm p} = 5{\text{μ}}{\rm m/s}$, $ {\tilde y_0} $ = 0.7, V_p > V_{p, cr}

Figure 8. CA simulated time evolution of liquid pool velocity for a SCN–0.3 wt.% ACE alloy at different temperature gradients and (a) $ V_{\rm p} = 0.6{\text{μ}}{\rm m/s}$, $ {\tilde y_0}$ = 0.3, V_p < V_{p, cr}; (b) $ V_{\rm p} = 5{\text{μ}}{\rm m/s}$, ${\tilde y_0}$ = 0.7, V_p > V_{p, cr}.

DownLoad: Full-Size Img PowerPoint

图 9 CA模拟的不同成分SCN–ACE合金熔池在G = 14°C/mm时迁移速度随时间的变化 (a) ${V_{\rm p} = 0.2 \;{\text{μ}}{\rm m/s}}$, ${\tilde y_0}$ = 0.4, V_p < V_{p, cr}; (b) $ V_{\rm p} = 6\;{\text{μ}}{\rm m/s}$, ${\tilde y_0}$ = 0.7, V_p > V_{p, cr}

Figure 9. CA simulated time evolution of liquid pool velocity for SCN-ACE alloys at G = 14°C/mm, different compositions and (a) $ V_{\rm p} = 0.2 \;{\text{μ}}{\rm m/s}$, ${\tilde y_0}$ = 0.4, V_p < V_{p, cr}; (b) $ V_{\rm p} = 6\;{\text{μ}}{\rm m/s}$, ${\tilde y_0}$ = 0.7, V_p > V_{p, cr}.

DownLoad: Full-Size Img PowerPoint

表 1 本文工作采用的物性参数^[15,28]

Table 1. The physical parameters used in the present work^[15,28].

符号物理意义数值

D_l/m²·s^–1 溶质在液相中的扩散系数 1 × 10^–9
k 平衡分配系数 0.1
m_l/K·(wt.%)^–1 液相线斜率 –2.8
T_m/°C 纯SCN的熔点 58.081

DownLoad: CSV

map

[1]	Rettenmayr M 2009 Int. Mater. Rev. 54 1 Google Scholar
[2]	Pfann W G 1955 Trans. AIME 203 961
[3]	Tiller W A 1963 J. Appl. Phys. 34 2757 Google Scholar
[4]	Allen D J, Hunt J D 1976 Metall. Mater. Trans. A 7 767 Google Scholar
[5]	Kinoshita K, Arai Y, Inatomi Y, Tsukada T, Miyata H, Tanaka R 2016 J. Cryst. Growth 455 49 Google Scholar
[6]	Wang H, Li S, Li X, Zhong H 2017 J. Cryst. Growth 466 56 Google Scholar
[7]	Ma X, Yoshikawa T, Morita K 2014 Sci. Adv. Mater. 6 1697 Google Scholar
[8]	Shirzadi A A, Wallach E R 1999 Acta Mater. 47 3551 Google Scholar
[9]	Nguyen-Thi H, Reinhart G, Buffet A, Schenk T, Mangelinck-Noel N, Jung H, Bergeon N, Billia B, Hartwig J, Baruchel J 2008 J. Cryst. Growth 310 2906 Google Scholar
[10]	Buchmann M, Rettenmayr M 2005 J. Cryst. Growth 284 544 Google Scholar
[11]	Bösenberg U, Buchmann M, Rettenmayr M 2007 J. Cryst. Growth 304 281 Google Scholar
[12]	Löffler A, Reuther K, Engelhardt H, Liu D, Rettenmayr M 2015 Acta Mater. 91 34 Google Scholar
[13]	Liu D M, Li X Z, Su Y Q, Peng P, Luo L S, Guo J J, Fu H Z 2012 Acta Mater. 60 2679 Google Scholar
[14]	Liu D M, Li X Z, Su Y Q, Rettenmayr M, Guo J J, Fu H Z 2014 Appl. Phys. A 116 1821 Google Scholar
[15]	Pan S Y, Zhang Q Y, Zhu M F, Rettenmayr M 2015 Acta Mater. 86 229 Google Scholar
[16]	朱鸣芳, 汤倩玉, 张庆宇, 潘诗琰, 孙东科 2016 金属学报 52 1297 Google Scholar Zhu M F, Tang Q Y, Zhang Q Y, Pan S Y, Sun D K 2016 Acta Metall. Sin. 52 1297 Google Scholar
[17]	陈瑞, 许庆彦, 柳百成 2014 63 188102 Google Scholar Chen R, Xu Q Y, Liu B C 2014 Acta Phys. Sin . 63 188102 Google Scholar
[18]	张云鹏, 林鑫, 魏雷, 王猛, 彭东剑, 黄卫东 2012 61 228106 Google Scholar Zhang Y P, Lin X, Wei L, Wang M, Peng D J, Huang W D 2012 Acta Phys. Sin. 61 228106 Google Scholar
[19]	江鸿翔, 赵九洲 2011 金属学报 47 1099 Jiang H X, Zhao J Z 2011 Acta Metall. Sin. 47 1099
[20]	Zhu M F, Stefanescu D M 2007 Acta Mater. 55 1741 Google Scholar
[21]	Pan S, Zhu M 2010 Acta Mater. 58 340 Google Scholar
[22]	李强, 李殿中, 钱百年 2004 53 3477 Google Scholar Li Q, Li D Z, Qian B N 2004 Acta Phys. Sin. 53 3477 Google Scholar
[23]	Wei L, Lin X, Wang M, Huang W D 2015 Chin. Phys. B 24 078108 Google Scholar
[24]	Zhang Q Y, Fang H, Xue H, Pan S Y, Rettenmayr M, Zhu M F 2017 Sci. Rep. 7 17809 Google Scholar
[25]	朱鸣芳, 邢丽科, 方辉, 张庆宇, 汤倩玉, 潘诗琰 2018 金属学报 54 789 Google Scholar Zhu M F, Xing L K, Fang H, Zhang Q Y, Tang Q Y, Pan S Y 2018 Acta Metall. Sin. 54 789 Google Scholar
[26]	Zhang Q Y, Xue H, Tang Q Y, Pan S Y, Rettenmayr M, Zhu M F 2018 Comput. Mater. Sci. 146 20
[27]	Zhang Q Y, Fang H, Xue H, Tang Q Y, Pan S Y, Rettenmayr M, Zhu M F 2018 Scr. Mater. 151 28 Google Scholar
[28]	Farup I, Drezet J M, Rappaz M 2001 Acta Mater. 49 1261 Google Scholar

[1]	Liang Jing-Yun, Zhang Li-Li, Luan Xi-Dao, Guo Jin-Lin, Lao Song-Yang, Xie Yu-Xiang. Multi-section cellular automata model of traffic flow. Acta Physica Sinica, 2017, 66(19): 194501. doi: 10.7498/aps.66.194501
[2]	Jiang Han, Chen Ming-Wen, Wang Tao, Wang Zi-Dong. Effects of anisotropic interface kinetics and surface tension on deep cellular crystal growth in directional solidification. Acta Physica Sinica, 2017, 66(10): 106801. doi: 10.7498/aps.66.106801
[3]	Wei Lei, Lin Xin, Wang Meng, Huang Wei-Dong. Cellular automaton simulation of the molten pool of laser solid forming process. Acta Physica Sinica, 2015, 64(1): 018103. doi: 10.7498/aps.64.018103
[4]	Han Ri-Hong, Dong Wen-Chao, Lu Shan-Ping, Li Dian-Zhong, Li Yi-Yi. Macro-micro coupled simulation of competitive dendrite growth in different areas of the welding pool. Acta Physica Sinica, 2014, 63(22): 228103. doi: 10.7498/aps.63.228103
[5]	Chen Ming-Wen, Chen Yi-Chen, Zhang Wen-Long, Liu Xiu-Min, Wang Zi-Dong. Effect of anisotropic surface tension on deep cellular crystal growth in directional solidification. Acta Physica Sinica, 2014, 63(3): 038101. doi: 10.7498/aps.63.038101
[6]	Chen Rui, Xu Qing-Yan, Liu Bai-Cheng. Simulation of dendritic competitive growth during directional solidification using modified cellular automaton method. Acta Physica Sinica, 2014, 63(18): 188102. doi: 10.7498/aps.63.188102
[7]	Yong Gui, Huang Hai-Jun, Xu Yan. A cellular automata model of pedestrian evacuation in rooms with squared rhombus cells. Acta Physica Sinica, 2013, 62(1): 010506. doi: 10.7498/aps.62.010506
[8]	Wang Xian-Bin, Lin Xin, Wang Li-Lin, Yu Hong-Lei, Wang Meng, Huang Wei-Dong. Influence of liquid flow on cellular and dendritic spacings. Acta Physica Sinica, 2013, 62(7): 078102. doi: 10.7498/aps.62.078102
[9]	Shi Yu-Feng, Xu Qing-Yan, Liu Bai-Cheng. Simulation and experimental research of melt convection on dendrite morphology evolution. Acta Physica Sinica, 2011, 60(12): 126101. doi: 10.7498/aps.60.126101
[10]	Li Qing-Ding, Dong Li-Yun, Dai Shi-Qiang. Investigation on traffic bottleneck induce by bus stopping with a two-lane cellular automaton model. Acta Physica Sinica, 2009, 58(11): 7584-7590. doi: 10.7498/aps.58.7584
[11]	Huang Feng, Di Hong-Shuang, Wang Guang-Shan. Modelling of solidification microstructure evolution of twin-roll casting magnesium strip using cellular automaton. Acta Physica Sinica, 2009, 58(13): 313-S318. doi: 10.7498/aps.58.313
[12]	Shan Bo-Wei, Lin Xin, Wei Lei, Huang Wei-Dong. A cellular automaton model for dendrite solidification of pure substance. Acta Physica Sinica, 2009, 58(2): 1132-1138. doi: 10.7498/aps.58.1132
[13]	Mei Chao-Qun, Huang Hai-Jun, Tang Tie-Qiao. A cellular automaton model for studying the on-ramp control of highway. Acta Physica Sinica, 2008, 57(8): 4786-4793. doi: 10.7498/aps.57.4786
[14]	Yue Hao, Shao Chun-Fu, Chen Xiao-Ming, Hao He-Rui. Simulation of bi-directional pedestrian flow based on cellular automata model. Acta Physica Sinica, 2008, 57(11): 6901-6908. doi: 10.7498/aps.57.6901
[15]	Zhang Wen-Zhu, Yuan Jian, Yu Zhe, Xu Zan-Xin, Shan Xiu-Ming. Study of the global behavior of wireless sensor networks based on cellular automata. Acta Physica Sinica, 2008, 57(11): 6896-6900. doi: 10.7498/aps.57.6896
[16]	Guo Si-Ling, Wei Yan-Fang, Xue Yu. On the characteristics of phase transition in CA traffic models. Acta Physica Sinica, 2006, 55(7): 3336-3342. doi: 10.7498/aps.55.3336
[17]	Wu Ke-Fei, Kong Ling-Jiang, Liu Mu-Ren. The study of a cellular automaton NS and WWH mixed model for traffic flow on a two-lane roadway. Acta Physica Sinica, 2006, 55(12): 6275-6280. doi: 10.7498/aps.55.6275
[18]	Hua Wei, Lin Bo-Liang. One-dimensional traffic cellular automaton model with considering the vehicle moving status. Acta Physica Sinica, 2005, 54(6): 2595-2599. doi: 10.7498/aps.54.2595
[19]	Mou Yong-Biao, Zhong Cheng-Wen. Cellular automaton model of traffic flow based on safety driving. Acta Physica Sinica, 2005, 54(12): 5597-5601. doi: 10.7498/aps.54.5597
[20]	Li Mei-E, Yang Gen-Cang, Zhou Yao-He. Phase field modeling of directional solidification of a binary alloy at high velocities. Acta Physica Sinica, 2005, 54(1): 454-459. doi: 10.7498/aps.54.454

Catalog

Vol. 68, Issue 4 - 2019-02-20

Metrics

Abstract views: 7740
PDF Downloads: 74
Cited By: 0

姓名
邮箱
手机号码
标题
留言内容
验证码

Search

Article

留言板