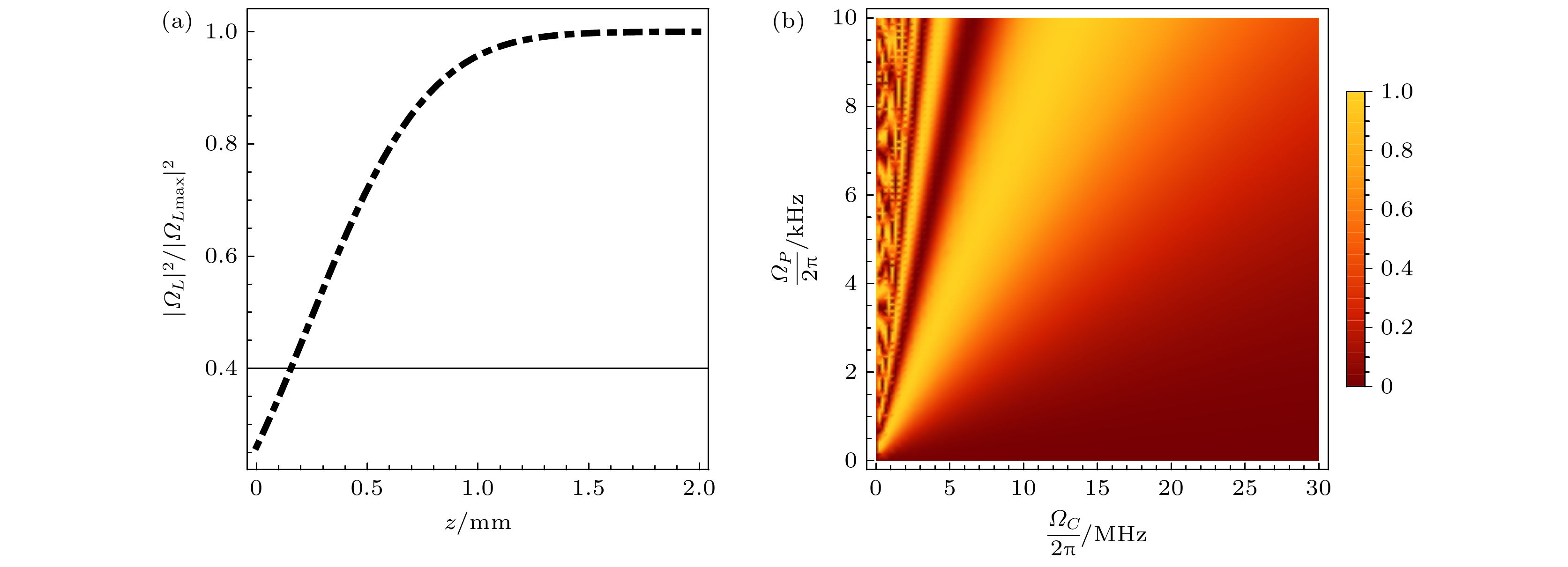
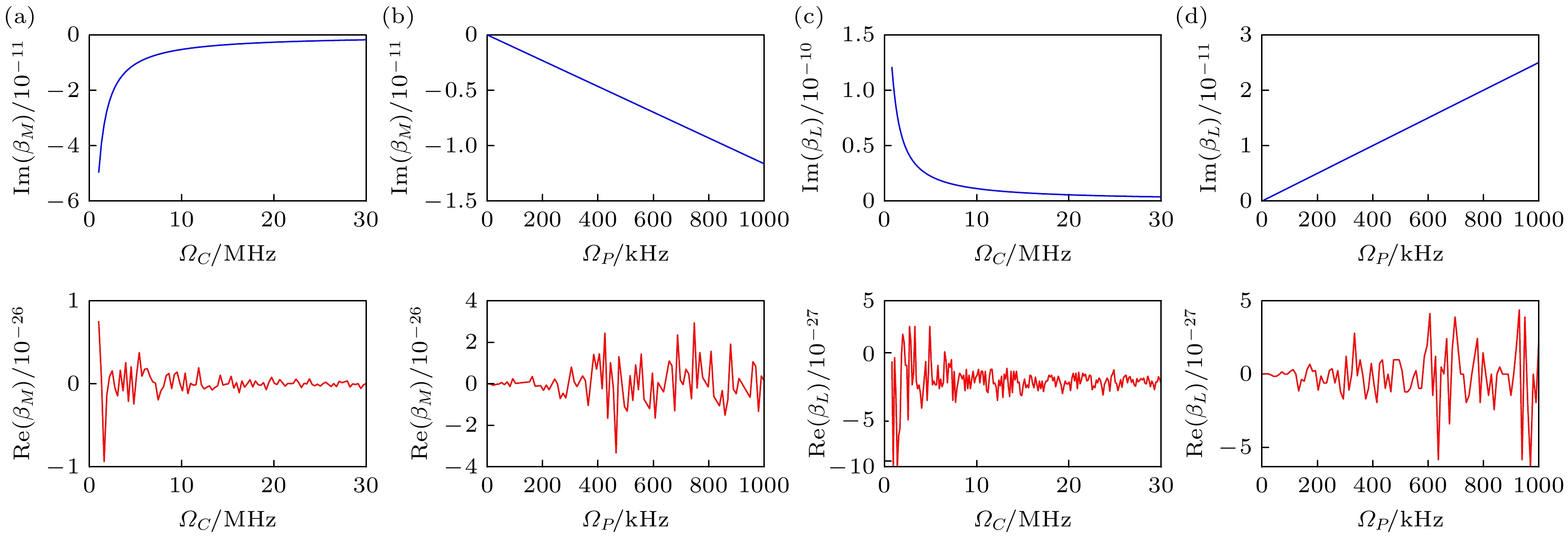
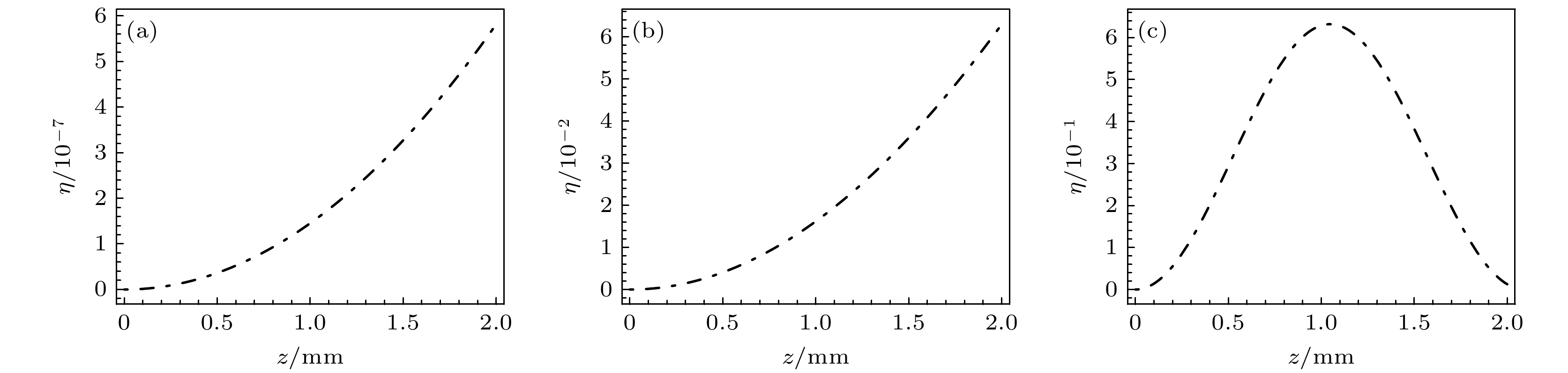
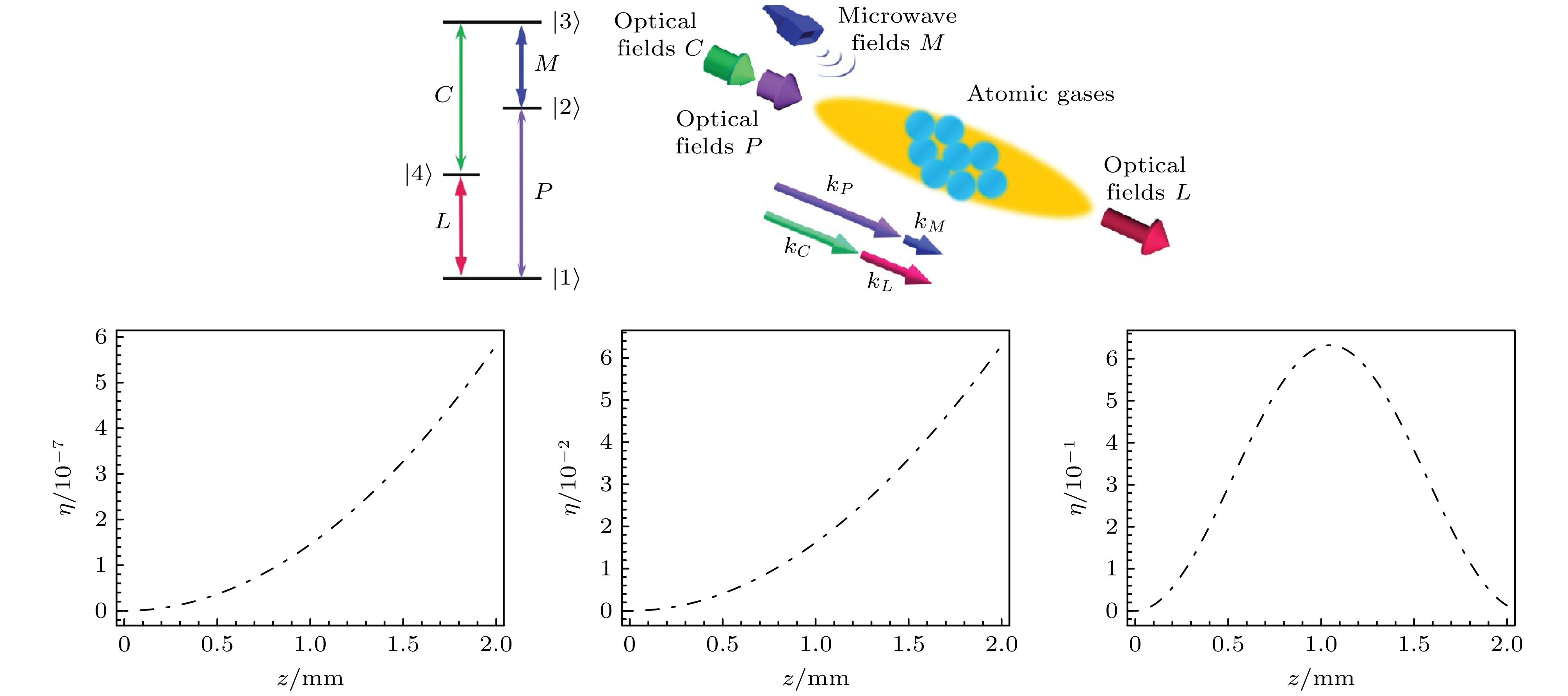
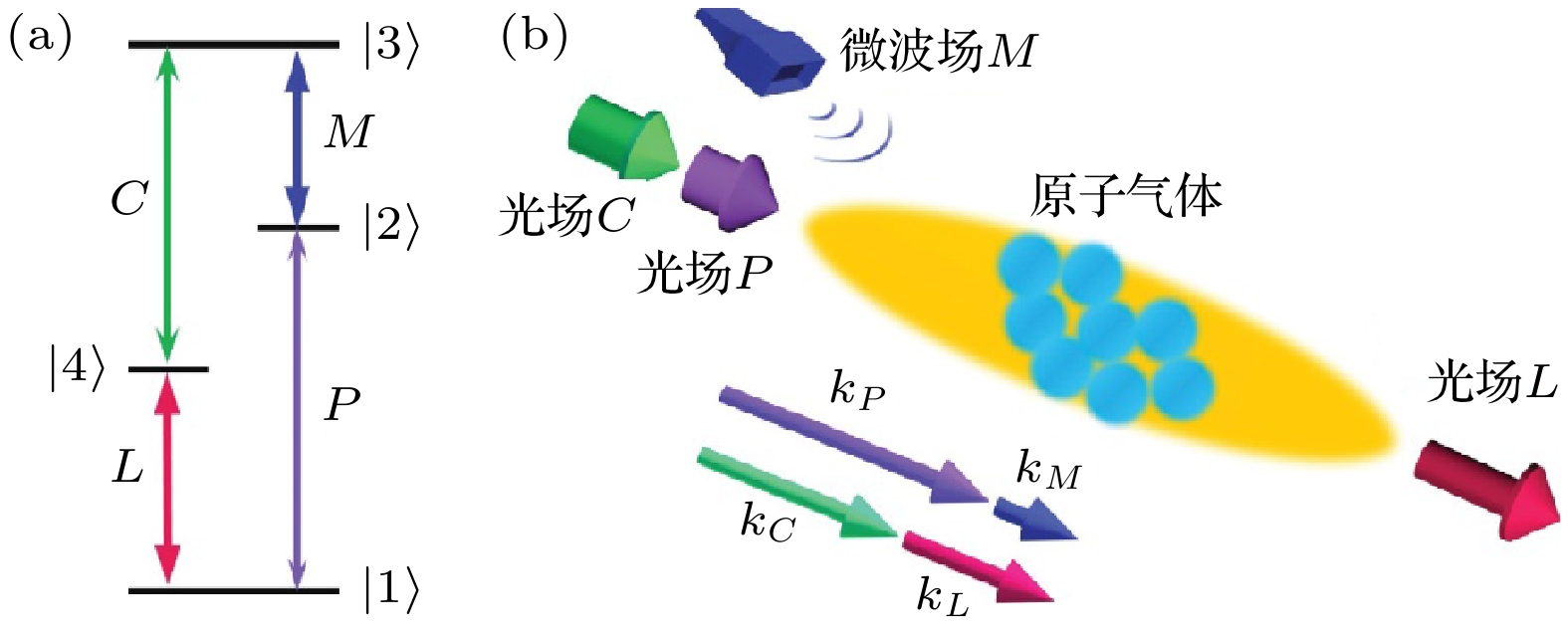
-
微波-光波转换是混合量子网络的核心技术, 然而热原子系综中的多普勒展宽效应常常成为限制转换效率的瓶颈. 本文提出基于室温里德伯原子的四波混频转换新机制, 采用密度矩阵法和微扰法结合麦克斯韦方程, 推导出双梯形四能级四波混频过程中表征微波场与光场之间相干系数的解析表达式, 并由此获得四波混频转换效率的解析表达式. 利用铯蒸气作为介质, 详细分析了四波混频效率的传播特性, 并探讨了激光场强度和多普勒效应对转换效率的影响. 研究结果表明, 原子的热运动引起的失谐效应会降低共振耦合效率, 当多普勒频率小于自然线宽时, 转换效率可显著提高. 本研究不仅为室温条件下的微波-光波转换提供了新的理论指导和实验方案, 而且对于推动量子信息技术的进步具有重要意义.Microwave-to-optics conversion is a core technology for hybrid quantum networks, enabling the integration of microwave and optical frequency domains essential for quantum communication and quantum information processing. However, the Doppler broadening effect in thermal atomic ensembles often severely limits the conversion efficiency. This study aims to propose a novel mechanism for microwave-to-optics conversion using four-wave mixing (FWM) in room-temperature Rydberg atoms, addressing the challenges posed by Doppler broadening and providing a theoretical framework for practical applications. We develop a theoretical model based on the coupled Maxwell-Bloch equations to describe the FWM process in a symmetric double-ladder four-level system. The density matrix method and perturbation method combined with Maxwell’s equations are used to derive an analytical expression for the coherence coefficient between the microwave field and the optical field. This coherence coefficient characterizes the energy transfer between the microwave and optical fields and is used to obtain an analytical expression for the FWM conversion efficiency. We use cesium vapor as a medium to analyze the propagation characteristics of the FWM efficiency and explore the effects of laser field intensity and the Doppler effect on the conversion efficiency. Our analysis reveals that the detuning effect caused by the thermal motion of atoms significantly reduces the resonance coupling efficiency. Specifically, when the Doppler frequency is lower than the natural linewidth, the conversion efficiency can be notably improved. In a Doppler-free environment, the conversion efficiency approaches unity at an optimal propagation distance. In contrast, in room-temperature cesium vapor (300 K), the conversion efficiency is significantly reduced due to Doppler broadening. However, by cooling the atoms to microkelvin temperatures, the Doppler broadening can be minimized, leading to a substantial increase in conversion efficiency. This study provides new theoretical guidance and experimental schemes for microwave-to-optics conversion at room temperature. The proposed mechanism based on Rydberg atoms provides a promising approach to overcoming the limitations imposed by Doppler broadening. Our findings are of great significance for advancing quantum information technology, especially in the context of developing efficient quantum networks.
-
Keywords:
- four-wave mixing /
- Rydberg atom /
- Doppler effect /
- quantum coherence
[1] Kimble H J 2008 Nature 453 1023
Google Scholar
[2] Lambert N J, Rueda A, Sedlmeir F, Schwefel H G L 2020 Adv. Quantum Technol. 3 1900077
Google Scholar
[3] Han X, Fu W, Zou C L, Jiang L, Tang H X 2021 Optica 8 1050
Google Scholar
[4] Lauk N, Sinclair N, Barzanjeh S, Covey J P, Saffman M, Spiropulu M, Simon C 2020 Quantum Sci. Technol. 5 020501
Google Scholar
[5] Strekalov D V, Savchenkov A A, Matsko A B, Yu N 2009 Opt. Lett. 34 713
Google Scholar
[6] 刘瑶, 何军, 苏楠, 蔡婷, 刘智慧, 刁文婷, 王军民 2023 72 060303
Google Scholar
Liu Y, He J, Su N, Cai T, Liu Z H, Diao W T, Wang J M 2023 Acta Phys. Sin. 72 060303
Google Scholar
[7] Zibrov A S, Matsko A B, Scully M O 2002 Phys. Rev. Lett. 89 103601
Google Scholar
[8] Han J S, Vogt T, Gross C, Jaksch D, Kiffner M, Li W H 2018 Phys. Rev. Lett. 120 093201
Google Scholar
[9] Vogt T, Gross C, Han J S, Sambit B P, Mark L, Kiffner M, Li W H 2019 Phys. Rev. A 99 023822
Google Scholar
[10] Tu H T, Liao K Y, Zhang Z X, Liu X H, Zheng S Y, Yang S Z, Zhang X D, Yan H, Zhu S L 2022 Nat. Photonics 16 291
Google Scholar
[11] Sebastian B, Uliana P, Mateusz M, Michał P 2024 Nat. Photonics 18 32
Google Scholar
[12] Kumar A, Suleymanzade A, Stone M, Taneja L, Anferov A, Schuster D I, Simon J 2023 Nature 615 614
Google Scholar
[13] Fan L, Zou C L, Cheng R, Guo X, Han X, Gong Z, Wang S, Tang H X 2018 Sci. Adv. 4 eaar4994
Google Scholar
[14] Higginbotham A P, Burns P S, Urmey M D, Peterson R W, Kampel N S, Brubaker B M, Smith G, Lehnert K W, Regal C A 2018 Nat. Phys. 14 1038
Google Scholar
[15] Mirhosseini M, Sipahigil A, Kalaee M, Painter O 2020 Nature 588 599
Google Scholar
[16] Delaney R D, Urmey M D, Mittal S, Brubaker B M, Kindem J M, Burns P S, Regal C A, Lehnert K W 2022 Nature 606 489
Google Scholar
[17] Petrosyan D, Mølmer K, Fortágh J, Saffman M 2019 New J. Phys. 21 073033
Google Scholar
[18] 苗强, 吴德伟 2025 激光与光电子学进展 62 0100004
Google Scholar
Miao Q, Wu D W 2025 Laser Optoelectron. Prog. 62 0100004
Google Scholar
[19] Covey J P, Sipahigil Alp, Saffman M 2019 Phys. Rev. A 100 012307
Google Scholar
[20] Kiffner M, Feizpour A, Kaczmarek K T, Jaksch D, Nunn J 2016 New J. Phys. 18 093030
Google Scholar
[21] Demtröder W 2008 Laser Spectroscopy (Berlin: Springer) pp70–75
-
图 1 四波混频示意图 (a) 对称梯形原子结构图; (b) 实现微波-光学转换的实验装置示意图
Fig. 1. Schematic diagrams of four-wave mixing: (a) Symmetric ladder configuration; (b) geometry of the setup enabling microwave-to-optical conversion.
图 2 无多普勒效应结果图 (a) 生成场L在空间位置的分布图; (b) 共振时转换效率与控制场和泵浦场的关系图
Fig. 2. Result of Doppler effect free: (a) Intensities of the converted field L versus position z; (b) 2D density map of the efficiency for the all-resonant case versus ${\varOmega _C}$and $ {\varOmega _P} $.
图 3 室温下互相干系数实部与虚部与控制场和泵浦场的关系图
Fig. 3. Relationship between the real and imaginary parts of the coefficient $ {\beta _M} $ and $ {\beta _L} $ at room temperature versus $ {\varOmega _C} $ and $ {\varOmega _P} $
图 4 不同温度下转换效率与空间位置的关系图 (a) T = 300 K; (b) T = 3 mK; (c) T = 30 μK
Fig. 4. Relationship between conversion efficiency and spatial position at different temperatures: (a) T = 300 K; (b) T = 3 mK; (c) T = 30 μK.
-
[1] Kimble H J 2008 Nature 453 1023
Google Scholar
[2] Lambert N J, Rueda A, Sedlmeir F, Schwefel H G L 2020 Adv. Quantum Technol. 3 1900077
Google Scholar
[3] Han X, Fu W, Zou C L, Jiang L, Tang H X 2021 Optica 8 1050
Google Scholar
[4] Lauk N, Sinclair N, Barzanjeh S, Covey J P, Saffman M, Spiropulu M, Simon C 2020 Quantum Sci. Technol. 5 020501
Google Scholar
[5] Strekalov D V, Savchenkov A A, Matsko A B, Yu N 2009 Opt. Lett. 34 713
Google Scholar
[6] 刘瑶, 何军, 苏楠, 蔡婷, 刘智慧, 刁文婷, 王军民 2023 72 060303
Google Scholar
Liu Y, He J, Su N, Cai T, Liu Z H, Diao W T, Wang J M 2023 Acta Phys. Sin. 72 060303
Google Scholar
[7] Zibrov A S, Matsko A B, Scully M O 2002 Phys. Rev. Lett. 89 103601
Google Scholar
[8] Han J S, Vogt T, Gross C, Jaksch D, Kiffner M, Li W H 2018 Phys. Rev. Lett. 120 093201
Google Scholar
[9] Vogt T, Gross C, Han J S, Sambit B P, Mark L, Kiffner M, Li W H 2019 Phys. Rev. A 99 023822
Google Scholar
[10] Tu H T, Liao K Y, Zhang Z X, Liu X H, Zheng S Y, Yang S Z, Zhang X D, Yan H, Zhu S L 2022 Nat. Photonics 16 291
Google Scholar
[11] Sebastian B, Uliana P, Mateusz M, Michał P 2024 Nat. Photonics 18 32
Google Scholar
[12] Kumar A, Suleymanzade A, Stone M, Taneja L, Anferov A, Schuster D I, Simon J 2023 Nature 615 614
Google Scholar
[13] Fan L, Zou C L, Cheng R, Guo X, Han X, Gong Z, Wang S, Tang H X 2018 Sci. Adv. 4 eaar4994
Google Scholar
[14] Higginbotham A P, Burns P S, Urmey M D, Peterson R W, Kampel N S, Brubaker B M, Smith G, Lehnert K W, Regal C A 2018 Nat. Phys. 14 1038
Google Scholar
[15] Mirhosseini M, Sipahigil A, Kalaee M, Painter O 2020 Nature 588 599
Google Scholar
[16] Delaney R D, Urmey M D, Mittal S, Brubaker B M, Kindem J M, Burns P S, Regal C A, Lehnert K W 2022 Nature 606 489
Google Scholar
[17] Petrosyan D, Mølmer K, Fortágh J, Saffman M 2019 New J. Phys. 21 073033
Google Scholar
[18] 苗强, 吴德伟 2025 激光与光电子学进展 62 0100004
Google Scholar
Miao Q, Wu D W 2025 Laser Optoelectron. Prog. 62 0100004
Google Scholar
[19] Covey J P, Sipahigil Alp, Saffman M 2019 Phys. Rev. A 100 012307
Google Scholar
[20] Kiffner M, Feizpour A, Kaczmarek K T, Jaksch D, Nunn J 2016 New J. Phys. 18 093030
Google Scholar
[21] Demtröder W 2008 Laser Spectroscopy (Berlin: Springer) pp70–75
下载:
计量
- 文章访问数: 482
- PDF下载量: 8
- 被引次数: 0
