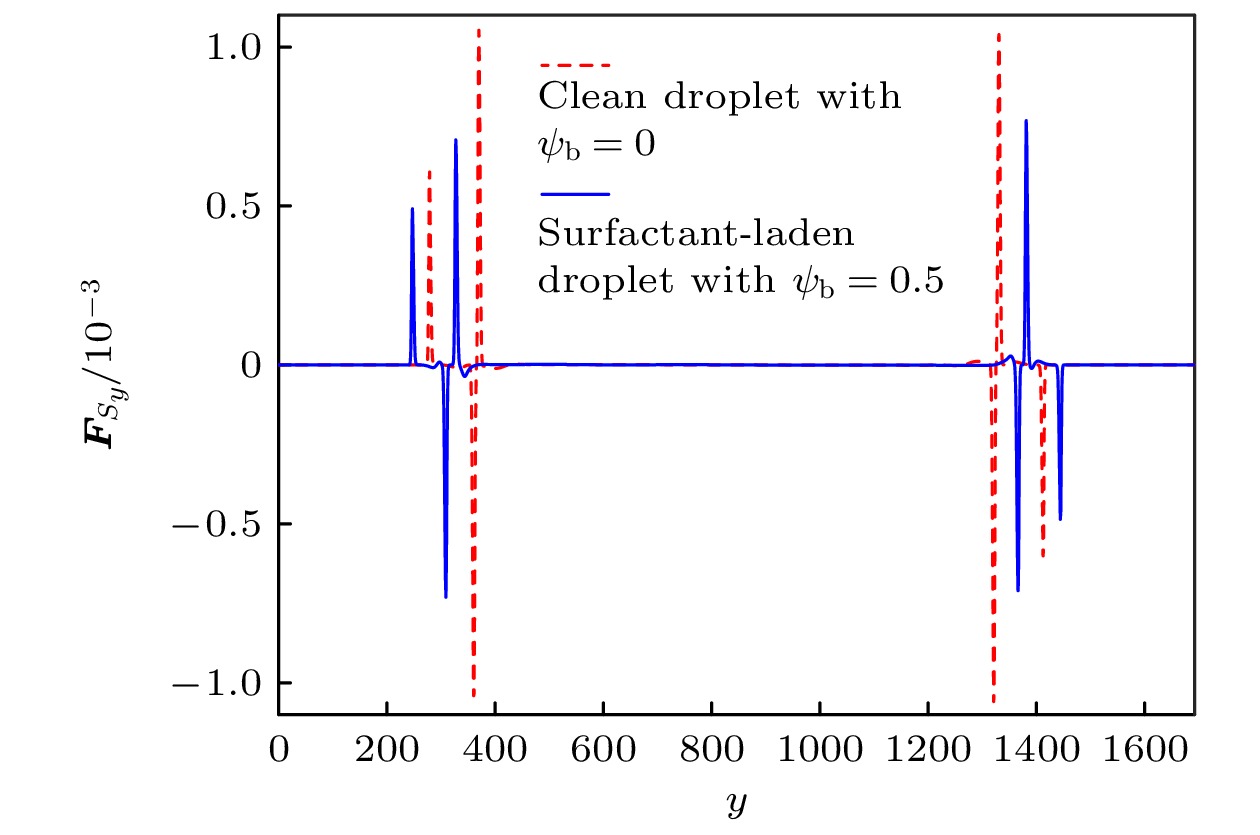
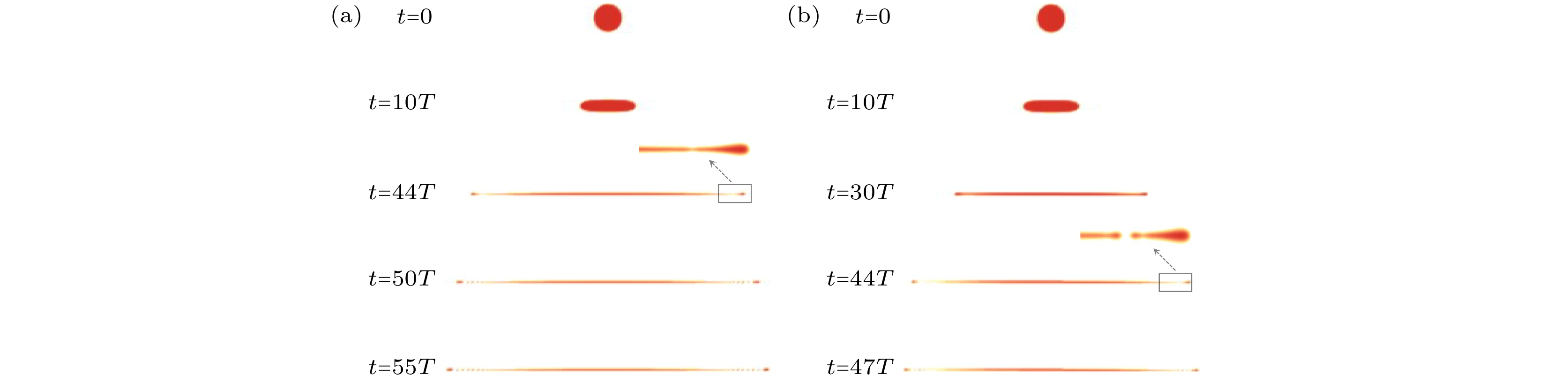
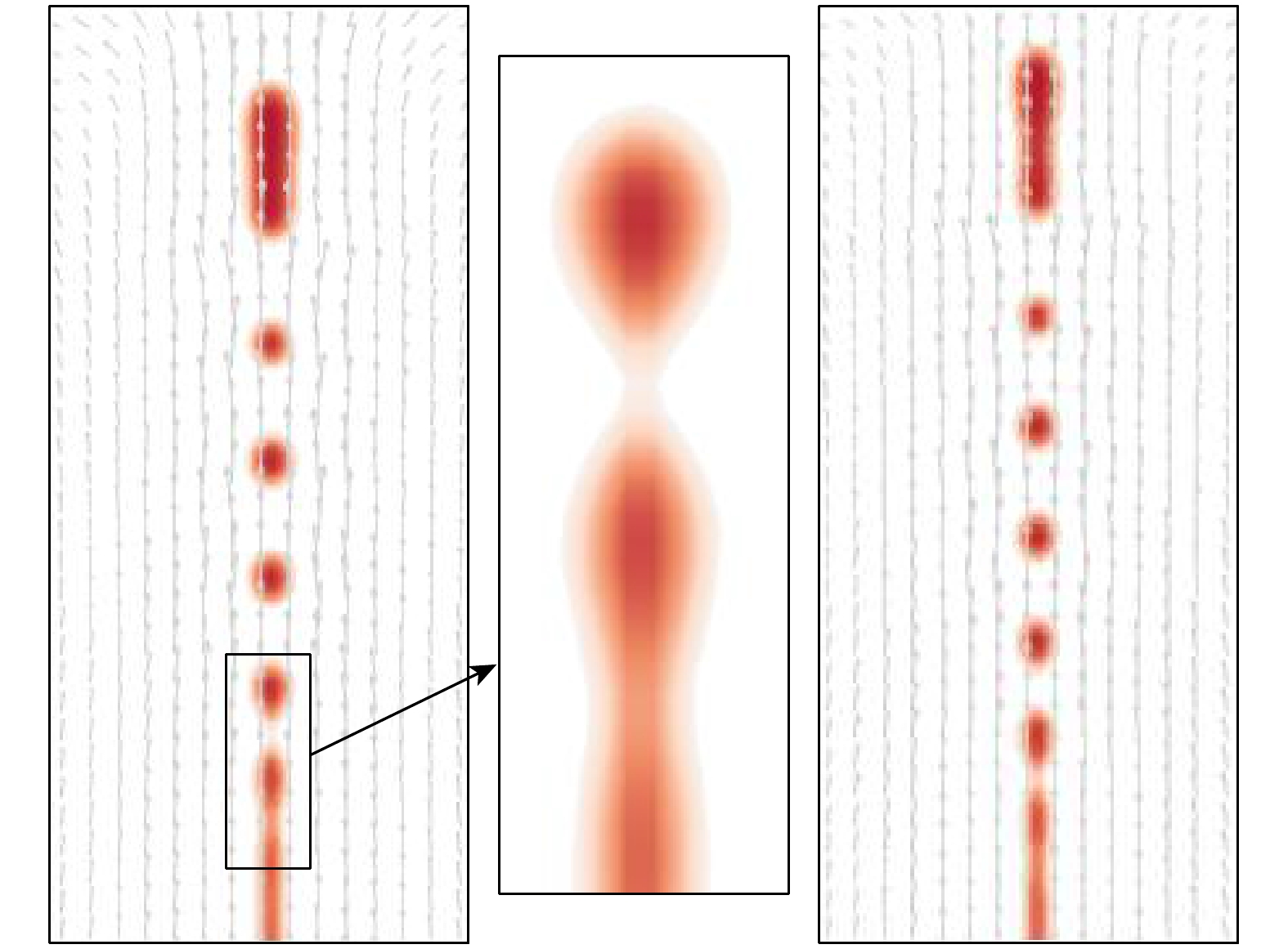
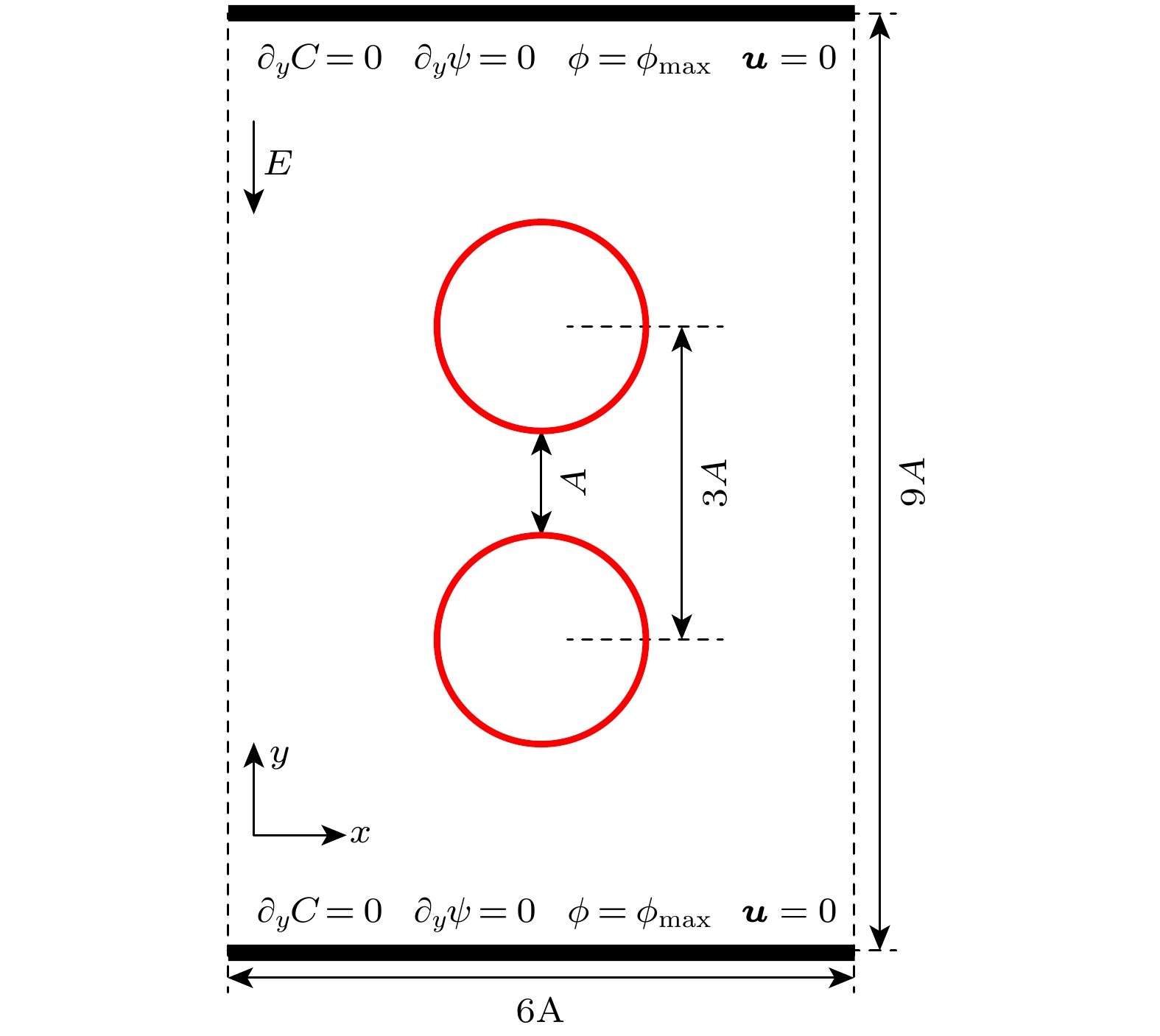
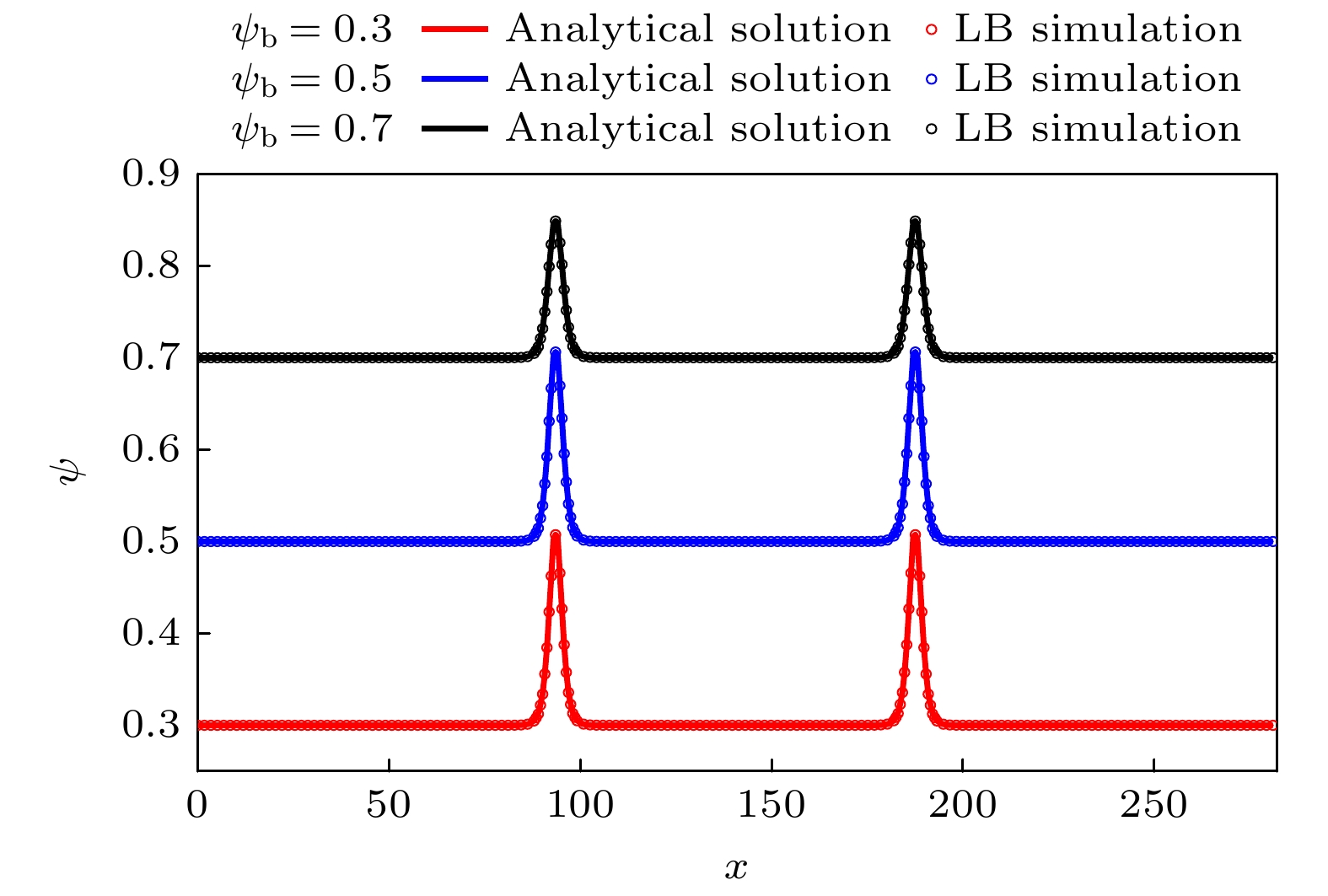
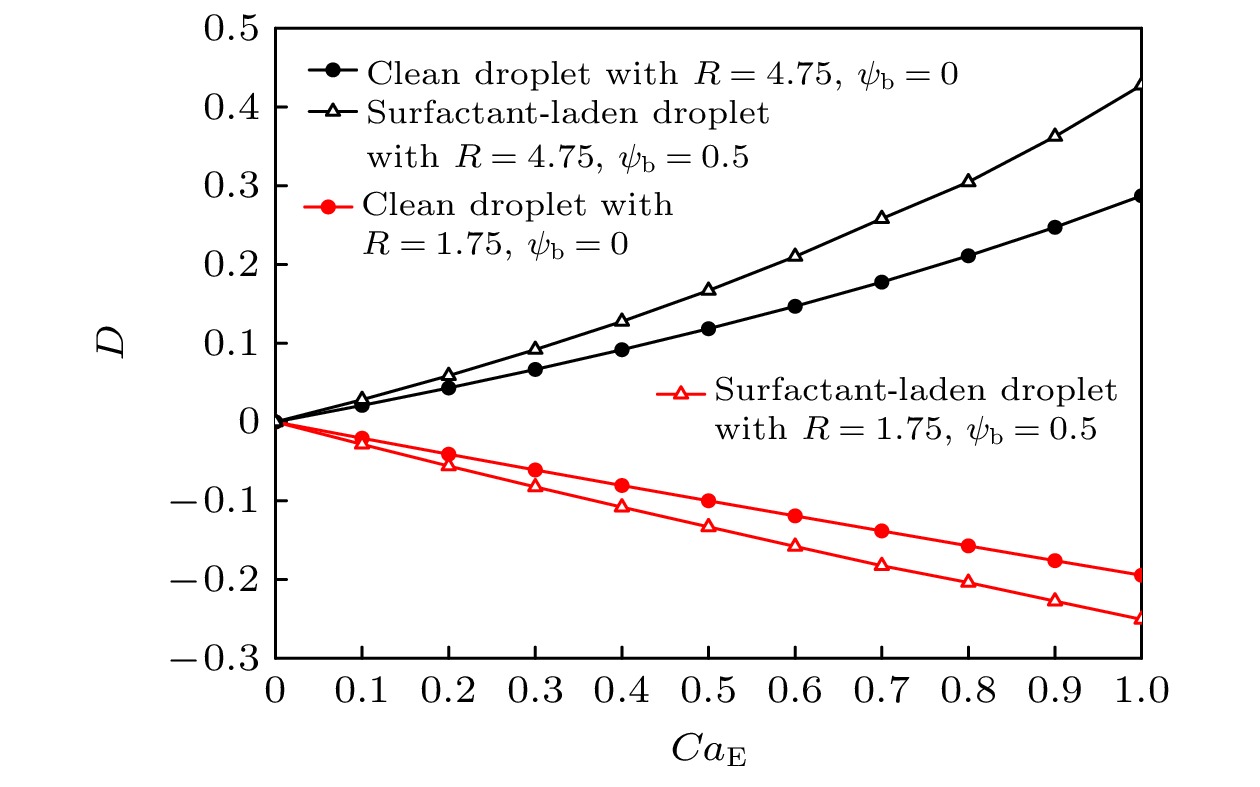
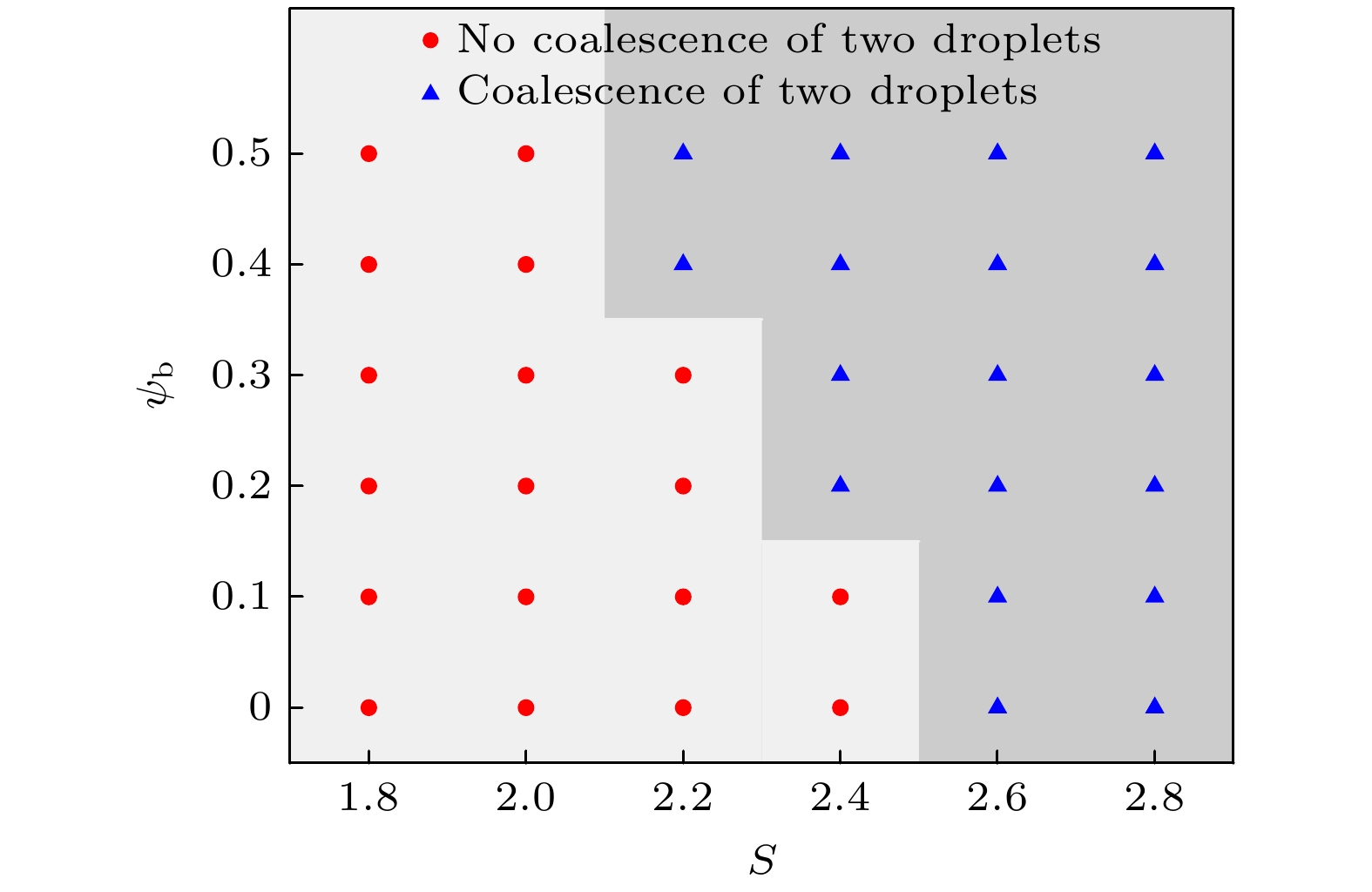
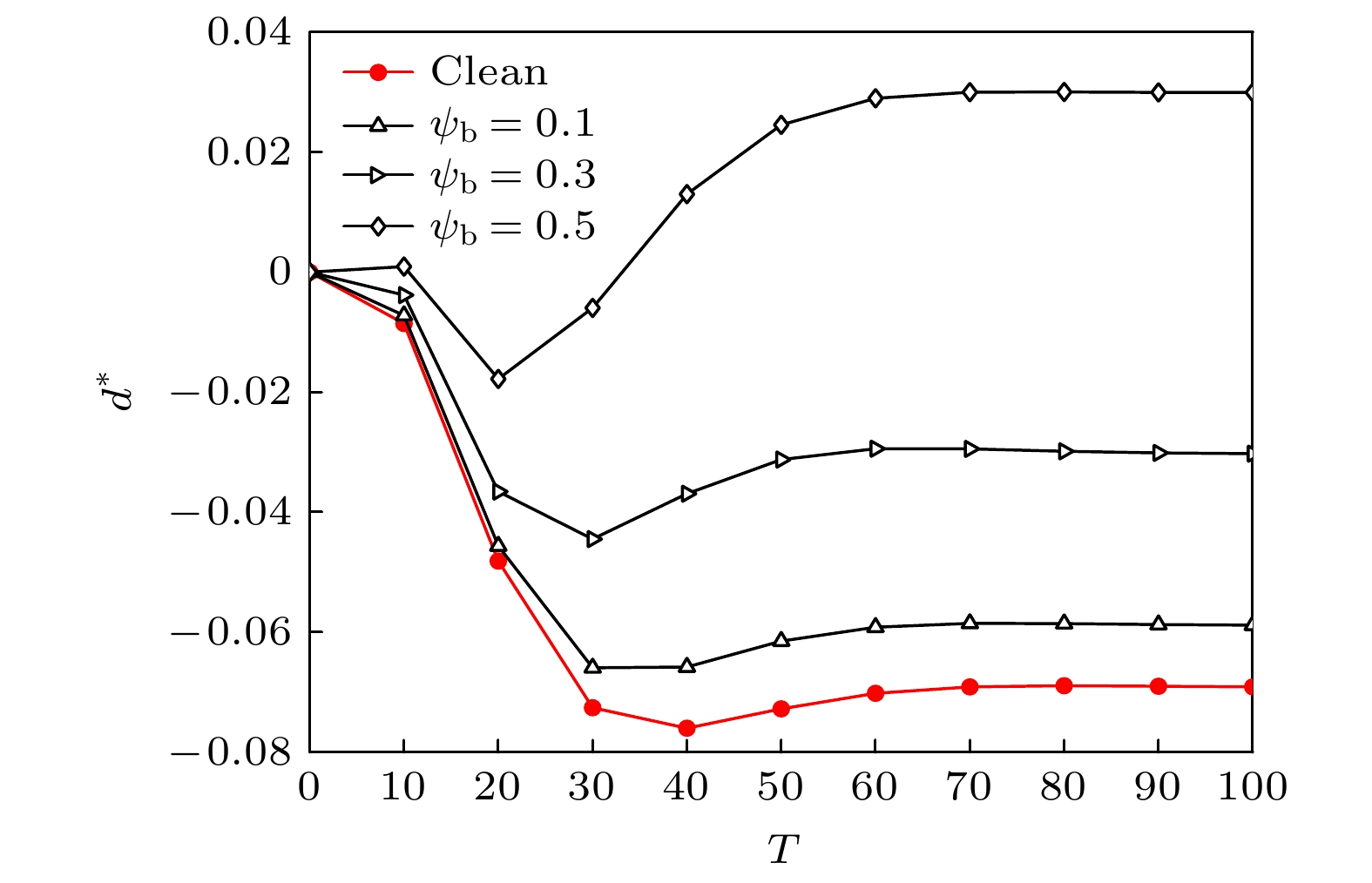
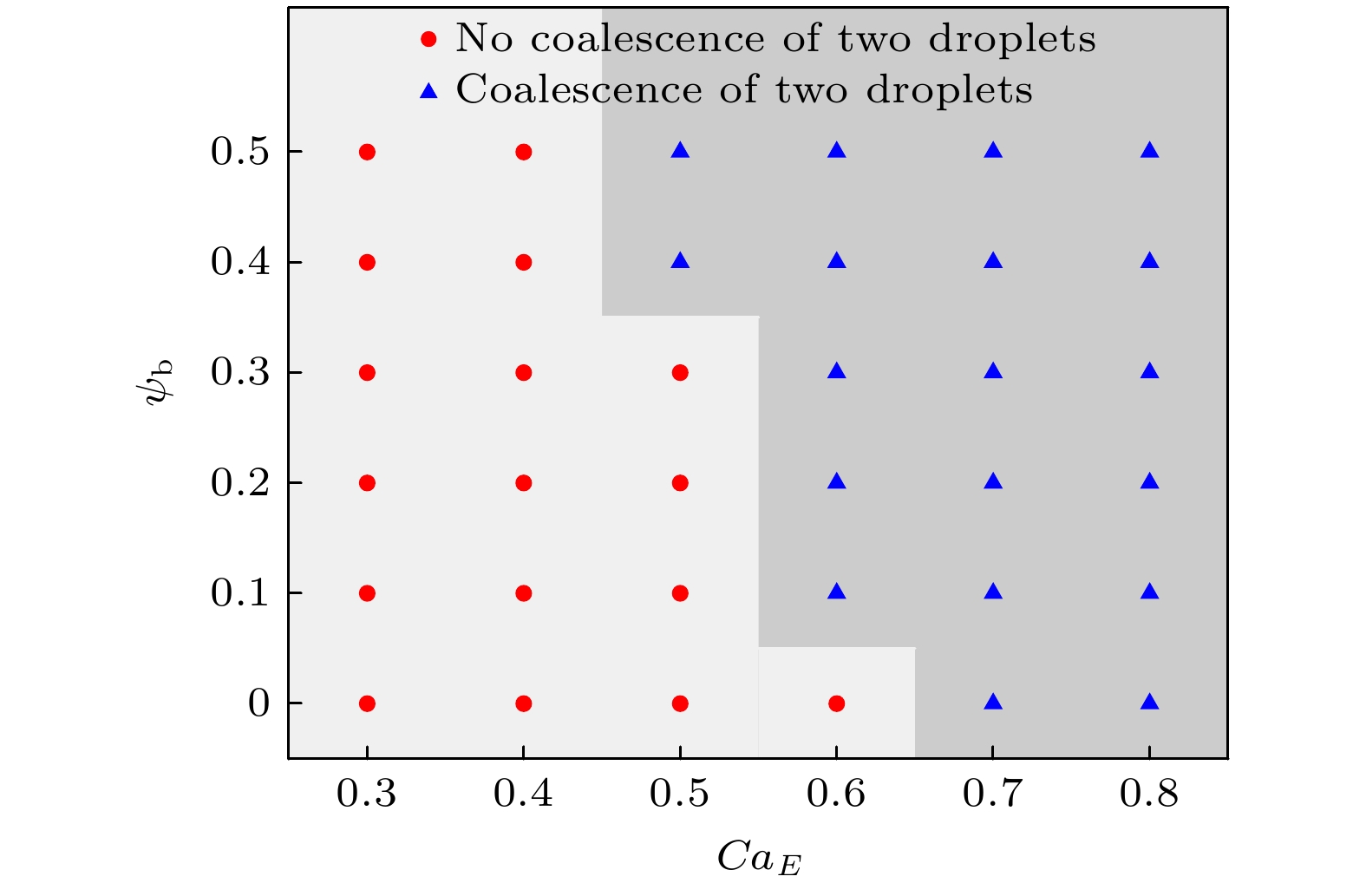
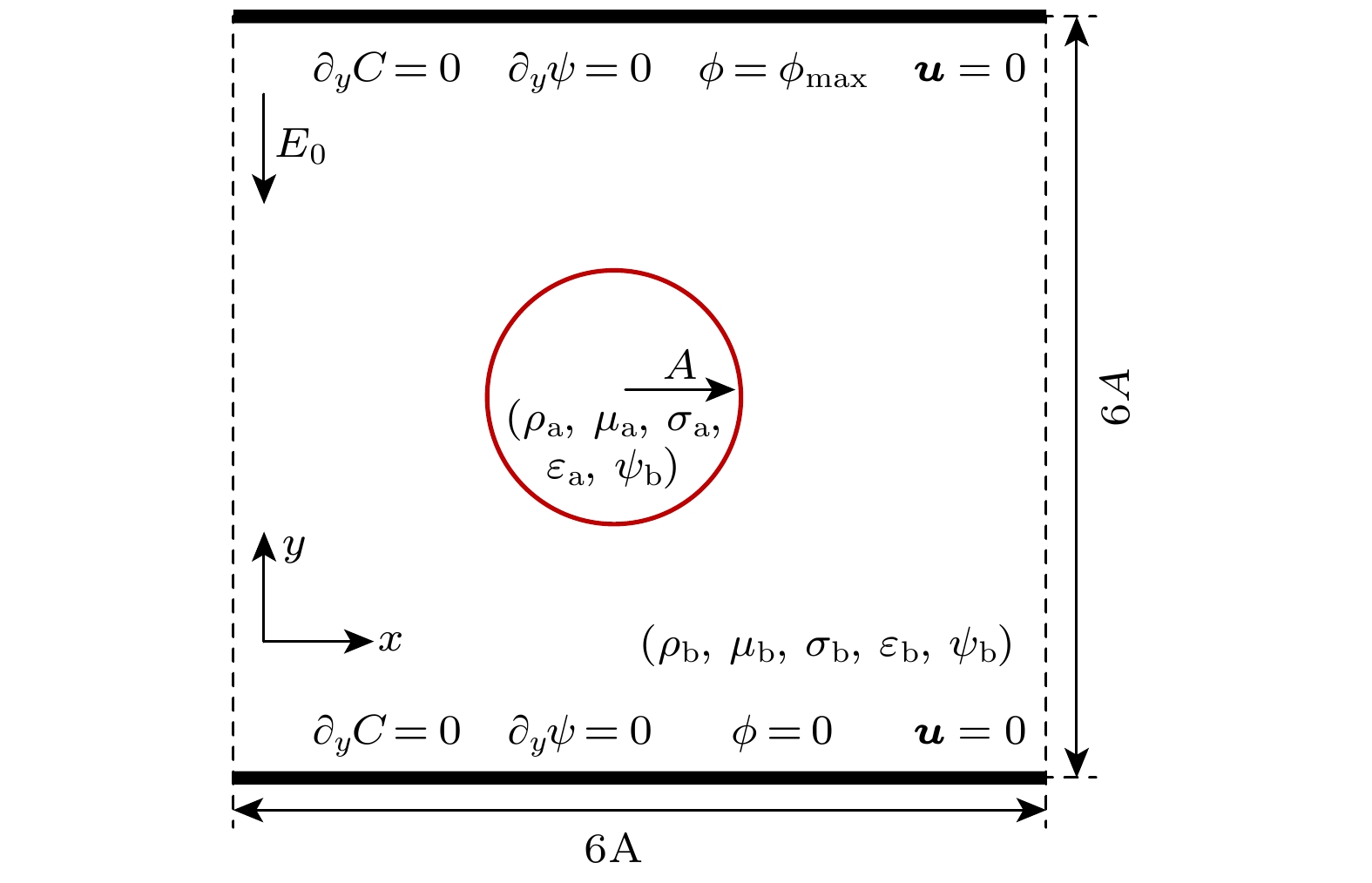
-
利用基于相场理论的格子Boltzmann方法研究了匀强电场作用下含可溶性表面活性剂液滴的动力学行为. 首先通过模拟静态液滴表面活性剂浓度分布和漏电介质液滴在电场作用下形变两个基准问题验证了方法的可靠性. 其次, 本文重点研究了含表面活性剂液滴在电场作用下的形变、破裂和聚合行为. 研究发现, 对于形变行为, 单液滴存在扁长型和扁平型两种形变模式, 表面活性剂浓度越高, 液滴形变越大; 对于破裂行为, 单液滴存在细丝状和窄颈状两种破裂模式, 含表面活性剂的液滴更容易发生破裂行为; 对于聚合行为, 双液滴存在形变聚合和吸引聚合两种过程, 表面活性剂促进其形变聚合, 但抑制其吸引聚合.
-
关键词:
- 格子Boltzmann方法 /
- 可溶性表面活性剂 /
- 漏电介质液滴
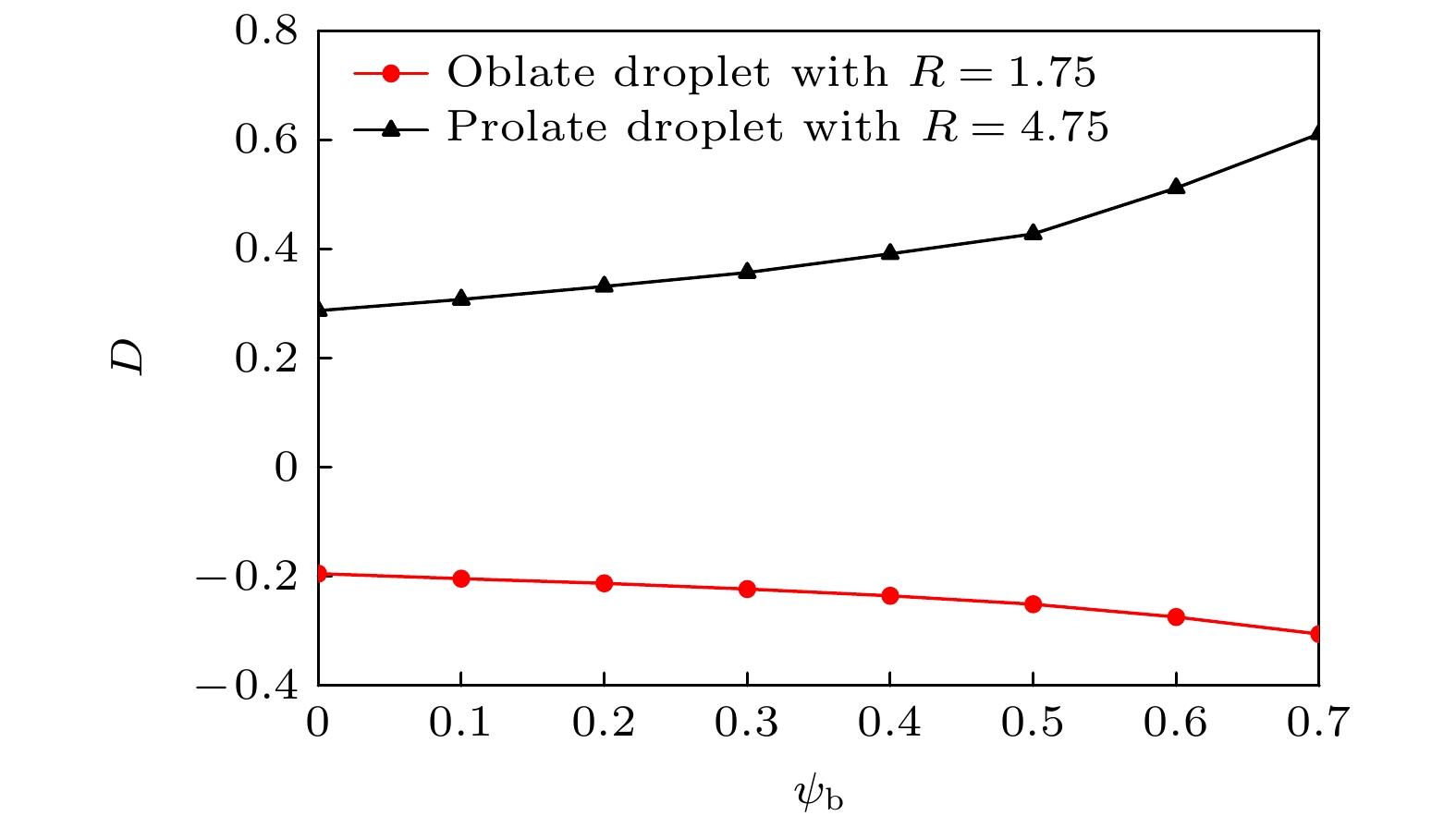
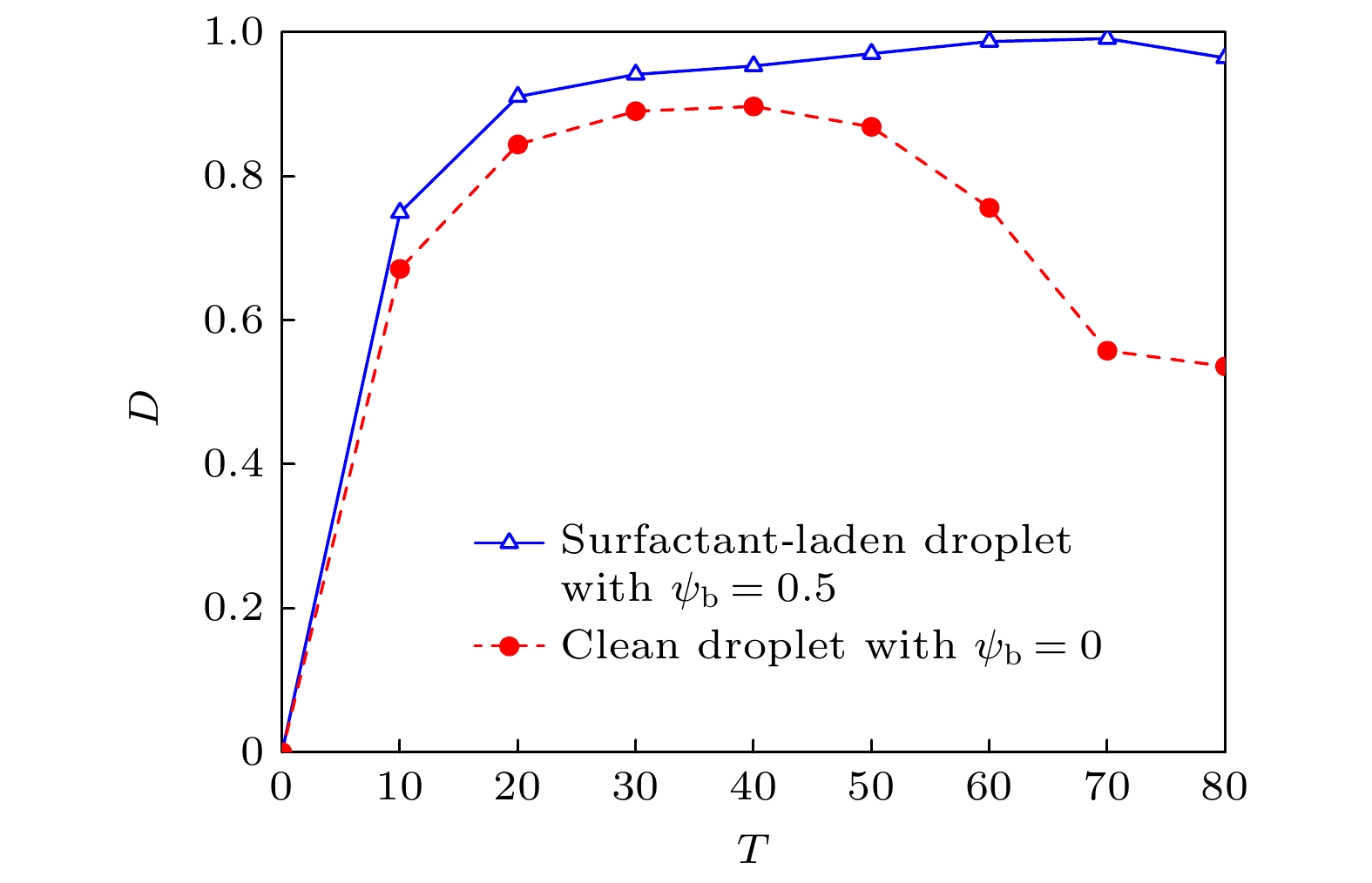
This paper adopts the phase-field based lattice Boltzmann (LB) method to study the dynamic behaviors of soluble surfactant-laden droplets in a uniform electric field. First, two benchmark problems including the surfactant concentration distribution on a static droplet and the deformation of a leaky dielectric droplet in an electric field, are used to validate the reliability of the LB method. Then, we investigate the deformation, breakup, and coalescence behaviors of surfactant-laden droplets in an electric field. The obtained results are shown below. 1) Regarding deformation, the single droplet exhibits two distinct deformation modes: Prolate and oblate shapes. A higher electric capillary number and a higher concentration of bulk surfactants both promote greater droplet deformation. 2) Regarding breakup, a single droplet exhibits two distinct breakup modes: filamentous breakup and conical jetting breakup. Droplets containing surfactants are more like to break up. Specifically, surfactants reduce the retraction degree of the main droplet after filamentous breakup, while increasing the number of satellite droplets formed at the ends of the main droplet after jetting breakup. 3) Regarding coalescence, the double droplets exhibit two distinct processes: deformation coalescence and attractive coalescence. A higher electric capillary number facilitates droplet coalescence. Surfactants promote the deformation coalescence while retarding attractive coalescence, but the promotional effect dominates. Consequently, a higher concentration of bulk surfactants will enhance the tendency of droplet coalescence.[1] Salipante P F, Vlahovska P M 2010 Phys. Fluids 22 112110
Google Scholar
[2] Stone H A, Stroock A D, Ajdari A 2004 Annu. Rev. Fluid Mech. 36 381
Google Scholar
[3] Manikantan H, Squires T M 2020 J. Fluid Mech. 892 1
[4] O’konski C T, Thacher H C 1953 J. Phys. Chem. 57 955
Google Scholar
[5] Taylor G 1966 Proc. R. Soc. Lond. A 291 159
Google Scholar
[6] Sherwood J D 1988 J. Fluid Mech. 188 133
Google Scholar
[7] Tomar G, Gerlach D, Biswas G, Alleborn N, Sharma A, Durst F, Welch S W J, Delgado A 2007 J. Comput. Phys. 227 1267
Google Scholar
[8] Hua J S, Lim L K, Wang C H 2008 Phys. Fluids 20 113302
Google Scholar
[9] Teigen K E, Munkejord S T 2009 IEEE Trans. Dielectr. Electr. Insul. 16 475
Google Scholar
[10] Lin Y, Skjetne P, Carlson A 2012 Int. J. Multiphase Flow 45 1
Google Scholar
[11] Fakhari A, Bolster D 2017 J. Comput. Phys. 334 620
Google Scholar
[12] Yang Q, Li B Q, Ding Y 2013 Int. J. Multiphase Flow 57 1
Google Scholar
[13] Novick-Cohen A 2008 Handbook of Differential Equations: Evolutionary Equations (Vol. 4) (Amsterdam: North-Holland) p201
[14] Liu X, Chai Z H, Shi B C 2019 Phys. Fluids 31 092103
Google Scholar
[15] Liu X, Chai Z H, Shi B C 2021 Commun. Comput. Phys. 30 1346
Google Scholar
[16] Liu X, Chai Z H, Shi B C, Yuan X L 2024 Physica D 468 134294
Google Scholar
[17] Feng J Q 2002 J. Colloid Interface Sci. 246 112
Google Scholar
[18] Cui Y T, Wang N N, Liu H H 2019 Phys. Fluids 31 022105
Google Scholar
[19] Baret J C 2012 Lab Chip 12 422
Google Scholar
[20] Anna S L 2016 Annu. Rev. Fluid Mech. 48 285
Google Scholar
[21] Liu H H, Zhang Y H 2010 J. Comput. Phys. 229 9166
Google Scholar
[22] Ceniceros H D 2003 Phys. Fluids 15 245
Google Scholar
[23] Wooding R A, Morel–Seytoux H J 1976 Annu. Rev. Fluid Mech. 8 233
Google Scholar
[24] van der Sman R G M, van der Graaf S 2006 Rheol. Acta 46 3
Google Scholar
[25] van der Sman R G M, Meinders M B J 2016 Comput. Phys. Commun. 199 12
Google Scholar
[26] Shi Y, Tang G H, Cheng L H, Shuang H Q 2019 Comput. Fluids 179 508
Google Scholar
[27] Zong Y J, Zhang C H, Liang H, Wang L, Xu J R 2020 Phys. Fluids 32 122105
Google Scholar
[28] Ha J W, Yang S M 1995 J. Colloid Interface Sci. 175 369
Google Scholar
[29] Nganguia H, Young Y N, Vlahovska P M, Blawzdziewicz J, Zhang J, Lin H 2013 Phys. Fluids 25 092106
Google Scholar
[30] Painuly R, Kumar S, Anand V 2024 Colloids Surf., A 697 134389
Google Scholar
[31] Teigen K E, Munkejord S T 2010 Phys. Fluids 22 112104
Google Scholar
[32] Sorgentone C, Tornberg A, Vlahovska P M 2019 J. Comput. Phys. 389 111
Google Scholar
[33] Ha J W, Yang S M 1998 J. Colloid Interface Sci. 206 195
Google Scholar
[34] Li N, Pang Y, Sun Z, Li W, Sun Y, Sun X, Liu Y, Li B, Wang Z, Zeng H 2024 Fuel 358 130328
Google Scholar
[35] Wang H L, Chai Z H, Shi B C, Liang H 2016 Phys. Rev. E 94 033304
Google Scholar
[36] Soligo G, Roccon A, Soldati A 2019 J. Comput. Phys. 376 1292
Google Scholar
[37] Yun A, Li Y, Kim J 2014 Appl. Math. Comput. 229 422
[38] Chang C H, Franses E I 1995 Colloids Surf., A 100 1
Google Scholar
[39] Qian Y H, D’Humières D, Lallemand P 1992 EPL 17 479
Google Scholar
[40] Guo Z L, Shu C 2013 Lattice Boltzmann Method and Its Application in Engineering (Vol. 3) (Singapore: World Scientific) pp35–59
[41] Dong Q, Sau A 2018 Phys. Rev. Fluids 3 073701
Google Scholar
-
图 1 匀强电场作用下含表面活性剂液滴示意图
Fig. 1. Schematic diagram of a surfactant-laden droplet in a uniform electric field.
图 2 表面活性剂浓度的数值解与解析解对比
Fig. 2. A comparison between the numerical simulation and analytical solution of surfactant concentration.
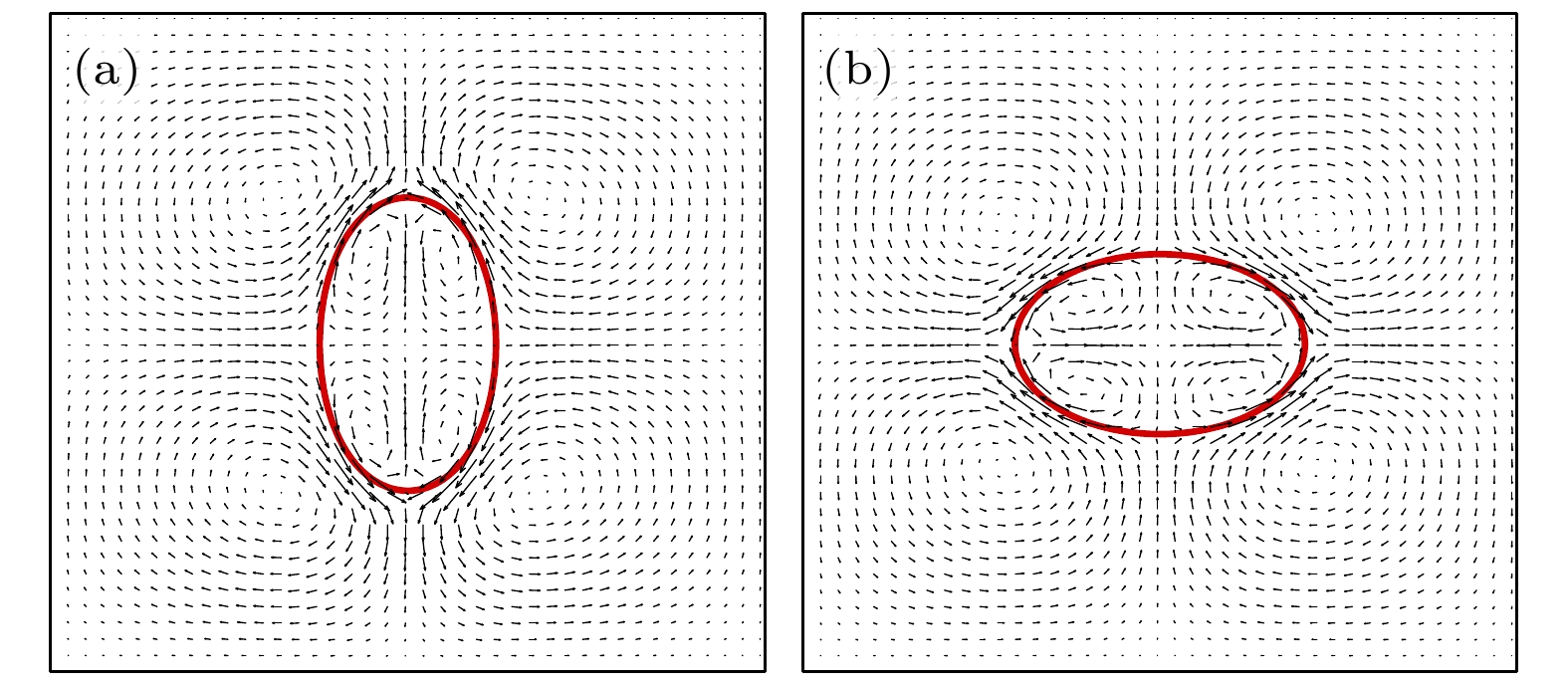
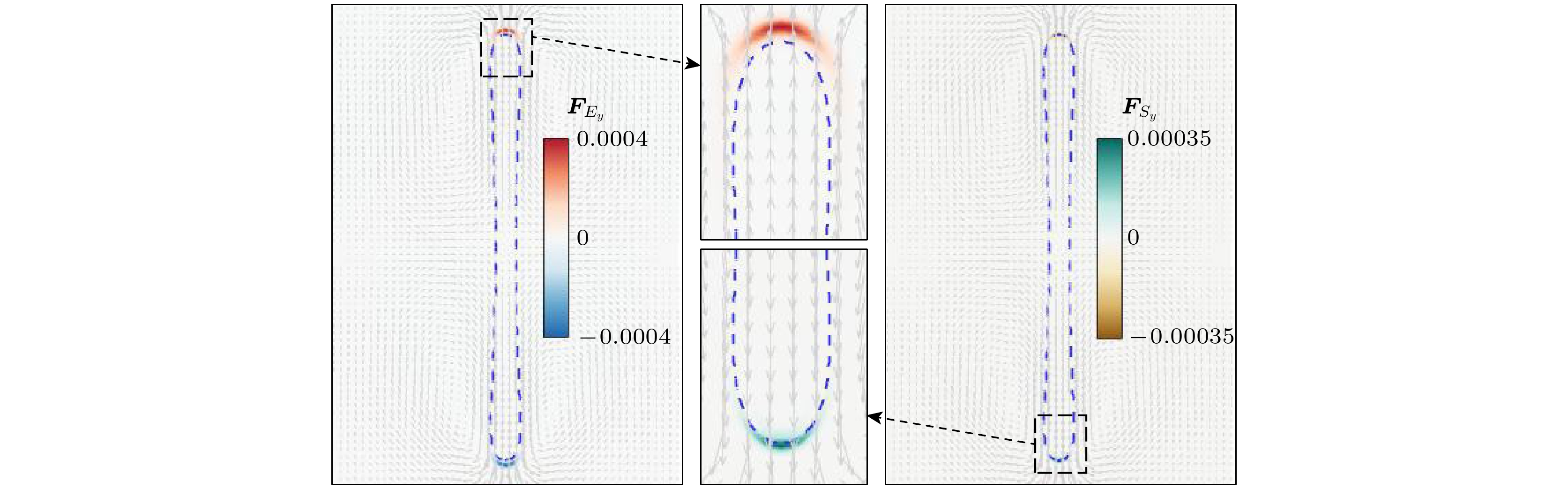
图 3 干净液滴 (a) 扁长型$ [(S, R) = (3.5, 4.75)] $, $ u_{{\mathrm{max}}} = $$ 0.00020 $; (b) 扁平型$ [(S, R) = (3.5, 1.75)] $,$ u_{{\mathrm{max}}} = 0.00043 $
Fig. 3. Clean droplet: (a) Prolate droplet $ [(S, R) = (3.5, $$ 4.75)] $, $ u_{{\mathrm{max}}} = 0.00020 $; (b) oblate droplet $ [(S, R) = (3.5, $$ 1.75)] $, $ u_{{\mathrm{max}}} = 0.00043 $.
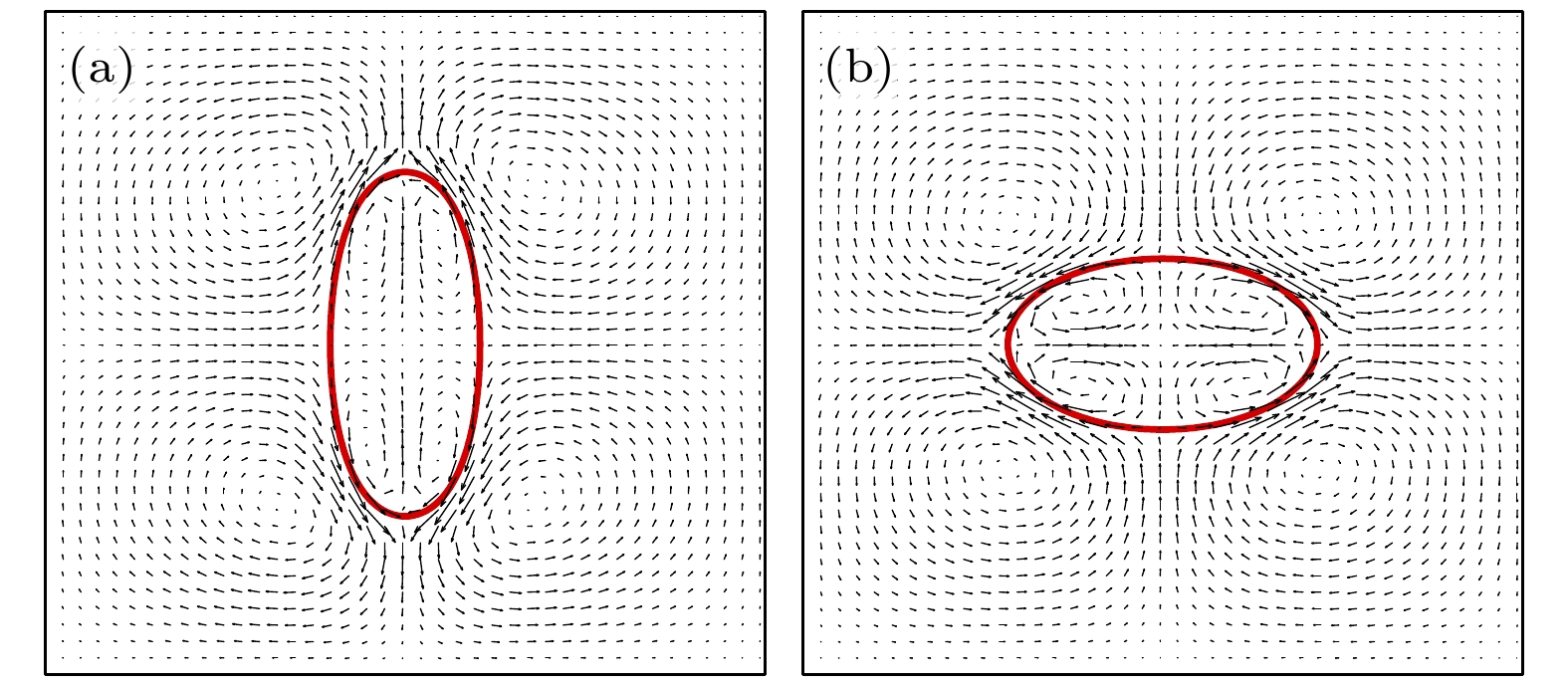
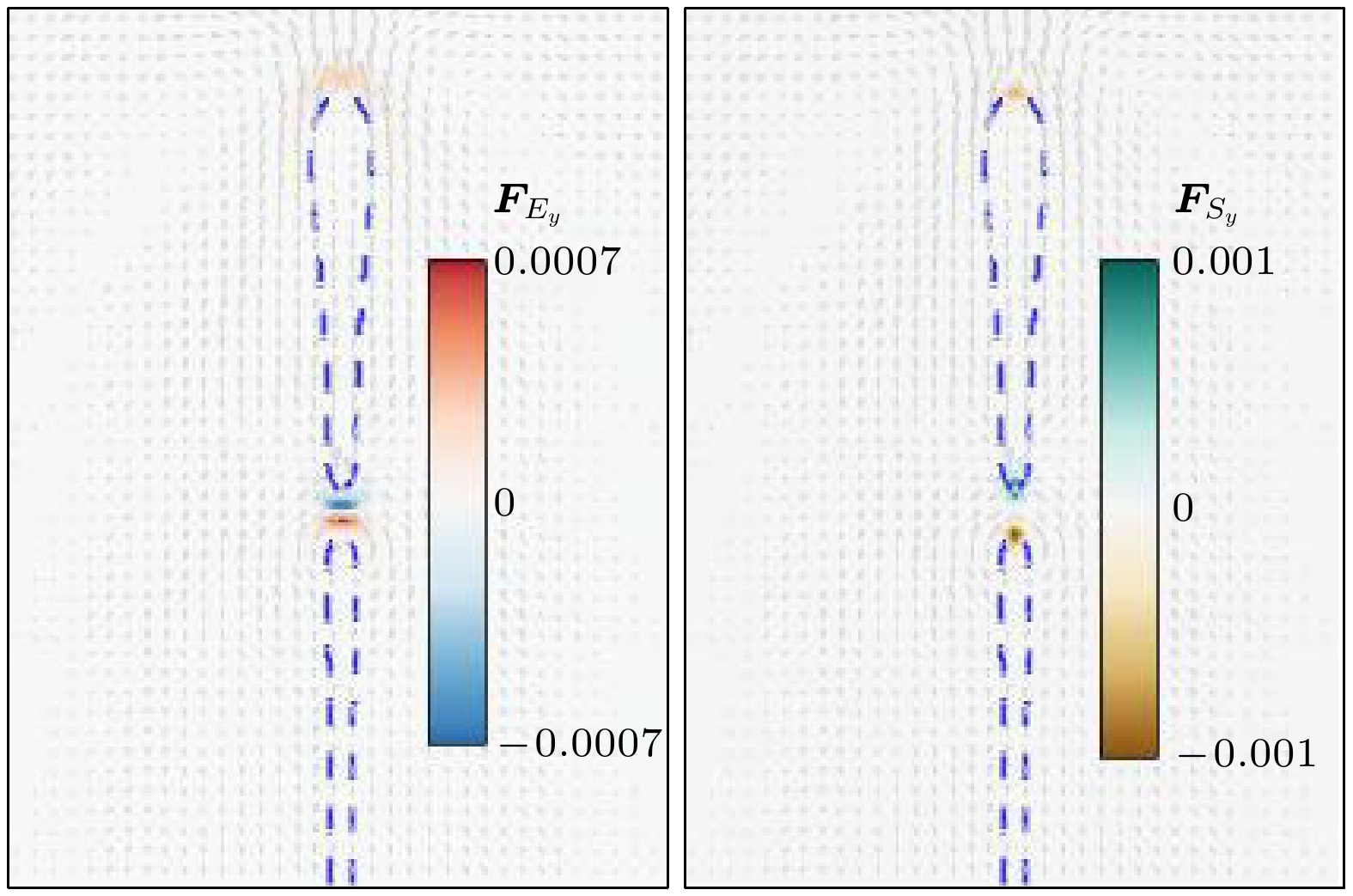
图 4 含表面活性剂液滴 (a) 扁长型$ [(S, R) = (3.5, 4.75)] $, $ u_{{\mathrm{max}}} = 0.00016 $; (b) 扁平型$ [(S, R) = (3.5, 1.75)] $, $ u_{{\mathrm{max}}} = $ 0.00034
Fig. 4. Surfactant-laden droplet: (a) Prolate droplet $ [(S, R) = $$ (3.5, 4.75)] $, $ u_{{\mathrm{max}}} = 0.00016 $; (b) oblate droplet $ [(S, R) = $$ (3.5, 1.75)] $, $ u_{{\mathrm{max}}} = 0.00034 $.
图 5 电毛细数对液滴形变因子的影响
Fig. 5. The effect of electric capillary number on the deformation factor of droplet.
图 6 体相区表面活性剂浓度对液滴形变因子的影响
Fig. 6. The effect of bulk surfactant concentration on the deformation factor of the droplet.
图 7 表面活性剂对扁长型液滴形变过程的影响
Fig. 7. The effect of surfactant on deformation factor of prolate droplet.
图 8 液滴的细丝状破裂过程 (a) 干净液滴($ \psi_{\mathrm{b}} = 0 $); (b) 含表面活性剂液滴($ \psi_{\mathrm{b}} = 0.5 $)
Fig. 8. The filamentous breakup process of droplet: (a) Clean droplet with $ \psi_{\mathrm{b}} = 0 $; (b) surfactant-laden droplet with $ \psi_{\mathrm{b}} = 0.5 $.
图 9 液滴形变过程中电场力与表面张力的比较
Fig. 9. A comparison between the electric field force and the surface tension force during the droplet deformation process.
图 10 液滴破裂后电场力与表面张力的比较
Fig. 10. A comparison between the electric field force and the surface tension after the breakup of droplet.
图 11 液滴破裂后中轴线上的表面张力分布
Fig. 11. The distribution of surface tension along the central line after the breakup of droplet.
图 12 液滴的窄颈状破裂过程 (a) 干净液滴($ \psi_{\mathrm{b}} = 0 $); (b) 含表面活性剂液滴($ \psi_{\mathrm{b}} = 0.5 $)
Fig. 12. The conical jetting breakup process of droplet: (a) Clean droplet with $ \psi_{\mathrm{b}} = 0 $; (b) surfactant-laden droplet with $ \psi_{\mathrm{b}} = 0.5 $
图 13 两种液滴破裂6T后末端的状态
Fig. 13. The end states of two kinds of droplets after they break up at 6T.
图 14 电场作用下双液滴物理工况示意图
Fig. 14. The schematic of two droplets under the effect of the electric field.
图 15 体相区表面活性剂浓度和介电系数比对双液滴动力学的影响
Fig. 15. The effects of bulk surfactant concentration and permittivity ratio on the dynamics of two droplets.
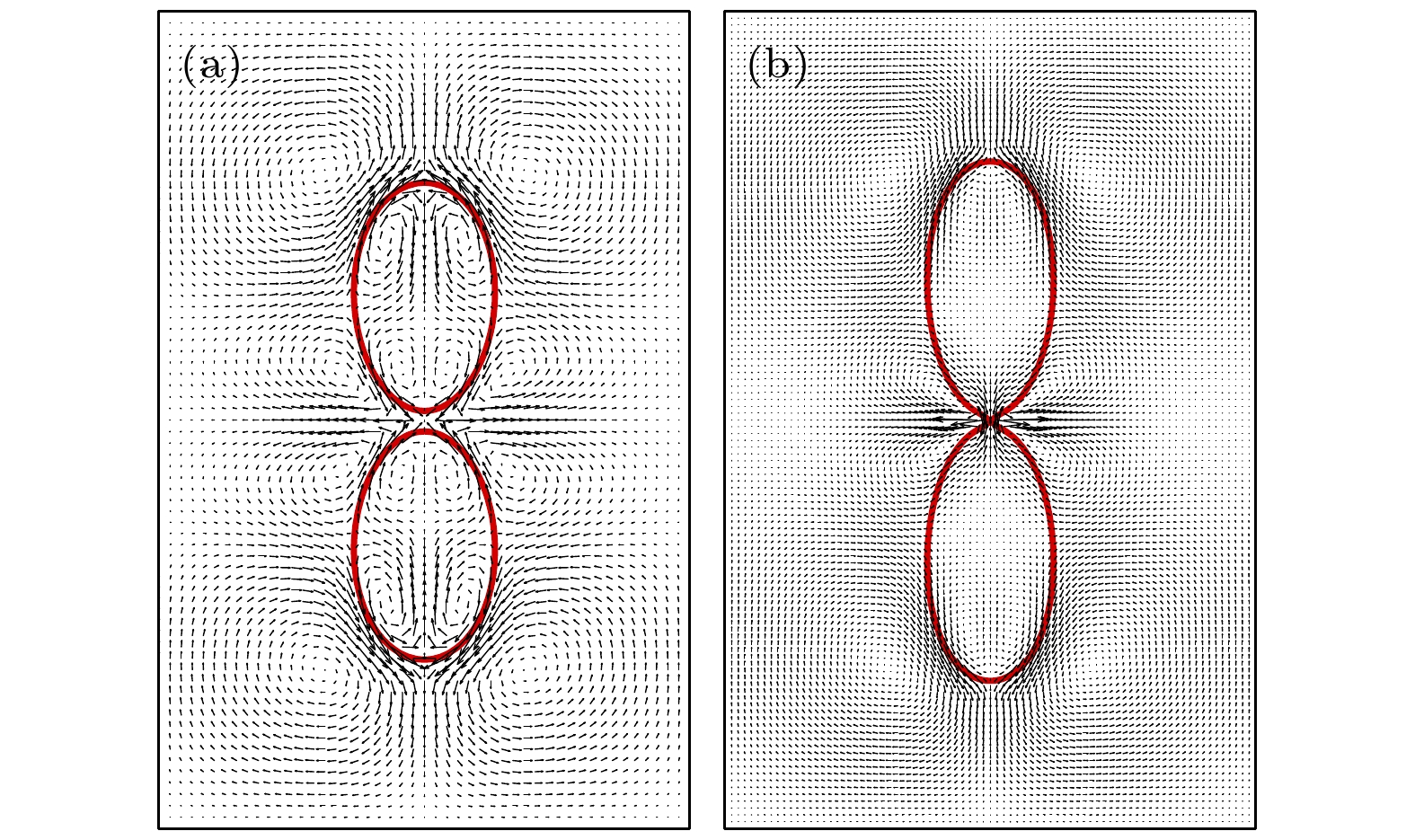
图 16 当$ S = 2.2 $, $ t = 30 T $时, 两液滴状态 (a) 干净液滴不聚合状态, $ u_{{\mathrm{max}}} = 0.00086 $; (b) 含表面活性剂液滴聚合状态($ \psi_{\mathrm{b}} = 0.5 $), $ u_{{\mathrm{max}}} = 0.00274 $
Fig. 16. The states of the two droplets under $ S = 2.2 $ and $ t = 30 T $: (a) Two clean droplets without coalescence, $ u_{{\mathrm{max}}} = 0.00086 $; (b) the coalescence of two surfactant-laden droplets ($ \psi_{\mathrm{b}} = 0.5 $), $ u_{{\mathrm{max}}} = 0.00274 $.
图 18 体相区表面活性剂浓度和电毛细数对双液滴的影响
Fig. 18. The effects of bulk surfactant concentration and electric capillary number on state of two droplets.
表 1 漏电介质液滴形变因子的数值解和理论解对比
Table 1. A comparison between the numerical results and analytical solution of the deformation factor of leaky dielectric droplet.
$ R $ $ S $ $ Ca_{\mathrm{E}} $ 形变因子$ D $ 本文结果 Taylor[5] Feng[17] Liu等[14] 其他数值结果 5 5 0.2 0.03543 0.03670 0.02960 0.03524 0.04080[10] 5 60 0.2 –0.25758 –0.40520 –0.27590 –0.25708 –0.25980[10] 1 2 0.2 –0.04826 –0.04380 –0.05000 –0.04751 –0.02377[10] 50 2 0.2 0.10733 0.10690 0.06520 0.10756 0.09931[10] 1.75 3.5 0.1 –0.02065 –0.02230 –0.02070 –0.02232 –0.02198[18] 3.25 3.5 0.1 0.00888 0.00850 0.00800 0.00833 0.00879[18] 4.75 3.5 0.1 0.02102 0.00228 0.01800 0.01953 0.02088[18] 
下载: 导出CSV
-
[1] Salipante P F, Vlahovska P M 2010 Phys. Fluids 22 112110
Google Scholar
[2] Stone H A, Stroock A D, Ajdari A 2004 Annu. Rev. Fluid Mech. 36 381
Google Scholar
[3] Manikantan H, Squires T M 2020 J. Fluid Mech. 892 1
[4] O’konski C T, Thacher H C 1953 J. Phys. Chem. 57 955
Google Scholar
[5] Taylor G 1966 Proc. R. Soc. Lond. A 291 159
Google Scholar
[6] Sherwood J D 1988 J. Fluid Mech. 188 133
Google Scholar
[7] Tomar G, Gerlach D, Biswas G, Alleborn N, Sharma A, Durst F, Welch S W J, Delgado A 2007 J. Comput. Phys. 227 1267
Google Scholar
[8] Hua J S, Lim L K, Wang C H 2008 Phys. Fluids 20 113302
Google Scholar
[9] Teigen K E, Munkejord S T 2009 IEEE Trans. Dielectr. Electr. Insul. 16 475
Google Scholar
[10] Lin Y, Skjetne P, Carlson A 2012 Int. J. Multiphase Flow 45 1
Google Scholar
[11] Fakhari A, Bolster D 2017 J. Comput. Phys. 334 620
Google Scholar
[12] Yang Q, Li B Q, Ding Y 2013 Int. J. Multiphase Flow 57 1
Google Scholar
[13] Novick-Cohen A 2008 Handbook of Differential Equations: Evolutionary Equations (Vol. 4) (Amsterdam: North-Holland) p201
[14] Liu X, Chai Z H, Shi B C 2019 Phys. Fluids 31 092103
Google Scholar
[15] Liu X, Chai Z H, Shi B C 2021 Commun. Comput. Phys. 30 1346
Google Scholar
[16] Liu X, Chai Z H, Shi B C, Yuan X L 2024 Physica D 468 134294
Google Scholar
[17] Feng J Q 2002 J. Colloid Interface Sci. 246 112
Google Scholar
[18] Cui Y T, Wang N N, Liu H H 2019 Phys. Fluids 31 022105
Google Scholar
[19] Baret J C 2012 Lab Chip 12 422
Google Scholar
[20] Anna S L 2016 Annu. Rev. Fluid Mech. 48 285
Google Scholar
[21] Liu H H, Zhang Y H 2010 J. Comput. Phys. 229 9166
Google Scholar
[22] Ceniceros H D 2003 Phys. Fluids 15 245
Google Scholar
[23] Wooding R A, Morel–Seytoux H J 1976 Annu. Rev. Fluid Mech. 8 233
Google Scholar
[24] van der Sman R G M, van der Graaf S 2006 Rheol. Acta 46 3
Google Scholar
[25] van der Sman R G M, Meinders M B J 2016 Comput. Phys. Commun. 199 12
Google Scholar
[26] Shi Y, Tang G H, Cheng L H, Shuang H Q 2019 Comput. Fluids 179 508
Google Scholar
[27] Zong Y J, Zhang C H, Liang H, Wang L, Xu J R 2020 Phys. Fluids 32 122105
Google Scholar
[28] Ha J W, Yang S M 1995 J. Colloid Interface Sci. 175 369
Google Scholar
[29] Nganguia H, Young Y N, Vlahovska P M, Blawzdziewicz J, Zhang J, Lin H 2013 Phys. Fluids 25 092106
Google Scholar
[30] Painuly R, Kumar S, Anand V 2024 Colloids Surf., A 697 134389
Google Scholar
[31] Teigen K E, Munkejord S T 2010 Phys. Fluids 22 112104
Google Scholar
[32] Sorgentone C, Tornberg A, Vlahovska P M 2019 J. Comput. Phys. 389 111
Google Scholar
[33] Ha J W, Yang S M 1998 J. Colloid Interface Sci. 206 195
Google Scholar
[34] Li N, Pang Y, Sun Z, Li W, Sun Y, Sun X, Liu Y, Li B, Wang Z, Zeng H 2024 Fuel 358 130328
Google Scholar
[35] Wang H L, Chai Z H, Shi B C, Liang H 2016 Phys. Rev. E 94 033304
Google Scholar
[36] Soligo G, Roccon A, Soldati A 2019 J. Comput. Phys. 376 1292
Google Scholar
[37] Yun A, Li Y, Kim J 2014 Appl. Math. Comput. 229 422
[38] Chang C H, Franses E I 1995 Colloids Surf., A 100 1
Google Scholar
[39] Qian Y H, D’Humières D, Lallemand P 1992 EPL 17 479
Google Scholar
[40] Guo Z L, Shu C 2013 Lattice Boltzmann Method and Its Application in Engineering (Vol. 3) (Singapore: World Scientific) pp35–59
[41] Dong Q, Sau A 2018 Phys. Rev. Fluids 3 073701
Google Scholar
下载:
计量
- 文章访问数: 381
- PDF下载量: 12
- 被引次数: 0
