-
通过对金星大气中云和霾进行详细的分层建模和辐射传输模拟, 并结合金星快车SPICAV IR仪器的近红外观测数据, 探讨了云和霾粒子的微物理性质及其对金星(盘)线偏振度的影响. 结果表明, 不同模式粒子的单次散射和线偏振特性在相位角和波长上呈现显著变化, 上层霾和云粒子(Mode 1和Mode 2)的微物理性质对金星的线偏振度影响尤为显著. Mode 1粒子的柱密度减小或模态半径增大均会使线偏振峰值增大, 而线偏振度对Mode 2粒子柱密度的变化与Mode 1趋势相反. 复折射率实部的变化对偏振特性影响显著, 而虚部影响较小. 此外, 线偏振度在金星盘上随波长、相位角及位置(中心与边缘)变化明显, 盘积分的线偏振特性对粒子微物理性质和大气水平不均匀性(如云量分布)高度敏感, 且光环现象清晰可见. 多层模型的模拟结果与SPICAV IR中低纬数据拟合较好, 这种详细分层建模为揭示金星大气中云和霾的微物理特性及其辐射传输特性提供了重要依据.
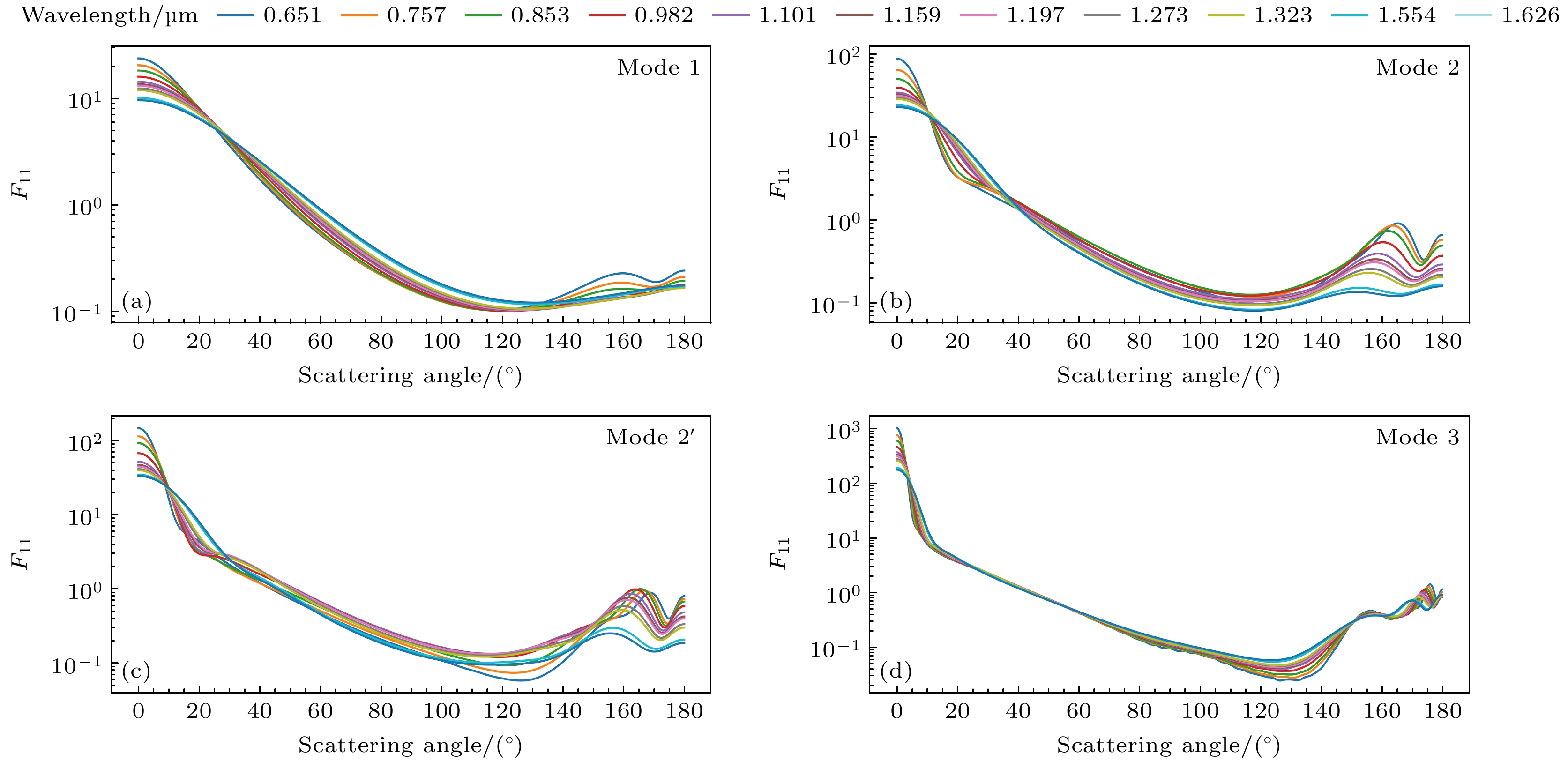
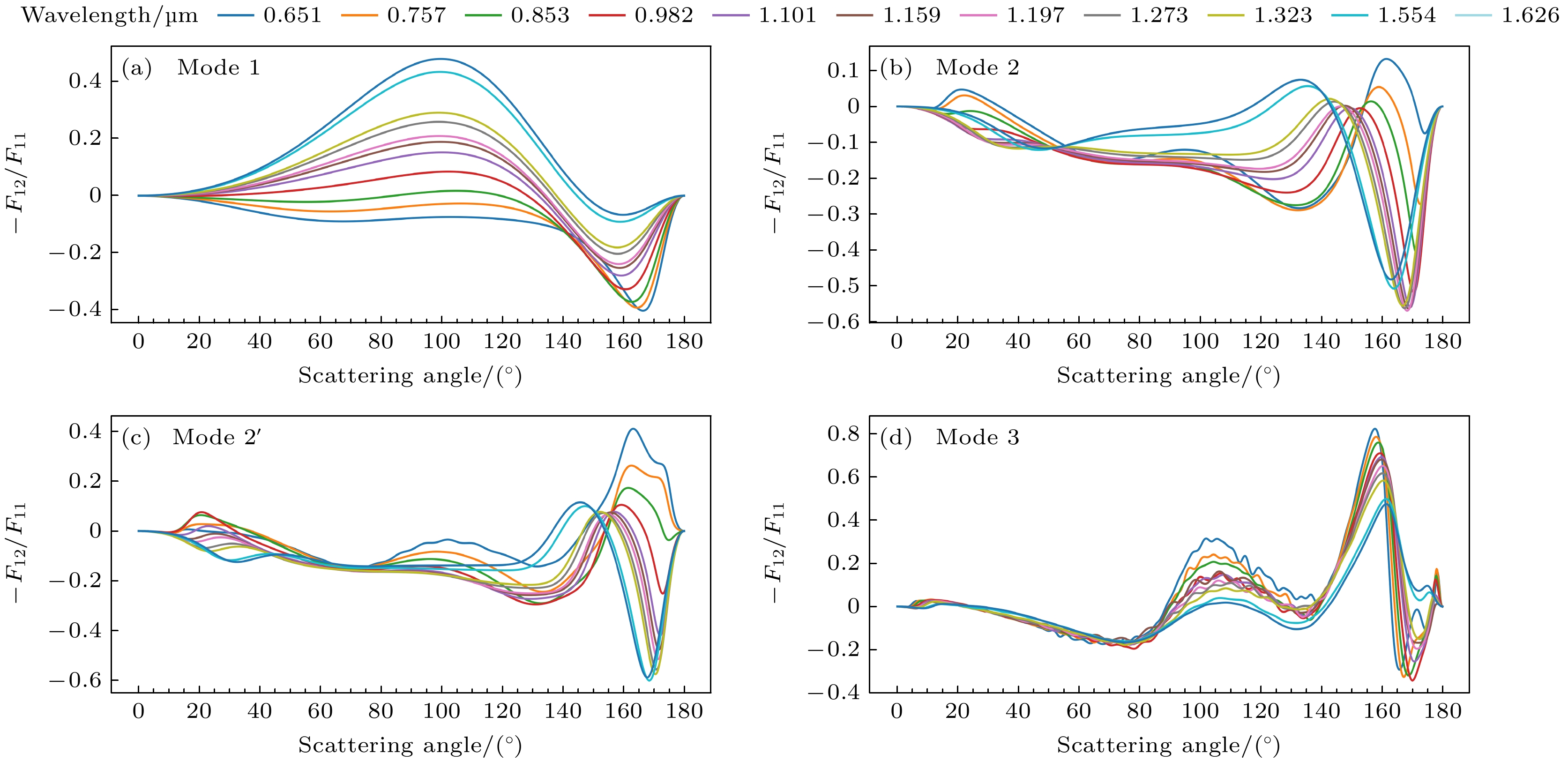
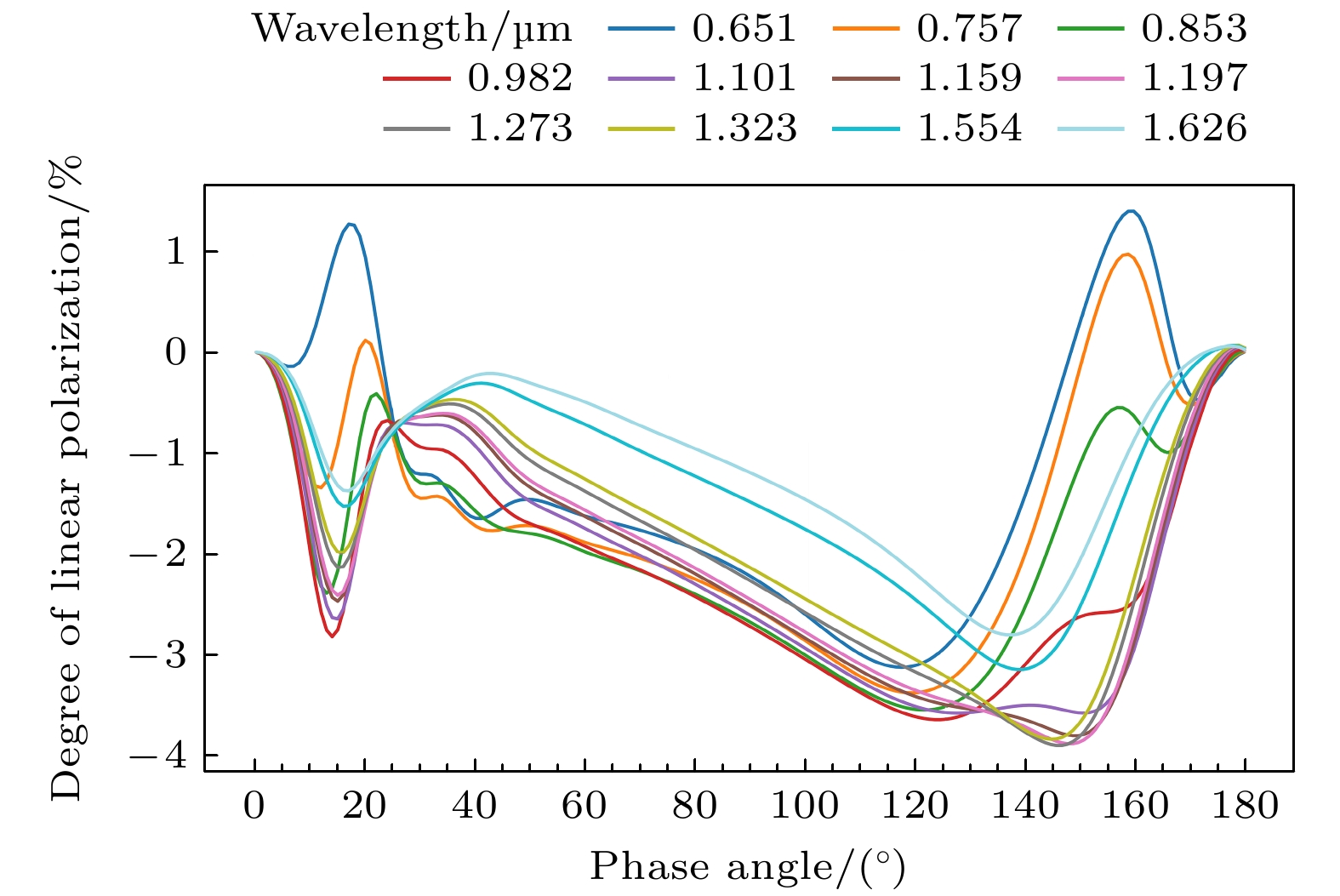
The PyMieDAP radiative transfer model is used in this work to simulate the radiation characteristics of Venus clouds and haze, thereby investigating how their microphysical characteristics affect linear polarization by comparing near-infrared polarization data from the SPICAV IR instrument on the Venus Express. The results show that single-scattered fluxes of the four particle modes decrease in a phase angle range from 0° to 120°, but increase near 160°. Mode 1 particles (upper haze) exhibit Rayleigh scattering characteristics, with polarization changing from positive to negative as the wavelength increases. Mode 2 and Mode 2' particles display two positive polarization peaks near 15° and 160°, respectively, with polarization reversing in the near-infrared. Mode 3 particles show oscillations in polarization near 105°, flipping from positive to negative between 155° and 165°. The primary polarization peak occurs near 15°, corresponding to the main rainbow, while a secondary peak between 150° and 160° is attributed to anomalous diffraction. The microphysical properties of upper clouds and haze (Mode 1 and Mode 2) significantly affect the linear polarization of Venus, while those of lower clouds (Mode 2' and Mode 3) have a minimum influence. A reduction in Mode 1 column density increases the polarization peak at the main rainbow, while an increase in Mode 2 column density has the opposite effect. Changes in modal radius enhance polarization peaks for Mode 1 and Mode 2, while increasing geometric standard deviation reduces polarization peaks and shifts their phase angles. The real part of the complex refractive index has a greater influence on polarization than the imaginary part. Simulations using the multilayer model show better agreement with SPICAV IR data and consistency with the larger particle sizes in Venus’ haze. The integrated linear polarization across the Venus disk varies with wavelength and phase angle, with the polarization being higher at the disk's edge. The variation in cloud coverage also influences polarization, with areas with fewer clouds exhibiting higher values. In the future, further research will be conducted on the influence of cloud and haze parameters on line polarization, for the inversion of these parameters is beyond the scope of this work. -
Keywords:
- Venusian clouds and haze /
- linear polarization /
- sensitivity analysis /
- microphysical properties
[1] Lyot B 1929 Ph. D. Dissertation (Paris: Université de Paris Paris
[2] Coffeen D L 1969 Astronom. J. 74 446
Google Scholar
[3] Dyck H, Forbes F, Shawl S 1971 Astronom. J. 76 901
Google Scholar
[4] Hansen J E, Hovenier J 1974 J. atmos. Sci. 31 1137
Google Scholar
[5] Esposito L, Knollenberg R, Marov M, Toon O, Turco R 1983 The Clouds and Hazes of Venus (University of Arizona Press) pp484−564
[6] Pollack J B, Dalton J B, Grinspoon D, Wattson R B, Freedman R, Crisp D, Allen D A, Bezard B, DeBergh C, Giver L P 1993 Icarus 103 1
Google Scholar
[7] Rossi L, Marcq E, Montmessin F, Fedorova A, Stam D, Bertaux J L, Korablev O 2015 Planet. Space Sci. 113 159
Google Scholar
[8] 李宜奇, 孙晓兵, 黄红莲, 刘晓, 提汝芳, 郑小兵, 樊依哲, 余海啸, 韦祎晨, 王宇轩, 王宇瑶 2024 红外与毫米波学报 43 657
Google Scholar
Li Y Q, Sun X B, Huang H L, Liu X, Ti R F, Zheng X B, Fan Y Z, Yu H X, Wei Y C, Wang Y X, Wang Y Y 2024 J. Infrared Millim. W. 43 657
Google Scholar
[9] Hansen J E, Travis L D 1974 Space Sci. Rev. 16 527
Google Scholar
[10] Stam D 2008 Astron. Astrophys. 482 989
Google Scholar
[11] Stam D, Hovenier J, Waters L 2004 Astron. Astrophys. 428 663
Google Scholar
[12] Bertaux J L, Nevejans D, Korablev O, et al. 2007 Planet. Space Sci. 55 1673
Google Scholar
[13] Svedhem H, Titov D, McCoy D, Lebreton J P, Barabash S, Bertaux J L, Drossart P, Formisano V, Häusler B, Korablev O 2007 Planet. Space Sci. 55 1636
Google Scholar
[14] Korablev O, Fedorova A, Bertaux J L, et al. 2012 Planet. Space Sci. 65 38
Google Scholar
[15] Rossi L, Berzosa-Molina J, Stam D M 2018 Astron. Astrophys. 616 A147
Google Scholar
[16] de Haan J F, Bosma P, Hovenier J 1987 Astron. Astrophys. 183 371
[17] Peterson P 2009 Int. J. Comput. Sci. Eng. 4 296
Google Scholar
[18] Zasova L, Moroz V, Linkin V, Khatuntsev I, Maiorov B 2006 Cosmic Res. 44 364
Google Scholar
[19] Braak C, De Haan J, Hovenier J, Travis L 2002 J. Geophys. Res. Planets 107 5
Google Scholar
[20] Knibbe W J J, de Haan J F, Hovenier J W, Travis L D 1998 J. Geophys. Res. Planets 103 8557
Google Scholar
[21] Palmer K F, Williams D 1975 Appl. Opt. 14 208
Google Scholar
[22] Haus R, Kappel D, Arnold G 2015 Planet. Space Sci. 117 262
Google Scholar
[23] Mie G 1908 Ann. Phys. 330 377
Google Scholar
[24] van de Hulst H C Van de Hulst H C, Twersky V 1957 Physics Today 10 28
Google Scholar
-
图 3 SPICAV IR 11个大气窗口波长处对应75% H2SO4溶液的复折射率
Fig. 3. SPICAV IR complex refractive index corresponding to 75% H2SO4 solution at 11 atmospheric window wavelengths.
图 4 四种模式粒子的单层光学厚度$ \tau $随波长和高度的变化
Fig. 4. Single-layer optical thickness τ of four modes of particles as a function of wavelength and height.
图 7 四种模式粒子的单次散射线偏振度
Fig. 7. Single scattering polarization for four modes of particles.
图 8 四种模式粒子多次散射的总线偏振度
Fig. 8. Total linear polarization degree of multiple scattering of particles in four modes.
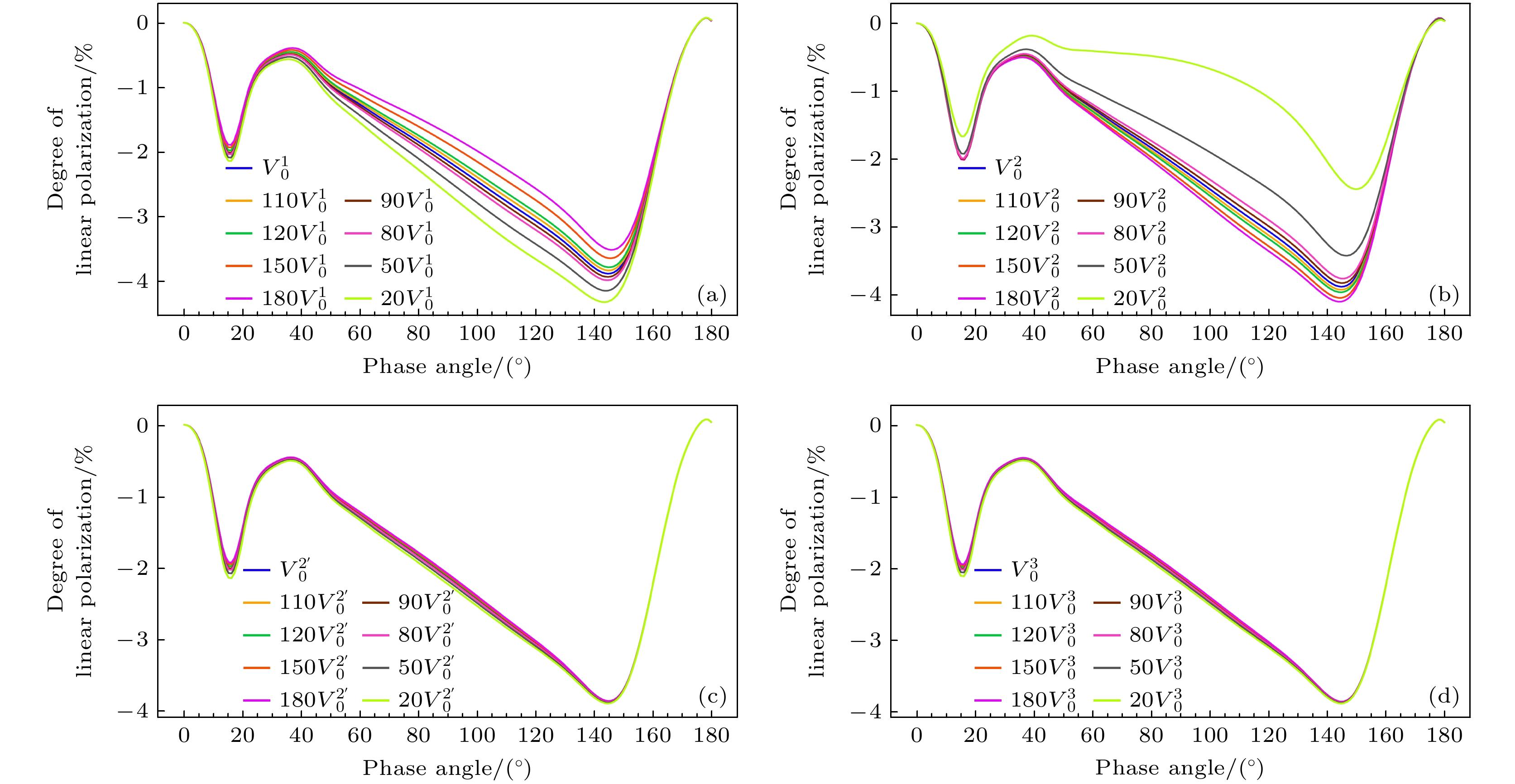
图 9 线偏振度对四种模式粒子柱密度变化的敏感性( $ {V}_{0}^{i} $代表粒子的柱密度(i =1 , 2, 2', 3), 对应4种不同的粒子模式)
Fig. 9. Sensitivity of linear polarization degree to changes in particle column density in four modes ($ {V}_{0}^{i} $ represents the column density of the particle, i = 1, 2, 2', 3, corresponding to four different particle modes).
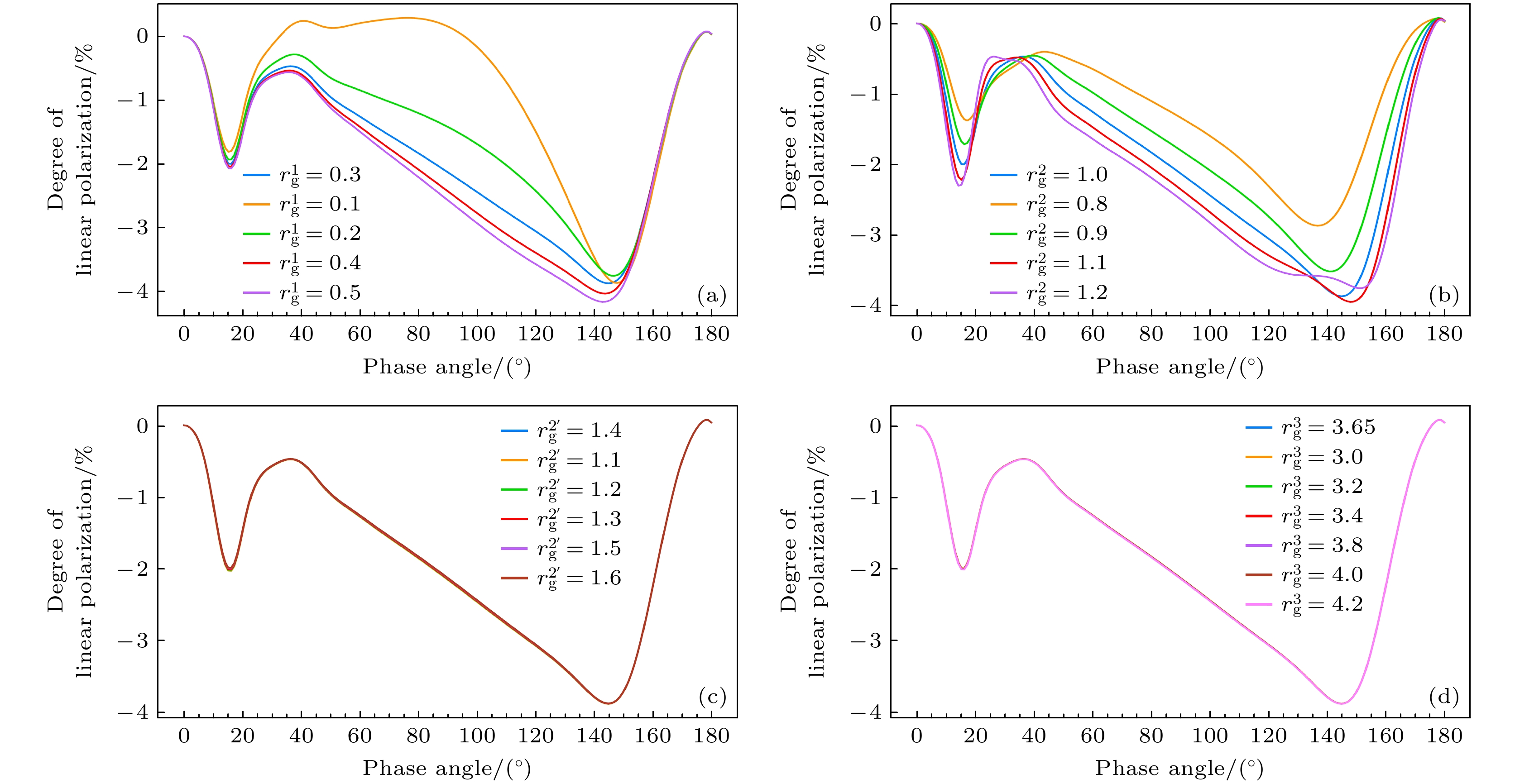
图 10 线偏振度对4种模式粒子模态半径变化的敏感性($ r_{\text{g}}^i $代表粒子的模态半径(i = 1, 2, 2', 3), 对应4种不同的粒子模式)
Fig. 10. Sensitivity of linear polarization degree to changes in modal radius of particles in four modes ($ r_{\text{g}}^i $ represents the modal radius of the particle, i = 1, 2, 2', 3, corresponding to four different particle modes).
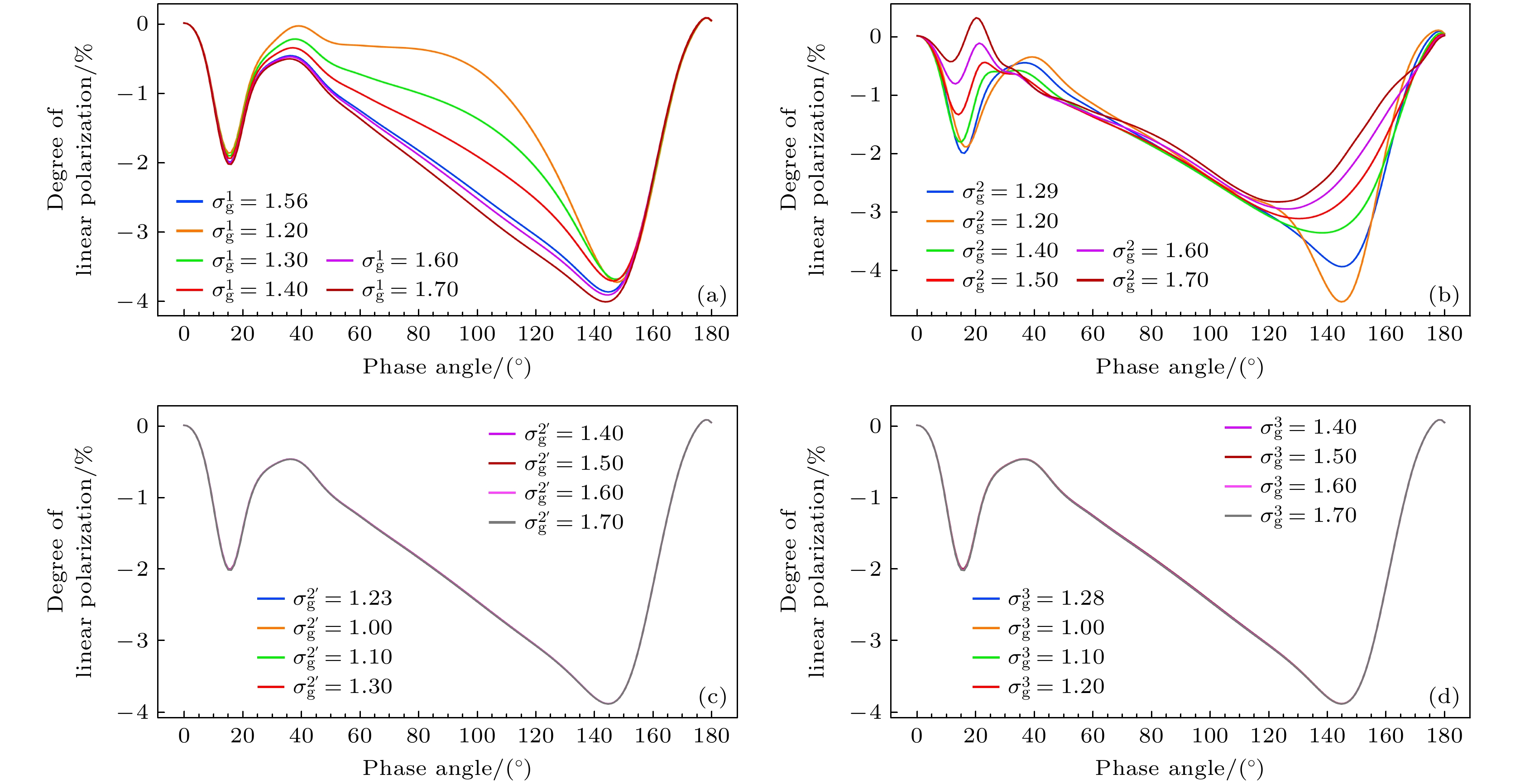
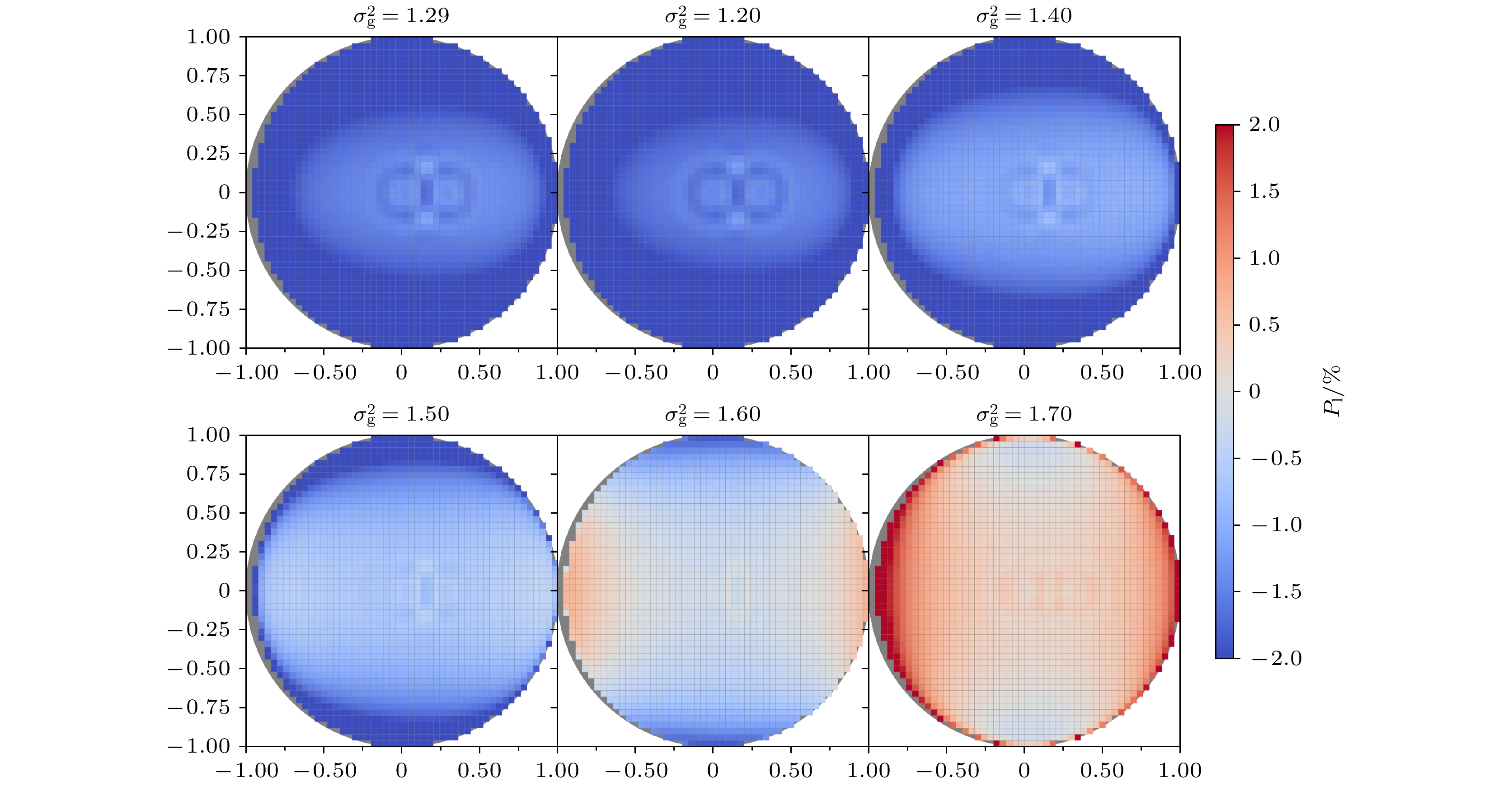
图 11 线偏振度对四种模式粒子几何标准差变化的敏感性($ \sigma _{\text{g}}^i $代表粒子的几何标准差(i = 1, 2, 2', 3), 对应4种不同的粒子模式)
Fig. 11. Sensitivity of linear polarization to the change of geometric standard deviation of particles in four modes ($ \sigma _{\text{g}}^i $ represents the geometric standard deviation of particles, i = 1, 2, 2', 3, corresponding to four different particle modes).
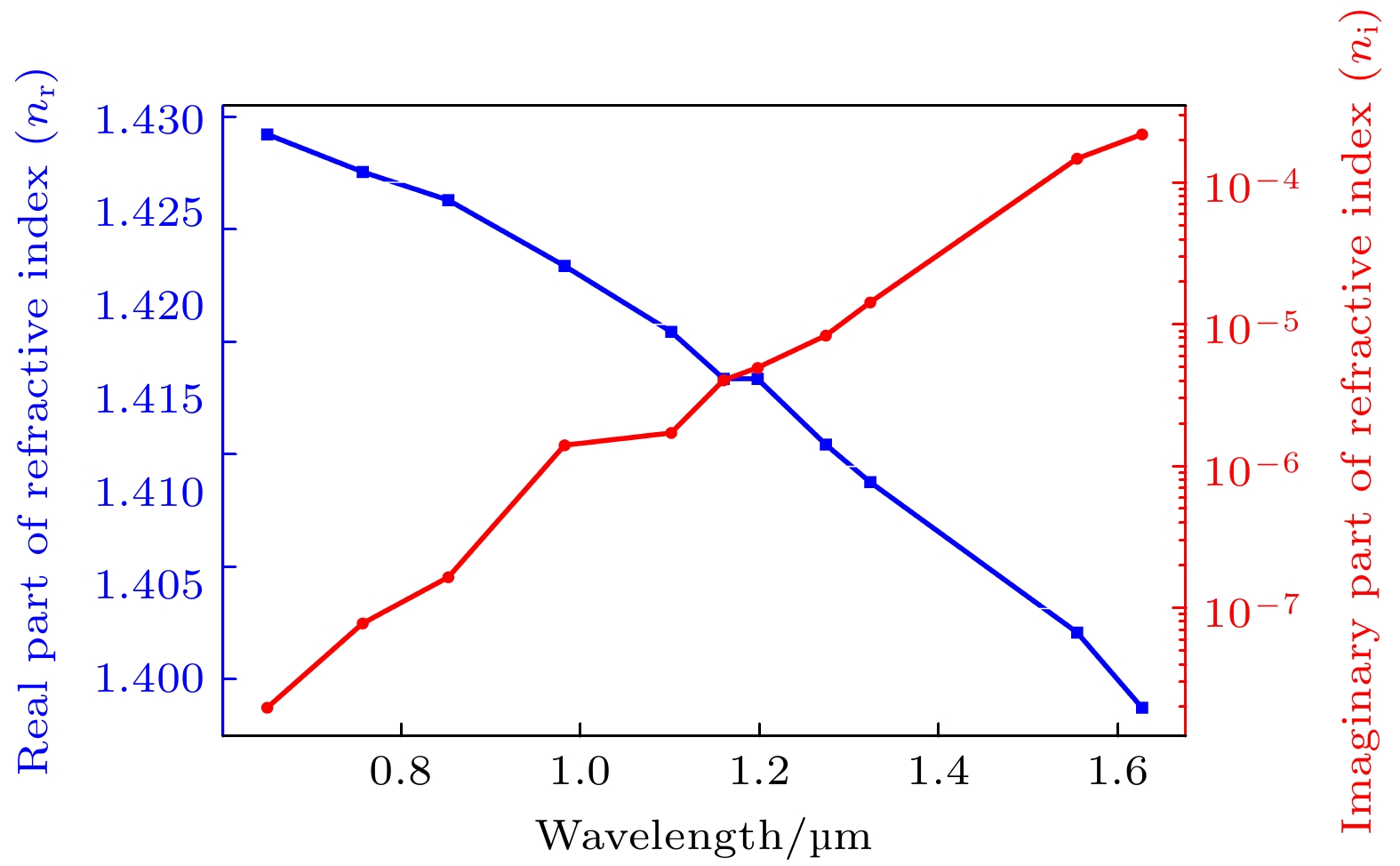
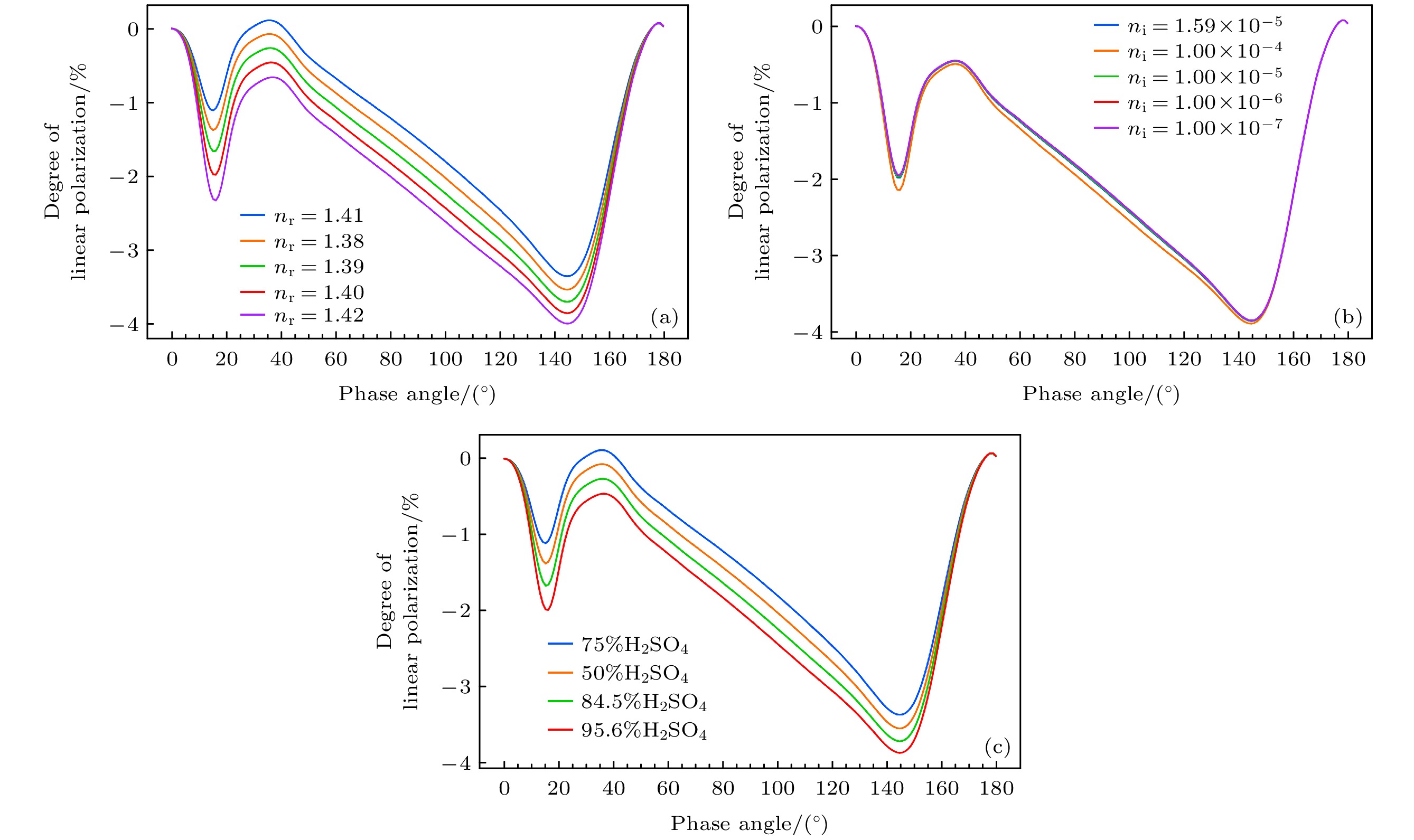
图 12 线偏振度对粒子复折射率和H2SO4浓度变化的敏感性($ {n}_{{\mathrm{r}}} $为折射率实部, $ {n}_{{\mathrm{i}}} $为折射率虚部)
Fig. 12. Sensitivity of linear polarization degree to changes in particle complex refractive index and H2SO4 concentration ($ {n}_{{\mathrm{r}}} $ is the real part of the refractive index, $ {n}_{{\mathrm{i}}} $ is the imaginary part of the refractive index).
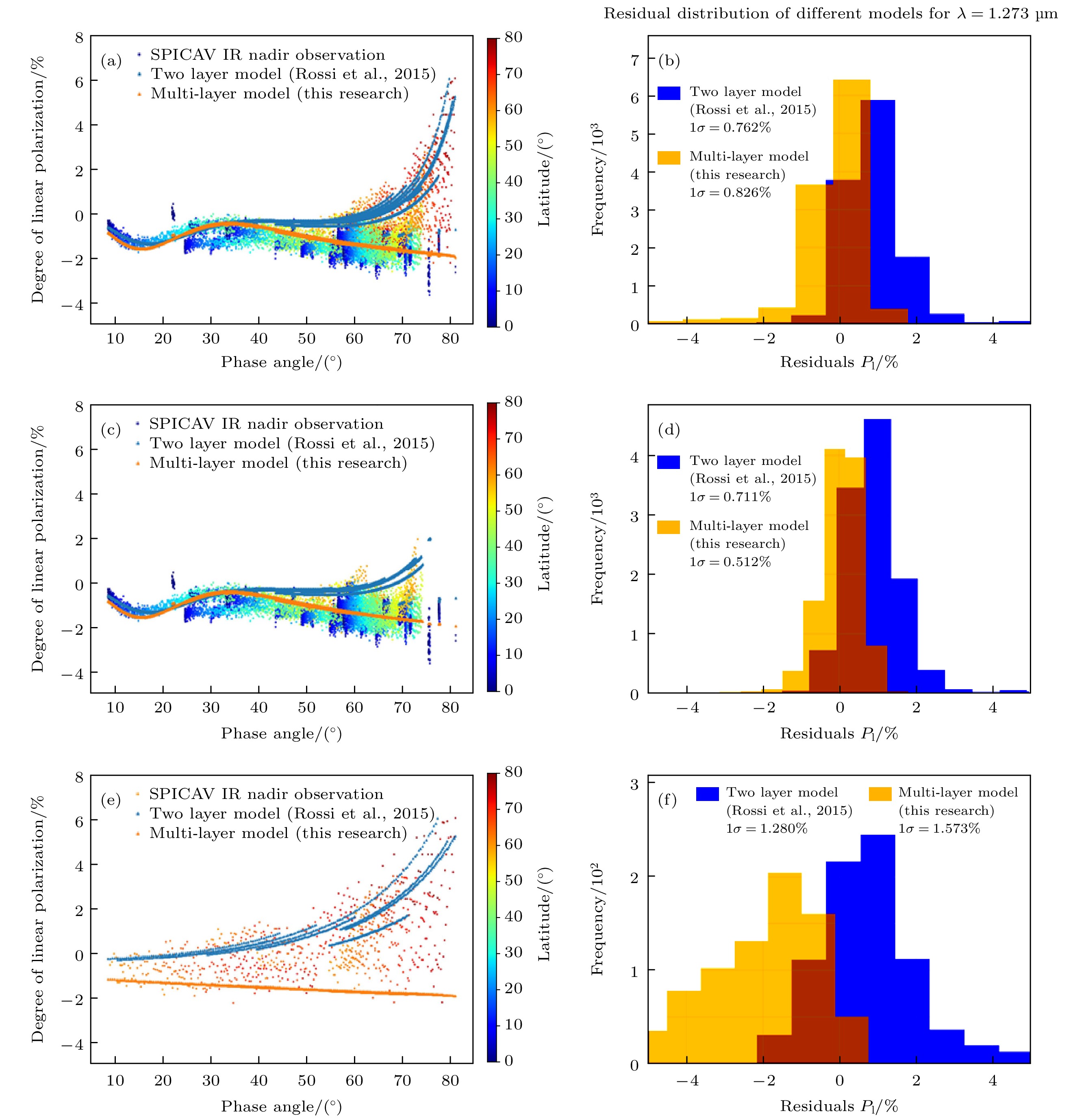
图 13 (a) 多层和双层模型的模拟结果与北半球SPICAV IR偏振数据的对比; (b)多层和双层模型模拟值与北半球SPICAV IR实测偏振数据间残差的1σ区间; (c), (d)对应北半球中低纬地区(0—60°N); (e), (f)对应北半球高纬地区(60°N—80°N)
Fig. 13. (a) Comparison of simulation results of multi-layer and double-layer models with SPICAV IR polarization data in the Northern Hemisphere; (b) 1σ interval of residuals between simulation values of multi-layer and double-layer models and measured polarization data of SPICAV IR in the Northern Hemisphere; (c), (d) correspond to the middle and low latitudes of the Northern Hemisphere (0−60°N); (e), (f) correspond to the high latitudes of the Northern Hemisphere (60°N−80°N)
图 14 相位角$ \alpha =0° $时不同波长下线偏振在金星盘上的积分结果
Fig. 14. Integration results of linear polarization on the disk of Venus at different wavelengths when the phase angle $ \alpha =0° $.
图 15 金星盘上的线偏振度随相位角的变化
Fig. 15. Variation of linear polarization degree with phase angle on the disk of Venus.
图 16 相位角$ \alpha =15° $时盘积分线偏振度对Mode 2粒子几何标准差$ \sigma _{\text{g}}^2 $的敏感性
Fig. 16. Sensitivity of disk integrated linear polarization degree to Mode 2 particle geometric standard deviation $ \sigma _{\text{g}}^2 $ when phase angle $ \alpha =15° $.
图 17 相位角$ \alpha =0° $时不同云量下金星盘积分线偏振度
Fig. 17. Integrated linear polarization degree of Venus disk under different cloud cover when phase angle $ \alpha =0° $.
表 1 SPICAV IR仪器SW和LW通道对应波长
Table 1. Wavelengths of SW and LW channels of SPICAV IR instrument.
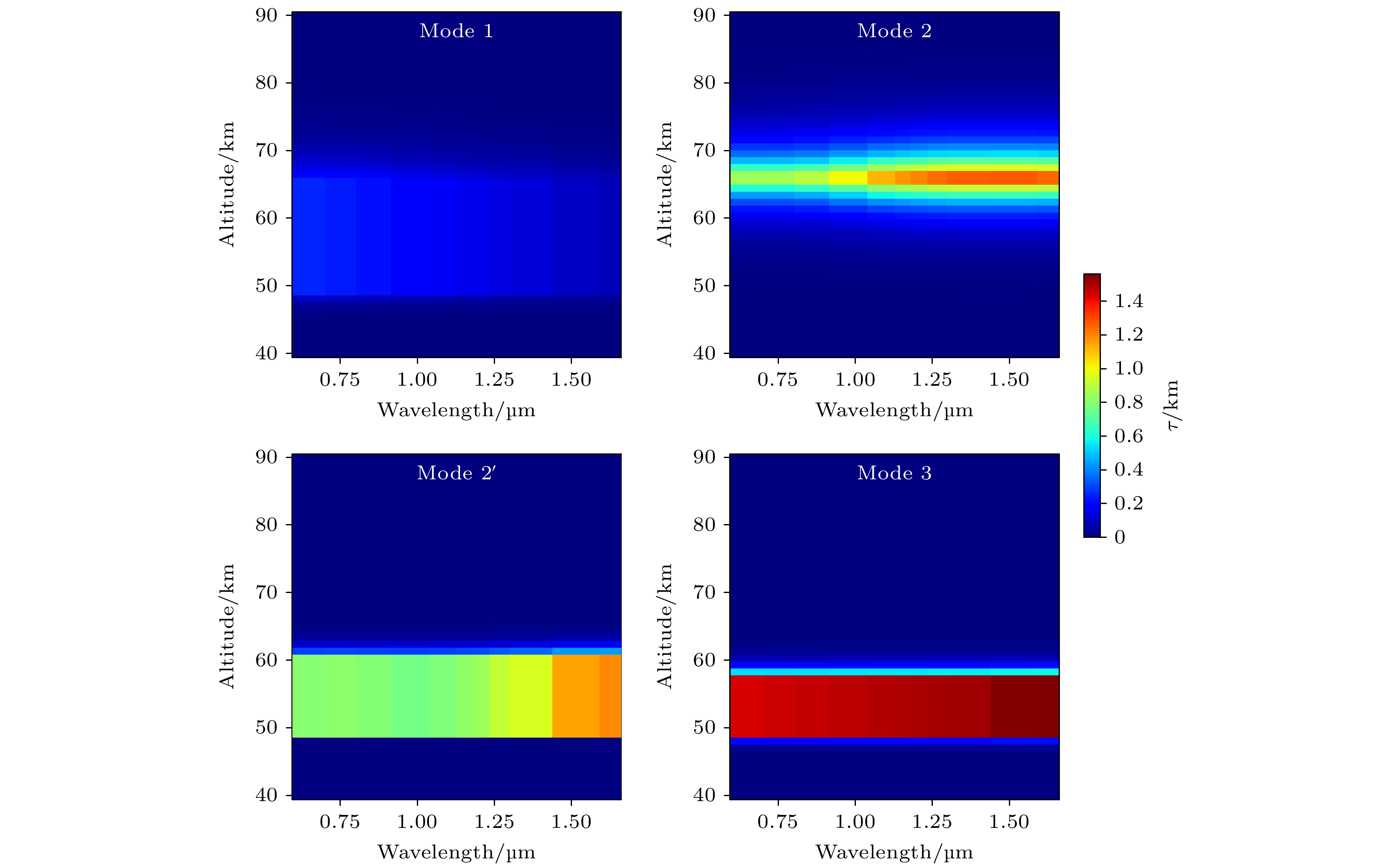
通道 DOTS处波长/nm SW 650.8, 757.2, 852.7, 982.3 LW 1101.1, 1159.6, 1197.3, 1273.4, 1323.0, 1553.7, 1626.0 
下载: 导出CSV
表 2 金星标准云模型的单模态参数
Table 2. Single-mode parameters of Venus standard cloud model.
模式 1 2 2' 3 峰值高度下限 zb/km 49.0 65.0 49.0 49.0 恒定峰值粒子数的层厚 zc/km 16.0 1.0 11.0 8.0 上层标高 Hup/km 3.5 3.5 1.0 1.0 下层标高 Hlo/km 1.0 3.0 0.1 0.5 峰值高度处的粒子数密度 N0/cm–3 193.5 100 50 14 粒子总柱浓度/(105 cm–2) 3966.19 749.56 605.0 133.0
下载: 导出CSV
-
[1] Lyot B 1929 Ph. D. Dissertation (Paris: Université de Paris Paris
[2] Coffeen D L 1969 Astronom. J. 74 446
Google Scholar
[3] Dyck H, Forbes F, Shawl S 1971 Astronom. J. 76 901
Google Scholar
[4] Hansen J E, Hovenier J 1974 J. atmos. Sci. 31 1137
Google Scholar
[5] Esposito L, Knollenberg R, Marov M, Toon O, Turco R 1983 The Clouds and Hazes of Venus (University of Arizona Press) pp484−564
[6] Pollack J B, Dalton J B, Grinspoon D, Wattson R B, Freedman R, Crisp D, Allen D A, Bezard B, DeBergh C, Giver L P 1993 Icarus 103 1
Google Scholar
[7] Rossi L, Marcq E, Montmessin F, Fedorova A, Stam D, Bertaux J L, Korablev O 2015 Planet. Space Sci. 113 159
Google Scholar
[8] 李宜奇, 孙晓兵, 黄红莲, 刘晓, 提汝芳, 郑小兵, 樊依哲, 余海啸, 韦祎晨, 王宇轩, 王宇瑶 2024 红外与毫米波学报 43 657
Google Scholar
Li Y Q, Sun X B, Huang H L, Liu X, Ti R F, Zheng X B, Fan Y Z, Yu H X, Wei Y C, Wang Y X, Wang Y Y 2024 J. Infrared Millim. W. 43 657
Google Scholar
[9] Hansen J E, Travis L D 1974 Space Sci. Rev. 16 527
Google Scholar
[10] Stam D 2008 Astron. Astrophys. 482 989
Google Scholar
[11] Stam D, Hovenier J, Waters L 2004 Astron. Astrophys. 428 663
Google Scholar
[12] Bertaux J L, Nevejans D, Korablev O, et al. 2007 Planet. Space Sci. 55 1673
Google Scholar
[13] Svedhem H, Titov D, McCoy D, Lebreton J P, Barabash S, Bertaux J L, Drossart P, Formisano V, Häusler B, Korablev O 2007 Planet. Space Sci. 55 1636
Google Scholar
[14] Korablev O, Fedorova A, Bertaux J L, et al. 2012 Planet. Space Sci. 65 38
Google Scholar
[15] Rossi L, Berzosa-Molina J, Stam D M 2018 Astron. Astrophys. 616 A147
Google Scholar
[16] de Haan J F, Bosma P, Hovenier J 1987 Astron. Astrophys. 183 371
[17] Peterson P 2009 Int. J. Comput. Sci. Eng. 4 296
Google Scholar
[18] Zasova L, Moroz V, Linkin V, Khatuntsev I, Maiorov B 2006 Cosmic Res. 44 364
Google Scholar
[19] Braak C, De Haan J, Hovenier J, Travis L 2002 J. Geophys. Res. Planets 107 5
Google Scholar
[20] Knibbe W J J, de Haan J F, Hovenier J W, Travis L D 1998 J. Geophys. Res. Planets 103 8557
Google Scholar
[21] Palmer K F, Williams D 1975 Appl. Opt. 14 208
Google Scholar
[22] Haus R, Kappel D, Arnold G 2015 Planet. Space Sci. 117 262
Google Scholar
[23] Mie G 1908 Ann. Phys. 330 377
Google Scholar
[24] van de Hulst H C Van de Hulst H C, Twersky V 1957 Physics Today 10 28
Google Scholar
下载:
计量
- 文章访问数: 375
- PDF下载量: 14
- 被引次数: 0
