-
Coherent population transfer in quantum systems is of fundamental importance in many fields such as atomic and molecular collision dynamics, and information processing for qubit systems. Stimulated Raman nonadiabatic passage technique, when implemented in an externally driven three-level system, provides an efficient approach for realizing accelerated population transfer while maintaining robust quantum coherence, with no need of rotating wave approximation. However, previous protocols employ multiple pulses and imply that Rabi frequencies have a few oscillations during dynamical evolution. In this work, under the condition of two-photon resonance, we use a gauge transformation method to inversely design a Λ-configuration three-level system that can be solved exactly. By using SU(3) transformation, we establish the relationship between Schrödinger representation and gauge representation, where the effective Hamiltonian is an Abelian operator. Subsequently, we construct the desired Hamiltonian and further investigate its dynamic behavior. The result shows that by imposing appropriate boundary conditions on the control parameters, high-fidelity population transfer can be achieved in ideal evolution. In addition, for the practical case with pulse truncation and intermediate state decay, the fidelities of specific models can reach about 99.996% and 99.983%, respectively. Compared with other existing nonadiabatic quantum control schemes, the present scheme has the distinctive advantages. We achieve the required quantum control by applying only a few sets of Stokes and pump pulses without introducing any additional microwave field. This method does not exhibit Rabi oscillations in the dynamic process, nor does it produce singularities in the pulse itself.
-
Keywords:
- three-level systems /
- SU(3) Lie algebra /
- without the rotating-wave approximation /
- nonadiabatic population transfer
[1] Goldner L S, Gerz C, Spreeuw R J C, et al. 1994 Phys. Rev. Lett. 72 997
Google Scholar
[2] Vitanov N V, Fleischhauer M, Shore B W, Bergmann K 2001 Adv. At. Mol. Opt. Phys. 46 55
[3] Ischenko A A, Weber P M, Miller R J D 2017 Chem. Rev. 117 11066
Google Scholar
[4] Meng S Y, Wu W 2009 Acta Phys. Sin. 58 5311
Google Scholar
[5] 周方, 文凯, 王良伟, 刘方德, 韩伟, 王鹏军, 黄良辉, 陈良超, 孟增明, 张靖 2021 70 154204
Google Scholar
Zhou F, Wen K, Wang L W, Liu F D, Han W, Wang P J, Huang L H, Chen L C, Meng Z M, Zhang J 2021 Acta Phys. Sin. 70 154204
Google Scholar
[6] Kumar P, Sarma A K 2013 Phys. Rev. A 87 025401
Google Scholar
[7] Ohta Y, Hoki K, Fujimura Y 2002 J. Chem. Phys. 116 7509
Google Scholar
[8] Sun G, Wen X, Mao B, Chen J, Yu Y, Wu P, Han S 2010 Nat. Commun. 1 51
Google Scholar
[9] Wei L F, Johansson J R, Cen L X, Ashhab S, Nori F 2008 Phys. Rev. Lett. 100 113601
Google Scholar
[10] Vepsäläinen A, Danilin S, Paraoanu G S 2019 Sci. Adv. 5 eaau5999
Google Scholar
[11] Giannelli L, Arimondo E 2014 Phys. Rev. A 89 033419
Google Scholar
[12] Chen X, Lizuain I, Ruschhaupt A, Guéry-Odelin D, Muga J G 2010 Phys. Rev. Lett. 105 123003
Google Scholar
[13] del Campo A 2013 Phys. Rev. Lett. 111 100502
Google Scholar
[14] Chen X, Muga J G 2012 Phys. Rev. A 86 033405
Google Scholar
[15] Huang B H, Kang Y H, Chen Y H, Wu Q C, Song J, Xia Y 2017 Phys. Rev. A 96 022314
Google Scholar
[16] Li W, Song Y 2022 J. Phys. B: At. Mol. Opt. Phys. 55 125501
Google Scholar
[17] Song Y, Kestner J P, Wang X, Sarma S D 2016 Phys. Rev. A 94 012321
Google Scholar
[18] Liu X, Fang G Y, Liao Q H, Liu S T 2014 Phys. Rev. A 90 062330
Google Scholar
[19] Sornborger A T, Cleland A N, Geller M R 2004 Phys. Rev. A 70 052315
Google Scholar
[20] Malz D, Nunnenkamp A 2016 Phys. Rev. A 94 053820
Google Scholar
[21] Scheuer J, Kong X, Said R S, et al. 2014 New J. Phys. 16 093022
Google Scholar
[22] Chen J, Wei L F 2015 Phys. Rev. A 91 023405
Google Scholar
[23] Kang Y H, Chen Y H, Huang B H, Song J, Xia Y 2017 Ann. Physik 529 1700004
Google Scholar
[24] Hioe F T 1985 Phys. Rev. A 32 2824
Google Scholar
[25] Lewis H R, Riesenfeld W B 1969 J. Math. Phys. 10 1458
Google Scholar
[26] Traverso A J, Sanchez G R, Yuan L, et al. 2012 Proc. Natl Acad. Sci. 109 15185
Google Scholar
-
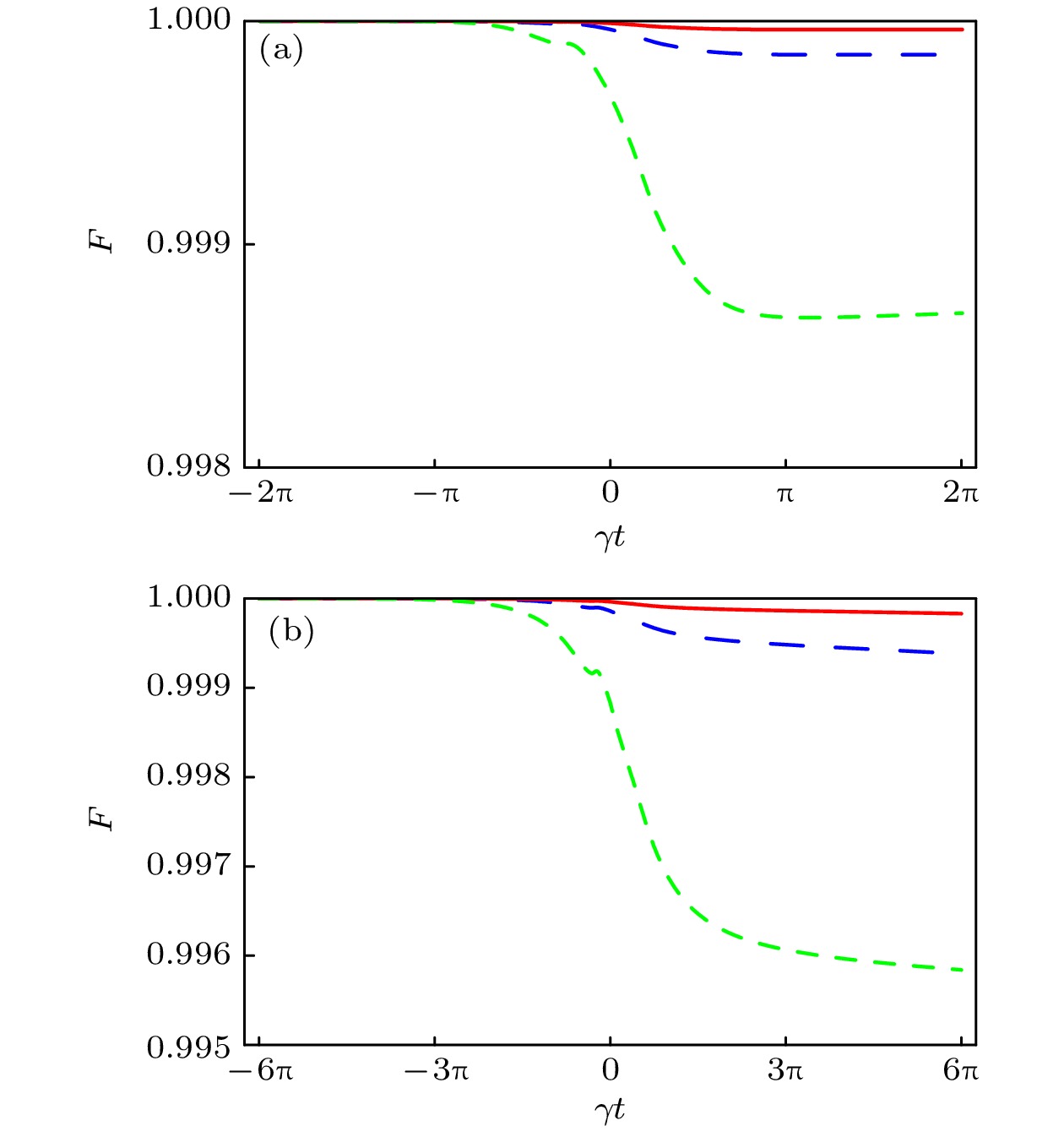
图 2 在量子态$|2\rangle$衰变的情况下, 保真度F相对于无量纲量$\gamma t$的演化. 这里分别设置参数$\varGamma/\gamma=0.005$(红实线), 0.01 (蓝虚线)和 0.03 (绿虚线) (a) 由方程(26)描述的模型, 保真度最终可以分别达到$F(2\pi)$ = 99.996%, 99.985%和99.869%; (b) 由方程(28)描述的模型, 保真度最终可以分别达到$F(6\pi)$ = 99.983%, 99.938%和99.584%
Fig. 2. Evolution of fidelity F as a function of the dimensionless quantity $\gamma t$, in the presence of decay. Here we have set $\varGamma/\gamma=0.005$(solid red), 0.01 (dashed blue), and 0.03 (dashed green): (a) For the model described by Eq. (26), the final fidelities can achieve as $F(2\pi)$ = 99.996%, 99.985%, and 99.869%; (b) for the model described by Eq. (28), the final fidelities can achieve as $F(6\pi)$ = 99.983%, 99.938% and 99.584%.
-
[1] Goldner L S, Gerz C, Spreeuw R J C, et al. 1994 Phys. Rev. Lett. 72 997
Google Scholar
[2] Vitanov N V, Fleischhauer M, Shore B W, Bergmann K 2001 Adv. At. Mol. Opt. Phys. 46 55
[3] Ischenko A A, Weber P M, Miller R J D 2017 Chem. Rev. 117 11066
Google Scholar
[4] Meng S Y, Wu W 2009 Acta Phys. Sin. 58 5311
Google Scholar
[5] 周方, 文凯, 王良伟, 刘方德, 韩伟, 王鹏军, 黄良辉, 陈良超, 孟增明, 张靖 2021 70 154204
Google Scholar
Zhou F, Wen K, Wang L W, Liu F D, Han W, Wang P J, Huang L H, Chen L C, Meng Z M, Zhang J 2021 Acta Phys. Sin. 70 154204
Google Scholar
[6] Kumar P, Sarma A K 2013 Phys. Rev. A 87 025401
Google Scholar
[7] Ohta Y, Hoki K, Fujimura Y 2002 J. Chem. Phys. 116 7509
Google Scholar
[8] Sun G, Wen X, Mao B, Chen J, Yu Y, Wu P, Han S 2010 Nat. Commun. 1 51
Google Scholar
[9] Wei L F, Johansson J R, Cen L X, Ashhab S, Nori F 2008 Phys. Rev. Lett. 100 113601
Google Scholar
[10] Vepsäläinen A, Danilin S, Paraoanu G S 2019 Sci. Adv. 5 eaau5999
Google Scholar
[11] Giannelli L, Arimondo E 2014 Phys. Rev. A 89 033419
Google Scholar
[12] Chen X, Lizuain I, Ruschhaupt A, Guéry-Odelin D, Muga J G 2010 Phys. Rev. Lett. 105 123003
Google Scholar
[13] del Campo A 2013 Phys. Rev. Lett. 111 100502
Google Scholar
[14] Chen X, Muga J G 2012 Phys. Rev. A 86 033405
Google Scholar
[15] Huang B H, Kang Y H, Chen Y H, Wu Q C, Song J, Xia Y 2017 Phys. Rev. A 96 022314
Google Scholar
[16] Li W, Song Y 2022 J. Phys. B: At. Mol. Opt. Phys. 55 125501
Google Scholar
[17] Song Y, Kestner J P, Wang X, Sarma S D 2016 Phys. Rev. A 94 012321
Google Scholar
[18] Liu X, Fang G Y, Liao Q H, Liu S T 2014 Phys. Rev. A 90 062330
Google Scholar
[19] Sornborger A T, Cleland A N, Geller M R 2004 Phys. Rev. A 70 052315
Google Scholar
[20] Malz D, Nunnenkamp A 2016 Phys. Rev. A 94 053820
Google Scholar
[21] Scheuer J, Kong X, Said R S, et al. 2014 New J. Phys. 16 093022
Google Scholar
[22] Chen J, Wei L F 2015 Phys. Rev. A 91 023405
Google Scholar
[23] Kang Y H, Chen Y H, Huang B H, Song J, Xia Y 2017 Ann. Physik 529 1700004
Google Scholar
[24] Hioe F T 1985 Phys. Rev. A 32 2824
Google Scholar
[25] Lewis H R, Riesenfeld W B 1969 J. Math. Phys. 10 1458
Google Scholar
[26] Traverso A J, Sanchez G R, Yuan L, et al. 2012 Proc. Natl Acad. Sci. 109 15185
Google Scholar
下载:
计量
- 文章访问数: 273
- PDF下载量: 2
- 被引次数: 0
