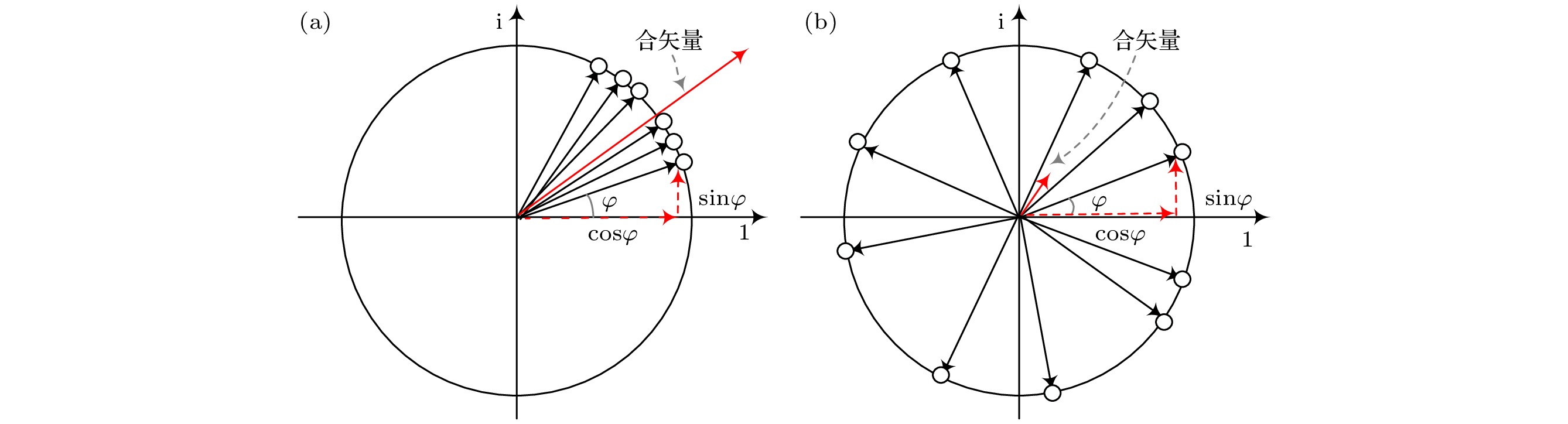
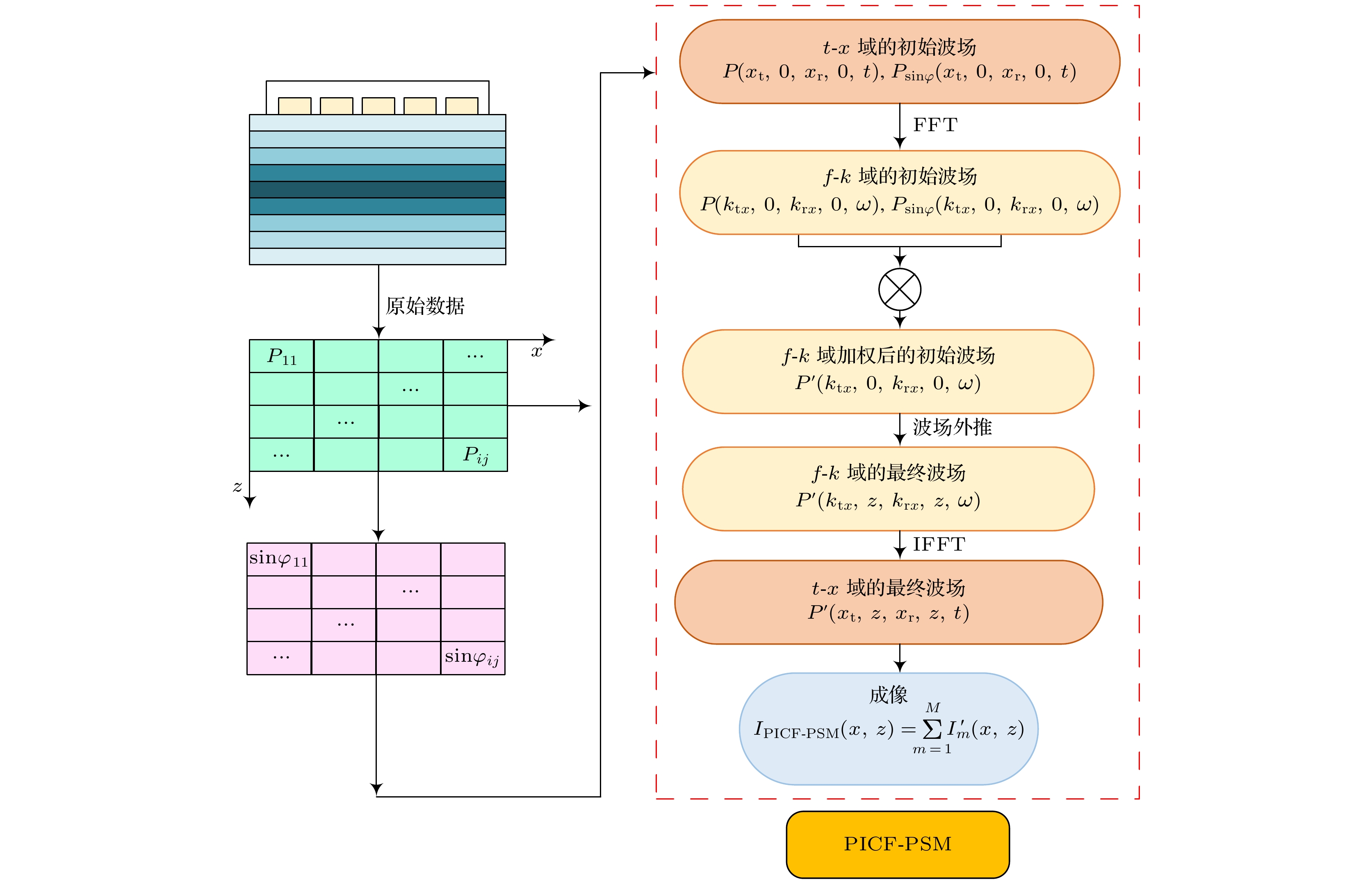
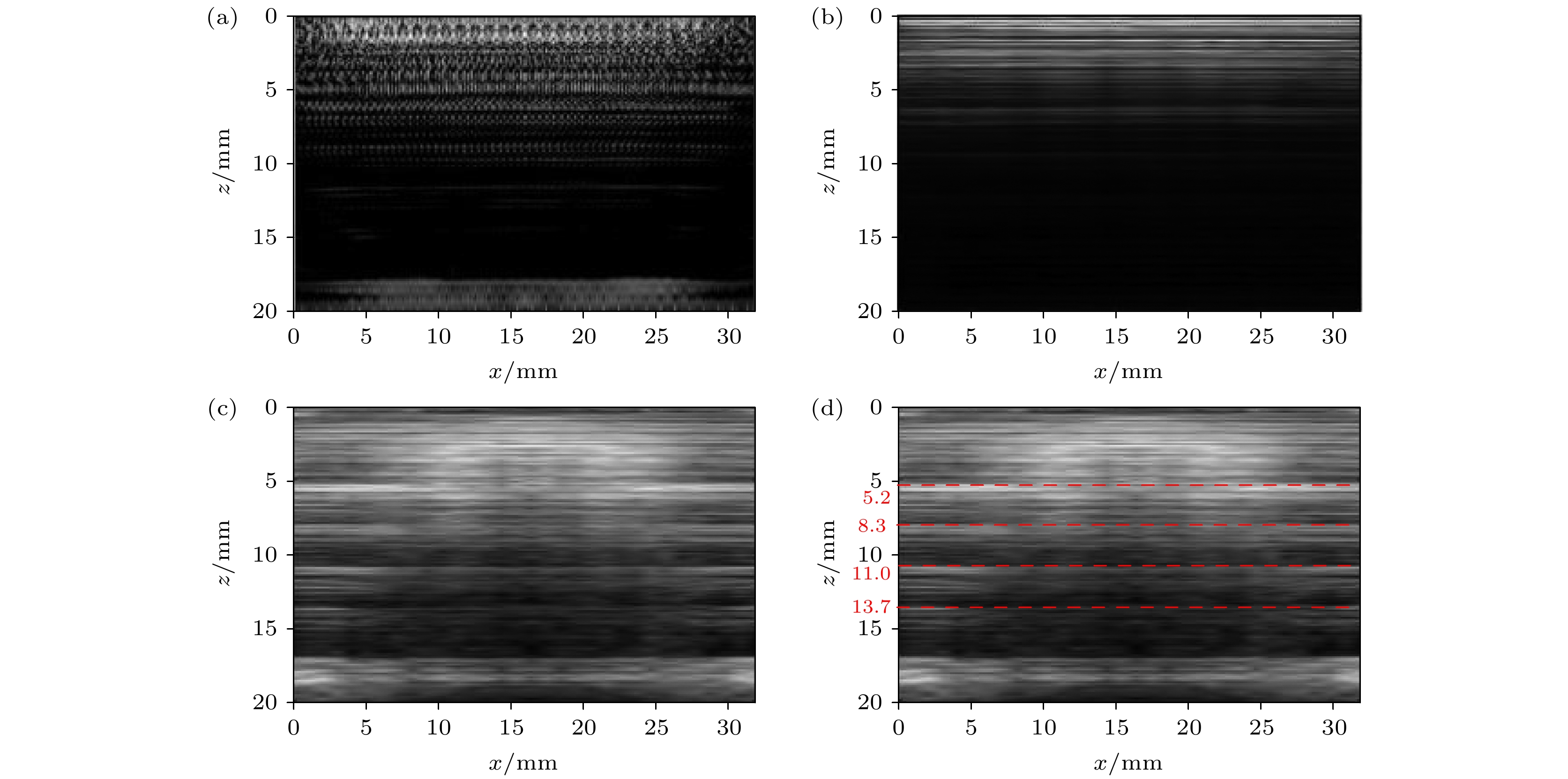
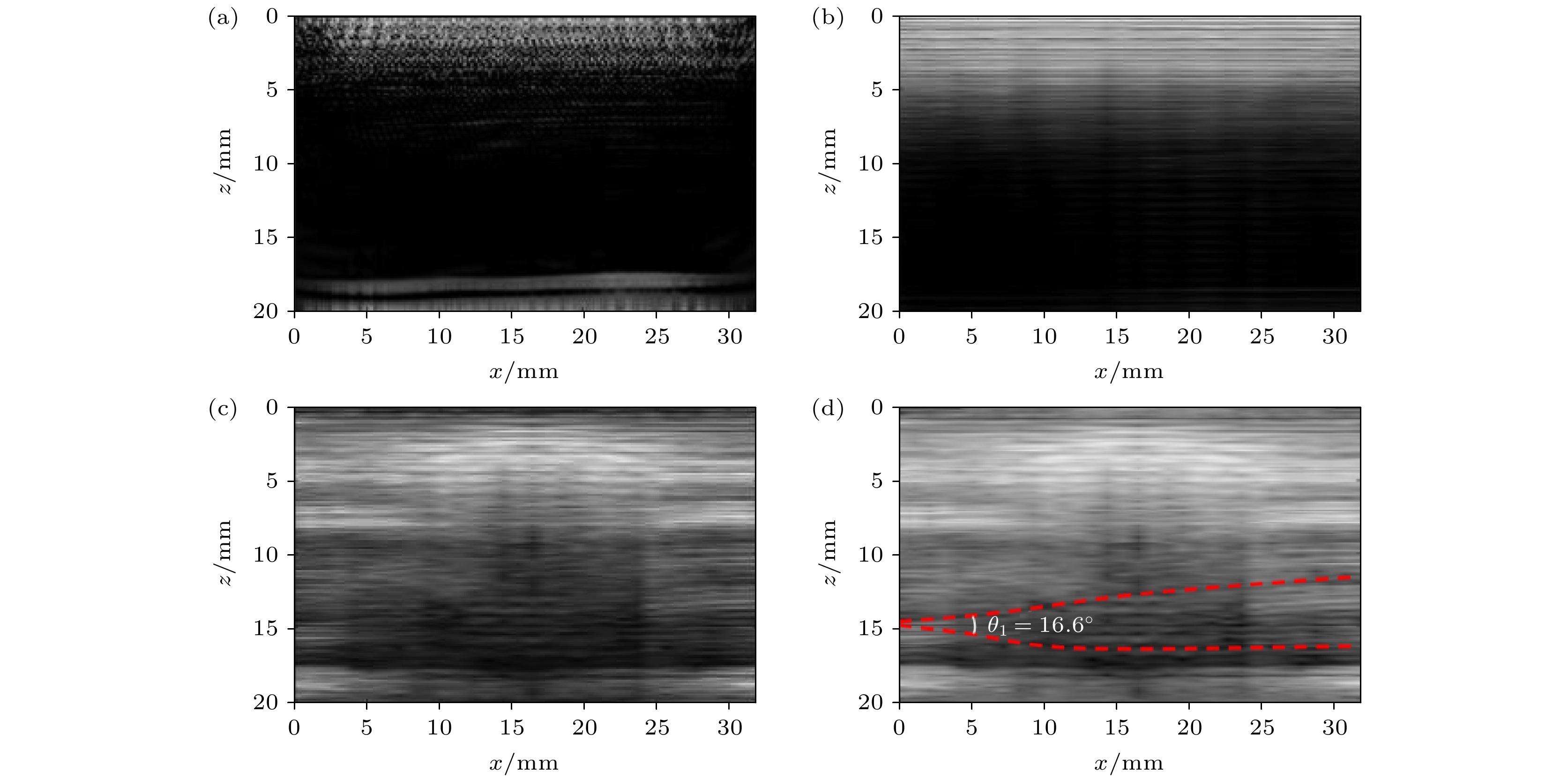
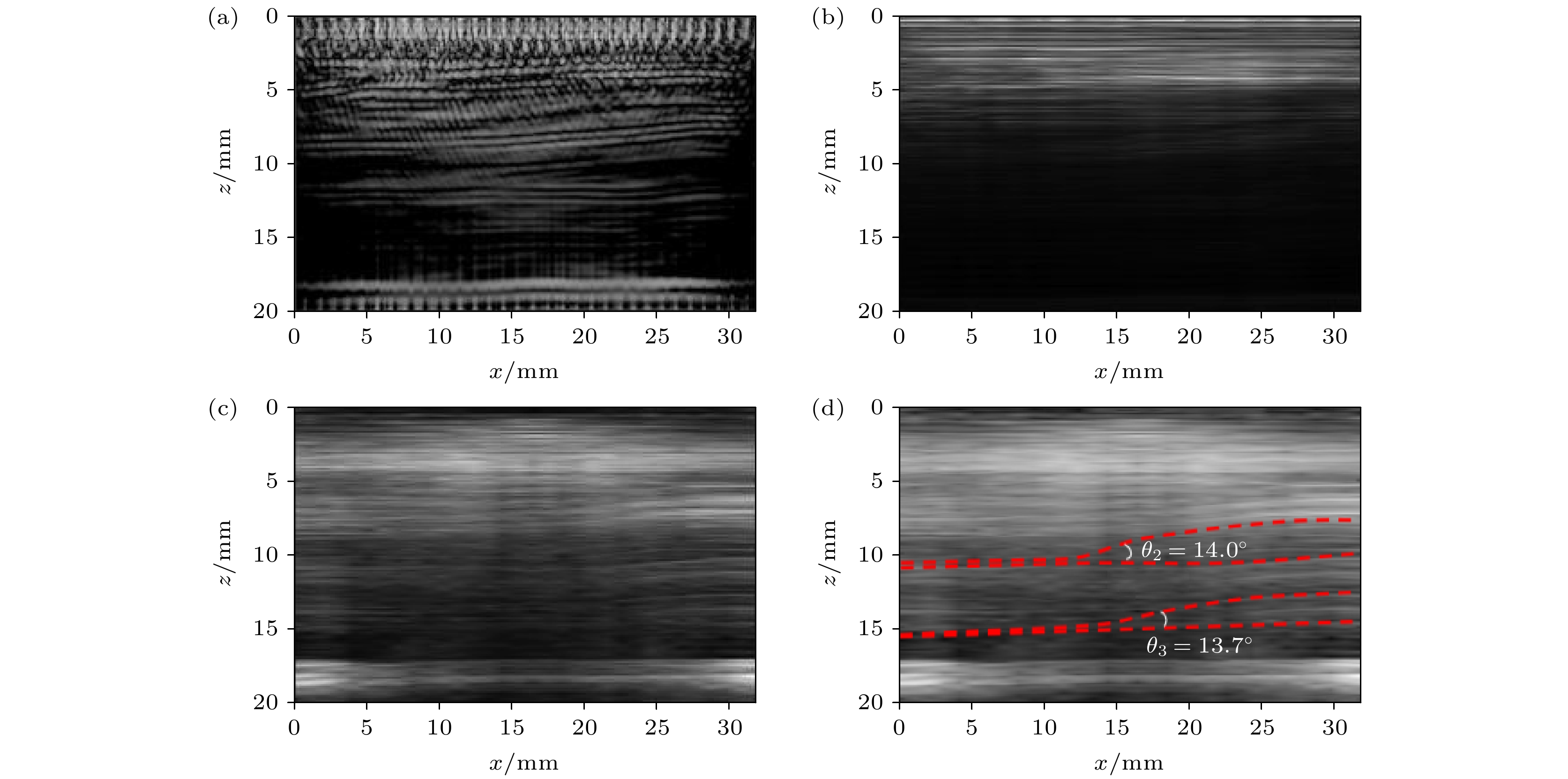
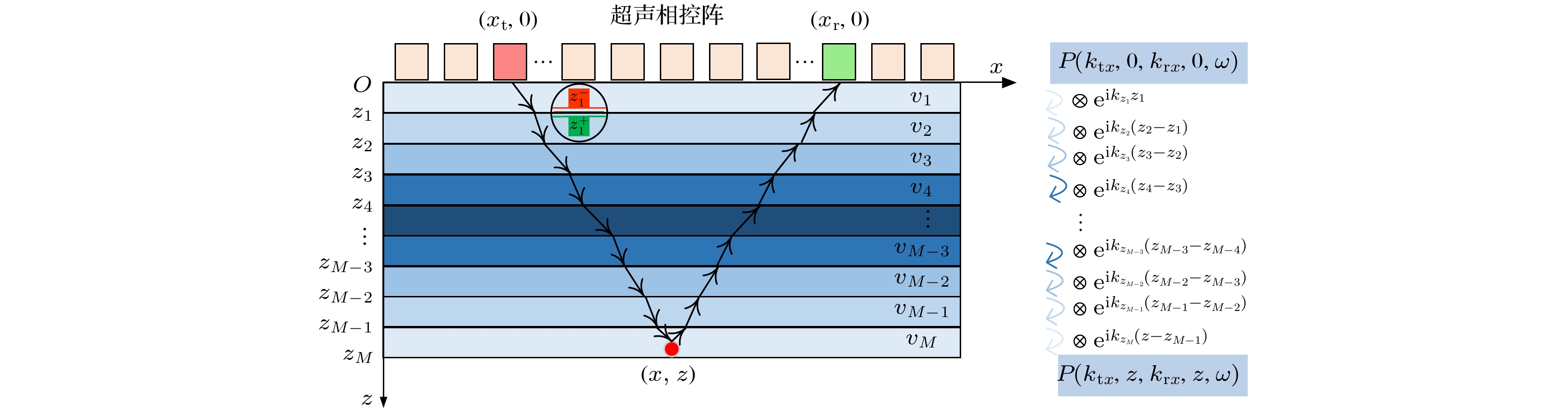
-
超声波的相位变化携带着组织结构的重要信息, 通过相位加权可提高超声图像的清晰度. 针对褶皱散射回波微弱、受噪声影响大、时域修正成像耗时长等问题, 提出一种基于相位虚部相干因子的频域相干成像方法. 首先提取波场信号中的相位信息, 然后采用环形统计获取相位虚部矩阵, 通过相位虚部矩阵与相位迁移成像(phase shift migration, PSM)中的原频域矩阵相乘构建相位虚部相干因子(phase imaginary coherence factor, PICF), 将相位虚部相干因子引入相位迁移成像, 并对各层迁移波场进行修正, 通过频域信号相乘恢复纤维纹理信息. 对厚度为18 mm的碳玻纤维复合材料板进行检测, 实验结果表明: 未加权的相位迁移成像在10 mm深度以后的纤维铺层信息丢失, 无法检测出深层区域的缺陷; 用PICF加权后PSM成像可检测出位于11, 15, 16 mm处的3个纤维褶皱, 褶皱缺陷成像清晰度和纹理细致度均得到提高, 褶皱角度的检测误差约为10%, 并且成像耗时仅为1.5 s, 运算效率比时域全聚焦成像(total focusing method, TFM)至少提高8.67倍.Ultrasonic phase changes carry critical information about tissue structures, and phase weighting can enhance the sharpness of ultrasonic images. Addressed here are challenges, such as the faint scattering echoes from folds, substantial noise interference, and the lengthy processing time involved in time-domain corrected imaging. Processed in this work is a frequency-domain coherent imaging method based on the coherence factor of the phase imaginary part. Firstly, the phase information in the wavefield signal is extracted, and then the phase imaginary part matrix is extracted by using circular statistics. Subsequent construction of the phase imaginary coherence factor (PICF) involves multiplying this matrix with the original frequency-domain matrix used in phase shift migration (PSM) imaging. By incorporating the PICF into phase migration imaging and adjusting the PICF of the migrating wavefield at each layer, fibre texture information can be efficiently recovered by frequency domain signal multiplication. In this paper, this technique is applied to the 18-mm-thick carbon-glass fiber composite boards. The experimental outcomes indicate that without PICF weighting, phase shift imaging loses the fiber layout information at depths exceeding 10 mm and cannot detect defects in deeper areas. The PICF-weighted PSM imaging identifies three fibre folds with depths of 11 mm, 15 mm and 16 mm, respectively. This method improves the imaging clarity and textural detail of folding defects, while maintaining a detection error of about 10% for folding angles. The imaging time is only 1.5 s, and its computational efficiency is at least 8.67 times that of time-domain TFM imaging.
[1] Teng G Y, Zhou X J, Yang C L, Zeng X 2018 Opt. Prec. Eng. 26 3108
Google Scholar
[2] Mukhopadhyay S, Jones M I, Hallett S R 2015 Compos. Pt. A-Appl. Sci. Manuf. 73 132
Google Scholar
[3] Gigante V, Aliotta L, Phuong V T, Coltelli M B, Cinelli P, Lazzeri A 2017 Compos. Sci. Technol. 152 129
Google Scholar
[4] Kulkarni P, Mali K D, Singh S 2020 Compos. Pt. A-Appl. Sci. Manuf. 137 106013
Google Scholar
[5] Xie N B, Smith R A, Mukhopadhyay S, Hallett S R 2018 Mater. Des. 140 7
Google Scholar
[6] Liu D, Fleck N A, Sutcliffe M F 2004 J. Mech. Phys. Solids 52 1481
Google Scholar
[7] Wang Z, Yang C L, Zhou X J, Teng Y H 2019 Russ. J. Nondestr. Test. 55 192
Google Scholar
[8] 陈越超, 周晓军, 杨辰龙, 李钊, 郑慧峰 2015 农业机械学报 46 372
Google Scholar
Chen Y C, Zhou X J, Yang C L, Li Z, Zheng H F 2015 Trans. Chin. Soc. Agricult. Machin. 46 372
Google Scholar
[9] Cruza J F, Camacho J 2016 IEEE Trans. Ultrason. Ferroelectr. Freq. Control 63 1581
Google Scholar
[10] 张海燕, 宋佳昕, 任燕, 朱琦, 马雪芬 2021 70 114301
Google Scholar
Zhang H Y, Song J X, Ren Y, Zhu Q, Ma X F 2021 Acta Phys. Sin. 70 114301
Google Scholar
[11] Zhang H Y, Ren Y, Song J X, Zhu Q, Ma X F 2021 J. Compos. Mater. 55 4633
Google Scholar
[12] Liu Z H, Chen L, Zhu Y P, Liu X Y, Lu Z J, He C F 2024 Ultrasonics 141 107321
Google Scholar
[13] Olofsson T 2010 IEEE Trans. Ultrason. Ferroelectr. Freq. Control 57 2522
Google Scholar
[14] Skjelvareid M H, Olofsson T, Birkelund Y, Larsen Y 2011 IEEE Trans. Ultrason. Ferroelectr. Freq. Control 58 1037
Google Scholar
[15] Wang Y D, Zheng C C, Peng H 2019 Comput. Biol. Med. 108 249
Google Scholar
[16] Yang C, Jiao Y, Jiang T Y, Xu Y W, Cui Y Y 2020 Appl. Sci. Basel 10 2250
[17] Camacho J, Parrilla M, Fritsch C 2009 IEEE Trans. Ultrason. Ferroelectr. Freq. Control 56 958
Google Scholar
[18] Cruza J F, Camacho J, Fritsch C 2017 NDT E. Int. 87 31
Google Scholar
[19] Prado V T, Higuti R T, Kitano C, Martínez-Graullera O 2014 IEEE Trans. Ultrason. Ferroelectr. Freq. Control 61 1204
Google Scholar
[20] Chen Y, Xiong Z H, Kong Q R, Ma X X, Chen M, Lu C 2023 Ultrasonics 128 106856
Google Scholar
[21] Nelson L J, Smith R A, Mienczakowski M 2018 Compos. Pt. A-Appl. Sci. Manuf. 104 108
Google Scholar
[22] Smith R A 2007 Mater. Eval. 65 697
[23] Garcia D, Le Tarnec L, Muth S, Montagnon E, Porée J, Cloutier G 2013 IEEE Trans. Ultrason. Ferroelectr. Freq. Control 60 1853
Google Scholar
[24] Ji K P, Zhao P, Zhuo C J, Jin H R, Chen M, Chen J, Ye S, Fu J Z 2022 Mech. Syst. Signal Proc. 174 109114
Google Scholar
[25] Lukomski T 2016 Ultrasonics 70 241
Google Scholar
[26] Schleicher J, Costa J C, Novais A 2008 Geophysics 73 S219
Google Scholar
[27] Pain D, Drinkwater B W 2013 J. Nondestruct. Eval. 32 215
Google Scholar
[28] Smith R A, Nelson L J, Mienczakowski M J, Wilcox P D 2018 IEEE Trans. Ultrason. Ferroelectr. Freq. Control 65 231
Google Scholar
-
图 1 超声相控阵多层层合板介质模型
Fig. 1. Ultrasonic phased array multi-layer laminated plate media model.
图 2 环形矢量 (a)集中分布的样本矢量; (b)散乱分布的样本矢量
Fig. 2. Circular vectors: (a) Centrally distributed sample vectors; (b) randomly distributed sample vectors.
图 4 CFRP (a)健康试样I; (b)褶皱试样II; (c)褶皱试样III
Fig. 4. CFRP: (a) Healthy sample I; (b) wrinkled sample II; (c) wrinkled sample III.
图 6 试样II的第16阵元的短时傅里叶变换 (a) fc = 2.5 MHz; (b) fc = 5 MHz
Fig. 6. Short-time Fourier transform of the 16th element of sample II: (a) fc = 2.5 MHz; (b) fc = 5 MHz.
图 7 试样I成像方法对比 (a) TFM; (b) PSM; (c) PICF-PSM; (d) PICF-PSM标注
Fig. 7. Comparison of imaging methods for sample I: (a) TFM; (b) PSM; (c) PICF-PSM; (d) PICF-PSM annotation diagram.
图 8 试样II成像方法对比 (a) TFM; (b) PSM; (c) PICF-PSM; (d) PICF-PSM标注
Fig. 8. Comparison of imaging methods for sample II: (a) TFM; (b) PSM; (c) PICF-PSM; (d) PICF-PSM annotation diagram.
图 9 试样III成像方法对比 (a) TFM; (b) PSM; (c) PICF-PSM; (d) PICF-PSM标注
Fig. 9. Comparison of imaging methods for sample III: (a) TFM; (b) PSM; (c) PICF-PSM; (d) PICF-PSM annotation diagram.
图 10 不同成像方法的清晰度评价
Fig. 10. Definition evaluation of different methods in frequency domain.
表 1 材料参数
Table 1. Parameters of materials.
试样 褶皱深度/mm 褶皱角度/(°) 健康试样I 无褶皱 褶皱试样II 16 15.2 褶皱试样III 11 12.6 15 12.4 
下载: 导出CSV
表 2 相控阵探头参数
Table 2. Parameters of phased array probes.
参数 探头A 探头B 阵元个数 32 32 阵元间隔/mm 1 1 阵元宽度/mm 0.9 0.9 中心频率/MHz 5 2.5 激励电源/V 70 70 采样频率/MHz 50 50 激励信号 5个周期的高斯正弦波 5个周期的高斯正弦波 激励方式 纵波 纵波
下载: 导出CSV
表 3 PICF-PSM成像的褶皱角误差
Table 3. Errors of samples with wrinkles in PICF-PSM imaging.
褶皱试样 实际褶皱
角度/(°)PICF-PSM检测
角度/(°)误差/% 试样II 15.2 16.6 9.22 试样III 12.6 14.0 11.1 12.4 13.7 10.48
下载: 导出CSV
表 4 不同成像算法计算耗时
Table 4. Calculation time of different imaging algorithms.
成像方法 计算时间/s 时域 TFM 13.0 频域 PSM 1.3 PICF-PSM 1.5
下载: 导出CSV
-
[1] Teng G Y, Zhou X J, Yang C L, Zeng X 2018 Opt. Prec. Eng. 26 3108
Google Scholar
[2] Mukhopadhyay S, Jones M I, Hallett S R 2015 Compos. Pt. A-Appl. Sci. Manuf. 73 132
Google Scholar
[3] Gigante V, Aliotta L, Phuong V T, Coltelli M B, Cinelli P, Lazzeri A 2017 Compos. Sci. Technol. 152 129
Google Scholar
[4] Kulkarni P, Mali K D, Singh S 2020 Compos. Pt. A-Appl. Sci. Manuf. 137 106013
Google Scholar
[5] Xie N B, Smith R A, Mukhopadhyay S, Hallett S R 2018 Mater. Des. 140 7
Google Scholar
[6] Liu D, Fleck N A, Sutcliffe M F 2004 J. Mech. Phys. Solids 52 1481
Google Scholar
[7] Wang Z, Yang C L, Zhou X J, Teng Y H 2019 Russ. J. Nondestr. Test. 55 192
Google Scholar
[8] 陈越超, 周晓军, 杨辰龙, 李钊, 郑慧峰 2015 农业机械学报 46 372
Google Scholar
Chen Y C, Zhou X J, Yang C L, Li Z, Zheng H F 2015 Trans. Chin. Soc. Agricult. Machin. 46 372
Google Scholar
[9] Cruza J F, Camacho J 2016 IEEE Trans. Ultrason. Ferroelectr. Freq. Control 63 1581
Google Scholar
[10] 张海燕, 宋佳昕, 任燕, 朱琦, 马雪芬 2021 70 114301
Google Scholar
Zhang H Y, Song J X, Ren Y, Zhu Q, Ma X F 2021 Acta Phys. Sin. 70 114301
Google Scholar
[11] Zhang H Y, Ren Y, Song J X, Zhu Q, Ma X F 2021 J. Compos. Mater. 55 4633
Google Scholar
[12] Liu Z H, Chen L, Zhu Y P, Liu X Y, Lu Z J, He C F 2024 Ultrasonics 141 107321
Google Scholar
[13] Olofsson T 2010 IEEE Trans. Ultrason. Ferroelectr. Freq. Control 57 2522
Google Scholar
[14] Skjelvareid M H, Olofsson T, Birkelund Y, Larsen Y 2011 IEEE Trans. Ultrason. Ferroelectr. Freq. Control 58 1037
Google Scholar
[15] Wang Y D, Zheng C C, Peng H 2019 Comput. Biol. Med. 108 249
Google Scholar
[16] Yang C, Jiao Y, Jiang T Y, Xu Y W, Cui Y Y 2020 Appl. Sci. Basel 10 2250
[17] Camacho J, Parrilla M, Fritsch C 2009 IEEE Trans. Ultrason. Ferroelectr. Freq. Control 56 958
Google Scholar
[18] Cruza J F, Camacho J, Fritsch C 2017 NDT E. Int. 87 31
Google Scholar
[19] Prado V T, Higuti R T, Kitano C, Martínez-Graullera O 2014 IEEE Trans. Ultrason. Ferroelectr. Freq. Control 61 1204
Google Scholar
[20] Chen Y, Xiong Z H, Kong Q R, Ma X X, Chen M, Lu C 2023 Ultrasonics 128 106856
Google Scholar
[21] Nelson L J, Smith R A, Mienczakowski M 2018 Compos. Pt. A-Appl. Sci. Manuf. 104 108
Google Scholar
[22] Smith R A 2007 Mater. Eval. 65 697
[23] Garcia D, Le Tarnec L, Muth S, Montagnon E, Porée J, Cloutier G 2013 IEEE Trans. Ultrason. Ferroelectr. Freq. Control 60 1853
Google Scholar
[24] Ji K P, Zhao P, Zhuo C J, Jin H R, Chen M, Chen J, Ye S, Fu J Z 2022 Mech. Syst. Signal Proc. 174 109114
Google Scholar
[25] Lukomski T 2016 Ultrasonics 70 241
Google Scholar
[26] Schleicher J, Costa J C, Novais A 2008 Geophysics 73 S219
Google Scholar
[27] Pain D, Drinkwater B W 2013 J. Nondestruct. Eval. 32 215
Google Scholar
[28] Smith R A, Nelson L J, Mienczakowski M J, Wilcox P D 2018 IEEE Trans. Ultrason. Ferroelectr. Freq. Control 65 231
Google Scholar
下载:
计量
- 文章访问数: 503
- PDF下载量: 12
- 被引次数: 0
