谐振型自偏置磁电换能器的建模与性能研究

谢冰鸿; 徐国凯; 雷保新; 肖绍球; 喻忠军; 朱大立

doi:10.7498/aps.73.20240615

摘要

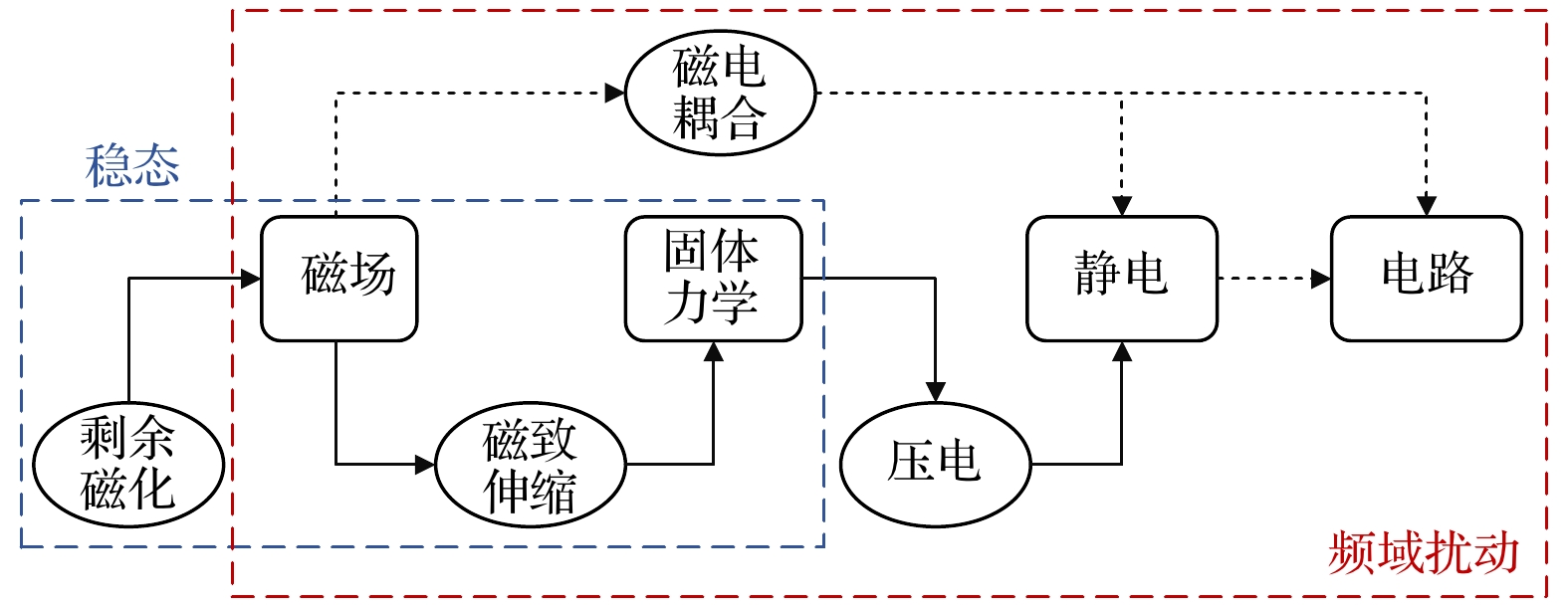
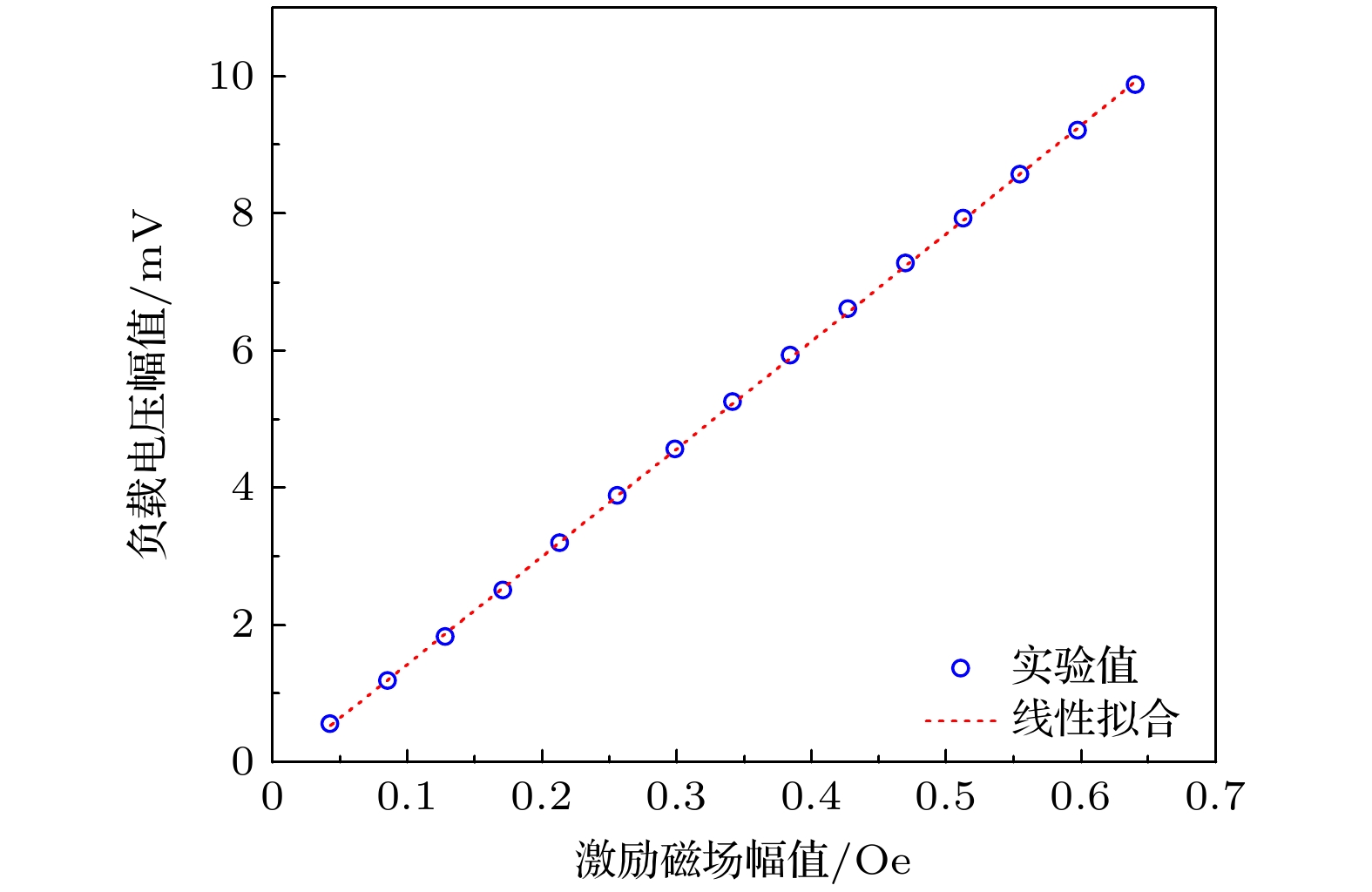
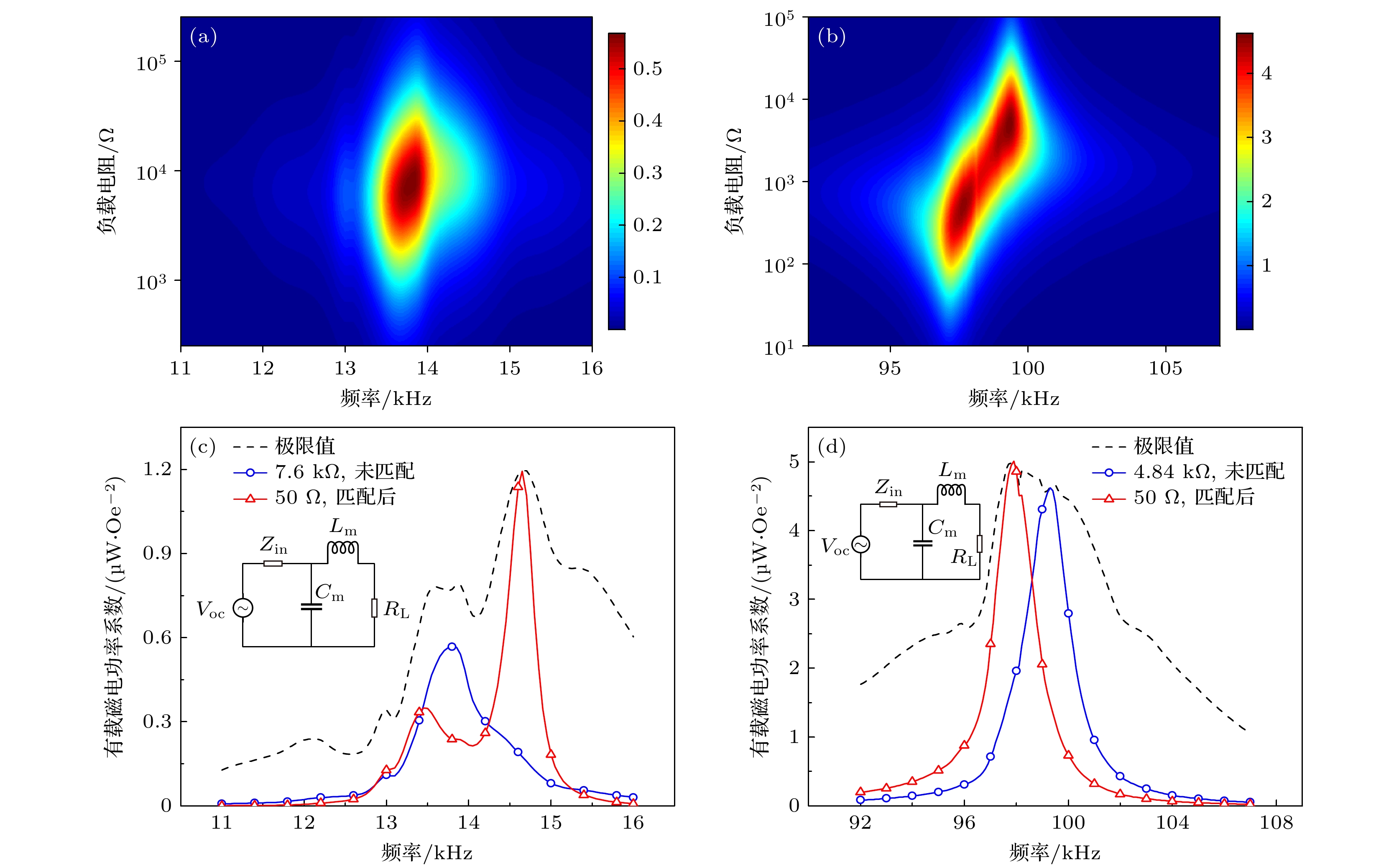
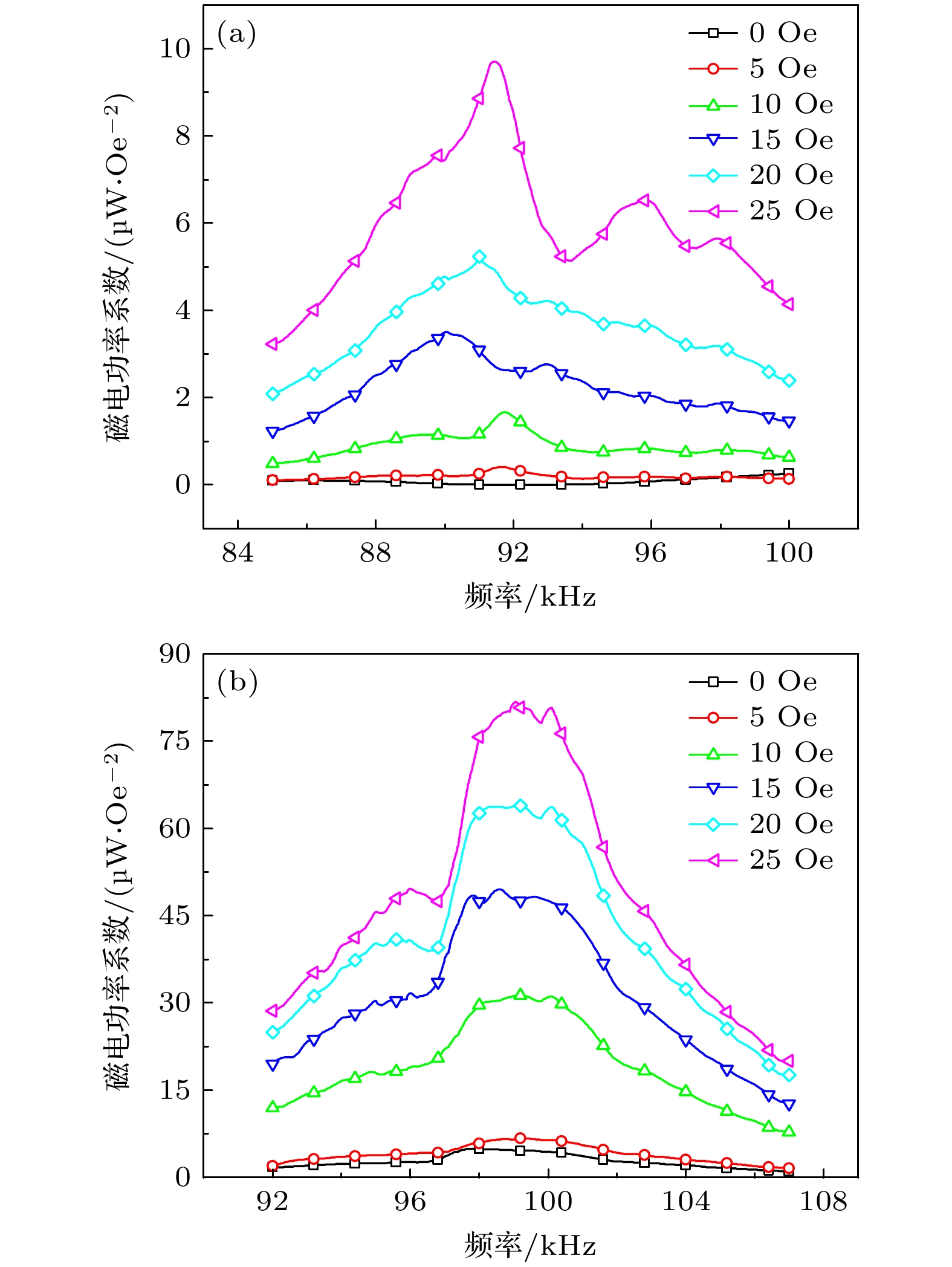
基于磁化等效和非线性磁致伸缩本构关系, 建立了L-T模式下的自偏置磁电换能器的多物理场耦合仿真模型, 研究了弯曲、伸缩谐振模式下的磁电耦合性能. 在所建模型基础上, 制备了相应的实验样品进行测试. 实测结果与仿真数据相吻合, 从而验证了模型的准确性和有效性. 实测结果表明, Metglas/Galfenol/PZT-5A结构在伸缩谐振模式下展现出更为显著的自偏置磁电效应, 其磁电系数为10.7 V·cm^–1·Oe^–1@99.4 kHz, 磁电功率系数为5.01 μW·Oe^–2@97.9 kHz. 无需阻抗匹配, 其有载磁电功率系数最高可达4.62 μW·Oe^–2@99.3 kHz. 施加外部偏置磁场至25 Oe, 磁电系数可提升至47.06 V·cm^–1·Oe^–1@99.4 kHz, 磁电功率系数提升至82.13 μW·Oe^–2@99 kHz. 进一步的仿真研究表明, 高磁导率层厚度的增加能显著提升自偏置磁电换能器的性能: 当Metglas层厚度增加至90 μm时, 磁电系数和功率系数分别提升至原先的2.47倍和6.96倍. 自偏置磁电换能器具备减少对外部偏置磁场依赖的能力, 为磁电复合材料在低频无线功率传输系统中的应用与发展提供了新途径.

关键词:

Abstract

Compared with single-phase multiferroic materials, magnetoelectric (ME) composites composed of piezoelectric and magnetostrictive materials have great ME coupling, and have received widespread attention in various application fields. The application of ME devices in wireless power transfer (WPT) is attractive due to their compactness and ability to operate at lower frequencies than conventional coils. However, traditional ME composites rely on permanent magnets or electromagnets to provide biased magnetic fields, thus leading to problems such as high noise, large size, and high cost, which significantly hinder the advancement of miniaturized and high-performance ME devices. To solve this problem, a self-biased ME laminated structure based on the magnetization grading effect is proposed in this work. Using the equivalent magnetization and nonlinear magnetostrictive constitutive relationship, a finite element simulation model for a self-biased ME transducer operating in L-T mode is constructed. The ME coupling performances without DC bias in bending vibration mode and stretching vibration mode are studied. Based on the model, the corresponding experimental samples are prepared for measurement. The measurement results are in agreement with the simulation data, thereby validating the accuracy and effectiveness of the model. The measured results show that the Metglas/Galfenol/PZT-5A structure can exhibit more significant self-biased ME effect under the stretching resonance mode than under bending resonance mode. Its ME coefficient attains a notable value of 10.7 V·cm^–1·Oe^–1 at 99.4 kHz, while ME power coefficient reaches 5.01 μW·Oe^–2 at 97.9 kHz. Its on-load ME power coefficient can reach up to 4.62 μW·Oe^–2 at 99.3 kHz without impedance matching. When an external bias magnetic field of 25 Oe is applied, these performance indexes increase significantly to 47.06 V·cm^–1·Oe^–1 at 99.4 kHz and 82.13 μW·Oe^–2 at 99.0 kHz, respectively. The simulation results further show that the performance of the self-biased ME transducer can be significantly improved by increasing the thickness of the high permeability layer. For example, by increasing the Metglas layer thickness from 30 μm to 90 μm, both the ME coefficient and ME power coefficient increase rapidly by 2.47 times and 6.96 times the original values, respectively. Self-biased ME transducers effectively reduce the dependence on external bias magnetic field, thereby providing a good approach for applying and developing ME composites in low-frequency WPT systems.

Keywords:

作者及机构信息

1.
中国科学院空天信息创新研究院, 北京　100094

2.
中国科学院信息工程研究所, 北京　100085

3.
中山大学系统科学与工程学院, 广州　510275

4.
中国科学院大学网络空间安全学院, 北京　100049

通信作者: 徐国凯, xugk3@mail2.sysu.edu.cn ; 肖绍球, xiaoshq8@mail.sysu.edu.cn ;

基金项目: 国家重点研究计划(批准号: 2021YFA0716500)和国家自然科学基金(批准号: 62171487)资助的课题.

Authors and contacts

1.
Institute of Aerospace Information Innovation, Chinese Academy of Sciences, Beijing 100094, China

2.
Institute of Information Engineering, Chinese Academy of Sciences, Beijing 100085, China

3.
School of Systems Science and Engineering, Sun Yat-sen University, Guangzhou 510275, China

4.
School of Cyberspace Security, University of Chinese Academy of Sciences, Beijing 100049, China

Corresponding author: Xu Guo-Kai, xugk3@mail2.sysu.edu.cn ; Xiao Shao-Qiu, xiaoshq8@mail.sysu.edu.cn ;

Funds: Project supported by the National Key Research and Development Program of China (Grant No. 2021YFA0716500) and the National Natural Science Foundation of China (Grant No. 62171487).

文章全文 : translate this paragraph

参考文献

[1]	Ou Z Y, Lu C J, Yang A C, Zhou H, Cao Z Q, Zhu R R, Gao H L 2019 Sens. Actuators A: Phys. 290 8 Google Scholar
[2]	Zhao Y X, Lu C J 2015 Rev. Sci. Instrum. 86 036101 Google Scholar
[3]	Chu Z Q, PourhosseiniAsl M, Dong S X 2018 J. Phys. D: Appl. Phys. 51 243001 Google Scholar
[4]	Mukherje D, Mallic D 2023 Appl. Phys. Lett. 122 014102 Google Scholar
[5]	Du Y J, Xu Y W, Wu J G, Qiao J C, Wang Z G, Hu Z Q, Jiang Z D, Liu M 2023 IEEE Trans. Antenn. Propag. 71 2167 Google Scholar
[6]	Niu Y P, Ren H 2021 Appl. Phys. Lett. 118 264104 Google Scholar
[7]	Sudersan S, Arockiarajan A 2019 Compos. Struct. 223 110924 Google Scholar
[8]	周勇, 李纯健, 潘昱融 2018 67 077702 Google Scholar Zhou Y, Li C J, Pan Y R 2018 Acta Phys. Sin. 67 077702 Google Scholar
[9]	Han J, Zhang J J, Gao Y W 2018 J. Magn. Magn. Mater. 466 200 Google Scholar
[10]	Yao H, Shi Y, Gao Y W 2016 J. Magn. Magn. Mater. 401 1046 Google Scholar
[11]	阳昌海, 文玉梅, 李平, 卞雷祥 2008 57 7292 Google Scholar Yang C H, Wen Y M, Li P, Bian L X 2008 Acta Phys. Sin. 57 7292 Google Scholar
[12]	Dong H M, Guo H H, Li J R, Li B J, Gan X X 2023 Phys. Scr. 98 065901 Google Scholar
[13]	Shi Y, Li L, Yang Y 2021 Chin. Phys. B 30 107503 Google Scholar
[14]	Lei B X, You Z X, Zhang Z D, Shi Y 2023 Acta Mech. Sin. 39 523120 Google Scholar
[15]	Niu L F, Shi Y, Gao Y W 2019 AIP Adv. 9 045216 Google Scholar
[16]	Kumar S D, Gupta S, Swain A B, Subramanian V, Padmanabhan M K, Mahajan R L 2021 J. Alloy. Compd. 858 157684 Google Scholar
[17]	Truong B D, Roundy S 2020 Smart Mater. Struct. 29 085053 Google Scholar
[18]	Lage E, Kirchhof C, Hrkac V, Kienle L, Jahns R, Knöchel R, Quandt E Meyners D 2012 Nature Mater. 11 523 Google Scholar
[19]	Röbisch V, Yarar E, Urs N O, Teliban I, Knöchel R, Mccoed J, Quandt E, Meyners D 2015 J. Appl. Phys. 117 17B513 Google Scholar
[20]	Zhou Y, Priya S 2014 J. Appl. Phys. 115 104107 Google Scholar
[21]	Zhang J J, Gao Y W 2015 Int. J. Solid. Struct. 69–70 291 Google Scholar
[22]	文玉梅, 王东, 李平, 陈蕾, 吴治峄 2011 60 097506 Google Scholar Wen Y M, Wang D, Li P, Cheng L, Wu Z Y 2011 Acta Phys. Sin. 60 097506 Google Scholar
[23]	Lu C J, Li P, Wen Y M, Yang A C, Yang C, Wang D C, He W, Zhang J T 2014 Chin. Phys. B 23 117503 Google Scholar
[24]	Chen L, Li P, Wen Y M, Zhu Y 2015 Compos. Struct. 119 685 Google Scholar
[25]	Lu C J, Li P, Wen Y M, Yang A C, He W, Zhang J T, Yang J, Wen J, Zhu Y, Yu M 2013 Appl. Phys. A 113 413 Google Scholar
[26]	Shi Y, Lei B X, Wang Y K, Ye J J 2022 Compos. Struct. 300 116164 Google Scholar
[27]	Zhang J, Du H, Xia X, Fang C, Weng G J 2020 Mech. Mater. 151 103609 Google Scholar
[28]	Ma J N, Xin C Z, Ma J, Lin Y H, Nan C W 2016 Mater. Res. Express 3 125012 Google Scholar
[29]	Huang D Y, Lu C J, Han B, Wang X, Li C X, Xu C B, Gui J G, Lin C H 2014 Appl. Phys. Lett. 105 263502 Google Scholar
[30]	Yang S C, Cho K H, Park C S, Priya S S 2011 Appl. Phys. Lett. 99 202904 Google Scholar
[31]	Truong B D 2020 IEEE Sens. J. 20 5322 Google Scholar
[32]	Hosur S, Sriramdas R, Karan S K, Liu N, Priya S, Kiani M 2021 IEEE Trans. Biomed. Circuits Syst. 15 1079 Google Scholar
[33]	Saha O, Truong B D, Roundy S 2022 Smart Mater. Struct. 31 113001 Google Scholar
[34]	Kim W, Tuppen C A, Alrashdan F, Singer A, Weirnick R, Robinson J T 2023 J. Appl. Phys. 134 094103 Google Scholar
[35]	Liu X, Zheng X J 2005 Acta Mech. Sin. 21 278 Google Scholar
[36]	李鸣鹤 2023 硕士学位论文 (长春: 吉林大学) Li M H 2023 M. S. Thesis (Changchun: Jilin University
[37]	谢冰鸿, 徐国凯, 肖绍球, 喻忠军, 朱大立 2023 72 117501 Google Scholar Xie B H, Xu G K, Xiao S Q, Yu Z J, Zhu D L 2023 Acta Phys. Sin. 72 117501 Google Scholar
[38]	罗志高 2019 大学物理实验 32 9 Google Scholar Luo Z G 2019 Phys. Exp. Coll. 32 9 Google Scholar
[39]	Li L, Chen X M 2008 Appl. Phys. Lett. 92 072903 Google Scholar
[40]	Zhang J T, Li P, Wen Y M, He W, Yang A C, Lu C J 2014 Sens. Actuators A 214 149 Google Scholar
[41]	Annapureddy V, Park S H, Song H, Ryu J 2023 J. Alloy. Compd. 957 170121 Google Scholar

施引文献

图 1 (a) 自偏置磁电换能器结构示意图; (b) 压电层的局部坐标系, 与空间坐标系一致; (c) 磁致伸缩层的局部坐标系

Fig. 1. (a) Schematic diagram of a self-biased magnetoelectric transducer; (b) local coordinate of the piezoelectric layer is consistent with the global coordinate; (c) local coordinate of the magnetostrictive layer.

下载: 全尺寸图片幻灯片

图 2 各接口之间的耦合及仿真计算方案

Fig. 2. Coupling between each interface and simulation calculation scheme.

下载: 全尺寸图片幻灯片

图 3 (a) 磁-力-电耦合等效电路; (b) 戴维南等效电路

Fig. 3. (a) Magneto-elastic-electric coupling equivalent circuit; (b) Thevenin equivalent circuit.

下载: 全尺寸图片幻灯片

图 4 自偏置磁电换能器样品及实验测量装置

Fig. 4. Self-biased magnetoelectric transducer sample and experimental equipment.

下载: 全尺寸图片幻灯片

图 5 不同振动模式下仿真与实测数据的对比　(a) 磁电系数; (b) 磁电功率系数

Fig. 5. Comparison of simulation and experimental data under different vibration modes: (a) Magnetoelectric coefficient; (b) magnetoelectric power coefficient.

下载: 全尺寸图片幻灯片

图 6 小信号磁场激励下, 自偏置磁电换能器负载电压的线性输出

Fig. 6. Linear output of load voltage of the self-biased magnetoelectric transducer under small signal magnetic field excitation.

下载: 全尺寸图片幻灯片

图 7 不同振动模式下的有载磁电功率系数　(a), (c) 弯曲模式; (b), (d) 伸缩模式

Fig. 7. Magnetoelectric power coefficient on load under different vibration modes: (a), (c) Bending mode; (b), (d) stretching mode.

下载: 全尺寸图片幻灯片

图 8 外部偏置磁场对磁电系数的影响　(a) 对照组; (b) 实验组

Fig. 8. The influence of external biased magnetic field on magnetoelectric coefficient: (a) Control group; (b) experimental group.

下载: 全尺寸图片幻灯片

图 9 外部偏置磁场对磁电功率系数的影响　(a) 对照组; (b) 实验组

Fig. 9. The influence of external biased magnetic field on magnetoelectric power coefficient: (a) Control group; (b) experimental group.

下载: 全尺寸图片幻灯片

图 10 仿真高磁导率层厚度的影响　(a) 磁电系数; (b) 磁电功率系数

Fig. 10. Simulate the effect of high permeability layer thickness: (a) Magnetoelectric coefficient; (b) magnetoelectric power coefficient.

下载: 全尺寸图片幻灯片

表 1 Galfenol和Metglas的材料参数

Table 1. Material parameters of Galfenol and Metglas.

名称	Galfenol	Metglas
密度/(${\text{kg}} \cdot {{\text{m}}^{{{ - 3}}}}$)	7972	7250
杨氏模量/GPa	70	100
泊松比	0.37	0.34
初始磁化率	27	—
饱和磁致伸缩系数/10^–6	320	—
饱和磁化强度/($ {\text{A}} \cdot {{\text{m}}^{{{ - 1}}}} $)	9.0×10⁵	—
电导率/($ {\text{S}} \cdot {{\text{m}}^{{{ - 1}}}} $)	1.23×10⁷	7.69×10⁵

下载: 导出CSV

表 2 不同自偏置磁电换能器的性能指标对比

Table 2. Performance comparison of different self-biased magnetoelectric transducers.

参考文献	体积/mm³	磁电系数/ (V·cm^–1·Oe^–1)	有载磁电功率系数/(μW·Oe^–2)
[4]	1.75	0.1328	14.0
[40]	201.6	28.0	0.323
[41]	121	4.2	—
本文	37.35	10.71	4.62

下载: 导出CSV

map

[1]	Ou Z Y, Lu C J, Yang A C, Zhou H, Cao Z Q, Zhu R R, Gao H L 2019 Sens. Actuators A: Phys. 290 8 Google Scholar
[2]	Zhao Y X, Lu C J 2015 Rev. Sci. Instrum. 86 036101 Google Scholar
[3]	Chu Z Q, PourhosseiniAsl M, Dong S X 2018 J. Phys. D: Appl. Phys. 51 243001 Google Scholar
[4]	Mukherje D, Mallic D 2023 Appl. Phys. Lett. 122 014102 Google Scholar
[5]	Du Y J, Xu Y W, Wu J G, Qiao J C, Wang Z G, Hu Z Q, Jiang Z D, Liu M 2023 IEEE Trans. Antenn. Propag. 71 2167 Google Scholar
[6]	Niu Y P, Ren H 2021 Appl. Phys. Lett. 118 264104 Google Scholar
[7]	Sudersan S, Arockiarajan A 2019 Compos. Struct. 223 110924 Google Scholar
[8]	周勇, 李纯健, 潘昱融 2018 67 077702 Google Scholar Zhou Y, Li C J, Pan Y R 2018 Acta Phys. Sin. 67 077702 Google Scholar
[9]	Han J, Zhang J J, Gao Y W 2018 J. Magn. Magn. Mater. 466 200 Google Scholar
[10]	Yao H, Shi Y, Gao Y W 2016 J. Magn. Magn. Mater. 401 1046 Google Scholar
[11]	阳昌海, 文玉梅, 李平, 卞雷祥 2008 57 7292 Google Scholar Yang C H, Wen Y M, Li P, Bian L X 2008 Acta Phys. Sin. 57 7292 Google Scholar
[12]	Dong H M, Guo H H, Li J R, Li B J, Gan X X 2023 Phys. Scr. 98 065901 Google Scholar
[13]	Shi Y, Li L, Yang Y 2021 Chin. Phys. B 30 107503 Google Scholar
[14]	Lei B X, You Z X, Zhang Z D, Shi Y 2023 Acta Mech. Sin. 39 523120 Google Scholar
[15]	Niu L F, Shi Y, Gao Y W 2019 AIP Adv. 9 045216 Google Scholar
[16]	Kumar S D, Gupta S, Swain A B, Subramanian V, Padmanabhan M K, Mahajan R L 2021 J. Alloy. Compd. 858 157684 Google Scholar
[17]	Truong B D, Roundy S 2020 Smart Mater. Struct. 29 085053 Google Scholar
[18]	Lage E, Kirchhof C, Hrkac V, Kienle L, Jahns R, Knöchel R, Quandt E Meyners D 2012 Nature Mater. 11 523 Google Scholar
[19]	Röbisch V, Yarar E, Urs N O, Teliban I, Knöchel R, Mccoed J, Quandt E, Meyners D 2015 J. Appl. Phys. 117 17B513 Google Scholar
[20]	Zhou Y, Priya S 2014 J. Appl. Phys. 115 104107 Google Scholar
[21]	Zhang J J, Gao Y W 2015 Int. J. Solid. Struct. 69–70 291 Google Scholar
[22]	文玉梅, 王东, 李平, 陈蕾, 吴治峄 2011 60 097506 Google Scholar Wen Y M, Wang D, Li P, Cheng L, Wu Z Y 2011 Acta Phys. Sin. 60 097506 Google Scholar
[23]	Lu C J, Li P, Wen Y M, Yang A C, Yang C, Wang D C, He W, Zhang J T 2014 Chin. Phys. B 23 117503 Google Scholar
[24]	Chen L, Li P, Wen Y M, Zhu Y 2015 Compos. Struct. 119 685 Google Scholar
[25]	Lu C J, Li P, Wen Y M, Yang A C, He W, Zhang J T, Yang J, Wen J, Zhu Y, Yu M 2013 Appl. Phys. A 113 413 Google Scholar
[26]	Shi Y, Lei B X, Wang Y K, Ye J J 2022 Compos. Struct. 300 116164 Google Scholar
[27]	Zhang J, Du H, Xia X, Fang C, Weng G J 2020 Mech. Mater. 151 103609 Google Scholar
[28]	Ma J N, Xin C Z, Ma J, Lin Y H, Nan C W 2016 Mater. Res. Express 3 125012 Google Scholar
[29]	Huang D Y, Lu C J, Han B, Wang X, Li C X, Xu C B, Gui J G, Lin C H 2014 Appl. Phys. Lett. 105 263502 Google Scholar
[30]	Yang S C, Cho K H, Park C S, Priya S S 2011 Appl. Phys. Lett. 99 202904 Google Scholar
[31]	Truong B D 2020 IEEE Sens. J. 20 5322 Google Scholar
[32]	Hosur S, Sriramdas R, Karan S K, Liu N, Priya S, Kiani M 2021 IEEE Trans. Biomed. Circuits Syst. 15 1079 Google Scholar
[33]	Saha O, Truong B D, Roundy S 2022 Smart Mater. Struct. 31 113001 Google Scholar
[34]	Kim W, Tuppen C A, Alrashdan F, Singer A, Weirnick R, Robinson J T 2023 J. Appl. Phys. 134 094103 Google Scholar
[35]	Liu X, Zheng X J 2005 Acta Mech. Sin. 21 278 Google Scholar
[36]	李鸣鹤 2023 硕士学位论文 (长春: 吉林大学) Li M H 2023 M. S. Thesis (Changchun: Jilin University
[37]	谢冰鸿, 徐国凯, 肖绍球, 喻忠军, 朱大立 2023 72 117501 Google Scholar Xie B H, Xu G K, Xiao S Q, Yu Z J, Zhu D L 2023 Acta Phys. Sin. 72 117501 Google Scholar
[38]	罗志高 2019 大学物理实验 32 9 Google Scholar Luo Z G 2019 Phys. Exp. Coll. 32 9 Google Scholar
[39]	Li L, Chen X M 2008 Appl. Phys. Lett. 92 072903 Google Scholar
[40]	Zhang J T, Li P, Wen Y M, He W, Yang A C, Lu C J 2014 Sens. Actuators A 214 149 Google Scholar
[41]	Annapureddy V, Park S H, Song H, Ryu J 2023 J. Alloy. Compd. 957 170121 Google Scholar

[1]	丰家峰, 陈星, 魏红祥, 陈鹏, 兰贵彬, 刘要稳, 郭经红, 黄辉, 韩秀峰. 自由层磁性交换偏置效应调控隧穿磁电阻磁传感单元性能. , 2023, 72(19): 197103. doi: 10.7498/aps.72.20231003
[2]	谢冰鸿, 徐国凯, 肖绍球, 喻忠军, 朱大立. 非线性磁电换能器模型的谐振磁电效应分析及其输出功率优化. , 2023, 72(11): 117501. doi: 10.7498/aps.72.20222277
[3]	芦佳, 甘渝林, 颜雷, 丁洪. EuS/Ta异质结的极大磁电阻效应. , 2021, 70(4): 047401. doi: 10.7498/aps.70.20201213
[4]	辛成舟, 马健男, 马静, 南策文. 伸缩-剪切模式自偏置铌酸锂基复合材料的磁电性能和高频谐振响应. , 2018, 67(15): 157502. doi: 10.7498/aps.67.20180810
[5]	李永超, 周航, 潘丹峰, 张浩, 万建国. Co/Co3O4/PZT多铁复合薄膜的交换偏置效应及其磁电耦合特性. , 2015, 64(9): 097701. doi: 10.7498/aps.64.097701
[6]	代显智. 基于能量转换原理的磁电层合材料低频磁电响应分析. , 2014, 63(20): 207501. doi: 10.7498/aps.63.207501
[7]	李平, 黄娴, 文玉梅. 偏置电压对磁致伸缩/压电层合换能结构磁电性能影响. , 2012, 61(13): 137504. doi: 10.7498/aps.61.137504
[8]	王巍, 罗小彬, 杨丽洁, 张宁. 层状磁电复合材料谐振频率下的巨磁电容效应. , 2011, 60(10): 107702. doi: 10.7498/aps.60.107702
[9]	鲍丙豪, 骆英. 纵向极化与磁化叠层复合材料磁电效应理论及计算. , 2011, 60(6): 067504. doi: 10.7498/aps.60.067504
[10]	许涌, 蔡建旺. 几种元素的界面插层对Ta/NiFe/Ta的各向异性磁电阻效应的影响. , 2011, 60(11): 117308. doi: 10.7498/aps.60.117308
[11]	陈蕾, 李平, 文玉梅, 王东. 高磁导率材料FeCuNbSiB对超磁致伸缩/压电层合材料磁电性能的影响. , 2011, 60(6): 067501. doi: 10.7498/aps.60.067501
[12]	代显智, 文玉梅, 李平, 杨进, 江小芳. 采用磁电换能器的振动能量采集器. , 2010, 59(3): 2137-2146. doi: 10.7498/aps.59.2137
[13]	阳昌海, 文玉梅, 李平, 卞雷祥. 偏置磁场对磁致伸缩/弹性/压电层合材料磁电效应的影响. , 2008, 57(11): 7292-7297. doi: 10.7498/aps.57.7292
[14]	万红, 谢立强, 吴学忠, 刘希从. TbDyFe/PZT层状复合材料的磁电效应研究. , 2005, 54(8): 3872-3877. doi: 10.7498/aps.54.3872
[15]	姜宏伟, 王艾玲, 郑鹉. 自旋阀中的各向异性磁电阻效应. , 2005, 54(5): 2338-2341. doi: 10.7498/aps.54.2338
[16]	万　红, 沈仁发, 吴学忠. 对称磁电层合板磁电转换效应理论研究. , 2005, 54(3): 1426-1430. doi: 10.7498/aps.54.1426
[17]	都有为, 王志明, 倪刚, 邢定钰, 徐庆宇. 高度取向石墨的巨磁电阻效应. , 2004, 53(4): 1191-1194. doi: 10.7498/aps.53.1191
[18]	李铁, 沈鸿烈, 沈勤我, 邹世昌. 不同过渡层上Co/Cu/Co三明治结构的巨磁电阻效应研究. , 1999, 48(13): 28-34. doi: 10.7498/aps.48.28
[19]	程荣胜, 李可斌, 李西军, 陈志祥, 熊曹水, 朱警生, 张裕恒. LaCaMnO/LaNdCaMnO/LaCaMnO三层膜中巨磁电阻增强效应. , 1998, 47(7): 1193-1200. doi: 10.7498/aps.47.1193
[20]	胡永健, 彭初兵, 方瑞宜, 李文君, 戴道生. [Fe/Cr]多层膜及掺入Si中介层后的层间耦合和磁电阻效应. , 1996, 45(10): 1744-1748. doi: 10.7498/aps.45.1744

计量

文章访问数: 752
PDF下载量: 34
被引次数: 0

姓名
邮箱
手机号码
标题
留言内容
验证码

搜索

留言板