-
高强度超声可激发生物组织空化, 软组织常被当作黏弹性介质, 因此, 黏弹性介质中气泡动力学行为研究可为超声生物治疗提供理论支持. 为探索组织液内多气泡动力学影响, 构建了球形液体腔内的球状泡团模型, 考虑了液体腔外黏弹性介质的动力学效应, 得到了球状泡群内气泡耦合振动方程, 并基于此分析了气泡的振动行为. 结果表明, 腔体以及泡群约束虽抑制了气泡振动, 但在一定程度上还可以增强气泡的非线性振动特性. 约束环境下气泡的非球形振动稳定性主要受驱动声波压力幅值和频率、气泡初始半径以及气泡数密度影响, 而腔体半径的影响随驱动压力的增加而增强; 存在最小不稳定驱动声压阈值, 不同初始半径的气泡不稳定振动阈值压力不同且不稳定分布区主要分布在小于4 μm的范围内; 驱动频率增大, 气泡振动不稳定区的声压阈值也随之增大, 且不稳定区域有减小的趋势; 随着气泡数密度的增加, 气泡不稳定区域逐渐向无规则的斑图状分布, 极易受到扰动发生不稳定振动而崩溃. 高频声波激励下平衡半径大于4 μm范围内气泡的惯性空化阈值受频率和气泡数密度的影响显著.Considering the interactions between bubbles in a multi-bubble system in a liquid micro-cavity, a spherical bubble cluster in a liquid cavity is modeled in order to describe the dynamical effect of the viscoelastic medium outside the liquid cavity on the oscillation of bubbles, and the coupled equations of bubbles are obtained. Subsequently, the acoustic response characteristics of bubbles are investigated by analyzing the radial oscillation, the stability of the non-spherical shape of bubbles and the threshold of inertial cavitation. The results show that the confinement of the cavity and the bubble cluster facilitates the suppression of bubble oscillation, however, it might enhance the nonlinear properties of bubbles to a certain extent. From the acoustic response curve at 1 MHz, it is found that the main resonance peaks shift leftward with the increase of the bubble number, which means a minor resonant radius can be obtained. The nonlinear stability of bubbles in a confined environment is mainly determined by acoustic pressure amplitude and frequency, the initial bubble radius, and bubble number density, while the effect of the cavity radius is enhanced with the increase of the driving pressure. There is a minimum unstable driving acoustic pressure threshold, depending on the initial bubble radius, and the unstable regions are mainly located in a range of less than 4 μm. With the increase in bubble number density, the strip-type stable region scattered of the unstable region in the map is gradually transformed into a random patch-like distribution, which indicates that the bubble oscillation under high acoustic pressure is more sensitive to the parameters, and it is very susceptible to interference, produces unstable oscillation and then collapses. When the bubble equilibrium radius is in a range greater than 4 μm, the influences of frequency and bubble number density on the inertial thresholds are particularly significant.
-
Keywords:
- spherical bubble cluster /
- liquid cavity /
- cavitation bubbles /
- coupled oscillation
[1] Kooiman K, Roovers S, Langeveld S A G, Kleven R T, Dewitte H, O'Reilly M A, Escoffre J M, Bouakaz A, Verweij M D, Hynynen K, Lentacker I, Stride E, Holland C K 2020 Ultrasound Med. Biol. 46 1296
Google Scholar
[2] Xi F, Feng Y, Chen Q, Chen L, Liu J 2022 Front. Oncol. 12 852454
Google Scholar
[3] Ellegala D B, Leong-Poi H, Carpenter J E, Klibanov A L, Kaul S, Shaffrey M E, Sklenar J, Lindner J R 2003 Circulation 108 336
Google Scholar
[4] Lanza G M, Abendschein D R, Hall C S, Scott M J, Scherrer D E, Houseman A, Miller J G, Wickline S A 2000 J. Am. Soc. Echocardiogr. 13 608
Google Scholar
[5] Lyons B, Balkaran J P R, Dunn-Lawless D, Lucian V, Keller S B, O'Reilly C S, Hu L A, Rubasingham J, Nair M, Carlisle R, Stride E, Gray M, Coussios C, Lu Y, Chen Z J 2023 Molecules 28 7733
Google Scholar
[6] Wischhusen J, Padilla F 2019 Irbm 40 10
Google Scholar
[7] Guzman H R, McNamara A J, Nguyen D X, Prausnitz M R 2003 Ultrasound Med. Biol. 29 1211
Google Scholar
[8] Liu Y, Yang H, Sakanishi A 2006 Biotechnol. Adv. 24 1
Google Scholar
[9] Unnikrishnan S, Klibanov A L 2012 Am. J. Roentgenol. 199 292
Google Scholar
[10] Villanueva F S, Jankowski R J, Klibanov S, Pina M L, Alber S M, Watkins S C, Brandenburger G H, Wagner W R 1998 Circulation 98 1
Google Scholar
[11] Schenk H J, Steppe K, Jansen S 2015 Trends Plant Sci. 20 199
Google Scholar
[12] Tanasawa I, Yang W J 1970 J. Appl. Phys. 41 4526
Google Scholar
[13] Wang Q X 2017 Phys. Fluids 29 072101
Google Scholar
[14] Vincent O, Marmottant P, Gonzalez-Avila S R, Ando K, Ohl C D 2014 Soft Matter 10 1455
Google Scholar
[15] Church C C, Yang X M 2006 AIP Conf. Proc. 838 217
Google Scholar
[16] Leonov K, Akhatov I 2021 Phys. Rev. E 104 015105
Google Scholar
[17] 张陶然, 莫润阳, 胡静, 陈时, 王成会, 郭建中 2021 70 124301
Google Scholar
Zhang T R, Mo R Y, Hu J, Chen S, Wang C H, Guo J Z 2021 Acta Phys. Sin. 70 124301
Google Scholar
[18] 张先梅, 王成会, 郭建中, 莫润阳, 胡静, 陈时 2021 70 214305
Google Scholar
Zhang X M, Wang C H, Guo J Z, Mo R Y, Hu J, Chen S 2021 Acta Phys. Sin. 70 214305
Google Scholar
[19] Zhang X M, Li F, Wang C H, Guo J Z, Mo R Y, Hu J, Chen S, He J X, Liu H H 2022 Ultrason. Sonochem. 84 105957
Google Scholar
[20] Gaudron R, Murakami K, Johnsen E 2020 J. Mech. Phys. Solids 143 104047
Google Scholar
[21] Zilonova E M, Solovchuk M, Sheu T W H 2019 Ultrason. Sonochem. 53 11
Google Scholar
[22] Yasui K, Iida Y, Tuziuti T, Kozuka T, Towata A 2008 Phys. Rev. E 77 016609
Google Scholar
[23] Wang X, Chen W, Zhou M, Zhang Z, Zhang L 2022 Ultrason. Sonochem. 84 105952
Google Scholar
[24] An Y 2011 Phys. Rev. E 83 066313
Google Scholar
[25] Zhang W, An Y 2013 Phys. Rev. E 87 053023
Google Scholar
[26] 王成会, 莫润阳, 胡静, 陈时 2015 64 234301
Google Scholar
Wang C H, Mo R Y, Hu J, Chen S 2015 Acta Phys. Sin. 64 234301
Google Scholar
[27] Xu L, Yao X R, Shen Y 2024 Chin. Phys. B 33 044702
Google Scholar
[28] Liu R, Huang C Y, Wu Y R, Hu J, Mo R Y, Wang C H 2024 Acta Phys. Sin. 73 084303 [刘睿, 黄晨阳, 武耀蓉, 胡静, 莫润阳, 王成会 2024 73 084303]
Google Scholar
Liu R, Huang C Y, Wu Y R, Hu J, Mo R Y, Wang C H 2024 Acta Phys. Sin. 73 084303
Google Scholar
[29] 李凡, 张先梅, 田华, 胡静, 陈时, 王成会, 郭建中, 莫润阳 2022 71 084303
Google Scholar
Li F, Zhang X M, Tian H, Hu J, Chen S, Wang C H, Guo J Z, Mo R Y 2022 Acta Phys. Sin. 71 084303
Google Scholar
[30] Vincent O, Marmottant P, Quinto-Su P A, Ohl C D 2012 Phys. Rev. Lett. 108 184502
Google Scholar
[31] Ma Y, Zhang G, Ma T 2022 Ultrason. Sonochem. 84 105953
Google Scholar
[32] Weninger K R, Camara C G, Putterman S J 2001 Phys. Rev. E 63 016310
Google Scholar
-
图 1 黏弹性介质包裹的液体腔中球状泡群
Fig. 1. Bubble cluster in a liquid confined in a viscoelastic medium.
图 2 不同模型下气泡振荡对比图 (a)本文模型(model 1)与球状泡群内气泡的耦合振动模型(model 2)以及单泡模型(single bubble)对比; (b)本文模型与弹性介质包裹的液体腔内单气泡空化模型(model 3)对比
Fig. 2. Comparison of different models of bubble oscillations: (a) The model in this paper (model 1) is compared with the coupled oscillation model of bubble cluster in the infinite liquid (model 2) and the single bubble model (single bubble); (b) the model in this paper (model 1) is compared with the model of a single bubble in a liquid cavity enclosed by elastic medium (model 3).
图 3 气泡振动特性 (a) 气泡振动分岔图; (b) 不同介质剪切模量下气泡径向振荡; (c) 气泡数量对气泡最大半径的影响; (d) 初始气泡半径对气泡最大半径的影响
Fig. 3. Bubble oscillations characteristics: (a) Bubble oscillations bifurcation diagram; (b) radial oscillations of bubble under different medium shear moduli; (c) effect of the number of bubbles on maximum bubble radius; (d) effect of initial bubble radius on maximum bubble radius.
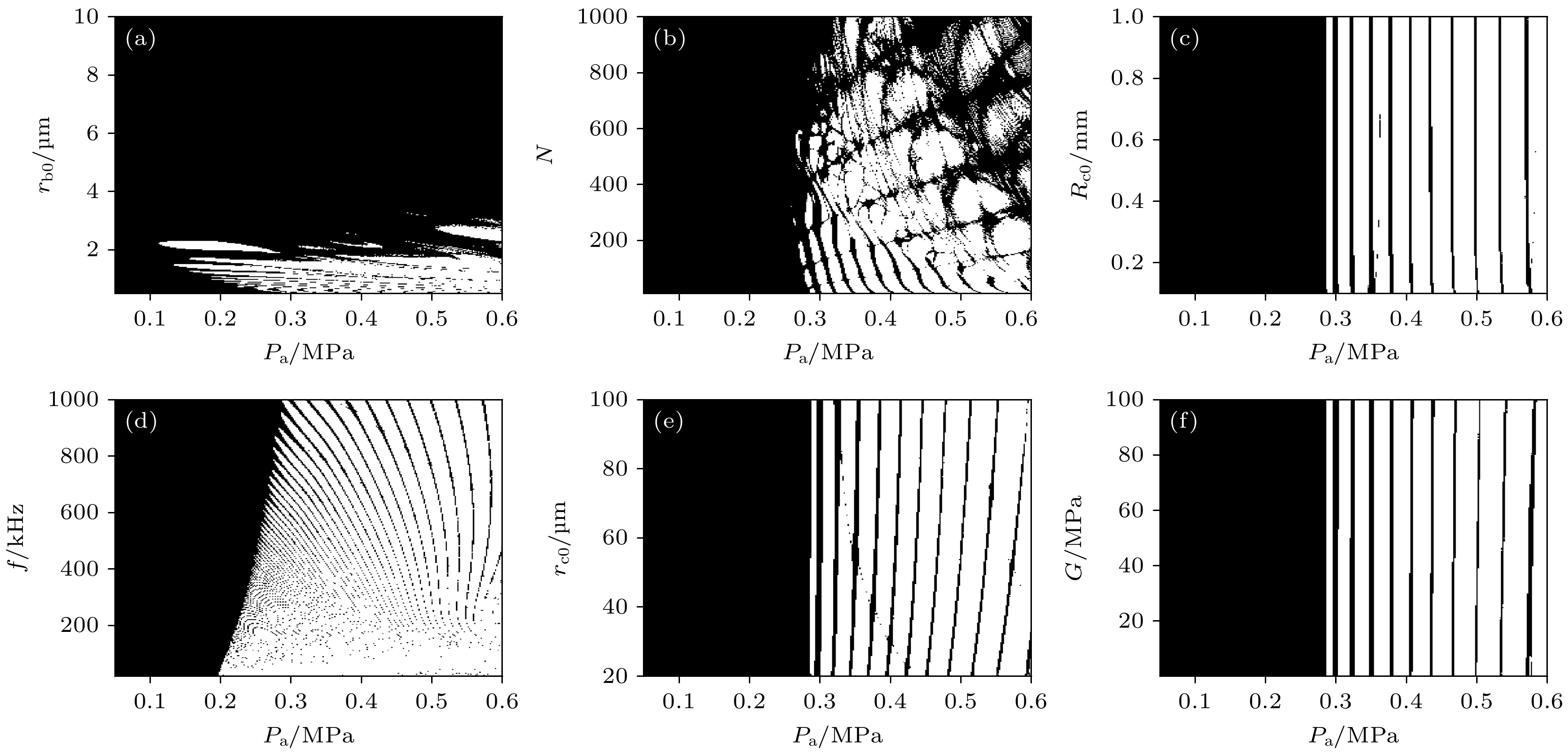
图 4 不同参数平面上气泡非球形系数与气泡半径比值$ {a_n}/{r_{{\text{b}}0}} $ (a) $ {r_{{\text{b0}}}}{\text{-}}{p_{\text{a}}} $参数平面; (b) $ N{\text{-}}{p_{\text{a}}} $参数平面; (c) $ {R_{{\text{c}}0}}{\text{-}}{p_{\text{a}}} $参数平面; (d) $ f{\text{-}}{p_{\text{a}}} $参数平面; (e) $ {r_{{\text{c0}}}}{\text{-}}{p_{\text{a}}} $参数平面; (f) $ G{\text{-}}{p_{\text{a}}} $参数平面(黑色, 稳定; 白色, 不稳定)
Fig. 4. Ratio of bubble nonsphericity coefficient to bubble radius in different parameter planes: (a) $ {r_{{\text{b0}}}}{\text{-}}{p_{\text{a}}} $ parameter plane; (b) $ N{\text{-}}{p_{\text{a}}} $ parameter plane; (c) $ {R_{{\text{c0}}}}{\text{-}}{p_{\text{a}}} $ parameter plane; (d) $ f{\text{-}}{p_{\text{a}}} $ parameter plane; (e) $ {r_{{\text{c0}}}}{\text{-}}{p_{\text{a}}} $ parameter plane; (f) $ G{\text{-}}{p_{\text{a}}} $ parameter plane (black, stable; white, unstable).
图 5 参数对气泡惯性空化阈值的影响 (a) 介质弹性; (b) 驱动频率; (c) 初始液体腔半径; (d) 气泡数量
Fig. 5. Influence of different parameters on the threshold of inertial cavitation of bubbles: (a) Shear modulus of medium; (b) driving frequency; (c) initial liquid cavity radius; (d) bubble number.
-
[1] Kooiman K, Roovers S, Langeveld S A G, Kleven R T, Dewitte H, O'Reilly M A, Escoffre J M, Bouakaz A, Verweij M D, Hynynen K, Lentacker I, Stride E, Holland C K 2020 Ultrasound Med. Biol. 46 1296
Google Scholar
[2] Xi F, Feng Y, Chen Q, Chen L, Liu J 2022 Front. Oncol. 12 852454
Google Scholar
[3] Ellegala D B, Leong-Poi H, Carpenter J E, Klibanov A L, Kaul S, Shaffrey M E, Sklenar J, Lindner J R 2003 Circulation 108 336
Google Scholar
[4] Lanza G M, Abendschein D R, Hall C S, Scott M J, Scherrer D E, Houseman A, Miller J G, Wickline S A 2000 J. Am. Soc. Echocardiogr. 13 608
Google Scholar
[5] Lyons B, Balkaran J P R, Dunn-Lawless D, Lucian V, Keller S B, O'Reilly C S, Hu L A, Rubasingham J, Nair M, Carlisle R, Stride E, Gray M, Coussios C, Lu Y, Chen Z J 2023 Molecules 28 7733
Google Scholar
[6] Wischhusen J, Padilla F 2019 Irbm 40 10
Google Scholar
[7] Guzman H R, McNamara A J, Nguyen D X, Prausnitz M R 2003 Ultrasound Med. Biol. 29 1211
Google Scholar
[8] Liu Y, Yang H, Sakanishi A 2006 Biotechnol. Adv. 24 1
Google Scholar
[9] Unnikrishnan S, Klibanov A L 2012 Am. J. Roentgenol. 199 292
Google Scholar
[10] Villanueva F S, Jankowski R J, Klibanov S, Pina M L, Alber S M, Watkins S C, Brandenburger G H, Wagner W R 1998 Circulation 98 1
Google Scholar
[11] Schenk H J, Steppe K, Jansen S 2015 Trends Plant Sci. 20 199
Google Scholar
[12] Tanasawa I, Yang W J 1970 J. Appl. Phys. 41 4526
Google Scholar
[13] Wang Q X 2017 Phys. Fluids 29 072101
Google Scholar
[14] Vincent O, Marmottant P, Gonzalez-Avila S R, Ando K, Ohl C D 2014 Soft Matter 10 1455
Google Scholar
[15] Church C C, Yang X M 2006 AIP Conf. Proc. 838 217
Google Scholar
[16] Leonov K, Akhatov I 2021 Phys. Rev. E 104 015105
Google Scholar
[17] 张陶然, 莫润阳, 胡静, 陈时, 王成会, 郭建中 2021 70 124301
Google Scholar
Zhang T R, Mo R Y, Hu J, Chen S, Wang C H, Guo J Z 2021 Acta Phys. Sin. 70 124301
Google Scholar
[18] 张先梅, 王成会, 郭建中, 莫润阳, 胡静, 陈时 2021 70 214305
Google Scholar
Zhang X M, Wang C H, Guo J Z, Mo R Y, Hu J, Chen S 2021 Acta Phys. Sin. 70 214305
Google Scholar
[19] Zhang X M, Li F, Wang C H, Guo J Z, Mo R Y, Hu J, Chen S, He J X, Liu H H 2022 Ultrason. Sonochem. 84 105957
Google Scholar
[20] Gaudron R, Murakami K, Johnsen E 2020 J. Mech. Phys. Solids 143 104047
Google Scholar
[21] Zilonova E M, Solovchuk M, Sheu T W H 2019 Ultrason. Sonochem. 53 11
Google Scholar
[22] Yasui K, Iida Y, Tuziuti T, Kozuka T, Towata A 2008 Phys. Rev. E 77 016609
Google Scholar
[23] Wang X, Chen W, Zhou M, Zhang Z, Zhang L 2022 Ultrason. Sonochem. 84 105952
Google Scholar
[24] An Y 2011 Phys. Rev. E 83 066313
Google Scholar
[25] Zhang W, An Y 2013 Phys. Rev. E 87 053023
Google Scholar
[26] 王成会, 莫润阳, 胡静, 陈时 2015 64 234301
Google Scholar
Wang C H, Mo R Y, Hu J, Chen S 2015 Acta Phys. Sin. 64 234301
Google Scholar
[27] Xu L, Yao X R, Shen Y 2024 Chin. Phys. B 33 044702
Google Scholar
[28] Liu R, Huang C Y, Wu Y R, Hu J, Mo R Y, Wang C H 2024 Acta Phys. Sin. 73 084303 [刘睿, 黄晨阳, 武耀蓉, 胡静, 莫润阳, 王成会 2024 73 084303]
Google Scholar
Liu R, Huang C Y, Wu Y R, Hu J, Mo R Y, Wang C H 2024 Acta Phys. Sin. 73 084303
Google Scholar
[29] 李凡, 张先梅, 田华, 胡静, 陈时, 王成会, 郭建中, 莫润阳 2022 71 084303
Google Scholar
Li F, Zhang X M, Tian H, Hu J, Chen S, Wang C H, Guo J Z, Mo R Y 2022 Acta Phys. Sin. 71 084303
Google Scholar
[30] Vincent O, Marmottant P, Quinto-Su P A, Ohl C D 2012 Phys. Rev. Lett. 108 184502
Google Scholar
[31] Ma Y, Zhang G, Ma T 2022 Ultrason. Sonochem. 84 105953
Google Scholar
[32] Weninger K R, Camara C G, Putterman S J 2001 Phys. Rev. E 63 016310
Google Scholar
下载:
计量
- 文章访问数: 1218
- PDF下载量: 36
- 被引次数: 0
